Х у график: Построение графика функции онлайн

Содержание

Графики функций у=ах²+n и у=а(х-m)². 9-й класс

(Приложение 1. Слайд 1)

Цели урока: ( Слайд 2)

расширить сведения о свойствах квадратичной функции;
ознакомить учащихся с графиками частных видов квадратичной функции – функций у = ах² + b, y = a (x – m)²;
научить строить графики квадратичной функции.

Оборудование: компьютер.

Ход урока

I. Организационный момент.

II. Актуализация знаний.

Проверка домашнего задания (разбор нерешенных задач, если они есть).
Контроль усвоения материала (письменный опрос).

Вариант 1.

Приведите основные свойства и график функции у = ах² при а > 0.

Постройте график функции:
а) y = – 2x²;

б)

Вариант 2.

Приведите основные свойства и график функции

у = ах² при а < 0.

Постройте график функции:

а) у = х²;

б) .

III. Изучение нового материала

Учитель: На предыдущем уроке мы рассмотрели два важнейших преобразования графика функции y = f(x).

1. График функции y = – f(x) получается из графика функции y = f(x) с помощью симметрии относительно оси абсцисс.

2. График функции y = аf(x) получается из графика функции y = f(x) растяжением вдоль оси ординат в а раз при а > 1 и сжатием в раз при
0 < а < 1.

Эти преобразования пригодны для любых функций.

Рассмотрим еще два важнейших преобразования графика функции y = f(x) + n и y = f(x – m).

3. График функции y = f(x) + n получается из графика функции y = f(x) с помощью параллельного переноса вдоль оси ординат

на |n| единиц: вверх при n > 0 и вниз при n < 0.

Пример 1.

Построим график функции у = х² + 1.

В соответствии с приведенным алгоритмом график функции у = х² + 1 получается из графика функции у = х² параллельным переносом вдоль оси ординат на 1 единицу вверх, т.к. n = 1 >0. (Слайд 3.)

Пример 2.

Построим график функции у = х² – 2.

В соответствии с приведенным алгоритмом график функции у = х² – 2 получается из графика функции у = х² параллельным переносом вдоль оси ординат на 2 единицы вниз, т.к. n = –2 < 0. (Слайд 4.)

4. График функции y = f(x – m) получается из графика функции

y = f(х) с помощью параллельного переноса вдоль оси абсцисс на |m| единиц: вправо при m > 0 и влево при m < 0.

Пример 3.

Построим график функции у = (х – 3)².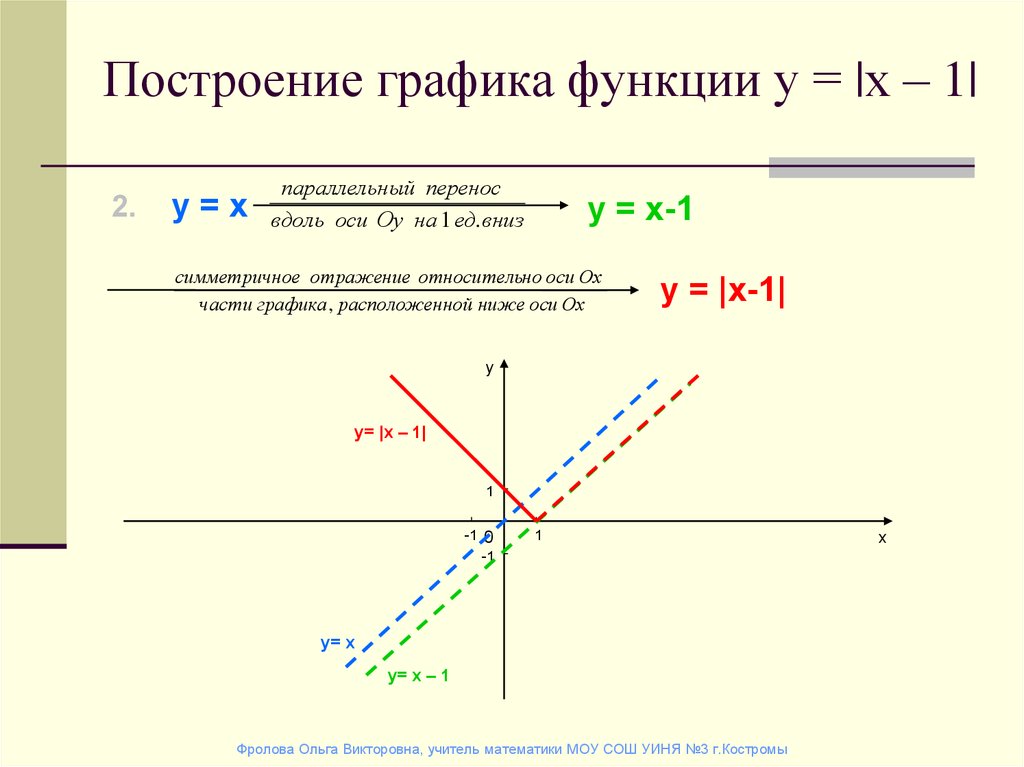

В соответствии с изложенным алгоритмом график функции у = (х – 3)²получается из графика функции у = х²параллельным переносом вдоль оси абсцисс на 3 единицы вправо, т.к. m = 3 > 0

(Слайд 5.)

Пример 4.

Построим график функции у = (х + 3)².

Запишем функцию в виде у = (х – (– 3))². Тогда в соответствии с изложенным ранее алгоритмом график функции у = (х + 3)² получается из графика функции у = х² параллельным переносом вдоль оси абсцисс на 3 единицы влево, т.к.

m = – 3 < 0. (Слайд 6.)

5. Полученные выводы позволяют понять, что представляет собой график функции

у = а(х – m)² + n . Рассмотрим, например, функцию

Пример 5.

Построить график функции у = (х – 3)² +1.

Ее график можно получить из графика функции у = х² с помощью двух параллельных переносов – сдвига параболы на 3 единицы вправо и на 1 единицу вверх.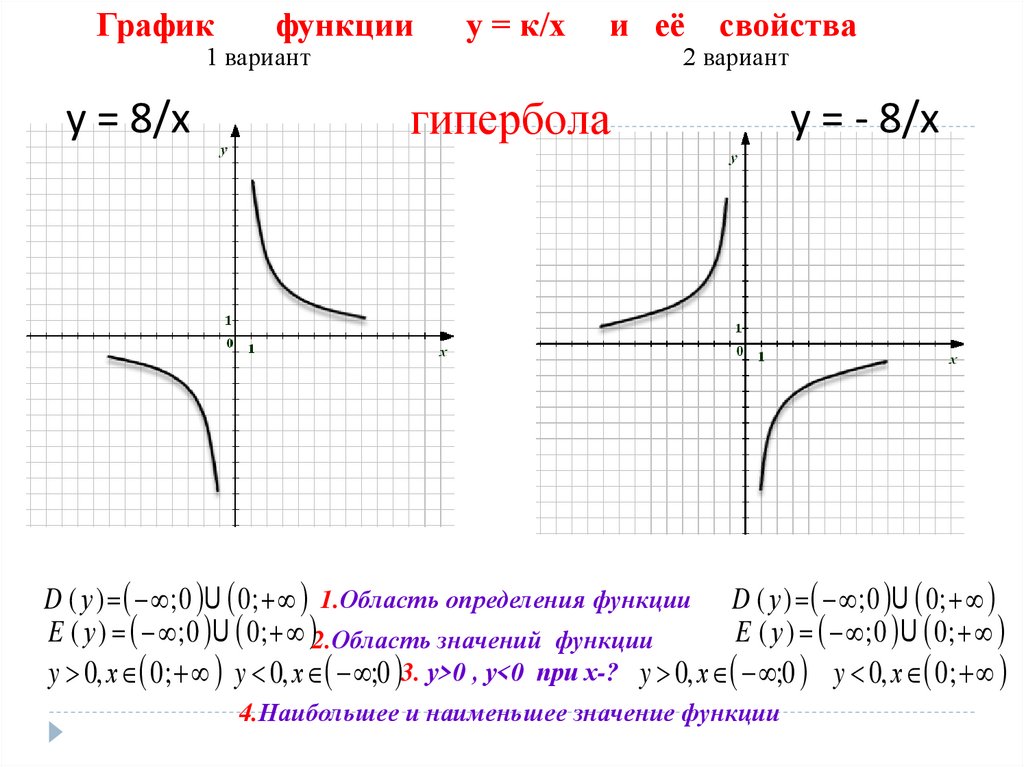 (Слайд 7.)

Пример 6.

Построить график функции у = (х + 3)² – 2.

Ее график можно получить из графика функции у = х² с помощью двух параллельных переносов – сдвига параболы на 3 единицы влево и на 2 единицы вниз.

(Слайд 8.)

IV. Вывод

Учитель. График функции у = а(х – m)² + n является параболой, которую можно получить из графика функции у = ах²с помощью двух параллельных переносов: сдвига вдоль оси х на т единиц вправо, если m > 0, или на – т единиц влево, если m < 0, и сдвига вдоль оси у на n единиц вверх, если n >0, или на – n единиц вниз, если n < 0.

Полученные нами выводы о преобразовании графиков применимы к любым функциям.

– График функции y = f(x) + n можно получить из графика функции y = f(x) с помощью параллельного переноса вдоль оси у на п единиц вверх, если n >0, или на – n единиц вниз, если n < 0.

– График функции y = f(x – т) можно получить из графика функции y = f(x)

с помощью параллельного переноса вдоль оси х на т единиц вправо, если m > 0, или на – т единиц влево, если m < 0.

– График функции y = f(x – т) + п можно получить из графика функции y = f(x) с помощью двух соответствующих параллельных переносов.

V. Тренировочные упражнения

Решить на уроке:

№ 106 (а,в), № 107 (а),
№ 109 (а,в,д) – устно,
№ 110 (б,в), № 114
№ 116 (а,в) – устно

Упражнения на повторение: № 117 (а), № 118 (а)

VI. Итог урока

1. Как из графика функции у = ах²можно получить у = ах² + n? (Слайд 9.)

– График функции у = ах² + n является параболой, которую можно получить из графика функции у = ах²с помощью параллельного переноса вдоль оси у на п единиц вверх, если n >0, или на –

n единиц вниз, если n < 0.

2. Как из графика функции у = ах²можно получить у = а(х – т)² ? (Слайд 10.)

– График функции у = а(х – т)²является параболой, которую можно получить из графика функции у = ах²с помощью параллельного переноса вдоль оси х на т единиц вправо, если m > 0, или на – т единиц влево, если m < 0.

3. Как из графика функции у = ах²можно получить у = а(х – m)² + n?

(Приложение. Слайд 11.)

– График функции у = а(х – m)² + n является параболой, которую можно получить из графика функции у = ах²с помощью двух параллельных переносов: сдвига вдоль оси х на т единиц вправо, если

m > 0, или на – т единиц влево, если m < 0, и сдвига вдоль оси у на n единиц вверх, если n >0, или на – n единиц вниз, если n < 0.

VII. Домашнее задание (Слайд 12.) п. 6, № 106 (б, г), № 107 (б), № 110 (а, г), № 117 (б).

Мордкович алгебра 8 класс 18.7 Постройте график функции y=4\x – Рамблер/класс

Интересные вопросы

Школа

Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?

Новости

Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?

Школа

Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?

Школа

Когда в 2018 году намечено проведение основного периода ЕГЭ?

Новости

Будет ли как-то улучшаться система проверки и организации итоговых сочинений?

Вузы

Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?

18.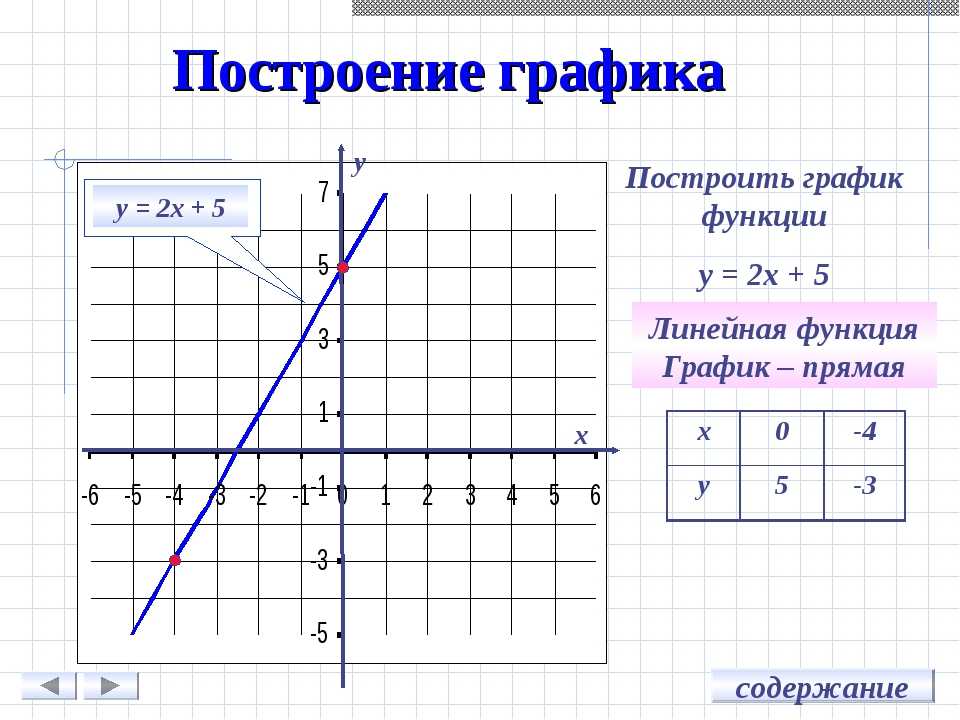 7.        а) Постройте график функции y=4\x
б)    Найдите, при каких значениях аргумента значение
функции равно 2.
в)     Выделите ту часть графика, которая соответствует
условию у > 2. При каких значениях х выполняется это
условие?
г)     При каких значениях х выполняется условие у < 2?

ответы

держи график и ответ

ваш ответ

Можно ввести 4000 cимволов

отправить

дежурный

Нажимая кнопку «отправить», вы принимаете условия пользовательского соглашения

похожие темы

Психология

ЕГЭ

10 класс

9 класс

похожие вопросы 5

Домашняя контрольная работа № 3 Вариант 2 10. При каких значениях р уравнение… Мордкович 8 класс алгебра

10. При каких значениях р уравнение -х 2 + 6х — 2 = р:
а) не имеет корней;
б) имеет один корень; (Подробнее. ..)

ГДЗМордкович А.Г.Алгебра8 класс

Когда скорость изменения функции будет наибольшей или наименьшей? Алгебра 10-11 класс Колмогоров Упр 308

Совсем я в точных науках не сильна) Кто поможет?) Найдите значения аргумента из промежутка [-2; 5], при которых скорость изменения (Подробнее…)

ГДЗ11 классКолмогоров А.Н.Алгебра

Приготовление раствора сахара и расчёт его массовой доли в растворе. Химия. 8 класс. Габриелян. ГДЗ. Хим. практикум № 1. Практ. работа № 5.

Попробуйте провести следующий опыт. Приготовление раствора
сахара и расчёт его массовой доли в растворе.
Отмерьте мерным (Подробнее…)

ГДЗШкола8 классХимияГабриелян О.С.

16. Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)… Цыбулько И. П. Русский язык ЕГЭ-2017 ГДЗ. Вариант 13.

16.
Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)
в предложении должна(-ы) стоять запятая(-ые). (Подробнее…)

ГДЗЕГЭРусский языкЦыбулько И.П.

ЕГЭ-2017 Цыбулько И. П. Русский язык ГДЗ. Вариант 13. 18. Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)…

18.
Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)
в предложении должна(-ы) стоять запятая(-ые). (Подробнее…)

ГДЗЕГЭРусский языкЦыбулько И.П.

3-8 9 Оценить квадратный корень из 12 10 Оценить квадратный корень из 20 11 Оценить квадратный корень из 50 94 18 Оценить квадратный корень из 45 19 Оценить квадратный корень из 32 20 Оценить квадратный корень из 18 92

Декартова плоскость (график XY): определение, квадранты, ордината, абсцисса

Квадранты
Ордината и абсцисса Определение
Нарисуйте график на декартовой плоскости
График XY в сравнении с графиком в декартовых координатах

Происхождение

Начало полярных координат

Декартова форма

A Декартова плоскость — это график с одной осью x и одной осью y (поэтому его иногда называют графиком XY).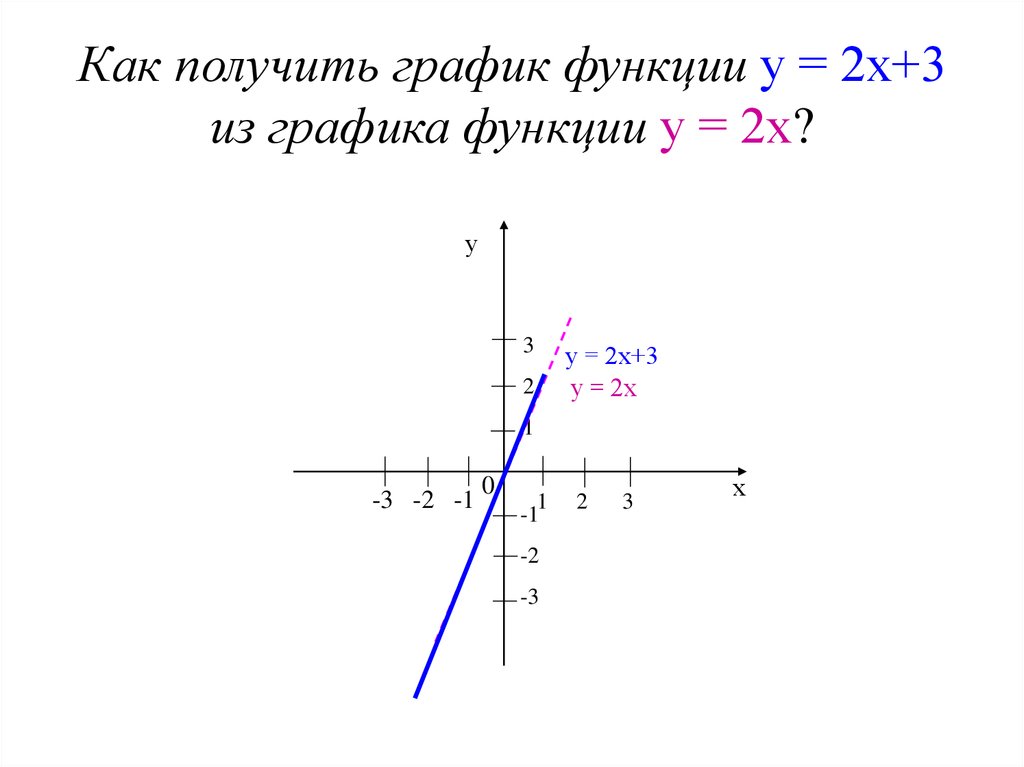 Эти две оси перпендикулярны друг другу. Начало (O) находится точно в центре графика. Числа справа от нуля на оси x положительны; числа слева от нуля отрицательные. Для оси Y числа ниже нуля являются отрицательными, а числа выше — положительными.

Проще говоря: 909:40 Декартова плоскость — это просто числовая линия с другой числовой линией под прямым углом.

Декартова плоскость сопоставляет точку на плоскости с парой чисел, расположенных на осях x и y. Каждая точка на плоскости имеет уникальный набор чисел, называемый упорядоченными парами . Первая точка, которую вы получите, всегда будет в части X графика, а второе число всегда будет Y. Например, (2,3) означает 2 пробела по оси x и 3 по оси y.

Декартова плоскость с несколькими упорядоченными парами, представляющими точки на графике.

Граф назван в честь математика 16 века Рене Декарта.
Квадранты декартовой плоскости
Квадранты составляют большую часть работы, когда дело доходит до тригонометрии.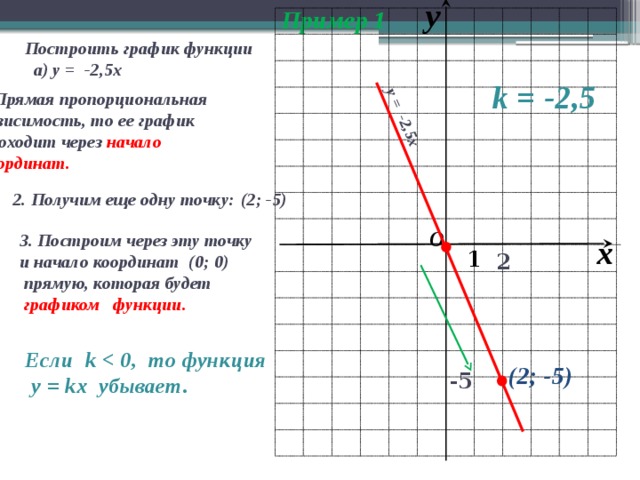 Когда дело доходит до триггера, вам нужно знать о четырех углах графика.
Первый квадрант = вверху справа.
Второй квадрант = вверху слева.
Третий квадрант = нижний левый.
Четвертый квадрант = нижний правый угол.

В этом примере первое число в списке упорядоченных номеров (-1) находится там, где точка находится на оси x. Другими словами, точка находится на один пробел левее нуля. Второе число (-2) указывает, где точка находится на оси Y. Другими словами, точка находится на два пробела ниже нуля.
Интересный факт: Изобретение этой системы было революционным для своего времени. Это дало нам первую систематическую связь между алгеброй и геометрией.
Ордината и абсцисса относятся к упорядоченным парам на декартовой плоскости.
Абсцисса — это значение x (первое число в упорядоченной паре).
Ордината — это значение y (второе число в упорядоченной паре).
На приведенном выше графике показаны четыре упорядоченные пары:
Первая точка (-3,1), -3 является абсциссой.
Для второй точки (2,3) ордината 3.
Далее точка (0,0), 0 — это абсцисса и ордината.
Для точки -1,5, -2,5, -1,5 это абсцисса, а -2,5 это ордината.
Не забывайте, что первая точка, которую вы получите, всегда будет на X части графика, а второе число всегда будет на Y.
Ордината и абсцисса: другие определения и использование обычно используются для описания первой и второй точек в системе координат, иногда они используются для обозначения чего-то немного другого.
Некоторые словари утверждают, что эти термины представляют собой расстояние между двумя точками . Например, Merriam-Webster утверждает, что ансцисса — это «горизонтальная координата точки в плоской декартовой системе координат, полученная путем измерения параллельно оси x». Будьте осторожны, так как это определение работает только с положительными числами!
На более ранних уроках геометрии ось X называлась абсциссой, а ось Y — ординатой. Например, «Журнал экспериментальной медицины» от 189 г.6 говорится, что «…ось абсцисс разделена на шесть-одиннадцать сегментов, каждый из которых соответствует периоду в одну неделю, а ордината разделена на десять сегментов, представляющих абстрактные единицы от 1 до 10». В некоторых науках, таких как физика и астрономия, некоторые ученые до сих пор используют это определение.
Эти два термина также могут использоваться в наклонной системе координат . В то время как оси в декартовой плоскости перпендикулярны, оси в наклонной системе координат — нет.
Я очень рекомендую вам заглянуть в блог Джейсона Дайера, где он проделывает весь путь до Фибоначчи (ок. 1170 – ок. 1250), чтобы найти происхождение слов. То есть, если вы действительно заинтересованы в чтении более запутанных аспектов ординаты и абсциссы и истории, стоящей за терминами!
Допустим, вам дали такую функцию, как f(x) = x ² – 2 (или, что то же самое, y = x ² – 2) и попросили нарисовать график на декартовой плоскости . Для решения задачи необходимо:
Выберите значения x для ввода в формулу. Обычно вам нужно выбирать целые числа (целые числа плюс ноль и отрицательные числа, такие как -10, 3, 1, 7…), потому что с ними легче работать.
Создайте несколько координат (x, y).
Нанесите точки на декартову плоскость.
Нарисуйте кривую или линию графика.
Нарисуйте график на декартовой плоскости: Пример
Пример вопроса №1: Нарисуйте график y = x ² – 2 на декартовой плоскости.
Шаг 1: Выберите ваши значения x . Вам решать, какие значения выбрать для ваших значений x, но выбирайте числа, которые легко вычислить. Хорошей отправной точкой является несколько значений около нуля: -2, -1, 0, -1, 2. Или вы можете попробовать -10, -5, 0, 5, 10.
Шаг 2: Введите x- значения из шага 1 в функцию. Для этого замените «x» в формуле на число, которое вы выбрали для x. Давайте использовать -2, -1, 0, -1, 2.
у = х ^-2 – 2 = 2
г = х ^-1 – 2 = -1
у = х ⁰ – 2 = -2
у = х ¹ – 2 = -1
у = х ² – 2 = 2
Шаг 3: Создайте таблицу значений из шагов 1 и 2. Этот шаг необязателен, но он может помочь вам увидеть точки (x, y) более четко:

Шаг 4: График точки.

Шаг 5: Нарисуйте кривую или линию графика. На самом деле это просто соединение точек.
Если на данный момент вы не уверены в форме графика, вернитесь к шагу 1 и выберите еще пару значений x, чтобы завершить картину.
Шаг 6: Проверьте свою работу. Вы можете использовать графический калькулятор: я использовал его на Desmos.com для построения графиков здесь.
Если вы не можете использовать графический калькулятор, введите в качестве входных данных случайное значение x, например, x = 9,2 или x = 7,5.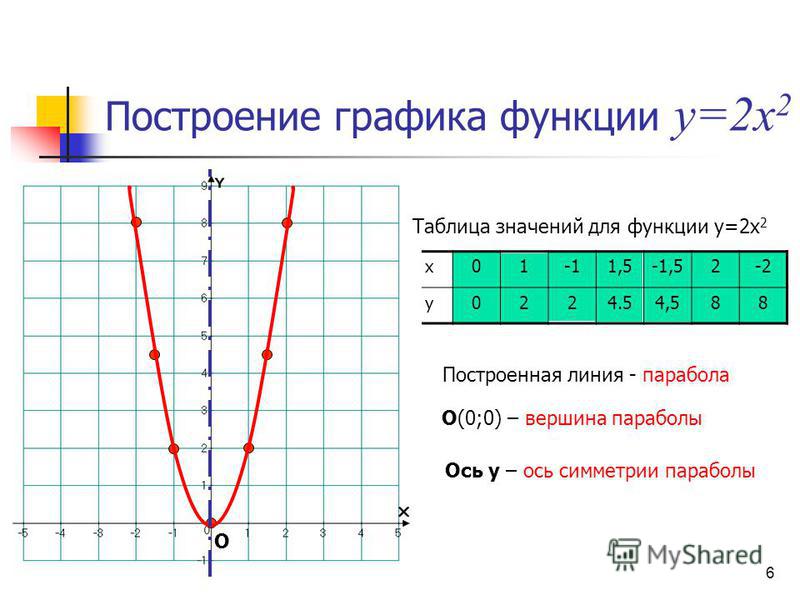 Если вы правильно нарисовали график, ваша новая точка будет лежать на линии, которую вы нарисовали.
Совет : Если у вас нет линейной функции, которая всегда дает прямой график, нарисуйте кривую от каждой точки к следующей вместо серии прямых линий.
Декартова плоскость (или декартова координатная диаграмма) — это практически то же самое, что и диаграмма X Y. Это связано с тем, что график XY является основным графиком, на котором вы можете построить простой график ряда координат, построить график рассеяния или линейный график. Что отличает декартов график от вашего стандартного графика? На этом графике основное внимание уделяется четырем углам, а также традиционным X и Y 9.0909
Подобно декартовой плоскости, график XY представляет собой график с двумя осями (оси — это множественное число оси):
Горизонтальная линия, идущая слева направо (ось X).
Вертикальная линия, идущая вверх и вниз (ось Y).

Нанесение точек на график XY
Чтобы нанести точку, перемещайтесь по оси x, чтобы найти первую координату (первое число), затем перемещайтесь вверх или вниз, чтобы найти вторую координату. После этого нарисуйте точку на этом пересечении. Посмотрите видео, чтобы узнать, как нанести две точки на график XY:
Как нанести точки на график XY
Посмотрите это видео на YouTube.
Видео не видно? Кликните сюда.
Первая точка, которую вы получите, всегда будет находиться на X части графика, а второе число всегда будет Y. Например, (2,3) означает 2 пробела по оси x и 3 по оси y. ось.
Набор точек на графике XY называется точечной диаграммой, поскольку он выглядит как разрозненный набор точек.
Построить график X Y онлайн: Сразу нужно убедиться, что вы нарисовали свои очки в правильном месте. Это можно сделать, воспользовавшись онлайн-калькулятором на канале Discovery. Введите свои очки (убедитесь, что вы используете круглые скобки, например: » (2,3)», а затем нажмите Нарисуйте их . На следующем изображении показана точка (2,3), нарисованная в графическом редакторе:

Исходная точка — это опорная точка, используемая для определения всех остальных точек; неподвижная точка, на которую ссылаются при описании геометрии пространства.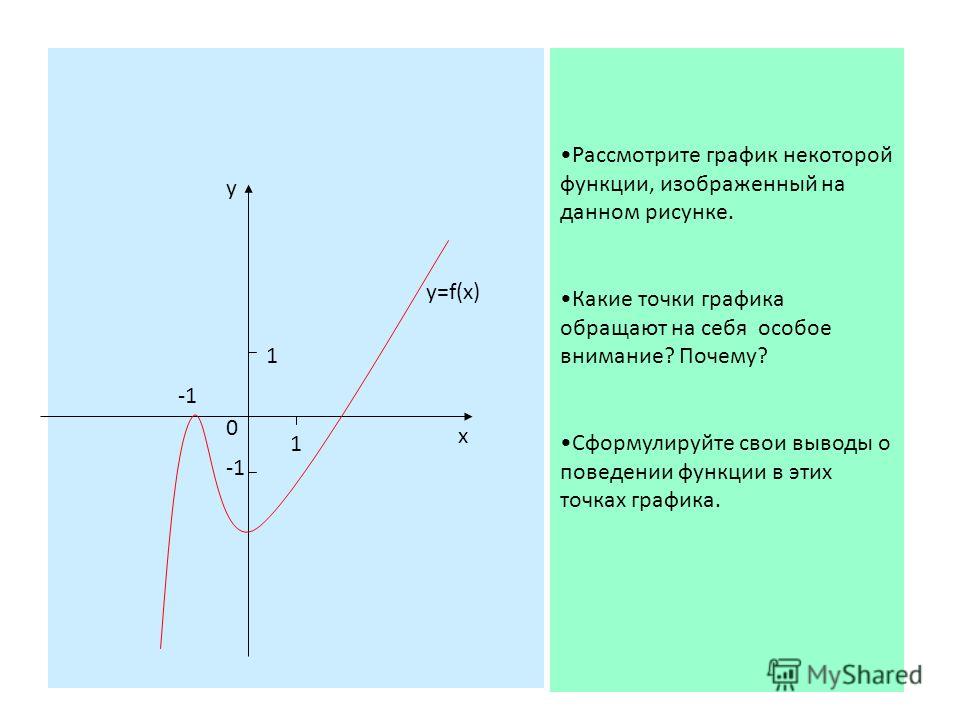 Помня об этом, ее часто обозначают буквой О, а координаты всегда равны нулю.
В одном измерении мы просто записываем начало координат как 0; это точка, с которой мы начинаем нумерацию на числовой прямой. Вы можете идти в любом из двух направлений:
Идя налево, вы будете считать отрицательные числа
Идя направо, вы будете считать с положительными числами.
В любом случае вы можете пройти бесконечное расстояние (до бесконечности или отрицательной бесконечности).
Числовая линия, показывающая расстояние от -1 до 1. 0 находится в центре.

В двух измерениях, использующих декартову плоскость, началом является точка пересечения осей x и y. Эта точка записывается как (0, 0).
В трех измерениях начало координат равно (0, 0, 0) и определяется как место пересечения осей x, y и z.

В размерах n начало координат будет местом пересечения осей n , и каждая координата будет равна нулю.

Начало в полярной системе координат также называется полюс (не путать с полюсом функции в комплексном анализе, который является изолированной особенностью). Каждая точка определяется углом и лучом (линия, которая начинается в заданных координатах и продолжается до бесконечности) от полюса. Полюсом в полярной системе координат является (0, φ), где 0 — это пересечение осей, а φ — это угол, на который мы поворачиваем.
Monsterman222 (собственная работа) [CC BY-SA 3.0 (http://creativecommons.org/licenses/by-sa/3.0)], через Wikimedia Commons

Сдвиги
Исходная точка произвольна и может быть смещена для удобства. Если вы работаете в двухмерных декартовых координатах и смещаете начало от (0, 0) к месту, которое было определено как (a, b), вам нужно будет добавить (-a, -b) к координатам каждой точки .
Например, предположим, что вы решили изменить свой исходный пункт на точку, в которую вы звонили (2, 4).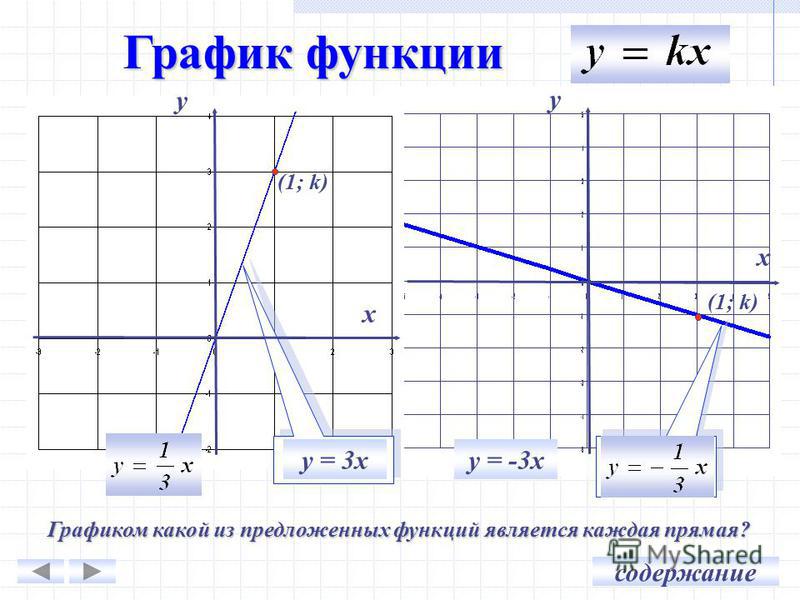 Следующее (2, 4) равно (0, 0) = O, ваше прежнее (0, 0) равно (-2, -4), а точка (3, 5) есть (1, 1).
Если вы работаете с трехмерной геометрией и хотите переключиться на точку, ранее обозначенную как (6, 7, 8), вы должны перевести каждую точку из старой системы в новую, добавив (-6, — 7, -8) к координатам каждой точки. После этого точка (20,20,20) станет (14, 13, 12).
Декартова форма
Декартова форма (также называемая Декартовым представлением или прямоугольной формой ) может относиться к любой функции или отношению, записанному с использованием координат (x, y) или (x, y, z). Однако в большинстве случаев этот термин относится к определенному способу записи комплексных чисел.
Его иногда называют «прямоугольной формой», потому что точка в пространстве, отнесенная к осям x и y, образует форму прямоугольника.
Декартова плоскость с несколькими упорядоченными парами, которые можно изобразить в виде прямоугольников.
Декартова форма комплексного числа
Комплексные числа имеют две формы: декартову и полярную форму. «Обычный» способ (по крайней мере, первый способ, которым вы учитесь выражать комплексные числа) — это декартова форма: z = x + yi, , где:
z = комплексное число,
x = действительная часть z,
i = мнимая часть z.
Правая часть этого уравнения, x + yi, , называется декартовой формой .
Другим способом записи комплексных чисел является полярная форма , состоящая из двух частей: модуля и аргумента. Полярная форма выглядит следующим образом:
z = r∠θ
В декартовой форме комплексные числа можно легко изобразить на диаграмме Аргана.
Пример Вопрос 1 : Какова декартова форма комплексного числа (3 + i)(2 – i) ² – i ?.
Решение :
Используйте ФОЛЬГУ, чтобы расширить квадрат члена (2 – i) ² , что даст 3 – 4i.
Используйте алгебру, чтобы переписать новое расширенное уравнение (3 + i)(3 – 4i) ² – i
Расширение с использованием ФОЛЬГИ: 3 · 3 + 3(-4i) + i · 3 + i (-4i) -i
Упростите и объедините аналогичные термины: : 9 – 12i + 3i + 4 = 13 – 9i -i = 13 – 10i
Решение (в декартовой форме) 13 – 10i.
Пример: перевод полярной формы в декартову форму
Пример вопроса 2 : Что такое декартова форма z = 3∠40°?
Помните SOHCATOA из тригонометрии? Вы можете использовать это для преобразования в декартову форму. Во-первых, график может помочь вам визуализировать, где находятся различные части:
Комплексное число z = 3∠40°
Итак:
cos 40° = ON / 3
Решение для ON дает:
ON = 3 cos 40° = 2,298
А,
sin 40° = NP / 3 :
NP = 3 sin 40° = 1,928
Декартова форма z = 2,298 + 1,928i
Ссылки
Center for Excellence.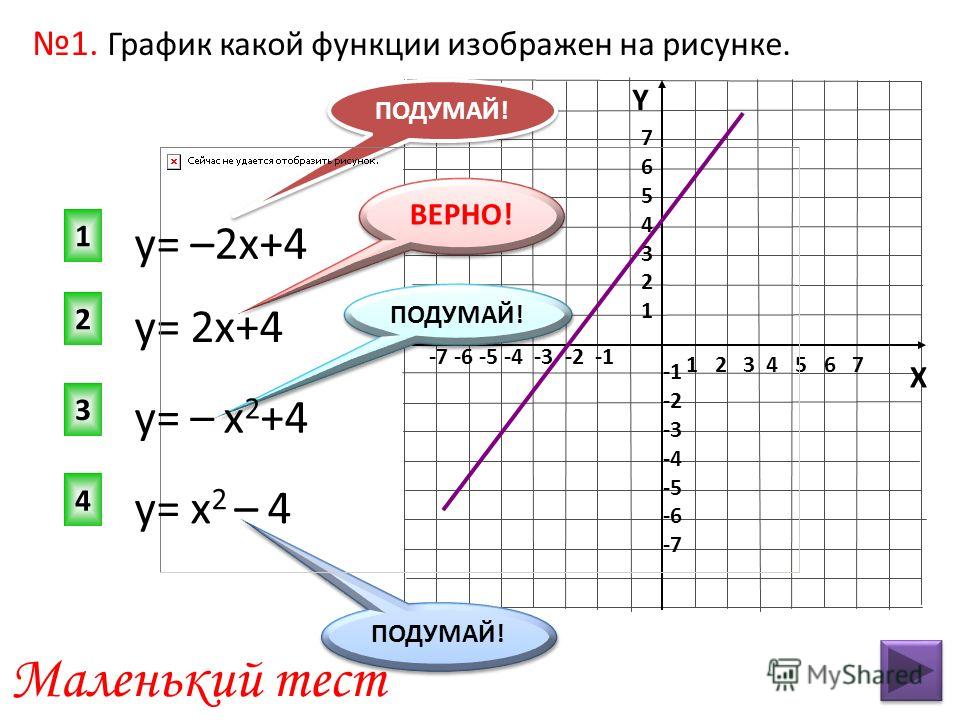 Сигма. Полярная форма комплексного числа. Получено 12 января 2020 г. с: http://www.mathcentre.ac.uk/resources/sigma%20complex%20number%20leaflets/sigma-complex10-2009.-1.pdf
Уорнер, С. Чистая математика для начинающих: элементарное введение в логику, теорию множеств, абстрактную алгебру, теорию чисел, реальный анализ, топологию, комплексный анализ и линейную алгебру в мягкой обложке — 29 сентября 2019 г. Получить 800.
Томас Р. Комплексные числа. Получено 12 января 2020 г. с: https://home.cc.umanitoba.ca/~thomas/Courses/ComplexRSDT.pdf
ЦИФРОВАТЬ ЭТО КАК:
Стефани Глен . «Декартова плоскость (график XY): определение, квадранты, ордината, абсцисса» из StatisticsHowTo.com : Элементарная статистика для всех нас! https://www.statisticshowto.com/calculus-definitions/cartesian-plane-quadrants-ordinate-abscissa/
————————————————— ————————-
Нужна помощь с домашним заданием или контрольным вопросом? С Chegg Study вы можете получить пошаговые ответы на свои вопросы от эксперта в данной области.
No related posts.