Теперь достаточно зажать левую кнопку мыши на нижней точки готовой ячейки и растянуть таблицу, чтобы формула автоматически подставилась в остальные ячейки, и вы могли сразу ознакомиться с результатом.
Перейдите на вкладку вставки и выберите раздел с рекомендуемыми диаграммами.
В списке отыщите точечную диаграмму, которая подойдет для составления подходящего графика.
Вставьте ее в таблицу и ознакомьтесь с результатом. На следующем скриншоте вы видите параболу и значения X, при которых она получилась правильной (такую часто показывают в примерах на математике).
Всего 7 простых шагов потребовалось для достижения желаемого результата. Вы можете подставлять свои значения в таблицу и изменять их в любое время, следя за тем, как перестраивается график функций.
Комьюнити теперь в Телеграм
Подпишитесь и будьте в курсе последних IT-новостей
Подписаться
График функции y=sin(x)
y=sin(x) – вторая функция, которую мы возьмем за пример. Может показаться, что ее составление осуществляется сложнее, хотя на самом деле это не так. Дело в том, что Excel сам посчитает значения, а вам останется только задать известные числа и вставить простой линейный график для вывода результатов на экран.
Может показаться, что ее составление осуществляется сложнее, хотя на самом деле это не так. Дело в том, что Excel сам посчитает значения, а вам останется только задать известные числа и вставить простой линейный график для вывода результатов на экран.
-
Если вам будет проще, впишите в отдельную клетку функцию, укажите интервал и шаг. Так вы не запутаетесь при дальнейшем заполнении ячеек.
-
Добавьте два столбца, в которые будут вписаны значения каждой оси. Это нужно не только для обозначения чисел, но и для их вычисления при помощи функций программы.
-
Начните вписывать значения X с необходимым интервалом и шагом. Кстати, вы можете заполнить всего несколько полей, а затем растянуть клетки таким же образом, как было показано в предыдущем примере, чтобы они подставились автоматически до конца вашего интервала.
-
Теперь более сложное, но не страшное действие – определение значения Y.
 Понятно, что он равняется синусу X, значит, нужно вписать функцию =SIN(A1), где вместо A1 используйте нужную ячейку, а затем растяните функцию на оставшийся интервал.
Понятно, что он равняется синусу X, значит, нужно вписать функцию =SIN(A1), где вместо A1 используйте нужную ячейку, а затем растяните функцию на оставшийся интервал. -
На следующем скриншоте вы видите результат заполнения таблицы. Используйте округление для удаления лишних знаков после запятой.
-
Вставьте обычную линейчатую диаграмму и ознакомьтесь с результатом.
На примере этих двух функций уже можно понять, как работает построение графиков в Экселе. При использовании других функций просто учитывайте особенности заполнения ячеек и не забывайте о том, что вам не нужно ничего считать, поскольку Excel все сделает за вас после указания необходимой формулы.
Личный опыт
Наши постоянные авторы и читатели делятся лайфхаками, основанными на личном опыте. Полная свобода самовыражения.
Рекомендуем
Графики функций.
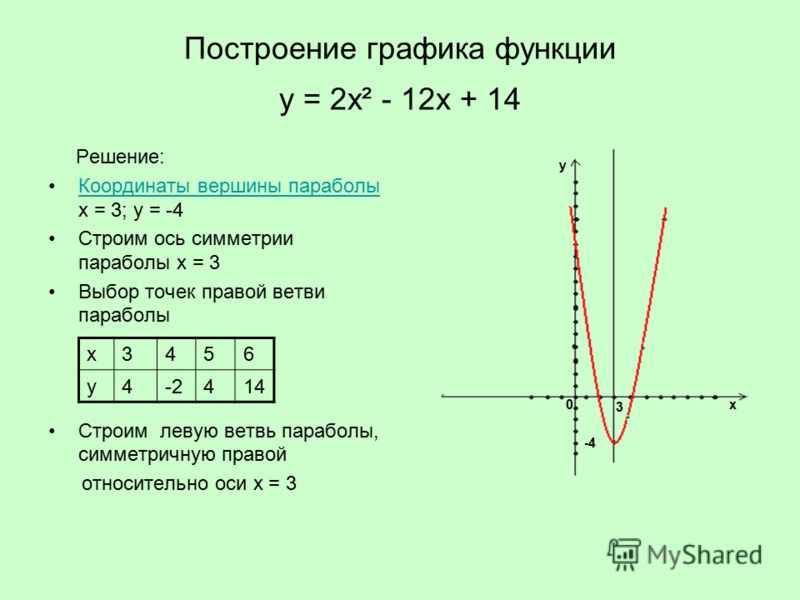 Простейшие построения. Прямая на плоскости
Простейшие построения. Прямая на плоскости
График функции — это наглядный образ некоторой функции f(x). Здесь каждому значению х соответствует единственное значение y. Это множество точек на плоскости, координаты которых удовлетворяют заданному уравнению y = f(x).График уравнения — это множество всех точек плоскости, которые удовлетворяют заданному уравнению, т.е. обращают уравнение в верное числовое равенство. Зависимость в данном случае не обязательно является функцией.Рассмотрим ряд элементарных функций, таких, как прямая, парабола, гипербола, их свойства и правила построения. |
Но для начала покажем на примере отличие графика функции от графика уравнения.
График функции — для каждого значения Х единственное значение Y
График функции — для каждого значения Х единственное значение Y
График уравнения — для некоторого значения Х могут существовать несколько значений Y, не функция.
1. Прямая. Уравнение прямой y = kx + b.
Прямая задается линейной функцией , т.е. уравнением первой степени вида y = kx + b.
при k>0 график функции возрастает (y=3x+1, k=3, k>0), при k<0 график функции убывает (y=-3x+1, k=-3, k<0)
график функции возрастает k=3, k>0
график функции убывает k=-3, k<0
Рассмотрим частные случаи расположения линейных функций.y = kx — график функции проходит через начало координат, т.е. точку О(0;0),
y = c (c = const) — график функции параллелен оси Ox,
x = c (c = const) — график функции параллелен оси Oy.
y = kx — график функции проходит через начало координат, т.е. точку О(0;0)
y = c (c = const) — график функции параллелен оси Ox
x = c (c = const) — график функции параллелен оси Oy
Для построения прямой достаточно получить координаты двух точек, принадлежащих заданному уравнению.
Как построить прямую? Покажем на примере.
Дано уравнение прямой: y=-2x+3. Необходимо построить график функции.
Возьмем два произвольных значения переменной х, например х = -1 и х = 5. Найдем для каждого из них соответствующее значение переменной у. Как это сделать? Подставить выбранные значения х в заданное уравнение.
y(-1) = -2·(-1)+3=5
y(5) = -2·5+3=-7
Получаем две точки с координатами: (-1;5) и (5;-7). Выносим их на координатную плоскость и проводим через них прямую.
На что указывают параметры k,b в уравнении прямой y = kx + b?
Параметр k — указывает на наклон прямой.
Параметр b — координата точки пересечения заданной прямой с осью OY. Так как y = k·0 + b (х=0 — уравнение оси OY)
Наклон прямой в зависимости от k. k>0 — угол острый
Наклон прямой в зависимости от k. k<0 — угол тупой
Точки пересечения прямых с осью OY
Параметр k в уравнении прямой y = kx + b есть угловой коэффициент этой прямой.
k=tgα, α — угол меду положительным направлением оси ОХ и прямой.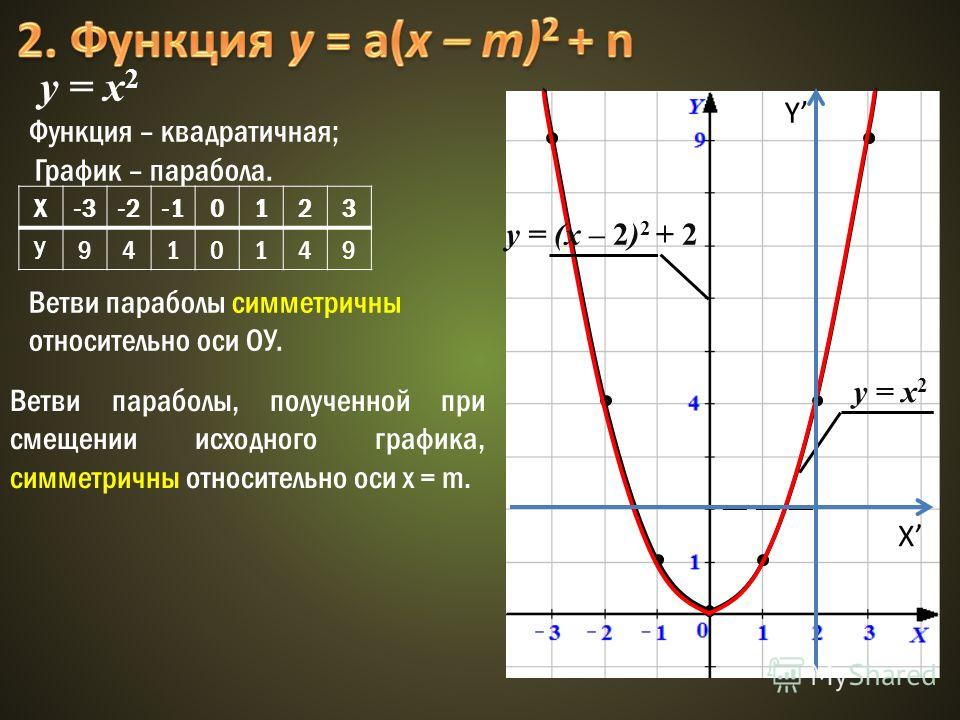
Угловые коэффициенты всех параллельных прямых равны.
Угловые коэффициенты перпендикулярных прямых взаимно обратны по величине и противоположны по знаку.
Для наглядности покажем утверждения на конкретных примерах.
Угловой коэффициент прямой
Угловой коэффициент параллельных прямых
Угловой коэффициент перпендикулярных прямых
Уравнения прямой на плоскости.
Построим некоторые уравнения прямых в зависимости от исходных данных, приведем формулы и рассмотрим конкретные примеры.
Коротко уточним используемые ниже понятия:
Угол наклона прямой — угол меду положительным направлением оси ОХ и прямой.
Нормальный вектор прямой — вектор, перпендикулярный искомой прямой.
Направляющий вектор прямой — вектор, параллельный искомой прямой.
Уравнение прямой по заданной точке и углу наклона. Дано: A(xA; yA), α
Уравнение прямой по двум точкам
Уравнение прямой по точке и нормальному (направляющему) вектору/div>
2.
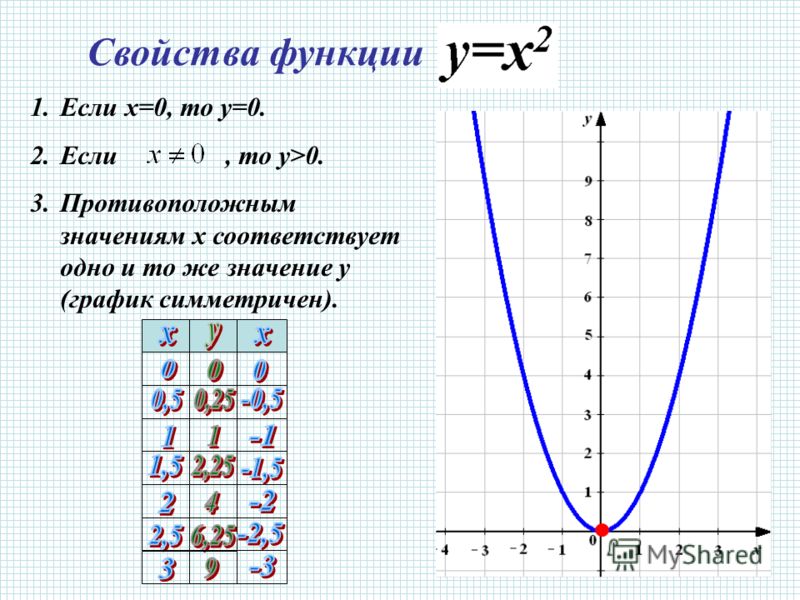 Парабола.
Парабола.Парабола задается квадратичной функцией вида y = ax2 + bx + c.
3. Гипербола.
4. Кубическая парабола.
графиков разброса (XY)
На точечной диаграмме (XY) есть точки, которые показывают взаимосвязь между двумя наборами данных.
В этом примере каждая точка показывает вес одного человека в зависимости от его роста.
(Данные отображаются на графике как «Декартовы (x, y) координаты»)
Пример:
Местный магазин мороженого отслеживает количество продаваемого мороженого в зависимости от полуденной температуры в этот день. Вот их цифры за последние 12 дней:
| Продажи мороженого в зависимости от температуры | |
| Температура °C | Продажа мороженого |
|---|---|
| 14,2° | 215 долларов |
| 16,4° | $325 |
| 11,9° | 185 $ |
| 15,2° | |
| 18,5° | 406 $ |
| 22,1° | $522 |
| 19,4° | 412 $ |
| 25,1° | 614 $ |
| 23,4° | $544 |
| 18,1° | $421 |
| 22,6° | $445 |
| 17,2° | 408 $ |
А вот те же данные, что и на точечной диаграмме:
Теперь легко увидеть, что более теплая погода приводит к увеличению продаж , но связь не идеальна.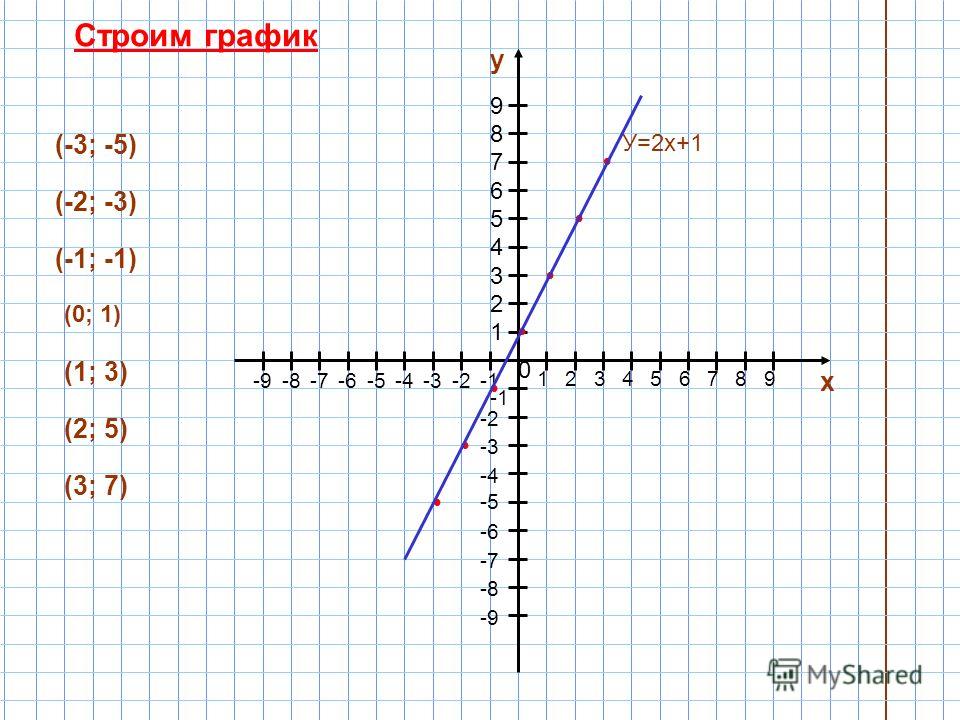
Линия Best Fit
Мы также можем нарисовать «Линию наилучшего соответствия» (также называемую «Линия тренда») на нашем точечном графике:
Постарайтесь провести линию как можно ближе ко всем точкам и на столько же точек выше линии, сколько и ниже.Но для большей точности мы можем рассчитать линию, используя регрессию наименьших квадратов и калькулятор наименьших квадратов.
Пример: повышение уровня моря
Точечная диаграмма повышения уровня моря: | |
| И здесь я нарисовал «Линию наилучшего соответствия». |
Интерполяция и экстраполяция
Интерполяция — это место, где мы находим значение внутри нашего набора точек данных.
Здесь мы используем линейную интерполяцию для оценки продаж при 21 °C.
Экстраполяция — это место, где мы находим значение за пределами нашего набора точек данных.
Здесь мы используем
Осторожно: Экстраполяция может дать вводящие в заблуждение результаты, потому что мы находимся на «неизведанной территории».
Помимо графика (как показано выше) мы можем создать формулу, которая поможет нам.
Пример: уравнение прямой линии
Мы можем оценить уравнение прямой линии по двум точкам на графике выше
Оценим две точки на прямой вблизи фактических значений: (12°, 180 долл. США) и (25°, 610 долл. США). )
Сначала найдем наклон:
| уклон «м» | = изменение у изменить на х |
| = 610 $ − 180 $ 25° − 12° | |
| = 430 долларов 13° | |
| = 33 (округлено) |
Теперь подставьте угол наклона и точку (12°, $180) в формулу «точка-наклон»:
Подставить известные значения: y − 180 = 3(x − 12)
Прибавить 180 к обеим сторонам: y = 33(x − 12) + 180
Разложить 33(x − 12): y = 33x − 396 + 180
Упрощение: y = 33x − 216
ИНТЕРПОЛЯЦИЯ
Теперь мы можем использовать это уравнение, чтобы интерполировать стоимость продажи при 21°:
y = 33×21° − 216 = $477
EXTRApolating
И на экстраполировать продажную стоимость при 29°:
− − 16y9 = 3
значения близки к тому, что мы получили на графике. Но это не значит, что они более (или менее) точны. Все они являются лишь оценками.
Но это не значит, что они более (или менее) точны. Все они являются лишь оценками.
Не используйте экстраполяцию слишком далеко! Каких продаж вы ожидаете при 0°?
y = 33×0° − 216 = − $216
Хммм… Минус $216 ? Мы экстраполировали слишком далеко!
Примечание: мы использовали линейную (на основе линии
Корреляция
Когда два набора данных тесно связаны друг с другом, мы говорим, что они имеют высокую корреляцию .
Слово «Корреляция» состоит из Co- (что означает «вместе») и Связь
- Корреляция Положительная , когда значения увеличивают вместе, и
- Корреляция Отрицательная когда одно значение уменьшается когда другое увеличивается
Вот так:
(Подробнее о корреляции)
Отрицательная корреляция
Корреляции могут быть отрицательными, что означает, что — это корреляция, но одно значение уменьшается по мере увеличения другого значения.
Пример: коэффициент рождаемости и доходКоэффициент рождаемости имеет тенденцию быть на ниже в более богатых странах.
Ниже приведена точечная диаграмма примерно для 100 разных стран. |
|
Имеет отрицательную корреляцию (линия наклонена вниз)
Примечание.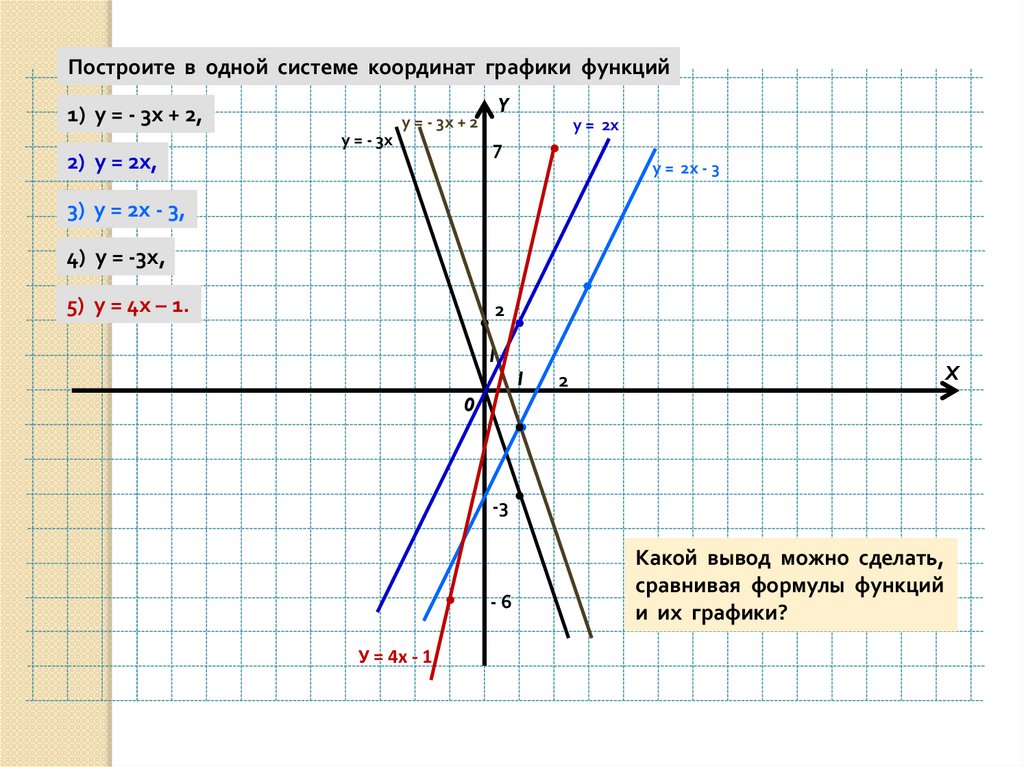

 Понятно, что он равняется синусу X, значит, нужно вписать функцию =SIN(A1), где вместо A1 используйте нужную ячейку, а затем растяните функцию на оставшийся интервал.
Понятно, что он равняется синусу X, значит, нужно вписать функцию =SIN(A1), где вместо A1 используйте нужную ячейку, а затем растяните функцию на оставшийся интервал.