Хорда радиус диаметр: Определение окружности ,центра радиуса, хорды и диаметра

Окружность, круг. Хорды, дуги

11.105. В окружности радиуса 26 см проведена хорда, равная 28 см. Найти длину отрезка, соединяющего середину хорды с центром окружности.

Ответ: 10 см.

11.106. Найти расстояние от центра окружности до хорды, равной 6 см, если радиус окружности равен 5 см.

Ответ: 4 см.

11.107. Хорда пересекает диаметр под углом 30° и делит его на два отрезка длиной 2 см и 6 см. Найти расстояние от центра круга до хорды.

Ответ: 2 см.

11.108. В окружности с центром в точке О проведены хорда AB и радиус OD, которые пересекаются в точке C, причем известно, что см,см. Найти хорду.

Ответ: 80 см.

11.109. На окружности с центром

О лежит точка В. АВ – хорда, АС – касательная, Найти уголАОВ.

Ответ: 70°.

11.110. В угол величиной 60° вписана окружность. Найти расстояние от центра окружности до вершины угла, если радиус окружности равен 7,5 см.

Ответ: 15 см.

11.111. В круговой сектор, дуга которого содержит 60°, вписан круг. Найти отношение площади этого круга к площади сектора.

Ответ: 2/3.

11.112. В круговой сектор вписана окружность, радиус которой в три раза меньше радиуса сектора. Найти величину центрального угла сектора.

Ответ: 60°.

11.113. К окружности радиуса 5 см в точке В проведена касательная, на которой отмечена точка А на расстоянии 12 см от точки

В. Найти расстояние от точки А до центра окружности.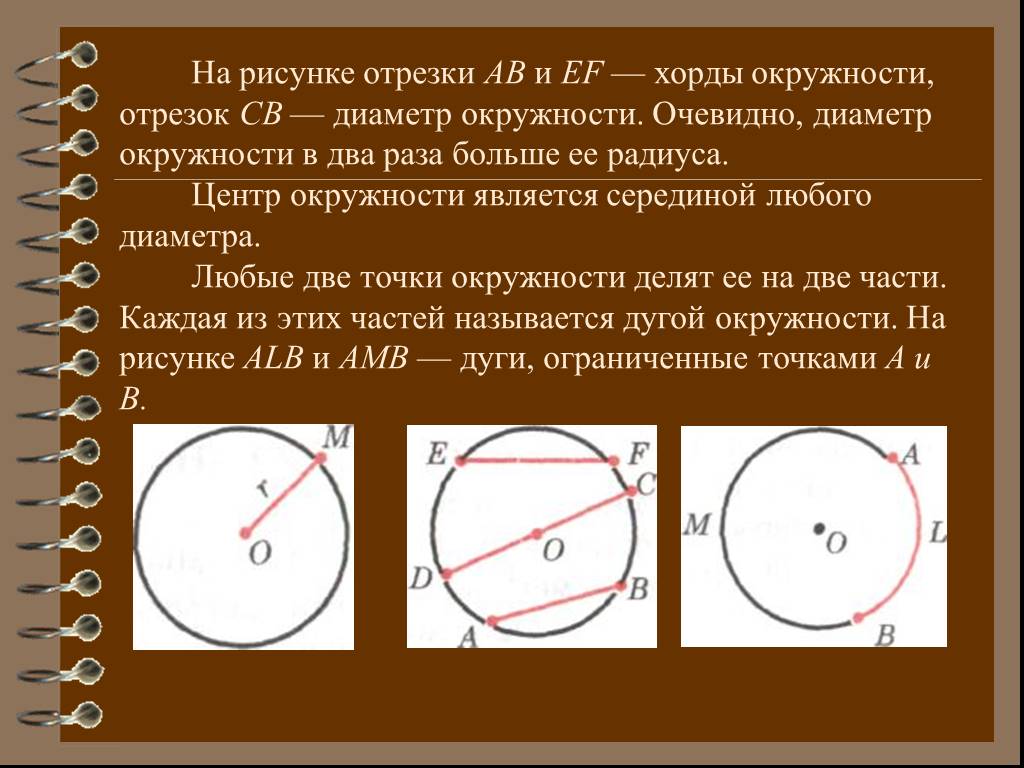

Ответ: 13 см.

11.114. Длина окружности равна 4π см. Найти площадь квадрата, вписанного в эту окружность.

Ответ: 8 см².

11.115. В круг вписан квадрат со стороной, равной см. Найти площадь круга.

Ответ: 2 см².

11.116. Найти площадь круга, если известно, что длина окружности круга вдвое меньшей площади равна 6π см.

Ответ: 18 см².

11.117. Центральный угол окружности на 50° больше вписанного угла, опирающегося на ту же дугу. Найти величину дуги.

Ответ: 100°.

11.118. Окружность радиуса 2 см разогнута в дугу радиуса 15 см. Найти центральный угол.

Ответ: 48°.

11.119. Круг радиуса 6 см делится концентрической окружностью на две части – на круг радиуса r и кольцо, площади которых относятся как 1 : 3. Найти r.

Ответ: 3 см.

11.120. Площадь кругового сектора равна 0,1π  см², радиус круга равен 1 см. Найти величину угла, опирающегося на дугу сектора с вершиной на окружности.

Ответ: 18°.

11.121. Две окружности, каждая из которых вписана в угол величиной 60°, касаются друг друга внешним образом. Найти расстояние от точки касания окружностей до стороны угла, если радиус большей окружности равен 23 см.

Ответ: 11,5 см.

11.122. Общая хорда двух пересекающихся окружностей видна из их центров под углами 90° и 120°. Найти расстояние между центрами окружностей, лежащими по одну сторону от хорды, если длина хорды равна см.

Ответ: 0,25 см.

11.123. Из точки К, лежащей на окружности, проведены касательная к окружности и хорда КА. Угол между ними равен 60°. Найти длину меньшей дуги, отсекаемой хордой КА, если радиус окружности равен см.

Ответ: 2 см.

11.124. Из точки А, лежащей вне круга, проведены касатель­ная к кругу и секущая. Найти, во сколько раз отрезок секущей, лежащей внутри круга, больше отрезка секущей, находящегося вне круга, если расстояние от точки

А до точки касания в 3 раза больше, чем длина отрезка, лежащего вне круга.

Ответ: в 8 раз.

11.125. В окружности радиуса см из одного конца диаметра проведена касательная, а из другого – хорда, стягивающая дугу в 120°. Хорда продолжена до пересечения с касательной. Найти внешний отрезок секущей.

Ответ: 1 см.

11.126. Длина окружности, в которую вписан правильный шестиугольник, равна см. Найти длину окружности, вписанной в этот шестиугольник.

Ответ: 1,5 см.

11.127. В окружности с центром О проведены диаметр АВ и хорда ВС, угол АОС равен 60°. Найти угол АВС.

Ответ: 30°.

Хорда рисунок — 81 фото

Две хорды из одной точки окружности

Взаимно перпендикулярные хорды

Хорда и диаметр окружности

Хорда равна радиусу окружности

Пересекающиеся хорды

Если хорда равна радиусу

Симметрия хорд

Внутренний образ окружности

Хорда стягивающая дугу в 60 равна радиусу окружности

Хорда окружности

Перпендикулярные хорды

Вписанный угол опирающийся на диаметр прямой

Перпендикулярные хорды в окружности

Что такое хорда окружности в геометрии

Укажите центр радиус хорда и диаметр

Свойства дуги окружности

Хорда и касательная к окружности

Хорды MN И pk пересекаются

Построить окружность с центром в точке с и радиусом 2см

Две взаимно перпендикулярные хорды

Рисунок окружности с радиусом хордой и диаметром

Секущие и касательные к окружности формулы

Радиус сегмента круга формула

Хорда равна радиусу

Трисекция хорды

Углы в окружности опирающиеся на одну хорду

Части круга геометрия

Высота сегмента окружности

Окружность хорда радиус диаметр касательная

Поворот окружности геометрия

Круг радиусом 6 см

Расстояние от центра окружности до хорды

Хорда сечения шара

Касание окружностей внешним и внутренним образом

Профиль naca 23009

Стринг арт схемы

Tangente

Дуга в геометрии

Строение глаза рисунок

Цветы эскиз

Восточная хорда в Москве схема

Ракушка скетч

Одежда рисунок Эстетика

Пищеварительная система круглоротых схема

Юго-Восточная хорда в Москве схема

Северо-Восточная хорда подробная схема 2020

Северо Восточная хорда схема 2020

Растения одной линией

МКАД ТТК кольца

Парадокс Бертрана

Эскизы тату Минимализм

Головохордовые ланцетник

Диаметр 10 см . радиус 5си

1/4 Хорды

Хорда АВ равна 18 см

Сегмент окружности

Скетчбук для рисования одежды

Нежная круглая рамка

Temel Tasarym эскиз курушка

Хорда окружности формула

Линии в круге радиус диаметр

Схема внутреннего строения ланцетника

Две перпендикулярные хорды

Общая хорда двух пересекающихся окружностей

Хорда АВ

Хорда стягивает дугу

Усики хорды карандашом для детей

Окружность радиус хорда диаметр круг

Свойства касательной к окружности

Задачи на центральные и вписанные углы 8 класс

Хорда ab стягивает дугу равную 125

Юго-Восточная хорда в Москве

Хорда сферы

Эмблема круги Соединенные отрезками

Отрисовка эллипса

Диаметр окружности равен 60мм

Комментарии (0)

Написать

Информация
Посетители, находящиеся в группе Гости, не могут оставлять комментарии к данной публикации.

Объясните следующее i Окружность ii Радиус iii Центр iv Диаметр v Хорда vi Внутренняя часть круга…

Перейти к

• Круги Упражнение 14.1

• Зная свои числа
• Игра с числами
• Целые числа
• Действия над целыми числами
• Отрицательное число и целые числа
• Фракции
• Десятичные
• Введение в алгебру
• Соотношение, пропорция и унитарный метод
• Основные геометрические понятия
• Углы
• Треугольники
• Круги
• Пара прямых и поперечная
• Понимание трехмерных форм
• Симметрия
• Основные геометрические инструменты
• Геометрические построения
• Измерение
• Обработка данных Представление данных
• Обработка данных – II
• Гистограммы обработки данных

Главная > РД Шарма Решения Класс 6 Математика > Глава 13 — Круги > Круги Упражнение 14.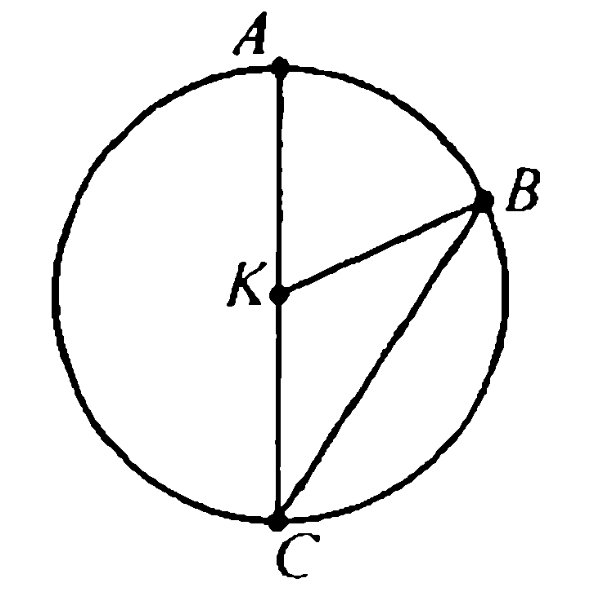 1 > Вопрос 1

Вопрос 1 Круги Упражнение 14.1

Объясните следующее:

(i) Окружность

(ii) Радиус

(iii) Центр

(iv) Диаметр

(v) Хорда

(vi) Внутренняя часть круга.

Ответ:

(i) Окружность – это набор всех тех точек на плоскости, расстояние до которых от фиксированной точки остается постоянным.

(ii) Радиус – Радиус окружности – это расстояние между всеми точками окружности и ее центром.

(iii) Центр – Центром окружности является фиксированная точка, находящаяся на постоянном расстоянии от всех точек.

(iv) Диаметр – Отрезок, проходящий через центр окружности и имеющий концы на окружности, называется называется диаметром окружности.

(v) Хорда – Отрезок, концы которого лежат на окружности, называется хордой окружности.

(vi) Внутренняя часть круга – Часть плоскости внутри круга, состоящая из всех точек, называется внутренней частью круга. круг.

Связанные вопросы

Возьмите точку в тетради и начертите окружности радиусами 4 см, 3 см и 6,5 см, каждая из которых имеет одинаковые цен. ..

Нарисуйте окружность с центром О и любым радиусом. Начертите AC и BD два перпендикулярных диаметра окружности…

Начертите окружность с центром О и радиусом 6 см. Отметьте точки P, Q, R такие, что (i) P лежит на окружности, (…

Возьмите две точки А и В на странице своей записной книжки. Нарисуйте окружность с центром А, которая проходит через…

Начертите полукруг с центром О и радиусом 5 см. Диаметр, определяющий полуокружность,…

Диаметр круга 14 см, найдите его радиус.

Фейсбук WhatsApp

Копировать ссылку

Было ли это полезно?

Упражнения

Круги Упражнение 14. 1

Главы

Знание ваших номеров

Игра с номерами

целые числа

Операции на целых числах

Отрицательные числа и целые числа

Фракции

Decimals

Введение в Algebra

. Основные геометрические понятия

Углы

Треугольники

Окружности

Пара прямых и поперечная

Понимание трехмерных фигур

Симметрия

Основные геометрические инструменты

Геометрические построения

Измерение

Обработка данных Представление данных

Обработка данных – II

Обработка данных Гистограммы

Курсы

Быстрые ссылки

Условия и политика

Условия и политика

2022 © Quality Tutorials Pvt Ltd Все права защищены

Касательные, хорды и дуги – Окружности и Пи – Матигон

Сбросить прогресс

Это приведет к удалению вашего прогресса и данных чата для всех глав этого курса, и это действие нельзя будет отменить!

Выберите одно из ключевых слов слева. ..

В предыдущих разделах вы узнали названия, данные нескольким различным частям круга, таким как центр, радиус, диаметр и окружность. Однако есть много геометрических элементов, связанных с окружностью, которые нам понадобятся для решения более сложных задач:

• Секущая — это линия, пересекающая окружность в двух точках.
• Хорда — это отрезок, концы которого лежат на окружности.
• Касательная — это линия, которая касается окружности ровно в одной точке. Это называется точкой касания .
• Дуга — это часть окружности окружности.
• Сектор — это часть внутренней части круга, ограниченная дугой и двумя радиусами .
• Наконец, сегмент — это часть внутренней части круга, ограниченная дуга и хорда .

В этом разделе мы рассмотрим отношения между всеми этими элементами и докажем теоремы об их свойствах.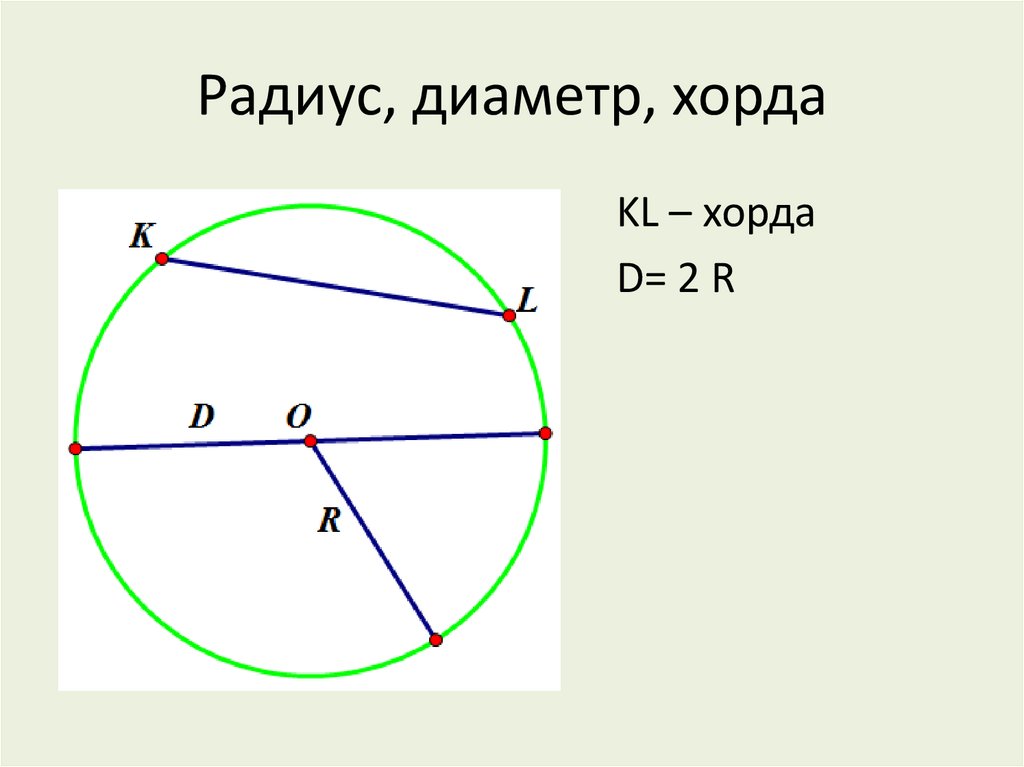 Пока не беспокойтесь о запоминании всех определений — вы всегда можете воспользоваться глоссарием.

Касательные

СКОРО!

Аккорды

СКОРО!

Дуги и секторы

Большинство ученых Древней Греции сходились во мнении, что Земля представляет собой шар. Доказательств было предостаточно: от кораблей, исчезающих за горизонтом в море, до кругового движения звезд в ночное время.

К сожалению, никто точно не знал, насколько велика Земля – примерно до 200 г. до н.э., когда математик Эратосфен нашел оригинальный способ измерить радиус Земли, используя базовую геометрию. Все, что нам нужно, это немного больше знаний об дугах и секторах окружности.

Как вы можете видеть на схеме, дуга является частью окружности, а сектор является частью окружности.

Дуга между двумя точками A и B часто записывается как AB⌒. Это определение немного двусмысленно: есть вторая дуга, соединяющая A и B , но идет наоборот по кругу.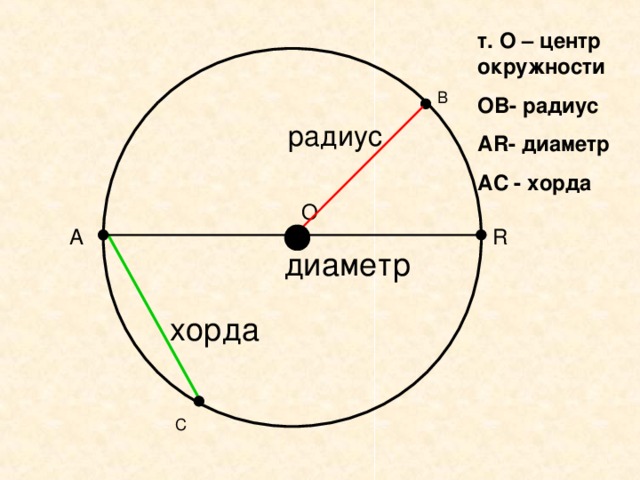

Меньшая из двух дуг называется малой дугой , а большая называется большой дугой . Если точки A и B находятся точно друг напротив друга, обе дуги имеют одинаковую длину и равны .

Чтобы найти длину дуги или площадь сектора, нам нужно знать соответствующий угол в центре круга: он называется центральным углом.

Обратите внимание, что дуга, сектор и угол составляют одну и ту же пропорцию полного круга. Например, если центральный угол равен , он занимает полный круг.

Это означает, что длина дуги также равна 14 полной длины окружности круга, а площадь сектора равна 14 полной площади окружности.

Мы можем выразить это соотношение в виде уравнения:

длина дугиокружность=площадь окружности=центральный угол

Теперь мы можем изменить эти уравнения, чтобы найти любую интересующую нас переменную. Например,

arc length	=	circumference×c360
	=	2πr×c360

sector area	=	circle area ×c360
	=	πr2×c360

, где r — радиус окружности, а r — центральный угол.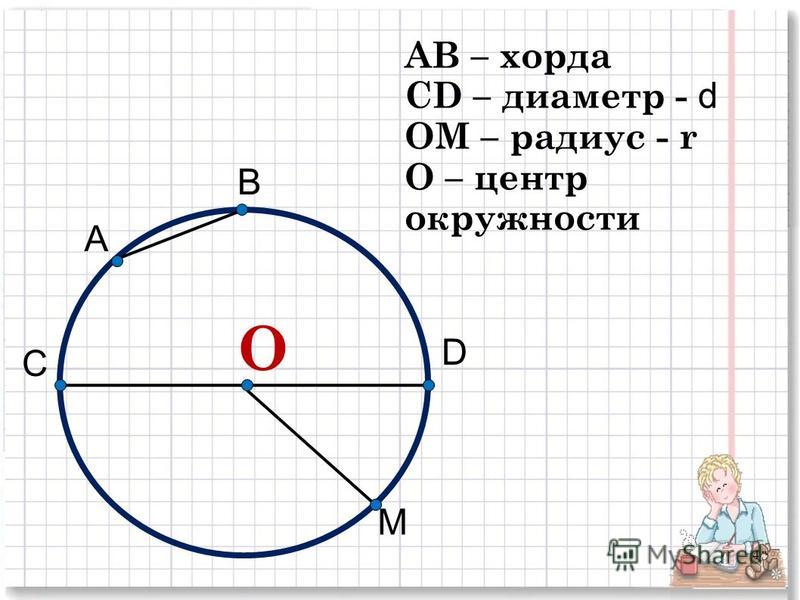

Если центральный угол измеряется в радианах, а не в градусах, мы можем использовать те же уравнения, но должны заменить 360° на: = r×c

sector area	=	πr2×c2π
	=	12r2c

Обратите внимание, как уравнения стали намного проще, и π везде сокращается. Это потому, что, как вы, возможно, помните, определение радианов — это длина дуги в окружности с радиусом 1.

Теперь давайте посмотрим, как мы можем использовать дуги и сектора для вычисления окружности Земли.

В Древнем Египте город Суенет располагался вдоль реки Нил. Свенет был известен колодцем с любопытным свойством: каждый год был один момент, когда солнечный свет достигал самого дна колодца — в полдень 21 июня, в день 9-го числа.0188 летнего солнцестояния . Именно в это время было освещено дно колодца, но не его стенки, а это означало, что Солнце стояло прямо над колодцем.

Древние египтяне измеряли большие расстояния, подсчитывая количество шагов, необходимых для ходьбы.

Некоторые источники говорят, что «Колодец Эратосфена» находился на острове Элефантина на реке Нил.

Математик Эратосфен жил в Александрии , примерно в 800 км к северу от Свенета, где он был директором Великой библиотеки. В центре города Александрии стоял обелиск, высокий узкий монумент с вершиной в форме пирамиды.

Эратосфен заметил, что в полдень в день летнего солнцестояния обелиск отбрасывал тень, а это означало, что солнце было , а не прямо над ним. Он пришел к выводу, что это произошло из-за кривизны Земли, и понял, что это можно использовать для расчета окружности нашей планеты.

Здесь вы можете увидеть колодец в Свенете, а также обелиск в Александрии. Солнечные лучи падают прямо в колодец, но падают на обелиск под углом и отбрасывают тень.

Эратосфен измерил, что угол тени составляет 7,2°. Это то же самое, что и центральный угол дуги от Александрии до Свенета, потому что это углы.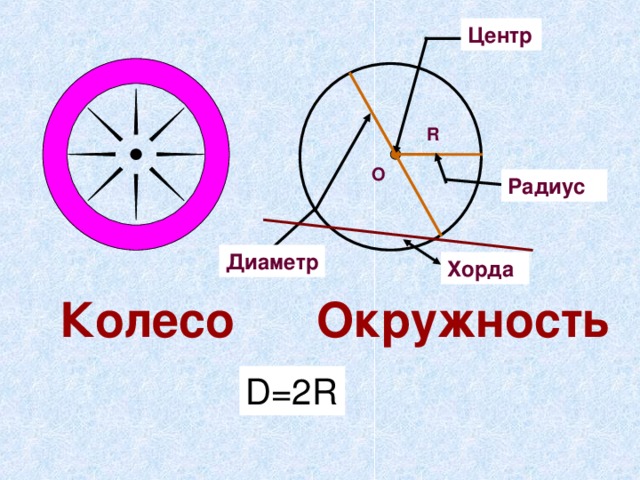

Теперь мы можем использовать уравнение для длины дуги, которое мы вывели выше:

длина дуги окружность=°360°

Если мы переставим это, мы обнаружим, что окружность Земли равна

окружность=360°7,2°×800 км=км

Наконец, мы знаем, что длина окружности равна C=2πr, поэтому радиус Земли равен

rEarth=40000км2π≈6400км.

Измерение Эратосфена было одним из важнейших экспериментов древности. Его оценка размера Земли была на удивление точной, особенно если учесть, что у него был доступ только к самым элементарным измерительным инструментам.

Конечно, его первоначальные результаты трудно перевести в современные единицы измерения, такие как километры. В Древней Греции расстояние измерялось в стадиях (примерно 160 м), но универсального эталона не существовало. В каждой области была своя версия, и мы не знаем, какую из них использовал Эратосфен.

В последующие века ученые пытались использовать другие методы для расчета радиуса Земли – иногда с очень разными и неверными результатами.