Игрек в квадрате равен икс в квадрате: x в квадрате y в квадрате

-1) и найдите его значение при x=1/3…

Какие цифры можно записать вместо * чтобы вычислении оказались верными…

При совместной работе двух контролёров они могут за 8 часов работы проверить 48 изготовленных аппаратов. Первый контролёр при той же производительности может выполнить одни всю эту работу за 12 часов. Сколько времени потребуется второму контролёру на всю эту работу, если он будет работать одни и с той же производительностью, как раньше….

В равенстве 2(1.5x-0.5) = 7х+*
Замените * таким выражением, чтобы получившееся уравнение:
1. Не имело корней
2. Имело бесконечно много корней
3. Имело один корень…

Реальная математика, огэ. ..

Математика

Литература

Алгебра

Русский язык

Геометрия

Английский язык

Химия

Физика

Биология

Другие предметы

История

Обществознание

Окружающий мир

География

Українська мова

Українська література

Қазақ тiлi

Беларуская мова

Информатика

Экономика

Музыка

Право

Французский язык

Немецкий язык

МХК

ОБЖ

Психология

формула, примеры, как решать, доказательство

Основные понятия

Квадратное уравнение — это ax² + bx + c = 0, где a — первый коэффициент, не равный нулю, b — второй коэффициент, c — свободный член.

Существует три вида квадратных уравнений:

• не имеют корней;
• имеют один корень;
• имеют два различных корня.

Чтобы определить, сколько корней имеет уравнение, нужно обратить внимание на дискриминант. Формула для его поиска записывается так: D = b² − 4ac. Его свойства:

• если D < 0, корней нет;
• если D = 0, есть один корень;
• если D > 0, есть два различных корня.

В случае, когда второй коэффициент четный, можно воспользоваться формулой нахождения дискриминанта , где .

В математике теоремой принято называть утверждение, у которого ранее было сформулировано доказательство.

Практикующий детский психолог Екатерина Мурашова

Бесплатный курс для современных мам и пап от Екатерины Мурашовой. Запишитесь и участвуйте в розыгрыше 8 уроков

Формула Виета

---

---

Если в школьной геометрии чаще всего используется теорема Пифагора, то в школьной алгебре ведущую роль занимают формулы Виета. Теорема звучит так: 

Теорема Виета Рассмотрим квадратное уравнение, в котором первый коэффициент равен 1: . Такие уравнения называют приведенными квадратными уравнениями. Сумма корней равна второму коэффициенту с противоположным знаком, а произведение корней равняется свободному члену.

Если дано x² + bx + c = 0, где x₁ и x₂ являются корнями, то справедливы два равенства:

Знак системы, который принято обозначать фигурной скобкой, означает, что значения x₁ и x₂ удовлетворяют обоим равенствам.

Рассмотрим теорему Виета на примере: x² + 4x + 3 = 0.

Пока неизвестно, какие корни имеет данное уравнение. Но в соответствии с теоремой можно записать, что сумма этих корней равна второму коэффициенту с противоположным знаком. Он равен четырем, значит будем использовать минус четыре:

Произведение корней по теореме соответствует свободному члену. В данном случае свободным членом является число три. Значит:

Необходимо проверить равна ли сумма корней −4, а произведение 3. Для этого найдем корни уравнения x² + 4x + 3 = 0. Воспользуемся формулами для чётного второго коэффициента:

Получилось, что корнями уравнения являются числа −1 и −3. Их сумма равняется второму коэффициенту с противоположным знаком, а значит решение верное.

Произведение корней −1 и −3 по теореме Виета должно равняться свободному члену, то есть числу 3. Это условие также выполняется:

Результат проделанных вычислений в том, что мы убедились в справедливости выражения:

Обучение на курсах по математике помогает быстрее разобраться в новых темах и подтянуть оценки в школе.

Доказательство теоремы Виета

Дано квадратное уравнение x² + bx + c = 0. Если его дискриминант больше нуля, то оно имеет два корня, сумма которых равна второму коэффициенту с противоположным знаком, а произведение корней равно свободному члену:

Докажем, что следующие равенства верны

• x₁ + x₂ = −b,
• x₁ * x₂ = c.

Формулы корней

Чтобы найти сумму корней x₁ и x₂ подставим вместо них то, что соответствует им из правой части формул корней. Напомним, что в данном квадратном уравнении x

2 + bx + c = 0 старший коэффициент равен единице. Значит после подстановки знаменатель будет равен 2.

1. Объединим числитель и знаменатель в правой части.

    

2. Раскроем скобки и приведем подобные члены:

    

3. Сократим дробь полученную дробь на 2, остается −b:

    

Мы доказали: x₁ + x₂ = −b.

Далее произведем аналогичные действия, чтобы доказать о равенстве x₁ * x₂ свободному члену c.

1. Подставим вместо x₁ и x₂ соответствующие части из формул корней квадратного уравнения:

    

2. Перемножаем числители и знаменатели между собой:

    

3. Очевидно, в числителе содержится произведение суммы и разности двух выражений.
   Поэтому воспользуемся тождеством (a + b) * (a − b) = a² − b². Получаем:

    

4. Далее произведем трансформации в числителе:

    

5. Нам известно, что D = b² − 4ac. Подставим это выражение вместо D.

    

6. Далее раскроем скобки и приведем подобные члены:

    

7. Сократим:

    

Мы доказали: x₁ * x₂ = c.

Значит сумма корней приведённого квадратного уравнения x² + bx + c = 0 равна второму коэффициенту с противоположным знаком (x₁ + x₂ = −b), а произведение корней равно свободному члену (x₁ * x₂= c). Теорема доказана.

Учёба без слёз (бесплатный гайд для родителей)

Пошаговый гайд от Екатерины Мурашовой о том, как перестать делать уроки за ребёнка и выстроить здоровые отношения с учёбой.

Обратная теорема Виета

Когда дана сумма и произведение корней квадратного уравнения, принято начинать подбор подходящих корней. Теорема, обратная теореме Виета, при таких условиях может быть главным помощником. Она формулируется так:

Обратная теорема Виета   Если числа x₁ и x₂ таковы, что их сумма равна второму коэффициенту уравнения x2 + bx + c = 0, взятому с противоположным знаком, а их произведение равно свободному члену, то эти числа являются корнями x2 + bx + c = 0.

Обратные теоремы зачастую сформулированы так, что их утверждением является заключение первой теоремы. Так, при доказательстве теоремы Виета стало понятно, что сумма x₁ и x₂ равна −b, а их произведение равно c. В обратной теореме это является утверждением.

Докажем теорему, обратную теореме Виета

Корни x₁ и x₂ обозначим как m и n. Тогда утверждение будет звучать следующим образом: если сумма чисел m и n равна второму коэффициенту x² + bx + c = 0, взятому с противоположным знаком, а произведение равно свободному члену, то числа m и n являются корнями x² + bx + c = 0.

Зафиксируем, что сумма m и n равна −b, а произведение равно c.

Чтобы доказать, что числа m и n являются корнями уравнения, нужно поочередно подставить буквы m и n вместо x, затем выполнить возможные тождественные преобразования. Если в результате преобразований левая часть станет равна нулю, то это будет означать, что числа m и n являются корнями x² + bx + c = 0.

1. Выразим b из равенства m + n = −b. Это можно сделать, умножив обе части на −1:

2. Подставим m в уравнение вместо x, выражение −m − n подставим вместо b, а выражение mn — вместо c:

При x = m получается верное равенство. Значит число m является искомым корнем.

3. Аналогично докажем, что число n является корнем уравнения. Подставим вместо x букву n, а вместо c подставим m * n, поскольку c = m * n.
   
   При x = n получается верное равенство. Значит число n является искомым корнем.

Мы доказали: числа m и n являются корнями уравнения x² + bx + c = 0.

Примеры

Для закрепления знаний рассмотрим примеры решения уравнений по теореме, обратной теореме Виета.

Дано: x² − 6x + 8 = 0.

Для начала запишем сумму и произведение корней уравнения. Сумма будет равна 6, так как второй коэффициент равен −6. А произведение корней равно 8.

Имея эти два равенства можно подобрать подходящие корни, которые будут удовлетворять как равенству обоим равенствам системы.

Подбор корней удобнее выполнять с помощью их произведения. Число 8 можно получить путем перемножения чисел 4 и 2 либо 1 и 8. Но значения x₁ и x₂ надо подбирать так, чтобы они удовлетворяли и второму равенству тоже.

Можно сделать вывод, что значения 1 и 8 не подходят, так как они не удовлетворяют равенству x₁ + x₂ = 6. Значения 4 и 2 подходят обоим равенствам:

Значит числа 4 и 2 являются корнями уравнения x² − 6x + 8 = 0.

Неприведенное квадратное уравнение 

Теорема Виета выполняется только тогда, когда квадратное уравнение является приведённым, то есть его первый коэффициент равен единице:

ax² + bx + c = 0, где а = 1.

Если квадратное уравнение не является приведенным, но задание связано с применением теоремы, нужно обе части разделить на коэффициент, который располагается перед x².

1. Получилось следующее приведенное уравнение:

2. Получается, второй коэффициент при x равен , свободный член — . Значит сумма и произведение корней будут иметь вид:

3. Рассмотрим пример неприведенного уравнения: 4x² + 5x + 1 = 0. Разделим обе его части на коэффициент перед x², то есть на 4.

4. Получилось приведённое квадратное уравнение. Второй коэффициент которого равен , а свободный член .
5. Тогда в соответствии с теоремой Виета получаем:

6. Метод подбора помогает найти корни: −1 и 

 

---

---

Умный в гору не пойдет / Хабр

Доброго дня, хабровчане!

Поделюсь с Вами одним численным алгоритмом вычислительной математики для построения оптимального пути движения на сложной поверхности. Под оптимальностью понимается построение такого маршрута, который проходит по карте местности, огибая все локальные экстремумы (возвышенности и впадины), обеспечивая таким образом некоторую степень минимизации перепада высот и длину всего маршрута.

Входная поверхность задана множеством точек (облаком точек) в трехмерном евклидовом пространстве и имитирует собой ландшафт со всеми его неровностями: возвышенности, холмы, горы, овраги, впадины, разломы и т. д. В качестве начального условия выбирается любая точка на поверхности.

Задачу можно рассматривать как продолжение уже имеющегося маршрута. Куда в конце концов упрется наш искомый путь нам неважно, — главное начать, а там как пойдет, чтобы он обогнул неровности. Алгоритм также не гарантирует прохождения маршрута через какие-либо заранее заданные точки из входного множества точек. Гладкость входной поверхности сильно влияет на гладкость и адекватность получаемого решения.

Алгоритм имеет эвристическую природу, поэтому в данной статье не приводятся строгие математические доказательства существования и единственности найденного решения.

Постановка задачи

В декартовой прямоугольной системе координат на плоскости задана равномерная сетка:

где — узлы сетки; — шаги сеток по осии, соответственно. В каждом узле сетки задано значение , представляющее собой высоту карты (ландшафта) местности в рассматриваемой точке. Значения , образующие исследуемую поверхность, могут быть отрицательными — в таком случае высоту карты следует понимать как глубину относительно некоторой нулевой отметки .

В качестве начального условия задана точка , которая может представлять собой крайнюю точку уже известного маршрута. Его необходимо продолжить далее через всю карту к плоскости , рисунок 1.

Рисунок 1. Пример ландшафта местности — исследуемая поверхность, заданная множеством точек. Синим цветом отмечена часть известного маршрута. Красная точка — начальное условие, точка из которой необходимо продолжить маршрут.

Численный алгоритм

Рассмотрим три ближайшие к соседние точки поверхности — , находящиеся на соседнем слое по оси . Одна из этих точек лежит на том же слое по оси , что и , а остальные лежат по диагонали к точке , рисунок 2.

Рисунок 2. Соседние точки по оси Ox для начального условия.

Вычислительный алгоритм построения оптимального маршрута является итерационным. На каждой итерации из трех соседних точек необходимо найти такую, сумма квадрата расстояния и квадрата тангенса угла наклона к которой является минимальной.

Для упрощения выкладок введем следующие обозначения:

— расстояние от точки до точки ;

— тангенс угла, одна сторона которого — это отрезок, соединяющий и, а другая сторона — отрезок, соединяющий и основание перпендикуляра, опущенного из точки на плоскость перпендикулярную оси и проходящую через точку (углы , рисунок 3).

Рисунок 3. Схематический чертеж исследуемого множества точек. Начало искомого пути z, который необходимо продолжить и три соседние точки поверхности — P_1, P_2, P_3, из которых нужно будет вы- брать одну, удовлетворяющую условию минимизации. Точки B_k — это основания перпендикуляров, опущенных из точек P_k

Таким образом, в данных обозначениях смысл вышеописанного алгоритма в следующем: используя начальное условие — последнюю точку известного маршрута,, нам необходимо найти такую точку , чтобы выполнялось условие минимизации:

После нахождения данной точки необходимо принять ее в качестве начального условия для следующей итерации. В результате на каждой итерации мы будем получать новые точки искомого оптимального пути.

Смысл слагаемых в (1) следующий: первое слагаемое отвечает за выбор точки с наименьшим расстоянием до предыдущей, и, как следствие, для минимизации суммарной длины полученного маршрута; второе слагаемое в виде квадрата тангенса необходимо для минимизации перепада высот. Таким образом, вышеописанный алгоритм будет прокладывать маршрут, стараясь обходить все локальные экстремумы, что мы и увидим в
экспериментах. Вместо тангенса можно было бы с тем же успехом использовать синус, что никак не повлияет на результат работы алгоритма.

В процессе расчетов может оказаться, что точкабудет находиться на крайнем слое по оси (или ) — в таком случае необходимо рассматривать не три соседние точки , а две — одна из которых лежит «по прямой», а другая «по диагонали» к точке, при этом алгоритм построения оптимального маршрута никак не изменится.

Сложность алгоритма составляет и зависит от «длины» карты, на которой необходимо проложить искомый маршрут. На каждой итерации необходимо проверять по 2-3 точки и находить минимальное значение (1).

Реализация алгоритма

Исходники находятся здесь

Определим свой класс для точки в пространстве:

class Point3D:
    def __init__(self, N, M, z, PositionalParameter):
        self.N = N
        self. M = M
        self.z = z
        self.PositionalParameter = PositionalParameter

Для удобства вместо и я использовал и , соответственно. PositionalParameter будет равен единице для точек и нулю для точки дабы немного упростить вычисления квадратов, упомянутых в формуле (1).

Определим функцию для подсчета квадрата расстояния:

def GetSquareOfDistance(point, testedPoint, dy):
    """Возвращает относительный квадрат расстояния до проверяемой точки"""
    return math.pow(point.z - testedPoint.z, 2.0) + testedPoint.PositionalParameter * dy * dy

point — это точка , testedPoint — точка , — шаг по оси .

На самом деле здесь не совсем квадрат расстояния, а немного упрощенное значение, которое не учитывает шаг , т.к. для поиска минимального значения в (1) его можно выкинуть (предоставлю читателю возможность это проверить).

А также функцию для подсчета квадрата тангенса:

def GetTangentSquare(point, testedPoint, dx, dy):
    """Возвращает квадрат тангенса угла между точками"""
    return math. pow(point.z - testedPoint.z, 2.0) / (dx * dx + testedPoint.PositionalParameter * dy * dy)

В отдельном файле были определены функции для формирования поверхностей как функции двух переменных:

import math
# Возвращает сумму квадрата синуса первого аргумента и квадрата косинуса второго аргумента
# x - первый аргумент
# y - второй аргумент
def SinSquarePlusCosSquare(x, y):
    return math.sin(x) * math.sin(x) + math.cos(y) * math.cos(y)
# Функция Гаусса (двумерная гауссиана). 
# Описание параметров (раздел "Многомерные обобщения"): https://ru.wikipedia.org/wiki/%D0%93%D0%B0%D1%83%D1%81%D1%81%D0%BE%D0%B2%D0%B0_%D1%84%D1%83%D0%BD%D0%BA%D1%86%D0%B8%D1%8F
# x, y              - точка плоскости, в которой необходимо вычислить Гауссиан
# A                 - высота колокола
# sigmaX, sigmaY    - размах колокола по оси Ox и Oy, соответственно
# x0                - сдвиг пика по оси Ox
# y0                - сдвиг пика по оси Oy
def Gaussian(x, y, A, sigmaX, sigmaY, x0, y0):
    xx = (x - x0) * (x - x0) / (2. 0 * math.pow(sigmaX, 2.0))
    yy = (y - y0) * (y - y0) / (2.0 * math.pow(sigmaY, 2.0))
    return A * math.exp(-(xx + yy))

Гауссиан отлично подходит для имитации отдельно стоящей горы. А с помощью композиции можно создавать горные цепи разной длины и сложности. SinSquarePlusCosSquare создает, как Вы уже догадались, подобие холмистого рельефа.

В конце расчета маршрут записывается в файл как массив трехмерных точек.

Результаты численного решения

На следующих рисунках показаны результаты численных экспериментов нахождения оптимальных маршрутов. Для имитации ландшафта местности использовались различные аналитические поверхности. Все размерности даны в условных единицах, шаг сеток во всех расчетах по обеим осям был взят равным

В качестве имитации горы использовалась функция Гаусса.А это вид сверху

Холмистый рельеф. Имитация с помощью функции

Имитация холмистого ландшафта. Хорошо видно как маршрут (белая линия) обходит локальные экстремумы.

а это вид сверху:

Вид сверху

Вот еще один интересный вариант ландшафта. Наложение нескольких функций Гаусса и поверхности заданной формулой :

Горы и впадиныВид сверху

Спасибо за прочтение!

Все доработки и усовершенствования оставляю Вам.

учим разгадывать шифровки из букв, картинок и цифр

Математика и логика для детей / Ребусы

Рассказываем по порядку правила составления и решения ребусов. Перед вами задания с пояснениями и подсказками, чтобы отработать алгоритм поиска ответа. С ЛогикЛайк вы научитесь решать любые ребусы и другие задания на логику. У нас есть всё, что вы искали!

Попробуйте наш курс развития логики!

Выберите возраст ученика для старта

4-6 лет

1 класс

2 класс

3 класс

4-5 класс

старше

На платформе LogicLike. com 3500 логических заданий с ответами: ребусы, задачи, вопросы и головоломки.

Что такое ребус?

Ребус – это занимательная головоломка, шифровка одного или нескольких слов с помощью иллюстраций, букв, цифр и символов. Разгадать ребус – значит расшифровать слово, словосочетание или целую фразу, задуманную автором.

Юный почемучка требует объяснить «Зачем вообще решать ребусы?!» Шпаргалка о пользе – вам в помощь.

Польза ребусов для детей и взрослых

• развивается логика: чтобы правильно «считать» картинку, нужно порассуждать над взаимным расположением элементов головоломки, подобрать верные правила;
• развивается память: если в ребусе зашифровано длинное слово, нужно запоминать разгаданные части слова или фразы, а также ошибочные предположения;
• развивается нестандартное мышление: картинку-шифровку можно интерпретировать по-разному, а решение ребусов на скорость может превратиться в увлекательную игру;
• регулярные тренировки развивают сообразительность и скорость мышления;
• увеличивается словарный запас.

ЛогикЛайк – полный комплекс для развития детей 4-12 лет

Логика

Память и внимание

Окружающий мир

Загадки

Математика

Шахматы

Технологии

Начать занятия

Как научиться разгадывать ребусы?

Шаг за шагом мы познакомим вас с примерами занимательных головоломок разного уровня сложности. Часть заданий мы приводим с ответами и описанием решения.

Одолеете весь материал от и до – сможете решать подобные ребусы на раз-два.

Базовые правила чтения ребусов

• Ребусы читаются слева направо, в отдельных случаях – сверху вниз. Могут быть исключения, о которых составители задания могут сообщить текстом или стрелками.
• Знаки препинания и пробелы не учитываются. Это правило актуально для больших и сложных ребусов, в которых зашифровано длинное слово или целая фраза.
• Любая картинка или символ в шифровке имеют значение. Ни одна запятая или изображение не даётся в ребусе просто так. Картинка и символ могут обозначать слово целиком либо часть слова в зависимости от других условий ребуса.
• Все слова в ребусе читаются в именительном падеже, а вот с единственным и множественным числом нужно быть внимательным. Если на картинке изображена пара ног, глаз или несколько фруктов, автор ребуса наверняка хочет, чтобы вы прочитали слово во множественном числе.

• Одна из самых сложных задач в ребусе – понять, «что хотел сказать автор?». Иными словами, правильно интерпретировать картинку. На рисунке вы можете «видеть» собаку, но автор мог загадать слово «пёс» или вообще «Хатико». Мальчик со светлыми волосами может быть словом «мальчик» или словом «блондин».
• Решение у ребуса всегда одно! А если несколько, об этом вас должен предупредить автор.
• Взялись за решение большого сложного ребуса? Будьте готовы, что в нём зашифровано предложение, в котором будут не только существительные, но и другие части речи.

Запятые в ребусах

Среди самых простых ребусов, которые можно предложить дошкольникам или младшим школьникам – ребусы, в которых рядом с картинкой стоит одна или несколько запятых. Запятые показывают, что у слова, которое изображает картинка, нужно убрать букву. Иногда запятые рисуют перевернутыми, но это значения не имеет.

Рассмотрим суть правила на примере двух ребусов ниже. Количество запятых равно количеству букв, которые нужно убрать.

Запятые слева – убираем 3 буквы в начале слова.

Узнать ответ

Ответ:

лампочка — почка.

2 запятые до картинки — убираем 2 буквы в начале слова, 1 запятая после картинки – убираем последнюю букву в слове.

Узнать ответ

Ответ:

облако — лак.

Расскажите ребёнку, что нужно быть внимательным, мыслить нестандартно и всегда придумывать несколько вариантов решения.

Выберите возраст ребёнка,

чтобы начать занятия

5-8 лет

9-14 лет

Учимся решать ребусы с буквами

Буквы в ребусах дополняют картинки и помогают создавать более сложные головоломки. Если одна или несколько букв стоят слева или справа от картинки, значит их нужно добавить к слову в начале или в конце.

Видим на рисунке РОТ, прибавляем к началу слова букву К и получаем слово КРОТ.

Буквы в ребусах могут сочетаться с другими символами и знаками.

В этом ребусе сочетается рисунок, запятые и буквы. Читать его нужно так: от слова ЗОНТ отнимаем две буквы в конце (две запятые справа) и получаем слог ЗО.

Узнать ответ

Ответ:

УЗОР.

Решение

Перед «ЗО» прибавляем букву «У», после – «Р». Получаем слово УЗОР.

Знак «=» между двумя буквами означает, что букву из слова на картинке нужно заменить на ту, которая стоит после «=».

В слове «ЦАПЛЯ» букву «Ц» меняем на «К».

Узнать ответ

Ответ:

Капля.

Вместо буквы первой в равенстве может стоять цифра. Тогда необходимо посчитать, какая по счёту буква соответствует цифре, и заменить её на ту, которая стоит после «=».

Третья по счёту буква в слове УХО – О.

Узнать ответ

Ответ:

Муха.

Решение

По условиям ребуса меняем букву «О» на «А», и к слову «УХА» прибавляем букву «М».

Если буква рядом с картинкой зачеркнута, её нужно убрать из слова.

У слова «СЛОН» забираем букву «Л» и получаем слово «СОН».

Выберите возраст ребёнка, чтобы начать занятия

4-5 лет

9-14 лет

Более 2 000 000 детей развивают логику, память, внимание и кругозор на сайте и в приложении.

Буквенные ребусы (без картинок)

Зашифровать слово для ребуса можно без рисунков и символов, а только с помощью букв. В этом случае обращаем внимание на то, как буквы или слоги расположены относительно друг друга, и выбираем подходящий предлог.

• Если одна буква, слог или слово стоит над другим, читать их надо с предлогами «над» или «под».
• Когда одна буква расположилась за другой, выбираем между предлогами «за» или «перед».
• В одну букву может быть вписана другая или несколько. В этом случае используем предлог «в».

Слог «ГА» расположен «ПОД» слогом «РУ».

Узнать ответ

Ответ:

Подруга.

За буквой «К» стоит слог «НИ». Но в этом ребусе предлог «за» нам не подходит, значит пробуем «перед».

Узнать ответ

Ответ:

Передник.

В большую букву «А» вписан слог «ТА».

Узнать ответ

Ответ:

Вата.

Рисунки в ребусах

Если обыкновенная картинка в ребусе обозначает слово, то перевёрнутая требует прочитать то же слово справа налево. Может сочетаться с буквами, цифрами и различными символами.

В этом ребусе слово «ЗУБР» читаем наоборот и получаем «РБУЗ».

Узнать ответ

Ответ:

Арбуз.

Стрелка рядом с рисунком указывает налево? Автор ребуса требует прочесть слово в обратном направлении.

Вместо «КИТ» читаем «ТИК».

Узнать ответ

Ответ:

Бантик.

Решение

«БАН» + «ТИК» = «БАНТИК».

Решаем ребусы с цифрами

Самый простой вариант использования цифр в ребусах — для замены части слова.

Узнать ответ

Ответ:

Сорока.

Если цифра рядом с рисунком зачеркнута, нужно убрать её из слова.

Слово «ТОРТ» читаем наоборот и отнимаем у получившегося слова «ТРОТ» первую букву «Т».

Узнать ответ

Ответ:

Рот.

В ребусе над рисунком может располагаться ряд чисел. Если чисел ровно столько, сколько и букв в слове, просто меняем буквы местами, как указывает числовой ряд.

В слове «КАБАН» 5 букв и столько же букв изображено над рисунком. Просто выстраиваем буквы в порядке, указанном в числовом ряду, и получаем новое слово.

Узнать ответ

Ответ:

БАНКА.

Если цифр над или под рисунком меньше, чем букв в слове, значит для разгадки используем только те, что соответствуют цифрам в числовом ряду.

Легко заметить, что цифр в загадке меньше, чем букв в слове «КРОКОДИЛ» или «АЛЛИГАТОР». Осталось выбрать верное слово и буквы из него.

Узнать ответ

Ответ:

Кролик.

Решение

Из букв слова «КРОКОДИЛ» мы собрали новое слово – КРОЛИК.

Задания на логику – отличный вариант совместных занятий с детьми. Ищите ключи к тайным шифрам в картинках, устраивайте соревнования на скорость между командами друзей. Разгадывайте интеллектуальные загадки и развивайте логику и мышление вместе с ЛогикЛайк.

Развиваем мышление и кругозор

Более 2 000 000 детей и родителей со всего мира уже занимаются на сайте ЛогикЛайк.

Начать занятия! Начать занятия!

Система Икс плюс ✅ игрек равно 6 икс квадрат минус игрек квадрат равно 12

dsanavskiy77

скорость реки-х км/ч

по течению реки-(х+2)км/ч

против течении-(х-2)км/ч

по условию

30/(х+2)+13/(х-2)=1,5

30(х-2)+13(х+2)=1,5(х-2)(х+2)

1,5x^2-43x+28=0

d=1681

x1=28

x2=2/3

ответ: 28км/ч

romabogomolov1

ну у синуса знаки в четвертях

++

—

а у косинуса

-+

-+

значит син

а=6п/5 — ето 216*, знак —

а=-п/6 — ет -30*, знак —

а=5п\6 — ет 150*, знак +

а=п/10 — ет 18*, знак +

кос

а=6п/5 — ето 216*, знак —

а=-п/6 — ет -30*, знак +

а=5п\6 — ет 150*, знак —

а=п/10 — ет 18*, знак +

SuperArtem52

x + y = 6

x² — y² = 12

(x — y)(x + y) = 12

6(x — y) = 12

x — y = 2

2x = 8

x = 4

y = 2

ответ (4, 2)

Karamelka3467

Решение системы уравнений  х=4

                                                      у=2

Объяснение:

х+у=6

х²-у²=12

Выразим х через у в первом уравнении, подставим выражение во второе уравнение и вычислим у:

х=6-у

(6-у)²-у²=12

36-12у+у²-у²=12

-12у=12-36

-12у= -24

у=2

х=6-у

х=6-2

х=4

Решение системы уравнений  х=4

                                                      у=2

Найдено 3 ответ(ов)

Показать ответы

Знаешь ответ?

Похожие вопросы:

Алгебра, 26. 2 — 4x — 5 = 0. так как a> 0, то ветви этой параболы направлены вверх, вершина вниз. тогда можно найти ко…

ответов: 2

Алгебра, 28.02.2019, маша9393

Разложить на множители: 1) 2) 3) 4) 5) 6)…

количество красных шариков относиться к белым, как 5/9, то есть белых 4/9.16 относится 4/9, х=4 5*4=20 красных шариков  …Подробнее

количество красных шариков относиться к белым, как 5/9, то есть белых 4/9.16 относится 4/9, х=4 5*4=20 красных шариков  …

ответов: 4

Алгебра, 28.02.2019, Dianochka2346587

Постройте график функции заданой формулой f(x)=4.5x f(x)=-…

3ч20мин переводим в часы, 3ч20мин=10/3ч, скорость лодки по течению реки равно 30: 10/3=9км/ч, а скорость против течения реки 28: 4=7км/ч, скорость течения реки равно (9-7): 2=1км/ч…Подробнее

3ч20мин переводим в часы, 3ч20мин=10/3ч, скорость лодки по течению реки равно 30: 10/3=9км/ч, а скорость против течения реки 28: 4=7км/ч, скорость течения реки равно (9-7): 2=1км/ч. ..

ответов: 2

Алгебра, 28.02.2019, денил55

.(При каких значения x функция y=f(x) обращается в нуль, принимает положительнны…

2. -2х=65/19-29/19 -2х=40/19 х=40/19разделиь на -2/1 х=-1целая1/19…Подробнее

2. -2х=65/19-29/19 -2х=40/19 х=40/19разделиь на -2/1 х=-1целая1/19…

ответов: 2

Алгебра, 28.02.2019, паша535

.(Втрех цехах работает 310 человек. в первом цехе рабочих в 1.5 раза больше чем…

х- надо взять 1 сплава, у — 2-го 0,2х+0,45у=0,3х+0,3у  0,45у-0,3у=0,3х-0,2х  1,5у=0,1х 0,1х/0,15у=1х: 1,5у=2х/3у  ответ 2: 3, т.е нужно взять три части с 20% соде…Подробнее

х- надо взять 1 сплава, у — 2-го 0,2х+0,45у=0,3х+0,3у  0,45у-0,3у=0,3х-0,2х  1,5у=0,1х 0,1х/0,15у=1х: 1,5у=2х/3у  ответ 2: 3, т.е нужно взять три части с 20% соде…

ответов: 3

Алгебра, 28.02.2019, elisavetafolst

. 2=24 т.к. числа в квадрате для начала мы не обращяем внимания на знаки сразу же откидываем числа 9 так как 81 уже перебор, затем 8, 6 их квадрат 64 и 36 второй…

ответов: 4

Алгебра, 01.03.2019, ОлесяБычкова

Во время распродажи новая цена холодильника состовляет 0.85% от старой цены. на…

решаем 4 уравнения 1) 3=(5х-10)/3, 9=5х-10,5х=19, х=19/5=3,8 2)10=(5х-10)/3, 5х-10=30, 5х=40, х=8 3)2/3=(5х-10), 2=15х-30,15х=32, х=15/32 4)0=(5x-10)/3, 5x-10=0, 5x=10, x=2…Подробнее

решаем 4 уравнения 1) 3=(5х-10)/3, 9=5х-10,5х=19, х=19/5=3,8 2)10=(5х-10)/3, 5х-10=30, 5х=40, х=8 3)2/3=(5х-10), 2=15х-30,15х=32, х=15/32 4)0=(5x-10)/3, 5x-10=0, 5x=10, x=2…

ответов: 2

Алгебра, 01.03.2019, shovkoplyas123456

Из двух пунктов , расстояние между которыми 18 км , одновременно навстречу друг…

обозначим длину за x, а ширину за y, тогда: периметр: 2x+2y = 70 площадь первоначального прямоугольника: s = xy площадь прямоугольника после изменения длин его сторон: (x-5)(y+. ..Подробнее

обозначим длину за x, а ширину за y, тогда: периметр: 2x+2y = 70 площадь первоначального прямоугольника: s = xy площадь прямоугольника после изменения длин его сторон: (x-5)(y+…

ответов: 2

Алгебра, 02.03.2019, markkolk77R

Дві точки рівномірно обертаються по двох колах. перша з них повний оберт на 5 се…

2а-аб=-б2 а(2-б)=-б2 а=-б2/(2-б)…Подробнее

2а-аб=-б2 а(2-б)=-б2 а=-б2/(2-б)…

ответов: 4

3-8 9 Оценить квадратный корень из 12 10 Оценить квадратный корень из 20 11 Оценить квадратный корень из 50 94 18 Оценить квадратный корень из 45 19 Оценить квадратный корень из 32 20 Оценить квадратный корень из 18 92

Видео-урок: Линейно-квадратичные системы уравнений

Стенограмма видео

В этом видео мы научимся решать линейно-квадратичные системы уравнений. Начнем с обсуждения того, что линейно-квадратичная система уравнений на самом деле такова. Это не так страшно, как кажется. Это система двух уравнений в одно из которых является линейным уравнением, а другое квадратным.

Помните, что линейное уравнение — это одно в котором наивысшая степень каждой появляющейся переменной равна единице и ни одной из переменные перемножаются. Например, уравнение 𝑦 равно два 𝑥 — линейное уравнение. И если бы вы нарисовали его график, это будет представлено прямой линией. Квадратное уравнение, однако, тот, в котором будет по крайней мере один квадрат члена. Например, уравнение 𝑥 квадрат плюс 𝑦 в квадрате равно пяти — это квадратное уравнение. Мы также можем видеть уравнения, которые включают термины, когда две переменные перемножаются, например, уравнение 𝑥 плюс два 𝑥𝑦 равно трем.

Если бы вам нужно было построить график квадратное уравнение, оно дает какую-то кривую. В случае 𝑥 в квадрате плюс 𝑦 квадрат равен пяти, это круг. С графической точки зрения, решение линейно-квадратичной системы уравнений эквивалентно нахождению координаты любых точек пересечения двух графиков.

Теперь мы будем в основном использовать метод решения одновременных уравнений подстановкой. Поэтому вы должны убедиться, что вы уже знакомы и удобны с этим методом. Вам также должно быть удобно решение квадратных уравнений с одной переменной методом факторизации. Мы рассмотрим некоторые приложения эти методы к сформулированным проблемам и проблемам, включающим точки пересечения прямые линии и кривые. Давайте рассмотрим наш первый пример тогда.

Решить одновременную уравнения 𝑦 равно 𝑥 минус два, 𝑥 минус два в квадрате плюс 𝑦 минус три квадрат равен девяти.

Первое, на что следует обратить внимание, это что это линейно-квадратичная система уравнений. Первое уравнение 𝑦 равно 𝑥 минус два — это линейное уравнение, как наивысшая степень 𝑥 и 𝑦, которая появляется является одним. И второе уравнение 𝑥 минус два в квадрате плюс 𝑦 минус три в квадрате равно девять — это квадратное число. уравнение, потому что как только мы распределим скобки, у нас будут оба 𝑥 в квадрате и 𝑦 в квадрате.

Мы собираемся использовать метод замены для решения этой задачи. Теперь наше первое уравнение 𝑦 равно 𝑥 минус два. И мы замечаем, что выражение 𝑥 минус два появляется во втором уравнении. Итак, что мы можем сделать, это заменить 𝑥 минус два с 𝑦 во втором уравнении. Это дает 𝑦 в квадрате плюс 𝑦 минус три в квадрате равно девять. Итак, у нас есть уравнение в 𝑦 только. Это квадратное уравнение, которое мы можем решить.

Начнем с распределения скобки в 𝑦 минус три в квадрате. А мы помним, что 𝑦 минус три в квадрате означает 𝑦 минус три, умноженное на 𝑦 минус три. Итак, когда мы распределяем скобки, у нас есть четыре термина. И эти четыре термина затем упростить до 𝑦 в квадрате минус шесть 𝑦 плюс девять. Собирая похожие термины на в левой части у нас есть квадратное уравнение два 𝑦 в квадрате минус шесть 𝑦 плюс девять равно девяти.

Теперь мы замечаем, что, поскольку у нас есть Положительные девять с каждой стороны, эти два члена будут прямо сокращать друг друга out, что эквивалентно вычитанию девяти из каждой части уравнения. Это оставляет нас с упрощенное уравнение два 𝑦 в квадрате минус шесть 𝑦 равно нулю, которое мы можем решить по факторингу. Наибольший общий делитель два 𝑦 в квадрате и минус шесть 𝑦 равно двум 𝑦. А чтобы сделать два 𝑦 в квадрате, мы нужно умножить два 𝑦 на 𝑦. А чтобы сделать минус шесть 𝑦, мы нужно умножить два 𝑦 на минус три. Так что наш квадратичный в его факторизованная форма равна двум 𝑦, умноженным на 𝑦 минус три, равно нулю.

Для решения берем каждый множитель в свою очередь, установить его равным нулю, а затем решить полученное линейное уравнение. Первое уравнение равно двум 𝑦 равно нулю, что мы можем решить, разделив каждую сторону на два, чтобы найти, что 𝑦 равно равен нулю. Второе уравнение 𝑦 минус три равно нулю. Решаем, добавляя три к каждая сторона, дающая 𝑦, равна трем. Таким образом, мы обнаруживаем, что наше решение эти одновременные уравнения включают два 𝑦-значения, 𝑦 равно нулю и 𝑦 равняется трем.

Теперь нам нужно найти соответствующие 𝑥-значения. И для этого подставляем каждое 𝑦-значение в линейное уравнение. Это должно быть линейное уравнение в который мы подставляем, потому что возможно, что на квадратичной кривой существует более одной точки, где 𝑦 равно нулю или 𝑦 равно трем. Но на линейном графике прямая, будет только одна точка, где 𝑦 равно нулю и одна точка где 𝑦 равно трем. Таким образом, мы должны заменить в линейное уравнение.

Когда 𝑦 равно нулю, мы имеем ноль равен 𝑥 минус два. И прибавив по два с каждой стороны, мы найдите, что 𝑥 равно двум. Когда 𝑦 равно трем, мы имеем что три равно 𝑥 минус два. И прибавив по два с каждой стороны, мы найти, что 𝑥 равно пяти. Таким образом, решение этой пары одновременных уравнений — это две пары 𝑥𝑦-значений. 𝑥 равно двум и 𝑦 равно ноль и 𝑥 равно пяти и 𝑦 равно трем.

Важно понимать что эти решения идут парами. И мы не можем смешивать и сочетать 𝑥- и 𝑦-значения. Например, 𝑥 равно двум и 𝑦 равно трем, не является допустимым решением этой пары одновременных уравнений, что вы можете подтвердить, подставив значения в линейное уравнение или, действительно, квадратичный.

Помните, мы использовали метод замена, чтобы ответить на этот вопрос, заменив 𝑥 минус два на 𝑦. Также было бы можно заменить 𝑦 во втором наборе скобок на 𝑥 минус два на дайте уравнение только в 𝑥. В этом случае мы бы нашли наши решения для 𝑥 сначала, а затем подставить его обратно в линейное уравнение чтобы найти наши решения для 𝑦. Наш окончательный ответ таков: 𝑥 равно двум и 𝑦 равно нулю или 𝑥 равно пяти и 𝑦 равно трем.

В следующем примере мы увидим, как мы можем применить эти методы к сформулированной задаче.

Сумма двух чисел равна 11 а сумма их квадратов равна 65. Что это за числа?

Важно отметить что мы не должны отвечать на этот вопрос методом проб и ошибок. Нам нужно использовать формальный подход. Мы собираемся использовать немного алгебры чтобы ответить на проблему. Итак, мы позволим двум числам быть обозначается буквами 𝑥 и 𝑦. Сейчас мы собираемся выразить информация в вопросе в виде уравнений с участием 𝑥 и 𝑦. Во-первых, сумма двух число равно 11. Это дает нам уравнение 𝑥 плюс 𝑦 равно 11,

Во-вторых, нам сказали, что сумма их квадратов равна 65. Это дает нам уравнение 𝑥 в квадрате плюс 𝑦 в квадрате равно 65. Теперь у нас есть линейно-квадратичное система уравнений. Первое уравнение линейное, а второй квадратичный. Мы собираемся использовать метод подстановки для решения этих двух уравнений одновременно. Начнем с перестановки линейное уравнение, чтобы дать одну переменную через другую. А в этой задаче нет не имеет значения, какую переменную мы выбираем, потому что проблема в равной степени сложным или одинаково простым по обеим переменным. Я решил переписать уравнение один как 𝑦 равно 11 минус 𝑥.

Теперь возьмем это выражение для 𝑦 через 𝑥 и подставить во второе уравнение, то есть в Квадратное уравнение. Давая 𝑥 в квадрате плюс 11 минус 𝑥 все в квадрате равно 65. Теперь у нас есть квадратное уравнение только с одной переменной 𝑥. Мы можем распространять осторожно заключайте скобки, помня, что 11 минус 𝑥 все в квадрате означает 11 минус 𝑥 умножается на 11 минус 𝑥, что упрощается до 121 минус 22𝑥 плюс 𝑥 в квадрате. Мы можем сгруппировать подобные термины на левая часть — это 𝑥 в квадрате плюс 𝑥 в квадрате — получается два 𝑥 в квадрате. И при этом вычесть 65 с каждой стороны, чтобы получить квадратное уравнение два 𝑥 в квадрате минус 22 𝑥 плюс 56 равно нулю.

Теперь мы замечаем в этой точке что каждый из коэффициентов в нашем уравнении является четным числом. Таким образом, мы можем упростить, разделив все уравнение на два. Это упрощает квадратное уравнение 𝑥 в квадрате минус 11𝑥 плюс 28 равно нулю. Теперь мы хотим решить эту уравнение для 𝑥. Итак, мы сначала смотрим, есть ли это уравнение можно разложить на множители. Как коэффициент 𝑥 квадрат в нашем уравнении равен единице, первый член в каждом наборе скобок будет просто быть 𝑥, потому что 𝑥, умноженное на 𝑥, дает 𝑥 в квадрате. И чтобы завершить скобки, мы ищем два числа, сумма которых является коэффициентом 𝑥 — это минус 11 — и чей продукт является постоянным членом — это 28.

Принимая во внимание факторы 28, мы видим, что если мы выберем два числа минус семь и минус четыре, тогда их произведение действительно равно 28, потому что минус, умноженный на минус дает позитив. И их сумма действительно отрицательное 11. Итак, это два числа мы ищем, чтобы завершить наши скобки. У нас есть наш квадратик в его тогда в факторизованной форме. 𝑥 минус семь умножить на 𝑥 минус четыре равно нулю.

Для решения берем каждый множитель в свою очередь, приравняйте его к нулю и решите полученное уравнение. У нас есть 𝑥 минус семь равно ноль, который можно решить, прибавив семь к каждой стороне, чтобы получить 𝑥 равно семи, и тогда 𝑥 минус четыре равно нулю, что мы решаем, добавляя четыре к каждой стороне чтобы дать 𝑥 равно четырем. Тогда мы нашли решение для 𝑥. Есть два возможных ценности. 𝑥 равно четырем или 𝑥 равно семи.

Теперь нам нужно найти соответствующие 𝑦-значения, что мы можем сделать, подставив каждое 𝑥-значение по очереди в линейное уравнение, которое, помните, было 𝑦 равно 11 минус 𝑥. Когда 𝑥 равно семи, мы найдите, что 𝑦 равно 11 минус семь, что равно четырем. А когда 𝑥 равно четырем, мы находим, что 𝑦 равно 11 минус четыре, что равно семи. Так что у нас точно так же значения для 𝑦, как мы сделали для 𝑥.

Причина в том, что в начале задачи мы просто позволяем двум числам быть представлены 𝑥 и 𝑦. Мы не уточнили, 𝑥 или 𝑦 было большим числом. Итак, мы нашли то же решение дважды. Два числа семь и четыре. И то и другое может быть 𝑥 и тогда другой будет 𝑦. Мы, конечно, можем проверить наш ответьте, во-первых, подтвердив, что сумма наших двух чисел равна 11, какое из конечно, а, во-вторых, подтвердив, что сумма их квадратов — семь в квадрате плюс четыре в квадрате, что равно 49.плюс 16 — действительно равно 65.

Итак, сначала сформулировав информацию в вопросе в виде линейно-квадратичной системы уравнений, а затем решив эту пару одновременных уравнений методом подстановки, мы обнаружили, что два числа, которые мы ищем, — это семь и четыре.

Теперь одно действительно полезное приложение из этих приемов заключается в нахождении точек пересечения прямой и кривая, как упоминалось в самом начале видео. Теперь рассмотрим пример этот тип.

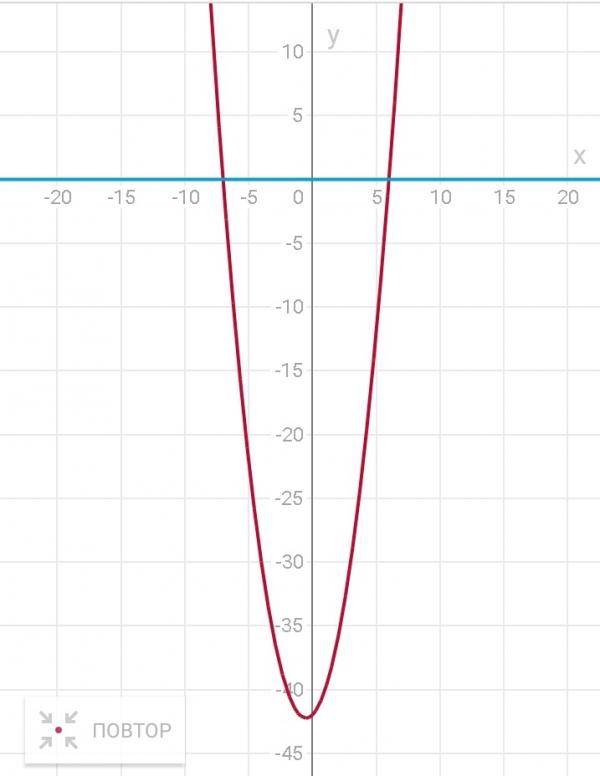
Найдите множество точек пересечение графиков 𝑥 минус 𝑦 равно нулю и шести 𝑥 в квадрате минус 𝑦 в квадрате равно 45.

Итак, нас попросили найти точки пересечения 𝑥 минус 𝑦 равны нулю, что является прямой линией, и шесть 𝑥 в квадрате минус 𝑦 в квадрате равно 45, что является кривой. Это эквивалентно решению линейно-квадратичная система уравнений 𝑥 минус 𝑦 равно нулю, шесть 𝑥 в квадрате минус 𝑦 в квадрате равно 45. Мы собираемся сделать это, используя метод замещения. Начнем с перестановки линейное уравнение, чтобы дать одну переменную через другую. Мы находим, что 𝑥 равно 𝑦.

Сейчас мы заменим наше выражение для 𝑥 во второе уравнение. Это дает шесть 𝑦 в квадрате минус 𝑦 в квадрате равно 45. С таким же успехом мы могли бы иметь подставил 𝑦 равно 𝑥 во второе уравнение, что дало бы шесть 𝑥 в квадрате минус 𝑥 в квадрате равно 45. Оба подхода приведут нас к такое же решение. Теперь мы можем решить этот квадратный уравнение для 𝑦.

Упрощение левой стороны, шесть 𝑦 в квадрате минус 𝑦 в квадрате, дает пять 𝑦 в квадрате. Затем мы можем разделить на пять, что дает 𝑦 в квадрате равно девяти, и решить с помощью извлечения квадратного корня. Вспоминая, надо брать плюс или минус квадратный корень. Итак, мы имеем, что 𝑦 равно плюс или минус квадратный корень из девяти, что равно положительному или отрицательному трем.

Найдя наши 𝑦-значения, мы теперь нужно найти соответствующие 𝑥-значения, подставив в линейную часть уравнение. И это очень простой. Поскольку наше линейное уравнение может быть выраженное как 𝑥 равно 𝑦, то каждое 𝑥-значение точно такое же, как соответствующее 𝑦-значение. Тогда мы находим, что есть два точки пересечения этих графиков, точки три, три и точка минус три, минус три, которые мы можем выразить как множество, содержащее эти две координаты.

Сейчас нельзя сразу узнать, как выглядит график шести 𝑥 в квадрате минус 𝑦 в квадрате равно 45 как. Но если у вас есть доступ к графический калькулятор или какое-либо графическое программное обеспечение для построения графиков, затем вы можете построить эти два графика. 𝑥 минус 𝑦 равно нулю прямая и шесть 𝑥 в квадрате минус 𝑦 в квадрате равно 45 — это то, что известно как гипербола. И, рассматривая эти два графиков, вы можете подтвердить, что две точки пересечения действительно являются точки, которые мы дали здесь.

В нашем последнем примере мы Рассмотрим задачу, в которой две переменные перемножаются вместе в одном из двух уравнения.

Учитывая, что 𝑥 в квадрате плюс 𝑥𝑦 равно 18 и 𝑥 плюс 𝑦 равно шести, найдите значение 𝑥.

У нас есть линейно-квадратичная система уравнений. Первое уравнение 𝑥 плюс 𝑦 равно шести является линейным. И второе уравнение 𝑥 квадрат плюс 𝑥𝑦 равно 18 является квадратичным, потому что он включает в себя член в квадрате 𝑥 а также термин 𝑥𝑦, где две переменные перемножаются. Нас не просят полностью решить эту систему уравнений, а просто найти значение 𝑥. Итак, мы собираемся сделать это, используя метод замещения.

Начнем с перестановки первое уравнение, дающее 𝑦, равно шести минус 𝑥, потому что это дает выражение для 𝑦 через 𝑥, которое мы можем подставить во второе уравнение, чтобы получить уравнение только в 𝑥. Это дает уравнение 𝑥 квадрат плюс 𝑥 умножить на шесть минус 𝑥 равно 18. Теперь у нас есть квадратное уравнение в 𝑥, которое мы можем решить.

Распределяем скобки в левой части, чтобы получить 𝑥 в квадрате плюс шесть 𝑥 минус 𝑥 в квадрате равно 18. И теперь мы видим, что 𝑥 квадрат и отрицательный 𝑥 в квадрате компенсируют друг друга. Итак, фактически наше уравнение сводится к линейному уравнению. У нас шесть 𝑥 равно 18. И это уравнение можно решить разделив каждую сторону на шесть, чтобы получить 𝑥 равно трем. Итак, подставив 𝑦 равно шесть минус 𝑥 во второе уравнение, мы создали уравнение в 𝑥 только которое тогда мы могли бы найти значение 𝑥.

Конечно, нас не просят найти значение 𝑦 в этой задаче. Но если бы нам было нужно, мы могли бы подставьте значение 𝑥, которое мы только что нашли, обратно в наше линейное уравнение, 𝑦 равно шести минус 𝑥, чтобы найти соответствующее значение 𝑦. Наше решение проблемы что значение 𝑥 равно трем.

Давайте теперь подытожим то, что мы видели в этом видео. Во-первых, линейно-квадратичная система уравнений — это просто система из двух уравнений, одно из которых линейное, а второе другой квадратичен. Решаем такие системы уравнений с помощью метода замещения. Преобразуем линейное уравнение в задаем одну переменную через другую, а затем подставляем наше выражение вместо эту переменную в квадратное уравнение. Затем решаем полученное квадратное уравнение, обычно с помощью факторинга. Затем мы подставляем значение или значения, которые мы нашли для первой переменной обратно в линейное уравнение, чтобы найти соответствующие значения для второго.

Мы должны помнить, что наши решения приходите парами. Поэтому мы должны представить наше решение как соответствующие пары двух переменных. Мы не можем смешивать и сочетать разные значения. Мы также видели в этом видео, что это метод может быть применен к числовым задачам. И особенно полезно приложение заключается в нахождении координат любых точек пересечения между прямая линия и кривая.

8.1 — Конические

8.1 — Конические

Коники получили свое название из-за того, что они могут быть образованы переходом плоскость через конус с двойным ворсом. Имеются четыре конических сечения и три вырожденных случаев, однако в этом классе мы рассмотрим пять вырожденных случаев, которые можно составить из общего уравнения второй степени.

Общая форма уравнения второй степени определяется как Ax ² + Bxy + Cy ² + Дх + Еу + Ф = 0

Определение конических сечений осмотром

Чтобы определить коническое сечение путем осмотра, заполните все квадраты, которые необходимы, чтобы переменные были с одной стороны, а константа с другой. правая сторона. Любая переменная в квадрате ниже может быть заменена количеством. То есть вместо x ² + y ² = 1 может быть (x-2) ² + y ² = 1

Круг

х ² + у ² = 1

Оба квадрата членов присутствуют, оба положительны, оба имеют один и тот же коэффициент. Правая часть положительная. Если правая сторона равен нулю, это точка. Если правая часть отрицательна, то нет графика.

Эллипс

3x ² + 4 года ² = 1

Присутствуют оба квадрата членов, оба положительны, но имеют различные коэффициенты. Правая часть должна быть положительной. Если право Сторона стороны равна нулю, это точка. Если правая часть отрицательна, то графика нет.

Гипербола

х ² — у ² = 1

Присутствуют оба квадрата членов, но один положительный, а другой отрицательно. Коэффициенты могут быть, а могут и не совпадать, это не имеет значения. Правая часть не равна нулю. Если правая часть равна нулю, то пересекающиеся линии.

Парабола

х ² + у = 1

Обе переменные присутствуют, но одна возводится в квадрат, а другая линейный.

Линия

х + у = 1

Ни одна из переменных не возведена в квадрат.

Точка

х ² + у ² = 0

Окружность (или эллипс), правая сторона которой равна нулю.

Нет графика

x ² + у ² = -1

Окружность (или эллипс) с отрицательной правой стороной.

Пересекающиеся линии

х ² — у ² = 0

Гипербола, правая часть которой равна нулю.

Параллельные линии

х ² = 1

Одна переменная возведена в квадрат, а другая отсутствует. Право Сторона стороны должна быть положительной. Если правая часть равна нулю, то это линия (x ² = 0, поэтому x = 0), и если правая часть отрицательна (x ² = -1), то графика нет.

Парабола

Парабола — это «множество всех точек плоскости, равноудалённых от неподвижная точка (фокус) и неподвижная линия (директриса)».

Расстояния до любой точки (x,y) параболы от фокуса (0,p) и направляющая y=-p равны друг другу. Это можно использовать для разработки уравнение параболы.

Если вы возьмете определение параболы и проработаете алгебру, вы можете разработать уравнение параболы. Вы можете нажать на ссылку, если хотите увидеть развитие, но краткое версия в том, что стандартная форма х ² = 4шт.

• Начальная точка — вершина в точке (h,k)
• Существует ось симметрии, содержащая фокус и вершину и перпендикулярна директрисе.
• Переместить p единиц по оси симметрии от вершины к фокусу.
• Переместить -p единиц по оси симметрии от вершины к директриса (которая является линией).
• Фокус находится в пределах кривой.

Парабола обладает тем свойством, что любой сигнал (свет, звук и т. д.), поступающий парабола, параллельная оси симметрии, будет отражаться через фокус (вот почему спутниковые тарелки и те параболические антенны, которые сыщики использовать для подслушивания разговоров). Кроме того, любой сигнал, исходящий от фокус будет отражаться параллельно оси симметрии (поэтому фонарики Работа).

Круг

Окружность — это «множество всех точек плоскости, равноудаленных от фиксированная точка (центр)».

Стандартная форма круга с центром в начале координат: x ² + y ² = r ² , где r — радиус окружности.

Эллипс

Эллипс — это «множество всех точек на плоскости, сумма которых расстояния от двух неподвижных точек (фокусов) постоянны».

Сумма расстояний до любой точки эллипса (x,y) от двух фокусы (c,0) и (-c,0) является константой. Эта константа будет 2а.

Если мы допустим d ₁ и d ₂ – расстояния от фокусов до точки, тогда d ₁ + d ₂ = 2a.

Вы можете использовать это определение для вывода уравнения эллипса, но ниже я приведу краткую форму.

Эллипс представляет собой вытянутую окружность. Начните с единичного круга (круг с радиусом 1) с центром в начале координат. Растянуть вершину от x=1 до x=a и точки от y=1 до y=b. То, что вы сделали, умножается каждый x на a и умножается каждый y на b.

В форме перевода вы представляете, что x делится на a и y делится б. Итак, уравнение окружности меняется с x ² + y ² = 1 на (x/a) ² + (y/b) ² = 1, и это стандартное уравнение для эллипса с центром в происхождении.

• Центр является отправной точкой в ​​(h,k).
• Большая ось содержит фокусы и вершины.
• Длина большой оси = 2a. Это также константа, что сумма расстояния должны складываться, чтобы быть.
• Длина малой оси = 2b.
• Расстояние между фокусами = 2c.
• Фокусы находятся внутри кривой.
• Поскольку вершины находятся дальше всего от центра, наибольшая из трех длин, и отношение Пифагора: a ² = b ² + c ² .

Гипербола

Гипербола — это «множество всех точек плоскости, разность которых расстояний от двух неподвижных точек (фокусов) постоянна».

Разница расстояний до любой точки гиперболы (x,y) от два фокуса (c, 0) и (-c, 0) являются константой. Эта константа будет 2а.

Если положить d ₁ и d ₂ расстояния от фокусов до точки, то | д ₁ — д ₂ | = 2а.

Абсолютное значение равно разнице, поэтому оно всегда положительное.

Вы можете использовать это определение для вывода уравнения гиперболы, но ниже я приведу краткую форму.

Единственная разница в определении гиперболы и эллипса состоит в том, что гипербола — это разность расстояний от фокусов, которая является постоянной, а эллипс — это сумма расстояний от фокусов, которая является постоянной.

Вместо уравнения (x/a) ² + (y/b) ² = 1, уравнение (x/a) ² — (y/b) ² = 1.

Однако графики сильно отличаются.

• Центр является отправной точкой в ​​(h,k).
• Поперечная ось содержит фокусы и вершины.
• Длина поперечной оси = 2a. Это также константа, которую разница расстояний должна быть.
• Длина сопряженной оси = 2b.
• Расстояние между фокусами = 2c.
• Фокусы находятся внутри кривой.
• Так как фокусы находятся дальше всего от центра, c является самым большим из трех длин, а пифагорейское соотношение: a ² + б ² = с ² .

Стандартные формы

В таблице ниже приведены стандартные формы трех основных конических сечений. в зависимости от направления главной оси. Для параболы ось — это «ось симметрии» и делит параболу пополам. Для эллипса это называется «большая ось» и является более длинной осью. Для гиперболы осью является «поперечная ось» и проходит между вершинами.

	Горизонтальная ось	Вертикальная ось
Парбола
Эллипс
Гипербола

 

Возведение в квадрат, чтобы найти вершину параболы — объяснение!

Нахождение формулы

Purplemath

Парабола — это кривая, которую вы получаете, когда рисуете квадратное уравнение формы y = a x ²  + b x  + c. Вы нарисовали эти кривые и, вероятно, познакомились с вершиной, которая является самой верхней (или самой нижней) точкой параболы (в зависимости от направления, в котором открывается парабола).

Но теперь вас просят найти именно вершину, и — конечно! — они затрудняют поиск вершины на графе. Чтобы найти координаты вершины, вам нужно «заполнить квадрат».

Содержимое продолжается ниже

MathHelp.com

Преобразования функций / переводы

Почему я должен заполнять квадрат?

Завершение квадрата, когда имеешь дело с квадратным уравнением параболы, переформатирует это квадратное уравнение в вершинную форму; из этой формы вершины вы можете прочитать координаты вершины параболы. Когда эти координаты запутаны — скажем, (−¾, 3,7) — завершение квадрата — единственный способ быть уверенным в точных x — и y — значения для вершины.

Могу ли я использовать свой калькулятор, чтобы найти вершину?

Да, вы, вероятно, можете использовать свой графический калькулятор, чтобы хотя бы приблизиться к значениям, но простые дробные значения, такие как

1/7, часто будут указываться как неконечные десятичные дроби; в этом случае на экране будет отображаться «0,1428571», что не очень полезно, особенно когда ваши ответы должны быть «точными».

Кроме того, ваш инструктор может решить, чтобы по крайней мере часть теста была без калькуляторов [и без телефонов], поэтому вам, вероятно, нужно знать, как сделать это вручную.

Какая форма вершины квадратичной параболы?

Вершинная форма квадратного уравнения параболы выглядит следующим образом: h , k ) — вершина.

a в вершинной форме такое же, как и в y = a x ²  + b x  + c; то есть оба a имеют точно такое же значение.

Знак «а» (плюс или минус) указывает, открывается квадратная парабола вверх или вниз. Подумайте об этом так: положительный a рисует улыбающееся лицо, а отрицательный a рисует хмурое лицо. (Да, глупо держать в голове эту картинку, но с ней очень легко запомнить, как работает старший коэффициент.)

---

---

Когда они хотят, чтобы вы нашли точные координаты вершины параболы, они обычно не дают вам квадратичную вершинную форму; вместо этого они обычно дают вам квадратичный в обычном y = a x ²  + b x  +  c формат. Как вы конвертируете из обычного формата в формат вершин? Используя технику завершения квадрата. Вот пример:

• Найдите вершину y = 3 x ²  + 2 x  − 1

Это мое исходное уравнение:

y = 3 x ² + 2 x − 1

Во-первых, я перенесу свободное число на другую сторону уравнения, с y :

y + 1 = 3 x ² + 2 x Теперь

9 9090 Вынесем все, что умножается на квадрат члена, имея в виду, что:

«Разложить на множители» не означает «заставить исчезнуть» или «разделить на другую сторону»; «фактор» означает «разделить вперед».

Так что я просто вытащу эти 3 вперед, что даст мне:

Для завершения квадрата я создам пространство слева с помощью y , и, если а не просто 1, я также поставлю копию а впереди этого пространства. Мне понадобится это место и копия a, чтобы сохранить «сбалансированное» уравнение.

y + 1 + 3(   ) = 3( x ² + 2/3 +    )

Теперь я возьму половину коэффициента линейного x 9120 скобки в правой части (то есть я разделю этот коэффициент на два), не забывая о его знаке, возведу результат в квадрат и прибавлю к обеим частям внутри скобок . (Вот почему в первую очередь были созданы скобки.)

В левой части уравнения я умножу часть «а, умноженную на квадрат коэффициента» в левой части, и преобразую правая часть к квадратной форме. (Здесь я использую тот знак, который я отслеживал ранее, помещая этот знак в середину выражения, возведенного в квадрат.)

При необходимости я еще немного упростлю:

Теперь я перееду. свободный номер с левой стороны обратно на правую сторону:

Чтобы быть тщательным, я переформатирую в вершинную форму (что нужно убедиться, что знаки соответствуют формуле вершинной формы) и прочитаю значения h и k .

В этом случае, поскольку a = 3 (что является положительным числом), то это правая парабола (то есть кривая, открывающаяся вверх), а вершина

( h , k ) = ( ⁻¹ / ₃ , ⁻⁴ / ₃ ), является самой низкой точкой на графике.

вершина: ( h ,  k ) = (−1/3, −4/3)

---

Вы можете удивиться, почему я взял на себя труд переформатировать уравнение в «правильный» вид вершины :

Я сделал это, потому что формула формы вершины такова:

y = a( x − h ) ² + k

8

8 что значение, которое было вычтено из x , чтобы получить бином

x  +  ¹ / ₃ , было отрицательным значением. Потому что, чтобы получить «плюс» в упрощенном виде, надо было вычесть «минус»:

x + ¹ / ₃ = x — ( ^-1 / ₃ )

Обращаясь к свободному числу, пришитому после квадратной скобки, я вижу, что оно вычтено из скобки. Чтобы это соответствовало вершинной форме квадратичного числа, я преобразовал вычитание в добавление отрицательного числа, потому что:

+ ( ^{− 4} / ₃ ) = ^{− 4} / ₃

( h ,  k ) = (какое бы число ни находилось внутри части, возведенной в квадрат, каким бы ни было другое число)», не замечая того факта, что h -часть равна вычитанию , а k -часть равна добавил .

(Отчасти поэтому я блуждал по этому длинному «в стороне» выше, о том, почему вершина ( h , k ) имеет смысл, если подумать. Потому что, если вы понимаете логику ( h ,  k ), являющуюся вершиной, то вам, как правило, проще сохранить формулу прямо.)

к форме вершины, обращая внимание на знаки, тогда вы сможете избежать одной из наиболее частых ошибок в этих задачах (а именно, наличия неправильных знаков в координатах вершины). Убедитесь, что вы практикуете это до тех пор, пока вы не сможете постоянно правильно интерпретировать свои результаты.

---

Кстати, вы заметили, что координаты вершин не были целыми числами? Преподаватели начинают понимать, что учащиеся угадывают вершину по красивым картинкам в своих графических калькуляторах, и они знают, что учащиеся часто думают, что все ответы всегда либо целые числа, либо «аккуратные» дроби, такие как половина. Например, если экран калькулятора оценивает вершину как (0,48, 0,98), многие учащиеся предположат, что ответ должен быть «на самом деле» (0,5, 1), а не, скажем, 9.0909

( ¹² / ₂₅ , ⁴⁹ / ₅₀ ).

Итак, чтобы проверить, действительно ли ученики умеют находить вершину (а не просто угадывать десятичную аппроксимацию по картинке), учителя дают более сложные упражнения. Если вам сказали, что вы должны знать эту технику нахождения вершины, будьте уверены, что у вашего учителя есть способы проверить, действительно ли вы этому научились. Не планируйте использовать читы калькулятора.

Как заполнить квадрат?

Чтобы взять общее квадратное уравнение и переформатировать его так, чтобы можно было найти вершину соответствующей параболы, выполните следующие действия: с и и любыми свободными числами слева от «равно».

Если любое число a ≠ 1 умножить на x ² члена, вынесите его и поместите перед скобками, содержащими x -терминов.

Перепишите каждую часть уравнения, чтобы добавить место для завершения квадрата.

• Слева от y добавьте пустую скобку, умноженную на факторизованное значение a, если применимо.
• С правой стороны добавьте дополнительный пробел внутри скобок. (На эту скобку уже умножено a, если применимо.)

Возьмем коэффициент линейного x -члена — вместе с его знаком! — и умножить на половину.

Возведите это новое значение в квадрат и добавьте его в скобки с обеих сторон уравнения.

Преобразуйте правую часть в квадрат бинома (умножьте на a, если применимо).

Переместите все свободные числа с левой стороны на правую.

Убедитесь, что ваши знаки внутри формы вершины верны, а затем считайте значение вершины.

 

---

URL: https://www.purplemath.com/modules/sqrvertx.htm

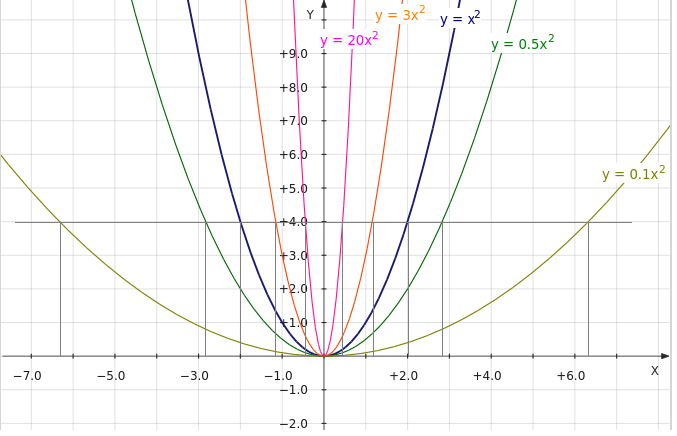
Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в преобразовании в вершинную форму. (Или пропустите виджет и перейдите к следующей странице. ) Попробуйте введенное упражнение или введите свое собственное упражнение. Затем нажмите кнопку и выберите «Найти форму вершины», чтобы сравнить свой ответ с ответом Mathway. 92 — кривая, называемая параболой. Чтобы начертить эту параболу, мы должны определить вершину, точку пересечения по оси Y, точку пересечения по оси X и несколько других точек по обе стороны от вершины кривой. Затем через эти точки проводится парабола.

Скачать PDF PDF Цитата страницы Цитировать Поделиться ссылкой Делиться

Ссылайтесь на эту страницу следующим образом:

«Как построить график х в квадрате?» eNotes Editorial , 10 октября 2020 г., https://www.enotes.com/homework-help/how-to-graph-x-squared-24739{2}+bx+c` , где a, b и c — действительные числа, а `a \ne 0` . Обратите внимание, что если a = 0,…

См.

Этот ответ сейчас

Начните 48-часовую бесплатную пробную версию , чтобы разблокировать этот и тысячи других ответов. Наслаждайтесь eNotes без рекламы и отмените подписку в любое время.

Получите 48 часов бесплатного доступа

Уже зарегистрированы? Войдите здесь. 9{2} = 4`; координаты этой точки (2, 4).

Найдя точки, через которые проходит парабола, мы можем теперь нанести их на график и построить через них параболу. Пожалуйста, обратитесь к приложенному графику.

Изображения:

Это изображение было помечено как неприемлемое Нажмите, чтобы снять отметку

Изображение (1 из 1)

Утверждено редакцией eNotes

Математика

Последний ответ опубликован 07 сентября 2010 г. в 12:47:25.

Что означают буквы R, Q, N и Z в математике?

14 ответов педагога

Математика

Последний ответ опубликован 03 августа 2010 г. в 00:41:32.

Если вы путешествуете  50 миль со скоростью 60 миль в час, сколько времени вам потребуется, чтобы добраться туда????

3 Ответы воспитателя

Математика

Последний ответ опубликован 27 ноября 2012 г. в 14:59:10.

Сформулируйте и докажите тест Раабе.

1 Ответ учителя

Математика

Последний ответ опубликован 24 октября 2012 г. в 5:48:10.

Как расположить 0,2, 0,22, 0,222, 0,2222 и 0,22222 на числовой прямой?

6 Ответы воспитателя 92 = 8 — это funkshun

, его equashun для серкеля вокруг (0,0) и radius = root (8)

ответил 5 марта 2013 г. по анонимно

Связанные вопросы

1 ответ

Центр и радиус x в квадрате плюс y в квадрате минус 8x плюс 6y равно -21

спросил 29 июня 2013 г. по алгебре 2 Ответы по анонимный | 607 просмотров

• центр и радиус окружности

1 ответ

график х в квадрате/4 плюс у в квадрате/25 равно 1

спросил 19 августа 2012 г. по алгебре 2 Ответы по анонимный | 536 просмотров

• построение графиков линейных уравнений

1 ответ

Сколько будет 3 в квадрате плюс 12 в квадрате равно x в квадрате

спросил 4 марта 2019 г. в ответы по геометрии по анонимный | 266 просмотров

1 ответ

-2 равно нулю f левая скобка x правая скобка пространство равно пробелу x в кубе плюс 7 x в квадрате плюс 4 x минус 12 , решите уравнение x в кубе плюс 7 x в квадрате плюс 4 x минус 12 равно 0 . 92 плюс 8т

спросил 23 апр. 2016 г. по алгебре 1 ответы по анонимный | 347 просмотров

• решение уравнений

1 ответ

x квадрат плюс 4x минус 5 равно 0

спросил 7 апр. 2014 г. по алгебре 2 Ответы по анонимный | 502 просмотров

• найти корень из х, равный 0

1 ответ

решить каждое уравнение, заполнив квадрат. R в квадрате плюс восемь r в квадрате равно сорок восемь

спросил 17 марта 2014 г. по алгебре 1 ответы по анонимный | 593 просмотров

• решение квадратных уравнений путем заполнения квадрата
• задачи по алгебре

1 ответ

5x в квадрате плюс 8x минус 1 равно 0 ….. что такое x?

спросил 5 сентября 2013 г. по алгебре 1 ответы по джхк | 820 просмотров

• предварительные задачи по алгебре

1 ответ

в квадрате

спросил 14 июня 2013 г. по алгебре 2 Ответы по анонимный | 537 просмотров

• задачи по алгебре
• алгебра

1 ответ

Какой ответ на вопрос 3x в квадрате равно 8x плюс 2

спросил 25 мая 2013 г. по алгебре 1 ответы по анонимный | 437 просмотров

• задача alrgbra
• решить с помощью квадратичной формулы

1 ответ

x квадрат плюс 10x равно -16

спросил 22 февраля 2013 г. по алгебре 1 ответы по анонимный | 772 просмотра

• задач по алгебре

1 ответ

Каков ответ на 2x в квадрате минус 5 плюс 3 равно 0?

спросил 17 января 2013 г. по алгебре 2 Ответы по анонимный | 626 просмотров

• задачи по алгебре

1 ответ

Предположим, что A в квадрате плюс B в квадрате равно C в квадрате и C равно 60, что такое A и B?

спросил 2 января 2013 г. в ответы по геометрии по анонимный | 962 просмотра

• задачи по геометрии

1 ответ

х в квадрате плюс х в квадрате равно 5 в квадрате

вопрос 4 декабря 2012 г. по алгебре 2 Ответы по анонимный | 674 просмотра

• в квадрате

1 ответ

3 больше х-2, ПЛЮС 7 больше х, равно -14 больше, х в квадрате минус 2х, что такое х?

спросил 27 ноября 2012 г. по алгебре 1 ответы по анонимный | 788 просмотров

1 ответ

что такое C, если 9x в квадрате минус 12x плюс C равно 0 ??

спросил 12 октября 2012 г. по алгебре 1 ответы по анонимный | 499 просмотров

• решение квадратных уравнений
• задачи по алгебре

2 ответа

Какой ответ на 2x в квадрате плюс 5x минус 12 равно 0?

спросил 18 марта 2012 г. по алгебре 1 ответы по анонимный | 3,7 тыс. просмотров

• задачи по алгебре
• решение уравнений методом факторизации

3 ответа

Как решить X в квадрате плюс Bx плюс C равно 0

спросил 4 октября 2011 г.

No related posts.