Интеграл как считать: Как решать интегралы для чайников, примеры решений

Несвойственные интегралы 1-го и 2-го рода

Несвойственный интеграл I рода

Если функция f(x) интегрирована за Риманом на каждом конечном промежутке [a;b], тогда несвойственный интеграл находят через предельный переход за формулой

и говорят, что несвойственный интеграл совпадающий, если существует такая конечная граница.
В противном случае (если граница бесконечна или не существует) говорят, что интеграл разбегается.

Несвойственный интеграл ІІ рода

Если функция f(x) неограничена в околе точки B и интегрирована за Риманом на каждом конечном промежутке , тогда несвойственный интеграл ІІ рода вычисляют по формуле

и говорят, что интеграл совпадающий, если существует его конечная граница. В противном случае (если граница бесконечна или не существует) говорят, что интеграл разбегается. Точка B называется особенной.

І. Вычислить интегралы

Начнем рассмотрение готовых ответов к несвойственным интегралам от простых к сложным заданиям.

Пример 2.147 (2334) Найти несвойственный интеграл
Имеем несвойственный интеграл І роду. Изменяем бесконечность на фиксированную точку из промежутка, вычисляем интеграл и после подстановки пределов интегрирования находим границу при следовании верхнего предела к бесконечности

 

Пример 2.148 ( 2335) Найти интеграл
Подинтегральная функция (логарифм) неопределенна в нуле, который отвечает нижней границе интегрирования. В соответствии с вышеприведенными формулами, имеем несвойственный интеграл второго рода. Для его нахождения переходим к границе в нуле, также выполняем интегрирование частями

Сам по себе интеграл не сложен в плане вычислений.
Замечание: в дальнейшем границу писать НЕ будем, а при вычисление несвойственных интегралов понимаем, что ищем значения границы в особенных точках (или в плюс минус бесконечности ) !!!

 

Пример 2.149 (2336) Вычислить интеграл
Разбиваем интеграл на 2 и находим несвойственные интегралы І рода

 

Пример 2. 150 (2337 ) Найти интеграл
Выполняем манипуляции идентичные, как и в предыдущем задании и приходим к несвойственным интегралам второго рода

 

Пример 2.151 ( 2338) Найти интеграл
Верхняя граница направляется к бесконечности, следовательно имеем несвойственный интеграл первого рода. Для нахождения предельного значения находим неопределенный интеграл и при подстановке пределов выносим переменную за скобки в числителе и знаменателе логарифма. В результате вклад бесконечно малых величин (1/x) направляется к нулю при переменной направляющейся к бесконечности. Таким образом находим главное значение интеграла

 

Пример 2.152 (2339) Найти интеграл

Решение: Вычислим последний интеграл методом Остроградського — метод не из простых, однако эффективный в подобных примерах:

возьмем производную от каждой части равенства (производная от интеграла равная подинтегральной функции)

Возведем дроби в правой части равенства к общему знаменателю и приравняем коэффициенты при соответствующих степенях x каждой части равенства

В результате получим систему из 4 линейных уравнений из которой находим 4 константы

Таким образом можем записать неопределенный интеграл в виде

Дальше подставляем пределы и находим границе дроби и арктангенса при переменной направляющейся к плюс минус бесконечности.

В конечной формуле можно еще избавиться от иррациональности в знаменателе, но это уже проделайте самостоятельно.

 

Пример 2.153 ( 2340)Найти интеграл

Вычислим последний интеграл методом неопределенных коэффициентов:

Записываем подинтегральные функции и, возведя их под общий знаменатель, 

а дальше приравняем коэффициенты при соответствующих степенях x каждой части равенства.
В результате решим систему трех уравнений и определим сталые

Подставим их в расписание и найдем неопределенный интеграл

после возведения под табличные формулы интегрирования получим логарифмы, которые группируем и арктангенс. 

В бесконечности выносим из числителя и знаменателя дроби под логарифмом слагаемое с самым старшим показателем переменной и сокращаем на него. Тогда получим логарифм единицы.
В нуле с точностью до наоборот, сталые оставляем — остальные слагаемые с переменными не дают вклада.
С арктангенсом ситуация более определена и его значение на пределе подставляем в формулу

 

Пример 2. 154 ( 2341)Вычислить интеграл
Покажем, как можно найти интеграл такого вида двумя способами.

І способ: расписание методом неопределенных коэффициентов:

Чему равен арктангенс в нуле, единице и бесконечности Вы должны знать на память при решении подобных заданий.
Здесь применили метод неопределенных коэффициентов (A=C=0; B=D=1/2) :

ІІ способ — через замену переменных:

Пределы интегрирования при замене переменных здесь стали другими (в нуле минус бесконечность).

 

Пример 2.155 (2342) Найти интеграл
Особенной точкой здесь является нуль, поскольку корень в знаменателе становится равным нулю, а подинтегральная функция направляется к бесконечности. Но это происходит на таком малом участке интегрирования, что вклад мизерен и в целом интеграл совпадающий.
Для его вычисления переходим под интегралом к новым переменным, находим новые пределы интегрирования и находим арктангенсы на краях

Вычисления не сложны, поскольку свели интегрирование под простой табличный интеграл.

 

Пример 2.156 (2343) Найти интеграл
В бесконечности подинтегральная функция направляется к нулю, поэтому делаем вывод, что имеем несвойственный интеграл І рода. Для его нахождения кое-как превращаем функцию и выполняем замену переменных

В результате сводим интеграл к логарифму, который упрощаем используя свойства логарифмов.

 

Пример 2.157 ( 2344) Найти интеграл
Имеем несвойственный интеграл І рода. Выполняем интегрирование частями

Второе слагаемое раскладываем методом неопределенных коэффициентов

В результате приходим к случаю когда имеем несвойственный интеграл І и ІІ рода одновременно, поэтому предел будет иметь вид

Здесь учтены следующие предельные переходы

Интеграл равен нулю.

 

Пример 2.158 (2345) Вычислить интеграл
В бесконечности подинтеграьная функция направляется к нулю — имеем І несвойственный интеграл.
Обозначив арктансенс через новую переменную определяем пределы интегрирования, дальше упрощаем функцию и интегрированием частями находим значение в крайних точках.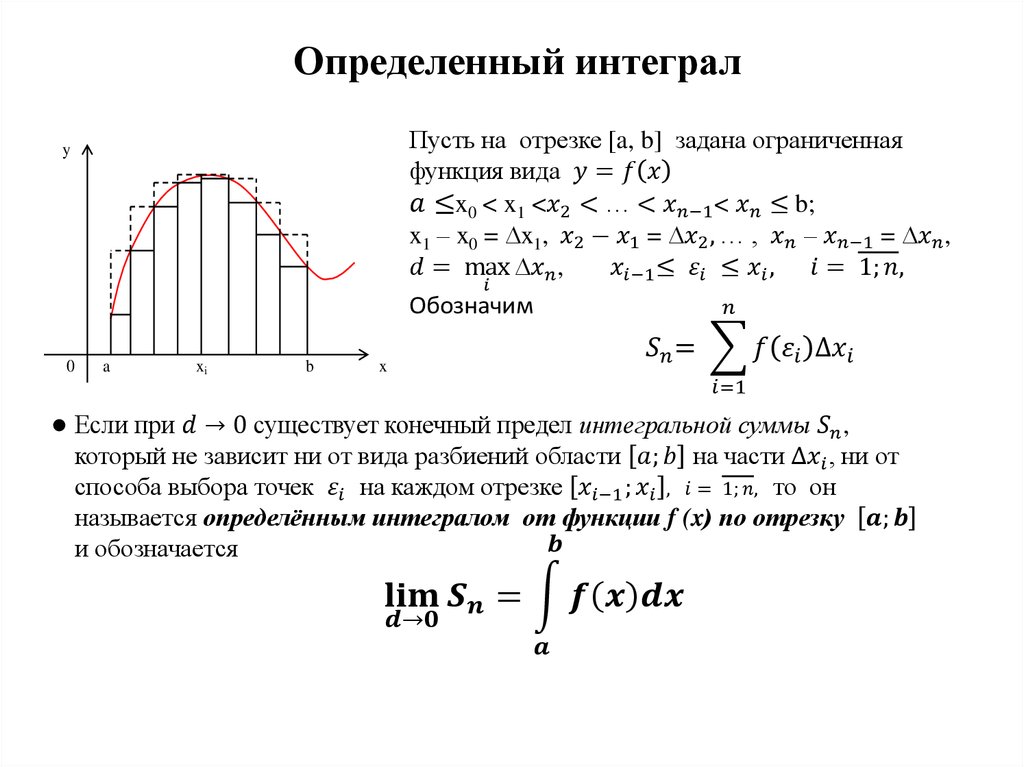

 

Пример 2.159 (2346) Найти интеграл
Неопределенный интеграл І рода решаем дважды применив интегрирование частями

В результате приходим к записи интеграла через самого себя, то есть рекуррентной формуле 

Перегруппировываем известные и неизвестные по разные стороны знака равенства

и выражаем

отсюда искомый интеграл

Метод не новый, и когда Вы имеете произведение экспоненты на синусы и косинусы без него не обойтись.

 

Пример 2.160 ( 2347) Найти интеграл
На бесконечности подынтегральное выражение дает бесконечно малую осциллирующую около нуля функцию.
Чтобы обойти такую неопределенность используем методику предыдущего примера. Дважды применив интегрирование частями

приходим к рекуррентной формуле

Из нее найти интеграл достаточно просто:
интегралы переносим в одну сторону, сталые в другую.

А дальше выполняем деления одной постоянной справа на множитель при интеграле

Отсюда и имеем искомый интеграл

Запомните методику последних двух заданий, на модулях и экзаменах на этом поплатилась значительная часть студентов.
Не будьте в их числе!

 

Пример 2.161 Найти интеграл
Имеем несвойственный интеграл І рода. Находим его и делаем вывод

что интеграл разбегается, поскольку преде не является конечным.

 

Пример 2.162 Найти интеграл
Экспоненту интегрировать не трудно, при отрицательном показателе она в бесконечности направляется к нулю

 

Пример 2.163 Вычислить интеграл
Интеграл по виду не сложный, однако при подстановке пределов многие из Вас пишут логарифм минус логарифм = бесконечность минус бесконечность, а дальше что границы не существует, а интеграл расходится.
А он совпадающий причем к нулю

В этом также легко убедиться проанализировав подинтегральную функцию, ее знаменатель положительный для положительных и отрицательных значений переменной, числитель непарная функция, следовательно интеграл справа от оси абсцисс нивелирует интеграл слева.

 

Пример 2.164 Найти интеграл
В знаменателе дроби выделяем полный квадрат и сводим интеграл под формулу арктангенса.

При следовании переменной к бесконечности арктангенс направляется к Pi/2, при минус бесконечности к — Pi/2.
В сумме получаем Int=Pi.

 

Пример 2.165 Найти интеграл

Имеем интеграл І рода. Покажем, что он расходится. Знаменатель на рассматриваемом промежутке удовлетворяет условие ln(x)<x-1, поэтому имеем следующее неравенство между функциями
,
Однако второй интеграл расходится

Поскольку функция принимает большие значения , то заданный интеграл также расходится!

 

Пример 2.166 Найти интеграл
Имеем несвойственный интеграл І рода. Его находим расписанием подинтегральной функции через простые множители, как это реализовать расписано дальше

Данный интеграл нашли методом неопределенных коэффициентов:

записываем функцию в виде расписания простых дробей

Дальше их возводим к общему знаменателю

приравняем коэффициенты при соответствующих степенях x в обеих частях равенства и находим сталіе A=1, B=-1; C=1 .
Их и подставляем в интеграл

 

Пример 2.167 Найти интеграл
Чтобы не раскладывать на простые дроби через неопределенные коэффициенты прибавим и отнимем в числителе единицу. Это позволит получить в числителе такой же множитель как и знаменатель и разложить дробь на два интегралы.
Дальнейшее их вычисление и определение пределов приведено в формуле
.

 

Пример 2.168 Найти интеграл
При переменной направляющейся к бесконечности функция, которая интегрируется направляется к нулю. Имеем несвойственный интеграл первого рода. Чтобы найти его значение выносим переменную из под корня знаменателя, переходим к новой переменной интегрирование (при этом изменяются пределы). В результате получим арксинус, который и вычисляем
.

 

Пример 2.169 Найти интеграл
Здесь необходимо, чтобы параметр превращался в нуль. Для других его значений несвойственный интеграл первого рода находим методом замены переменных. В результате приходим к логарифму, который расписываем к самому простому виду

 

Пример 2.170 Найти интеграл
Здесь в нуле надо найти предел, для этого вычисляем несвойственный интеграл, и подставляем пределы интегрирования.

Интеграл равен 0,5.

 

Пример 2.171 Найти интеграл
В нуле имеем особенность, которую при интегрировании необходимо обойти. Сначала превращаем функцию, чтобы перейти к новой переменной. Дальше применяем интегрирование частями, если множителем имеем экспоненту то это быстро приводит к конечному результату или рекуррентной формуле. Дальше подставляем пределы и анализируем, какие слагаемые сбегаются и к какой границе (значении).

 

Пример 2.172 Найти интеграл
В бесконечности синус осциллирует, если умножить на переменную то получим осциллирующую функцию с растущей амплитудой. Выполняем интегрирование частями и переходим к границе.

Поскольку последней границы не существует, то интеграл расходится.

 

Пример 2.173 Вычислить интеграл
Поскольку мы знаем к чему сводить подобные интегралы, то выполняем превращение функции в начале. Вы же можете обозначить корень из аргумента за новую переменную и в результате превращений прийти к тому же конечного интегралу. Самостоятельно проинтегрирував  частями, Вы получите, что интеграл равен единице

 

Пример 2.174 Найти интеграл

В подобных примерах нужно дважды применять интегрирование частями.

В результате придем к рекуррентной формуле

откуда и определяем интеграл

Данный интеграл — это классика интегрирования, если бы экспонента и синус имели множители при аргументах, то вычисления были не такие простые как в рассмотреном примере.

 

Пример 2.175 Найти интеграл
Здесь с первого взгляда может показаться, что интеграл не принадлежит к несвойственным. Однако, разложив знаменатель на одночлены, видим, что во внутренней точке имеет особенность, а именно разрыв второго рода.
При нахождении несвойственного интегралу второго рода при переходе к границам два логарифма упрощаем, по правилу разница логарифмов равна логарифму части. Таким образом лишь одно из слагаемых дает вклад

На графике функции эта особенность имеет вид

Пример 2.176 Найти интеграл
В единице корень в знаменателе превращается в нуль и функция там имеет вертикальную асимптоту. Чтобы ее обойти прибавим и отнимем в числителе единицы и распишем интеграл на два. Их вычисление уже не содержит никаких особенностей

График функции, не доходя до 1 справа имеет вид

Пример 2.177 Найти интеграл
Неопределенность в заданный интеграл вносит то что логарифм вблизи нуля направляется к минус бесконечности. Интегрируя частями, придем к особенности в нуле, Вы ее можете свести к следствию второй важной границы, мы же записываем конечное значение.

Для наглядности графики подинтегральной функции на указанном промежутке имеет вид

Как можно убедиться здесь все гладко и красиво.

 

Пример 2.178 Найти интеграл
При приближении к нулю за счет квадрата знаменателя функция растет к бесконечности. Но и при этом промежуток на котором это происходит направляется к нулю. Поэтому несвойственный интеграл существует и с помощью приведенной замены переменных находится без проблем

Найденный интеграл не что другое как площадь фигуры между функцией и осью ординат. За исключением особенности в нуле графики функции имеет вид верхней линии, а значение интеграла — заштрихованной на рисунке поверхности.

Пример 2.179 Найти интеграл
В единице логарифм направляется к минус бесконечности, чтобы учесть это выполняем замену переменных под интегралом

В результате предел равен бесконечности, поэтому заданный интеграл разбегается.
График подинтегральной функции в околі особенной точки имеет вид

Пример 2.180 Найти интеграл
При приближении к единице логарифм направляется к нулю, а функция к плюс бесконечности.
Чтобы вычислить несвойственный интеграл ІІ рода выполняем замену переменных и переходим к корневой функции в знаменателе, которая после интегрирования не имеет особенности

Значение интеграла равно площади заштрихованной фигуры.

Пример 2.181 Найти интеграл
Здесь свой вклад вносит точка x=0, поскольку в ней функция из двух сторон направляется к плюс бесконечности.
Разделим числитель на знаменатель и перепишем функцию в виде показателей переменной.
Дальше разделяем интеграл на два и находим значение в пределе.

Получили совпадающий интеграл. Вид функции приведен на рисунку

Пример 2.182 Найти интеграл
Здесь идентичная ситуация, в нуле имеем особенность. По схеме предыдущего задания находим два неопределенных интеграла

 

Пример 2.183 Найти интеграл
Здесь в нуле имеем особенность, но поскольку знаменатель в нуле непарный то график общей функции имеет в нуле разрыв второго рода. Такие функции интегрируемые и по схеме выше находим предел в нуле.

Около нуля график функции имеет вид

Пример 2.184 (2348) Найти интеграл

Вычислим нулевое приближение с устранимой особенностью в бесконечности

Дальше интегрированием частями находим значение для номера n

Получили рекуррентную формулу: I_n=n*I_{n — 1}, отсюда интеграл равен

На этом ознакомление с основными приемами нахождения несвойственных интегралов подходит к концу.
Больше готовых ответов на интегрирование функций ищите на страницах сайта.
Если нужна помощь, также обращайтесь!

Обзор методов вычисления интегралов по времени и пространству

Интегрирование — один из важнейших математических инструментов, особенно в численном моделировании. Например, дифференциальные уравнения в частных производных обычно выводятся из интегральных уравнений сохранения. Когда возникает необходимость численного решения уравнения в частных производных, интегрирование также играет важную роль. В этой статье приведен обзор методов и подходов интегрирования, доступных в COMSOL Multiphysics, а также конкретные примеры их использования.

Важность интегралов

В COMSOL используется метод конечных элементов, который преобразует описывающее некоторый процесс уравнение в частных производных в интегральное уравнение — другими словами, в слабую форму (weak form). При детальном и глубоком изучении формулировок, используемых в интерфейсах COMSOL, вы обнаружите, что множество граничных условий реализованы через интегралы. В качестве наиболее характерных примеров можно привести условия Total heat flux (Общий тепловой поток) или Floating potential (Плавающий потенциал). Вычисление интегралов также играет ключевую роль в процессе постобработки результатов, поскольку COMSOL рассчитывает большое количество вспомогательных величин через интегралы, например энергию электрического поля, скорость потока или общий тепловой поток. Разумеется, пользователи вольны использовать интегрирование в COMSOL в своих целях, и в этой статье мы объясним вам, как это делать максимально эффективно. {t_1}\int_{\Omega}F(u)\ \mathrm{d A} \mathrm{d} t

где [t_0,t_1] — это временной интервал, \Omega — это пространственная область, а F(u) — это произвольное выражение, включающее зависимую переменную u и произвольные функции от нее, в том числе производные по пространству, времени, а также любой другой величине.

Наиболее удобный способ вычисления интегралов — использование узла Derived Values (Расчет выражений) в разделе Results (Результаты) ленты Ribbon или дерева модели (Лента Ribbon отсутствует в том случае, если ваш компьютер работает не под управлением ОС Windows®).

Добавление операций расчета пространственных интегралов по объему, поверхности или линии в узле Derived Values (Расчет выражений)

Вы можете обратиться к любому доступному решению, выбрав соответствующий набор данных (data set). В поле Expression (Выражение) вводится подынтегральная функция, включающая зависимые или производные переменные. Для данных расчета во временной области пространственный интеграл вычисляется на каждом временном шаге. В качестве альтернативы, в окне Settings (Настройки) узла Data Series Operations (Операции с массивами данных) можно выбрать опцию Integral (Интегрирование), что позволит вычислить общий пространственно-временной интеграл.

Пример настроек вычисления интегралов по поверхности (Surface Integration) с дополнительным вычислением интеграла по времени в разделе Data Series Operations.

Оператор Average (Усреднение) — еще одна операция в разделе Derived Values, связанная с вычислением интегралов. Оператор вычисляет интеграл и делит его на объем, площадь или длину выбранной области. Операция Averageв узле Data Series Operations аналогично вводит деление на продолжительность временного диапазона. Операторы узла Derived Values — важный инструмент, однако их можно использовать только во время постобработки, а значит с их помощью можно рассчитать далеко не любой интеграл. Именно поэтому в COMSOL представлены другие более мощные и гибкие инструменты для вычисления интегралов. 2. Стационарное и нестационарное решение (в момент времени 100 секунд) представлены на иллюстрациях ниже.

Стационарное решение, нажмите на изображение для увеличения.

Нестационарное решение (для момента времени 100 секунд), нажмите на изображение для увеличения.

Вычисление пространственного интеграла с использованием операторов узла Component Coupling

Операторы узла Component Coupling (Сопряжение компонентов) используются в тех случаях, когда, например, в одном выражении объединяются несколько интегралов, или интегралы требуются в процессе вычислений, или требуется множество контурных интегралов. Операторы данного узла определяются в разделе Definitions (Определения). На этом этапе режультат использования оператора не просчитывается, а указываются только их название и выборки областей.

Добавление операторов через узел Component Couplings

В нашем примере мы для начала хотим вычислить пространственный интеграл для стационарного распределения температуры, равный

\int_{\Omega}T(x,y)\ \mathrm{d}x\mathrm{d}y = 301. 65

В пакете COMSOL оператор вычисления интеграла по умолчанию получает имя intop1.

Окно настроек оператора интегрирования.

Расчет результата интегрирования через оператор.

Теперь давайте рассмотрим, как оператор интегрирования может использоваться непосредственно в процессе расчета модели. С его помощью мы могли бы, например, выяснить, какая нагревательная мощность потребуется для получения средней температуры 303.15 К, то есть температуры, на 10 К превышающей температуру окружающей среды. Прежде всего нам необходимо вычислить разницу между требуемым и действительным средними значениями. Среднее значение вычисляется путем деления интеграла от T на интеграл от постоянной функции 1, который равен площади области. Нетрудно догадаться, что вычисление подобного вида легко выполнить с помощью представленного в COMSOL оператора Average (Усреднение), см. комментарии выше. По умолчанию данный оператор получает название aveop1. 2. Т.е. полученное значение можно задать в качестве граничного условия для общего входящего теплового потока, чтобы средняя температура в рассматриваемой области стала равна 303.15 К.

Вычисление неопределенного интеграла посредством оператора интегрирования

В своих обращениях в службу поддержки пользователи часто задают один и тот же вопрос: как рассчитать неопределенный пространственный интеграл? Для этой цели нам также пригодится оператор интегрирования, задаваемый через Component Couplings. Нахождение неопределенного интеграла — операция, обратная дифференцированию. Неопределенный интеграл позволяет вычислять площади произвольных областей, ограниченных графиками функций. Одна из самых важных прикладных задач — вычисление вероятностей в статистическом анализе. Для того чтобы это продемонстрировать, мы зафиксируем y=0 и обозначим неопределенный интеграл от T(x,0) как u(x). Это значит, что \frac{\partial u}{\partial x}=T(x,0). Тогда неопределенный интеграл имеет вид

u(\bar x) = \int_0^{\bar x}T(x,0)\mathrm{d} x

Здесь мы используем \bar x, чтобы отличать переменную интегрирования от внешней переменной. 1T(x,0)\cdot(x\leq\bar x)\ \mathrm{d} x

Во-вторых, нам понадобится оператор вычисления интеграла, который будет действовать на нижней границе области из примера. Давайте обозначим его как intop2. В-третьих, мы должны отличать переменную интегрирования от внешней переменной. Принятые обозначения для такого случая: x называется источником (source), а \bar x — точкой назначения (destination). При использовании операторов интегрирования доступен встроенный оператор dest, который позволяет явно оглашать, что соответствующее выражение не относится к переменным интегрирования. Точнее, это значит, что в COMSOL \bar x=dest(x). Объединив логическое выражение с оператором dest, мы получим выражение вида T*(x<=dest(x)), которое является именно тем входным выражением, которое требуется для intop2. Объединив все вместе, мы можем вычислить неопределенный интеграл, воспользовавшись выражением intop2(T*(x<=dest(x))). Результат данной операции можно проиллюстрировать следующим графиком:

Как построить график неопределенного интеграла с помощью оператора интегрирования, оператора dest и логического выражения.

В пакете COMSOL дополнительно доступны еще два оператора вычисления интеграла, а именно общая проекция (general projection) и линейная проекция (linear projection). Эти операторы можно использовать для получения множества контурных интегралов в любом направлении в области. Другими словами, вычисление интеграла производится только вдоль одного измерения. В результате мы получаем функцию размерности на единицу меньше, чем размерность области. Для двухмерного примера результатом будет одномерная функция, которая может быть рассчитана на любой границе. Более подробная информация об использовании данных операторов будет представлена в одной из следующих публикаций в нашем компоративном блоге.

Вычисление пространственного интеграла посредством дополнительного физического интерфейса

Наиболее гибким способом вычисления пространственных интегралов является техника с добавлением дополнительного PDE-интерфейса.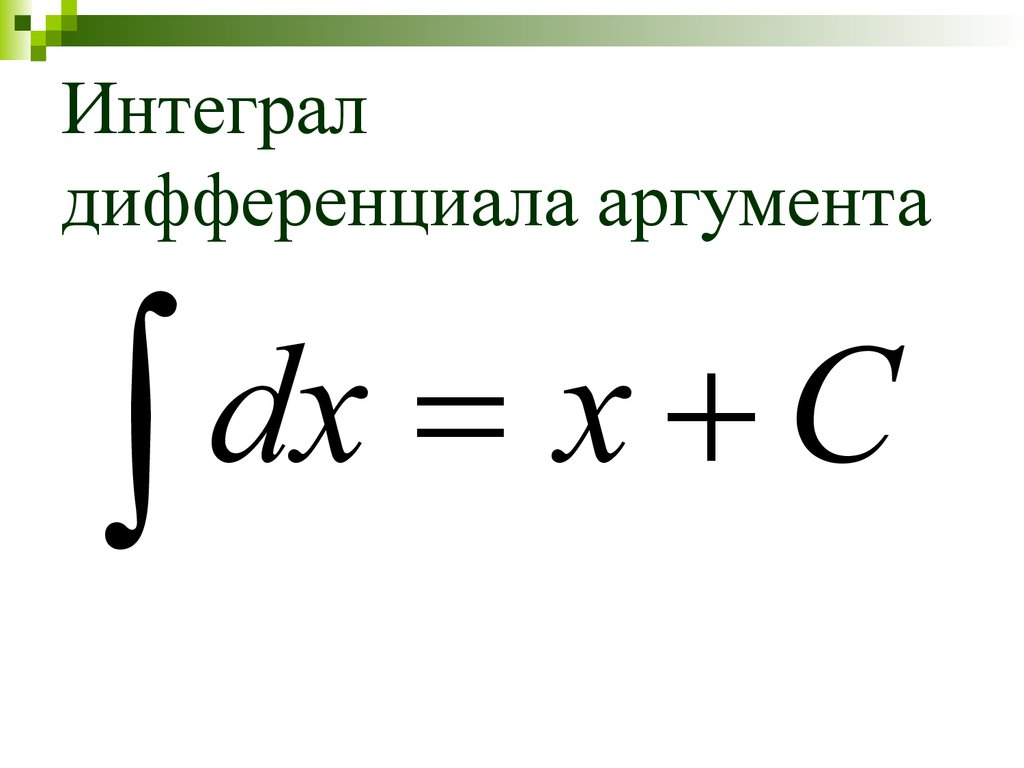 Давайте вспомним пример выше с неопределенным интегралом и предположим, что мы хотим вычислить неопределенный интеграл не только для y=0. Данная задача может быть сформулирована в виде дифференциального уравнения в частных производных

\frac{\partial u}{\partial x}=T(x,y)

с граничным условием типа Дирихле u=0 на левой границе. Расчет такого уравнения проще всего реализовать в физическом (математическом) интерфейсе Coefficient Form PDE (Дифференциальное уравнение в частных производных, коэффициентная форма записи), который потребует следующих настроек:

Вычисление пространственного интеграла посредством дополнительного PDE-интерфейса.

Зависимая переменная u представляет собой неопределенный интеграл по x и доступна в процессе расчета модели и в постобработке. Помимо гибкости, дополнительным преимуществом данного подхода является точность, так как интеграл рассчитывается не вспомогательными инструментами на основе уже определенного распределения переменной, а непосредственно в процессе расчета с учетом алгоритмов оценки погрешностей и т. {100}T(x,y,t)\ \mathrm{d} t

На поверхностном графике ниже представлен результирующий интеграл, являющийся функцией пространственных переменных (x,y):

Использование оператора timeavg – оператора вычисления интеграла по времени.

Схожие операторы существуют для вычисления интегралов на сферических зонах, а именно ballint, circint, diskint и sphint.

Вычисление временного интеграла посредством дополнительного физического интерфейса

В случае если временные интегралы нужно использовать непосредственно в модели в процессе расчета, вам будет необходимо задать их как дополнительные зависимые переменные. Аналогично представленному выше примеру с интерфейсом Coefficient Form PDE, это можно сделать, добавив ODE-интерфейс из раздела Mathematics. Предположим, например, что на каждом временном шаге требуется вычислять интеграл от величины общего теплового потока на промежутке от старта до текущего момента, который показывает накопленную энергию. Переменная для общего теплового потока рассчитывается в COMSOL автоматически и называется ht.tfluxMag. Интеграл может быть вычислен как дополнительная зависимая переменная с помощью узла Distributed ODE (Распределенное обыкновенное дифференциальное уравнение) интерфейса Domain ODEs and DAEs. Правой частью (источниковым членом) для доменного ОДЕ должна выступать подынтегральная функция, что и показано на иллюстрации ниже.

Использование дополнительного ODE-интерфейса для вычисления интеграла по времени.

В чем польза подобной техники? Полученный интеграл можно повторно использовать в других физических интерфейсах, поля в которых могут зависеть от накопленной в системе энергии. Более того, полученный резултат будет мгноменно доступен для всех видов постобработки, что удобнее и быстрее, чем использование встроенных операторов. Рекомендуем ознакомится с моделью Carbon Deposition in Hetereogeneous Catalysis (Образование сажевых отложений при гетерогенном катализе), в которой ОДЕ в области используется для вычисления пористости катализатора при наличии химических реакций в виде нестационарной полевой переменной.

Вычисление интеграла от аналитических функций и выражений

До сих пор мы демонстрировали, каким образом вычислять интеграл от искомых переменных в процессе расчета или при постобработке. Но не касались случая взятия интегралов от аналитических функций или выражений. Для этой операции в среде COMSOL доступен встроенный оператор integrate(expression, integration variable, lower bound, upper bound).

Выражение может представлять собой любую одномерную функцию, например sin(x). При этом допускается включение дополнительных переменных, например sin(x*y). Второй параметр определяет, по какой переменной вычисляется интеграл. Например, integrate(sin(x*y),y,0,1) выдает функцию переменной x, потому что интегрирование выполняется только по переменной y. Обратите внимание, что данный оператор также может использоваться для работы с аналитическими функциями, заданными в узле Definitions (Определения) текущего компонента.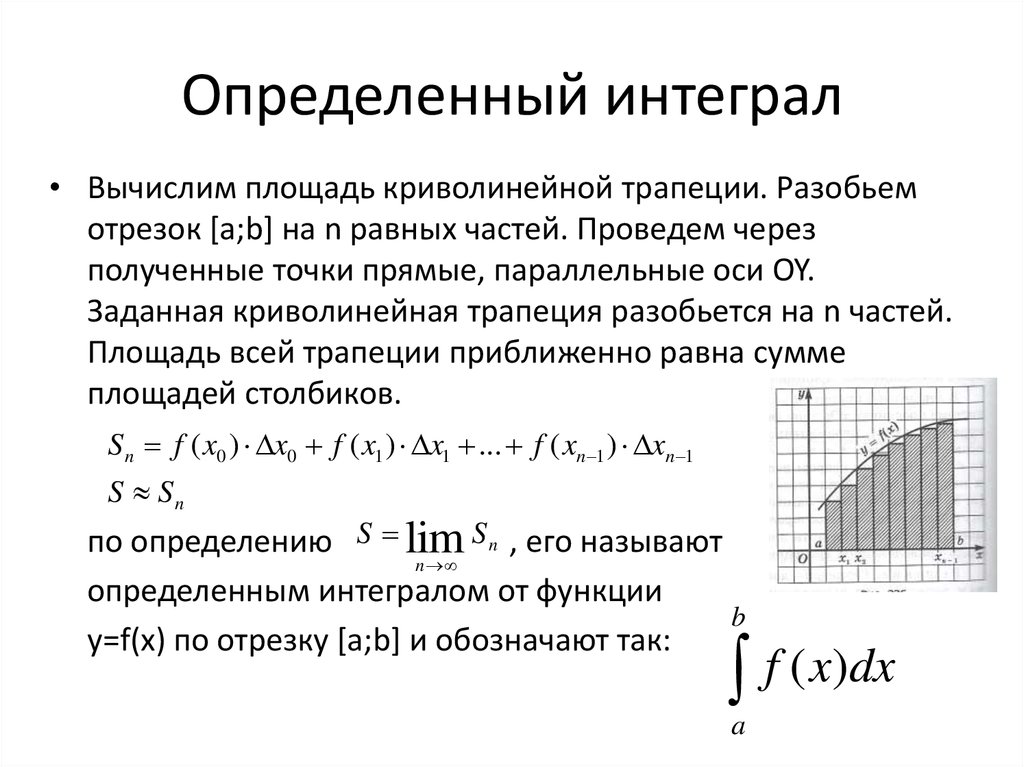

Добавление аналитической функции.

Вычисление интеграла от аналитической функции.

Материалы для дальнейшего изучения

• Модели, в которых использованы некоторые из рассмотренных операций (по состоянию на 29 января 2014 года)
  • Оператор интегрирования: Акустические характеристики глушителя
  • Глобальное уравнение для вычисления интеграла по времени: Управление процессами с помощью ПИД-регулятора
  • Глобальное уравнение для решения обрабной задачи (для обеспечения ограничений): Использование глобальных уравнений для обеспечения ограничений
  • Доменное ОДЕ для вычисления интеграла по времени: Уменьшение емкости литий-ионной аккумуляторной батареи (Capacity Fade of a Li-Ion Battery) и Образование сажевых отложений при гетерогенном катализе (Carbon Deposition in Heterogeneous Catalysis)
• Дополнительная информация в базе знаний (Knowledge Base): Вычисление интегралов по времени и пространству

Как находить интегральные выражения

Все ресурсы исчисления 1

10 Диагностические тесты 438 практических тестов Вопрос дня Карточки Learn by Concept

← Предыдущая 1 2 3 4 5 6 7 8 9 … 18 19 Следующая →

Исчисление 1 Помощь » Функции » Уравнения » Написание уравнений » Интегральные выражения » Как найти интегральные выражения

Какова площадь под кривой для ?

Возможные ответы:

Правильный ответ:

Объяснение:

По нормальным правилам экспоненты  , поэтому мы устанавливаем определенный интеграл

,

, который интегрируется с:

Сообщить об ошибке

Интегральная формула Гаусса утверждает, что

 .

Чему равен интеграл от

?

Возможные ответы:

Правильный ответ:

Пояснение:

Интегрируя по частям с

,  

, ,

получаем:

Сообщить об ошибке

Определить, учитывая, что

Определить.

Возможные ответы:

Правильный ответ:

Пояснение:

В этой задаче требуется вычислить неопределенный интеграл от заданной функции f’(x). Интегрируя каждый член функции по x, мы просто делим каждый коэффициент на (n+1), где n — значение показателя степени x для этого конкретного члена, а затем добавляем 1 к значению показателя степени каждого члена. Икс. Это дает нам:

Правильный ответ должен включать константу C, так как исходная функция могла иметь константу, которая не отражена в уравнении для ее производной.

 

Сообщить об ошибке

Каково значение следующего определенного интеграла?

Возможные ответы:

Правильный ответ:

Объяснение:

Начнем с интегрирования функции в скобках по x, а затем вычтем оценку нижнего предела из оценки верхнего предела:

Сообщить об ошибке. Правильный ответ:

Пояснение:

Эта задача призвана продемонстрировать одно из возможных приложений исчисления в области физики. Уравнение для работы, данное в физике, выглядит следующим образом:

Используя это уравнение, мы просто устанавливаем определенный интеграл с нашими границами, заданными интересующим нас интервалом в задаче: Чтобы толкнуть коробку с x=2 метра на x=5 метров, требуется 39,8 джоуля.

Сообщить об ошибке

Вычислить определенный интеграл в интервале .

Возможные ответы:

Правильный ответ:

Объяснение:

Чтобы решить эту задачу, мы должны знать, что

В этом случае у нас есть:

Наш первый шаг — интегрировать:

наши значения 

 

Сообщить об ошибке

Запишите выражение площади под следующей кривой от  до .

Возможные ответы:

Правильный ответ:

 

Объяснение:

Просто используйте интегральное выражение с заданными значениями x в качестве границ.

Не забудьте добавить dx!

Сообщить об ошибке

Вычислить определенный интеграл в интервале  .

Возможные ответы:

Правильный ответ:

Объяснение:

Чтобы решить эту задачу, мы должны помнить, что: 

В этом случае у нас есть: 

 

Наш первый шаг состоит в интеграции: в наших значениях  

Сообщить об ошибке

Вычислить определенный интеграл в интервале  

Возможные ответы:

Правильный ответ:

Объяснение:

Чтобы решить эту задачу, мы должны помнить, что:

В этом случае у нас есть:

Наш первый шаг — интегрировать:

Затем мы приходим к нашему решению, подключая значения

Сообщить об ошибке

Вычислить неопределенный интеграл.

Возможные ответы:

Правильный ответ:

Объяснение:

Нас просят интегрировать функцию.

Для этого нам нужно запомнить правило степени интегралов,

Используя это правило, мы можем вычислить следующий интеграл:

Сообщить об ошибке

← Предыдущий 1 5 6 3 7 4 8 9 … 18 19 Далее →

Уведомление об авторских правах

Все ресурсы исчисления 1

10 диагностических тестов 438 практических тестов Вопрос дня Карточки Learn by Concept

Интегральное исчисление в Python

В этом посте показано, как выполнить интегральное исчисление непрерывных и ограниченных реальных функций реальных переменных в Python. за счет использования общих библиотек Python, часто используемых в научных приложениях. Интегральные методы расчета здесь в основном численные, поскольку этот сайт посвящен вычислениям, однако также показаны некоторые аналитические методы.

Пост организован по примерам : каждый абзац содержит пример интеграла для вычисления и соответствующий фрагмент кода Python, который вычисляет его с помощью соответствующей библиотеки.

Для всех различных фрагментов кода, описанных в этом посте, требуется Python версии 3 и библиотека NumPy, в то время как по отдельности они требуют дополнительной библиотеки (и ее зависимостей, если таковые имеются) между SciPy и SymPy.

Мы благодарим профессора Фаусту Д’Акунцо из Preparazione 2.0 за теоретическую поддержку, оказанную в области интегрального исчисления с несколькими переменными.

Чтобы получить код, см. параграф «Полная загрузка кода» внизу этого поста.

Интеграция через SciPy

Интеграл функции одной переменной (с конечными экстремумами)

В интегральном исчислении определенный интеграл — это оператор, который для вещественнозначной функции вещественнозначной переменной и интервала $[a,b]$ (подмножества области определения) сопоставляет функции площадь, стягиваемую ее графиком в интервале $[a,b]$.

-x от x=1 до x=5′) подынтегральная функция = лямбда x: 2 * x * np.exp(-x) а = 1. б = 5. результат = spi.romberg (интегральное выражение, a, b) print(‘Результат ‘, результат) 9-x от х=1 до х=5 Результат 1.3

4006967394 Вот ссылка на код на GitHub.

Вычисление интеграла с трапецией

Функция трапеции представляет собой метод интегрирования функций с фиксированной выборкой, поэтому код сначала равномерно распределяет интервал интегрирования и для всех дискретных значений $x$ он вычисляет соответствующие значения $y$ а затем передает два набора дискретных значений $x$ и $y$ методу интегрирования. 9-x от х=1 до х=5 Результат 1.3

6624352673
 

Вот ссылка на код на GitHub.

Вычисление интеграла с помощью

cumulative_trapezoid

Функция cumulative_trapezoid также является методом интегрирования функций с фиксированной выборкой, а так сказанное про трапецию применимо.
Ниже приведен пример кода Python, который вычисляет интеграл, используя из 9-x от х=1 до х=5 Результат 1.3

6624352677
 

Вот ссылка на код на GitHub.

Вычисление интеграла с помощью

Симпсона

Функция simpson также является методом интегрирования функций с фиксированной выборкой, а так сказанное про трапецию применимо.
Ниже приведен пример кода Python, который вычисляет интеграл, используя симпсон функция 9-x от x=1 до x—>+inf Результат 1.4715177646857691 с ошибкой 3.7568301883294814e-10 Вот ссылка на код на GitHub.

Расчет длины дуги плоской кривой

Как известно, интегралы от функции одной переменной можно использовать и для вычисления длины дуги плоской кривой. Если кривая представлена ​​в виде $y=f(x)$ и является непрерывной и выводимой формула для расчета длины дуги кривой между $x=a$ и $x=b$ выглядит следующим образом: $$ \int_{a}^{b} \sqrt{1 + \left(\frac{\,dy}{\,dx}\right)^2} \,dx $$ 92} \, дх $$ аналитическое решение которого $\около 2. 3(t) от t=0 до t=2pi’) x = лямбда t : anp.cos(t) ** 3 y = лямбда t : anp.sin(t) ** 3 dx_dt = аг.град(х) dy_dt = ag.grad(y) подынтегральное выражение = лямбда t : anp.sqrt (dx_dt (t) ** 2 + dy_dt (t) ** 2) а = 0. б = 2 * отн.пи результат, ошибка = spi.quad (интегральное выражение, a, b) print(‘Результат ‘, результат, ‘с ошибкой’, ошибка) 93(t) от t=0 до t=2pi Результат 6.0 с ошибкой 6.616929226765933e-14 Вот ссылка на код на GitHub.

Двойной интеграл функции двух переменных

В интегральном исчислении определенный двойной интеграл — это оператор, который для заданной вещественной функции двух вещественных переменных и множества, включенного в область определения, связывает с функцией объем твердого тела (называемого цилиндроидом) между поверхностью, описываемой функцией, и плоскостью, содержащей данный набор. 9{-x y} \,dx dy $$ аналитическое решение которого $\около 1.0273$ проверяется онлайн через Wolfram Alpha. 2 от z=1 до z=2, y=z+1 до y=z+2 и от x=y+x до x=2(y+z)’) подынтегральная функция = лямбда x, y, z : x + y * z ** 2 bounds_z = лямбда: [1., 2.] bounds_y = лямбда z : [z+1, z+2] bounds_x = лямбда z, y : [y+z, 2 * (y+z)] ya=лямбда z: z + 1 yb=лямбда z: z + 2 ха = лямбда z, y : y + z xb=лямбда z, y : 2 * (y + z) результат, ошибка = spi.nquad (интегральное выражение, [bounds_x, bounds_y, bounds_z]) print(‘Результат ‘, результат, ‘с ошибкой’, ошибка) 92 от z=1 до z=2, y=z+1 до y=z+2 и от x=y+x до x=2(y+z) Результат 65.71944444444445 с ошибкой 1.659412309590769e-12 Вот ссылка на код на GitHub.

Интеграция через SymPy

Интеграл функции одной переменной (с конечными экстремумами)

В интегральном исчислении определенный интеграл — это оператор, который для вещественнозначной функции вещественнозначной переменной и интервала $[a,b]$ (подмножества области определения) сопоставляет функции площадь, стягиваемую ее графиком в интервале $[a,b]$. -x от x=1 до x=5′) х = sp.Symbol(‘x’) f = 2 * x * sp.exp(-x) примитив = sp.integrate(f, x) print(‘Примитив есть’, примитив) примитив_лямбда = sp.lambdify(x, примитив) а = 1. б = 5. интеграл = примитивная_лямбда(б) — примитивная_лямбда(а) print(‘Результат равен’, целое число) 9-x от х=1 до х=5 Примитив (-2*x — 2)*exp(-x) Результат 1.3

4006967436 Программа сначала вычисляет неопределенный интеграл, а затем применяя основную теорему интегрального исчисления, вычисляет значение интеграла.

Вот ссылка на код на GitHub.

Двойной интеграл функции двух переменных

В интегральном исчислении определенный двойной интеграл — это оператор, который для заданной вещественной функции двух вещественных переменных и множества, включенного в область определения, связывает с функцией объем твердого тела (называемого цилиндроидом) между поверхностью, описываемой функцией, и плоскостью, содержащей данный набор.