Знак интеграла | это… Что такое Знак интеграла?
Не следует путать с ʃ.
∫
Знак интеграла используется для обозначения интеграла в математике. Впервые он был использован немецким математиком и основателем дифференциального и интегрального исчислений Лейбницем в конце XVII века.
Символ (∫) образовался из буквы S (от лат. summa — сумма).
Содержание
|
Юникод
| Знак | Unicode | Название | HTML-представление | LaTeX | |||
|---|---|---|---|---|---|---|---|
| Позиция | Название | Шестнадцатеричное | Десятичное | Мнемоника | |||
| ∫ | U+222B | Integral | Интеграл | ∫ | ∫ | ∫ | \int |
| ∬ | U+222C | Double Integral | Двойной интеграл | ∬ | ∬ | \iint | |
| ∭ | U+222D | Triple Integral | Тройной интеграл | ∭ | ∭ | \iiint | |
| ∮ | U+222E | Contour Integral | Интеграл по контуру | ∮ | ∮ | \oint | |
| ∯ | U+222F | Surface Integral | Интеграл по поверхности | ∯ | ∯ | \oiint (требуется пакет esint) | |
| ∰ | U+2230 | Volume Integral | Интеграл по объёму | ∰ | ∰ | \oiiint (требуется пакет esint) | |
| ∱ | U+2231 | Clockwise Integral | Интеграл с правым обходом | ∱ | ∱ | ||
| ∲ | U+2232 | Clockwise Contour Integral | Интеграл по контуру с правым обходом | ∲ | ∲ | \ointclockwise (требуется пакет esint) | |
| ∳ | U+2233 | Anticlockwise Contour Integral | Интеграл по контуру с левым обходом | ∳ | ∳ | \ointctrclockwise (требуется пакет esint) | |
Традиции начертания
Русскоязычная традиция начертания знака интеграла отличается от принятой в некоторых западных странах.
См. также
- История математических обозначений
Ссылки
- Akademie Ausgabe Online (нем.)
- Полное собрание трудов (PDF)
- http://www.fileformat.info/info/unicode/char/222b/index.htm
Литература
- Александрова Н. В. История математических терминов, понятий, обозначений: Словарь-справочник. — СПб: ЛКИ, 2007. — 248 с.
Тема: кратные интегралы
26
ТИПОВОЕ ЗАДАНИЕ № 2
1. Двойной интеграл
Обозначим d наибольший
из диаметров областей . Диаметром замкнутой ограниченной области называется
наибольшее из расстояний между двумя
точками границы этой области. В каждой
области k выберем произвольную точку Pk (xk ,yk)
и составим интегральную
сумму функции f(x,y)Рисунок 1
(рис. 1).Определение. Двойным интегралом функции f(x,y) по области D называется предел интегральной суммы
,
если он существует.
Двойной интеграл обозначается
(1)
Замечание. Интегральная сумма S зависит от способа разбиения области D и выбора точек Pk (k=1,
…, n).
Однако, предел
,
если он существует, не зависит от способа
разбиения области D и выбора точек Pk .
2. Достаточное условие существования двойного интеграла. Двойной интеграл (1) существует, если функция f(x,y) непрерывна в D за исключением конечного числа кусочно-гладких кривых и ограничена в
В дальнейшем будем считать, что все рассматриваемые двойные интегралы существуют.
3. Геометрический смысл двойного интеграла. Если f(x,y) ≥0 в области D, то двойной интеграл (1) равен объему “цилиндрического” тела, изображенного на рис.1:
V = (2)
Пояснение. Цилиндрическое тело ограничено снизу областью D, сверху частью поверхности z=f(x,y), с боков вертикальными отрезками прямых, соединяющих границы этой поверхности и области D.
4. Некоторые свойства двойного интеграла.
Линейность. Если С – числовая константа, то
,
.
Аддитивность. Если область D
“разбита” на области D1 и D2, то
.
3) Площадь ограниченной области D равна
(3)
5. Вычисление двойного интеграла. Пусть область
D = {(x, y): a ≤ x ≤ b, φ1(x) ≤ y≤ φ2(x)}. (4)
Рисунок 2
Область D заключена в полосе между прямыми x = a, y = b, снизу и сверху ограничена соответственно кривыми y = φ1(x) и y = φ2(x) (рис. 2а).
Двойной интеграл (1) по области D (4) вычисляется переходом к повторному интегралу:
.
Этот повторный интеграл вычисляется следующим образом. Сначала вычисляется внутренний интеграл
по переменной y, при этом x считается постоянной. В результате получится функция от переменной x, а затем вычисляется “внешний” интеграл от этой функции по переменной x.
Замечание. Процесс перехода к повторному интегралу по формуле (5) часто называют расстановкой пределов интегрирования в двойном интеграле. При расстановке пределов интегрирования нужно помнить два момента. Во-первых, нижний предел интегрирования не должен превышать верхнего, во-вторых, пределы внешнего интеграла должны быть константами, а внутреннего должны в общем случае зависеть от переменной интегрирования внешнего интеграла.
Пусть теперь область D имеет вид (рис. 2б)
D =
{ (x, y) : c ≤ y ≤ d, ψ1(y) ≤ x ≤ ψ2(y) }.
(6)Тогда
. (7)
Предположим, что область D можно представить в виде (4) и (6) одновременно. Тогда имеет место равенство
(8)
Переход од одного повторного интеграла к другому в равенстве (8) называется изменением порядка интегрирования в двойном интеграле.
Примеры.
1) Изменить порядок интегрирования в повторном интеграле
Рисунок 3 Рисунок 4
Решение.Область интегрирования для первого интеграла задается неравенствами , , для второго интеграла – : , . Изобразим эти области на рис.3. и не имеют общих внутренних точек, а в сумме эти области дают одну область , которую можно описать неравенствами , .
Рисунок 5
2) Вычислить: I= ,
где D ограничена прямыми y=x и x=2
и гиперболой xy=1.
Решение. Область интегрирования изображена на рисунке 4. Решая систему, состоящую из уравнений прямой y=x и гиперболы xy=1, получим координаты точки их пересечения А(1,1). Для вычисления интеграла по области D удобно воспользоваться формулой (5). Пределы внешнего интеграла по x – это абсциссы самой левой и самой правой точек области D , т.е. 1 и 2. При , y будет изменяться в пределах . Следовательно,
.
Если применить формулу (7), то вычисления будут более громоздкими.
3). Вычислить I = где D область, ограниченная линиями x=0, , .
Решение. Найдём абсциссу точки пересечения прямых и : =2x Область интегрирования D изображена на рисунке 5.
D = { :, }
По формуле (7) имеем
.
Задача 1.
Изменить порядок интегрирования.
1.1. . 1.2. .
1.3. . 1.4. .
1.5. . 1.6. .
1.7. . 1.8. .
1.9. . 1.10. .
1.11. . 1.12. .
1.13. . 1.14. .
1.15. . 1.16. .
1.17. . 1.18. .
1.19. . 1.20. .
1.21. . 1.22. .
1.23. . 1.24. .
1.25. . 1.26. .
Задача 2. Вычислить.
2.1. 2.2.
2.3. 2.4.
2.5. 2.6.
2.7. 2.8.
2.9. 2.10.
2.11. 2.12.
2.13. 2.14.
2.15. 2.16.
2.17. 2.18.
2.19. 2.20.
2.21. 2.22.
2.23. 2.24.
2.25. 2.26.
2.27. 2.28.
Задача 3. Вычислить.
3.1. 3.2.
3.3. 3.4.
3.5. 3.6.
3.7. 3.8.
3.9. 3.10.
3.11. 3.12.
3.13. 3.14.
3.15. 3.16.
3.17. 3.18.
3.19. 3.
20.
3.21. 3.22.
3.23. 3.24.
3.25. 3.26.
3.27. 3.28.
6. Вычисление площади фигуры. Площадь плоской области , ограниченной простой замкнутой кривой, можно найти по формуле (3) из пункта 4
Рисунок 6
.
Пример. 4) Вычислить площадь фигуры, ограниченной кривыми , , .
Решение. Данная фигура D расположена в вертикальной полосе , а в ней ограничена снизу параболой , сверху прямой (рис. 6). По формуле (5) имеем
.
Задача 4. Найти площадь фигуры.
4.1. 4.2.
4.3. 4.4.
4.5. 4.6.
4.7. 4.8.
4.9.
4.10.
4.11.
4.12.
4.13. 4.14.
4.15. 4.16.
4.17. 4.18.
4.19.
4.20. 4.21.
4.22. 4.23.
4.24.
4.25. 4.26.
4.27. 4.28.
7.
Переход к
полярным координатам в двойном интеграле. Полярная
система координат состоит из луча Or.
Любая точка M ≠ O однозначно определяется полярным углом φ (0 ≤ φ <2π или –π < φ π) и полярным
радиусом r (r≥0)
(рис. 7а).
Для начала координат O радиус r = 0, а полярный
угол не определен.
Пусть декартова полуось Ox совпадает с полярным лучом Or (рис.7а).
Рисунок 7
Декартовы координаты выражаются через полярные по формулам
(9)
Полярные координаты выражаются через декартовы:
,
, (10)
.
Пусть область D в декартовых координатах преобразуется
в область Dr в
полярных координатах согласно формулам
(10).
Тогда интеграл (1) преобразуется в
двойной интеграл в полярных координатах
по формуле
(11)
Двойной интеграл (11) вычисляется переходом к повторному интегралу в полярных координатах. Пусть область Dr имеет вид (рис. 7б)
Dr = { (r, φ ) : α ≤ φ ≤ β, r1(φ) ≤ r≤ r2 (φ)},
где лучи φ = α и φ = β ограничивают сектор, в котором находится фигура Dr , кривые r = r1(φ), r = r2 (φ) ограничивают ее в этом секторе. Тогда
(12)
Замечание. При расстановке пределов интегрирования
в повторном интеграле нужно учесть, что
изменение полярного угла определяется
поворотом луча, исходящего из начала O вокруг него против хода часовой стрелки,
а изменение полярного радиуса определяется
движением точки вдоль луча в сторону
его возрастания.
Рисунок 7
Примеры. 5) Вычислить где D: x2 + y22x ≤ 0, y≤ 0.
Решение. Подставим в уравнение окружности x2 +y22x = 0 полярные координаты (9) и преобразуем: r22 rcosφ = 0 r =2cosφ. Получили уравнение полуокружности в полярных координатах. Поскольку y≤ 0, то D полукруг (рис.7). При этом .
При движении точки полукруга по лучу Оl от точки О до точки M полярный радиус r изменяется от 0 до координаты r=2cosφ точки M. Следовательно, 0 ≤ r ≤ 2cos φ.
.
Задача 5.
Найти площадь фигуры.
5.1. 5.2. 5.3.
5.4. 5.5. 5.6.
5.7. 5.8. 5.9.
5.10. 5.11. 5.12.
5.13. 5.14. 5.15.
5.16. 5.17. 5.18.
5.19. 5.20. 5.21.
5.22. 5.23. 5.24.
5.25. 5.26. 5.27.
8. Вычисление объема цилиндрического тела. Если в ограниченной области D, то объем цилиндрического тела (рис.1) вычисляется по формуле (2) пункта 3:
Замечание. Прежде чем перейти к примерам на
вычисление объёмов, заметим, что при
вычислении объёма какого-нибудь тела
полезно сделать пространственный
рисунок, который давал бы представление
о форме данного тела. Если же такого
рисунка не удаётся построить, то можно
ограничиться хотя бы рисунком, изображающим
только область интегрирования на
плоскости xOy.
Однако и в этом случае необходимо
представить себе, хотя бы в самых общих
чертах, то тело, объём которого требуется
найти.
Рисунок 8
Примеры. 6). Вычислить объём тела, ограниченного поверхностями , , , .
Решение. Поверхность – это параболический цилиндр с образующей, параллельной оси Oz, и направляющей параболой в плоскости xOy. Наклонная плоскость отсекает на осях координат равные отрезки. Плоскость проходит через ось Oz и прямую в плоскости xOy. – уравнение плоскости xOy. Тело, ограниченное этими поверхностями, изображено на рис.8. Т.к. данное тело цилиндрическое и , то для вычисления его объёма можно использовать формулу (2)
где D = { : , }. Следовательно,
.
7) Найти объем тела, ограниченного поверхностями , , .
Решение.
это круговой цилиндр радиуса 2, ось
которого совпадает с Оy.
параболоид, который пересекает цилиндр
по окружности радиуса 2 в плоскости (рис.
9).
координатная плоскость xOy.
Таким образом, тело ограничено сверху
параболоидом ,
снизу
кругом D , с боков
цилиндрической поверхностью .
Так как данное тело цилиндрическое и ,
то для вычисления его объема можно
использовать формулу (2)
Рисунок 9
где D ={ : , } круг в плоскости xOy (рис 9). Для вычисления этого интеграла перейдем к полярным координатам. При этом круг D преобразуется во множество Dr ={ : , }. По формуле (12) получим
Задача 6. Найти объем тела.
6.1. 6.2.
6.3. 6.4.
6.5. 6.6.
6.7. 6.8.
6.9. 6.10.
6.11. 6.12.
6.13. 6.14.
6.15. 6.16.
6.17. 6.18.
6.19. 6.20.
6.
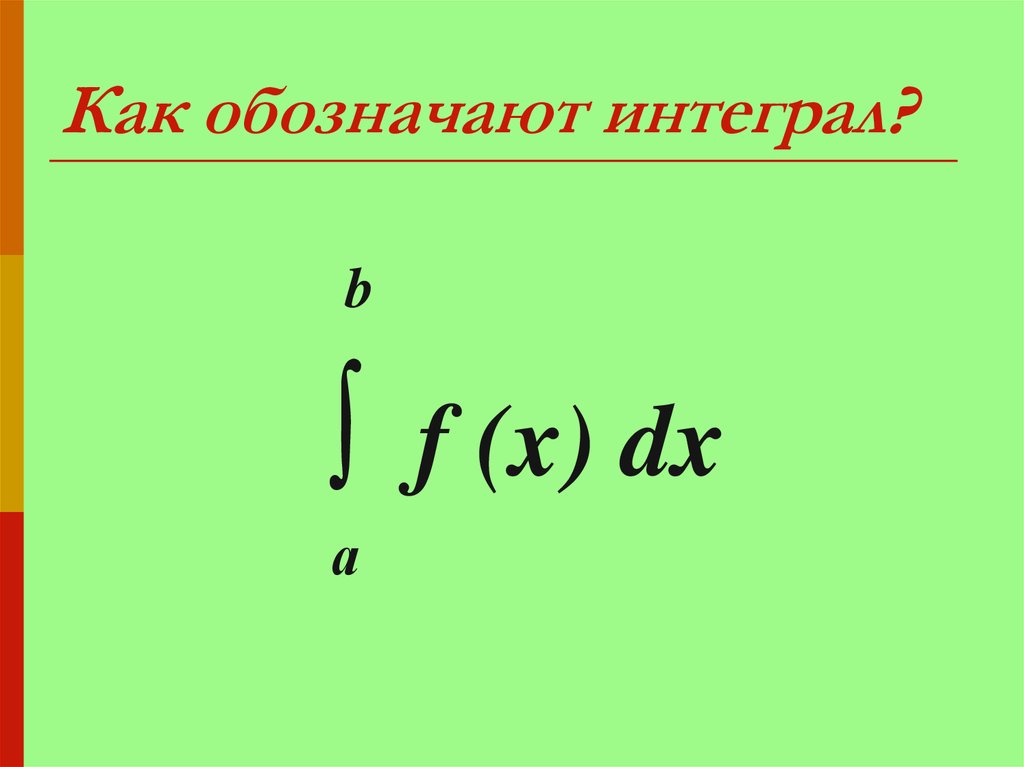21. 6.22.
6.23. 6.24.
6.25. 6.26.
6.27. 6.28.
9. Тройной интеграл. Пусть функция u = f(x,y,z) определена в ограниченной замкнутой области Ω пространства R3. Разобьём область Ω произвольным образом на n элементарных замкнутых областей ω1, … , ωn, имеющих объемы ω1, …, ωn соответственно. Обозначим d – наибольший из диаметров областей ω1, … , ωn. В каждой области ωk выберем произвольную точку Pk (xk, yk , zk) и составим интегральную сумму функции f(x, y, z)
.
Определение.
Тройным
интегралом от функции f(x, y, z) по области Ω называется предел интегральной суммы
,
если он существует.
Интеграция
Неопределенная интеграция означает антидифференцировку ; то есть, учитывая функцию ƒ ( x ), определите наиболее общую функцию F ( x ), производная которой равна ƒ ( x ). Символом этой операции является знак интеграла ∫, за которым следует подынтегральное выражение (интегрируемая функция) и дифференциал, такой как dx , который определяет переменную интегрирования.
С другой стороны, фундаментальная геометрическая интерпретация Определенная интеграция заключается в вычислении площади . То есть для функции ƒ( x ) и интервала a ≤ x ≤ b в ее области определения определенный интеграл от ƒ от a до b дает площадь, ограниченную кривой y = ƒ ( x ), ось x и вертикальные линии x = a и х = б .
Символом этой операции является знак интеграла с пределами интегрирования ( a и b ), ƒ a b , за которыми следуют функция и дифференциал, определяющий переменную интегрирования .
Рисунок 1
Из их определений видно, что процессы неопределенной интеграции и определенной интеграции действительно сильно различаются. неопределенный интеграл функции представляет собой совокупность функций, являющихся ее первообразными, тогда как определенный интеграл функции требует двух пределов интегрирования и дает численный результат, равный площади на плоскости xy . Однако тот факт, что обе операции называются «интегрированием» и обозначаются такими схожими символами, говорит о том, что между ними существует связь.
Основная теорема исчисления говорит, что дифференцирование (нахождение наклона кривой) является операцией, обратной определенному интегрированию (нахождению площади под кривой).
Более подробно, Часть I Основной теоремы говорит, что если функцию интегрировать (образовать определенный интеграл с переменным верхним пределом интегрирования), а затем продифференцировать результат, то восстанавливается исходная функция; то есть дифференциация «отменяет» интеграцию. Часть II дает связь между определенными и неопределенными интегралами. В нем говорится, что определенный интеграл можно вычислить, предварительно определив неопределенный интеграл (поэтому вычисление площади под кривой выполняется путем антидифференцирования).
- Основная теорема исчисления (Часть I ):
- Если I> ƒ является непрерывным, то D DX ∫ x A ƒ ( T ) DT = ƒ ( x ).
- Основная теорема исчисления (Часть II) :
- Если ƒ непрерывна с первообразной F , то ∫ b a ƒ( x ) d x = F ( b ) − F ).
Пример 1 : Вычисление интеграла
Используя первую формулу интегрирования в Таблице 1, каждая функция, производная которой равна ƒ( x ) = x 4 — 3 x 2 + x — 1, равна
, где c — произвольная константа.
ТАБЛИЦА 1 Формулы дифференцирования и интегрирования
Статья об интеграле+исчислении из The Free Dictionary
Интеграл+исчисление | Статья об интеграле+исчислении от The Free DictionaryИнтеграл+исчисление | Статья об интеграле+исчислении от The Free Dictionary
Слово, не найденное в Словаре и Энциклопедии.
Возможно, Вы имели в виду:
Пожалуйста, попробуйте слова отдельно:
интеграл исчисление
Некоторые статьи, соответствующие вашему запросу:
Не можете найти то, что ищете? Попробуйте выполнить поиск по сайту Google или помогите нам улучшить его, отправив свое определение.