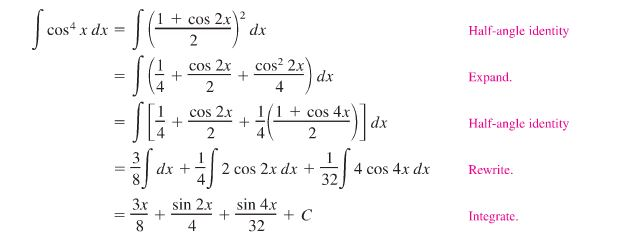Интеграл от косинуса в степени 4: Неопределенный интеграл от косинуса в четвертой степени

2

Интегрирование тригонометрических функций: методы и примеры

• Подынтегральное выражение можно преобразовать из произведения тригонометрических функций в сумму
• Интеграл произведения степеней синуса и косинуса одного и того же аргумента
• Использование метода замены переменной
• Универсальная тригонометрическая подстановка

Будут и задачи для самостоятельного решения, к которым можно посмотреть ответы.

Рассмотрим интегралы, в которых подынтегральная функция представляет собой произведение синусов и косинусов первой степени от икса, умноженного на разные множители, то есть интегралы вида

 (1)

Воспользовавшись известными тригонометрическими формулами

 (2)
 (3)
 (4)
можно преобразовать каждое из произведений в интегралах вида (31) в алгебраическую сумму и проинтегрировать по формулам

 (5)

и

 (6)

• Пригодится: тригонометрические тождества для преобразования выражений

Пример 1. Найти интеграл от тригонометрической функции

Решение. По формуле (2) при

имеем

Поэтому

Применяя далее формулу (5), получим

Пример 2. Найти интеграл от тригонометрической функции

Решение. По формуле (3) при получаем следующее преобразование подынтегрального выражения:

Поэтому

Применяя далее формулу (6), получим

Для самопроверки при расчетах можно воспользоваться

калькулятором неопределённых интегралов онлайн.

• Пригодится: тригонометрические тождества для преобразования выражений

Пример 3. Найти интеграл от тригонометрической функции

Решение. По формуле (4) при получаем следующее преобразование подынтегрального выражения:

Применяя формулу (6), получим

Рассмотрим теперь интегралы от функций, представляющих собой произведение степеней синуса и косинуса одного и того же аргумента, т.е.

 (7)

В частных случаях один из показателей (m или n) может равняться нулю.

При интегрировании таких функций используется то, что чётную степень косинуса можно выразить через синус, а дифференциал синуса равен cos 

x dx (или чётную степень синуса можно выразить через косинус, а дифференциал косинуса равен — sin x dx).

Следует различать два случая: 1) хотя бы один из показателей m и n нечётный; 2) оба показателя чётные.

Пусть имеет место первый случай, а именно показатель n = 2k + 1 — нечётный. Тогда, учитывая, что

получим

Подынтегральное выражение представлено в таком виде, что одна его часть – функция только синуса, а другая – дифференциал синуса. Теперь с помощью замены переменной t = sin x решение сводится к интегрированию многочлена относительно t

. Если же только степень m нечётна, то поступают аналогично, выделяя множитель sinx, выражая остальную часть подынтегральной функции через cos x и полагая t = cos x. Этот приём можно использовать и при интегрировании частного степеней синуса и косинуса, когда хотя бы один из показателей — нечётный. Всё дело в том, что частное степеней синуса и косинуса — это частный случай их произведения: когда тригонометрическая функция находится в знаменателе подынтегрального выражения, её степень — отрицательная. Но бывают и случаи частного тригонометрических функций, когда их степени — только чётные. О них — следующем абзаце.

Если же оба показателя m и n – чётные, то, используя тригонометрические формулы

понижают показатели степени синуса и косинуса, после чего получится интеграл того же типа, что и выше. Поэтому интегрирование следует продолжать по той же схеме. Если же один из чётных показателей — отрицательный, то есть рассматривается частное чётных степеней синуса и косинуса, то данная схема не годится. Тогда используется замена переменной в зависимости от того, как можно преобразовать подынтегральное выражение. Такой случай будет рассмотрен в следующем параграфе.

• Пригодится: тригонометрические тождества для преобразования выражений

Пример 4. Найти интеграл от тригонометрической функции

Решение. Показатель степени косинуса – нечётный. Поэтому представим

в виде

и произведём замену переменной t = sin x (тогда dt = cos x dx). Тогда получим

Возвращаясь к старой переменной, окончательно найдём

Для самопроверки при расчетах можно воспользоваться калькулятором неопределённых интегралов онлайн.

Пример 5. Найти интеграл от тригонометрической функции

.

Решение. Показатель степени косинуса, как и в предыдущем примере – нечётный, но больше. Представим

в виде

и произведём замену переменной t = sin x (тогда dt = cos x dx). Тогда получим

Раскроем скобки

и получим

Возвращаясь к старой переменной, получаем решение

Пример 6. Найти интеграл от тригонометрической функции

Решение. Показатели степени синуса и косинуса – чётные. Поэтому преобразуем подынтегральную функцию так:

Тогда получим

Во втором интеграле произведём замену переменной, полагая t = sin2x. Тогда (1/2)dt = cos2x dx. Следовательно,

а

Окончательно получаем

• Пригодится: тригонометрические тождества для преобразования выражений

Найти интеграл от тригонометрической функции самостоятельно, а затем посмотреть решение

Пример 7. Найти

интеграл от тригонометрической функции

.

Посмотреть правильное решение и ответ.

Нет времени вникать в решение? Можно заказать работу!

Метод замены переменной при интегировании тригонометрических функций можно применять в случаях, когда в подынтегральном выражении присутствует только синус или только косинус, произведение синуса и косинуса, в котором или синус или косинус — в первой степени, тангенс или котангенс, а также частное чётных степеней синуса и косинуса одного и того же аргумента. При этом можно производить перестановки не только sinx = t и sinx = t, но и tgx = t и ctgx = t.

Пример 8. Найти интеграл от тригонометрической функции

.

Решение. Произведём замену переменной: , тогда . Получившееся подынтегральное выражение легко интегрируется по таблице интегралов:

.

Возвращаясь к первоначальной переменной, окончательно получаем:

Для самопроверки при расчетах можно воспользоваться калькулятором неопределённых интегралов онлайн.

• Пригодится: тригонометрические тождества для преобразования выражений

Пример 9. Найти интеграл от тригонометрической функции

.

Решение. Преобразуем тангенс в отношение синуса и косинуса:

.

Произведём замену переменной: , тогда . Получившееся подынтегральное выражение представляет собой табличный интеграл со знаком минус:

.

Возвращаясь к первоначальной переменной, окончательно получаем:

.

Пример 10. Найти интеграл от тригонометрической функции

.

Решение. Произведём замену переменной: , тогда .

Преобразуем подынтегральное выражение, чтобы применить тригонометрическое тождество :

Производим замену переменной, не забывая перед интегралом поставить знак минус (смотрите выше, чему равно dt). Далее раскладываем подынтегральное выражение на множители и интегрируем по таблице:

.

Возвращаясь к первоначальной переменной, окончательно получаем:

.

Для самопроверки при расчетах можно воспользоваться

калькулятором неопределённых интегралов онлайн.

Найти интеграл от тригонометрической функции самостоятельно, а затем посмотреть решение

Пример 11. Найти интеграл от тригонометрической функции

.

Посмотреть правильное решение и ответ.

• Пригодится: тригонометрические тождества для преобразования выражений

Универсальную тригонометрическую подстановку можно применять в случаях, когда подынтегральное выражение не подпадает под случаи, разобранные в предыдущих параграфах. В основном, когда синус или косинус (или и то, и другое) находятся в знаменателе дроби.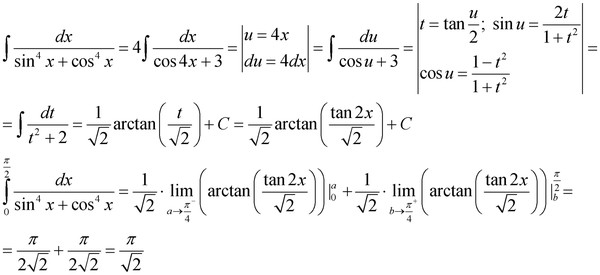 Доказано, что синус и косинус можно заменить другим выражением, содержащим тангенс половины исходного угла следующим образом:

где .

Тогда .

Но заметим, что универсальная тригонометрическая подстановка часто влечёт за собой довольно сложные алгебраические преобразования, поэтому её лучше применять, когда никакой другой метод не работает. Разберём примеры, когда вместе с универсальной тригонометрической подстановкой используются подведение под знак дифференциала и метод неопределённых коэффициентов.

Пример 12. Найти интеграл от тригонометрической функции

.

Решение. Решение. Воспользуемся универсальной тригонометрической подстановкой. Тогда
.

Дроби в числителе и знаменателе умножаем на , а двойку выносим и ставим перед знаком интеграла. Тогда

Чтобы в результате преобразований прийти к табличному интегралу, попытаемся получить в знаменателе полный квадрат. Для этого умножим числитель и знаменатель подынтегрального выражения на 2. Применяем интегрирование подведением под знак дифференциала. Получим

К полученному результату преобразований можем теперь применить табличный интеграл 21. В результате получаем окончательное решение:

.

Пример 13. Найти интеграл от тригонометрической функции

.

Решение. Решение. Воспользуемся универсальной тригонометрической подстановкой. Тогда
.

Дроби в числителе и знаменателе умножаем на , а двойку выносим и ставим перед знаком интеграла. Тогда

.

Чтобы в результате преобразований прийти к табличному интегралу, попытаемся получить в знаменателе полный квадрат. Для этого умножим числитель и знаменатель подынтегрального выражения на 3. Применяем интегрирование подведением под знак дифференциала. Получим

К полученному результату преобразований можем теперь применить табличный интеграл 21. В результате получаем окончательное решение:

.

Пример 14. Найти интеграл от тригонометрической функции

.

Решение. Решение. Воспользуемся универсальной тригонометрической подстановкой. Тогда

Используем метод неопределённых коэффициентов. Получим следующее подынтегральное выражение:

Чтобы найти коэффициенты, решим систему уравнений:

Теперь получаем:

Используем подведение под знак дифференциала:

К последнему слагаемому применяем замену переменной , тогда . Получаем:

Преобразуем и вернём на место первоначальную переменную и окончательно получим решение:

• Пригодится: тригонометрические тождества для преобразования выражений

Назад

Листать

Вперёд>>>

К началу страницы

Пройти тест по теме Интеграл

Начало темы «Интеграл»

Неопределённый интеграл: основные понятия, свойства, таблица неопределённых интегралов

Найти неопределённый интеграл: начала начал, примеры решений

Метод замены переменной в неопределённом интеграле

Интегрирование подведением под знак дифференциала

Метод интегрирования по частям

Интегрирование дробей

Интегрирование рациональных функций и метод неопределённых коэффициентов

Интегрирование некоторых иррациональных функций

Продолжение темы «Интеграл»

Определённый интеграл

Несобственные интегралы

Площадь плоской фигуры с помощью интеграла

Объём тела вращения с помощью интеграла

Вычисление двойных интегралов

Длина дуги кривой с помощью интеграла

Площадь поверхности вращения с помощью интеграла

Определение работы силы с помощью интеграла

исчисление — Определенный интеграл четных степеней косинуса.