Интеграл степенной функции: Интеграл степенной функции, x^n

{2}}}=3 \sqrt[3]{x}+C \)

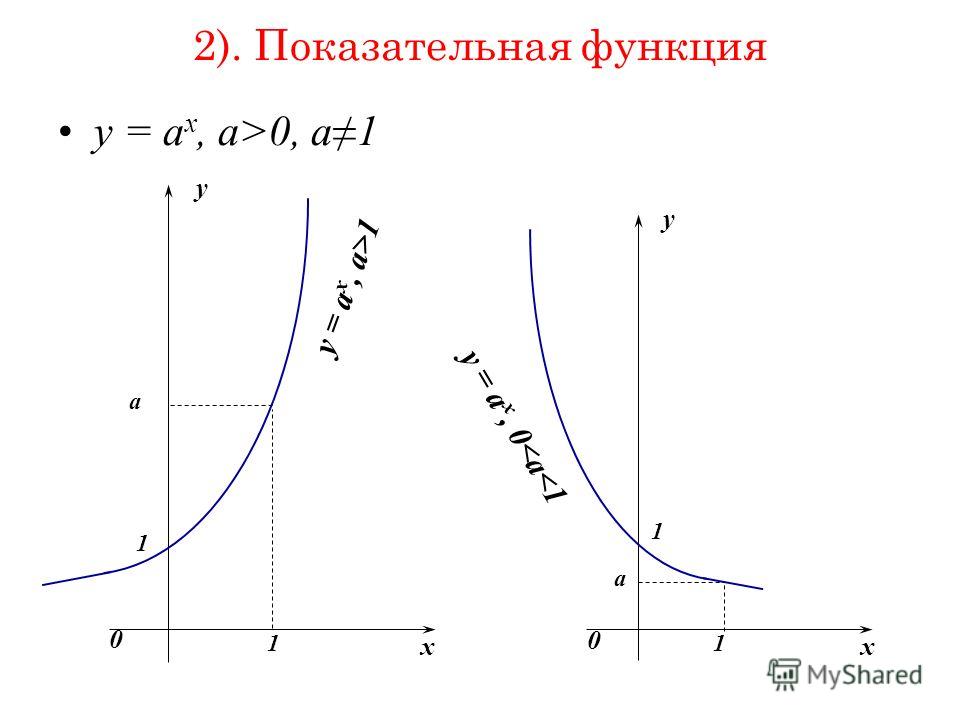
Физика

166

Реклама и PR

31

Педагогика

80

Психология

72

Социология

7

Астрономия

9

Биология

30

Культурология

86

Экология

8

Право и юриспруденция

36

Политология

13

Экономика

49

Финансы

9

История

16

Философия

8

Информатика

20

Право

35

Информационные технологии

6

Экономическая теория

7

Менеджент

719

Математика

338

Химия

20

Микро- и макроэкономика

1

Медицина

5

Государственное и муниципальное управление

2

География

542

Информационная безопасность

2

Аудит

11

Безопасность жизнедеятельности

3

Архитектура и строительство

1

Банковское дело

1

Рынок ценных бумаг

6

Менеджмент организации

2

Маркетинг

238

Кредит

3

Инвестиции

2

Журналистика

1

Конфликтология

15

Этика

9

Формулы дифференцирования Интеграл от экспоненты Интеграл от корня Интеграл от дроби Интеграл произведения функций

Узнать цену работы

Узнай цену

своей работы

Имя

Выбрать тип работыЧасть дипломаДипломнаяКурсоваяКонтрольнаяРешение задачРефератНаучно — исследовательскаяОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерскаяНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация в ВАКПубликация в ScopusДиплом MBAПовышение оригинальностиКопирайтингДругое

Принимаю  Политику  конфиденциальности

Подпишись на рассылку, чтобы не пропустить информацию об акциях

Таблица первообразных.

Таблица интегралов. Таблица неопределенных интегралов.

Таблица первообразных («интегралов»). Таблица интегралов. Табличные неопределенные интегралы.

(Простейшие интегралы и интегралы с параметром). Формулы интегрирования по частям. Формула Ньютона-Лейбница.

• Справочно: Таблица производных.
• Справочно: Таблицы неопределенных интегралов. Смолянский М.Л. ГИФМЛ 1963. (.djvu — 1Mb)

Таблица первообразных («интегралов»). Табличные неопределенные интегралы. (Простейшие интегралы и интегралы с параметром).

Интеграл степенной функции.	Интеграл степенной функции.
Интеграл, сводящийся к интегралу степенной функции, если загнать х под знак диффференциала.
—
Интеграл экспоненциальной функции.	Интеграл экспоненты, где a-постоянное число.
Интеграл сложной экспоненциальной функции.	Интеграл экспоненциальной функции.
—
Интеграл, равняющийся натуральному логарифму.	Интеграл : «Длинный логарифм».
	Интеграл : «Длинный логарифм».
Интеграл : «Высокий логарифм».	Интеграл, где х в числителе заводится под знак дифференциала (константу под знаком можно как прибавлять, так и отнимать), в итоге схож с интегралом, равным натуральному логарифму.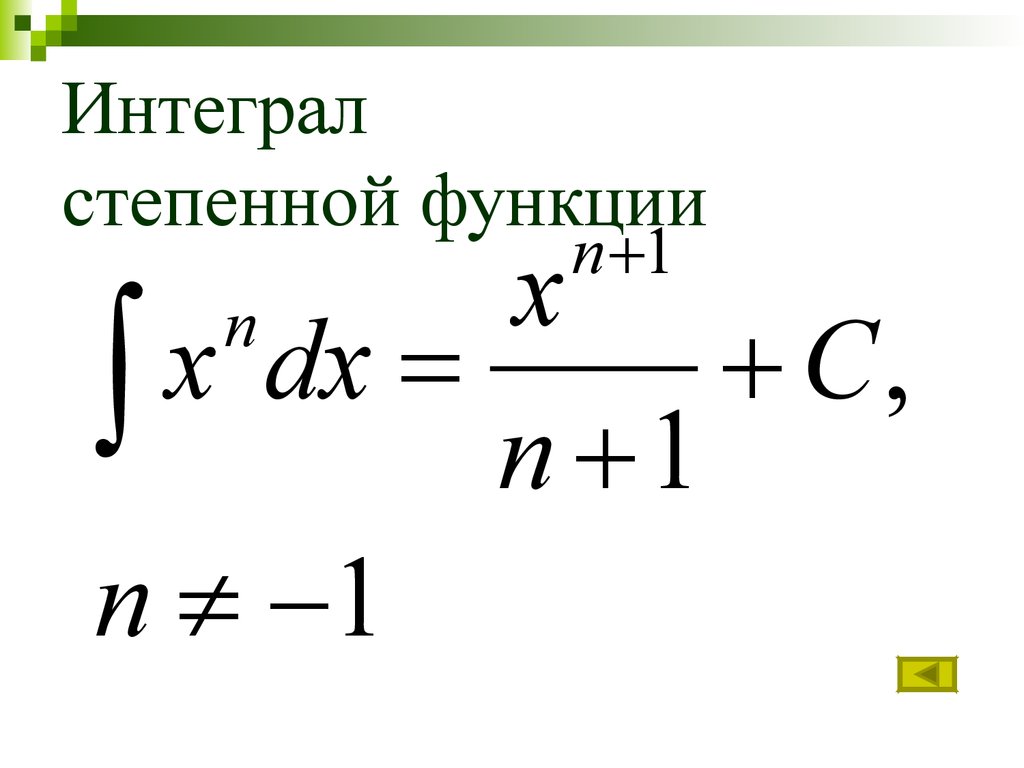
Интеграл : «Высокий логарифм».
—
Интеграл косинуса.	Интеграл синуса.
Интеграл, равный тангенсу.	Интеграл, равный котангенсу.
—
Интеграл, равный как арксинусу, так и арккосинусу	Интеграл, равный как арктангенсу, так и арккотангенсу.
Интеграл, равный как арксинусу, так и арккосинусу.	Интеграл, равный как арктангенсу, так и арккотангенсу.
Интеграл равный косекансу.	Интеграл, равный секансу.
Интеграл, равный арксекансу.	Интеграл, равный арккосекансу.
Интеграл, равный арксекансу.	Интеграл, равный арксекансу.
—
Интеграл, равный гиперболическому синусу.	Интеграл, равный гиперболическому косинусу.
Интеграл, равный гиперболическому тангенсу.	Интеграл, равный гиперболическому котангенсу.
Интеграл, равный гиперболическому синусу, где sinhx — гиперболический синус в ангийской версии.	Интеграл, равный гиперболическому косинусу, где sinhx — гиперболический синус в ангийской версии.
Интеграл, равный гиперболическому тангенсу.	Интеграл, равный гиперболическому котангенсу.
Интеграл, равный гиперболическому секансу.	Интеграл, равный гиперболическому косекансу.

• Справочно: Таблица производных.

Формулы интегрирования по частям. Правила интегрирования.

Формулы интегрирования по частям. Формула Ньютона-Лейбница.Правила интегрирования.

Интегрирование произведения (функции) на постоянную:
Интегрирование суммы функций:
Формула интегрирования по частям неопределенные интегралы:
Формула интегрирования по частям определенные интегралы:
Формула Ньютона-Лейбница определенные интегралы:	Где F(a),F(b)-значения первообразных в точках b и a соответственно.

Описание раздела: Таблица первообразных. Таблица интегралов.

Интеграл силы | Superprof

В этой статье вы узнаете, как рассчитать интеграл мощности. Но прежде чем приступить к нахождению интеграла мощности, сначала давайте посмотрим, что такое интегралы.

Что такое интегралы?

Интегралы функций рассчитываются с помощью процесса, известного как интегрирование . В математике интегрирование используется для вычисления значений важных величин, например, площади, объема, перемещения и т. д. Когда мы говорим, что собираемся вычислить интеграл от данной функции, то на самом деле имеем в виду, что мы вычислим определенный интеграл функции. Концепция интегрирования помогает нам найти проблемную функцию, учитывая производные функции. Это также помогает нам вычислить площадь, ограниченную графиком функции при некоторых ограничениях.

Основная теорема исчисления связывает процессы дифференцирования и интегрирования. На самом деле интегрирование — это , обратное дифференцированию . Поиск решений небольших задач на сложение прост и может выполняться как вручную, так и с помощью калькуляторов. Однако для более крупных задач используются методы интегрирования.

В следующем разделе мы увидим, как использовать степенное правило интегрирования для нахождения интегралов функций, включающих степени или показатели.

Лучшие репетиторы по математике

Поехали

Степенная формула для интегралов

Мы можем использовать интегральную степенную формулу для вычисления интегралов широкого диапазона многочленов, корней и рациональных функций. Формула степенного правила для вычисления интегралов степенной функции приведена ниже:

Чтобы использовать это правило, мы просто берем показатель степени и добавляем к нему единицу. Затем мы делим выражение с тем же числом. На последнем шаге мы добавляем константу C.

Теперь мы решим несколько примеров, в которых найдем интегралы от многочленов и корневые функции.

Пример 1

Найти

Решение

Сначала разложим интегралы, используя сложение/вычитание или умножение на константы. Следовательно, мы можем написать приведенную выше функцию следующим образом:

Теперь мы сдвинем константы перед знаком интеграла следующим образом:

Теперь мы применим степенное правило следующим образом:

На последнем шаге запишите окончательный ответ в наиболее упрощенной форме, например:

 

Пример 2

Найти

Решение

Сначала разложим интегралы с помощью сложения/вычитания. умножение на константы. Следовательно, мы можем записать приведенную выше функцию следующим образом:

Теперь мы сместим константы перед знаком интеграла следующим образом:

Теперь мы применим правило степени, чтобы найти интегралы от степеней и интеграла постоянное правило для вычисления интеграла от последнего члена вышеуказанного многочлена:

На последнем шаге запишите окончательный ответ в наиболее упрощенной форме, например:

 

Пример 3

Найдите

Решение

Сначала разложим интегралы с помощью сложения/вычитания. умножение на константы. Следовательно, мы можем записать приведенную выше функцию следующим образом:

Теперь мы сместим константы перед знаком интеграла следующим образом:

Теперь мы применим правило степени, чтобы найти интегралы от степеней и интеграла постоянное правило для вычисления интеграла от последнего члена вышеуказанного многочлена:

На последнем шаге запишите окончательный ответ в наиболее упрощенной форме, например:

 

Пример 4 вычитание или умножение на константы.

Следовательно, мы можем записать приведенную выше функцию следующим образом:

Теперь мы сместим константы перед знаком интеграла следующим образом:

Теперь мы применим правило степени, чтобы найти интегралы от степеней и интеграла постоянное правило для вычисления интеграла от последнего члена вышеуказанного многочлена:

На последнем шаге запишите окончательный ответ в его наиболее упрощенной форме, например:

 

Пример 5

Найти

Решение

Помните, что форма может быть записана в экспоненциальном виде. Следовательно, мы можем написать функцию следующим образом:

В следующем разделе мы будем применять правило мощности следующим образом:

Упростим приведенное выше выражение, чтобы получить окончательный ответ:

Мы также можем написать ответ в экспоненциальной форме, такой как это:

Пример 6

Найти

Решение

Напишите функцию в экспоненциальной форме. используя знак интеграла с обоими терминами, как показано ниже:

Используйте степенное правило для интегрирования функции следующим образом:

Упростите приведенное выше выражение, чтобы получить окончательный ответ:

Мы можем написать ответ в экспоненциальной форме, такой как это:

Пример 7

Найти

Решение

Мы можем переписать вышеупомянутое выражение в терминах экспонентов:

Переписывание. выше выражение, снова используя знак интегрирования с обоими членами:

На следующем шаге примените правило степени, чтобы найти интеграл функции следующим образом:

Упростите приведенное выше выражение, чтобы записать окончательный ответ:

 

Правило мощности: определение, формула и пример . Вы бы помыли посуду вручную, если бы у вас была посудомоечная машина? Или перепечатать абзац, если можно скопировать и вставить? То же самое можно сказать и о математике!

Возьмем, к примеру, производную.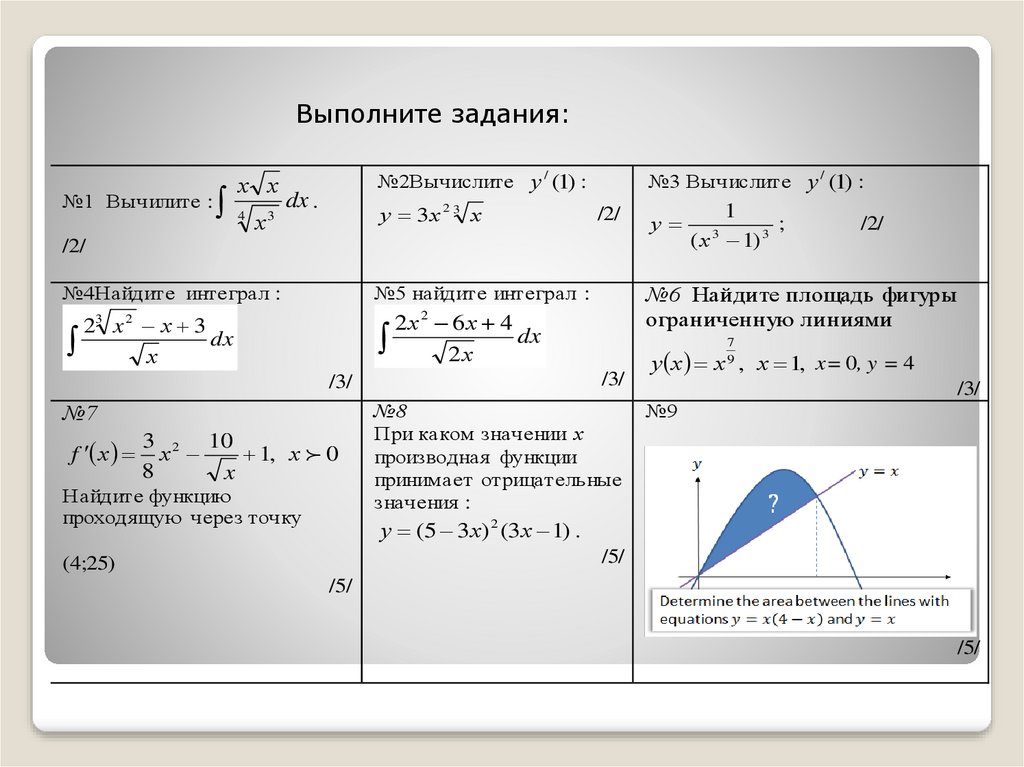 Нахождение производной функции — одна из основных операций исчисления. Однако использование пределов может занять много времени, так как требуется много шагов и множество алгебраических операций. Вот пример этого процесса.

Найдите производную f(x)=x2.

Используйте определение производной.

dfdx=limh→0f(x+h)-f(x)h

Вычислить f(x+h) и f(x).

dfdx=limh→0(x+h)2-x2h

Развернуть (x+h)2.

dfdx=limh→0x2+2xh+h3-x2h

Упрощение.

dfdx=limh→02x+h

Оценить предел.

dfdx=2x

Производная f(x)=x2isdfdx=2x.

Много шагов, да? Вместо того, чтобы выполнять все эти процедуры, в математическом анализе есть много формул, которые мы можем использовать для нахождения производных с меньшим количеством шагов, экономя наше время и умственную энергию. Эти формулы известны как производные правила, и одним из таких производных правил является правило степени .

Формула степенного правила и примеры

Одной из основных функций в исчислении является степенная функция.

Питание Функции — это функции, в которых переменная является основанием и возводится в любую степень действительного числа.

f(x)=xn

Эти функции необходимы в исчислении для создания более сложных функций, таких как полиномиальные функции или рациональные функции. Мы можем найти производную степенной функции, используя так называемое степенное правило. Давайте посмотрим на это.

Правило степеней — это формула для нахождения производной степенной функции. Пусть n — действительное число, тогда:

ddxxn=nxn-1

Это правило может сделать нахождение производных в исчислении намного проще! Давайте посмотрим на некоторые примеры.

Найдите производную f(x)=x5.

Определите мощность функции мощности. Эта функция имеет степень 5.

f(x)=x5

Дифференцируйте, используя правило степени.

dfdx=5×5-1

Упростите показатель степени.

dfdx=5×4

Производная от f(x)=x5isdfdx=5×4.

Мы можем использовать правило степени в сочетании с другими правилами дифференцирования, чтобы найти производную полиномиальной функции. Давайте рассмотрим пример этого процесса.

Найдите производную g(x)=3×4-2×3+x.

Используйте правила суммы, разности и постоянного множителя.

dgdx=3ddxx4-2ddxx3+ddxx

Дифференцируйте по правилу мощности.

dgdx=3(4×3)-2(3×2)+x0

Упрощение.

dgdx=12×3-6×2+1

Производная g(x)=3×4-2×3+xisdgdx=12×3-6×2+1.

Вывод степенного правила

Чтобы доказать степенное правило, мы рассмотрим производную от f(x)=xn, используя ограничения. Нам нужно найти такую ​​производную, используя пределы только один раз, доказав нашу формулу.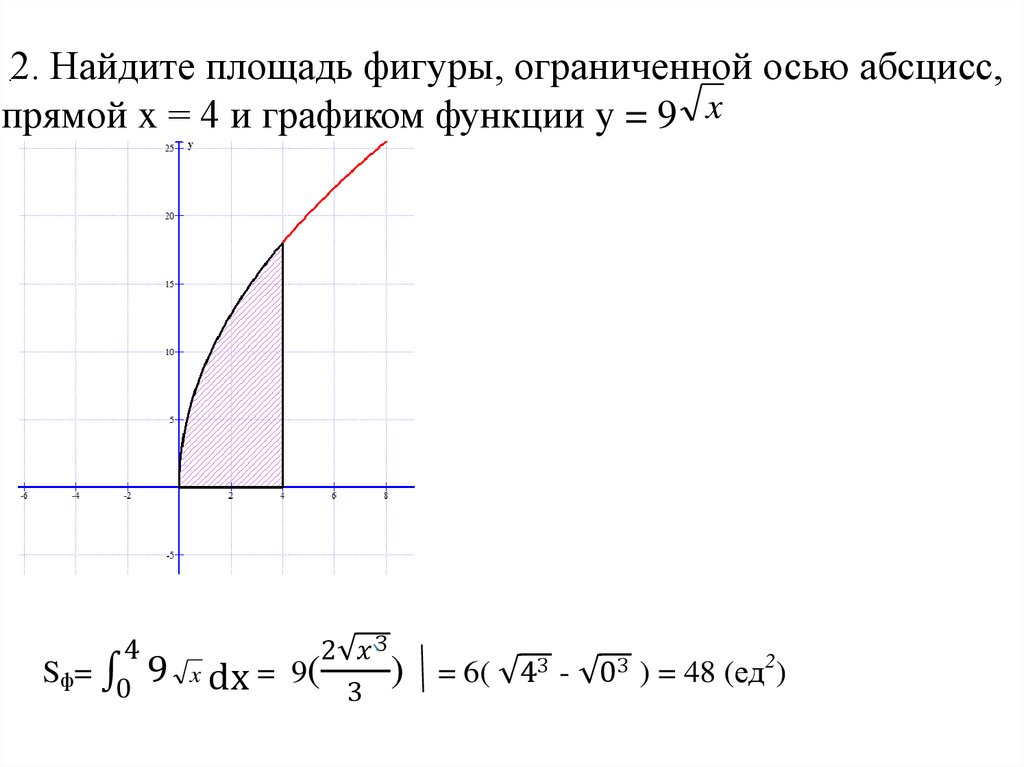 Затем мы можем использовать формулу всякий раз, когда нам нужно дифференцировать степенную функцию.

Начнем с определения производной.

ddxxn=limh→0f(x+h)-f(x)h

Затем оцените f(x+h) и f(x).

ddxxn=limh→0(x+h)n-xnh

Мы можем использовать биномиальную теорему, чтобы разложить (x+h)n.

(x+h)n=n0xn+n1xn-1h+n2xn-2h3+…+nnhn

Первые два биномиальных коэффициента равны 1 и n соответственно.

(x+h)n=xn+nxn-1h+n2xn-2h3+…+nnhn

Чтобы отразить определение производной, нам нужно вычесть xn и разделить на h в обеих частях уравнения.

Теперь у нас есть следующее выражение:

(x+h)n-xnh=nxn-1+n2xn-2h+…+nnhn-1

Когда мы берем предел, когда h стремится к 0, каждый член, содержащий h, исчезает. Следовательно, у нас осталось только nxn-1.

limh→0(x+h)n-xnh=nxn-1

Наконец, мы пришли к степенному правилу.

ddxxn=nxn-1

Степенное правило для отрицательных и дробных степеней

Мы доказали только случай с положительными целыми числами. Однако мы можем использовать правило мощности, когда мощности отрицательны. Формула та же.

Найдите производную g(x)=x-3.

Определите мощность функции мощности. В этом случае мощность равна -3.

g(x)=x-3

Дифференцируйте по степенному правилу.

dgdx=-3x-3-1

Упростите показатель степени.

dgdx=-3x-4

Мы также можем использовать правило степени для дробных степеней, как в случае функции квадратного корня.

Найдите производную h(x)=x.

Запишите корень в виде дробной степени.

h(x)=x12

Дифференцируйте по степенному правилу.

dhdx=12×12-1

Упростите питание.

dhdx=12x-12

Запишите в знаменателе отрицательную степень.

dhdx=121×12

Запишите мощность как корень.

dhdx=121x

Правило степени работает, когда n — любое действительное число. К счастью, формула одинакова для всех случаев!

Другие примеры правила степени

Исчисление полно различных функций, к которым мы можем применять правила дифференцирования. В этом разделе мы рассмотрим больше примеров производных с использованием степенного правила.

Найдите производную f(x)=2×4-x2.

Используйте правила суммы, разности и постоянного множителя.

dfdx=2ddxx4-ddxx2

Дифференцируйте с помощью правила степени.

dfdx=2(4×3)-2x

Упрощение.

dfdx=8×3-2x

В следующем примере рассматриваются отрицательные степени.

Найдите производную g(x)=x2+1×2.

Запишите мощность в знаменателе как отрицательную мощность.

g(x)=x2+x-2

Используйте правило сумм.

dgdx=ddx(x2)+ddx(x-2)

Дифференцируйте, используя правило степени.

dgdx=2x-2x-3

Запишите отрицательный показатель в качестве знаменателя.

dgdx=2x-2×3

Давайте посмотрим на другие корни, которые мы можем записать в виде дробных степеней.

Найдите производную h(x)=x3+1×5.

Запишите корень в виде дробной степени.

h(x)=x13+1×5

Запишите степень в знаменателе как отрицательную степень.

ч(х)=х13+х-5

Используйте правило сумм.

dhdx=ddxx13+ddxx-5

Различайте с помощью правила степени.

dhdx=13×13-1-5x-5-1

Упростите полномочия.

dhdx=13x-23-5x-6

Запишите отрицательные степени как знаменатели.

dhdx=131×23-5×6

Запишите дробные степени в виде степени и корня.

dhdx=131×23-5×6

При достаточной практике мы можем пропустить некоторые из этих шагов.

Распространенные ошибки при использовании правила степени

Мы не можем использовать правило степени, если переменная является степенью выражения.