Радиус и интервал сходимости степенного ряда — Студопедия
Из теоремы Абеля следует, что если степенной ряд сходится, при некотором значении х0, то этот ряд абсолютно сходится в промежутке изменения от -х0 до х0, (-х0;х0).
Если при некотором значении 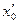 ряд расходится, то он расходится для всех х удовлетворяющих неравенствам
ряд расходится, то он расходится для всех х удовлетворяющих неравенствам 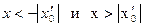 , или
, или 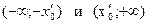 — интервалы расходимости.
— интервалы расходимости.
Определение: Интервал (-R;+R), внутри которого степенной ряд сходится, называется интервалом сходимости ряда. Половина интервала сходимости ряда называется радиусом сходимости.
(-R;+R)- интервал сходимости;
R- радиус сходимости.
На концах интервала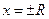
1. Если ряд (1) сходится в точке х=0, то R=0
2. Если ряд (1)сходится для любого х, то 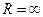
3. Если ряд (1) сходится в (-R;+R), то в x= -R и x= +R степенной ряд исследуется особо.
Укажем способ определения радиуса сходимости степенного ряда. 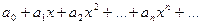 (1)
(1)
Рассмотрим ряд, составленный из абсолютных величин его членов:
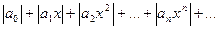 (4)
(4)
Для определения сходимости ряда (4) применим признак Даламбера. Допустим, что существует предел:
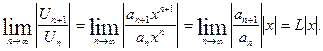
По признаку Даламбера ряд (4) сходится,
если 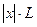
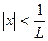 и расходится если
и расходится если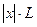 >1, т.е.
>1, т.е. 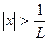 .
.
Из предыдущего следует, что интервал сходимости 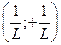 обозначим
обозначим 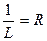 , тогда
, тогда 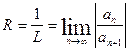 (по Даламберу).
(по Даламберу).
Аналогичным образом можно определить интервал сходимости по признаку Коши.
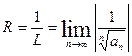 .
.
Рассмотрим примеры: Определить интервалы сходимости степенных рядов
1) 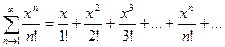
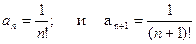
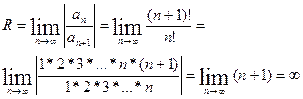
ряд сходится всюду  .
.
2)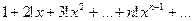
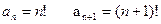
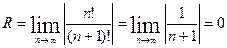
R=0. Ряд сходится в х=0.
3)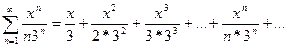
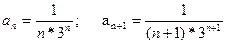
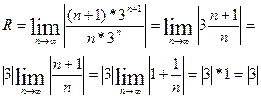
(-3;+3) — интервал сходимости. Исследуем ряд на концах:
х=-3.
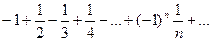 условно сходится
условно сходится
х=3
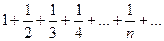 расходится
расходится
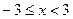 или [-3;3) интервал сходимости.
или [-3;3) интервал сходимости.
Сходимость степенных рядов — Студопедия
Выясним вопрос о сходимости степенного ряда (3).
Область сходимости степенного ряда (3) содержит по крайней мере одну точку: 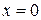 (ряд (4) сходится в точке
(ряд (4) сходится в точке 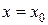 ).
).
2.1. Теорема Абеля
Об области сходимости степенного ряда можно судить, исходя из следующей теоремы:
Теорема 1 (Абель). Если степенной ряд (3) сходится при 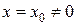 , то он абсолютно сходится при всех значениях х, удовлетворяющих неравенству
, то он абсолютно сходится при всех значениях х, удовлетворяющих неравенству 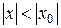 .
.
По условию ряд 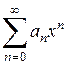 сходится. Следовательно, по необходимому признаку сходимости
сходится. Следовательно, по необходимому признаку сходимости 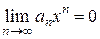 . Отсюда следует, что величина
. Отсюда следует, что величина 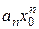 ограничена, т.е. найдется такое число M > 0, что для всех n выполняется неравенство
ограничена, т.е. найдется такое число M > 0, что для всех n выполняется неравенство 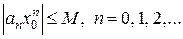
Пусть 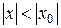
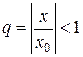 и, следовательно,
и, следовательно,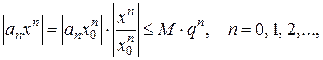
т. е. модуль каждого члена ряда (3) не превосходит соответствующего члена сходящегося 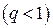 ряда геометрической прогрессии. Поэтому по признаку сравнения при
ряда геометрической прогрессии. Поэтому по признаку сравнения при 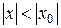 ряд (3) абсолютно сходящийся.
ряд (3) абсолютно сходящийся.
Следствие 1. Если ряд (3) расходится при 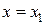 , то он расходится и при всех х , удовлетворяющих неравенству
, то он расходится и при всех х , удовлетворяющих неравенству 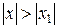 .
.
Действительно, если допустить сходимость ряда в точке 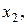
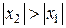 , то по теореме Абеля ряд сходится при всех х, для которых
, то по теореме Абеля ряд сходится при всех х, для которых 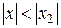 , и, в частности, в точке
, и, в частности, в точке 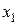 , что противоречит условию.
, что противоречит условию.2.2. Интервал и радиус сходимости степенного ряда
Из теоремы Абеля следует, что если 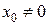 есть точка сходимости степенного ряда, то интервал
есть точка сходимости степенного ряда, то интервал 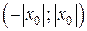 весь состоит из точек сходимости данного ряда; при всех значениях х вне этого интервала ряд (3) расходится.
весь состоит из точек сходимости данного ряда; при всех значениях х вне этого интервала ряд (3) расходится.
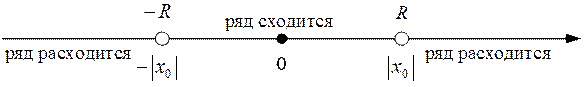
Рис. 1
Интервал 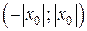 и называют интервалом сходимости степенного ряда. Положив
и называют интервалом сходимости степенного ряда. Положив 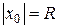 , интервал сходимости можно записать в виде
, интервал сходимости можно записать в виде 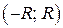 . Число R называют радиусом сходимости степенного ряда, т. е. R>0 – это такое число, что при всех х, для которых
. Число R называют радиусом сходимости степенного ряда, т. е. R>0 – это такое число, что при всех х, для которых 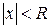 , ряд (3) абсолютно сходится, а при
, ряд (3) абсолютно сходится, а при 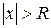 расходится (см. рис. 1).
расходится (см. рис. 1).
В частности, когда ряд (3) сходится лишь в одной точке 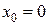 , то считаем, что R = 0. Если же ряд (3) сходится при всех значениях
, то считаем, что R = 0. Если же ряд (3) сходится при всех значениях 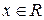
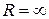 .
.Отметим, что на концах интервала сходимости (т. е. при 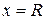 и при
и при 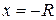 ) сходимость ряда проверяется в каждом случае отдельно.
) сходимость ряда проверяется в каждом случае отдельно.
Для нахождения радиуса сходимости степенного ряда (3) можно поступить следующим образом. Составим ряд из модулей членов данного степенного ряда
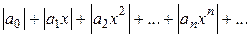
и применим к нему признак Даламбера. Допустим, что существует предел
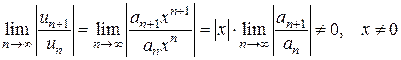
По признаку Даламбера ряд сходится, если 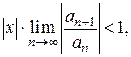 т. е. ряд сходится при тех значениях х, для которых
т. е. ряд сходится при тех значениях х, для которых
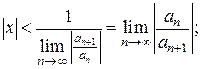
ряд, составленный из модулей членов ряда (3), расходится при тех значениях х, для которых 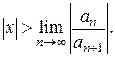 Таким образом, для ряда (3) радиус абсолютной сходимости
Таким образом, для ряда (3) радиус абсолютной сходимости
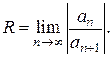 (5)
(5)
Аналогично, воспользовавшись радикальным признаком Коши, можно установить, что
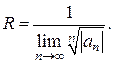 (6)
(6)
Замечания.
1.Если 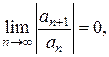 то можно убедиться, что ряд (3) абсолютно сходится на всей числовой оси. В этом случае
то можно убедиться, что ряд (3) абсолютно сходится на всей числовой оси. В этом случае 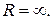
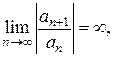 то
то 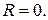
2. Интервал сходимости степенного ряда (4) находят из неравенства 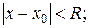 имеет вид
имеет вид 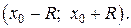
3. Если степенной ряд содержит не все степени х, т. е. задан неполный степенной ряд, то интервал сходимости ряда находят без определения радиуса сходимости (формулы (5) и (6)), а непосредственно применяя признак Даламбера (или Коши) для ряда, составленного из модулей членов данного ряда.
Пример 3. Найти область сходимости ряда 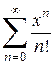 .
.
Решение. Воспользуемся формулой (5):
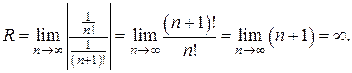
Следовательно, данный ряд абсолютно сходится на всей числовой оси.
Пример 4. Найти область сходимости ряда
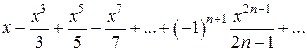 .
.
Решение. Заданный ряд неполный. Воспользуемся признаком Даламбера. Для данного ряда имеем:
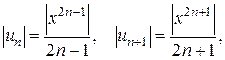
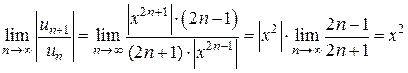 .
.
Ряд абсолютно сходится, если  Исследуем поведение ряда на концах интервала сходимости.
Исследуем поведение ряда на концах интервала сходимости.
При 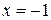 имеем ряд
имеем ряд 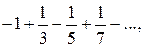 который сходится по признаку Лейбница.
который сходится по признаку Лейбница.
При 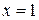 имеем ряд
имеем ряд 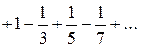 – это тоже сходящийся лейбницевский ряд. Следовательно, областью сходимости исходного ряда является отрезок
– это тоже сходящийся лейбницевский ряд. Следовательно, областью сходимости исходного ряда является отрезок 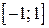 .
.
Пример 5. Найти область сходимости ряда
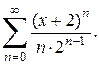
Решение. Находим радиус сходимости ряда по формуле (5):
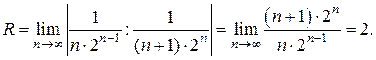
Следовательно, ряд сходится при 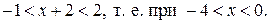
При 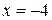 имеем ряд
имеем ряд
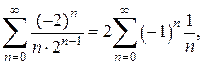
который сходится по признаку Лейбница.
При 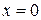 имеем расходящийся ряд
имеем расходящийся ряд
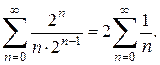
Следовательно, областью сходимости исходного ряда является полуотрезок 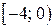 .
.
Интервал и радиус сходимости степенного ряда — КиберПедия
Из теоремы Абеля следует, что если 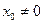 есть точка сходимости степенного ряда, то интервал
есть точка сходимости степенного ряда, то интервал  весь состоит из точек сходимости данного ряда; при всех значениях х вне этого интервала ряд
весь состоит из точек сходимости данного ряда; при всех значениях х вне этого интервала ряд  расходится.
расходится.
Интервал  и называют интервалом сходимости степенного ряда. Положив
и называют интервалом сходимости степенного ряда. Положив 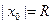 , интервал сходимости можно записать в виде ( -R;R). Число R называют радиусом сходимостистепенного ряда, т.е. R>0 – это такое число, что при всех х , для которых
, интервал сходимости можно записать в виде ( -R;R). Число R называют радиусом сходимостистепенного ряда, т.е. R>0 – это такое число, что при всех х , для которых 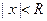 , ряд
, ряд  абсолютно сходится, а при
абсолютно сходится, а при 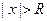 – расходится.
– расходится.
В частности, когда ряд  сходится лишь в одной точке
сходится лишь в одной точке  , то считаем, что R=0. Если же ряд сходится при всех значениях
, то считаем, что R=0. Если же ряд сходится при всех значениях 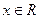 , то считаем, что
, то считаем, что 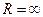 .
.
Отметим, что на концах интервала сходимости (т.е. при х= R и при х= -R ) сходимость ряда проверяется в каждом случае отдельно.
Для нахождения радиуса сходимости степенного ряда  можно поступить следующим образом. Составим ряд из модулей членов данного степенного ряда
можно поступить следующим образом. Составим ряд из модулей членов данного степенного ряда

и применим к нему признак Даламбера. Допустим, что существует предел
 ,
, 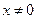
По признаку Даламбера ряд сходится, если  , т.е. ряд сходится при тех значениях х , для которых
, т.е. ряд сходится при тех значениях х , для которых  ; ряд, составленный из модулей члена ряда
; ряд, составленный из модулей члена ряда  , расходится при тех значениях х, для которых
, расходится при тех значениях х, для которых 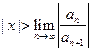 .Таким образом, для ряда
.Таким образом, для ряда  радиус абсолютной сходимости
радиус абсолютной сходимости

Аналогично, воспользовавшись радикальным признаком Коши, можно установить, что
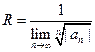
Свойства степенных рядов
1. Сумма S(x) степенного ряда  является непрерывной функцией в интервале сходимости ( -R;R).
является непрерывной функцией в интервале сходимости ( -R;R).
2. Степенные ряды 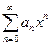 и
и  , имеющие радиусы сходимости соответственно
, имеющие радиусы сходимости соответственно 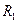 и
и 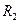 , можно почленно складывать, вычитать и умножать. Радиус сходимости произведения, суммы и разности рядов не меньше, чем меньшее из чисел
, можно почленно складывать, вычитать и умножать. Радиус сходимости произведения, суммы и разности рядов не меньше, чем меньшее из чисел 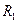 и
и 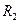 .
.
3. Степенной ряд внутри интервала сходимости можно почленно дифференцировать; при этом для ряда
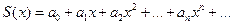
при –R<x<R выполняется равенство
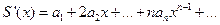
Степенной ряд можно почленно интегрировать на каждом отрезке, расположенном внутри интервала сходимости; при этом для ряда 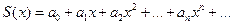 при –R<a<x<R выполняется равенство
при –R<a<x<R выполняется равенство

Ряды 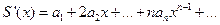 и
и  имеют тот же радиус сходимости, что и исходный степенной ряд.
имеют тот же радиус сходимости, что и исходный степенной ряд.
Разложение функций в степенные ряды
Ряды Тейлора и Маклорена
Как известно, для любой функции 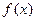 определенной в окрестности точки
определенной в окрестности точки 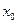 и имеющей в ней производные до ( n+1)- го порядка включительно, справедлива формула Тейлора:
и имеющей в ней производные до ( n+1)- го порядка включительно, справедлива формула Тейлора:
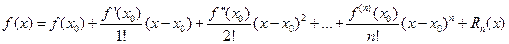
где  – остаточный член в форме Лагранжа. Число с можно записать в виде
– остаточный член в форме Лагранжа. Число с можно записать в виде  , где
, где 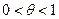 . Формулу
. Формулу 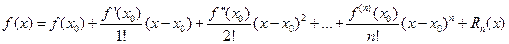 кратко можно записать в виде
кратко можно записать в виде 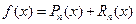 , где
, где 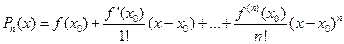 – многочлен Тейлора.
– многочлен Тейлора.
Если функция 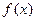 имеет производные любых порядков в окрестности точки
имеет производные любых порядков в окрестности точки 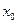 и остаточный член
и остаточный член 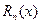 стремится к нулю при
стремится к нулю при  , то из формулы Тейлора получается разложение функции
, то из формулы Тейлора получается разложение функции 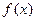 по степеням
по степеням 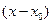 , называемое рядом Тейлора:
, называемое рядом Тейлора:
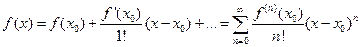
Если в ряде Тейлора положить  , то получим разложение функции по степеням х в так называемый ряд Маклорена :
, то получим разложение функции по степеням х в так называемый ряд Маклорена :
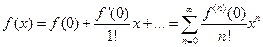
Отметим, что ряд Тейлора можно формально построить для любой бесконечно дифференцируемой функции в окрестности точки 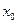 . Но отсюда еще не следует, что он будет сходиться к данной функции
. Но отсюда еще не следует, что он будет сходиться к данной функции 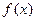 ; он может оказаться расходящимся или сходиться, но не к функции
; он может оказаться расходящимся или сходиться, но не к функции 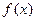 .
.
Теорема1
Для того чтобы ряд Тейлора 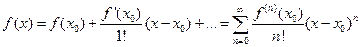 функции
функции 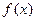 сходился к
сходился к 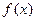 в точке х , необходимо и достаточно, чтобы в этой точке остаточный член формулы Тейлора
в точке х , необходимо и достаточно, чтобы в этой точке остаточный член формулы Тейлора 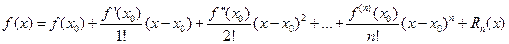 стремился к нулю при
стремился к нулю при  , т.е. чтобы
, т.е. чтобы 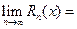 0.
0.
Пусть ряд Тейлора 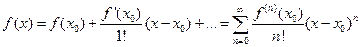 сходится к функции
сходится к функции 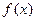 в некоторой окрестности точки
в некоторой окрестности точки 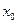 , т.е.
, т.е. 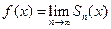 . Так как n -я частичная сумма
. Так как n -я частичная сумма  ряда
ряда 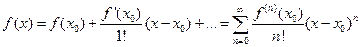 совпадает с многочленом Тейлора
совпадает с многочленом Тейлора 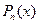 , т.е.
, т.е. 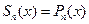 находим:
находим: 
Обратно, пусть 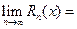 0. Тогда
0. Тогда 
Теорема2
Если модули всех производных функций 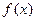 ограничены в окрестности точки
ограничены в окрестности точки 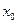 одним и тем же числом М>0, то для любого х из этой окрестности ряд Тейлора функции
одним и тем же числом М>0, то для любого х из этой окрестности ряд Тейлора функции 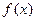 сходится к функции
сходится к функции 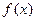 , т.е. имеет место разложение
, т.е. имеет место разложение 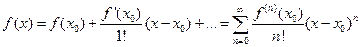 .
.
Согласно теореме1, достаточно показать, что 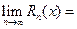 0. По условию теоремы2 для любого n имеет место неравенство
0. По условию теоремы2 для любого n имеет место неравенство 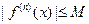 . Тогда имеем:
. Тогда имеем: 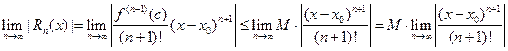
Осталось показать, что 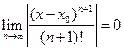 . Для этого рассмотрим ряд
. Для этого рассмотрим ряд 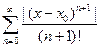
Так как 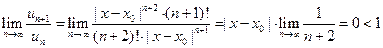 , то по признаку Даламбера этот ряд сходится на всей числовой оси. Но тогда, в силу необходимого признака сходимости,
, то по признаку Даламбера этот ряд сходится на всей числовой оси. Но тогда, в силу необходимого признака сходимости, 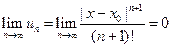
Следовательно, 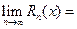 0
0
Разложение некоторых элементарных функций в ряд Тейлора (Маклорена)
Для разложения функции 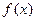 в ряд Маклорена
в ряд Маклорена 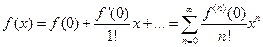 нужно:
нужно:
А) найти производные 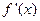 ,
, 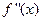 ,…,
,…, 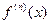 ,..;
,..;
Б) вычислить значения производных в точке  ;
;
В) написать ряд 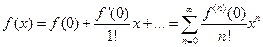 для заданной функции и найти его интервал сходимости;
для заданной функции и найти его интервал сходимости;
Ґ) найти интервал ( -R;R), в котором остаточный член ряда Маклорена 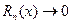 при
при  . Если такой интервал существует, то в нем функция
. Если такой интервал существует, то в нем функция 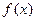 и сумма ряда Маклорена совпадают.
и сумма ряда Маклорена совпадают.
Приведем таблицу, содержащую разложения в ряд Маклорена некоторых элементарных функций:
Докажем формулу.
Пусть 
Имеем:
А) 
Б) 
В)  , т.е. ряд сходится в интервале
, т.е. ряд сходится в интервале 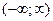 ;
;
Ґ) для всех 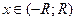 имеем
имеем 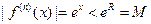 , т.е. все производные в этом интервале ограничены одним и тем же числом
, т.е. все производные в этом интервале ограничены одним и тем же числом 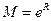 . Следовательно,
. Следовательно, 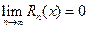 . Таким образом,
. Таким образом, 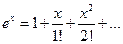 .
.
Докажем формулу.
Пусть f(x)=sin x
Имеем:
А) 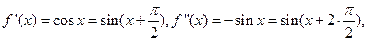
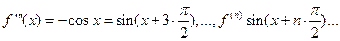
Б) 
В) 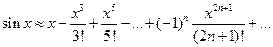 Легко проверить, что полученный ряд сходится на всей числовой оси, т.е. при всех
Легко проверить, что полученный ряд сходится на всей числовой оси, т.е. при всех 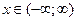
Ґ) любая производная функция f(x)=sin x по модулю не превосходит единицы, 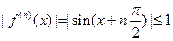 . Следовательно, имеет место разложение f(x)=sin x.
. Следовательно, имеет место разложение f(x)=sin x.
Докажем формулу
Пусть f(x)=cos x
Формулу f(x)=cos x можно доказать так же, как и формулу f(x)=sin x . Однако проще получить разложение функции cos x , воспользовавшись свойством 3 степенных рядов. Продифференцировав почленно ряд f(x)=sin x , получим:

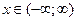
Докажем формулу
Пусть 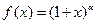 ,
, 
Имеем:
А) 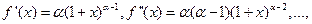
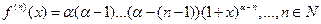
Б) 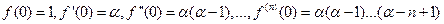
В) 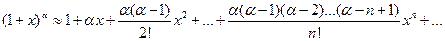
Ґ) 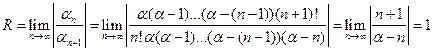 , т.е. составленный для функции
, т.е. составленный для функции 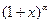 ряд сходится в интервале (-1;1), остаточный член
ряд сходится в интервале (-1;1), остаточный член  стремится к нулю при
стремится к нулю при 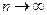 .
.
Ряд 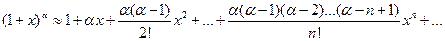 называется биномиальным . Если
называется биномиальным . Если 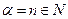 , то все члены ряда с ( n+1)- го номера равны 0, так как содержат множитель
, то все члены ряда с ( n+1)- го номера равны 0, так как содержат множитель 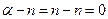 . В этом случае ряд представляет собой известную формулу бинома Ньютона:
. В этом случае ряд представляет собой известную формулу бинома Ньютона:

Докажем формулу
Пусть 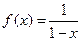
Формула может быть получена разными способами:
1)пользуясь правилом разложения функции в ряд;
2)рассматривая ряд 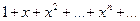 как ряд геометрической прогрессии, первый член которой равен 1 и знаменатель q=x; известно, что данный ряд сходится при
как ряд геометрической прогрессии, первый член которой равен 1 и знаменатель q=x; известно, что данный ряд сходится при 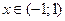 и его сумма равна
и его сумма равна 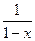
3)воспользовавшись формулой 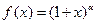 : положив в ней
: положив в ней 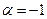 и заменив х на –х , получим формулу
и заменив х на –х , получим формулу 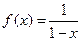 .
.
Докажем формулу
Пусть f(x)=ln (1+x)
Формула f(x)=ln (1+x ) также может быть доказана разными способами. Приведем один из них.
Рассмотрим равенство 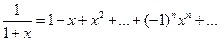 ,
,
справедливое для всех 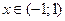 . Используя свойство 4 степенных рядов, проинтегрируем данный ряд на отрезке [0;x],
. Используя свойство 4 степенных рядов, проинтегрируем данный ряд на отрезке [0;x], 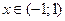 :
:
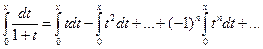
или
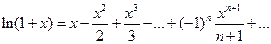
Докажем формулу
Пусть f(x)=arctg x
Положив в формуле 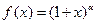
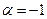 и заменив х на
и заменив х на  , получим равенство
, получим равенство
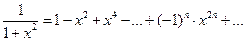
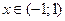
Тогда 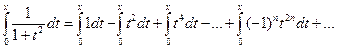
или
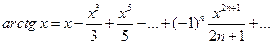
Докажем формулу
Пусть f(x)=arcsin x
Положив в формуле 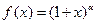
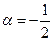 и заменив х на
и заменив х на  , получим равенство
, получим равенство
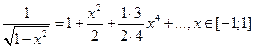
Тогда 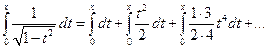
или
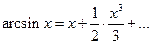
Степенные ряды. Интервал сходимости степенного ряда. Разложение функций в степенные ряды.
Степенным рядом называется ряд вида:
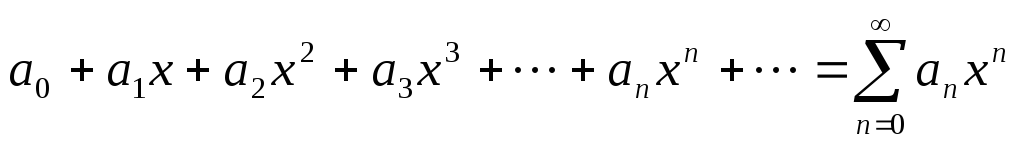 ,
,
где 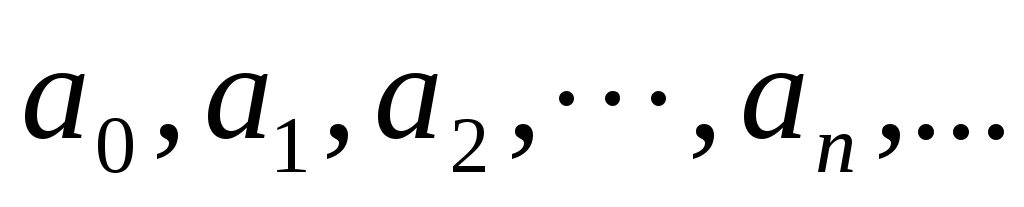 называются коэффициентами
степенного ряда.
называются коэффициентами
степенного ряда.
Придавая х различные числовые значения, будем
получать различные
числовые ряды, которые могут оказаться
сходящимися или расходящимися. Множество
тех значений х,
при которых степенной ряд
сходится,
называется областью его сходимости. Это множество всегда
не пусто, так как любой степенной ряд
сходится при 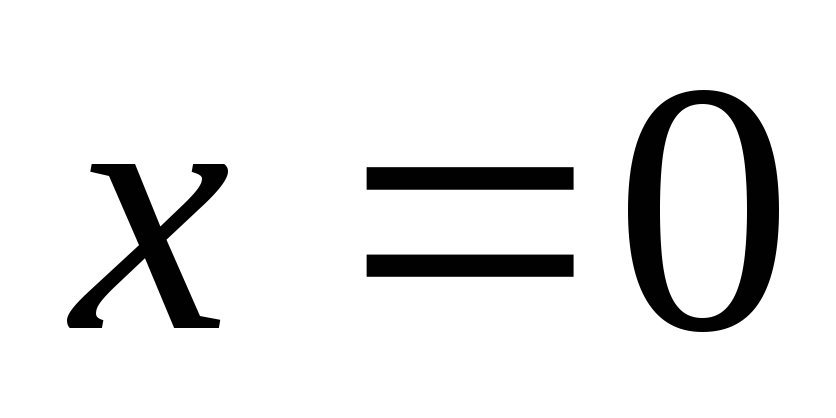 .
.
Очевидно, что частичная сумма степенного ряда
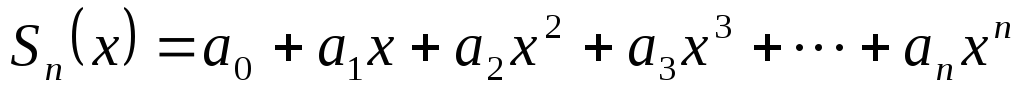
является
функцией переменной х. Поэтому и сумма ряда S
также является некоторой функцией
переменной х, определенной
в области сходимости ряда: 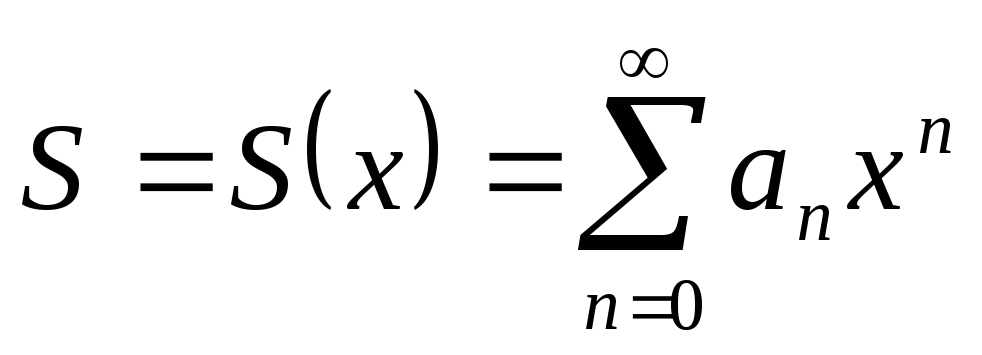 .
.
Рассмотрим теорему, имеющую важное значение в теории степенных рядов и касающуюся области сходимости степенного ряда.
Теорема Абеля. (Абель Нильс Хенрик (1802—1829) — норвежский математик).
1) Если степенной
ряд сходится
при 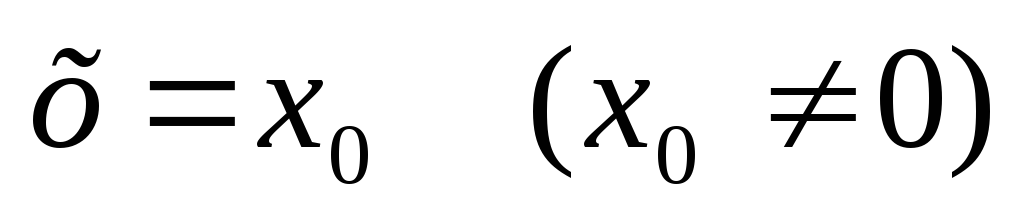 , то он сходится,
и притом абсолютно, для всех х,
удовлетворяющих условию
, то он сходится,
и притом абсолютно, для всех х,
удовлетворяющих условию 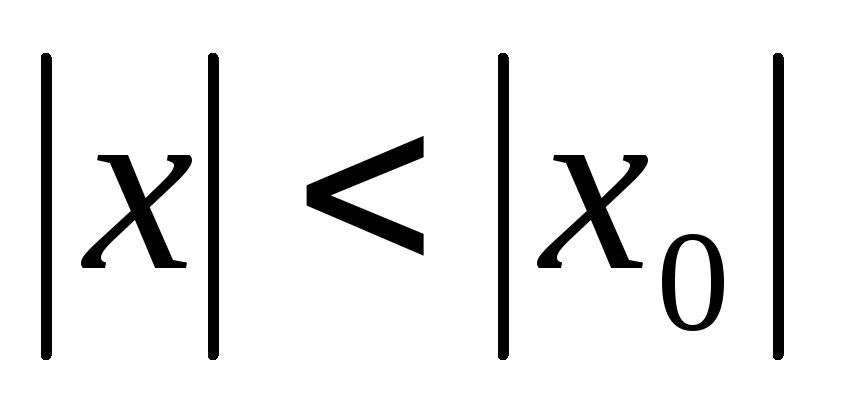 ;
;
2) если степенной
ряд расходится
при 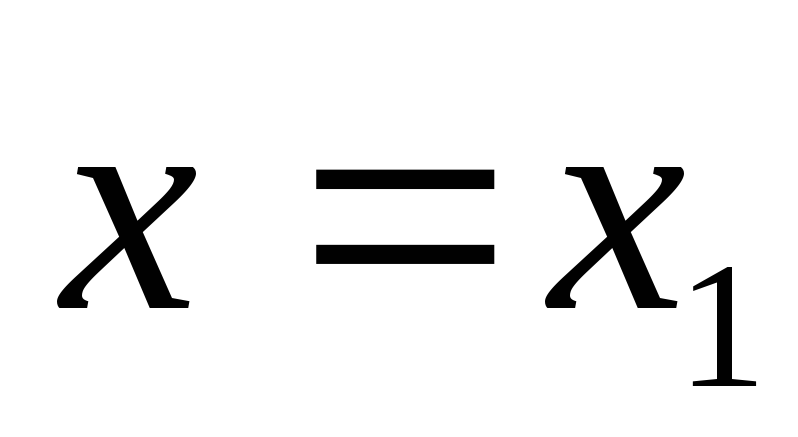 ,
то он расходится для всех х, удовлетворяющих
условию
,
то он расходится для всех х, удовлетворяющих
условию 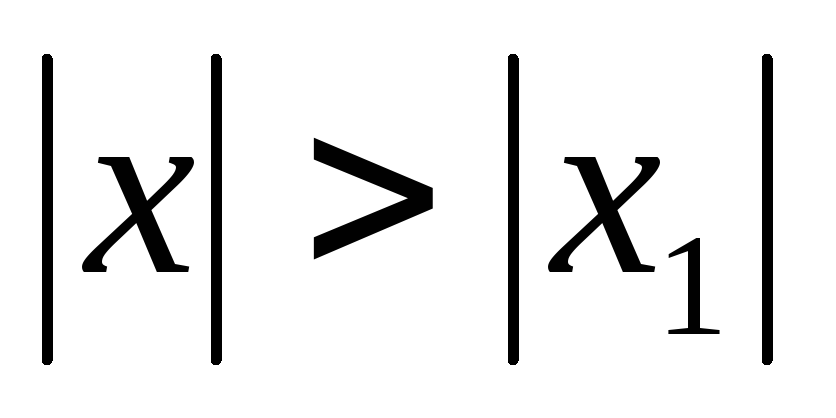 .
.
Теорема
Абеля утверждает, что если 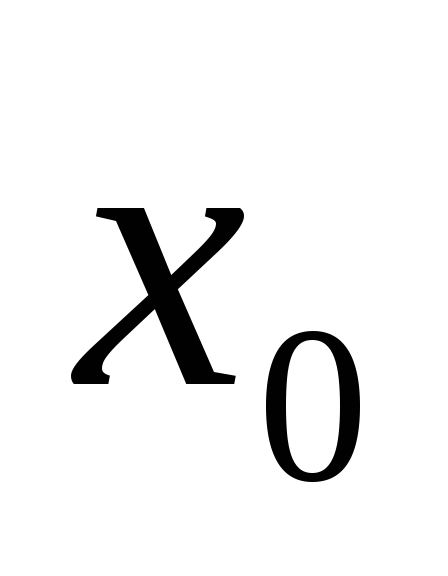 —
точка
сходимости степенного ряда, то во всех
точках, расположенных на интервале (
—
точка
сходимости степенного ряда, то во всех
точках, расположенных на интервале ( )
этот ряд сходится абсолютно, а
если
)
этот ряд сходится абсолютно, а
если 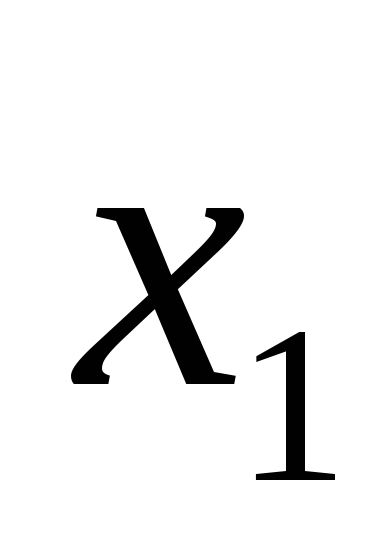 —точка
расходимости степенного ряда, то во
всех точках, расположенных вне интервала
(
—точка
расходимости степенного ряда, то во
всех точках, расположенных вне интервала
(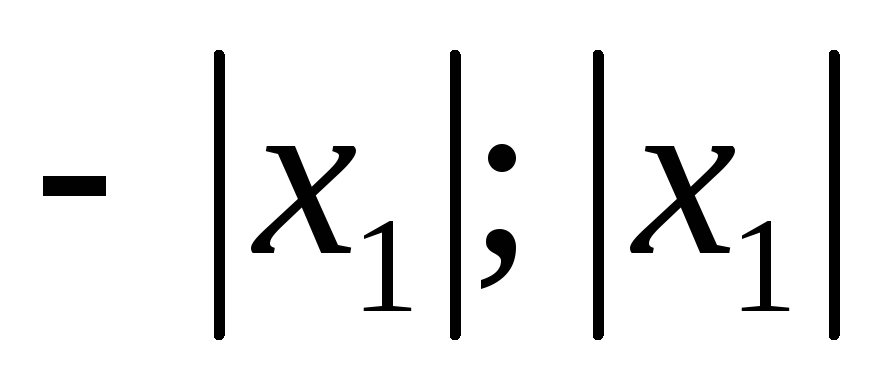 )
ряд расходится.
)
ряд расходится.
Отсюда вытекает следующая теорема:
Если
ряд 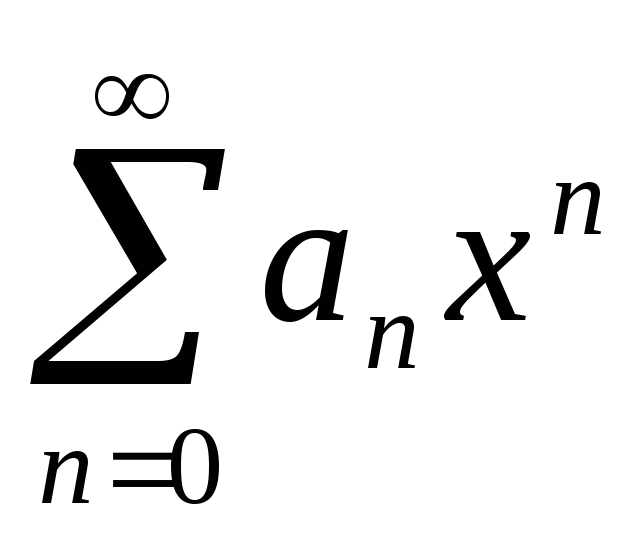 сходится не при всех значениях х и не только при
сходится не при всех значениях х и не только при 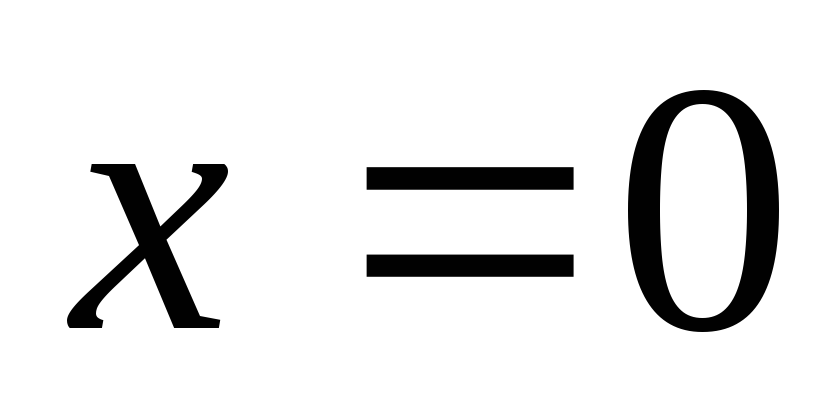 ,
то существует число
,
то существует число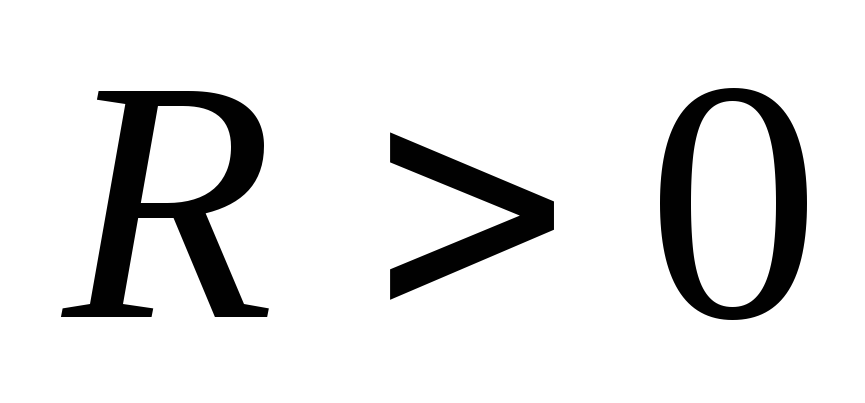 такое, что ряд
абсолютно сходится при
такое, что ряд
абсолютно сходится при 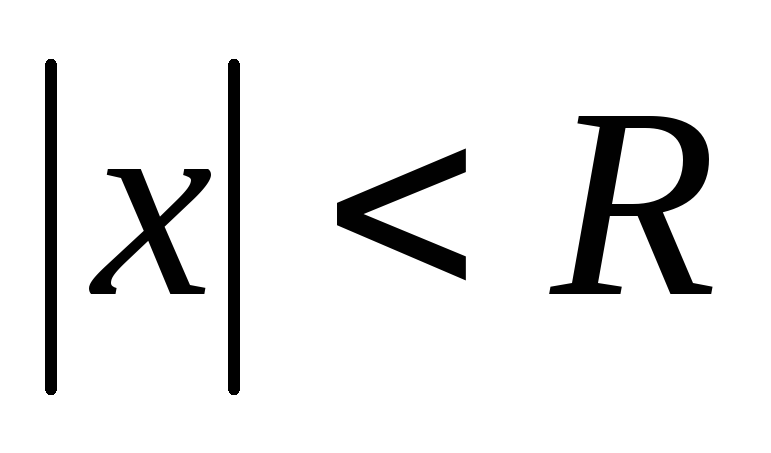 и расходится npu
и расходится npu 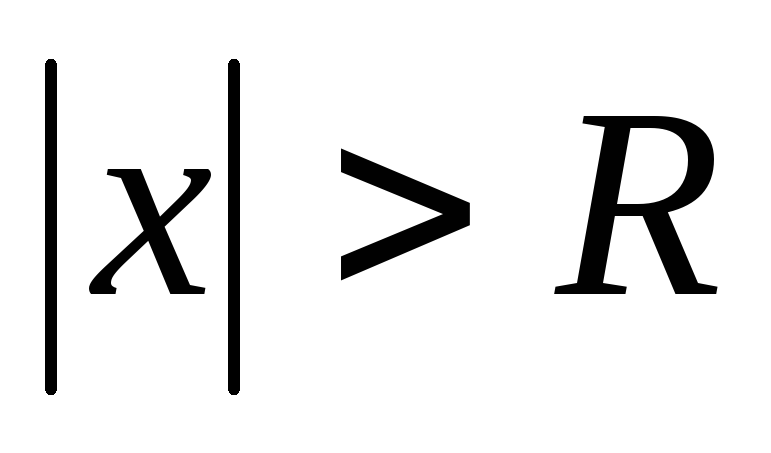 .
.
Интервал 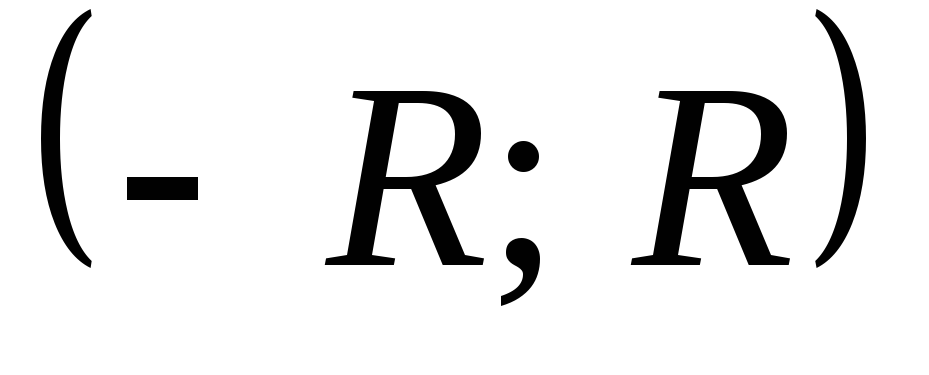 называетсяинтервалом
сходимости степенного ряда.
Число R называется радиусом
сходимости степенного
ряда. Отметим, что интервал сходимости у
некоторых рядов охватывает всю числовую
прямую (в этом случае пишут
называетсяинтервалом
сходимости степенного ряда.
Число R называется радиусом
сходимости степенного
ряда. Отметим, что интервал сходимости у
некоторых рядов охватывает всю числовую
прямую (в этом случае пишут 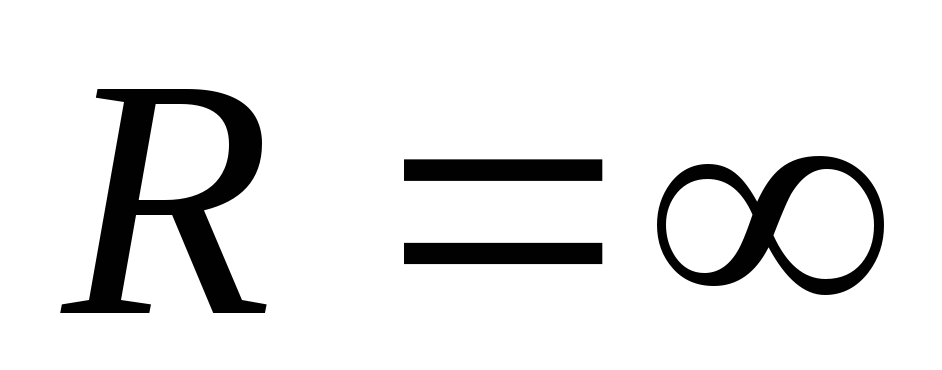 ),
у других вырождается в одну точку (
),
у других вырождается в одну точку (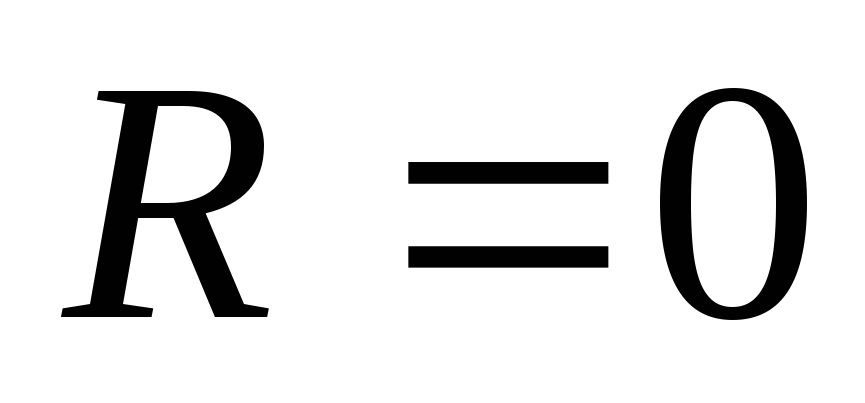 ).
).
Итак,
всякий степенной ряд имеет свой радиус
сходимости R.
При 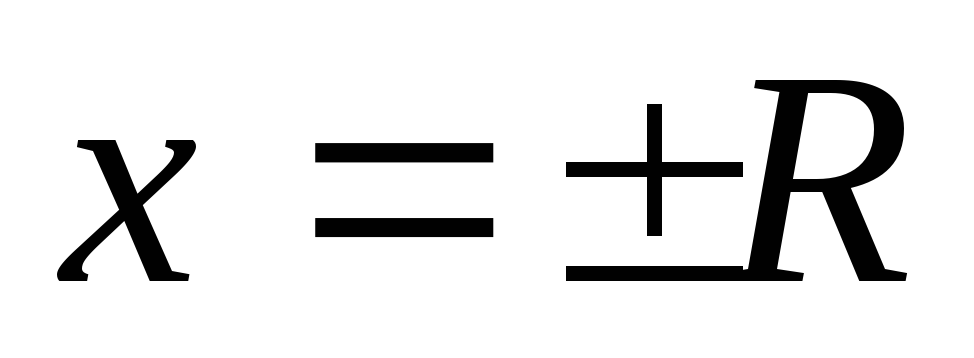 ряд может либо сходиться, либо расходиться.
Этот вопрос решается для каждого
конкретного ряда.
ряд может либо сходиться, либо расходиться.
Этот вопрос решается для каждого
конкретного ряда.
Приведем способ определения радиуса сходимости степенного ряда по признаку Даламбера.
Если
существует предел 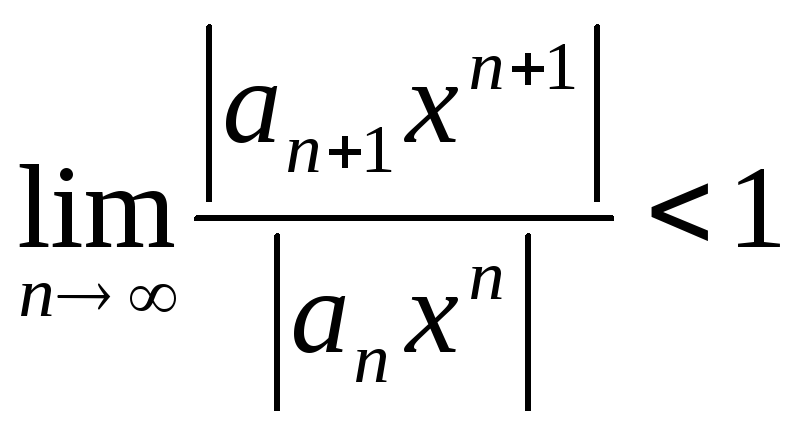 ,то радиус
сходимости ряда
,то радиус
сходимости ряда 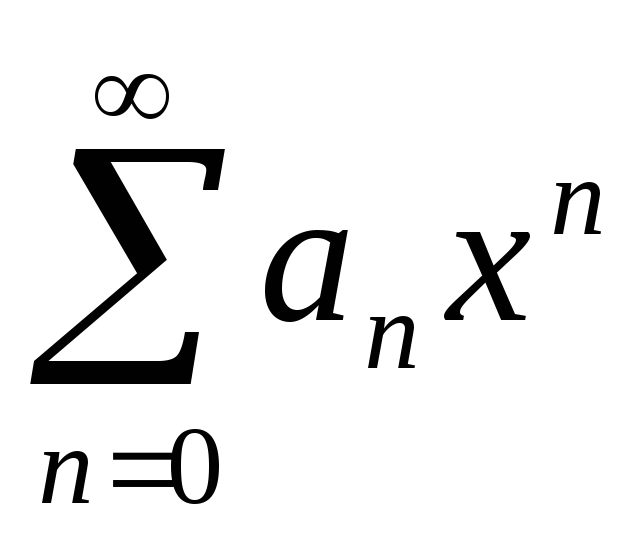 равен
равен 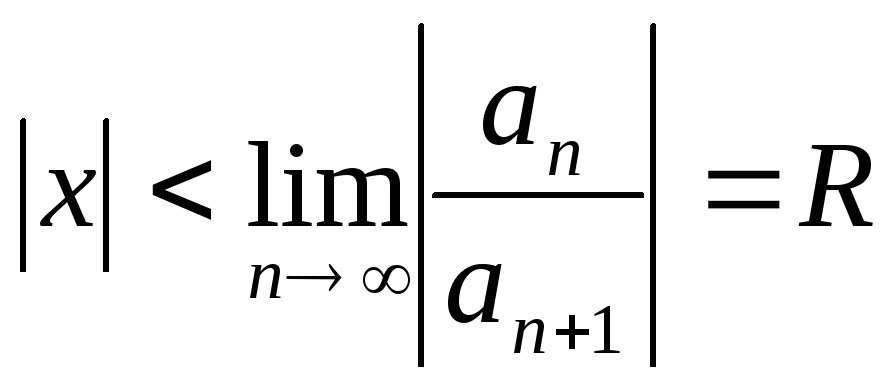 .
.
Свойства степенных рядов.
Пусть
функция 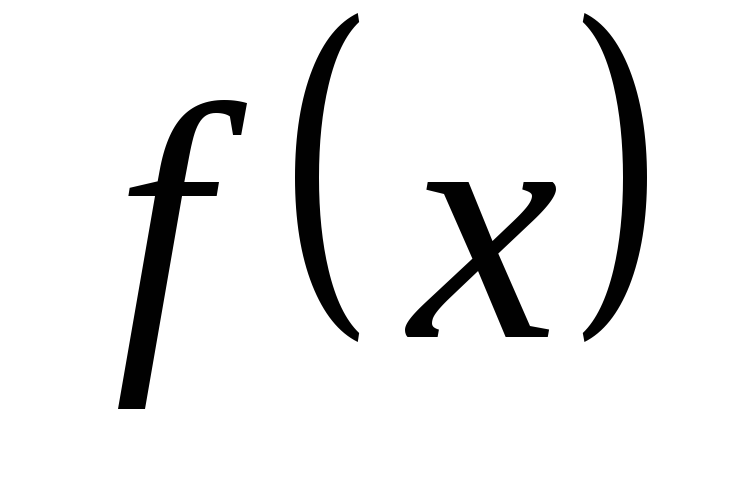 является
суммой
степенного ряда
является
суммой
степенного ряда
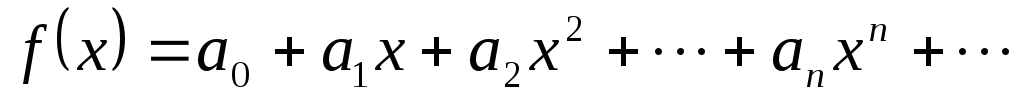 ,
,
интервал
сходимости которого 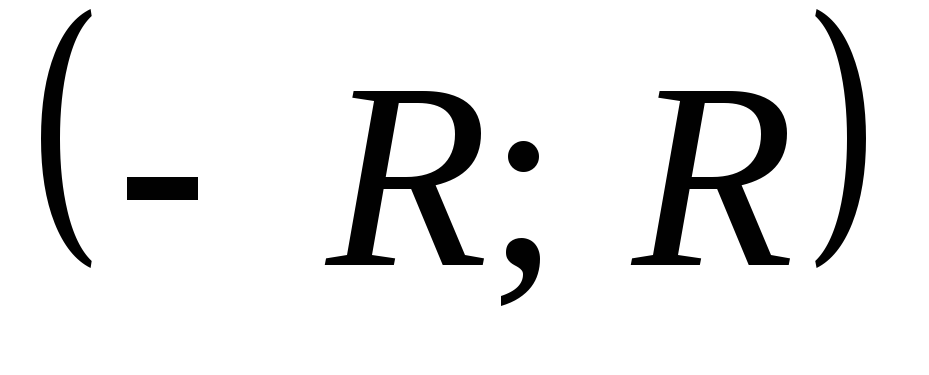 .
.
В
этом случае говорят, что на интервале 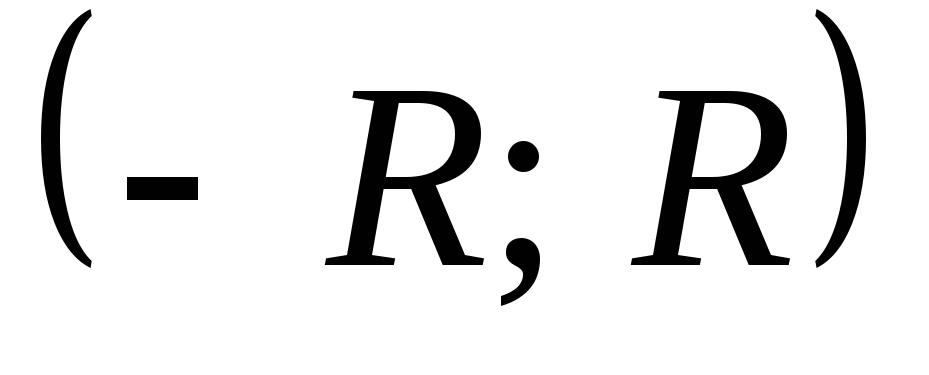 функция
функция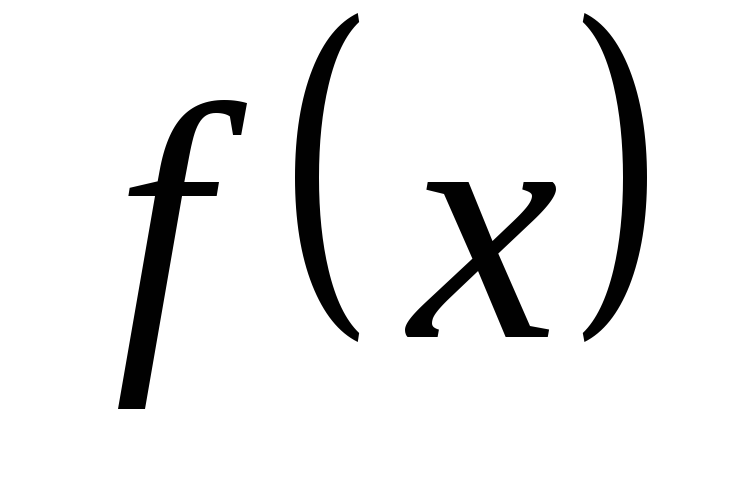 разлагается
в степенной ряд (или в ряд по степеням х).
разлагается
в степенной ряд (или в ряд по степеням х).
Имеют место две теоремы о свойствах степенных рядов.
Если функция
 на интервале
на интервале  разлагается в степенной ряд, то она
дифференцируема на этом интервале и
ее производная
разлагается в степенной ряд, то она
дифференцируема на этом интервале и
ее производная  может быть найдена почленным
дифференцированием ряда, т.е.:
может быть найдена почленным
дифференцированием ряда, т.е.:
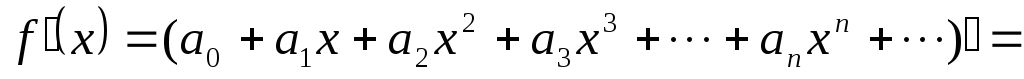
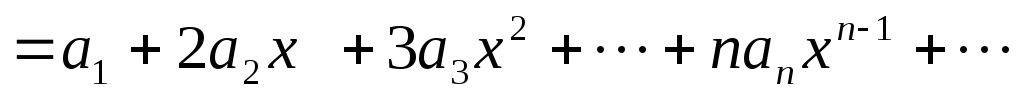 .
.
Аналогично
могут быть вычислены производные любого
порядка функции 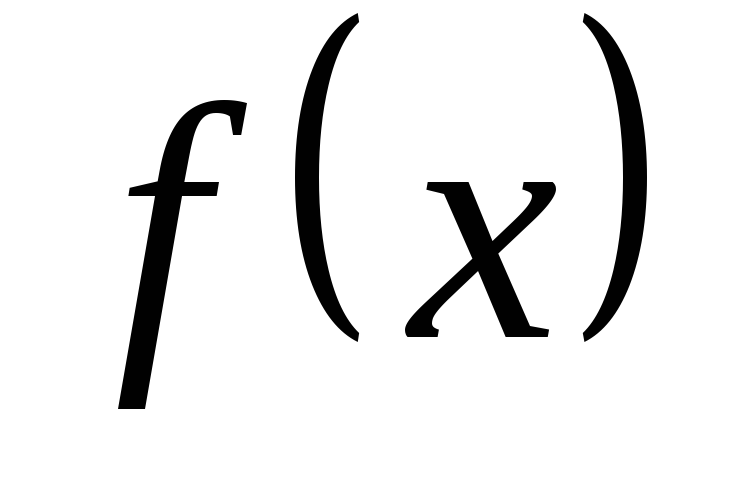 .
При этом соответствующие ряды имеют
тот же
интервал
сходимости, что и степенной ряд.
.
При этом соответствующие ряды имеют
тот же
интервал
сходимости, что и степенной ряд.
Если функция
 на интервале
на интервале  разлагается
в степенной ряд, то она
интегрируема в интервале
разлагается
в степенной ряд, то она
интегрируема в интервале  и интеграл
от нее может быть вычислен почленным
интегрированием степенного ряда,
т.е.,
если
и интеграл
от нее может быть вычислен почленным
интегрированием степенного ряда,
т.е.,
если  ,
то:
,
то:
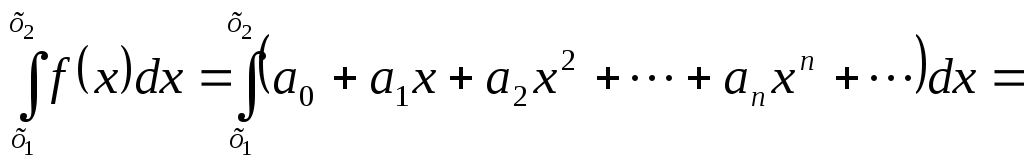
 +
+
+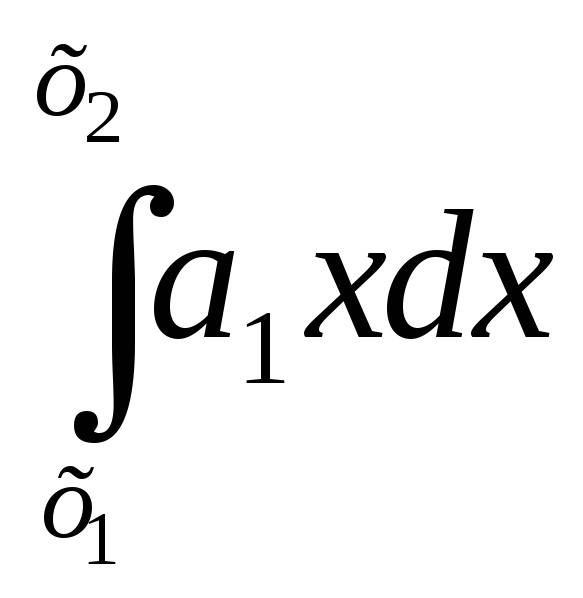 +
+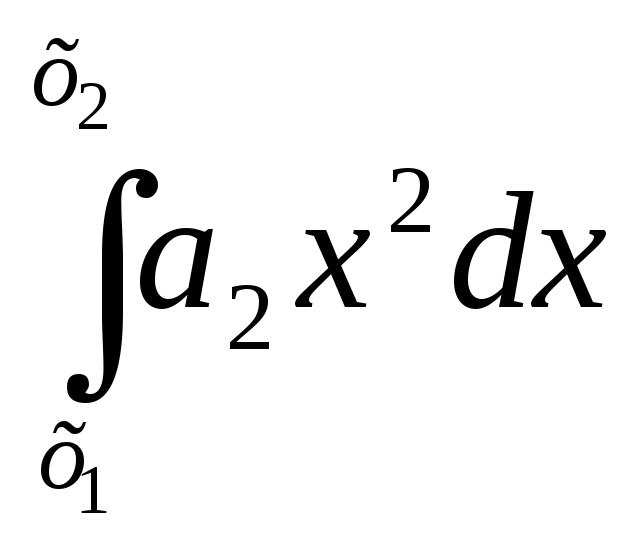 … +
… +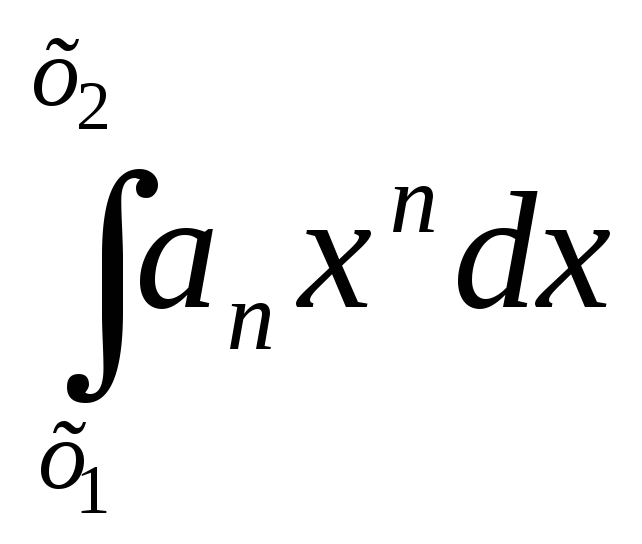 +….
+….
Теорема. Если функция 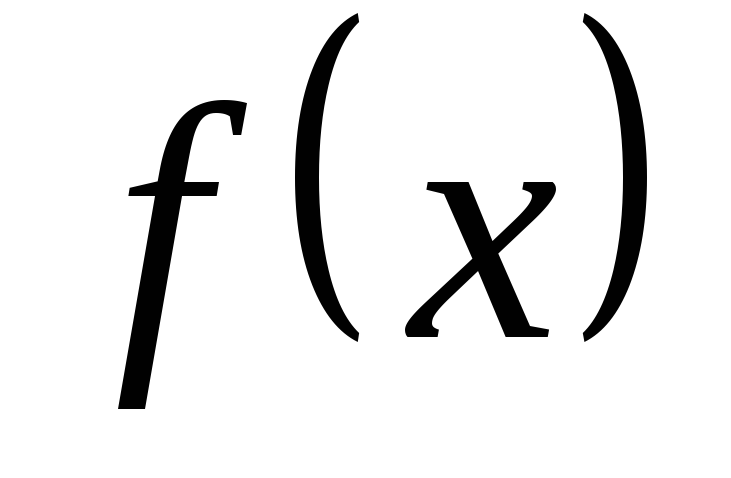 на интервале
на интервале 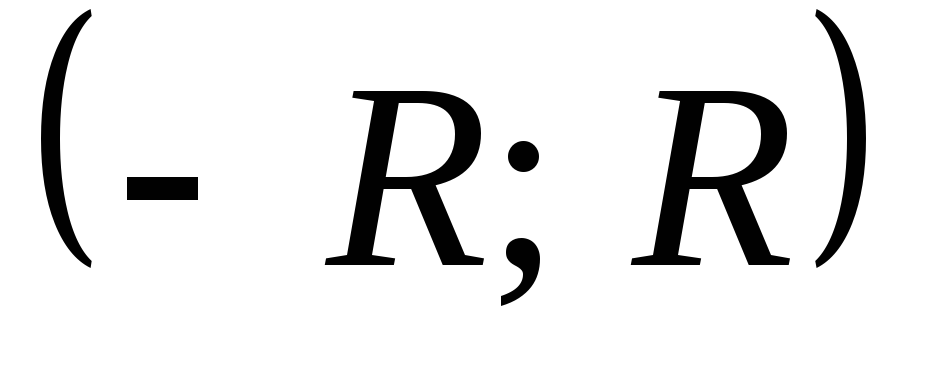 разлагается в степенной ряд:
разлагается в степенной ряд:
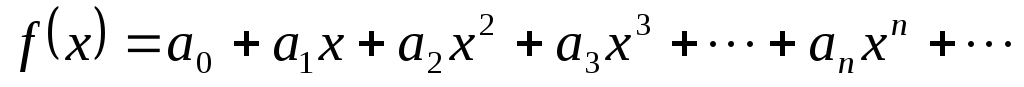 ,
,
то это разложение единственно.
Пусть
функция 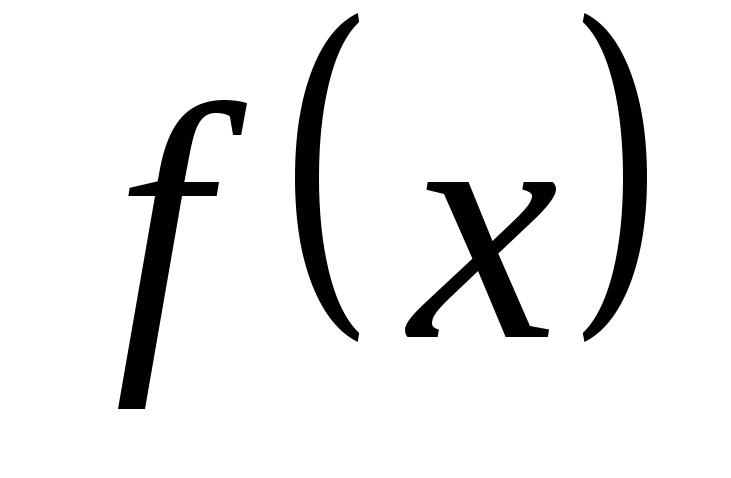 бесконечное число раз дифференцируема
в точке
бесконечное число раз дифференцируема
в точке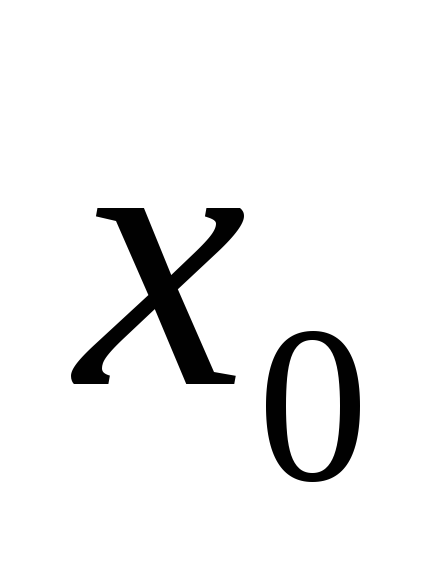 ,
тогда в окрестности этой точки функция
раскладывается в степенной ряд:
,
тогда в окрестности этой точки функция
раскладывается в степенной ряд:
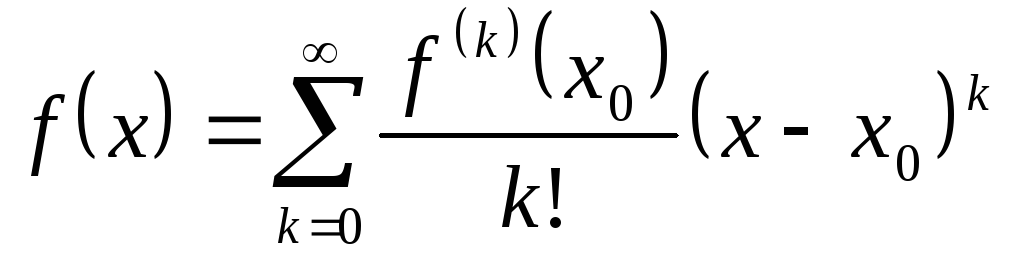 ,
,
называемый рядом Тейлора.
При 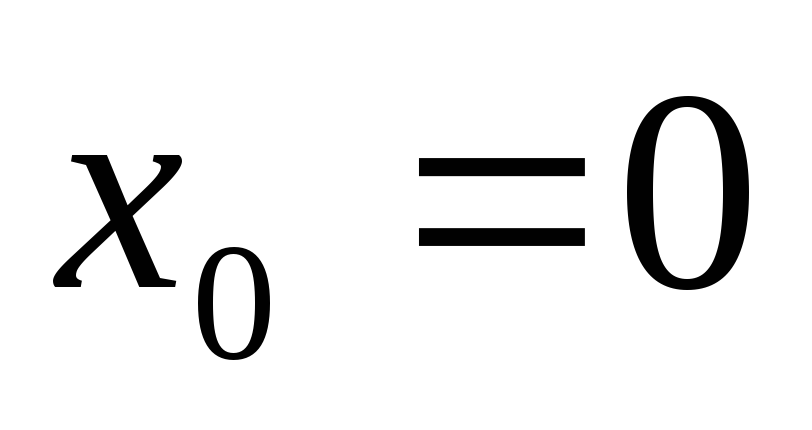 функция
функция разлагается в степенной ряд:
разлагается в степенной ряд:
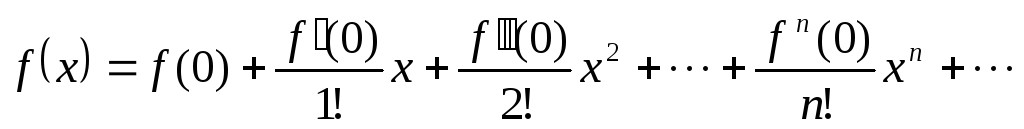 ,
,
называемый рядом Маклорена.
Для
того чтобы ряд Маклорена сходился
на 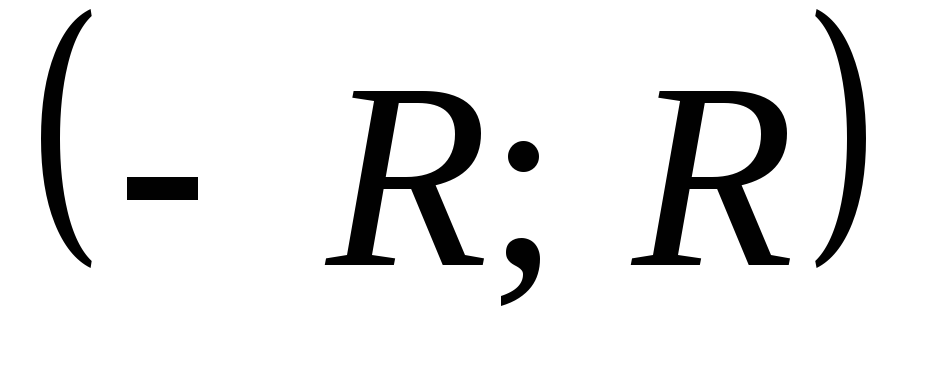 и имел своей
суммой функцию
и имел своей
суммой функцию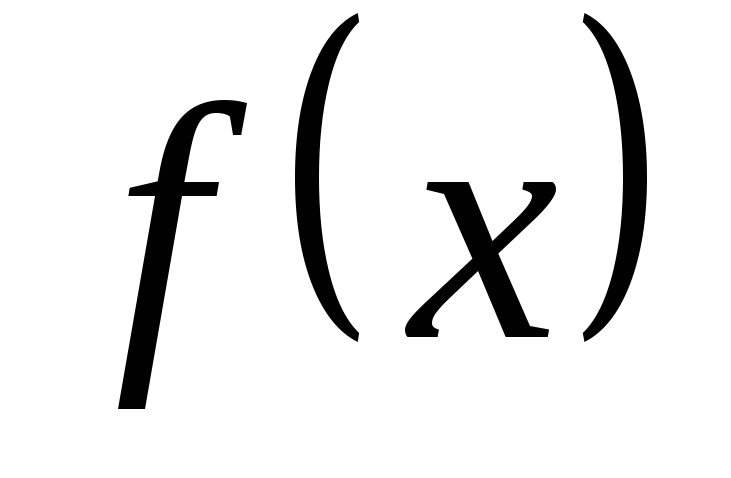 ,
необходимо и достаточно, чтобы на
,
необходимо и достаточно, чтобы на 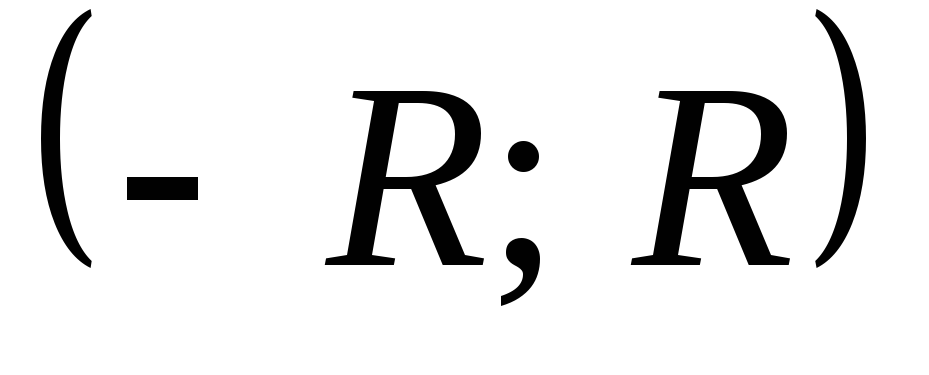 остаточный
член
остаточный
член 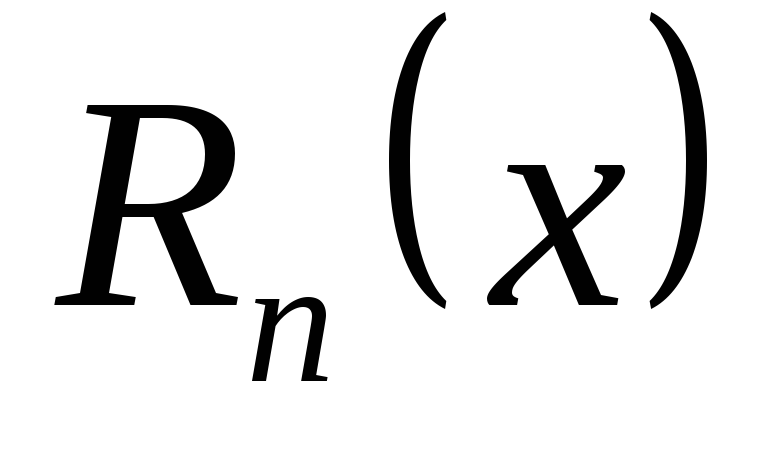 формулы Маклорена стремился к
нулю при
формулы Маклорена стремился к
нулю при 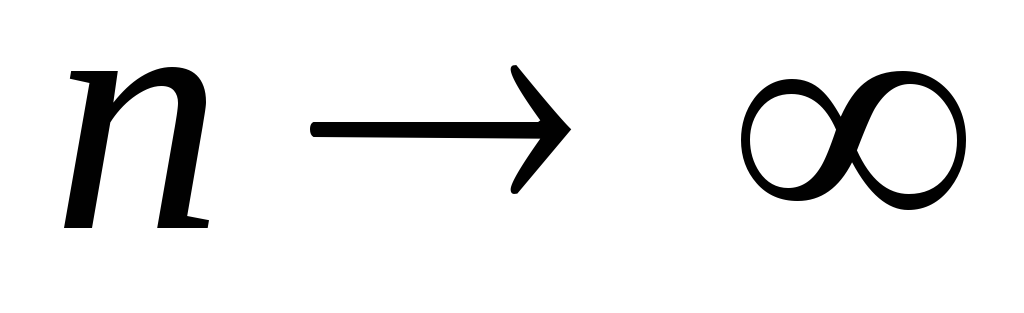 ,т.е.
,т.е. 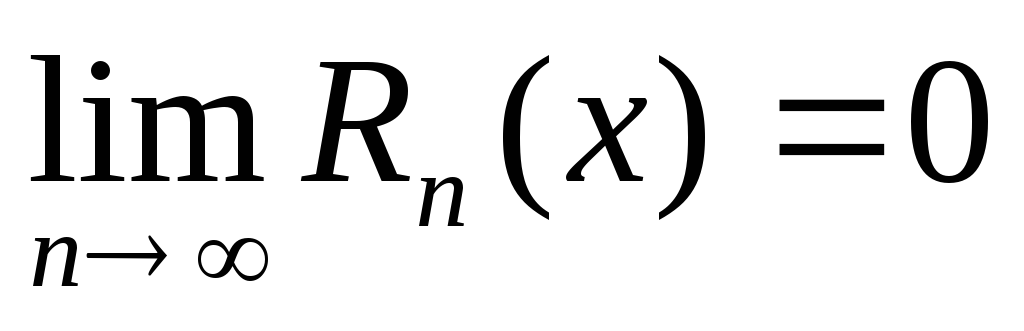 для любого
для любого 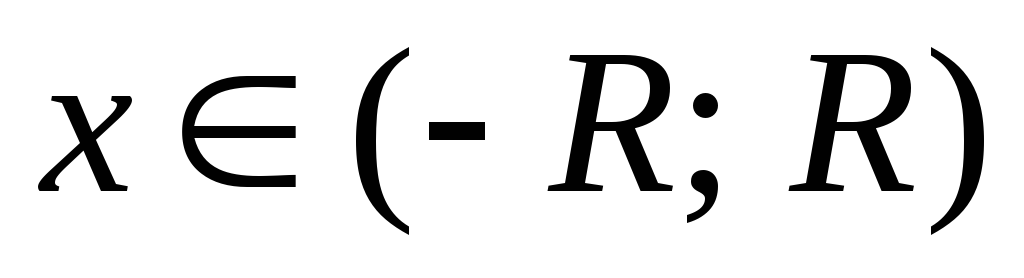 .
.
Рассмотрим разложения в ряд Маклорена некоторых элементарных функций:
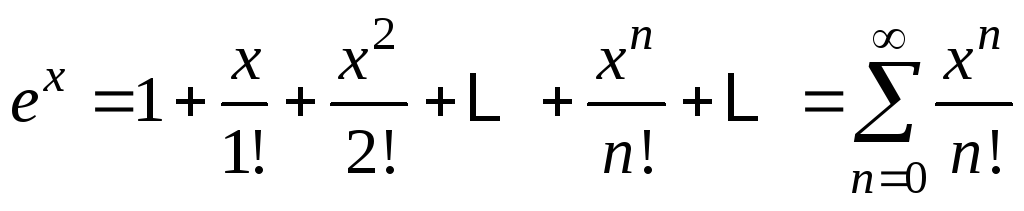 ;
;
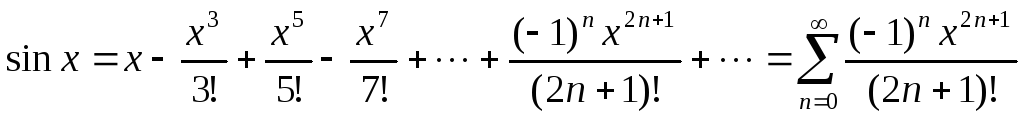
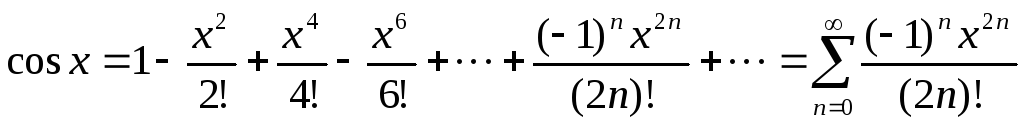 ;
;
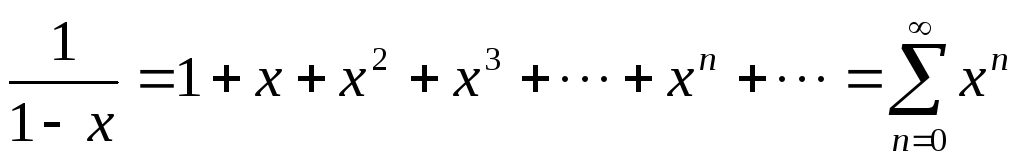 ;
;
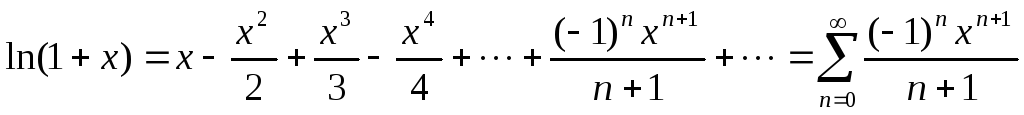
Радиус и область сходимости степенного ряда — Студопедия
Радиусом сходимости степенного ряда 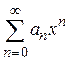 называется такое число R, при котором ряд сходится, если
называется такое число R, при котором ряд сходится, если 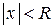 , и расходится, если
, и расходится, если 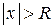 .
.
Для нахождения радиуса сходимости R составим ряд из абсолютных величин членов ряда 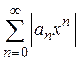 и применим признак Даламбера. Найдем
и применим признак Даламбера. Найдем
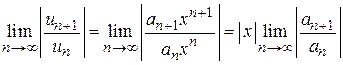 .
.
В соответствии с признаком Даламбера ряд сходится, если этот предел меньше единицы, т. е.
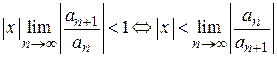 ,
,
и расходится, если 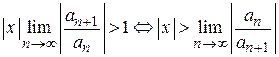 .
.
Отсюда следует, что радиус сходимости равен
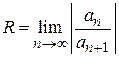 .
.
При использовании данной формулы необходимо не забывать, что в этой формуле 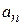 и
и 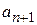 коэффициенты в членах степенного ряда при х в степени n и n+1, а не члены ряда.
коэффициенты в членах степенного ряда при х в степени n и n+1, а не члены ряда.
С помощью радиуса сходимости можно найти интервал сходимости ряда. При  степенной ряд сходится. Для того чтобы найти область сходимости, необходимо дополнительно исследовать сходимость ряда в граничных точках интервала сходимости
степенной ряд сходится. Для того чтобы найти область сходимости, необходимо дополнительно исследовать сходимость ряда в граничных точках интервала сходимости 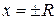 .
.
Пример 9.1. Найти область сходимости ряда 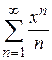 .
.
Находим радиус сходимости
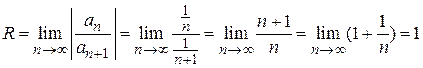 .
.
Интервал сходимости ряда 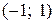 .
.
Исследуем сходимость ряда в граничных точках.
При 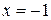 ряд имеет вид
ряд имеет вид 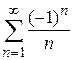 является знакочередующимся, его члены монотонно убывают и стремятся к нулю. По теореме Лейбница он сходится (см. пример 8.15).
является знакочередующимся, его члены монотонно убывают и стремятся к нулю. По теореме Лейбница он сходится (см. пример 8.15).
При 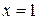 ряд
ряд 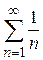 является гармоническим. Как известно он расходится.
является гармоническим. Как известно он расходится.
Следовательно, область сходимости ряда 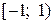 .
.
Пример 9.2. Найти область сходимости ряда 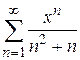 .
.
Находим радиус сходимости
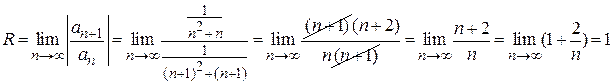 .
.
Интервал сходимости 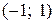 .
.
Исследуем сходимость ряда в граничных точках.
При 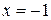 ряд имеет вид
ряд имеет вид 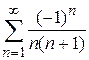 является знакочередующимся.
является знакочередующимся.
Члены ряда монотонно убывают 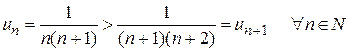
и стремятся к нулю 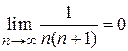 . По теореме Лейбница ряд сходится.
. По теореме Лейбница ряд сходится.
При 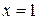 ряд имеет вид
ряд имеет вид 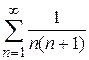 . Его сходимость исследуем по интегральному признаку Коши. Находим
. Его сходимость исследуем по интегральному признаку Коши. Находим
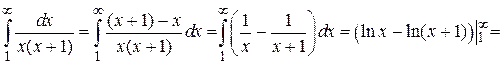
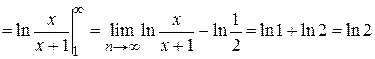 .
.
Интеграл сходится и ряд сходится.
Следовательно, область сходимости ряда 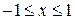 .
.
Пример 9.3. Найти область сходимости ряда 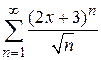 .
.
Введем новую переменную 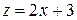 , ряд примет вид
, ряд примет вид 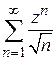 .
.
Найдем радиус сходимости этого ряда.
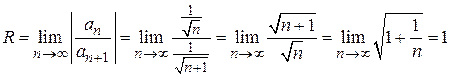 .
.
Интервал сходимости ряда 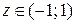 .
.
Исследуем сходимость ряда в граничных точках.
При 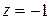 ряд имеет вид
ряд имеет вид 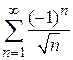 является знакочередующимся.
является знакочередующимся.
Члены ряда монотонно убывают 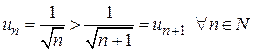
и стремятся к нулю 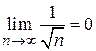 . По теореме Лейбница ряд сходится.
. По теореме Лейбница ряд сходится.
При 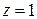 ряд имеет вид
ряд имеет вид 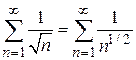 . Ряд расходится, так как степень n в знаменателе
. Ряд расходится, так как степень n в знаменателе 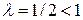 (см. пример 8.12).
(см. пример 8.12).
Область сходимости ряда 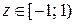 . Переходим к исходной переменной:
. Переходим к исходной переменной: 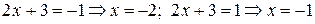
Область сходимости исходного ряда 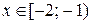 .
.
В отдельных случаях степенные ряды могут содержать только четные степени переменной 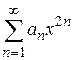 или нечетные степени
или нечетные степени 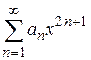 . Для нахождения радиуса сходимости ряда в таком случае составляется ряд из абсолютных величин этого ряда, а затем применяется признак Даламбера.
. Для нахождения радиуса сходимости ряда в таком случае составляется ряд из абсолютных величин этого ряда, а затем применяется признак Даламбера.
Для ряда с четными степенями 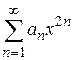 составляем ряд
составляем ряд 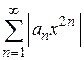 и применяем признак Даламбера
и применяем признак Даламбера 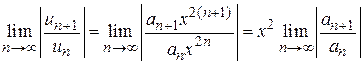 .
.
Ряд сходится, если 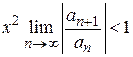 , т. е.
, т. е. 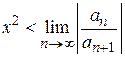 и расходится, если
и расходится, если 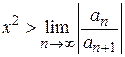 . Следовательно, можно определить квадрат радиуса сходимости такого ряда по формуле
. Следовательно, можно определить квадрат радиуса сходимости такого ряда по формуле
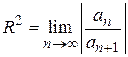 .
.
Для ряда с нечетными степенями 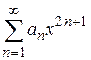 составляем ряд
составляем ряд 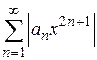 , применяем признак Даламбера
, применяем признак Даламбера 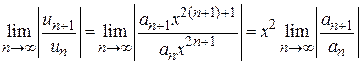 .
.
Ряд сходится, если 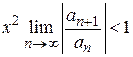 Û
Û 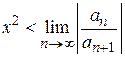 и расходится, если
и расходится, если
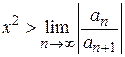 . Следовательно, в случае ряда с нечетными степенями справедлива та же формула для квадрата радиуса сходимости.
. Следовательно, в случае ряда с нечетными степенями справедлива та же формула для квадрата радиуса сходимости.
Пример 9.4. Найти область сходимости ряда 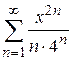 .
.
Находим 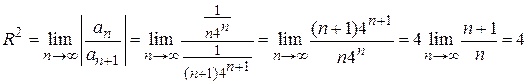 .
.
Радиус сходимости 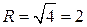 . Интервал сходимости ряда
. Интервал сходимости ряда  .
.
При 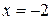
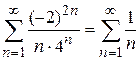 ряд расходится (гармонический).
ряд расходится (гармонический).
При 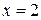
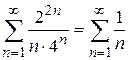 ряд расходится.
ряд расходится.
Область сходимости ряда  .
.
2.2. Интервал и радиус сходимости степенного ряда Примеры решения задач
Пример 1. Найти область сходимости степенного ряда:
а) 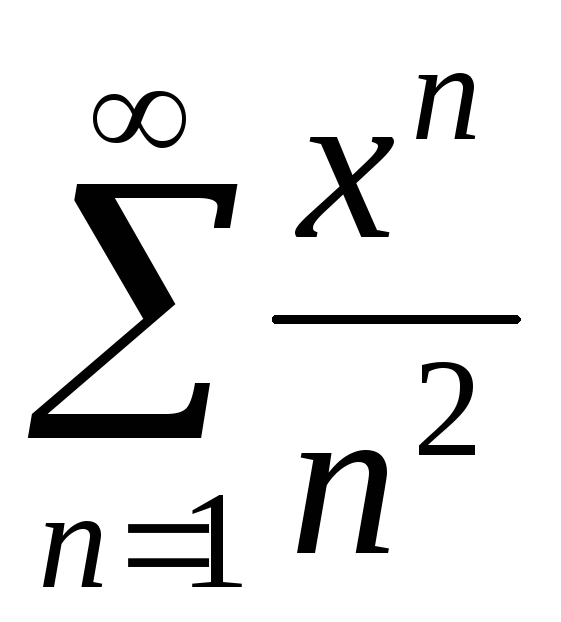 ; б)
; б)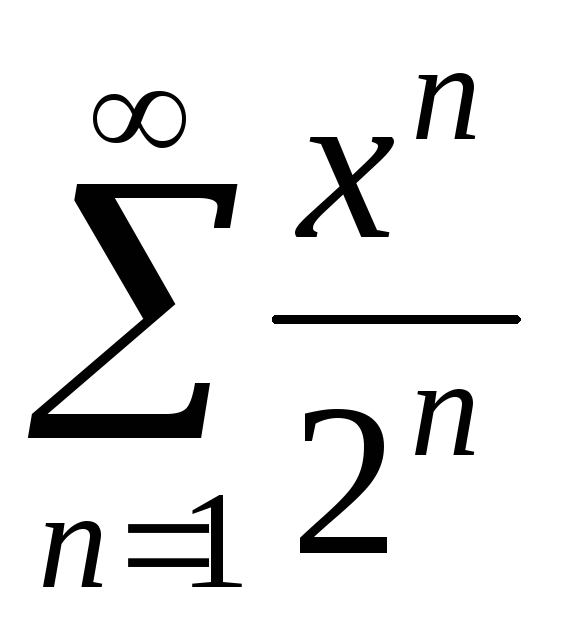 ;
;
в) 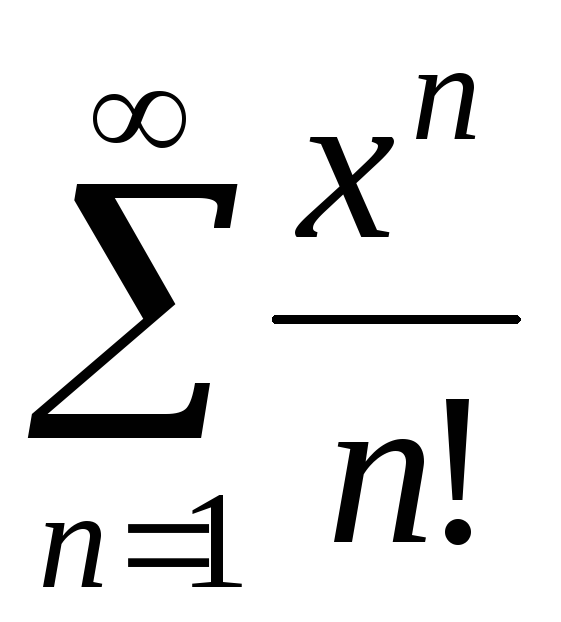 ; г)
; г)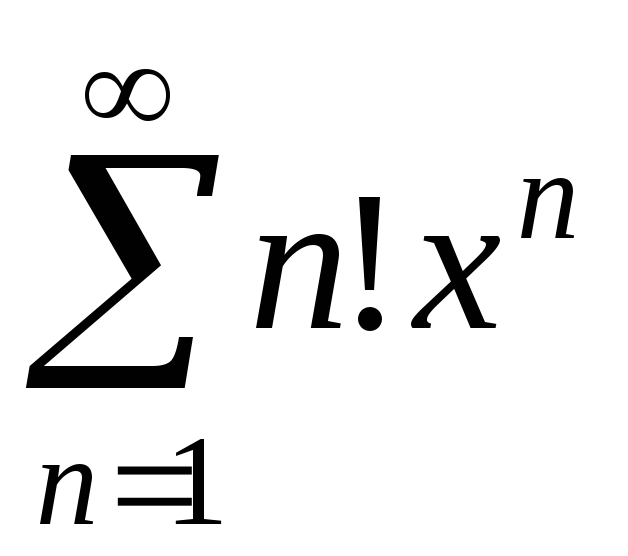 ;
;
д) 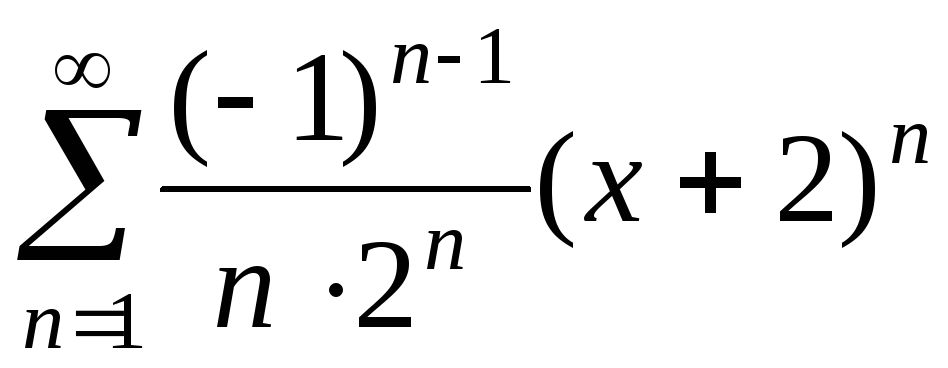 .
.
а) Найдем радиус сходимости R.
Так как 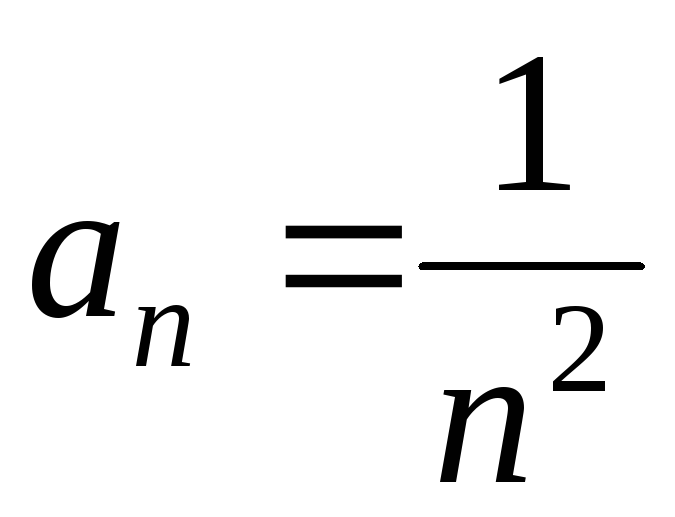 ,
,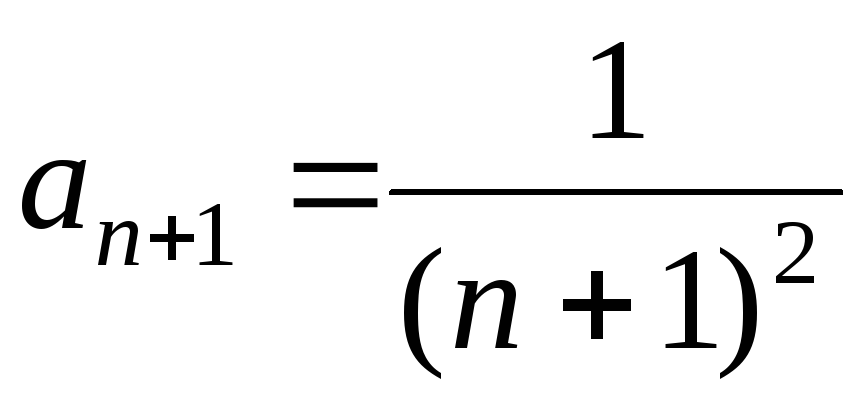 ,
то
,
то
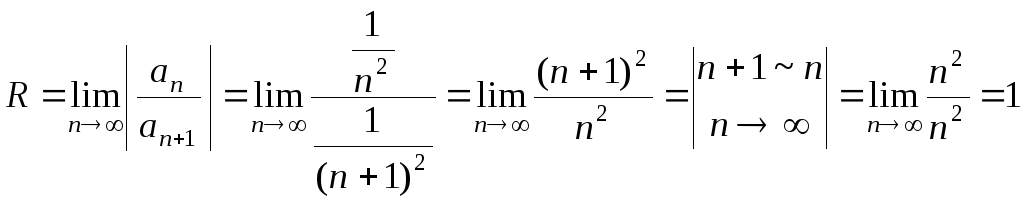 .
.
Итак, ряд сходится
абсолютно для всех x,
удовлетворяющих неравенству 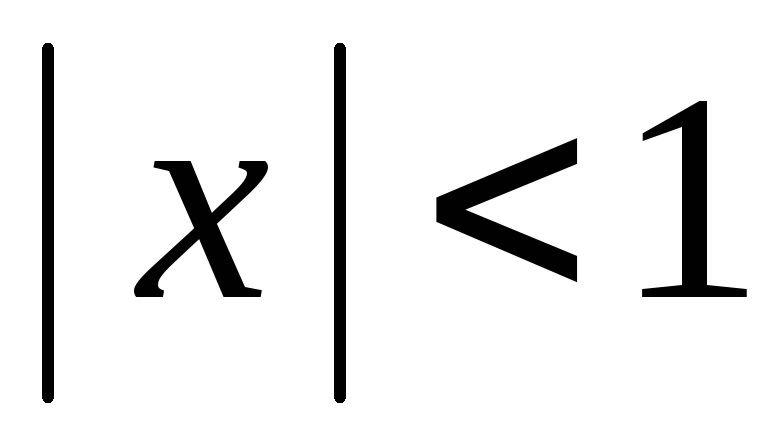 ,
то есть интервал сходимости ряда
,
то есть интервал сходимости ряда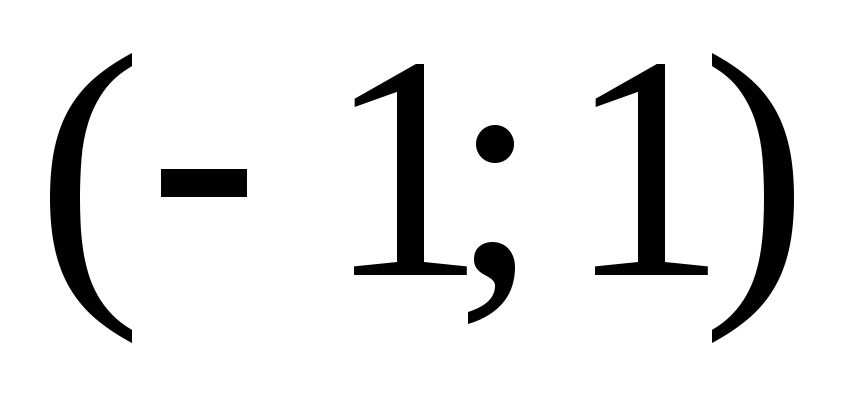 .
.
Исследуем на сходимость данный ряд на концах интервала сходимости.
При 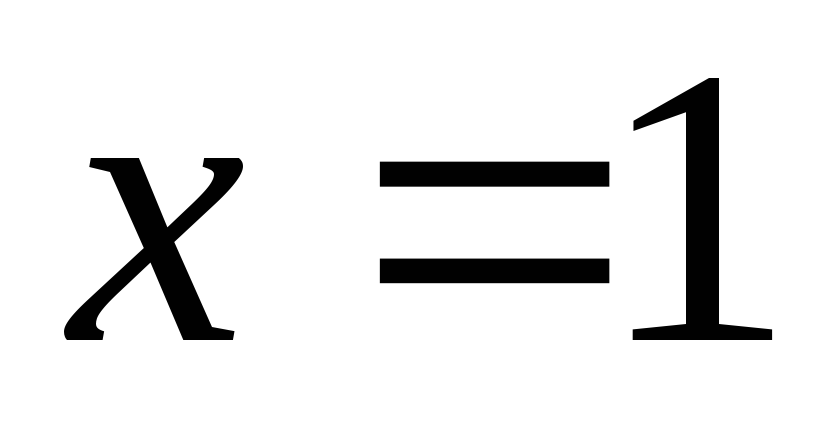 получаем
числовой ряд
получаем
числовой ряд 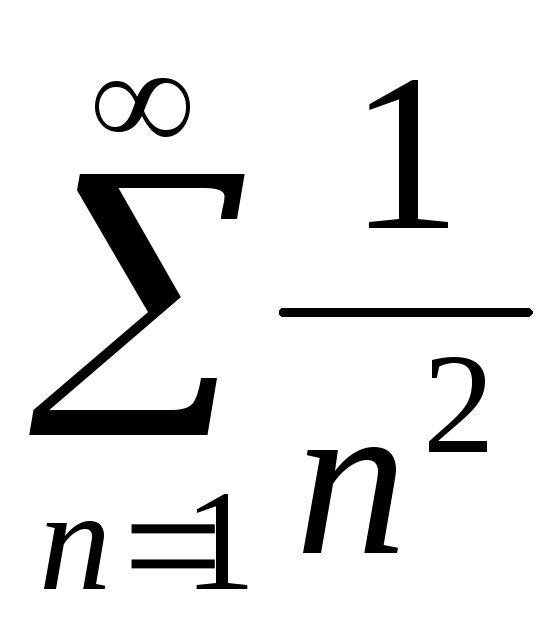 .
Этот ряд сходится, так как является
обобщенным гармоническим рядом
.
Этот ряд сходится, так как является
обобщенным гармоническим рядом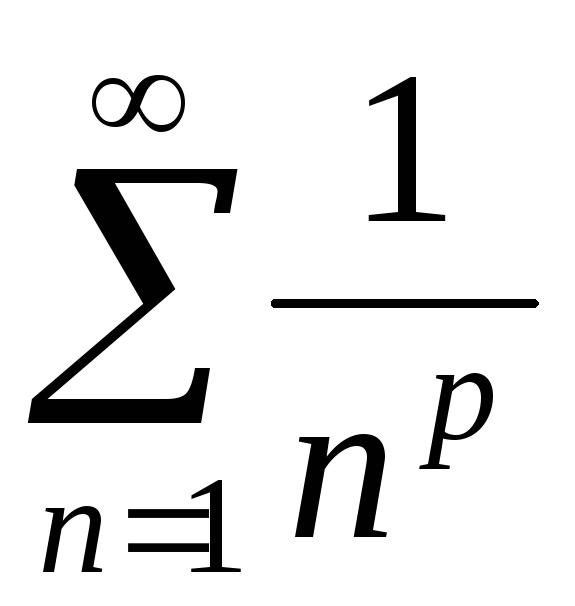 при
при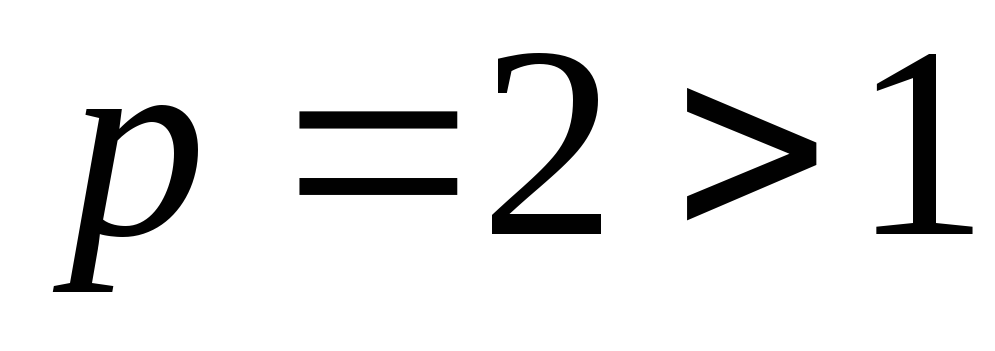 .
.
При 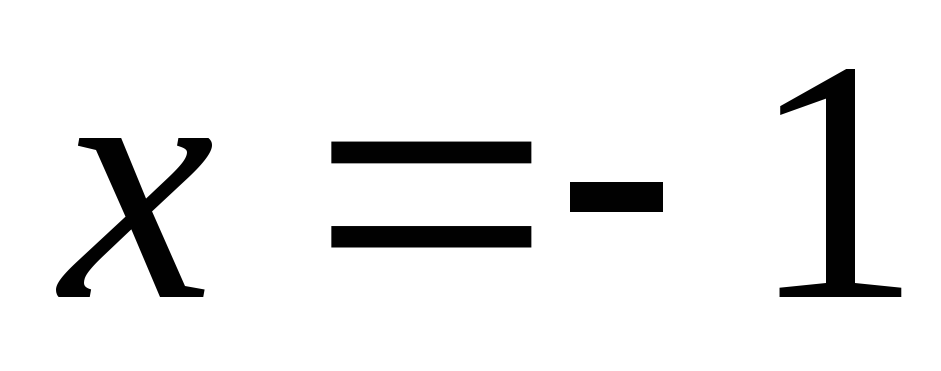 получаем
числовой ряд
получаем
числовой ряд 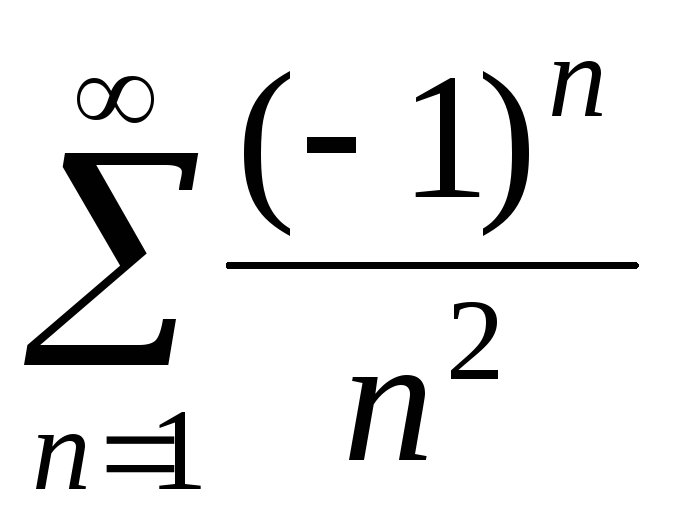 .
Этот ряд абсолютно сходящийся, так как
ряд, составленный из абсолютных величин
его членов
.
Этот ряд абсолютно сходящийся, так как
ряд, составленный из абсолютных величин
его членов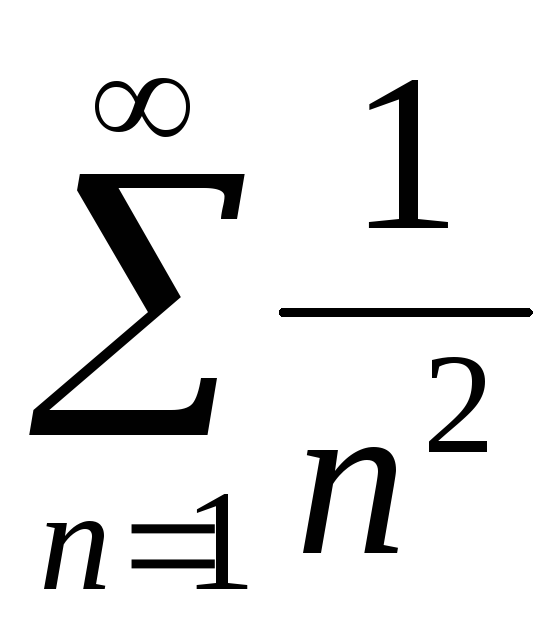 ,
сходящийся.
,
сходящийся.
Итак, область
сходимости данного ряда  .
.
б) Найдем радиус
сходимости R.
Так как 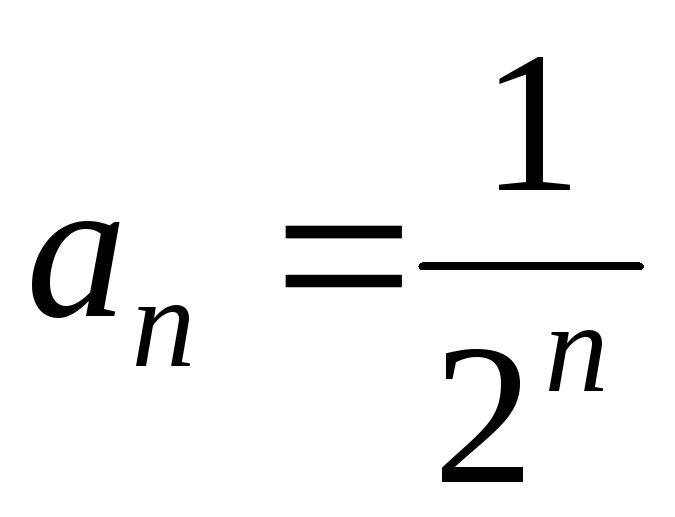 ,
то
,
то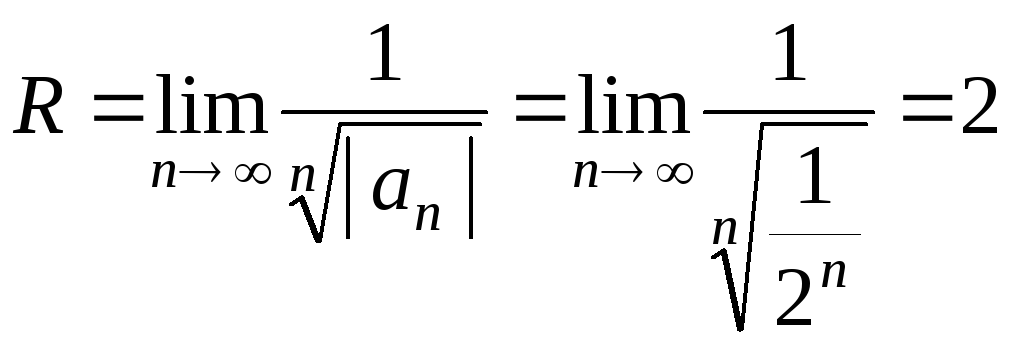 .
.
Итак, интервал
сходимости ряда 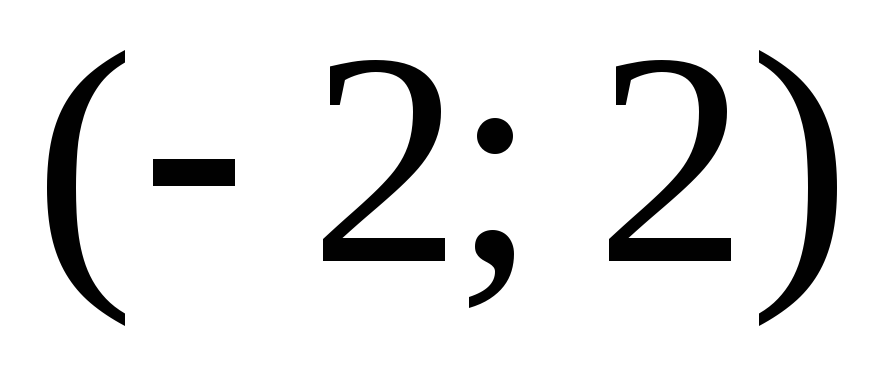 .
.
Исследуем на сходимость данный ряд на концах интервала сходимости.
При 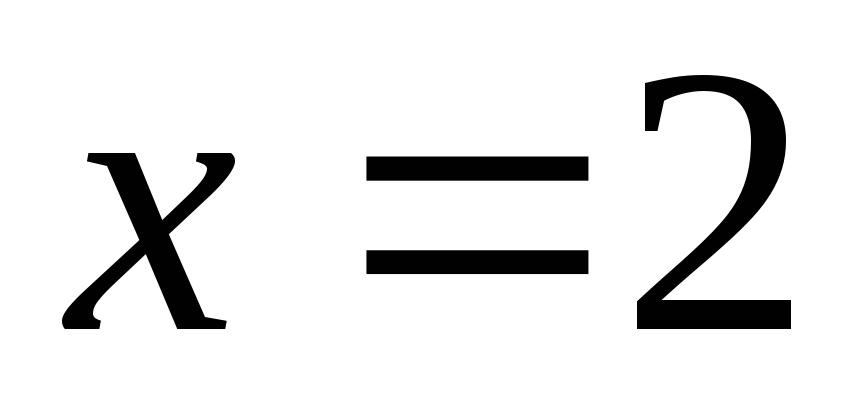 имеем числовой ряд
имеем числовой ряд 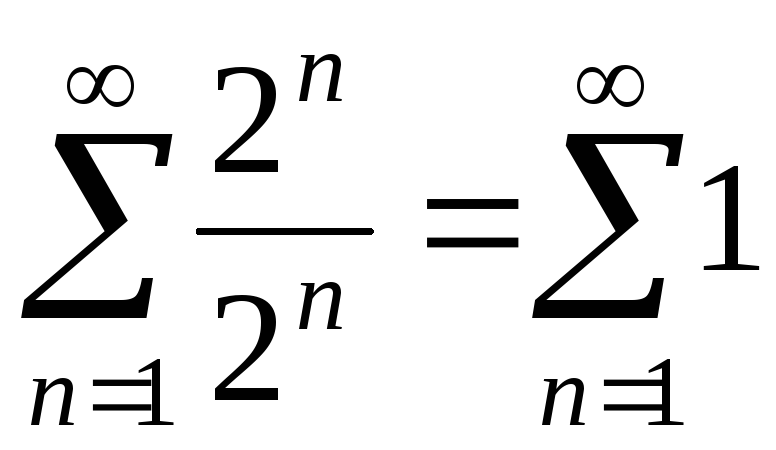 .
Этот ряд расходящийся, так как
.
Этот ряд расходящийся, так как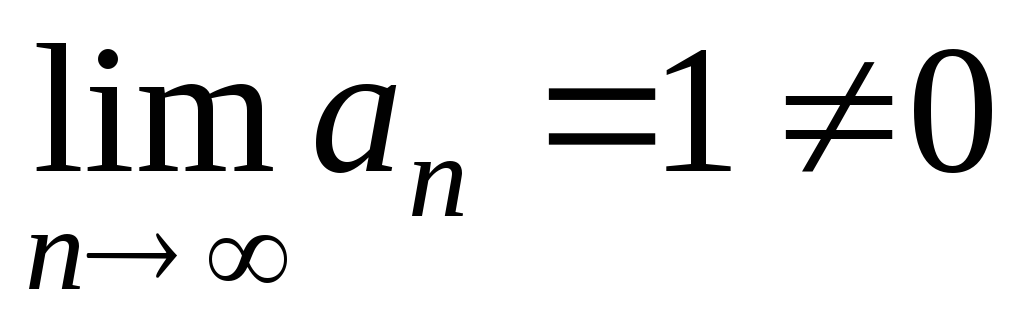 .
.
При 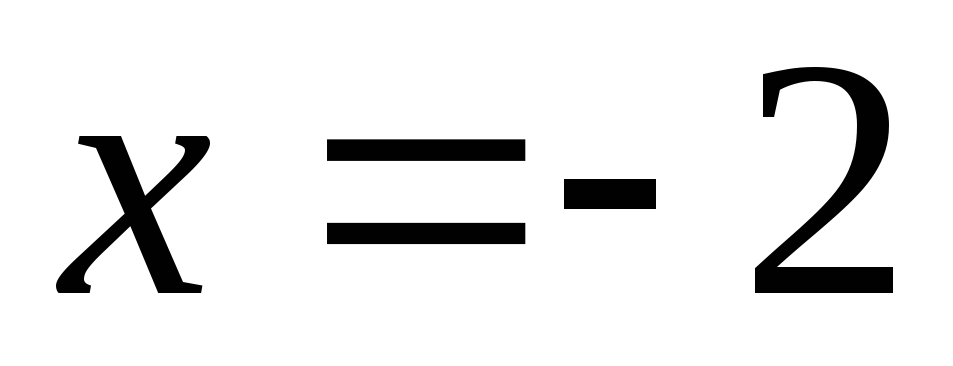 имеем числовой ряд
имеем числовой ряд 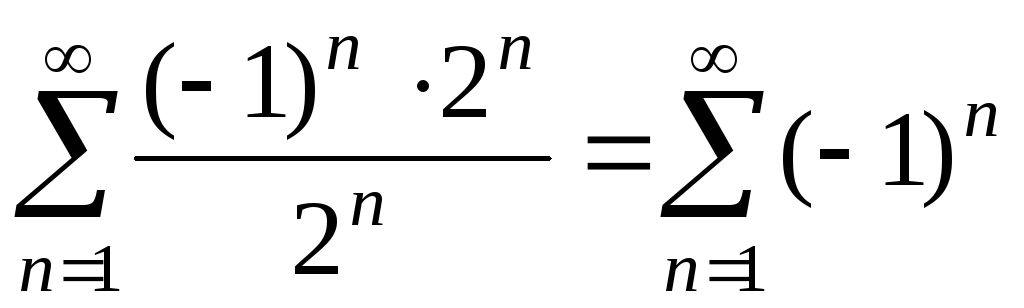 .
Этот ряд расходящийся, так как
.
Этот ряд расходящийся, так как не существует.
не существует.
Итак, область
сходимости данного ряда 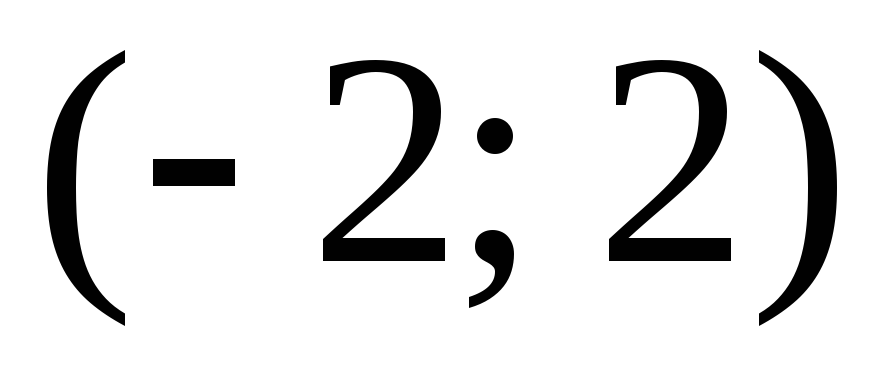 .
.
в) Найдем радиус
сходимости R.
Так как  ,
, то
то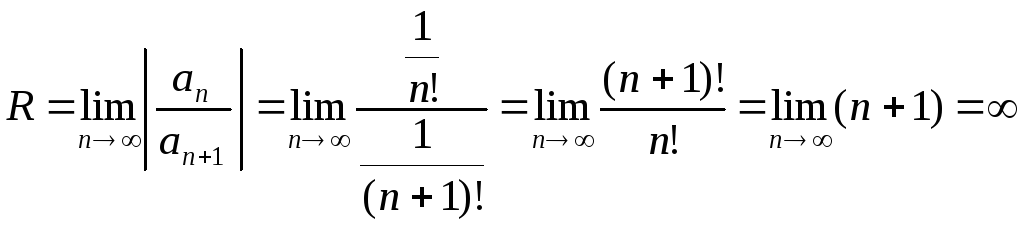 .
.
Итак, интервал
сходимости  .
Область сходимости данного ряда совпадает
с интервалом сходимости, то есть ряд
сходится при любом значении переменнойx.
.
Область сходимости данного ряда совпадает
с интервалом сходимости, то есть ряд
сходится при любом значении переменнойx.
г) Найдем радиус сходимости R.
Так как 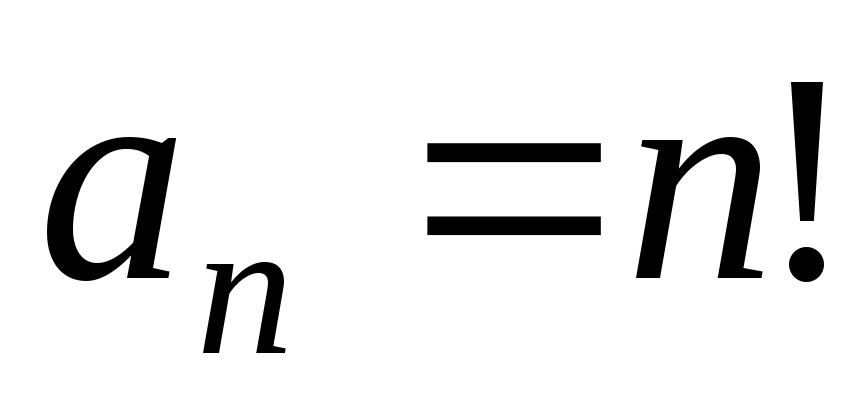 ,
,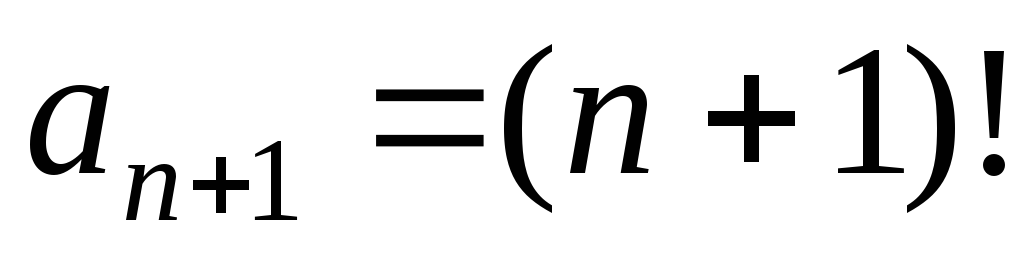 то
то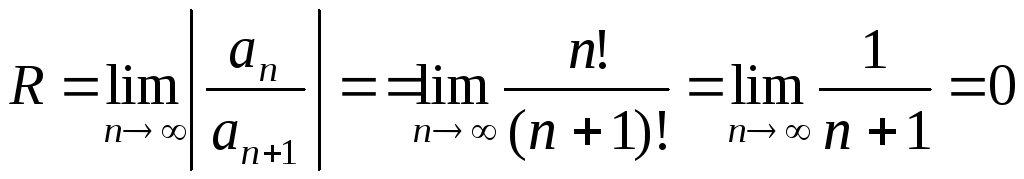 .
.
Так как 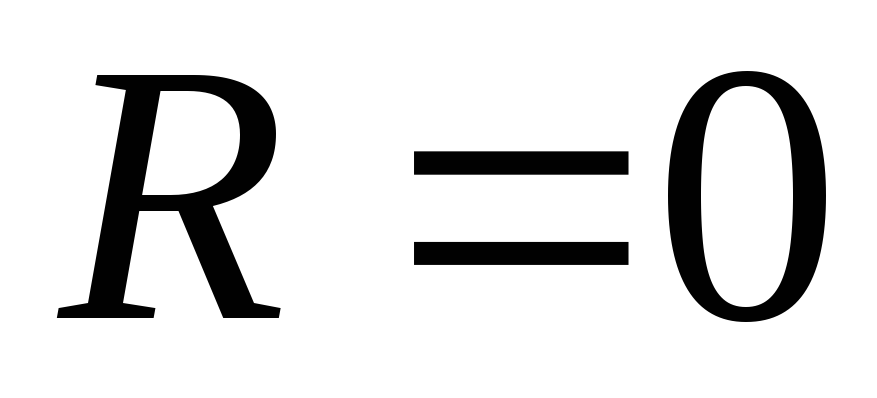 ,
то ряд сходится только в точке
,
то ряд сходится только в точке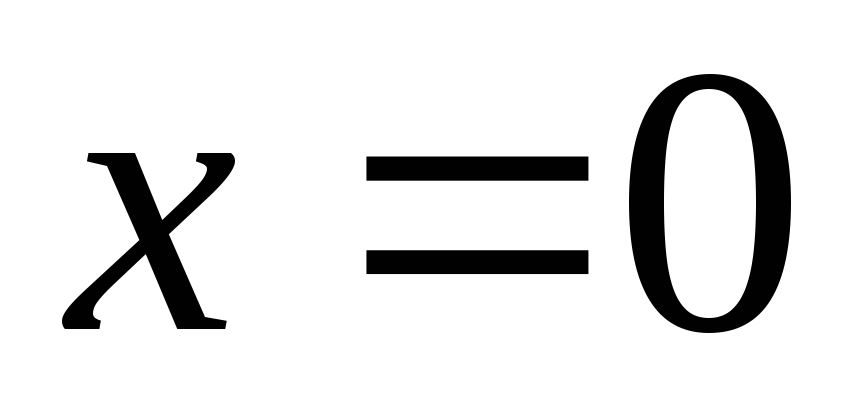 .
Значит, область сходимости данного ряда
представляет собой одну точку
.
Значит, область сходимости данного ряда
представляет собой одну точку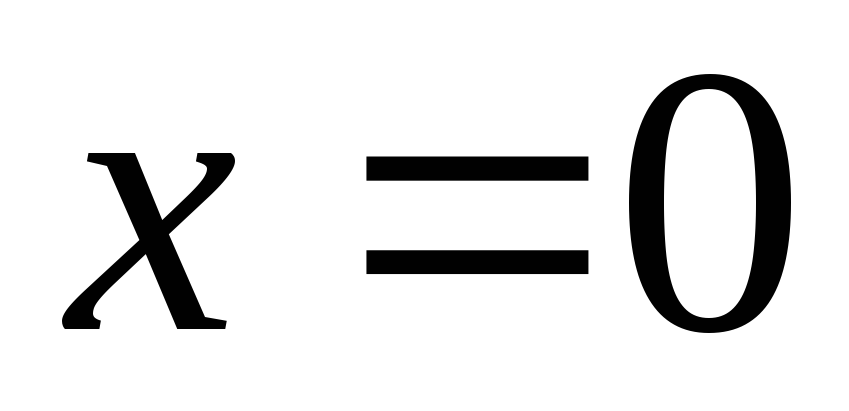 .
.
д) Найдем радиус сходимости R.
Так как 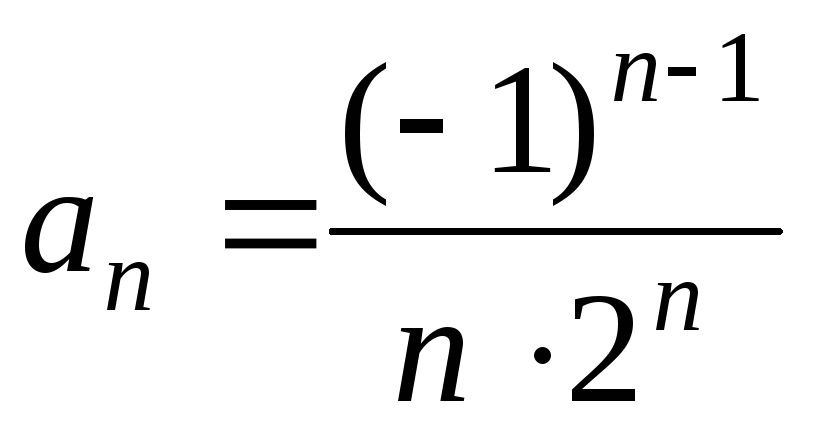 ,
,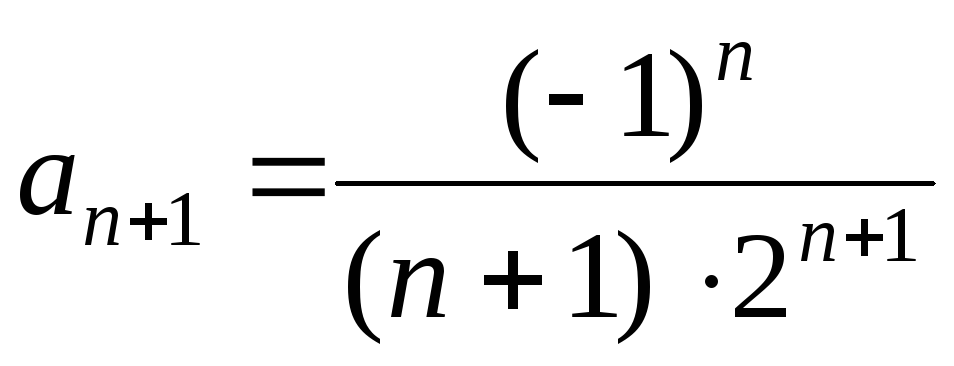 ,
то
,
то
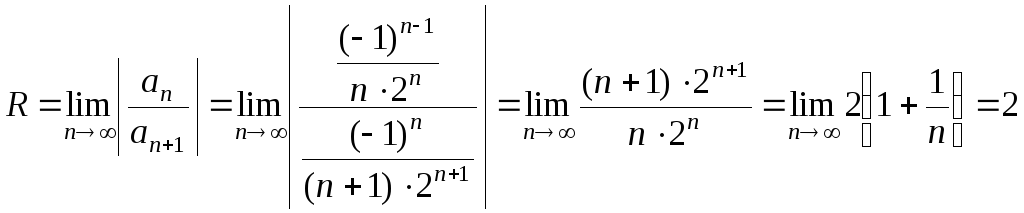 .
.
Итак, ряд сходится
абсолютно для всех x,
удовлетворяющих неравенству 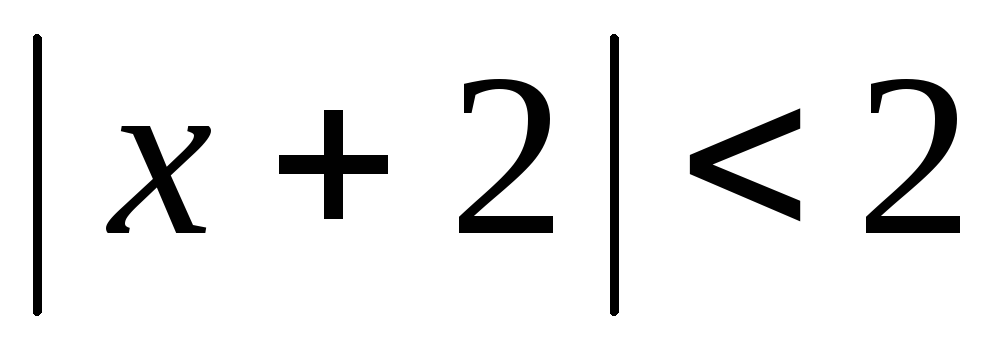 ,
то есть
,
то есть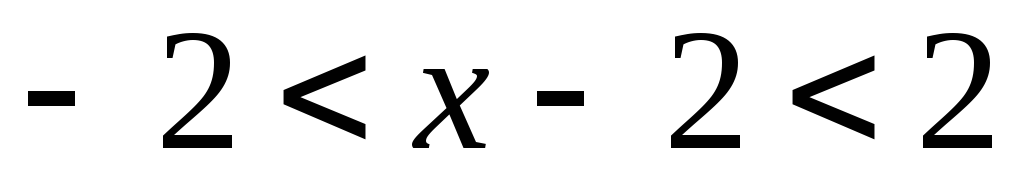 .
.
Отсюда 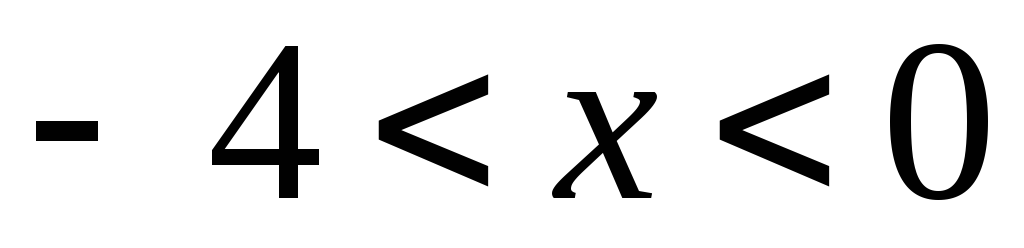 − интервал сходимости,
− интервал сходимости,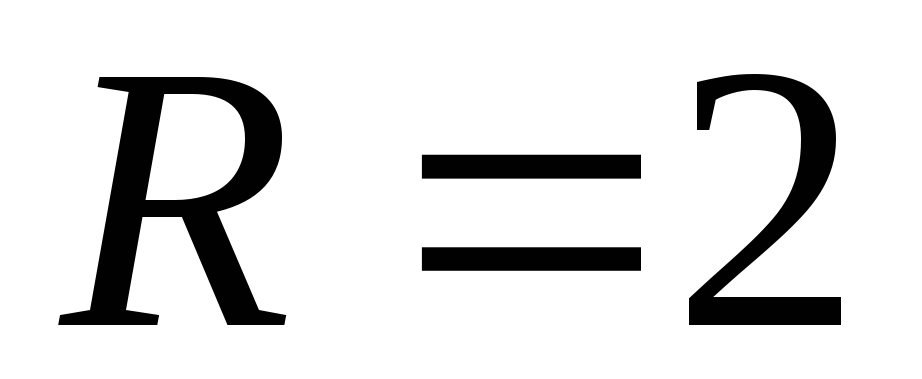 − радиус сходимости.
− радиус сходимости.
Исследуем данный ряд на сходимость на концах интервала сходимости.
При 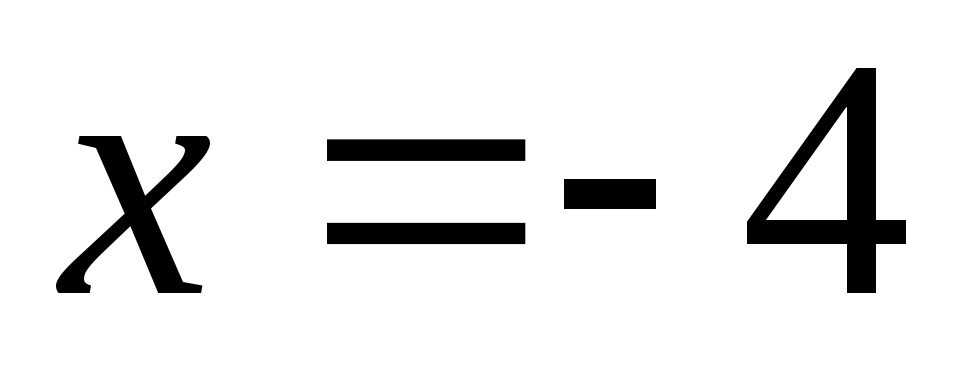 получаем числовой ряд
получаем числовой ряд
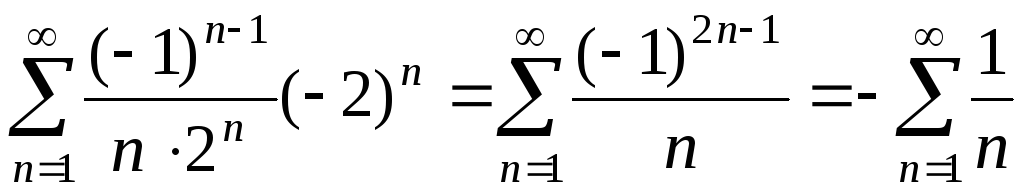 ,
,
который расходится (гармонический ряд).
При 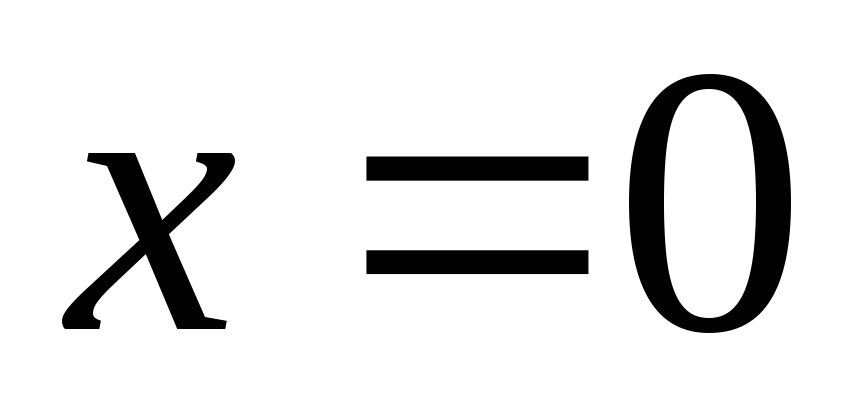 получаем числовой ряд
получаем числовой ряд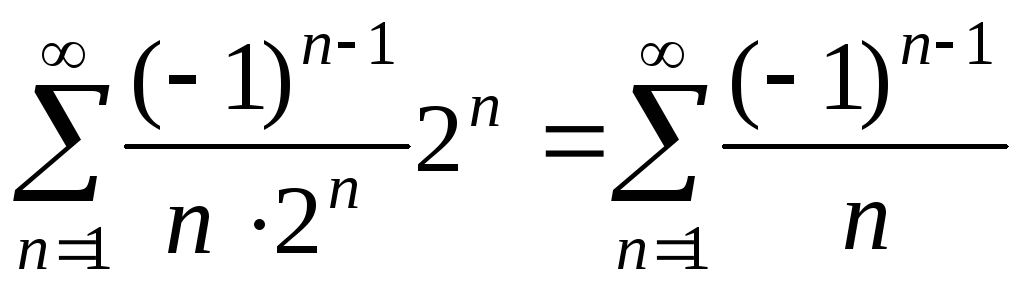 ,
который сходится условно (ряд сходится
по признаку Лейбница, а ряд, составленный
их абсолютных величин его членов,
расходится, так как является гармоническим).
,
который сходится условно (ряд сходится
по признаку Лейбница, а ряд, составленный
их абсолютных величин его членов,
расходится, так как является гармоническим).
Итак, область
сходимости ряда 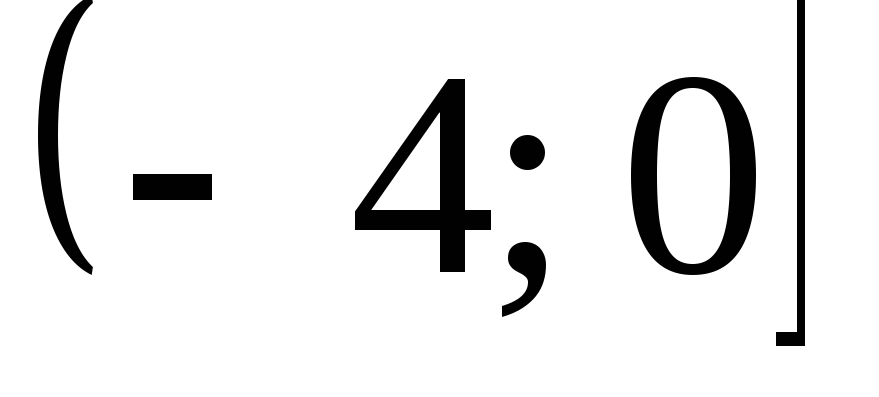 .
.
2.3. Ряды Тейлора и Маклорена.
Разложение функций в степенной ряд.
Приложение степенных рядов к приближенным вычислениям
Примеры решения задач
Пример 1. Разложить в степенной ряд функции:
а) 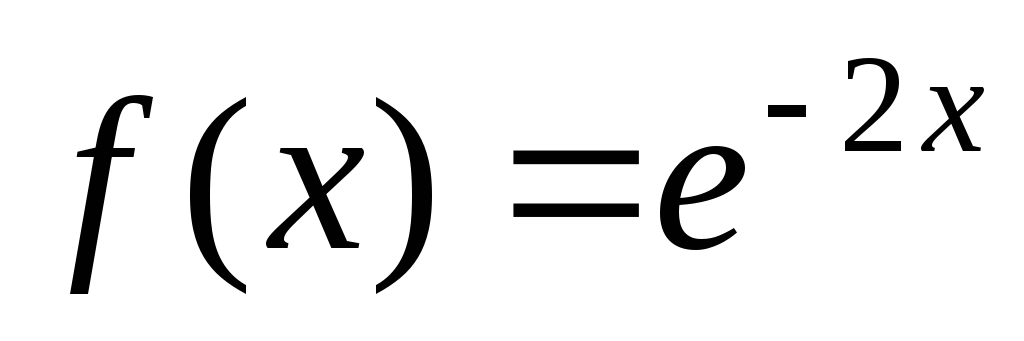 ; б)
; б)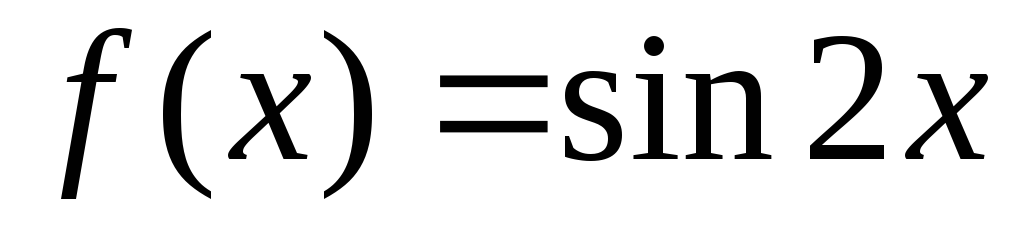 ;
;
в) 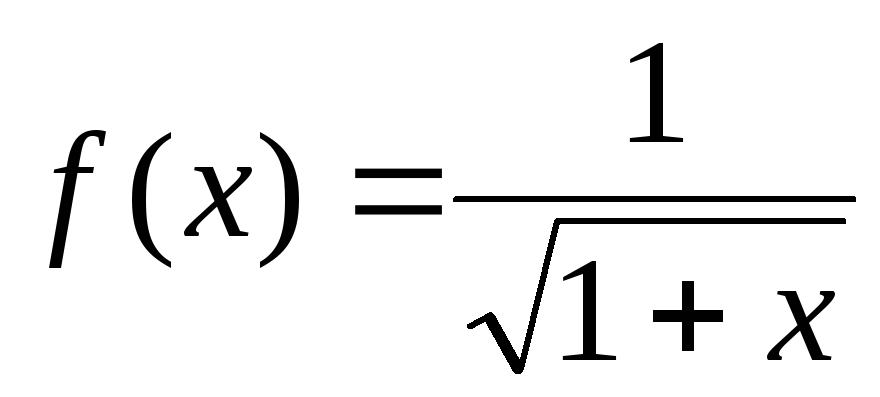 ; г)
; г)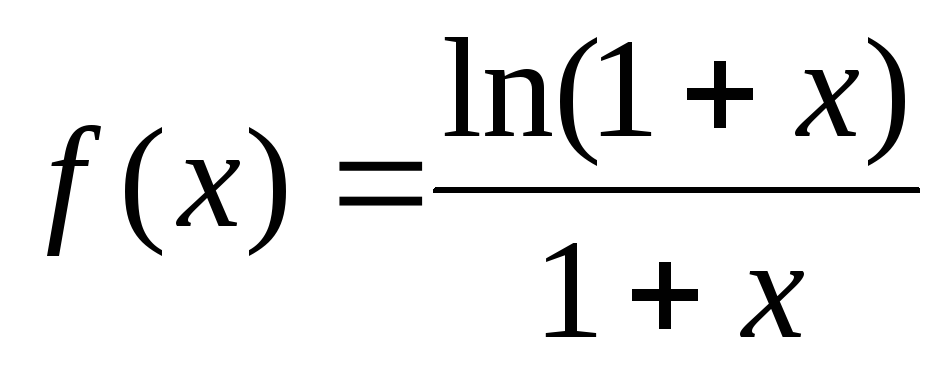 .
.
а) Заменив в формуле x на 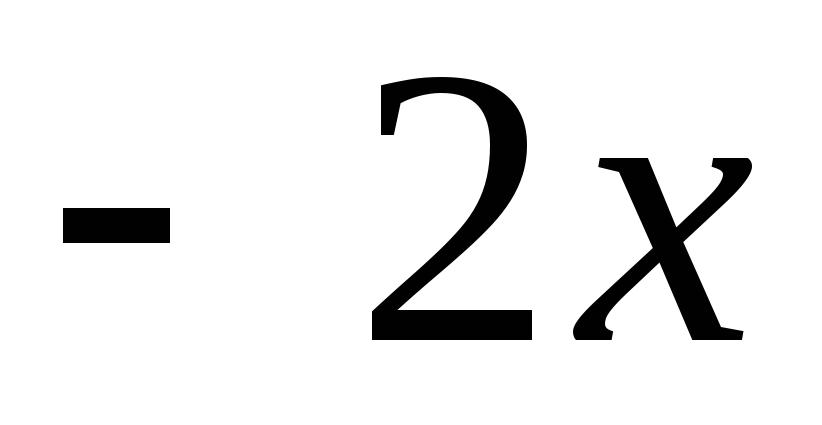 ,
получим искомое разложение:
,
получим искомое разложение:
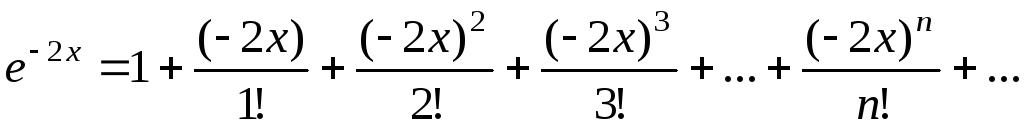 ,
где
,
где 
или
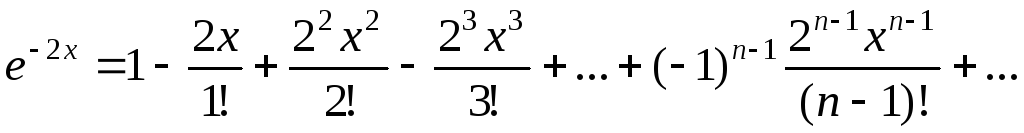 .
.
б) Заменяя в равенстве
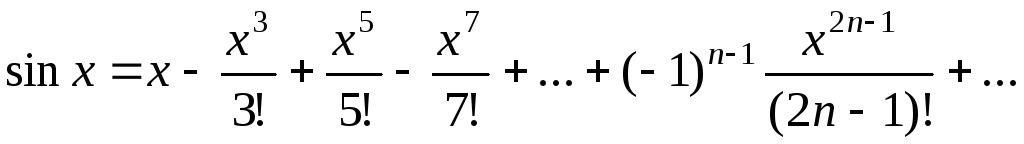 ,
где
,
где  x на
x на  ,
получим искомое разложение:
,
получим искомое разложение:
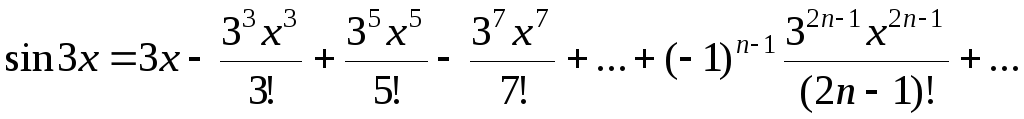 .
.
в) Данную функцию можно записать так: 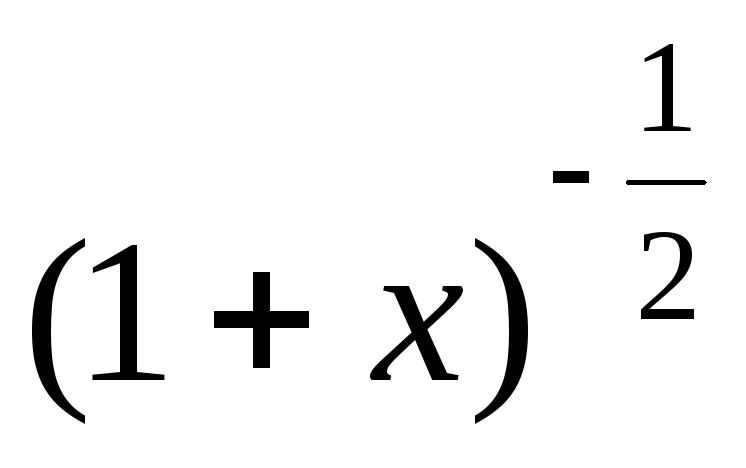 .
Чтобы найти искомый ряд, достаточно в
разложение
.
Чтобы найти искомый ряд, достаточно в
разложение
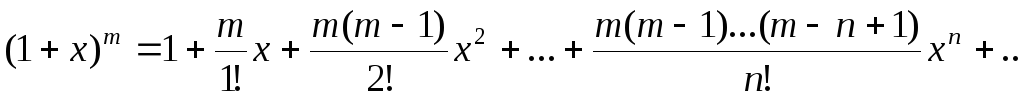 .,
где
.,
где 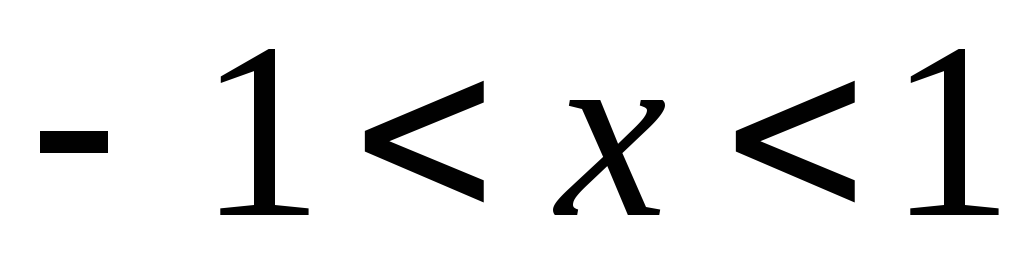 подставить
подставить 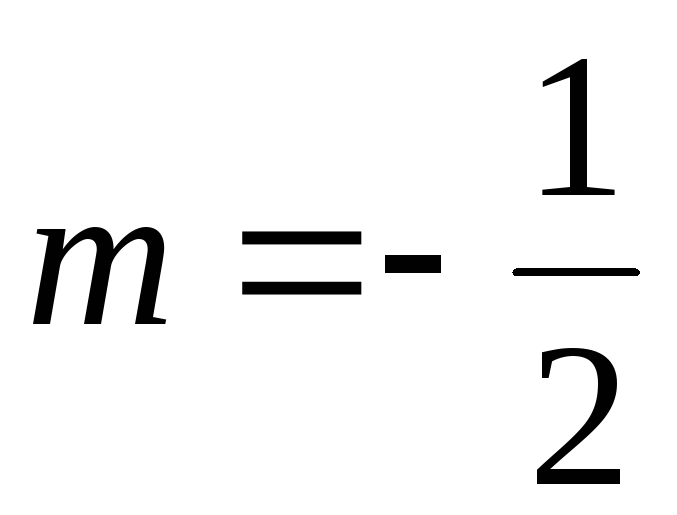 .
Тогда получим:
.
Тогда получим:
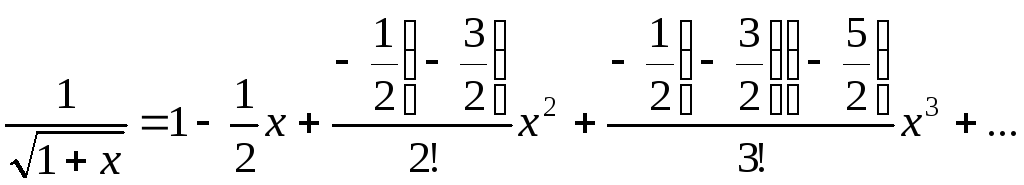
или
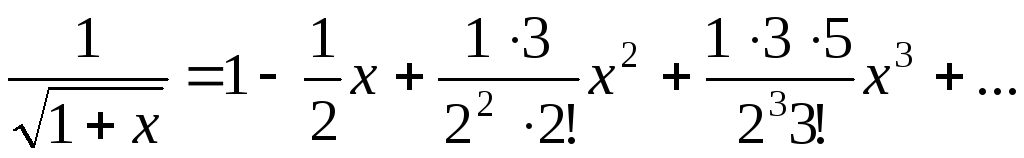 .
.
г) Данную функцию можно переписать так: 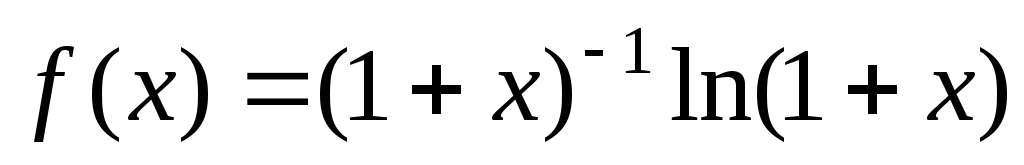 .
.
Функцию  можно разложить в степенной ряд, положив
в биномиальном ряде
можно разложить в степенной ряд, положив
в биномиальном ряде 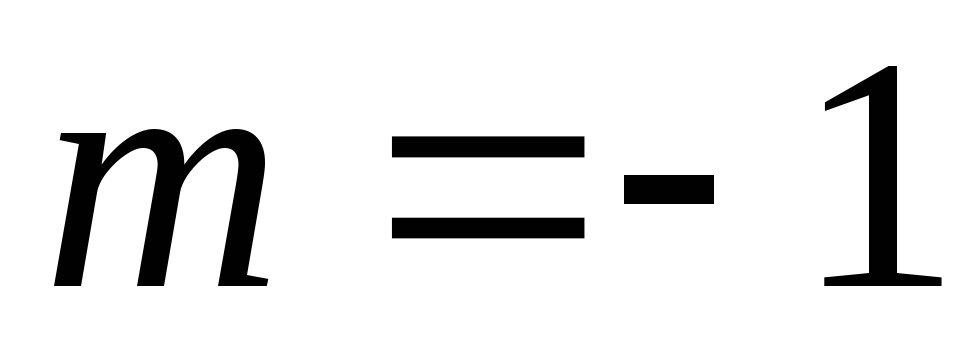 ,
получим
,
получим 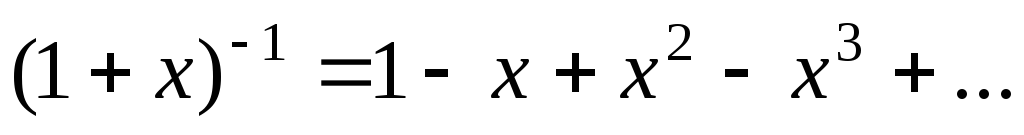 .
.
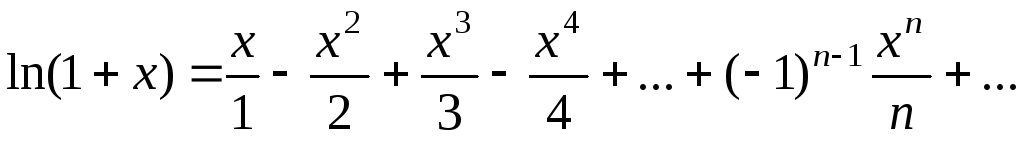 ,
где
,
где 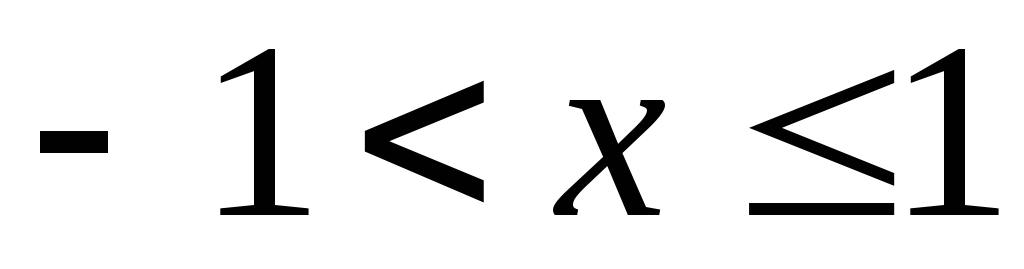 .
.
Чтобы получить искомое разложение, достаточно перемножить полученные ряды (ввиду абсолютной сходимости этих рядов).
Следовательно,
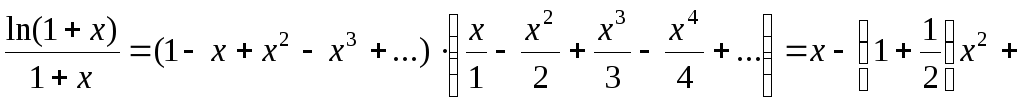
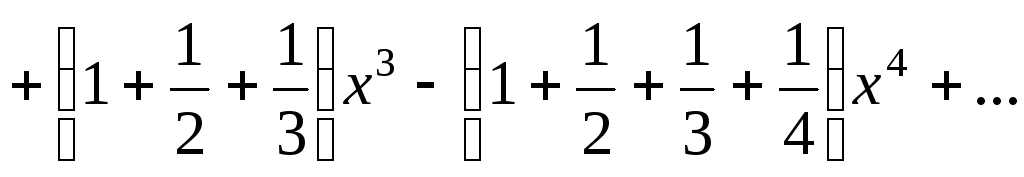 ,
где
,
где 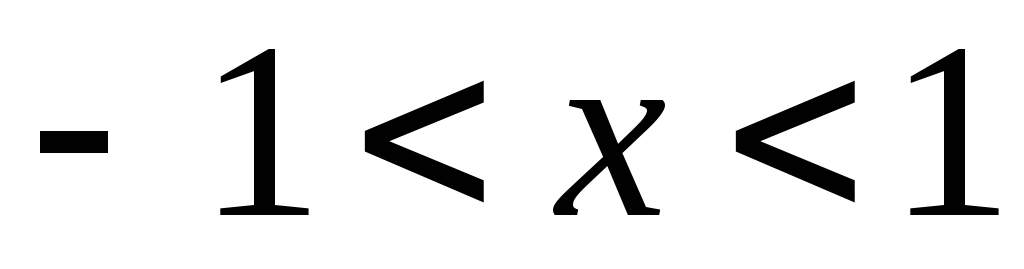 .
.
Пример 2. Найти приближенные значения данных функций:
а)  с точностью до 0,0001;
с точностью до 0,0001;
б) 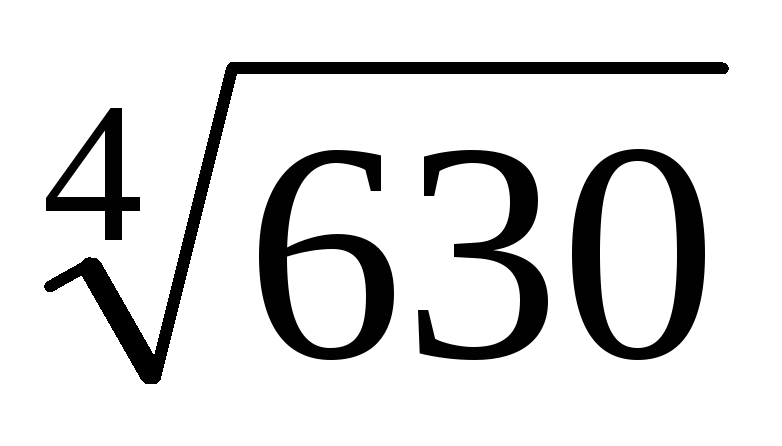 с точностью до 0,00001.
с точностью до 0,00001.
а) Так как 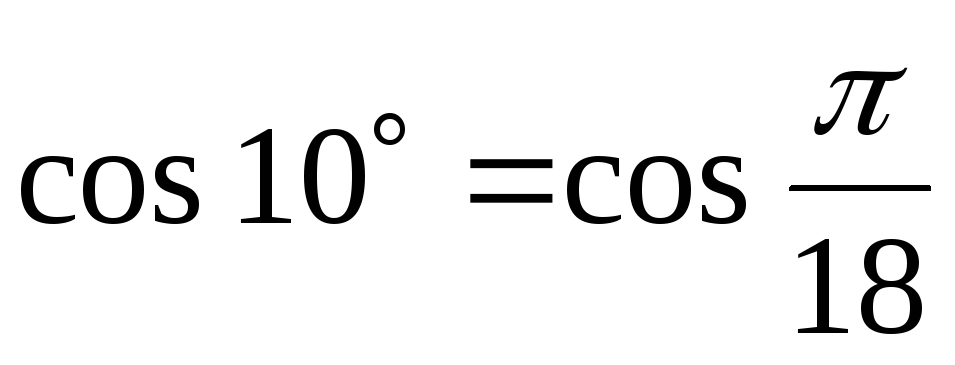 ,
то в разложение функции
,
то в разложение функции 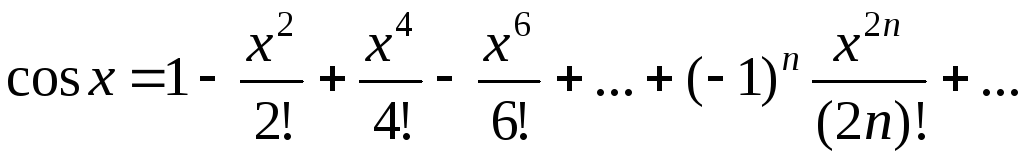 ,
где
,
где  подставим :
подставим :
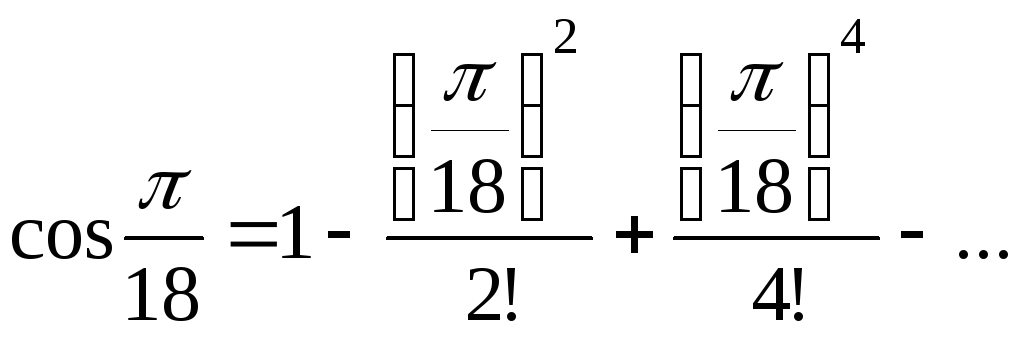 или
или 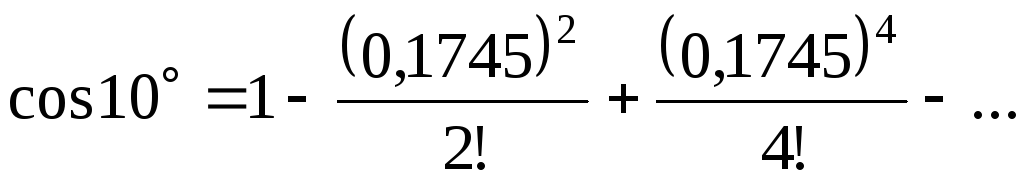
Так как 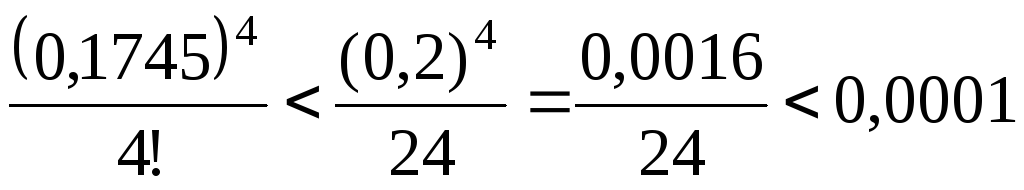 ,
то требуемая точность будет обеспечена,
если ограничиться только первыми двумя
членами полученного разложения.
,
то требуемая точность будет обеспечена,
если ограничиться только первыми двумя
членами полученного разложения.
Итак,
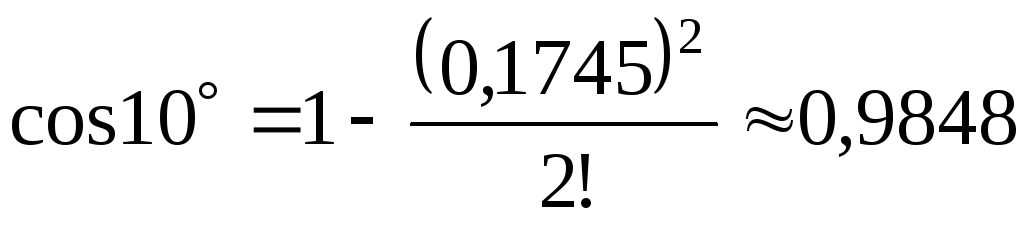 .
.
б) 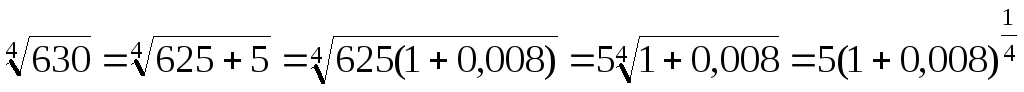 .
.
Используем биномиальный ряд
.,
где 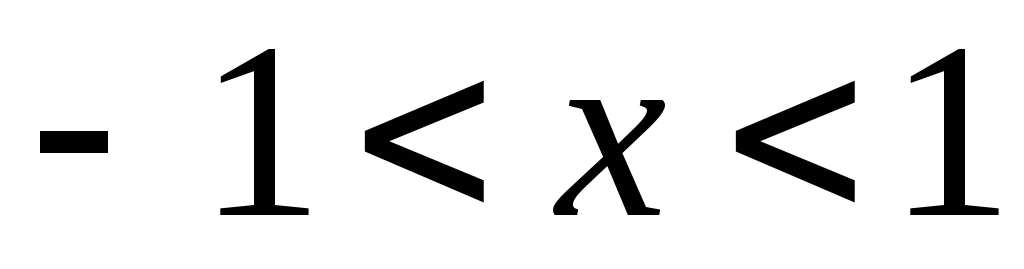 .
.
Полагая 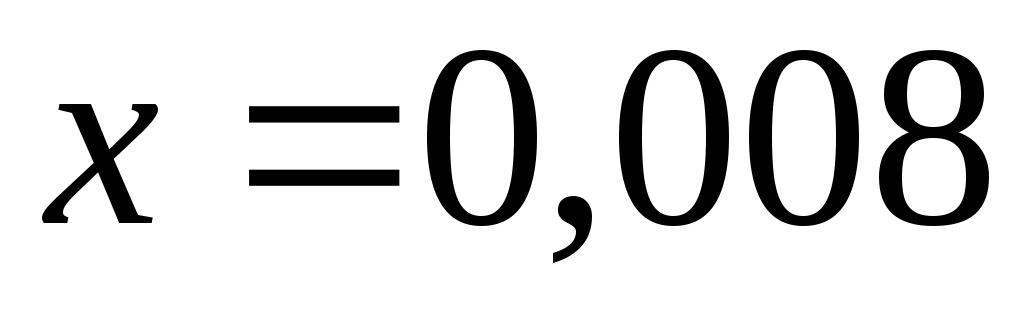 и
и 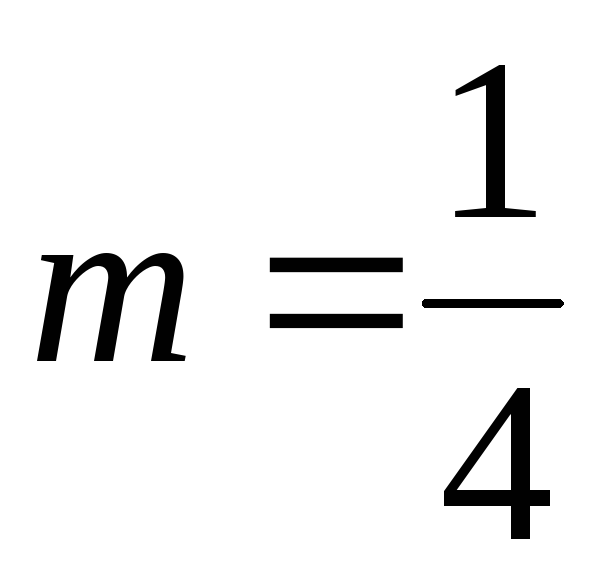 ,
получим следующее разложение:
,
получим следующее разложение:
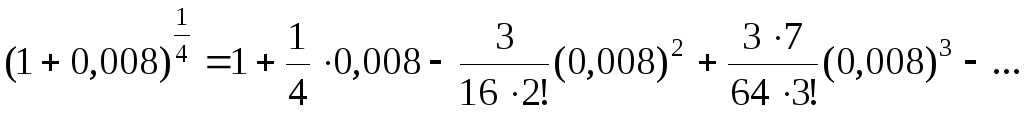
или
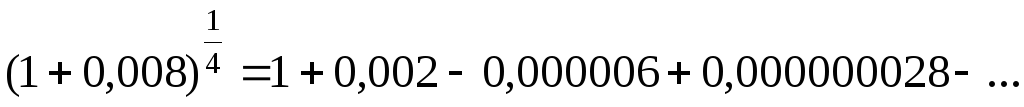 .
.
Если в последнем
знакочередующемся ряде учитывать только
первые два члена, а остальные отбросить,
то погрешность при вычислении  не превысит по абсолютной величине
0,000006. Тогда погрешность при вычислении
не превысит по абсолютной величине
0,000006. Тогда погрешность при вычислении 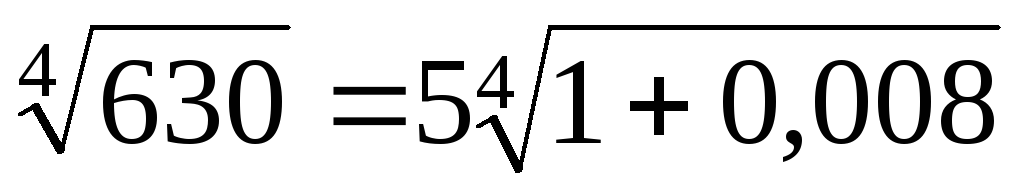 не превысит числа
не превысит числа 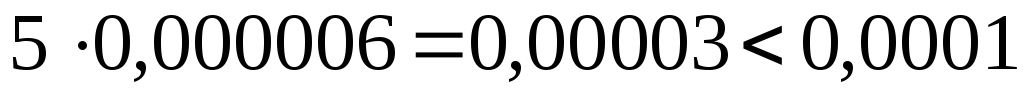 .
Следовательно,
.
Следовательно,
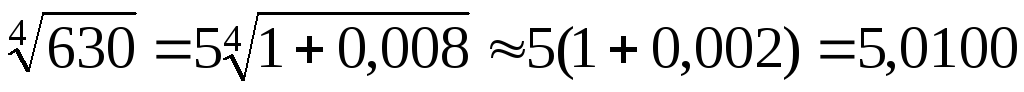 .
.
Пример 3. Вычислить с точностью до 0,001:
а) 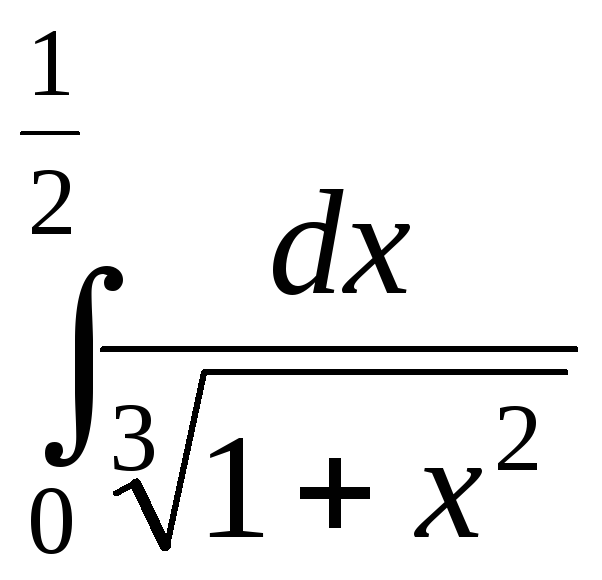 ; б)
; б) 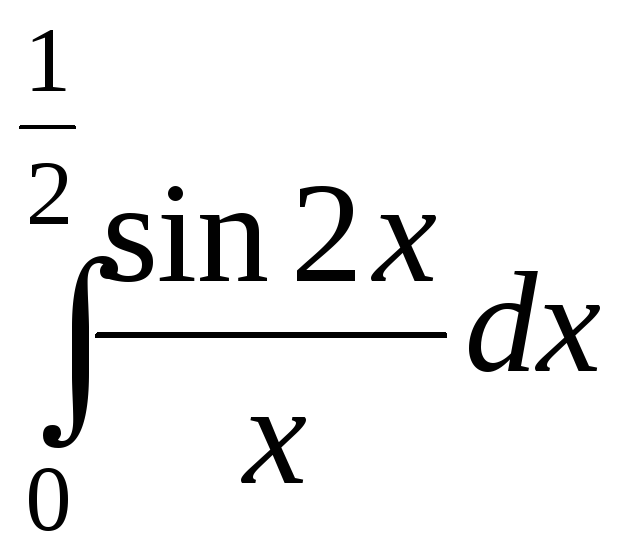 .
.
а) 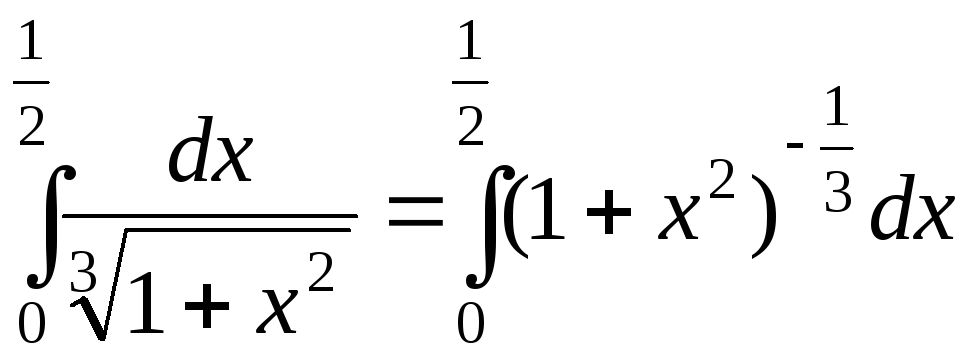 .
.
Разложим
подынтегральную функцию в степенной
ряд. Для этого подставим в биномиальный
ряд 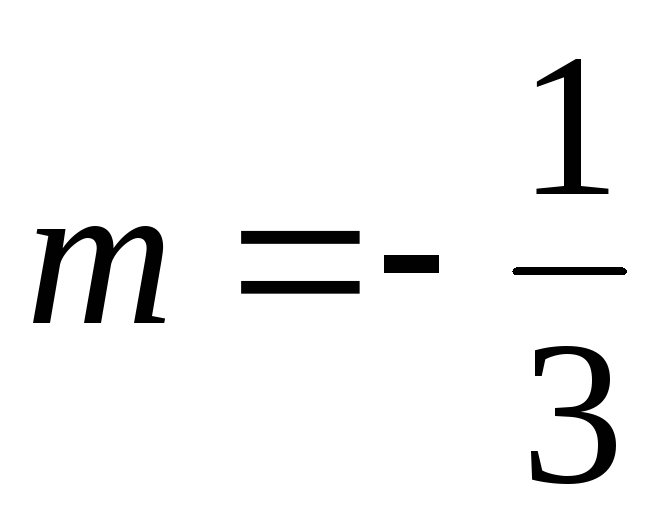 и заменим x на
и заменим x на 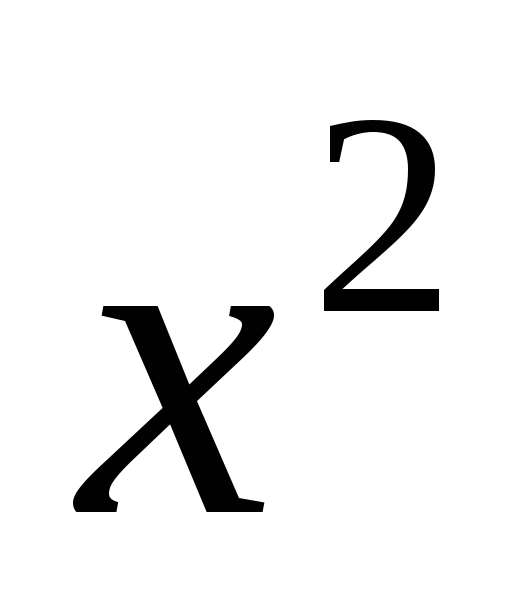 :
:
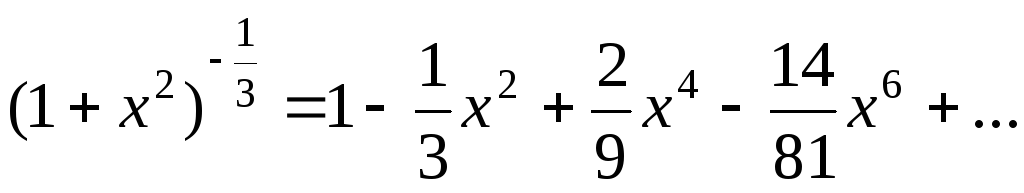 .
.
Так как отрезок
интегрирования 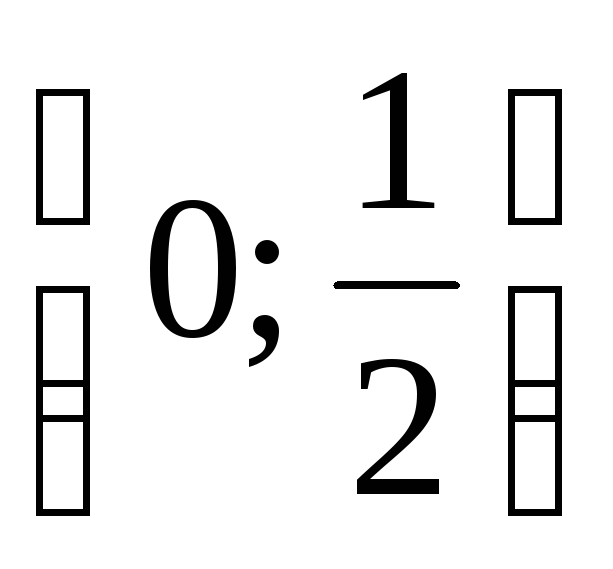 принадлежит области сходимости
полученного ряда
принадлежит области сходимости
полученного ряда 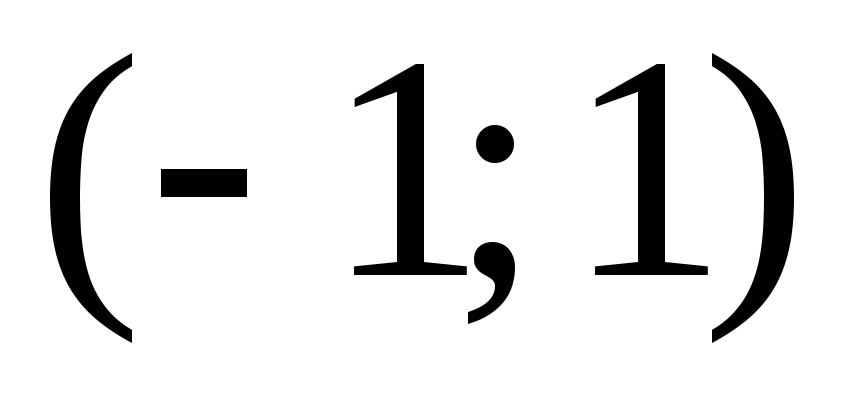 ,
то будем интегрировать почленно в
указанных пределах:
,
то будем интегрировать почленно в
указанных пределах:

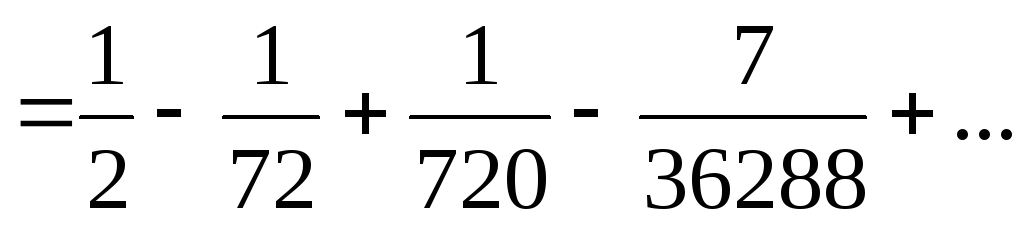 .
.
В полученном знакочередующемся ряде четвертый член по абсолютной величине меньше 0,001. Следовательно, требуемая точность будет обеспечена, если учитывать только первые три члена ряда.
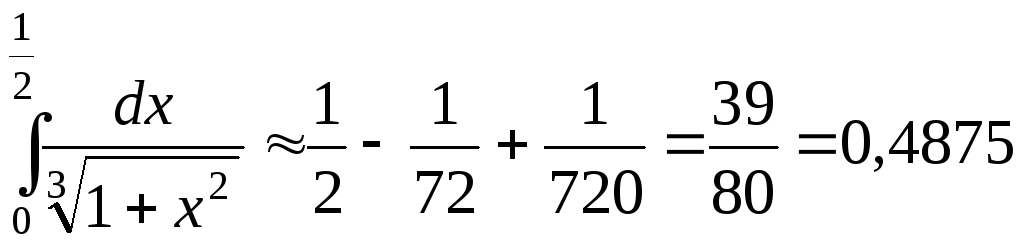 .
.
Так как первый из отброшенных членов имеет знак минус, то полученное приближенное значение будет с избытком. Поэтому ответ с точностью до 0,001 равен 0,487.
б) Предварительно представим подынтегральную функцию в виде степенного ряда. Заменим в разложении функции
 ,
где
,
где
x на 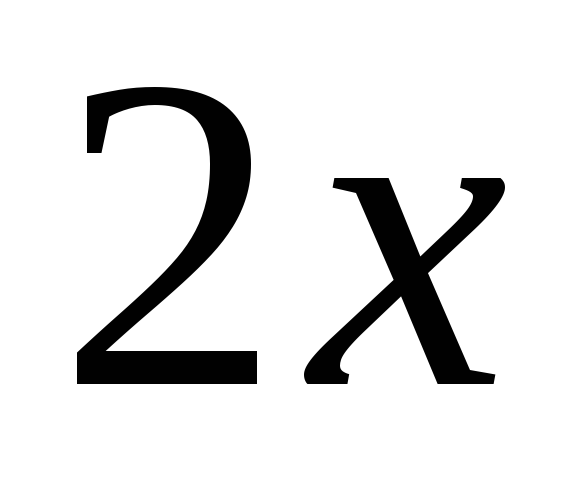 ,
получим:
,
получим:

Тогда 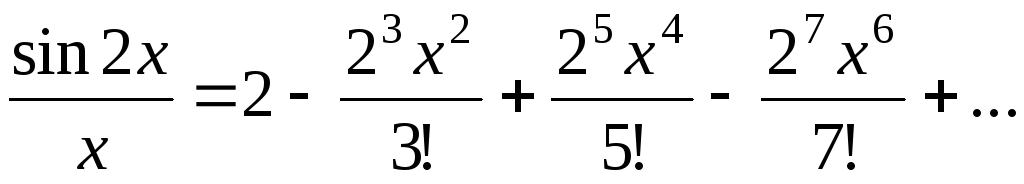 .
.
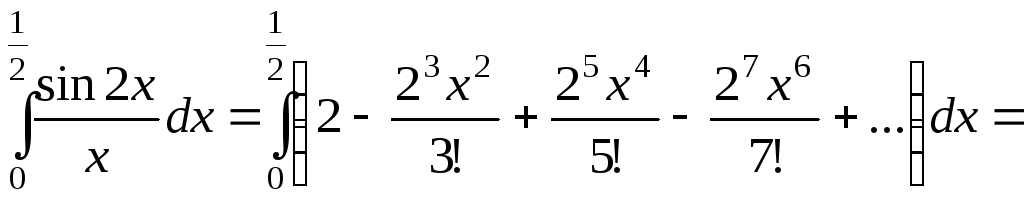
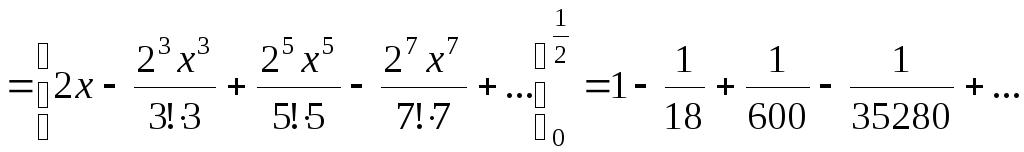 .
.
Полученный знакочередующийся ряд удовлетворяет условиям признака Лейбница. Четвертый член ряда по абсолютной величине меньше 0,001. Чтобы обеспечить требуемую точность, достаточно найти сумму первых трех членов.
Следовательно, 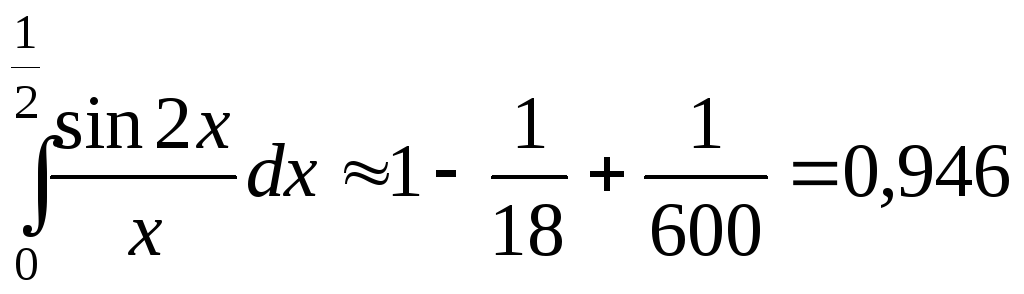 .
.
Интервал и радиус сходимости степенного ряда
⇐ ПредыдущаяСтр 3 из 3
Из теоремы Абеля следует, что если  есть точка сходимости степенного ряда, то интервал
есть точка сходимости степенного ряда, то интервал 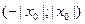 весь состоит из точек сходимости данного ряда; при всех значениях х вне этого интервала ряд
весь состоит из точек сходимости данного ряда; при всех значениях х вне этого интервала ряд 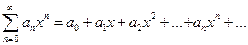 расходится.
расходится.
Интервал 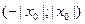 и называют интервалом сходимости степенного ряда. Положив
и называют интервалом сходимости степенного ряда. Положив 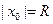 , интервал сходимости можно записать в виде (-R;R). Число R называют радиусом сходимости степенного ряда, т.е. R>0 – это такое число, что при всех х, для которых
, интервал сходимости можно записать в виде (-R;R). Число R называют радиусом сходимости степенного ряда, т.е. R>0 – это такое число, что при всех х, для которых  , ряд
, ряд 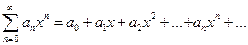 абсолютно сходится, а при
абсолютно сходится, а при 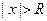 – расходится.
– расходится.
В частности, когда ряд 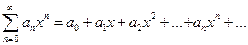 сходится лишь в одной точке
сходится лишь в одной точке 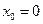 , то считаем, что R=0. Если же ряд сходится при всех значениях
, то считаем, что R=0. Если же ряд сходится при всех значениях 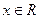 , то считаем, что
, то считаем, что 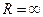 .
.
Отметим, что на концах интервала сходимости (т.е. при х=R и при х=-R) сходимость ряда проверяется в каждом случае отдельно.
Для нахождения радиуса сходимости степенного ряда 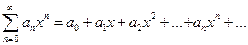 можно поступить следующим образом. Составим ряд из модулей членов данного степенного ряда
можно поступить следующим образом. Составим ряд из модулей членов данного степенного ряда

и применим к нему признак Даламбера. Допустим, что существует предел
 ,
, 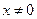
По признаку Даламбера ряд сходится, если  , т.е. ряд сходится при тех значениях х, для которых
, т.е. ряд сходится при тех значениях х, для которых  ; ряд, составленный из модулей члена ряда
; ряд, составленный из модулей члена ряда 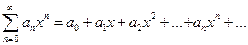 , расходится при тех значениях х, для которых
, расходится при тех значениях х, для которых 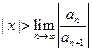 .Таким образом, для ряда
.Таким образом, для ряда  радиус абсолютной сходимости
радиус абсолютной сходимости

Аналогично, воспользовавшись радикальным признаком Коши, можно установить, что
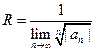
Свойства степенных рядов
1. Сумма S(x) степенного ряда 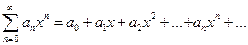 является непрерывной функцией в интервале сходимости (-R;R).
является непрерывной функцией в интервале сходимости (-R;R).
2. Степенные ряды 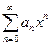 и
и  , имеющие радиусы сходимости соответственно
, имеющие радиусы сходимости соответственно 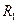 и
и 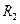 , можно почленно складывать, вычитать и умножать. Радиус сходимости произведения, суммы и разности рядов не меньше, чем меньшее из чисел
, можно почленно складывать, вычитать и умножать. Радиус сходимости произведения, суммы и разности рядов не меньше, чем меньшее из чисел 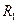 и
и 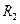 .
.
3. Степенной ряд внутри интервала сходимости можно почленно дифференцировать; при этом для ряда
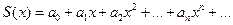
при –R<x<R выполняется равенство
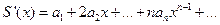
- Степенной ряд можно почленно интегрировать на каждом отрезке, расположенном внутри интервала сходимости; при этом для ряда
 при –R<a<x<R выполняется равенство
при –R<a<x<R выполняется равенство
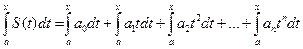
Ряды 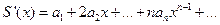 и
и 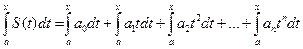 имеют тот же радиус сходимости, что и исходный степенной ряд.
имеют тот же радиус сходимости, что и исходный степенной ряд.
Разложение функций в степенные ряды
Ряды Тейлора и Маклорена
Как известно, для любой функции  определенной в окрестности точки
определенной в окрестности точки  и имеющей в ней производные до (n+1)-го порядка включительно, справедлива формула Тейлора:
и имеющей в ней производные до (n+1)-го порядка включительно, справедлива формула Тейлора:
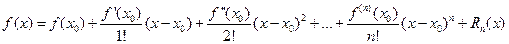
где 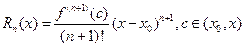 – остаточный член в форме Лагранжа. Число с можно записать в виде
– остаточный член в форме Лагранжа. Число с можно записать в виде 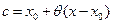 , где
, где 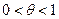 . Формулу
. Формулу 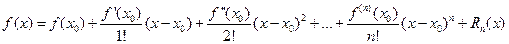 кратко можно записать в виде
кратко можно записать в виде 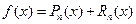 , где
, где 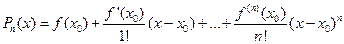 – многочлен Тейлора.
– многочлен Тейлора.
Если функция 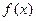 имеет производные любых порядков в окрестности точки
имеет производные любых порядков в окрестности точки  и остаточный член
и остаточный член 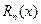 стремится к нулю при
стремится к нулю при  , то из формулы Тейлора получается разложение функции
, то из формулы Тейлора получается разложение функции 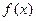 по степеням
по степеням 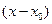 , называемое рядом Тейлора:
, называемое рядом Тейлора:
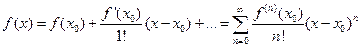
Если в ряде Тейлора положить 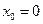 , то получим разложение функции по степеням х в так называемый ряд Маклорена:
, то получим разложение функции по степеням х в так называемый ряд Маклорена:
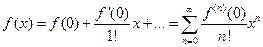
Отметим, что ряд Тейлора можно формально построить для любой бесконечно дифференцируемой функции в окрестности точки  . Но отсюда еще не следует, что он будет сходиться к данной функции
. Но отсюда еще не следует, что он будет сходиться к данной функции 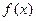 ; он может оказаться расходящимся или сходиться, но не к функции
; он может оказаться расходящимся или сходиться, но не к функции 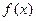 .
.
Теорема1
Для того чтобы ряд Тейлора 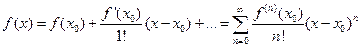 функции
функции 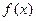 сходился к
сходился к 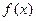 в точке х, необходимо и достаточно, чтобы в этой точке остаточный член формулы Тейлора
в точке х, необходимо и достаточно, чтобы в этой точке остаточный член формулы Тейлора 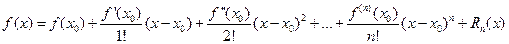 стремился к нулю при
стремился к нулю при  , т.е. чтобы
, т.е. чтобы 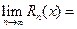 0.
0.
Пусть ряд Тейлора 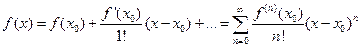 сходится к функции
сходится к функции 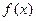 в некоторой окрестности точки
в некоторой окрестности точки  , т.е.
, т.е.  . Так как n-я частичная сумма
. Так как n-я частичная сумма  ряда
ряда 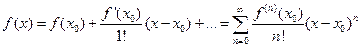 совпадает с многочленом Тейлора
совпадает с многочленом Тейлора 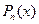 , т.е.
, т.е. 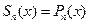 находим:
находим: 
Обратно, пусть 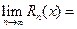 0. Тогда
0. Тогда 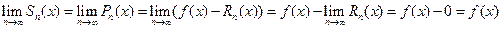
Теорема2
Если модули всех производных функций 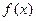 ограничены в окрестности точки
ограничены в окрестности точки  одним и тем же числом М>0, то для любого х из этой окрестности ряд Тейлора функции
одним и тем же числом М>0, то для любого х из этой окрестности ряд Тейлора функции 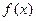 сходится к функции
сходится к функции 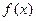 , т.е. имеет место разложение
, т.е. имеет место разложение 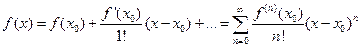 .
.
Согласно теореме1, достаточно показать, что 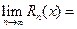 0. По условию теоремы2 для любого n имеет место неравенство
0. По условию теоремы2 для любого n имеет место неравенство 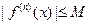 . Тогда имеем:
. Тогда имеем: 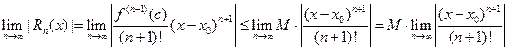
Осталось показать, что 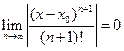 . Для этого рассмотрим ряд
. Для этого рассмотрим ряд 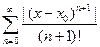
Так как 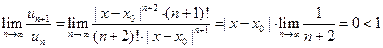 , то по признаку Даламбера этот ряд сходится на всей числовой оси. Но тогда, в силу необходимого признака сходимости,
, то по признаку Даламбера этот ряд сходится на всей числовой оси. Но тогда, в силу необходимого признака сходимости, 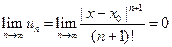
Следовательно, 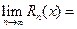 0
0
Разложение некоторых элементарных функций в ряд Тейлора (Маклорена)
Для разложения функции 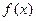 в ряд Маклорена
в ряд Маклорена 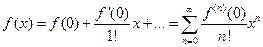 нужно:
нужно:
А) найти производные 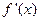 ,
, 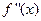 ,…,
,…, 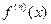 ,..;
,..;
Б) вычислить значения производных в точке 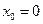 ;
;
В) написать ряд 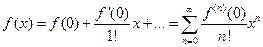 для заданной функции и найти его интервал сходимости;
для заданной функции и найти его интервал сходимости;
Ґ) найти интервал (-R;R), в котором остаточный член ряда Маклорена 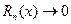 при
при 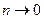 . Если такой интервал существует, то в нем функция
. Если такой интервал существует, то в нем функция  и сумма ряда Маклорена совпадают.
и сумма ряда Маклорена совпадают.
Приведем таблицу, содержащую разложения в ряд Маклорена некоторых элементарных функций:
Докажем формулу.
Пусть 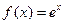
Имеем:
А) 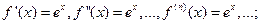
Б) 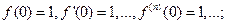
В) 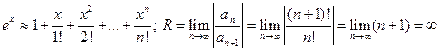 , т.е. ряд сходится в интервале
, т.е. ряд сходится в интервале 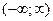 ;
;
Ґ) для всех 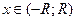 имеем
имеем 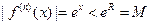 , т.е. все производные в этом интервале ограничены одним и тем же числом
, т.е. все производные в этом интервале ограничены одним и тем же числом 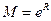 . Следовательно,
. Следовательно,  . Таким образом,
. Таким образом, 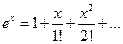 .
.
Докажем формулу.
Пусть f(x)=sin x
Имеем:
А) 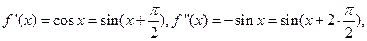
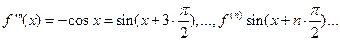
Б) 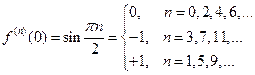
В) 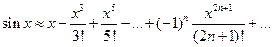 Легко проверить, что полученный ряд сходится на всей числовой оси, т.е. при всех
Легко проверить, что полученный ряд сходится на всей числовой оси, т.е. при всех 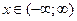
Ґ) любая производная функция f(x)=sin x по модулю не превосходит единицы,  . Следовательно, имеет место разложение f(x)=sin x.
. Следовательно, имеет место разложение f(x)=sin x.
Докажем формулу
Пусть f(x)=cos x
Формулу f(x)=cos x можно доказать так же, как и формулу f(x)=sin x. Однако проще получить разложение функции cos x, воспользовавшись свойством 3 степенных рядов. Продифференцировав почленно ряд f(x)=sin x, получим:
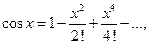
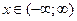
Докажем формулу
Пусть 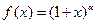 ,
, 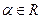
Имеем:
А) 
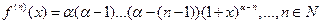
Б) 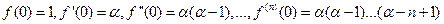
В) 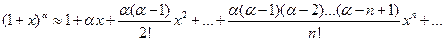
Ґ) 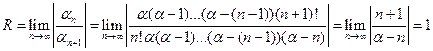 , т.е. составленный для функции
, т.е. составленный для функции 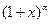 ряд сходится в интервале (-1;1), остаточный член
ряд сходится в интервале (-1;1), остаточный член 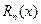 стремится к нулю при
стремится к нулю при  .
.
Ряд 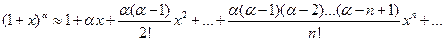 называется биномиальным. Если
называется биномиальным. Если 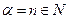 , то все члены ряда с (n+1)-го номера равны 0, так как содержат множитель
, то все члены ряда с (n+1)-го номера равны 0, так как содержат множитель 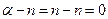 . В этом случае ряд представляет собой известную формулу бинома Ньютона:
. В этом случае ряд представляет собой известную формулу бинома Ньютона:
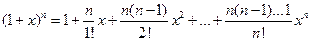
Докажем формулу
Пусть 
Формула может быть получена разными способами:
1)пользуясь правилом разложения функции в ряд;
2)рассматривая ряд  как ряд геометрической прогрессии, первый член которой равен 1 и знаменатель q=x; известно, что данный ряд сходится при
как ряд геометрической прогрессии, первый член которой равен 1 и знаменатель q=x; известно, что данный ряд сходится при 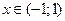 и его сумма равна
и его сумма равна 
3)воспользовавшись формулой 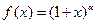 : положив в ней
: положив в ней 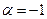 и заменив х на –х, получим формулу
и заменив х на –х, получим формулу  .
.
Докажем формулу
Пусть f(x)=ln (1+x)
Формула f(x)=ln (1+x) также может быть доказана разными способами. Приведем один из них.
Рассмотрим равенство  ,
,
справедливое для всех 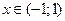 . Используя свойство 4 степенных рядов, проинтегрируем данный ряд на отрезке [0;x],
. Используя свойство 4 степенных рядов, проинтегрируем данный ряд на отрезке [0;x], 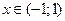 :
:
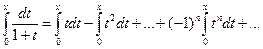
или
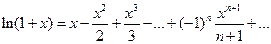
Докажем формулу
Пусть f(x)=arctg x
Положив в формуле 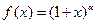
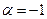 и заменив х на
и заменив х на  , получим равенство
, получим равенство

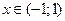
Тогда 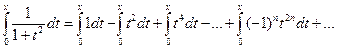
или

Докажем формулу
Пусть f(x)=arcsin x
Положив в формуле 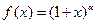
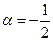 и заменив х на
и заменив х на 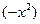 , получим равенство
, получим равенство
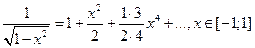
Тогда 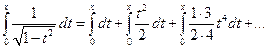
или
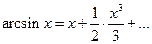
Правила определения интервала сходимости степенного ряда
ОРИГИНАЛЬНАЯ ПОЛНАЯ СТРАНИЦА : Правила определения интервала сходимости степенного ряда
ИЗУЧАЙТЕ ТЕМУ НА НЕСКОЛЬКИХ УРОВНЯХ :
ТАКЖЕ ВЫБЕРИТЕ :
В этой статье описывается правило, набор правил или процедура для определения набора значений для параметра, в котором сходятся ряд или интеграл, определенный в терминах этого параметра.
См. Другие правила определения интервала конвергенции
Заявление
Рассмотрим степенной ряд вида:
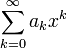
Приведенные здесь правила помогают определить радиус сходимости и интервал сходимости для этого степенного ряда с точки зрения того, как коэффициенты  растут или затухают с
растут или затухают с 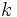 как
как  .
.
Ниже представлена таблица со всеми случаями:
| Словесное описание дела | Версия Lim sup для коэффициентов | Другая версия для коэффициентов | Заключение о радиусе схождения | Заключение об интервале схождения | Примеры функций  |
|---|---|---|---|---|---|
| коэффициенты убывают сверхэкспоненциально | 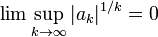 | [ПОКАЗАТЬ БОЛЬШЕ] Для любого 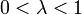 существует положительное целое число существует положительное целое число  такое, что такое, что 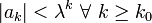 | 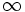 | все из 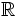 | , обратная функция с дважды экспоненциальным ростом, обратная экспоненте функции с полиномиальным ростом, обратная факториальной функции или функция факториального типа. |
| коэффициенты сверхэкспоненциально растут | 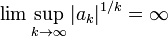 | 0 | 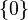 | функция с дважды экспоненциальным ростом, экспонента функции с полиномиальным ростом, факториальная функция или функция факториального типа | |
| коэффициенты растут или убывают экспоненциально | 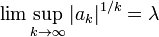 ( (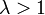 , если коэффициенты растут, , если коэффициенты растут,  , если коэффициенты уменьшаются) , если коэффициенты уменьшаются) | 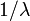 | Чтобы определить, включены ли конечные точки, мы используем тест разницы степеней или какой-либо его вариант (см. Ниже) | экспоненциальная функция, умноженная на экспоненциальную функцию на рациональную функцию, умноженную на функцию более медленного роста | |
| коэффициенты субэкспоненциально растут или убывают | 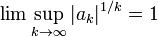 |  | Чтобы определить, включены ли конечные точки, мы используем тест разницы степеней или какой-либо его вариант (см. Ниже) | экспоненциальная функция, умноженная на экспоненциальную функцию на рациональную функцию, умноженную на функцию более медленного роста |
Пояснение
Результат почти сразу следует из корневого теста, примененного к серии 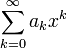 .Главное помнить, что термины этой серии — не
.Главное помнить, что термины этой серии — не  , а
, а 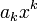 . Мы получили:
. Мы получили:
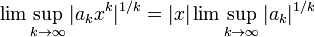
Радиус сходимости — это значение 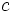 , которое удовлетворяет:
, которое удовлетворяет:
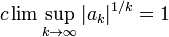
Это потому, что если 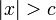 , то
, то 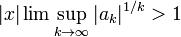 , поэтому ряд расходится по корневому тесту. Если
, поэтому ряд расходится по корневому тесту. Если 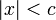 , то
, то 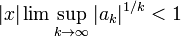 , поэтому ряд сходится по критерию корня. Случай
, поэтому ряд сходится по критерию корня. Случай 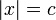 (конечные точки) не дает результатов для корневого теста, а остальная часть этой страницы объясняет, как работать с конечными точками.
(конечные точки) не дает результатов для корневого теста, а остальная часть этой страницы объясняет, как работать с конечными точками.
В приведенной выше таблице просто рассматриваются различные случаи для 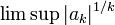 .
.
Иерархия функций
Список функций
Обозначение с большим числом  означает функцию, которая ограничена между постоянными положительными кратными
означает функцию, которая ограничена между постоянными положительными кратными 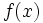 для достаточно большого
для достаточно большого 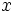 .
.
Ниже приведены функции со сверхэкспоненциальным ростом (который становится сверхэкспоненциальным затуханием, когда они появляются в знаменателе). Они расположены в порядке убывания роста:
- Двойные экспоненциальные функции, т.е.е., функции вида
 , где
, где  .
. - Функция формы
 , где
, где  , то есть функции, экспоненциально растущие в суперлинейной степени
, то есть функции, экспоненциально растущие в суперлинейной степени  . Внутри них, чем больше значение
. Внутри них, чем больше значение  , тем быстрее будет рост.
, тем быстрее будет рост. - Функции формы
 . Здесь живет факториальная функция.
. Здесь живет факториальная функция.
Единственные функции с экспоненциальным ростом — это функции вида  ,
, 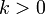 . Их обратные значения, которые являются функциями вида
. Их обратные значения, которые являются функциями вида 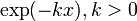 , дают примеры функций экспоненциального затухания.
, дают примеры функций экспоненциального затухания.
Вот функции субэкспоненциального роста (их обратные имеют субэкспоненциальное затухание):
- Функции формы
 ,
, 
- Функции, которые растут как полиномы или степенные функции, т. Е.
 . Чем больше значение
. Чем больше значение  , тем быстрее будет рост.
, тем быстрее будет рост. - Функции, которые растут как полилогарифмические функции, т. Е.
 .
.
Взаимодействие между функциями
- Взаимодействие суперэкспоненциалов : Произведение двух функций со сверхэкспоненциальным ростом все еще имеет сверхэкспоненциальный рост.Для частного двух функций со сверхэкспоненциальным ростом сначала выясните, какая из них находится выше в иерархии. Если числитель выше по иерархии, то в целом мы получаем сверхэкспоненциальный рост. Если знаменатель выше по иерархии, то в целом мы получаем суперэкспоненциальный спад. если они находятся в одном месте в иерархии, попробуйте выполнить алгебраическое упрощение и переписать и посмотреть, что у вас получится — вы можете получить что угодно.
- Взаимодействие между суперэкспоненциальным и экспоненциальным / субэкспоненциальным : Суперэкспоненциальный требует внимания.
- Взаимодействие между экспоненциальной и субэкспоненциальной : Мы по-прежнему получаем что-то экспоненциальное, но субэкспоненциальная часть имеет отношение к определению поведения конечной точки.
Помните, что все это функции в 
Прежде чем мы продолжим применять идеи этой иерархии функций к проблеме сходимости степенных рядов, нам нужно напомнить себе следующее: нас интересует рост или убывание коэффициентов  , степенного ряда, которые являются функциями из индексирующая переменная
, степенного ряда, которые являются функциями из индексирующая переменная 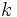 , а не
, а не 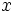 .Таким образом, везде, где мы видим
.Таким образом, везде, где мы видим 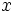 в приведенной выше иерархии, нам нужно заменить его на
в приведенной выше иерархии, нам нужно заменить его на 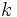 . Например,
. Например, 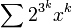 описывает двойной экспоненциальный рост коэффициентов.
описывает двойной экспоненциальный рост коэффициентов.
Определение интервала схождения
Сверхэкспоненциальный рост и спад
(Примечание: видео начинается с общего обсуждения правил, затем переходит к сверхэкспоненциальному росту и распаду)
Мы приводим ниже несколько примеров:
Субэкспоненциальный рост и распад: тест разности градусов
Здесь коэффициенты субэкспоненциально растут или убывают.Обратите внимание, что в этом случае радиус сходимости всегда равен 1. Чтобы определить интервал сходимости, нам нужно подключить конечные точки и использовать различные версии теста разности градусов. Тест на разность степеней говорит нам, что для ряда с терминами формы:
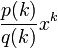
с 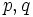 полиномами или, в более общем смысле, суммами степенных функций, мы имеем:
полиномами или, в более общем смысле, суммами степенных функций, мы имеем:
В случаях, когда тест на разность степеней не определен, нам может потребоваться использовать интегральный тест.
С помощью этих правил мы можем попробовать определить интервал сходимости в нескольких случаях:
Субэкспоненциальный рост и распад: тест на разность степеней с осторожностью, когда показатель степени кратен индексу суммирования
Мы рассмотрим несколько примеров, для которых мы можем использовать тест разницы в градусах, но должны делать это более тщательно.
Субэкспоненциальный рост и спад: примеры, в которых показатель степени является степенью индекса суммирования
(необходимо добавить больше, чтобы соответствовать примерам в видео).
Экспоненциальный рост или спад: тест на разность степеней коэффициентов
В этом случае коэффициенты растут или убывают экспоненциально. Хитрость здесь заключается в том, чтобы записать коэффициент как произведение чистой экспоненциальной функции (которая определяет радиус сходимости) и субэкспоненциальной функции (которая определяет, включены ли конечные точки, с помощью теста разности степеней, описанного выше). Обратите внимание, что вместо ![(-1,1), [-1,1), (-1,1],[-1,1]](/800/600/https/calculus.subwiki.org/w/images/math/8/9/d/89d7a4584e8454518d7789534479e8be.png) мы теперь имеем дело с интервалами, указанными с использованием радиуса сходимости.
мы теперь имеем дело с интервалами, указанными с использованием радиуса сходимости.
Теперь рассмотрим несколько случаев:
Экспоненциальный рост или спад: осторожное использование, когда показатель степени является кратным индексу суммирования
Мы рассматриваем случаи, когда появляются только некоторые степени 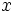 . В этих случаях мы должны быть осторожны при определении скорости экспоненциального роста, а также поведения конечной точки.
. В этих случаях мы должны быть осторожны при определении скорости экспоненциального роста, а также поведения конечной точки.
Например, для 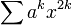 скорость экспоненциального роста коэффициентов составляет
скорость экспоненциального роста коэффициентов составляет 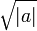 , а радиус сходимости равен
, а радиус сходимости равен 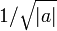 .
.
Хитрые примеры
(Дополнительные примеры будут добавлены из видео)
,Понимание интервала конвергенции
- Образование
- Математика
- Исчисление
- Понимание интервала конвергенции
Марк Зегарелли
В отличие от геометрического ряда и ряда p , степенной ряд часто сходится или расходится в зависимости от своего значения x . Это приводит к новой концепции при работе со степенными рядами: интервал сходимости.
Интервал сходимости для степенного ряда — это набор значений x , для которых этот ряд сходится.
Интервал схождения никогда не бывает пустым
Каждый степенной ряд сходится для некоторого значения x . То есть, интервал сходимости для степенного ряда никогда не бывает пустым множеством.
Хотя этот факт имеет полезные последствия, на самом деле это довольно просто. Например, взгляните на следующую серию мощности:
Когда x = 0, этот ряд оценивается как 1 + 0 + 0 + 0 +…, поэтому он, очевидно, сходится к 1.Точно так же взгляните на эту серию мощности:
На этот раз, когда x = –5, ряд сходится к 0, так же тривиально, как и в последнем примере.
Обратите внимание, что в обоих этих примерах ряд сходится тривиально при x = a для степенного ряда с центром a .
Три возможности для интервала конвергенции
Для интервала сходимости любого степенного ряда существуют три возможности:
Ряд сходится, только когда x = a .
Ряд сходится на некотором интервале (открытом или закрытом с обоих концов) с центром в и .
Ряд сходится для всех реальных значений x .
Например, предположим, что вы хотите найти интервал сходимости для:
Этот степенной ряд центрируется в 0, поэтому он сходится, когда x = 0. Используя тест отношения, вы можете узнать, сходится ли он для любых других значений x . Для начала установите следующий лимит:
Чтобы оценить этот предел, начните с отмены x n в числителе и знаменателе:
Далее раздаем, убрав скобки в числителе:
В настоящее время этот предел имеет вид
, поэтому примените правило Л’Опиталя, дифференцируя переменную n :
Из этого результата тест соотношения говорит вам, что серия:
Сходится, когда –1 < x <1
Расходится, когда x <–1 и x > 1
Может сходиться или расходиться, если x = 1 и x = –1
К счастью, легко увидеть, что происходит в этих двух оставшихся случаях.Вот как выглядит ряд, когда x = 1:
Ясно, что серии расходятся. Вот как это выглядит, когда x = –1:
Этот чередующийся ряд сильно колеблется между отрицательными и положительными значениями, поэтому он также расходится.
В качестве последнего примера предположим, что вы хотите найти интервал сходимости для следующего ряда:
Центром этого ряда является 0, поэтому он сходится, когда x = 0.Реальный вопрос заключается в том, сходится ли он для других значений x . Поскольку это чередующийся ряд, вы применяете тест отношения к его положительной версии, чтобы увидеть, можете ли вы показать, что он абсолютно сходится:
Во-первых, вы хотите немного упростить это:
Затем вы расширяете экспоненты и факториалы:
На этом этапе возможны многие отмены:
На этот раз предел находится между –1 и 1 для всех значений x . Этот результат говорит вам, что ряд сходится абсолютно для всех значений x , , поэтому чередующийся ряд также сходится для всех значений x .
Об авторе книги
Марк Зегарелли , преподаватель математики и писатель с 25-летним профессиональным опытом, любит делать техническую информацию кристально понятной и интересной для обычных читателей.Он является автором Логика для чайников и Основы математики и предварительной алгебры для чайников . ,(1 / n)] = R. Те же выводы, основанные на стоимости R.Эти тесты полезны, потому что они имеют явный способ нахождения «границы» между сходящимся / расходящимся поведением. При нахождении радиуса сходимости мы применим один из тестов и фактически ограничим его значениями <1 (заставляя его сходиться). Поскольку мы смотрим на степенной ряд, а не на обычный бесконечный ряд, предел будет равен (что-то в терминах x) <1 . Затем мы можем определить, какие значения x действительно удовлетворяют неравенству.
Степенный ряд записывается как сумма по a_n * (x-c) n . A_n — это коэффициенты, а c — «центральная точка» ряда степеней (включение x = c исключает все члены, кроме a_0). Когда вы применяете тесты отношения / корня, вы хотите расположить вещи от (что-то в терминах x) <1 до | x-c |
- Примените тест корня к абсолютному значению степенного ряда; установить предел до значений <1.
lim_ (n-> inf): | [2 ((n + 1)! / 3 (n + 1) ) * x (n + 1) ] / [2 (n! / 3 n ) x n ] | <1
- Упростите все в пределах лимита (2 с отмена; (n + 1)! / N! = N + 1; 3 n /3 (n + 1) = 1/3; x (n + 1) / х п = х)
lim_ (n-> inf): | [(n + 1) / 3] * x | <1
- Оцените предел и поместите его в форму | x-c |
| ∞ * x | <1 или | x | <1 / ∞ или | x | <0
- Следовательно, ваш радиус сходимости r = 0.
- Ваш интервал сходимости простирается от c-r
Если бы мы получили любое другое ненулевое значение для r, мы бы определили открытый интервал , где степенной ряд абсолютно сходится. Следующим шагом будет проверка двух конечных точек интервала, чтобы увидеть, действительно ли весь интервал конвергенции был открытым, закрытым или полуоткрытым. Просто вставьте каждое значение конечной точки в x в исходной формуле степенного ряда, а затем примените один из стандартных тестов сходимости к полученному бесконечному ряду.
,
 на интервале
на интервале 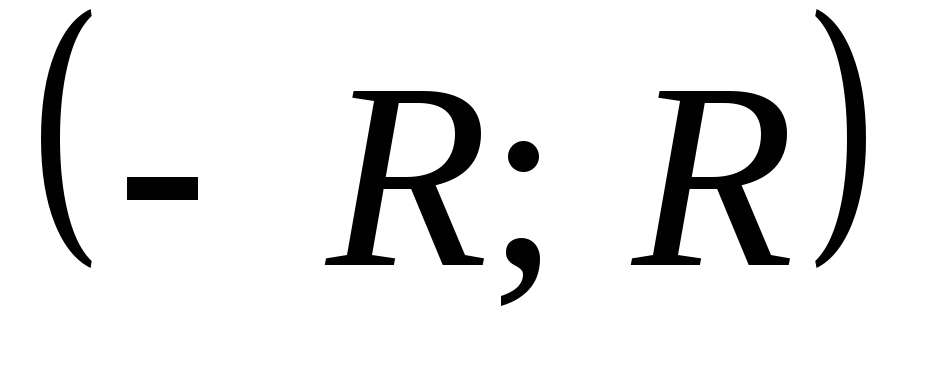 разлагается в степенной ряд, то она
дифференцируема на этом интервале и
ее производная
разлагается в степенной ряд, то она
дифференцируема на этом интервале и
ее производная 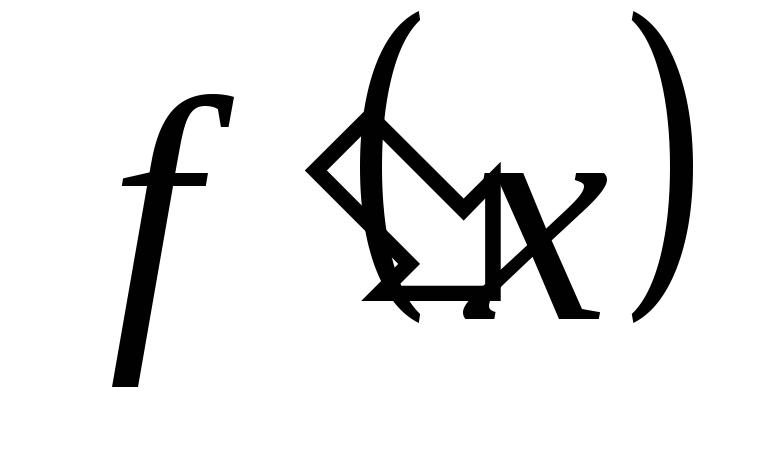 может быть найдена почленным
дифференцированием ряда, т.е.:
может быть найдена почленным
дифференцированием ряда, т.е.: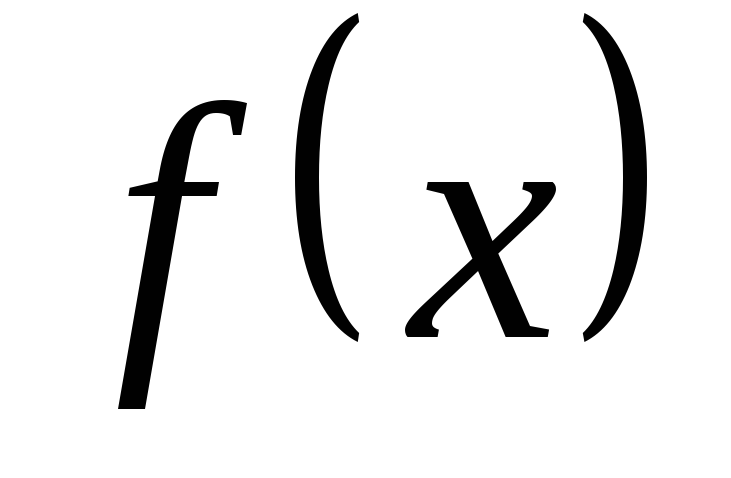 на интервале
на интервале 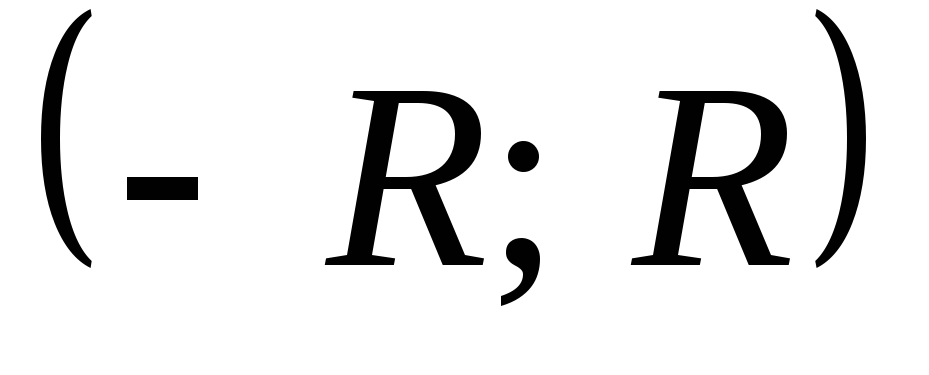 разлагается
в степенной ряд, то она
интегрируема в интервале
разлагается
в степенной ряд, то она
интегрируема в интервале 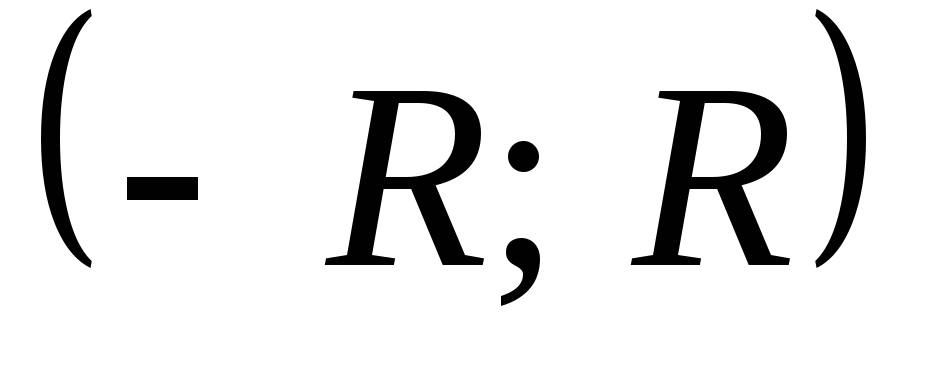 и интеграл
от нее может быть вычислен почленным
интегрированием степенного ряда,
т.е.,
если
и интеграл
от нее может быть вычислен почленным
интегрированием степенного ряда,
т.е.,
если 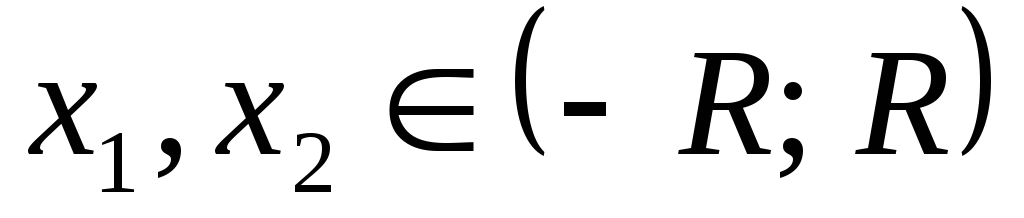 ,
то:
,
то: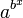 , где
, где  .
. , где
, где 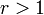 , то есть функции, экспоненциально растущие в суперлинейной степени
, то есть функции, экспоненциально растущие в суперлинейной степени  , тем быстрее будет рост.
, тем быстрее будет рост.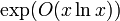 . Здесь живет факториальная функция.
. Здесь живет факториальная функция.
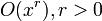 . Чем больше значение
. Чем больше значение 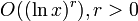 .
.