Некоторые из самых крутых чисел иррациональны
В Mathnasium of Littleton некоторые из наших любимых чисел иррациональны. Каждый год 14 марта мы отмечаем «день числа пи» пирогами и мероприятиями, связанными с этим иррациональным числом, но нам нравятся и другие иррациональные числа!
Что такое иррациональное число?
Иррациональное число — это число, которое нельзя представить как отношение двух чисел. Это число, в котором цифры справа от десятичной дроби идут бесконечно без повторяющегося шаблона. Это означает, что целые числа никогда не бывают иррациональными, потому что единственным числом после запятой будет 0. Нам нравится идея, что иррациональные числа существуют вечно. Это просто сбивает с толку.
4 Известные иррациональные числа
1) Пи описывает отношение длины окружности к ее диаметру. Для основных расчетов число Пи используется число 3,142.
2) Phi Φ (произносится как фие) описывает соотношение отрезков, разделенных определенным образом.
3) Квадратный корень из 2 — еще одно известное иррациональное число. Приблизительный квадратный корень из 2 равен 1,414. Нам нравится это число, потому что вы можете доказать, что оно иррационально.
4) Число e или число Эйлера является основанием натуральных логарифмов. Приблизительное значение e равно 2,718. Нам нравится e, потому что он используется для расчета непрерывного начисления процентов, например, для расчета возврата инвестиций.
Кто не любит зарабатывать деньги? Для тех, кто не удовлетворен просто выходом на три знака после запятой, вот ссылка на первые пять миллионов цифр. Есть ли практическое применение иррациональным числам?
Ученые, бухгалтеры и инженеры полагаются на электронную почту в большей части своей работы. Они либо оставляют число в символьной форме, либо решают, насколько точно (сколько цифр) им нужно использовать.
Неразумно, но весело
Одна только мысль о том, что иррациональные числа существуют, вызывает ряд интересных вопросов. Они предлагают любителям математики, таким как мы, увлекательные творческие упражнения, например, доказательство иррациональности числа. Они дают людям, которые сомневаются в математике, некоторые интересные вещи для размышлений.
Вот несколько вопросов об иррациональных числах, которые заинтересуют вас.
Как ранние математики обнаружили существование иррациональных чисел?
В какой момент они сдались и решили, что числа справа от десятичных знаков никогда не будут повторяться и никогда не остановятся?
Как далеко они просчитали, прежде чем принять это решение… 1000 мест….
10 000 мест?
Сколько существует иррациональных чисел? Можно подумать, что рациональных чисел больше, чем иррациональных, но верно как раз обратное. Числа бесконечны, поэтому существует бесконечное количество как рациональных, так и иррациональных чисел. Рациональные числа теоретически счетны, а иррациональные — нет, поэтому некоторые математики говорят, что иррациональных чисел больше, чем рациональных. Это означает, что некоторые наборы бесконечности больше, чем другие наборы бесконечности! Как это для умопомрачительной мысли!
Можно ли представить иррациональные числа в виде дроби? Нет! Вы не можете выразить рациональные числа в виде дроби, потому что дроби — это отношения между двумя числами. 33,3333333333 … с повторением 3-х по-прежнему является рациональным числом. Это можно записать как 100/3. Вот почему иррациональные числа обычно обозначают такими символами, как π, Φ и e. Это единственный правильный способ написать их.
С математической точки зрения иррациональные числа являются «реальными» или «мнимыми»? Они настоящие.
Существует целый другой набор чисел, известный как «воображаемый», и тем не менее они все еще существуют. Мнимые числа нельзя назвать рациональными или иррациональными. Это тема для другого дня.
Иррациональные числа и математика Литтлтона
Мы любим думать о высшей математике. Вам не обязательно быть на продвинутом курсе математики, чтобы начать думать о продвинутых математических темах. Если вы хотите, чтобы другие статьи пробудили ваше математическое творчество, ознакомьтесь с:
Математический взгляд на снежинки
6 способов для студентов, изучающих математику с ускоренным и углубленным изучением математики, снова увлечься математикой
10 забавных способов включить математику во время школьных каникул
Долгая поездка на машине
Почему Mathnasium of Littleton любит математические игры?
Я никогда не буду использовать математический анализ после окончания средней школы
Книги по математике выше 1,2,3
Математические фильмы для всей семьи
Математические навыки, которым должен научиться семилетний ребенок
Математик в центре внимания Кэтрин Г.
Джонсон
Число ноль
Великая традиция арифметики
В вашем доме есть любитель математики? Приведите их в Матназиум Литтлтона. Им будет предоставлена свобода заниматься математикой просто для удовольствия и в своем собственном темпе. Также прочитайте 5 лучших математических занятий, которые нужно пройти для успеха и карьеры в математике 21-го века
У вас дома есть ненавистник математики? Это ЧП!!! Пожалуйста, прочитайте Нормально ли ненавидеть математику? Затем пригласите их, чтобы мы могли помочь им встать на путь.
Это защищено авторским правом. Mathnasium of Littleton имеет разрешение на его использование. Другие филиалы Mathnasium должны узнать об этом по адресу http://hdwrite.com
Иррациональные числа
Иррациональное число — это число, которое нельзя записать в виде обыкновенной дроби двух целых чисел. Он является частью набора действительных чисел наряду с рациональными числами. Его также можно определить как набор действительных чисел, которые не являются рациональными числами.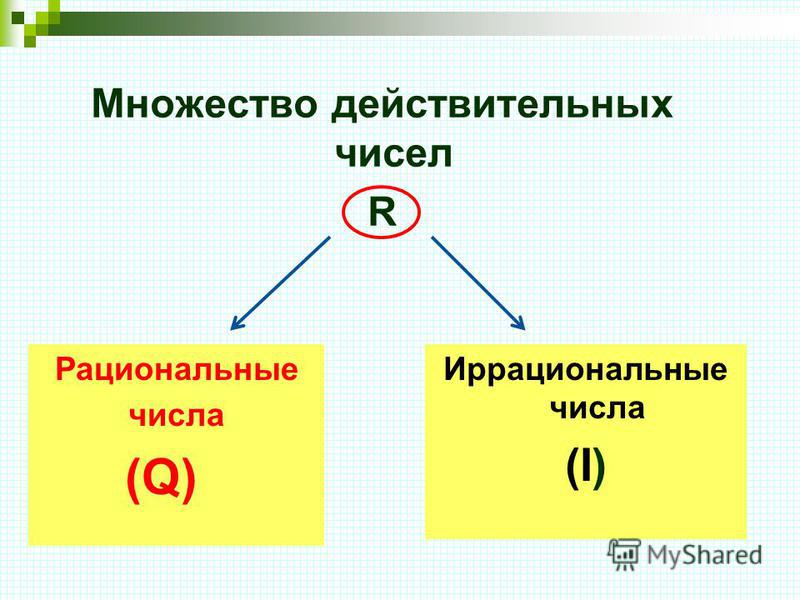
Когда иррациональное число преобразуется в десятичную форму, оно является неконечным десятичным числом, которое не повторяется. Обратите внимание, что неконечная десятичная дробь, которая повторяется, является рациональным числом, а не иррациональным числом.
Примеры
Ниже приведены некоторые из наиболее известных иррациональных чисел:
| π | = | 3.14159… |
| и | = | 2,71828… |
| = | 1.41421… |
Независимо от количества знаков после запятой, до которого мы вычисляем эти значения, после них всегда будет другая цифра, отсюда и термин неконечная десятичная дробь.
Как подмножество действительных чисел, иррациональные числа обладают теми же свойствами, что и действительные числа. Ниже приведены некоторые свойства иррациональных чисел, связанные с их рациональными аналогами.
- Сумма иррационального числа и рационального числа иррациональна.
- Произведение иррационального числа на рациональное число иррационально, если рациональное число не равно 0.
- Два иррациональных числа могут иметь или не иметь наименьшее общее кратное.
- Иррациональные числа не замыкаются при сложении, вычитании, умножении и делении. Это в отличие от рациональных чисел, которые закрыты для всех этих операций.
Что касается последнего пункта списка, свойства замыкания, это означает, что операции, затрагивающие только набор иррациональных чисел, могут привести к числам, которые являются членами различных наборов, таких как рациональные числа:
Сложение и вычитание
Сложение а вычитание иррациональных чисел может привести либо к иррациональному, либо к рациональному числу. Всякий раз, когда операции между двумя иррациональными числами могут привести к числу, которое не является иррациональным, оно не замыкается при выполнении этой операции.
Примеры
Сложение:
(рациональное)
Вычитание:
(рациональное)
Умножение и деление
Иррациональные числа также не замыкаются при умножении и делении.