Используя координатную прямую,найдите пересечение,объедин… -reshimne.ru
Новые вопросы
Ответы
Эти множества не пересекаются.
Пересечение: А /\ В = пустое множество.
Объединение: A U B = (-oo; 1] U (3; 7]
Разность множеств — это элементы одного множества, которые не входят в другое.
Если множества не пересекаются, то разность равна уменьшаемому.
A — B = A = (-oo; 1]
B — A = B = (3; 7]
Похожие вопросы
В 3кг бараницы содержится 0,5кг белков. Сколько белков содержится в 4,5кг баранины?
Заранее спасибо)…
В 4 тонн медной руды вмешается 25 кг чистой меди.Сколько меди вмешается в 6 тонн руды?…
Найдите суммудлин всех ребер прямоугольного паралелепипеда измерения которого равны 13 . 16.21…
16.21…
Найдите сумму. № 2
Помогите пожулуйста!
…
Определите величину угла:
а)градусная мера которого составляет 7/30 (это дробь)
развернутого угла.
б) 4/ 17 (это дробь) которого ровны 12 градусов…
1,7+6=7,7 и 0,5-1,7=-1,2…
Математика
Литература
Алгебра
Русский язык
Геометрия
Английский язык
Химия
Физика
Биология
Другие предметы
История
Обществознание
Окружающий мир
Українська мова
Українська література
Қазақ тiлi
Беларуская мова
Информатика
Экономика
МузыкаПраво
Французский язык
Немецкий язык
МХК
ОБЖ
Психология
Тема: «Объединение и пересечение промежутков»
Просмотр содержимого документа
План урока по математике | Тема: «Объединение и пересечение промежутков» | Объем и содержание устной и письменной работы: уметь находить промежутки пересечения и объединения | Словарная работа: числовая прямая, отрезок, интервал, луч, открытый луч, неравенство строгие и нестрогие | |||||||||||||||||||
Класс: | 6Г, | |||||||||||||||||||||
Дата: | 12. | Применяемые технологии: игровая технология | Оборудование: Доска, мел, карточки | |||||||||||||||||||
Цель урока: | -ученики с низкой мотивацией к концу урока смогут определить и записать пересечение и объединение промежутков -ученики с средней мотивацией смогут изображать промежутки пересечения и объединения на числовой прямой -ученики с высокой мотивацией смогут самостоятельно составлять неравенства с использованием приобретенных знаний -развивать навыки работы в группе | Уровень С:Аширов Э, Заболотников О, Кадырбек А, Полилов Р, Копец Н, Мерекеева Ж. Уровень В: Андакулова И, Валеева С, Марашан Д, Неутова К, Собянина Г, Суслопарова А, Трофимова Е, Шагеева Р, Омарова А,Короткова Н Уровень А:Грабовецкая М, Нурбекова М, Демченко М, Самигулина А. | ||||||||||||||||||||
Ожидаемый результат: | знать: — обозначение пересечения и объединения промежутков; уметь: — изображать пересечения и объединения промежутков; понимать: — алгоритм нахождения пересечения и объединения промежутков Умение работать в группе | |||||||||||||||||||||
Ход урока: | Цели и задачи этапа | Временные сроки | Методы и приемы | Деятельность учителя | Деятельность ученика | |||||||||||||||||
1.Организационный момент 2.Создание психологического настроя. | Цель: проверка готовности учащихся, их настрой на работу. | 1мин | Ребята, послушайте, какая тишина! Цель нашего урока это повторить и закрепить знания и умения по теме «Объединение и пересечение числовых промежутков. Девизом к сегодняшнему уроку будут слова древнегреческого математика Фалеса: — Что есть больше всего на свете? – Пространство. — Что быстрее всего? – Ум. — Что мудрее всего? – Время. — Что приятнее всего? – Достичь желаемого. Хочется, чтобы каждый из вас на сегодняшнем уроке достич желаемого результата | Приветствуют учителя, проверяют свою готовность к уроку. Класс разбит на 4 группы — экипаж. Экипажам машин предстоит совершить пробег по местности с множеством препятствий. Преодолеть эти препятствия сможет экипаж который умеет находить пересечение и объединение числовых промежутков. Жюри для оценки решений учащихся можно сформировать из учащихсякоторые не были на прошлых уроках | ||||||||||||||||||
3.Самоопределение к деятельности | Цель: проверить у учащихся умение находить пересечение и объединение промежутков | 4мин | Проверка д/з | 3. 1) (-3,4; 3] [-4; 5)=(-3,4; 3] целые числа -3,-2,-1,0,1,2,3 2) (-9;11] = целые числа -4,-3,-2,-1,0,1,2,3 3)(-∞; целые числа 0,1,2,3,4,5,6,7 4)(-6 целые числа -5,-4,-3,-2,-1,0 №966 стр 248 1) наименьшее целое число 3 2)(-∞; наименьшее число 0 3)(-∞;+∞)∩ наименьшее число -7 4)(-5,1;9,1)∩ (-∞;+∞)=(-5,1;9,1) наименьшее -5 | Открывают тетради. Докладывают о выполнении домашнего задания учащимися. В случае отсутствия домашнего задания, учащимся даётся консультация после уроков) | |||||||||||||||||
4.Актуализация знаний | Цель:повторить виды числовых промежутков и способы их записи. | 4мин | «Теоретический». | Каждой команде задаются вопросы по очереди. Отвечает по очереди каждый член команды. 1. Какой знак используют для пересечения?( )  Если стоят круглые скобки? (точки не закрашиваютя знак неравенства строгий) Если стоят круглые скобки? (точки не закрашиваютя знак неравенства строгий)4. Если стоят квадратные скобки?(точки закрашиваются и знак неравентва не строгий)? | Учащиеся устно отвечают на вопросы учителя | |||||||||||||||||
4 Самооценивание и взаимоценивание | Цель проверить качество усвоения материала. Результат: находить объединения и пересечения числовых промежутков. | 30мин | Метод: послушать- сговориться- обсудить | «Разминка». Эстафета 1 экипаж. Уровень А 1.Найдите промежутки пересечения и объединения, запишите с помощью обозначений. 2 .С помощью координатной прямой найдите пересечение и объединение промежутков: а) [-4; 8] и [0; 5]; Уровень В 3. [-3; 6] и [0; 2], запишите с помощью обозначений. Найдите наименьшее целое число, лежащее на пересечений промежутков. Уровень С 4. Используя координатную прямую, найдите объединение промежутков [-1; 8] и [3; 4] , запишите с помощью обозначений. Найдите наибольшее целое число, удовлетворяющее объединению промежутка. Запишите в виде неравенства промежуток объединения 2 экипаж. Уровень А 1.Найдите промежутки пересечения и объединения, запишите с помощью обозначений. 2.С помощью координатной прямой найдите пересечение и объединение промежутков: а) (1;7) и (4; 9) Уровень В 3. Используя координатную прямую, найдите пересечение промежутков [-3; 11] и [6; 15]; запишите с помощью обозначений. Найдите наименьшее натуральное число, лежащее на пересечений промежутков. Уровень С 4. Используя координатную прямую, найдите объединение промежутков (1;7) и (4; 9), запишите с помощью обозначений. Найдите наибольшее целое число, удовлетворяющее объединению промежутка. Запишите в виде неравенства промежуток объединения 3 экипаж. Уровень А 1.Найдите промежутки пересечения и объединения, запишите с помощью обозначений 2.Спомощью координатной прямой найдите пересечение и объединение промежутков: б) [ -5; 5] и[ -3;7] Уровень В 3. Используя координатную прямую, найдите пересечение промежутков (-3; 2) и [-5; 1]; запишите с помощью обозначений. Найдите наибольшее целое число, лежащее на пересечений промежутков. Уровень С 4. Используя координатную прямую, найдите объединение промежутков (-4;1) и [ 5; 6]запишите с помощью обозначений. 4 экипаж. Уровень А 1.Найдите промежутки пересечения и объединения, запишите с помощью обозначений 2.С помощью координатной прямой найдите пересечение и объединение промежутков: б) ) [ -5;0) и (-2;4] Уровень В 3. Используя координатную прямую, найдите пересечение промежутков [-4; 8] и [0; 5]; запишите с помощью обозначений. Найдите наибольшее целое число, лежащее на пересечений промежутков. Уровень С 4. Используя координатную прямую, найдите объединение промежутков [ -4; 3] и[ -1;7) запишите с помощью обозначений. Найдите наибольшее целое число, удовлетворяющее объединению промежутка. Запишите в виде неравенства промежуток объединения Авария. Группам дается изображение промежутков где необходимо найти ошибку. Экипаж-1 1.[-2; 3) (1; 5]= [-2; 5) 2.[-2; 3) (1; 5]= (1; 5) Экипаж-2 1.[1; 5] [3; 7]= (3; 5) 2.[1; 5] [3; 7]= [1; 7] Экипаж-3 1.[-2; 3] [1; 6]= [1; 3] 2 .[-2; 3] [1; 6]= [-2; 6] Экипаж-4 1.[-2; 1) (3; 5]= 2.[-2; 1) (3; 5]=[-2; 1) (3; 5] Привал. Самое время заняться гимнастикой, чтобы голова и тело отдохнули от работы! Гонки по пересеченной местности. Командам предлагается выполнить одинаковые задания. Каждая команда может заработать верное решение каждого задания. 1.Изобразите на координатной прямой Найдите пересечение и объединение промежутков. Запишите: а) (1;7) (4; 9)=(1;9) (1;7) (4; 9)=(4;7) [ -5; 5] [ -3;7]= | Каждая команда получает лист с заданием. Учащиеся выполняют задания по одному, передают лист следующему ученику. Участвует каждый член команды. После выполнения последнего задания лист сдаётся на проверку жюри. Каждый ученик получает карточку с заданием, и решает у доски соответствующим уровню учащегося. Его команды выполняет это задание на местах. Карточки сдаются для проверки жюри. Работа в грруппе Выполняют указанные предписания на месте. | |||||||||||||||||
8. | Закрепить полученные знания. | 3мин | Резерв При наличии времени командам предлагается разгадать по одному ребусу и творческомузаданию, в котором зашифрован математический термин. Найдите пересечение и объединение множеств А и В: а)А = {1,5,6,7,10,12,14}, В={2,3,5,8,9,11,12}. б)А = {А, Б, Г, Д, Е, Ж, К} В={Б, В, Е, К, Л, М}. в)А= {Оля, Петя, Юра, Лена, Вова}, В={Катя, Петя, Витя, Лена, Миша}. в)А= { Математика }, В={ Литература }. « Математические ребусы». | Отрабатывают действия, соответствующие мыслительным операциям анализа, синтеза, сравнения, обобщения. | ||||||||||||||||||
9.Рефлексия | Цель: оценить свою работу. | 1 мин | Для меня сегодняшний урок…» |
| Определяют степень своего продвижения к цели. Отмечают свое настроение. | |||||||||||||||||
10.Домашнее задание | Дифференцированное домашнее задание | 1 мин. | ИКТ | Задаётся дифференцированное домашнее задание: – базовый уровень:. №968 стр247 – продвинутый уровень. №969 стр247 -высокий уровень №971 стр247 | Запись в дневниках.. Выбирают для себя оптимальный уровень задания. | |||||||||||||||||
PDF РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ НЕРАВЕНСТВ Обзор устройства Система линейных неравенств Система линейных неравенств – это совокупность линейных неравенств с одинаковыми переменными. Решением является любая упорядоченная пара, удовлетворяющая каждому из неравенств. Построить график системы линейных неравенств
Пересечение (03:58) Теперь добавим в систему неравенств третью линию x < 1 и исследуем пересечение всех трех линий.
Для определения системы неравенств по графику:
Стоп! Перейдите к вопросам 1–4 по этому разделу, затем вернитесь, чтобы перейти к следующему разделу. Линейное программирование
Если есть максимальное и минимальное значение целевой функции, то оно всегда находится в одной из вершин допустимой области.
Давайте повторим, что мы уже узнали о линейном программировании. В следующих нескольких вопросах и/или утверждениях прочитайте и заполните пробелы о линейном программировании. Используйте термины из данного банка слов. Решив, какие термины подходят лучше всего, нажмите, чтобы открыть ответы. неравенства, ограничения «Нажмите здесь», чтобы проверить ответ. Точки в допустимой области являются __________ системы. набор растворов «Нажмите здесь», чтобы проверить ответ. Угловые точки сформированного многоугольника являются _________ допустимой области. вершин «Нажмите здесь», чтобы проверить ответ. Функция, которую нужно максимизировать или минимизировать, называется __________. целевая функция «Нажмите здесь», чтобы проверить ответ. Какие значимые значения всегда встречаются в вершинах допустимой области? максимальное и минимальное значения «Нажмите здесь», чтобы проверить ответ. Линейное программирование — бизнес-ограничения (04:36)
Останавливаться! Перейдите к вопросам № 5–23, чтобы завершить этот модуль. |
Системы нелинейных уравнений и неравенств: две переменные
Цели обучения
В этом разделе вы:
- Решите систему нелинейных уравнений с помощью подстановки.
- Решите систему нелинейных уравнений методом исключения.
- Нарисуйте график нелинейного неравенства.
- Нарисуйте график системы нелинейных неравенств.
Комета Галлея ((Рисунок)) совершает оборот вокруг Солнца примерно раз в 75 лет. Его путь можно рассматривать как очень вытянутый эллипс. Другие кометы следуют аналогичным путям в космосе. Эти орбитальные траектории можно изучать с помощью систем уравнений. Эти системы, однако, отличаются от тех, которые мы рассмотрели в предыдущем разделе, потому что уравнения не являются линейными.
Рис. 1. Комета Галлея (кредит: «NASA Blueshift»/Flickr)
В этом разделе мы рассмотрим пересечение параболы и прямой, окружности и прямой, окружности и эллипса. Методы решения систем нелинейных уравнений аналогичны методам решения линейных уравнений.
Методы решения систем нелинейных уравнений аналогичны методам решения линейных уравнений.
Решение системы нелинейных уравнений с помощью подстановки
Система нелинейных уравнений — это система двух или более уравнений с двумя или более переменными, содержащая хотя бы одно нелинейное уравнение. Напомним, что линейное уравнение может иметь вид [латекс]\,Ах+Ву+С=0.\,[/латекс] Любое уравнение, которое нельзя записать в таком виде в нелинейное. Метод подстановки, который мы использовали для линейных систем, — это тот же метод, который мы будем использовать для нелинейных систем. Мы решаем одно уравнение для одной переменной, а затем подставляем результат во второе уравнение для решения другой переменной и так далее. Однако есть вариации возможных результатов.
Пересечение параболы и прямой
Существует три возможных типа решений системы нелинейных уравнений, включающих параболу и прямую.
Возможные типы решений для точек пересечения параболы и прямой
(Рисунок) иллюстрирует возможные наборы решений для системы уравнений, включающей параболу и прямую.
- Нет решения. Линия никогда не пересечет параболу.
- Одно решение. Прямая касается параболы и пересекает параболу ровно в одной точке.
- Два решения. Прямая пересекает параболу внутри и пересекает параболу в двух точках.
Рис. 2.
Дана система уравнений, содержащая прямую и параболу, найти решение.
- Решите линейное уравнение для одной из переменных.
- Подставьте выражение, полученное на первом шаге, в уравнение параболы.
- Найдите оставшуюся переменную.
- Проверьте свои решения в обоих уравнениях. 9{2}-y=0\hfill \end{массив}[/latex]
Показать решение
Пересечение окружности и прямой
Как и в случае с параболой и прямой, при решении системы уравнений, представляющей окружность и прямую, возможны три исхода.
Возможные типы решений для точек пересечения окружности и прямой
(Рисунок) иллюстрирует возможные наборы решений для системы уравнений, включающей окружность и прямую.

- Нет решения. Линия не пересекает окружность.
- Одно решение. Прямая касается окружности и пересекает окружность ровно в одной точке.
- Два решения. Прямая пересекает окружность и пересекает ее в двух точках.
Рисунок 4.
Как
Дана система уравнений, содержащая прямую и окружность, найти решение.
- Решите линейное уравнение для одной из переменных.
- Подставьте выражение, полученное на первом шаге, в уравнение для окружности. 9{2}=10\hfill \\ \,\,\,x-3y=-10\hfill \end{array}[/latex]
Показать решение
Решение системы нелинейных уравнений с помощью исключения
Мы видели, что подстановка часто является предпочтительным методом, когда система уравнений включает линейное уравнение и нелинейное уравнение. Однако, когда оба уравнения в системе имеют одинаковые переменные второй степени, решить их методом исключения путем сложения часто проще, чем подстановкой.
 Как правило, исключение является гораздо более простым методом, когда система включает только два уравнения с двумя переменными (система два на два), а не система три на три, поскольку шагов меньше. В качестве примера исследуем возможные типы решений при решении системы уравнений, представляющих окружность и эллипс.
Как правило, исключение является гораздо более простым методом, когда система включает только два уравнения с двумя переменными (система два на два), а не система три на три, поскольку шагов меньше. В качестве примера исследуем возможные типы решений при решении системы уравнений, представляющих окружность и эллипс.Возможные типы решений для точек пересечения окружности и эллипса
(Рисунок) иллюстрирует возможные наборы решений для системы уравнений, включающей окружность и эллипс.
- Нет решения. Окружность и эллипс не пересекаются. Одна фигура находится внутри другой или круг и эллипс находятся на расстоянии друг от друга.
- Одно решение. Окружность и эллипс касаются друг друга и пересекаются ровно в одной точке. 9{2}=10\end{массив}[/latex]
Показать решение
График нелинейного неравенства
Все уравнения в системах, с которыми мы сталкивались до сих пор, включали равенства, но мы также можем столкнуться с системами, включающими неравенства.
 Мы уже научились отображать линейные неравенства, изображая соответствующее уравнение, а затем заштриховывая область, представленную символом неравенства. Теперь мы выполним аналогичные шаги для построения графика нелинейного неравенства, чтобы научиться решать системы нелинейных неравенств. Нелинейное неравенство — это неравенство, содержащее нелинейное выражение. График нелинейного неравенства очень похож на график линейного неравенства.
Мы уже научились отображать линейные неравенства, изображая соответствующее уравнение, а затем заштриховывая область, представленную символом неравенства. Теперь мы выполним аналогичные шаги для построения графика нелинейного неравенства, чтобы научиться решать системы нелинейных неравенств. Нелинейное неравенство — это неравенство, содержащее нелинейное выражение. График нелинейного неравенства очень похож на график линейного неравенства.Напомним, что когда неравенство больше, чем,[latex]\,y>a,[/latex]или меньше, чем,[latex]\,y
Рисунок 8. (а) пример [латекс]\,у>а;\,[/латекс] (б) пример [латекс]\,у\ге а;\,[/латекс] (c) пример [латекс]\,y
Как
Дано неравенство, ограниченное параболой, начертите график.

- Нарисуйте параболу, как если бы это было уравнение. Это граница области, которая является набором решений.
- Если граница включена в область (оператор [latex]\,\le \,[/latex]или [latex]\,\ge [/latex]), парабола изображается сплошной линией.
- Если граница не входит в область (оператор < или >), парабола изображается пунктирной линией.
- Проверьте точку в одной из областей, чтобы определить, удовлетворяет ли она условию неравенства. Если утверждение истинно, набор решений представляет собой область, включающую точку. Если утверждение неверно, набор решений представляет собой область по другую сторону линии границы.
- Закрасьте область, представляющую набор решений.
Построение неравенства для параболы 9{2}+1.[/latex]
Показать решение
Построение графика системы нелинейных неравенств
Теперь, когда мы научились строить графики нелинейных неравенств, мы можем научиться строить графики систем нелинейных неравенств.
 Система нелинейных неравенств — это система двух или более неравенств с двумя или более переменными, содержащая хотя бы одно неравенство, которое не является линейным. Построение графика системы нелинейных неравенств аналогично построению графика системы линейных неравенств. Разница в том, что наш график может привести к большему количеству заштрихованных областей, представляющих решение, чем мы находим в системе линейных неравенств. Решением нелинейной системы неравенств является область графика, в которой перекрываются заштрихованные области графика каждого неравенства или где области пересекаются, называемая допустимой областью.
Система нелинейных неравенств — это система двух или более неравенств с двумя или более переменными, содержащая хотя бы одно неравенство, которое не является линейным. Построение графика системы нелинейных неравенств аналогично построению графика системы линейных неравенств. Разница в том, что наш график может привести к большему количеству заштрихованных областей, представляющих решение, чем мы находим в системе линейных неравенств. Решением нелинейной системы неравенств является область графика, в которой перекрываются заштрихованные области графика каждого неравенства или где области пересекаются, называемая допустимой областью.Как
Дана система нелинейных неравенств, нарисуйте график.
- Найдите точки пересечения, решив соответствующую систему нелинейных уравнений.
- Нарисуйте график нелинейных уравнений.
- Найдите заштрихованные области каждого неравенства.
- Определите возможную область как пересечение заштрихованных областей каждого неравенства или набора точек, общих для каждого неравенства.

График системы неравенств 9{2}-1\hfill \\ x-y\ge -1\hfill \end{array}[/latex]
Показать решение
Доступ к этим онлайн-ресурсам для получения дополнительных инструкций и практики с нелинейными уравнениями.
- Решение системы нелинейных уравнений с помощью замены
- Решение системы нелинейных уравнений методом исключения
Ключевые понятия
- Существует три возможных типа решений системы уравнений, представляющих прямую и параболу: (1) нет решения, прямая не пересекает параболу; (2) одно решение, прямая касается параболы; 3) два решения, прямая пересекает параболу в двух точках. См. (Рисунок).
- Возможны три типа решений системы уравнений, представляющих окружность и прямую: (1) нет решения, прямая не пересекает окружность; (2) одно решение, прямая касается параболы; (3) два решения, прямая пересекает окружность в двух точках. См. (Рисунок).
- Существует пять возможных типов решений системы нелинейных уравнений, представляющих эллипс и окружность: <(1) решения нет, окружность и эллипс не пересекаются; (2) одно решение, окружность и эллипс касаются друг друга; (3) два решения, окружность и эллипс пересекаются в двух точках; (4) три решения, окружность и эллипс пересекаются в трех местах; (5) четыре решения, окружность и эллипс пересекаются в четырех точках.
 См. (Рисунок).
См. (Рисунок). - Неравенство рисуется почти так же, как уравнение, за исключением того, что > или <, мы рисуем пунктирную линию и заштриховываем область, содержащую набор решений. См. (Рисунок).
- Неравенства решаются так же, как и равенства, но решения систем неравенств должны удовлетворять обоим неравенствам. См. (Рисунок).
Упражнения по разделам
Вербальные
Объясните, может ли система двух нелинейных уравнений иметь ровно два решения. А если ровно три? Если нет, объясните почему. Если да, приведите пример такой системы в виде графика и объясните, почему ваш выбор дает два или три ответа.
Показать решение
При построении графика неравенства объясните, почему нам нужно проверить только одну точку, чтобы определить, является ли решением вся область?
Когда вы рисуете систему неравенств, всегда ли будет допустимая область? Если да, объясните почему. Если нет, приведите пример графа неравенств, не имеющего допустимой области.


 02.15г
02.15г
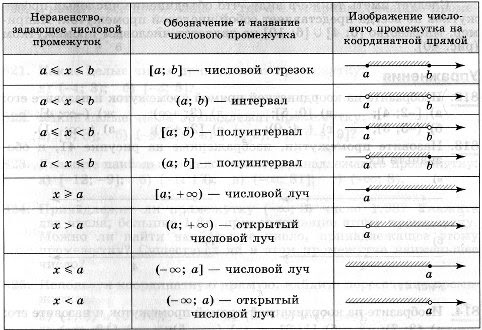
 Проверка д/з №964 стр 248
Проверка д/з №964 стр 248 Используя координатную прямую, найдите пересечение промежутков
Используя координатную прямую, найдите пересечение промежутков
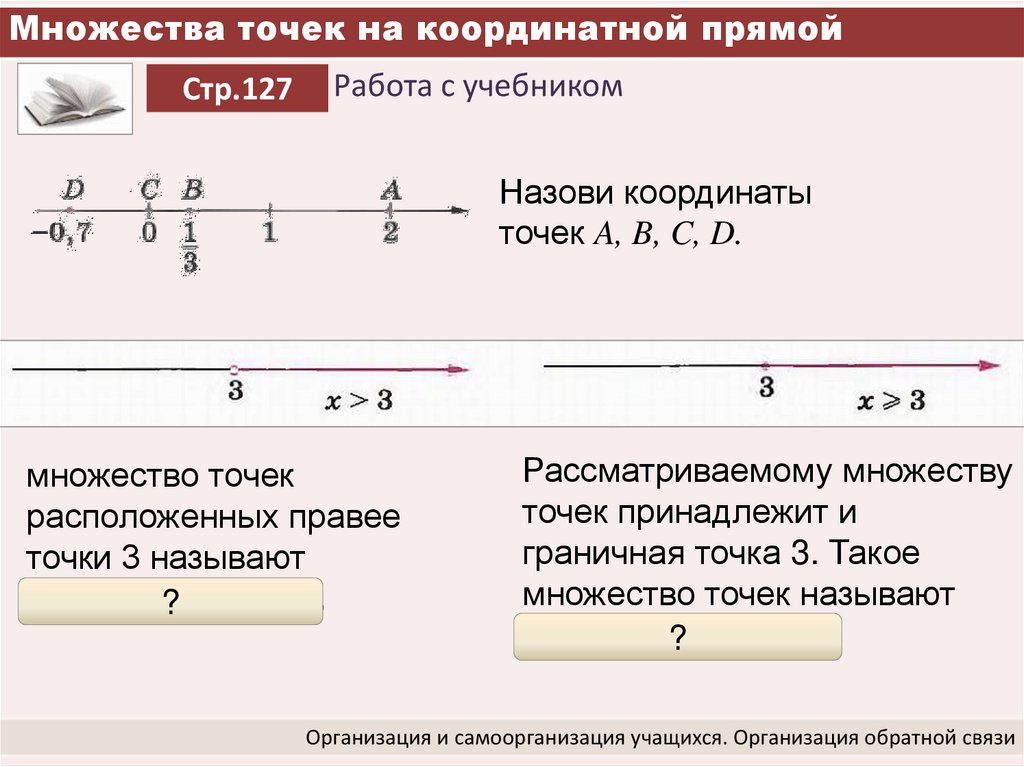 Найдите наибольшее целое число, удовлетворяющее объединению промежутка. Запишите в виде неравенства промежуток объединения
Найдите наибольшее целое число, удовлетворяющее объединению промежутка. Запишите в виде неравенства промежуток объединения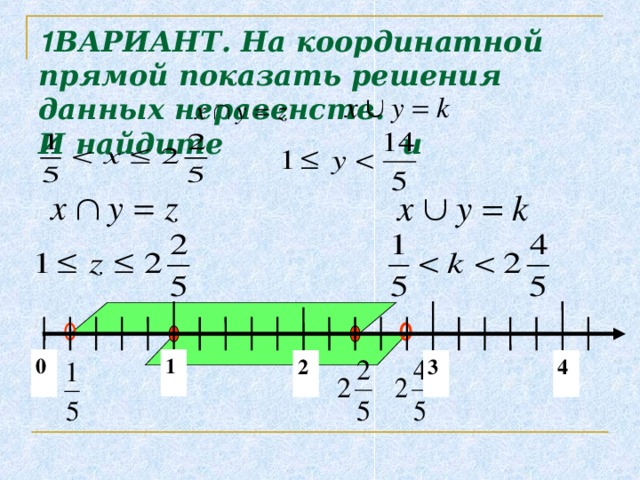

 Финишная прямая.
Финишная прямая. интересно
интересно Например, линейное неравенство можно использовать для моделирования расстояния, которое может проехать автомобиль с заданным коэффициентом экономии топлива, используя не более двадцати двух галлонов бензина. В этом модуле вы будете решать и строить графики линейных неравенств с двумя переменными, а затем писать и строить графики набора ограничений для задачи линейного программирования.
Например, линейное неравенство можно использовать для моделирования расстояния, которое может проехать автомобиль с заданным коэффициентом экономии топлива, используя не более двадцати двух галлонов бензина. В этом модуле вы будете решать и строить графики линейных неравенств с двумя переменными, а затем писать и строить графики набора ограничений для задачи линейного программирования.



 Назовите координаты вершин допустимой области. Найдите максимальное и минимальное значения целевой функции P = 3 x + y.
Назовите координаты вершин допустимой области. Найдите максимальное и минимальное значения целевой функции P = 3 x + y.  Сформированный многоугольник представляет собой треугольник с вершинами в точках (1, 4), (3, 0) и (1,0).
Сформированный многоугольник представляет собой треугольник с вершинами в точках (1, 4), (3, 0) и (1,0).

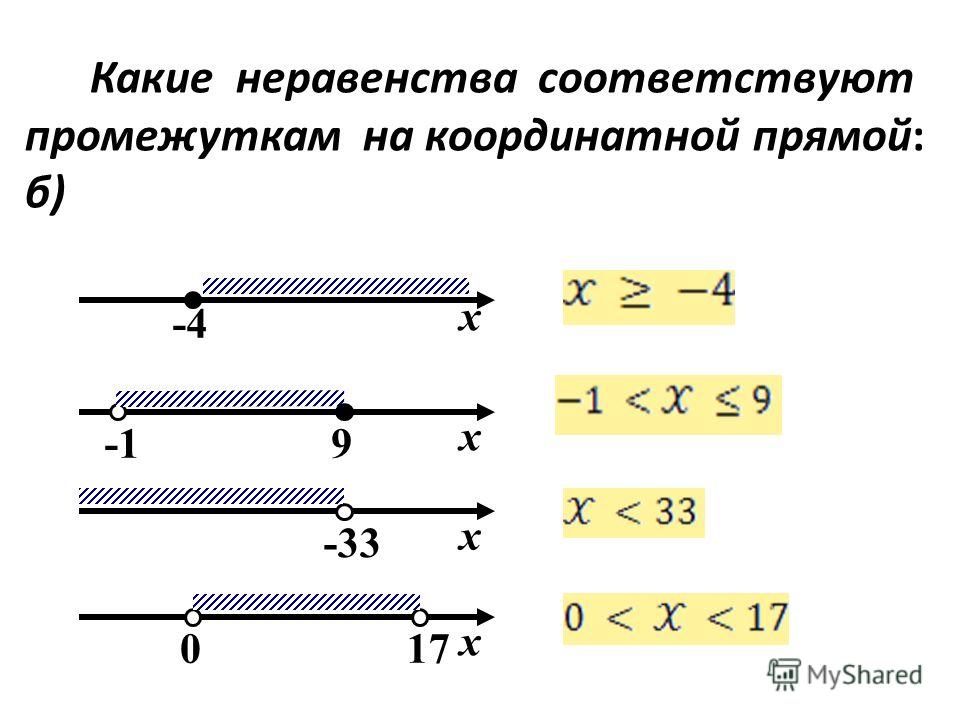


 Как правило, исключение является гораздо более простым методом, когда система включает только два уравнения с двумя переменными (система два на два), а не система три на три, поскольку шагов меньше. В качестве примера исследуем возможные типы решений при решении системы уравнений, представляющих окружность и эллипс.
Как правило, исключение является гораздо более простым методом, когда система включает только два уравнения с двумя переменными (система два на два), а не система три на три, поскольку шагов меньше. В качестве примера исследуем возможные типы решений при решении системы уравнений, представляющих окружность и эллипс.
 Система нелинейных неравенств — это система двух или более неравенств с двумя или более переменными, содержащая хотя бы одно неравенство, которое не является линейным. Построение графика системы нелинейных неравенств аналогично построению графика системы линейных неравенств. Разница в том, что наш график может привести к большему количеству заштрихованных областей, представляющих решение, чем мы находим в системе линейных неравенств. Решением нелинейной системы неравенств является область графика, в которой перекрываются заштрихованные области графика каждого неравенства или где области пересекаются, называемая допустимой областью.
Система нелинейных неравенств — это система двух или более неравенств с двумя или более переменными, содержащая хотя бы одно неравенство, которое не является линейным. Построение графика системы нелинейных неравенств аналогично построению графика системы линейных неравенств. Разница в том, что наш график может привести к большему количеству заштрихованных областей, представляющих решение, чем мы находим в системе линейных неравенств. Решением нелинейной системы неравенств является область графика, в которой перекрываются заштрихованные области графика каждого неравенства или где области пересекаются, называемая допустимой областью.
 См. (Рисунок).
См. (Рисунок).