Как найти условные экстремумы функции двух и более переменных
В задачах оптимизации возникает необходимость найти экстремумы функции двух и более переменных при условии, что существует связь между переменными этой связи, заданная уравнением . В этом случае говорят, что требуется найти условный экстремум.
Для того чтобы найти условный экстремум требуется находить частные производные и решать системы уравнений Существует алгоритм нахождения условного экстремума из трёх шагов, который сейчас и разберём на примере, и геометрический смысл условного экстремума, который должен дойти до каждого при разборе этого самого примера.
Итак, алгоритм, который разберём на примере самой распространённой задачи — нахождение условного экстремума функции двух переменных..
Шаг 1. Вводится функция Лагранжа
,
где первое слагаемое — сама исходная функция, а второе слагаемое со знаком минус —
левая часть уравнения условия связи, умноженная на (лямбда) — множитель Лагранжа.
Пример 1. Найти условные экстремумы функции двух переменных , выражающей площадь прямоугольника через его стороны x и y при условии , означающем, что существует верёвка, которой можно ограничить этот прямоугольник, и длина этой верёвки равна 100.
Шаг 1. Решение. Приведём уравнение условия связи к требуемому виду с нулём в правой части:
.
Составим функцию Лагранжа:
.
Шаг 2. Составляем систему уравнений из равенств частных производных нулю и уравения условия связи (необходимый признак существования условного экстремума):
Решения этой системы уравнений являются точками возможного условного экстремума — стационарными точками или, как ещё говорят, критическими точками.
Пример 1. Шаг 2.
Решение.
Найдём частные производные функции Лагранжа и составим из их равенств нулю и
уравнения условия связи систему уравнений:
Из первого и второго уравнений выразим соответственно x и y:
Подставим эти выражения в третье уравнение и найдём значение множителя Лагранжа:
Подставим теперь значение множителя Лагранжа в выражения для x и y и найдём значения переменных исходной функции:
Получили и . Эти значения являются также координатами стационарной точки. Таким образом, получили стационарную точку .
Шаг 3. Пусть является стационарной точкой, найденной на шаге 2. Чтобы определить, является ли условный экстремум минимумом или максимумом, нужно найти второй дифференциал функции Лагранжа
и в полученном выражении подставить вместо «лямбды» её значения (значения множителя Лагранжа), найденные
на шаге 2.
Если значение второго дифференциала функции Лагранжа меньше нуля (), то стационарная точка является точкой максимума, если больше нуля (), то стационарная точка является точкой минимума. Если значение второго дифференциала функции Лагранжа равно нулю, то требуются дополнительные исследования, но такие случаи практически не попадаются в задачах, задаваемых студентам.
Координаты стационарных точек подставляются в исходную точку и, таким образом, мы окончательно находим условные экстремумы (или минимум и максимум или что-то одно из этих экстремумом).
Пример 1. Шаг 3.
Решение. Найдём второй дифференциал функции Лагранжа:
В нашем случае, так как первое и третье составляющие равны нулю, нам не придётся подставлять в них значения множителя Лагранжа. Зато нужно найти отношения между дифференциалами dx и dy:
Так как полученные значения — противоположные по знаку, то получаем, что в любом
случае .
Теперь можем найти значение условного экстремума исходной функции, являющееся максимумом:
.
Это заданная исходной функцией максимальная площадь прямоугольника, который можно ограничить верёвкой, длина которой равна 100.
Нет времени вникать в решение? Можно заказать работу!
Пример 2. Найти условные экстремумы функции двух переменных при условии .
Решение.
Шаг 1. Составим функцию Лагранжа:
.
Шаг 2. Найдём частные производные функции Лагранжа и составим из их равенств нулю и уравнения условия связи систему уравнений:
Из первого и второго уравнений выразим соответственно x и y:
Подставим эти выражения в третье уравнение и найдём значения множителя Лагранжа:
Подставим теперь значение множителя Лагранжа в выражения для x и y и найдём значения переменных исходной функции при двух значениях множителя Лагранжа:
Эти значения икса и игрека
являются координатами двух стационарных точек.
Таким образом, получили стационарные точки
.
Шаг 3. Найдём частные производные второго порядка функции Лагранжа:
:
Найдём второй дифференциал функции Лагранжа по формуле
:
.
Установим знак второго дифференциала функции Лагранжа при значении множителя Лагранжа :
Получили значение, меньшее нуля, следовательно, точка — точка условного максимума:
.
Установим знак второго дифференциала функции Лагранжа при значении множителя Лагранжа :
Получили значение, большее нуля, следовательно, точка
— точка
.
Таким образом, условные экстремумы заданной функции найдены.
Пример 3. Найти условные экстремумы функции двух переменных
при условии .
Решение.
Шаг 1. Составим функцию Лагранжа:
.
Шаг 2. Найдём частные производные функции Лагранжа и составим из их равенств нулю и уравнения условия связи систему уравнений:
Из первого и второго уравнений выразим соответственно x и y:
Получаем, что , однако подстановка этих значений переменных в третье уравнение системы не даёт верного равенства. Поэтому считаем, что на самом деле второй сомножитель равенства равен нулю: . Отсюда получаем
Ищем координаты стационарных точек при значении множителя Лагранжа . Тогда из выражений для икса и игрека из системы уравнений следует, что . Из третьего уравнения системы получаем:
Получили две стационарные точки:
Ищем координаты стационарных точек при значении множителя Лагранжа .
Тогда из выражений для икса и игрека из системы уравнений следует, что .
На основании вычислений двух первых стационарных точек получилаем ещё две стационарные точки:
Шаг 3. Найдём частные производные второго порядка функции Лагранжа:
:
Найдём второй дифференциал функции Лагранжа по формуле
:
.
Установим знак второго дифференциала функции Лагранжа при значении множителя Лагранжа :
Получили значение, меньшее нуля, следовательно, точки — точки условного максимума:
.
Установим знак второго дифференциала функции Лагранжа при значении множителя Лагранжа :
Получили значение, большее нуля, следовательно, точки — точки условного минимума:
.
Таким образом, условные экстремумы заданной функции найдены.
Аналогичным образом можно находить условные экстремумы функций трёх и более переменных.
К началу страницы
Пройти тест по теме Функции нескольких переменных
Функции нескольких переменных
- Функция двух и более переменных. Её область определения
- Поверхности второго порядка
- Частные производные
- Касательная плоскость и нормаль к поверхности
- Производная по направлению, градиент функции
- Экстремумы функции двух переменных
- Условные экстремумы и функция Лагранжа
3.22. Условный экстремум функции нескольких переменных
3.22.1. Постановка задачи
Требуется найти экстремум функции при условии, что переменные x и y удовлетворяют уравнению .
Геометрически это
можно представить следующим образом
(рис.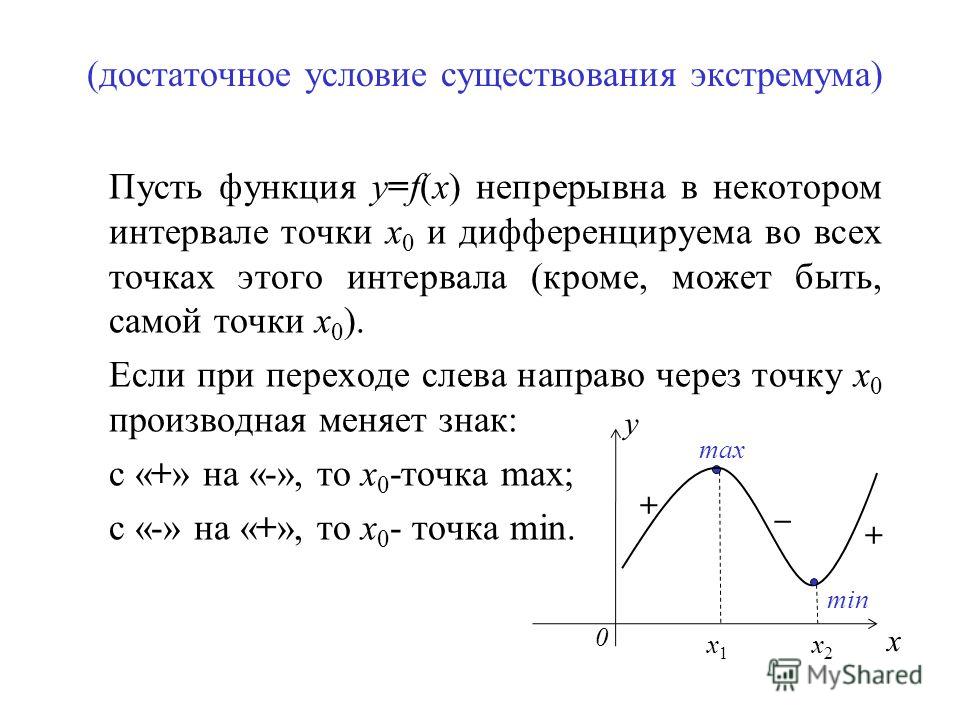
53).
Рис. 53 |
3.22.2. Нахождение критических точек
Будем считать, что уравнение задает неявно функцию . Подставим эту функцию в функцию , получим функцию одной переменной . Для нахождения экстремума этой функции используем необходимый признак. Найдем критические точки, в которых производная равна нулю
.
Также подставим в уравнение и продифференцируем по х
.
Решим систему
Второе равенство
умножим на некоторый множитель
и прибавим к первому.
Получим
Будем считать, что . Тогда множитель можно подобрать так, чтобы . В этом случае уравнение
распадется на два уравнения. Получится система
Эти два уравнения совместно с уравнением образуют систему уравнений для нахождения критических точек
Критические точки, найденные при решении этой системы, необходимо проверить на наличие в них экстремума с помощью достаточного признака.
3.22.3. Метод множителей Лагранжа
Нетрудно заметить, что левые части уравнений системы для нахождения критических точек являются частными производными функции вида
.
Составленная таким образом функция называется функцией Лагранжа, а множитель называется множителем Лагранжа.
Систему для нахождения критических точек с помощью функции Лагранжа можно записать в виде
В случае n переменных задача на условный экстремум
формулируется следующим образом.
Найти экстремум функции , если независимые переменные удовлетворяют системе ограничений
В этом случае функция Лагранжа имеет вид
.
Данную функцию исследуют на обычный безусловный экстремум.
Система для нахождения критических точек имеет вид
или в более компактной записи
В результате решения данной системы с n + m переменными могут быть найдены критические точки .
3.22.4. Достаточный признак условного экстремума функции двух переменных
Пусть решается задача на условный экстремум
Запишем функцию Лагранжа
.
Составим систему для нахождения критических точек
Пусть в результате
решения этой системы найдена критическая
точка
.
Тогда в этой точке равны нулю частные
производные
,
следовательно, и дифференциал первого порядка .
Наличие экстремума функции в точке определяется по тому, что является или нет знакоопределенной функцией приращение функции в окрестности этой точки. Ввиду того, что дифференциал первого порядка в этой точке равен нулю, в первом приближении . Если в критической точке , то и точка является точкой минимума. Если же , и точка является точкой максимума.
Дифференциал второго порядка функции трех переменных является квадратичной формой относительно .
.
В матричной записи этот дифференциал имеет вид
.
Данную квадратичную форму можно исследовать на знакоопределееность с помощью критерия Сильвестра.
Согласно данному
критерию, для того чтобы квадратичная
форма была знакоположительной в некоторой
-окрестности
точки
,
т. е.
,
должны быть положительными все три
главных минора матрицы этой формы.
, , .
В этом случае функция будет иметь минимум в точке .
Для того чтобы квадратичная форма была знакоотрицательной в некоторой -окрестности точки , т.е. , должны быть отрицательными первый и третий главные минора матрицы, а второй минор положительный.
. , .
В этом случае функция будет иметь максимум в точке .
В более удобном виде достаточный признак на условный экстремум функции двух переменных в критической точке записывают в виде одного определителя
.
Если > 0, то точка минимума, если < 0, то точка максимума.
Пример 3.27. Найти наибольший объем и длину ребер прямоугольного параллелепипеда, если его полная поверхность равна 2а.
Обозначим длины
ребер параллелепипеда через x, y, z. Тогда его объем
,
а полная поверхность равняется
.
Поделим это равенство на 2, получим
уравнение,
которое является ограничением при
нахождении максимального объема
параллелепипеда. Таким образом, задача
формулируется следующим образом.
Найти максимум функции
при условии, что ее переменные удовлетворяют уравнению
.
Запишем функцию Лагранжа
.
Составим систему уравнений для нахождения критических точек.
Умножим первое уравнение на х, второе на y, а третье на z и сложим, получим
Подставим это значение в систему уравнений и поделим первое уравнение на yz, второе на xz, а третье на xy.
.
Отсюда получаем
,
,
.
Из равенства получаем .
Так как все ребра параллелепипеда равны , то объем .
Пример 3.28. Найти условные экстремумы функции при (Рис. 54).
Рис. 54
Запишем функцию Лагранжа
.
Составим систему для нахождения критических точек
Из первого и второго уравнений найдем .
Из третьего уравнения получим .
Тогда , .
Критические точки , исследуем на экстремум по достаточному признаку.
Найдем частные производные второго порядка: , , , , , .
Вычисляем значения этих производных в критической точке и составляем определитель .
, , ,
, , .
.
Следовательно, в
точке функция имеет локальный максимум.
Вычисляем значение функции в этой точке
.
Вычисляем значения производных функции в критической точке и составляем определитель .
, , ,
, , .
.
Следовательно, в точке функция имеет локальный минимум. .
О т в е т. в точке ;
в точке .
Расчет— Условный экстремум, нужна помощь в поиске экстремумов при расчете.
спросил
Изменено 7 лет, 7 месяцев назад
Просмотрено 1к раз
$\begingroup$
Найдите условные экстремумы следующих $$u=xyz$$, если $$(1) x^2+y^2+z^2=1,x+y+z=0.
2-1) + \mu (x+y+z) $, теперь производя производные по x, y , z равно нулю, я получаю систему:
$ \phi_x’=yz+2\lambda x+ \mu $
$\phi _y’=xz+2\lambda y+ \mu $
$\phi _z’=xy+2\lambda z+ \mu$
С помощью этих систем и (1) найдено 6 точек. Я не умею считать эти баллы. Может ли кто-нибудь помочь с расчетом, я не знаю, как получить результат. $\endgroup$
$\begingroup$ 93-\frac{\xi}{2}$ имеет следующий график:
для того, чтобы $f(\xi)=u$ имела три действительных решения, $u$ должно находиться между значениями $f$ в его стационарные точки, т.е.:
$$ u\in\left[-\frac{1}{3\sqrt{6}},\frac{1}{3\sqrt{6}}\right].$$
$\endgroup$
3
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
частная производная — Определение условных экстремумов функции
спросил
Изменено 4 года, 11 месяцев назад
Просмотрено 201 раз
$\begingroup$
Пытаюсь определить условные экстремумы следующего вопроса:
- Определить точку плоскости $2x-y+2z=16$, ближайшую к началу координат.
но я не до конца понял вопрос. Если я правильно интерпретирую вопрос, то:
- Функция будет следующей: $f(x,y,z) = 2x+2y+2z=16$.
- Условие будет примерно таким: $x + y = ?$.
Но я не уверен, как именно интерпретировать условие из вопроса. Какие-либо предложения?
- частная производная
- условное ожидание
- теорема об экстремальном значении
$\endgroup$
3
$\begingroup$
Расстояние от точки $(x,y,z)$ на плоскости до начала координат $(0,0,0)$ равно 92\quad\text{при условии} \quad 2x−y+2z=16.