Как корень уравнения: Как найти корень уровнения? — ответ на Uchi.ru

Уравнения и неравенства. Нестандартные методы решения

Уравнения и неравенства. Нестандартные методы решения

С.Н. Олехник, М.К. Потапов, П.И. Пасиченко Уравнения и неравенства. Нестандартные методы решения: Справочник. Справочник посвящен задачам, которые для школьников считаются задачами повышенной трудности, требующим нестандартных методов решений. Приводятся методы решений уравнений и неравенств, основанные на геометрических соображениях, свойствах функций (монотонности, ограниченности, четности), применении производной. Книга ставит своей целью познакомить школьников с различными, основанными на материале программы общеобразовательной средней школы, методами решения, казалось бы трудных задач, проиллюстрировать широкие возможности использования хорошо усвоенных школьных знаний и привить читателю навыки употреблять нестандартные методы рассуждений при решении задач. Для школьников, абитуриентов, руководителей математических кружков, учителей и всех любителей решать задачи. Оглавление От авторов Глава I. Алгебраические уравнения и неравенства § 1.1. Разложение многочлена на множители 1.1.2. Применение формул сокращенного умножения. 1.1.3. Выделение полного квадрата. 1.1.4. Группировка. 1.1.5. Метод неопределенных коэффициентов. 1.1.6. Подбор корня многочлена по его старшему и свободному коэффициентам. 1.1.7. Метод введения параметра. 1.1.8. Метод введения новой неизвестной. 1.1.9. Комбинирование различных методов. § 1.2. Простейшие способы решения алгебраических уравнений § 1.3. Симметрические и возвратные уравнения 1.3.2. Симметрические уравнения четвертой степени. 1.3.3. Возвратные уравнения. 1.3.4. Уравнения четвертой степени с дополнительными условиями на коэффициенты. § 1.4. Некоторые искусственные способы решения алгебраических уравнений 1. 4.2. Угадывание корня уравнения. 1.4.3. Использование симметричности уравнения. 1.4.4. Использование суперпозиции функций. 1.4.5. Исследование уравнения на промежутках действительной оси. § 1.5. Решение алгебраических неравенств 1.5.2. Метод интервалов. 1.5.3. Обобщенный метод интервалов. Глава II. Уравнения и неравенства, содержащие радикалы, степени, логарифмы и модули § 2.1. Уравнения и неравенства, содержащие неизвестную под знаком корня 2.1.4. Умножение уравнения или неравенства на функцию. § 2.2. Уравнения и неравенства, содержащие неизвестную в основании логарифмов 2.2.2. Переход к основанию, содержащему неизвестную. 2.2.3. Уравнения вида … 2.2.5. Неравенства вида … § 2.3. Уравнения и неравенства, содержащие неизвестную в основании и показателе степени § 2.4. Уравнения и неравенства, содержащие неизвестную под знаком абсолютной величины 2.4.6. Использование свойств абсолютной величины. Глава III. Способ замены неизвестных при решении уравнений § 3. 1. Алгебраические уравнения § 3.2. Рациональные уравнения § 3.3. Иррациональные уравнения 3.3.3. Сведение решения иррационального уравнения к решению тригонометрического уравнения. § 3.4. Уравнения вида § 3.5. Решение некоторых уравнений сведением их к решению систем уравнений относительно новых неизвестных Глава IV. Решение уравнений и неравенств с использованием свойств входящих в них функций § 4.1. Применение основных свойств функций 4.1.2. Использование ограниченности функций. 4.1.3. Использование монотонности. 4.1.4. Использование графиков. 4.1.5. Метод интервалов для непрерывных функций. § 4.2. Решение некоторых уравнений и неравенств сведением их к решению систем уравнений или неравенств относительно той же неизвестной 4.2.3. Использование ограниченности функций. 4.2.4. Использование свойств синуса и косинуса. 4.2.5. Использование числовых неравенств. § 4.3. Применение производной 4.3.2. Использование наибольшего и наименьшего значений функции. 4.3.3. Применение теоремы Лагранжа. Дополнения

Вычисление корней уравнения

Вычисление корней уравнения Вычисление корней уравнения

Корнем уравнения f(x) = 0 является такое, возможно не единственное, значение x = x^*, при котором имеет место тождество f(x^*) = 0. Для сложных функций не существует методов точного нахождения корня, но существуют методы приближённого вычисления корня с заданной точностью. Найти корень с заданной точностью – значит найти такое приближенное значение корня

x, которое мало отличается от точного значения корня x^*, так что выполняется неравенство |x^* – x| < ε, где ε – малая положительная величина (см. рис. 1).

Рис. 1. Точное и приближённое значения корня уравнения

Метод деления отрезка пополам предполагает постепенное сужение отрезка, на котором находится корень уравнения.

Пусть задан некий отрезок [a, b], на котором находится один корень уравнения. Найдём середину отрезка и определим, в какой части отрезка – левой или правой – находится корень уравнения. Именно эта половина отрезка будет взята в качестве следующего приближения. Таким образом, будем уменьшать длину отрезка, пока она не станет меньше

ε. В качестве корня берётся середина отрезка, и, таким образом, корень уравнения находится с точностью ε / 2. Рис. 2 иллюстрирует метод деления отрезка пополам.

Рис. 2. Метод деления отрезка пополам

Для того чтобы определить в какой части отрезка находится корень уравнения, надо сравнить знаки f(a) и f(x). Если знаки не совпадают, значит на отрезке [a, x] функция пересекает ось x, и корень уравнения находится на этом отрезке. В этом случае необходимо правую границу отрезка перенести в точку x (см. рис. 2-а). Если знаки совпадают, значит на отрезке [a, x] функция не пересекает ось x, и корень уравнения находится на отрезке [x

, b]. В этом случае необходимо левую границу отрезка перенести в точку x (см. рис. 2-б).

Совпадение знаков f(a) и f(x) можно проверить, используя неравенство f(a) * f(x) < 0, – два числа с разными знаками имеют отрицательное произведение.

Формальное описание метода деления отрезка пополам
while <длина отрезка больше точности> do begin <найти середину отрезка x> if <знаки f(a) и f(x) не совпадают> then <перенести правую границу в точку x> else <перенести левую границу в точку x> end;

Приведём уравнение f(x) = 0 при помощи некоторых тождественных преобразований к виду x = φ(x).

Такое преобразование можно произвести разными способами, и при этом будут получаться разные функции φ(x) в правой части уравнения. Уравнение f(x) = 0 эквивалентно уравнению x = λ(x)∙f(x) при любой функции λ(x) ≠ 0. Таким образом, можно взять φ(x) = λ(x)∙f(x) и при этом выбрать функцию λ(x) ≠ 0 так, чтобы функция φ(x) удовлетворяла тем свойствам, которые понадобятся нам для обеспечения нахождения корня уравнения. В простейшем случае в качестве λ(x) выбирается неравная 0 постоянная. Этот вариант удобен с точки зрения задания в программе функции λ(x) и, в то же время, позволяет подобрать такое значение постоянной, которое обеспечит быстрое и точное нахождение корня уравнения.

Для нахождения корня уравнения x = φ(x) выберем какое-либо начальное приближение x₀ (расположенное, по возможности, близко к корню x^*). Далее будем вычислять последующие приближения

x₁, x₂, …, x_i, x_{i + 1}, … по формуле x_{i + 1} = φ(x_i).

Заметим следующее: тот факт, что x^* – корень уравнения x = φ(x), означает, что x^* есть абсцисса точки пересечения графика y = φ(x) с прямой y = x. Если при каком-либо x_i вычислено значение x_{i + 1} = φ(x_i) и взято в качестве нового аргумента функции, то это означает, что через точку графика (x_i, φ(x_i)) проводится горизонталь до прямой y = x, а оттуда опускается перпендикуляр на ось x. Там и будет находиться новый аргумент x_{i + 1}.

Для метода простых итераций необходимо одно начальное приближение, в качестве которого можно взять середину отрезка [a, b]. Процесс вычисления прекращается, когда разность между двумя текущими приближениями становится меньше точности, т.е. когда выполняется условие |x_{i + 1} – x_i| < ε, где ε – заданная точность вычисления.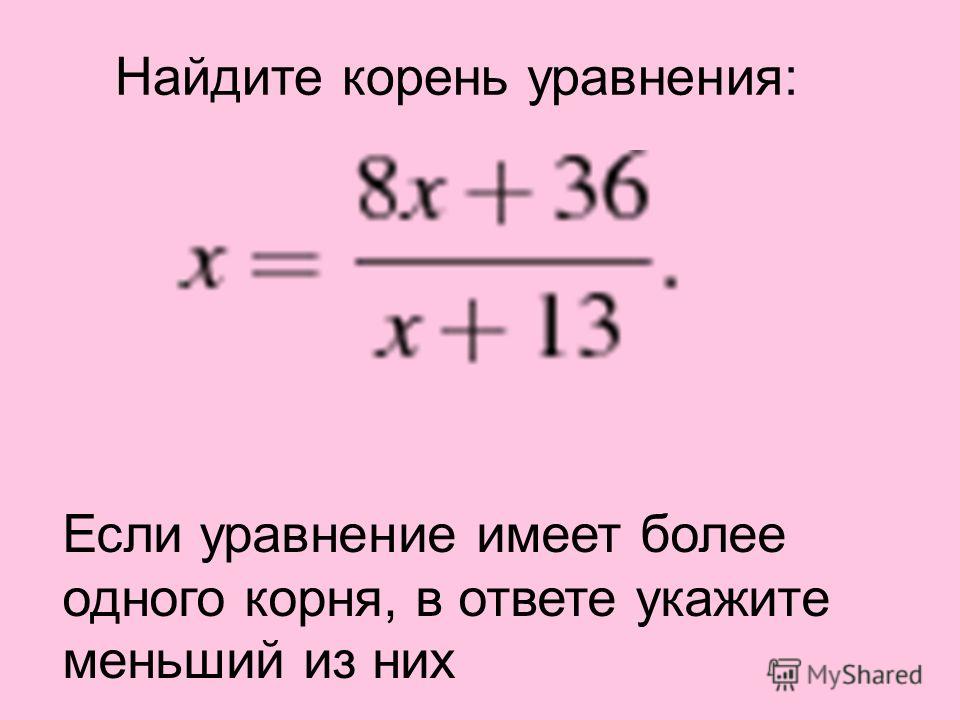 Рис. 2 иллюстрирует метод простых итераций.

Рис. 3. Метод простых итераций

Метод простых итераций сходится к корню уравнения при условии, что функция φ(x) в окрестностях корня уравнения не изменяется слишком быстро, т.е. график функции не сильно отклонён от горизонтальной прямой. Введение коэффициента λ(x) позволяет обеспечить желаемое поведение функции φ(x).

Формальное описание метода простых итераций

repeat   <сохраняем старое приближение>   <вычисляем новое приближение> until <разность между двумя текущими приближениями меньше точности>;

Мы видим, что в алгоритмах поиска корней уравнения так же, как и при нахождении суммы ряда, невозможно заранее определить, сколько итераций потребуется для нахождения корня. Это зависит от заданных начальных приближений, от точности и, конечно, от самой функции. Поэтому мы снова должны использовать циклы с неизвестным количеством повторов тела цикла. В описании метода деления отрезка пополам использовался цикл «пока», а в описании метода секущих – цикл «до». Однако это не является жёстким правилом, в любом методе можно использовать любой цикл. Главное, надо помнить, что цикл «пока» продолжается при истинности условия, а цикл «до» завершается при истинности условия. Поэтому при замене одного цикла на другой необходимо также поменять условие на противоположное.

Видео с вопросами: Нахождение корня квадратного уравнения по другому корню

Видеозапись

Учитывая, что минус 10 является уравнение два 𝑥 в квадрате плюс 13𝑥 минус 70 равно нулю, чему равно другое корень?

Нам сказали, что минус 10 — это корень нашего уравнения, что означает, что наш квадрат должен быть равен нулю, когда 𝑥 равно минус 10. По сути, это решение уравнение два 𝑥 в квадрате плюс 13𝑥 минус 70 равно нулю. Теперь, что это на самом деле означает, что 𝑥 плюс 10 должно быть умножено на два 𝑥 в квадрате плюс 13𝑥 минус 70. Два 𝑥 в квадрате плюс 13𝑥 минус 70 поэтому можно записать как 𝑥 плюс 10 раз какой-то другой бином.

Теперь давайте присвоим этому биному форма. Допустим, это в форме 𝑎𝑥 плюс 𝑏, где 𝑎 и 𝑏 — вещественные константы. Что мы собираемся сделать, это Распределите скобки в правой части этого уравнения и посмотрите, что мы получать. Начнем с умножения 𝑥 на 𝑎𝑥. Это 𝑎𝑥 в квадрате. Затем мы умножаем внешний условия. Это в 𝑥 раз 𝑏, то есть 𝑏𝑥. Далее умножаем внутренний условия. Это в 10 раз больше 𝑎𝑥, то есть 10𝑎𝑥. И, наконец, умножаем 10 на 𝑏, чтобы дать нам 10𝑏. Итак, мы находим, что это равно два 𝑥 в квадрате плюс 13𝑥 минус 70.

Теперь мы используем процесс под названием сравнение коэффициентов. Смотрим на коэффициенты нашего различные термины. Начнем со сравнения наших коэффициенты 𝑥 в квадрате. С левой стороны у нас есть два. А с правой стороны, коэффициент 𝑥 в квадрате равен 𝑎. Поэтому, когда мы сравниваем коэффициенты 𝑥 в квадрате, находим 𝑎 равно двум.

Теперь мы можем сравнить коэффициенты из 𝑥. На самом же деле мы собираемся сравнить константы. Можно сказать, что это коэффициенты 𝑥 в степени нулевых членов. В левой части наша постоянная отрицательно 70. И в правой части имеем 10𝑏. Таким образом, минус 70 равняется 10𝑏. И так делим на 10 решить для 𝑏. 𝑏 поэтому равно отрицательному Семь. Это означает, что наш квадратичный выражение можно записать как 𝑥 плюс 10 умножить на два 𝑥 минус семь. Мы заменили 𝑎 и 𝑏 на их решения.

Но мы знаем, что используем это чтобы решить уравнение два 𝑥 в квадрате плюс 13𝑥 минус 70 равно нулю. Мы уже знаем, что у нас есть один корень из минус 10. Это можно найти, установив 𝑥 плюс 10 равен нулю. Теперь мы собираемся установить два 𝑥 минус семь равны нулю и найти 𝑥. Мы добавим семь к обеим сторонам это уравнение так, что два 𝑥 равно семи. И тогда мы разделим на два. Итак, 𝑥 равно семи больше двух или 3.5. И мы могли бы проверить это решение с помощью подставив 𝑥 равно семи больше двух в наше исходное уравнение, убедившись, что он действительно равен нулю. 92+kx-6=0$ равно $3$, а $k$ является константой.

 

Количество А	$\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \;\;\;\;\;\;\;\;\;\;\;\;$	Количество В
	$\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \;\;\;\;\;\;\;\;\;\;\;\;$
Стоимость $k$	$\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \;\;\;\;\;\;\;\;\;\;\;\;$	$-1$

1. Количество A больше.
2. Количество B больше.
3. Обе величины равны.
4. Отношения не могут быть определены из предоставленной информации

Итак, вы пытались быть хорошим сдающим экзамен и практиковаться для GRE с помощью PowerPrep онлайн. Нуууу, тогда у вас есть вопросы по разделу количественных показателей, в частности, по вопросу 8 раздела 4 практического теста 1. Эти вопросы проверяют наши Решение квадратных уравнений знания могут быть довольно сложными, но не бойтесь, PrepScholar прикроет вашу спину!

Изучите вопрос

Давайте поищем в задаче подсказки относительно того, что она будет тестировать, так как это поможет переключить наши мысли на мысли о том, какой тип математических знаний мы будем использовать для решения этого вопроса. Обратите внимание на любые слова, которые относятся к математике, и на что-нибудь особенное в отношении того, как выглядят числа, и отметьте их на бумаге.

Для вопросов, ищущих 92)$, мы должны ожидать, что проблема потребует нашего умения Решение квадратных уравнений .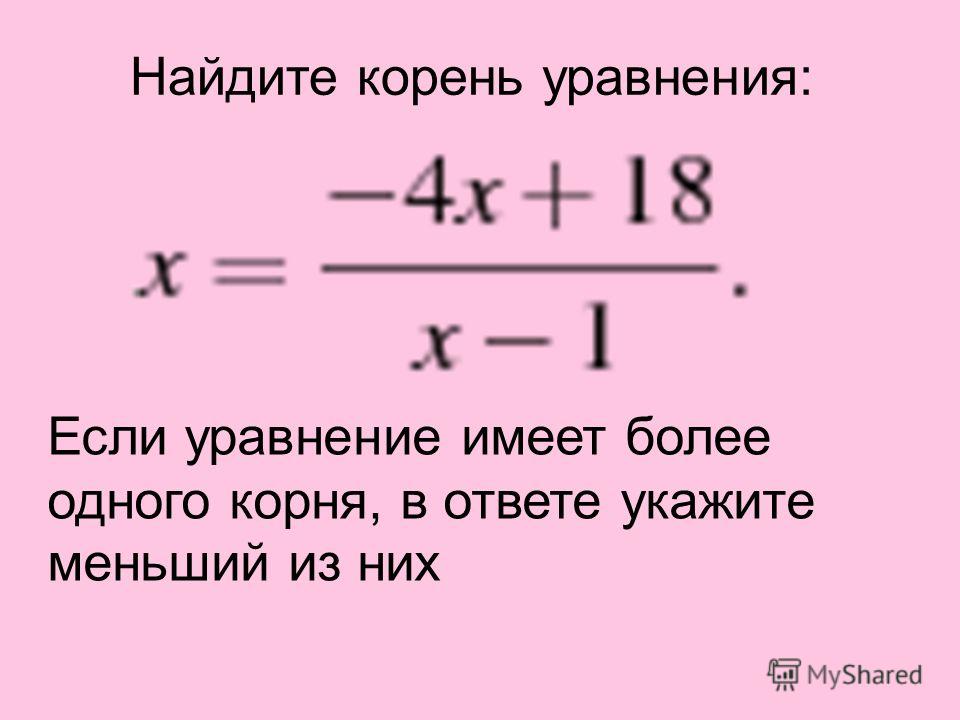 Давайте держать в уме то, что мы узнали об этом навыке, когда мы подходим к этому вопросу.

Что мы знаем?

Давайте внимательно прочитаем вопрос и составим список вещей, которые мы знаем.

 

1. У нас есть квадратное уравнение с $x$ и $k$
2. Один корень уравнения равен $3$
3. Мы хотим сравнить $k$ с определенным значением 92+кх-6=0$. Мы знаем, что если бы у нас было значение $x$ для подстановки в это уравнение, то мы могли бы просто решить его для $k$. Итак, , давайте посмотрим, сможем ли мы найти значение $x$, удовлетворяющее квадратному уравнению .

   Мы знаем, что корень квадратного уравнения говорит нам, что если мы подставим значение корня для $x$, то уравнение будет равно $0$ . Итак, давайте решим этот вопрос, подставив $x=-1$, а затем упростим уравнение, пока мы не сможем найти $k$, а затем сравним $k$ с $-1$. 92+к·3-6$ $=$ $0$ $9+3k-6$ $=$ $0$ $3+3k$ $=$ $0$ 3 тысячи долларов $=$ $-3$ $k$ $=$ $-1$

   Поскольку количество A ($k$) равно $-1$, мы видим, что обе величины равны.

   No related posts.