Как на калькуляторе посчитать логарифм: Как вычислить на калькуляторе логарифм 🚩 калькулятор с логарифмами 🚩 Математика

Содержание

Как использовать калькулятор Windows 10

Встроенный калькулятор Windows прошел долгий путь с момента его появления в Windows 1.0 в 1985 году. Он включает в себя различные режимы, вычисление даты и некоторые удобные функции ежедневных преобразований.

Переключение между режимами калькулятора

Как вы увидите ниже, калькулятор делает намного больше, чем простое сложение, вычитание, умножение и деление. Вы можете выбрать один из четырех режимов, в зависимости от ваших потребностей.

Чтобы переключиться между режимами, нажмите кнопку меню в верхнем левом углу, а затем выберите режим из следующих параметров.

Вот на что способны эти режимы.

Стандартный режим

Стандартный режим полезен для основных математических операций, таких как сложение, вычитание, умножение и деление, а также поиска квадратных корней, вычисления процентов и работы с простыми функциями. Вероятно, это режим, в котором большинство людей будет чувствовать себя комфортно.

Инженерный режим

Инженерный режим калькулятора представляет собой расширенный в стандартный режим, предоставляя вам дополнительные функции, которые вы найдёте в типичном научном калькуляторе. В дополнение к операторам стандартного режима он содержит функции типа log, mod, exp, тригонометрические градусы и SIN, COS и TAN.

Режим программиста

Этот режим предназначен для программистов. Он добавляет возможность переключения между различными системами счисления – двоичная, десятичная, шестнадцатеричная и восьмеричная. Он также добавляет новые операции для работы с логическими затворами: Or, And, Xor, Not и битами – Lsh, Rsh, RoR и RoL.

Кроме того, режим Программист позволяет переключаться между байтами (8 бит), Word (16 бит), DWord (32 бита) и QWord (64 бита) и имеет возможность переключения на бинарный бит.

Режим расчета даты

Режим расчета даты – удобный инструмент, который позволяет рассчитать разницу между двумя конкретными датами. Это идеально подходит для выяснения таких вещей, сколько дней осталось до следующего отпуска.

Все, что вам нужно сделать, это выбрать дату начала и окончания, а калькулятор будет определять месяцы, недели и дни между ними.

Преобразование измерений в калькуляторе

Вы нашли рецепт, но он требует использования жидких унций, или совершаете покупки в интернете, а все цены в евро?

Нажмите кнопку меню калькулятора и выберите тип преобразования из списка в разделе «Преобразователь».

Нажмите первое измерение – это будет вход – и выберите единицу измерения из предоставленного списка.

Нажмите второе измерение – это будет выход – и выберите там единицу измерения.

Теперь введите своё значение, и калькулятор преобразует его для вас. Он также показывает несколько других связанных преобразований внизу.

Сохранение значений в памяти

Если вы часто используете определенные числа и не хотите вводить их в свой калькулятор каждый раз, хранить их в памяти калькулятора. Это супер полезная функция, доступная в режимах стандарт, инженерный и программист. Вы будете управлять функциями памяти с помощью кнопок MS, MR, M+, M- и MC.

Вот как они работают:

MS: сохранить новое значение в памяти.
MR: вставить значение из памяти.
M+: добавляет значение из поля ввода к самому последнему сохраненному значению.
M-: вычитает значение на входе из последнего сохраненного значения.
MC: очищает все значения из памяти.
M: отображает все значения, сохраненные в памяти.

Использование кнопок MR, M+ и M- работает также, как и на физическом калькуляторе. Однако, в калькуляторе Windows у вас также есть доступ к любым другим значениям, которые вы сохранили в памяти во время текущего сеанса. Чтобы увидеть их, нажмите кнопку M со стрелкой вниз справа. Затем вы можете щелкнуть любое значение, чтобы вставить его.

Если вы предпочитаете, чтобы ваша очередь памяти всегда открывалась, измените размер калькулятора по горизонтали, и тогда она должна открыться.

История вычислений калькулятора

Если вам нужно взглянуть на все вычисления, выполненные в текущем сеансе, они хранятся в удобной истории калькулятора.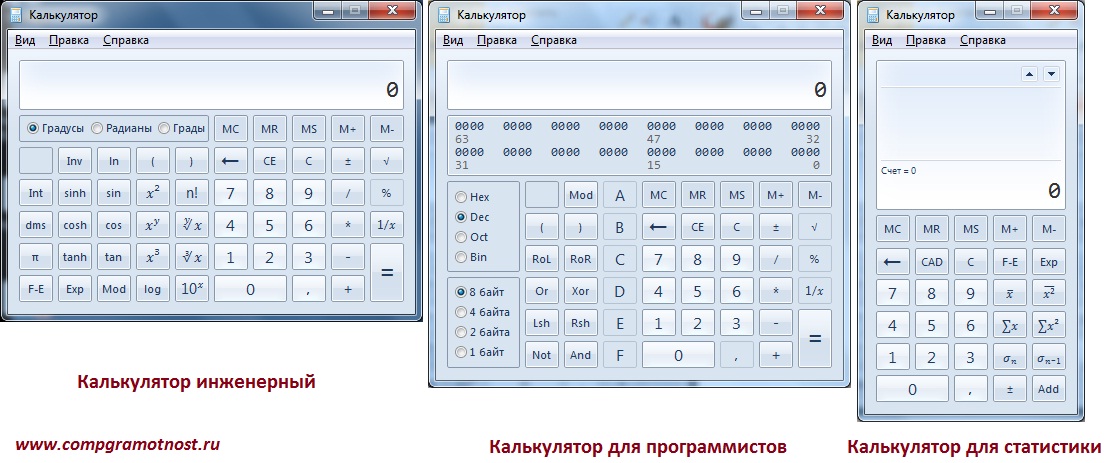 Калькулятор сохраняет историю даже при переключении режимов, но она удаляется, когда вы закрываете приложение.

Доступ к истории калькулятора

Существует два способа доступа к истории внутри приложения. Первый – щелкнуть кнопку истории, расположенную в верхнем правом углу. Это показывает список последних вычислений. Щелчок по чему-либо в истории загрузит его обратно в поле ввода калькулятора.

Если вы хотите сохранить историю открытой, измените размер окна калькулятора по горизонтали, и оно должно появиться, когда окно достаточно велико.

Удаление истории калькулятора

Вы можете удалить отдельные записи из своей истории или удалить всю историю сразу.

Чтобы удалить отдельную запись, щелкните её правой кнопкой мыши и выберите команду «Удалить». Чтобы удалить всю историю, щелкните значок маленькой корзины в правом нижнем углу панели.

Горячие клавиши Калькулятора

В приложении Calculator доступны сочетания клавиш, позволяющие выполнять некоторые вычисления намного легче и быстрее. Полный список этих сочетаний можно найти на странице «Горячие клавиши Microsoft Windows», но вот несколько наиболее полезных:

Alt + (1-4): Удерживайте нажатой клавишу Alt и нажмите любое число от одного до четырех, чтобы переключиться в разные режимы калькулятора.
Del: очистить текущий вход (это работает как ключ CE на калькуляторе)

Esc: очистить все входные данные (это работает как клавиша C на калькуляторе)
Ctrl + H: включение и отключение истории.

Наверное, это больше, чем вы когда-либо хотели знать о калькуляторе Windows. Тем не менее, это недооцененный инструмент, который содержит множество полезных функций.

Расчет с громкоговорителями — TOA Electronics

Значение и расчеты децибел

Децибел (русское обозначение: дБ; международное: dB) выражает отношение двух значений энергетической величины десятичным логарифмом этого отношения. Децибел – не физическая величина (как, напр., метр). Использование логарифмического отношения определяет восприятие человеческим ухом гораздо лучше, чем линейные величины. К тому же оно позволяет выразить соотношение воспринимаемого звукового давления (слухового порога) к предельно переносимому звуковому давлению (болевому порогу) не как 1 : 3 000 000, а гораздо более наглядно – от 0 до 130 дБ. Общий расчет выглядит следующим образом: log (значение/заданное значение). При этом используется десятичный логарифм, обозначенный на калькуляторе символом «log». Сама единица называется «бел», десятая часть обозначается приставкой «деци-», в результате получается децибел. Он выражает соотношение мощностей. Для звукового давления, напряжения, тока используется коэффициент 20.

Соотношение мощностей в дБ:
10 x log₁₀ (мощность/заданная мощность) или 10 x log₁₀ (P/P₀)

Соотношение звукового давления, напряжения или тока в дБ:
20 x log₁₀ (значение/заданное значение)

Для определения соотношения звукового давления используется значение слухового порога, равное 20 мкПа (микропаскалям). В этом случае заданное значение является постоянным, поэтому к «дБ» добавляется «SPL». В настоящее время появилась тенденция говорить об уровнях звукового давления, не используя «SPL». Другие ссылки:

Заданное значение	1 мкВ	1 мВ	0,775 В	1 В	20 мкПа
Dezibel	дБ мкВ	дБ мВ	дБн	дБВ	дБ SPL

Следующая таблица представляет некоторую соотнесенность для расчетов физических величин и отношений между ними, а также их отношение в децибелах.

Физич	Умножение	Деление	< 1	1	> 1	Отрицат
	⇩	⇩	⇩	⇩	⇩	⇩
Децибел	Сложение	Вычитание	Отрицат	0	Положит	невозможно

Пример 1: Входной сигнал 1 мВ (милливольт) в усилителе повышается до выходного сигнала 1 000 мВ.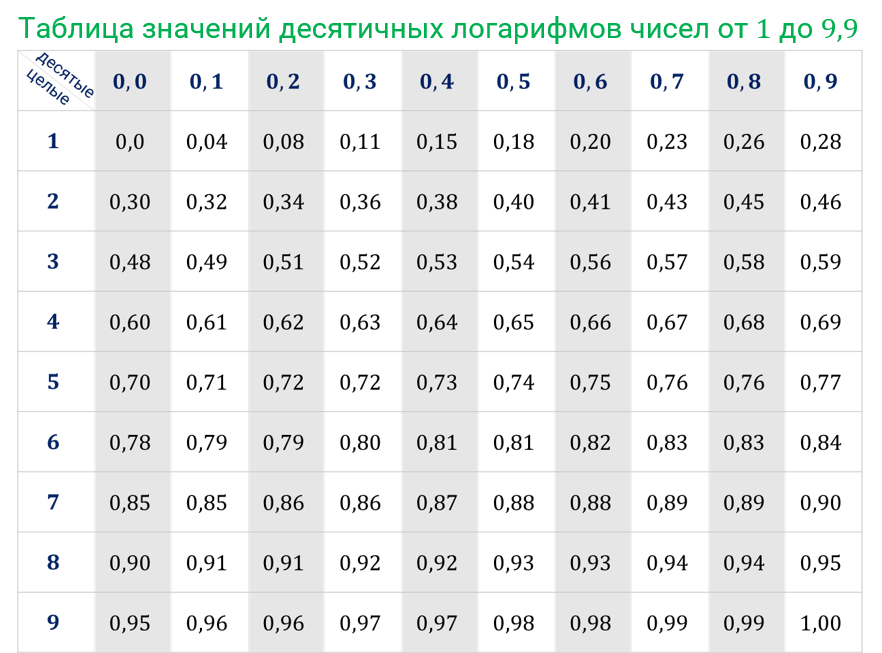 Следовательно, имеет место тысячекратное усиление (1 000 : 1), или 20 x log (1 000 / 1) = +60 дБ.

Пример 2: Аттенюатор ослабляет напряжение в десять раз. Соотношение между значением на входе и выходе 0,1 / 1 = 0,1. В децибелах: 20 x log (0,1 / 1) = -20 дБ.

Пример 3: Аттенюатор (пример 2) подключен после усилителя (пример 1). Тогда общее усиление выглядит так: 1 000 x 0,1 = 100. В децибелах: 60 дБ + (-20 дБ) = 60 дБ – 20 дБ = 40 дБ.

Уровень звукового давления при определенной мощности

Если уровень звукового давления указан в дБ, его можно использовать для расчетов. Технический паспорт громкоговорителя указывает, например, для номинального уровня звукового давления (1 Вт / 1 м): 95 дБ. Это значит, что уровень звукового давления громкоговорителя при мощности 1 ватт на расстоянии 1 метр равен 95 дБ. Из приведенной таблицы можно узнать, на сколько децибел повысится уровень звукового давления громкоговорителя при указанной мощности.

Мощность (Вт)	1	2	5	6	10	15	20	30	50	100
Повышение уровня звукового давления (дБ)	0	3	7	8	10	12	13	15	17	20

В таблице указано, что при мощности 6 ватт к 95 дБ нужно добавить 8 дБ. В итоге при мощности 6 ватт на расстоянии 1 метр получим 103 дБ SPL. Для расчета также можно использовать математическую формулу, дающую тот же результат: p₁ = p_n + 10 x log(P)

p₁: Уровень звукового давления (дБ) p_n: Номинальный уровень звукового давления (дБ) P: входная мощность (Вт)

При каждом повышении мощности в два раза уровень звукового давления повышается на 3 дБ.

Log Calculator — Z SCORE TABLE

Log Calculator

Log калькулятор — это мощный онлайн-инструмент, с помощью которого можно быстро и легко вычислить логарифмические значения. Благодаря удобному интерфейсу этот калькулятор является отличным ресурсом для всех, кому необходимо работать с логарифмами, включая студентов, исследователей и специалистов в различных областях. Калькулятор может решать как обычные, так и натуральные логарифмические функции, что делает его универсальным инструментом для широкого круга приложений. Просто введите основание и аргумент, и калькулятор выдаст вам логарифмическое значение. Он также может предоставить объяснения логарифмических вычислений, что делает его отличным ресурсом для образовательных целей. Изучаете ли вы математику, инженерное дело или любую другую область, требующую логарифмических вычислений, калькулятор логарифмов — это полезный и надежный способ получить нужные вам ответы. Это быстро, просто и бесплатно, так что попробуйте прямо сейчас и упростите свои логарифмические вычисления.

Log Calculator

Provide any two values to calculate log

_b x = y

Value (x):
Base (b):
Value (y):

91 Советы по расчету с помощью Micros…

Пожалуйста, включите JavaScript0007

Инструкции по использованию калькулятора логарифмов

Это простой калькулятор для расчета логарифмов. Чтобы использовать калькулятор, выполните следующие действия:

Введите значение x в поле ввода «Значение (x)». Это значение, для которого вы хотите вычислить логарифм.
Введите основание логарифма в поле ввода «Основание (b)». По умолчанию в качестве базы установлено значение «е», что представляет собой натуральный логарифм. Вы можете изменить базу на любое другое значение, введя его в поле ввода.
Введите значение y в поле ввода «Значение (y)». Это результат логарифмирования.
Нажмите на кнопку «Рассчитать», чтобы получить ответ. Результат отобразится в поле «Результат» внизу.

Обратите внимание, что калькулятор может вычислить любые два из трех значений (x, b и y) и вычислит третье значение. Итак, если вы введете значение x и y, калькулятор рассчитает базу. Точно так же, если вы введете основание и значение y, калькулятор рассчитает значение x.

Логарифмы: важная математическая функция

Логарифмы — это математическая концепция, которая играет жизненно важную роль в различных областях науки, включая науку, инженерию, финансы и другие. Они являются важным инструментом, который помогает нам решать сложные уравнения и упрощать математические задачи. В этой статье мы обсудим, что такое логарифмы, их свойства и значение в различных областях.

Что такое логарифмы? 93 равно 1000.

Свойства логарифмов

Логарифмы обладают несколькими свойствами, которые необходимы при решении математических уравнений. Вот некоторые из этих свойств:

Свойство продукта: logb (xy) = logb (x) + logb (y)
Это свойство указывает, что логарифм произведения двух чисел равен сумме логарифмов каждого числа.

Свойство частного логарифмов гласит, что логарифм частного двух чисел по общему основанию «b» равен разности между логарифмами отдельных чисел с одинаковым основанием «b». Математически это можно выразить как logb(x/y) = logb(x) — logb(y). 9у) = у logb(x).

Применение логарифмов

Логарифмы имеют множество применений в реальных сценариях и широко используются в различных областях исследований. Некоторые из областей, где используются логарифмы, включают:

В финансы логарифмы используются для расчета сложных процентных ставок. Например, если вы вкладываете 1000 долларов на сберегательный счет с годовой процентной ставкой 5%, начисляемой ежемесячно, сумму денег, которую вы будете иметь через 10 лет, можно рассчитать по формуле: 9-5)
pH = 5

В физике логарифмы используются для измерения интенсивности землетрясений по шкале Рихтера. Магнитуда землетрясения измеряется по шкале Рихтера, которая представляет собой логарифмическую шкалу, которая оценивает амплитуду сейсмических волн, вызванных землетрясением. Например, землетрясение магнитудой 7 баллов по шкале Рихтера в 10 раз мощнее землетрясения магнитудой 6 баллов.0004, логарифмы используются для измерения уровня сигнала электрических цепей и интенсивности звука. Например, шкала в децибелах (дБ), используемая для измерения интенсивности звука, представляет собой логарифмическую шкалу, которая связывает интенсивность звука с эталонной интенсивностью. Формула для уровня децибел:

дБ = 10 log(I/I0)

В этом контексте «I» представляет интенсивность звука, а «I0» — эталонную интенсивность. Звук, который в 10 раз интенсивнее эталонного звука, имеет уровень децибел 10 дБ.

В информатика логарифмы используются в таких алгоритмах, как алгоритмы двоичного поиска и сортировки. Например, при бинарном поиске алгоритм многократно делит отсортированный массив на две половины, пока не найдет нужный элемент. Количество раз деления массива пропорционально логарифму размера массива. Это делает бинарный поиск очень эффективным алгоритмом для поиска в больших массивах.

В статистика , логарифмы используются для преобразования данных, которые искажены или имеют широкий диапазон значений. Например, если данные подчиняются степенному закону распределения, логарифмирование данных может преобразовать их в нормальное распределение. Это упрощает анализ и сравнение данных с использованием статистических методов.

В биология логарифмы используются для измерения интенсивности света с использованием шкалы поглощения. Поглощение раствора определяется как отрицательный логарифм пропускания света через раствор. Это позволяет ученым измерять концентрацию вещества в растворе, сравнивая его абсорбцию со стандартной кривой.

Это всего лишь несколько примеров использования логарифмов в различных областях. Логарифмы — это мощный математический инструмент, который позволяет нам преобразовывать мультипликативные отношения в аддитивные и сжимать большие диапазоны значений в меньшие. Они необходимы во многих областях науки, техники и математики и используются в повседневной жизни, даже если мы этого не осознаем.

Решение уравнений с помощью логарифмов

Логарифмы можно использовать для упрощения сложных уравнений путем преобразования задач на умножение и деление в более простые задачи на сложение и вычитание.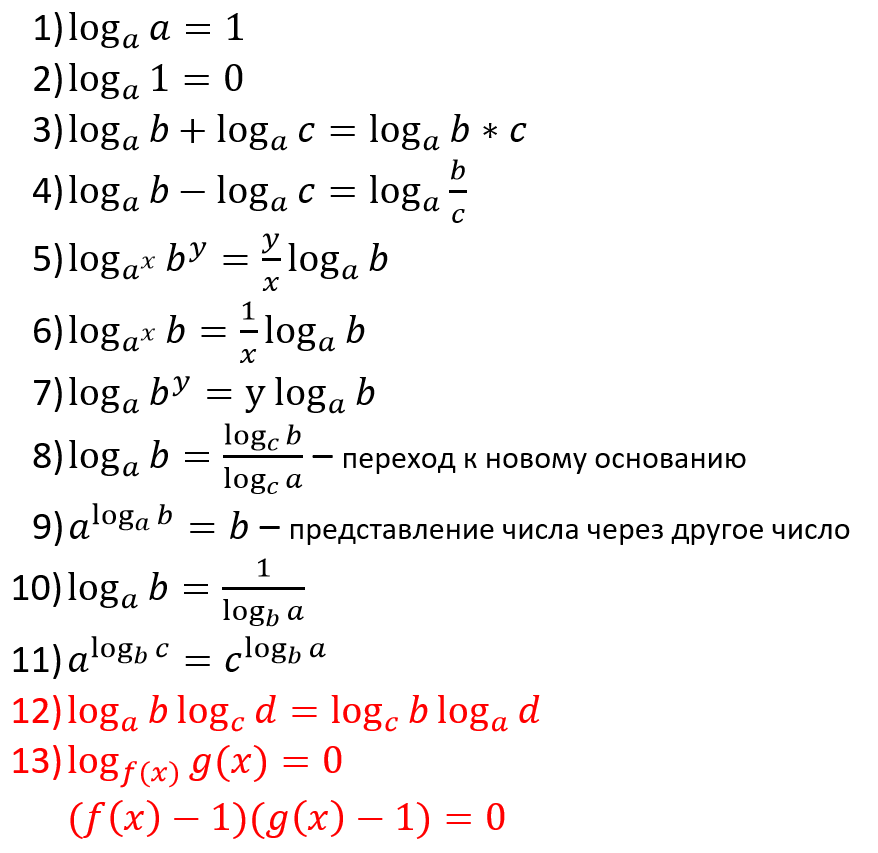 x = 8. Логарифмируя обе части уравнения по основанию 2, мы получаем: 9x = 8 равно x = 3.

Подводя итог, можно сказать, что логарифмы — это важная математическая функция, имеющая многочисленные применения в различных областях науки. Они помогают нам решать сложные уравнения и упрощать математические задачи, делая изучение математики более эффективным и результативным. Понимая свойства логарифмов, мы можем использовать их для решения сложных уравнений и получения информации о различных сценариях реального мира. Применения логарифмов огромны, и они являются важным инструментом, который помогает нам понимать и анализировать мир вокруг нас.

Посетите нас на z-table.com, чтобы получить больше математических и статистических калькуляторов.

Каково значение E в журнале? Как рассчитать значение Log E в калькуляторе?

Каково значение E In Log — часто задаваемый вопрос в математике. Значение e в натуральном логарифме (log) представляет собой математическую константу, приблизительно равную 2,71828. Это значение имеет решающее значение во многих математических формулах и имеет важные приложения в различных областях науки и техники. Каково значение E In Log, можно определить с помощью различных методов, включая исчисление и численные приближения. Знание значения e в log важно для понимания поведения экспоненциальных и логарифмических функций. Независимо от того, работаете ли вы с финансовыми данными, моделируете темпы роста или изучаете поведение сложных систем, важно понимать, в чем ценность E In Log.

Источник изображения: Fresherslive

Каково значение E в логарифме

Значение e в логарифме — это математическая константа, которая широко используется в различных областях науки, техники и математики. Эта константа, обозначаемая символом «е», является фундаментальной константой в исчислении и играет важную роль во многих математических формулах. Значение e в log приблизительно равно 2,71828 и является иррациональным числом, что означает, что его нельзя выразить в виде конечного десятичного числа или дроби.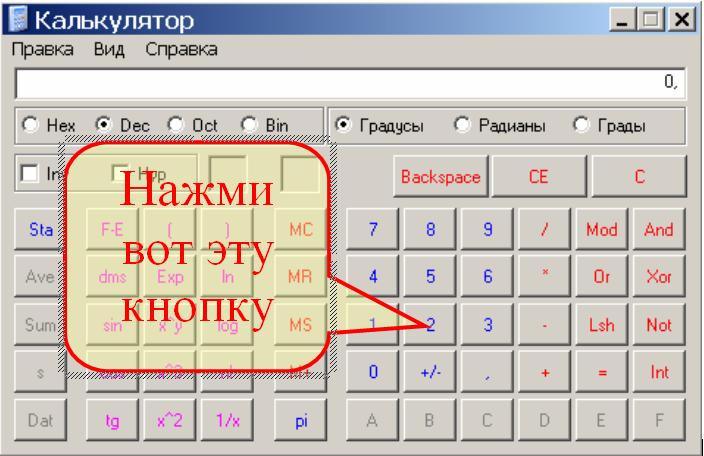

Константа e также известна как число Эйлера, названное в честь знаменитого математика Леонарда Эйлера, который впервые ввел ее в 18 веке. Значение e в log можно найти с помощью различных методов, включая численные приближения и бесконечные ряды.

Значение e in log важно во многих приложениях, включая финансовое моделирование, физику и инженерию. В финансах он используется для расчета сложных процентов и моделирования роста инвестиционных портфелей. В физике константа e используется для описания поведения многих физических явлений, включая радиоактивный распад и распределение энергетических уровней в атомах. В технике он используется для проектирования сложных систем, таких как схемы, системы управления и сети связи.

Таким образом, значение e в log является фундаментальной константой в математике, которая используется во многих приложениях. Это ключевой элемент в понимании экспоненциальных и логарифмических функций и имеет важное значение в самых разных областях, от финансов до физики и техники.

Как вычислить значение журнала E в калькуляторе

Вычисление значения log e в калькуляторе — это простой процесс. Большинство научных калькуляторов имеют функцию натурального логарифма (ln), которая вычисляет логарифм по основанию e.

Чтобы найти логарифмическое значение числа с помощью калькулятора, выполните следующие действия:

Включите калькулятор и убедитесь, что он находится в правильном режиме. Для вычисления натуральных логарифмов он должен быть в радианах.
Введите число, значение журнала которого вы хотите найти.
Нажмите кнопку натурального логарифма (ln) на вашем калькуляторе. Обычно его обозначают «ln» или «log e».
Калькулятор отобразит натуральный логарифм введенного вами числа. Это логарифмическое значение числа. 91,6094″ на калькуляторе, чтобы получить результат, который примерно равен 5.
Стоит отметить, что функция натурального логарифма и функция основания e взаимозаменяемы, и обе они дают одинаковый результат.
Однако использование функции натурального логарифма обычно более просто и удобно.
В некоторых случаях может потребоваться найти значение log e более сложного выражения или уравнения. В этих случаях вы можете использовать правила логарифмирования, чтобы упростить выражение, а затем использовать функцию натурального логарифма, чтобы найти значение log e. Эти правила включают правило произведения, правило частного и правило мощности.
Таким образом, вычисление значения log e числа в калькуляторе — это простой процесс, который можно выполнить с помощью функции натурального логарифма или функции основания e. Это важное математическое понятие, имеющее многочисленные применения в науке, технике и финансах.
Что такое формула Log E?
Формула для log e, также известная как натуральный логарифм или ln, выглядит следующим образом:
ln(x) = log e (x) = y
где x — аргумент логарифма, а y — значение логарифма. 9y = x, мы можем использовать функцию натурального логарифма, чтобы найти ln(x) = y.

Например, если мы хотим найти натуральный логарифм числа 10, мы можем использовать формулу ln(10) = log e (10) = y. Решая у, получаем:
у = ln(10) = 2,3026
Это означает, что e нужно возвести в степень 2,3026, чтобы получить значение 10.
Натуральный логарифм имеет важные применения в различных областях науки, включая исчисление, физику и финансы. Это фундаментальное математическое понятие, которое широко используется во многих областях математики и естественных наук. 92 ≈ 7,389.
Натуральный логарифм обладает многими полезными свойствами в математике и естественных науках, включая вычисления, статистику и физику. Он часто используется для моделирования экспоненциального роста и распада, такого как распад радиоактивных материалов или рост населения. Он также используется в финансовом моделировании для расчета сложных процентов и нормы прибыли на инвестиции.

Обратным значением натурального логарифма является экспоненциальная функция, которую часто записывают как exp(x) или e^x. Экспоненциальная функция обычно используется для моделирования экспоненциального роста и затухания, а также является важной функцией в исчислении и дифференциальных уравнениях.
Таким образом, натуральный логарифм e имеет значение 1, и это фундаментальное математическое понятие со многими важными приложениями в различных областях исследований.
Что такое e In Log?
В математике буква «е» в логарифме относится к математической константе, известной как число Эйлера или натуральное основание, которое обозначается буквой «е». Это иррациональное число, приблизительно равное 2,71828.
Логарифм по основанию e, также называемый натуральным логарифмом, обозначается «ln» и определяется как функция, обратная экспоненциальной функции по основанию e. Другими словами, натуральный логарифм дает показатель степени, в которую необходимо возвести основание e, чтобы получить заданное значение.
Например, если у нас есть значение «x» и мы хотим найти натуральный логарифм «x», мы можем использовать уравнение ln(x) = y, где «y» — это показатель степени, к которому относится основание e. нужно поднять, чтобы получить значение «x». Итак, если мы хотим найти натуральный логарифм самого e, мы имеем ln(e) = 1, потому что e, возведенное в степень 1, равно e.
Значение «е» в логарифмическом выражении играет важную роль во многих математических функциях и формулах, включая экспоненциальный рост и затухание, сложные проценты и вычисления. Это фундаментальная математическая константа, имеющая многочисленные применения в различных областях науки, включая физику, химию, биологию и финансы.
Каково значение базы E журнала 1?
Значение логарифмической базы e числа x равно 0. Это связано с тем, что логарифмическая база e числа x — это степень, в которую нужно возвести e, чтобы получить x. В этом случае e в степени 0 равно 1. Следовательно, логарифмическая база e от 1 равна 0.
В общем случае для любого основания b логарифм b по основанию 1 всегда равен 0. Это связано с тем, что любое число, возведенное в степень 0, всегда равно 1. Таким образом, логарифм 1 по любому основанию всегда равен 0 .
Тот факт, что основание логарифма b по основанию 1 всегда равно 0, является полезным свойством логарифмов, которое используется во многих областях математики и естественных наук. Это позволяет нам упростить логарифмические выражения и выполнять вычисления более эффективно.
Логарифмы используются для решения уравнений, включающих экспоненциальные функции, а также для сравнения значений, которые варьируются в большом диапазоне. Они обычно используются в финансах для расчета нормы прибыли на инвестиции и в информатике для измерения сложности алгоритмов.
Помимо практического применения, логарифмы имеют богатую историю в математике. Впервые они были введены шотландским математиком Джоном Нейпиром в 17 веке, а позже были развиты многими другими математиками, в том числе Леонардом Эйлером, который ввел обозначение натурального логарифма как ln(x).
Логарифмы являются фундаментальной концепцией математики и имеют множество применений в естественных, социальных и инженерных науках. Их важность заключается в их способности преобразовывать экспоненциальные функции в линейные функции, что делает их мощным инструментом математического анализа и моделирования.
Является ли E тем же, что и Log10?
Нет, «e» и «log10» не одно и то же.
«E» относится к математической константе, называемой числом Эйлера или натуральным основанием, которое приблизительно равно 2,71828. «E» используется в качестве основания для функции натурального логарифма, которая обозначается «ln». Натуральный логарифм дает показатель степени, в которую необходимо возвести основание «е», чтобы получить заданное значение.
С другой стороны, «log10» относится к функции логарифмирования по основанию 10. Логарифмирование по основанию 10 дает показатель степени, до которого необходимо возвести основание 10, чтобы получить заданное значение. Например, log10(100) = 2, потому что 10, возведенное в степень 2, дает 100.
Хотя функция натурального логарифма и функция логарифма по основанию 10 связаны, это не одно и то же. В натуральном логарифме в качестве основания используется «e», а в логарифме с основанием 10 используется 10 в качестве основания. Они имеют разные свойства и приложения в математике, естественных науках и технике.
Таким образом, «e» и «log10» — это не одно и то же, поскольку они относятся к разным математическим понятиям и функциям.
Что такое значение E в журнале — Часто задаваемые вопросы
1. Каково значение e в журнале?
Значение e в логарифме относится к основанию натурального логарифма, обозначается как «e» и имеет приблизительное значение 2,71828.
2. Почему e используется как основание для логарифмов?
E используется в качестве основы для логарифмов, потому что он обладает некоторыми уникальными математическими свойствами, которые делают его полезным в различных областях математики и естественных наук, включая вычисления и экспоненциальный рост и затухание.
No related posts.