Кратные числа в таблице
4.1
Средняя оценка: 4.1
Всего получено оценок: 243.
4.1
Средняя оценка: 4.1
Всего получено оценок: 243.
Математика имеет много специфических понятий, среди которых кратное число и делимость чисел. Сегодня мы разберем понятие кратности, а так же все понятия из математики 6 класса, которые связаны с кратностью.
Деление
Операция деления является обратной для операции умножения. Деление показывает, сколько раз одно число умножили на другое, чтобы получить изначальный результат. Для нахождения результата простейших операций деления пользуются таблицей умножения.
Для более сложных примеров пользуются деление в столбик. Так же различают деление с остатком, нацело и деление с дробным остатком:
- Деление с остатком. Деление с остатком подразумевает, что получился целый результат и такой же целый остаток, который записывается рядом с результатом.
- Деление нацело означает, что в результате деления получилось целое число без всяких остатков.
- Дробный остаток записывается через запятую. Если в результате деления не получается поделить число нацело, то можно продолжить делить для того, чтобы получить десятичную дробь.
Так же вместо деления всегда можно записать обычную или неправильную дробь, но в качестве ответа такая запись не подойдет.
Отрицательные числа так же можно поделить нацело. Так же, как и в делении отрицательных чисел на положительные и положительные на отрицательные. Нельзя так же забывать, что на деление действует правило знаков. То есть деление отрицательного числа на положительное дает отрицательный результат. Деление отрицательного числа на отрицательное – положительный результат.
Кратность и делимость
Разберем эти понятия на числе 9. Так для числа 9 кратными будут 18, 27, 36 и так далее. То есть кратными называют числа, которые можно поделить на заданное число нацело.
Делимостью же называют способность самого числа поделиться нацело.
То есть для 9 делителями будут числа 9,3,1. Число делителей – ограниченно, число кратных – нет.
Бывают числа кратные для нескольких значений одновременно.
Для нескольких чисел существует два понятия, связанных с делимостью и кратностью:
- НОД или наибольший общий делитель. Это наибольшее число, на которое можно поделить нацело все числа заданного ряда. Обратите внимание, что речь идет о ряде чисел, то есть 2 и более.
- НОК или наименьшее общее кратное. Это наименьшее число, которое делиться на все числа ряда.
Иногда ученики пытаются найти таблицу кратных чисел. Но такого материала просто не существует. Нельзя свести в одну таблицу все числа. А для наиболее простых от 1 до 10 существует таблица умножения.
Что мы узнали?
Тест по теме
Доска почёта
Чтобы попасть сюда — пройдите тест.
Анна Ножеева
4/5
Оценка статьи
4.1
Средняя оценка: 4.1
Всего получено оценок: 243.
А какая ваша оценка?
Делители и кратные
Цели: начать формирование представления о делимости натуральных чисел, делителе и кратном натурального числа; ввести понятия делитель, кратное; научить находить делители числа и кратные числа; содействовать формированию интереса к учению.
Ход урока
I. Организационный момент
II. Актуализация опорных знаний
Учитель говорит о действии деления.
Деление — это действие разложения величины на равные части. Например, 6 яблок разделить поровну на двоих детей. Конечно, и 5 яблок можно поделить между двумя детьми, но для этого придётся одно из яблок разрезать пополам.
Возможно и деление с остатком.
Сегодня мы рассмотрим деление натуральных чисел, когда числа делятся без остатка.
Рассмотрим простой пример.
На день рождения Маша получила 8 воздушных шаров. Она решила поделиться со своей подругой Леной и пригласила её в гости.
«Нам двоим достанется по 4 шарика», — подумала Маша
Но праздник был бы не таким веселым, если бы в гости не заглянул друг Коля.
«Как же теперь делить воздушные шары?» — подумала Лена.
8 шариков не разделишь поровну на трёх друзей. Ведь воздушные шары не яблоки, их не разрежешь на части.
Но Коля пришёл не один, а вместе с братом Ваней.
«Ну, что ж, проблема решена, — подумала именинница, — теперь каждому из нас достанется по 2 шарика».
III. Изучение нового материала
а) Рассмотрим данный пример с математической точки зрения.
8 шаров делится на 2 и 4. Но 8 не делится нацело на 3.
Говорят, что числа 2 и 4 являются делителями числа 8, а число 3 не является делителем восьми.
Делителем b натурального числа а называют натуральное число b, на которое а делится без остатка.
Число 8 имеет 4 делителя: 1,2,4 и 8.
Важно понимать различие понятия делится от понятия делить.
Можно делить 5 на 2 и получить 2,5. Но верно будет и то, что 5 не делится на 2. (имеется ввиду поровну)
Например,
6 делится на 3;
30 делится на 10;
7 не делится на 2.
Разберём ещё одно простое задание: найти все делители числа 12. Перебираем все натуральные числа до 12. Записываем только те, которые делятся на 12.
Делители 12: 1, 2, 3, 4, 6, 12.
б) Ёще одним важным понятием темы будет понятие «кратное».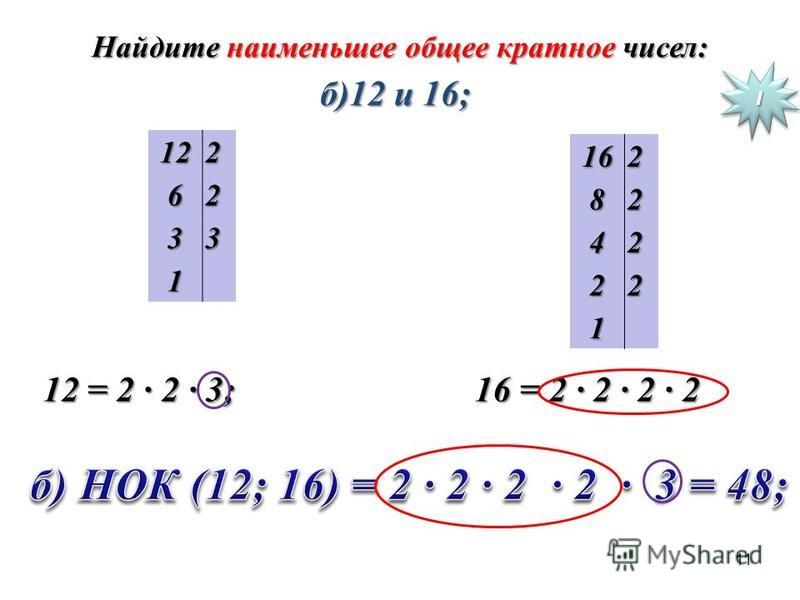
Если натуральное числа а делится на натуральное число b, то число а называют кратным числа b.
Другими словами, число а кратно числу b — значит а делится на b.
В примере с шариками 8 делится на 2, можно сказать, 8 кратно двум.
Вот например, несколько чисел кратных семи:
7, 14, 21, 70… Все эти числа делятся на 7.
Запишем 5 чисел кратных 10:
10, 100, 1000, 10 000, 1 000 000.
в) Теперь поговорим о количестве делителей и кратных.
Для числа 6 делителей будет 4: 1,2,3 и 6.
Теперь запишем кратные 6: 6, 12, 18, 600, 6000… Все числа и не запишешь.
Запомним, любое натуральное число имеет бесконечно много кратных.
IV.Закрепление и практическое применение знаний
Решение заданий в учебнике: устно № 3, № 5.
Письменно № 6 и № 7.
Как найти кратные числа?
••• изображение клавиатуры от vashistha pathak с сайта Fotolia.com
Обновлено 24 апреля 2017 г.
Автор: Fatima Farakh
Определение кратности числа является одним из самых важных математических навыков, которым необходимо овладеть в жизни. Несколько чисел используются в течение дня в самых разных областях, начиная от выполнения простых транзакций в магазине и заканчивая сложными научными и математическими расчетами, лежащими в основе физики и компьютерных наук. Числа, кратные числам, лежат в основе математики и должны быть ясно поняты всеми детьми и молодыми людьми, чтобы они могли правильно использовать их в своей повседневной жизни.
- Базовые математические навыки
- Калькулятор (дополнительно)
Вы можете использовать калькулятор, чтобы найти кратные большего числа.
Сосредоточьтесь и обратите внимание на каждую цифру. Незначительная оплошность при вычислении чисел и выполнении уравнений вызовет ошибку при нахождении кратных чисел.
Выберите число, для которого вы хотите найти кратное, и умножьте его, продолжая целые числа. Например, если вы хотите найти числа, кратные 2, выполните следующие вычисления: 2 * 1 = 2, 2 * 2 = 4, 2 * 3 = 6 и продолжайте с другими целыми числами. В другом примере числа, кратные числу 5, можно найти, выполнив следующие вычисления: 5 * 1 = 5, 5 * 2 = 10, 5 * 3 = 15, 5 * 4 = 20 и 5 * 5 = 25.
Определить, можно ли разделить число без остатка. Множественное число должно иметь возможность делиться на исходное число, для которого вы ищете кратное, без остатка. Например, 8 кратно 2, а так как 2 * 4 = 8, то 8/2 = 4. В этом примере 2 и 4 также являются множителями 8, и остатков не осталось. Сравните это с делением 12 на 5. При делении 12 на 5 получается остаток 2, а это значит, что 12 не кратно 5.
Проанализируйте, как умножается число. Кратность числа – это результат умножения числа на целое число. Например, умножьте 2,5 (не целое число) на 5 (целое число). Результат равен 12,5, что означает, что 12,5 кратно 2,5, поскольку оно было умножено на 5 (целое число). Сравните это с умножением 2,5 на 5,5. Результат 13,75. В этом случае 13,75 нельзя назвать кратным 2,5, так как оно не умножалось на целое число, например 1, 2, 3, 4 или 5.
Найдите НОК (наименьшее общее кратное), просмотрев кратные двух или более целых чисел. Например, проанализируйте числа, кратные 2 и 5, и найдите общее кратное между числами, кратными 2 и 5.
НОК будет наименьшим кратным из общих кратных 2 и 5. В приведенном примере НОК 2 и 5 равно 10.
Вещи, которые вам понадобятся
Предупреждения
Статьи по теме
Советы
- Вы можете использовать калькулятор, чтобы найти кратность большего числа.
Предупреждения
- Сосредоточьтесь и обратите внимание на каждую цифру. Незначительная оплошность при вычислении чисел и выполнении уравнений вызовет ошибку при нахождении кратных чисел.
Об авторе
Фатима Фарах профессионально пишет с 2001 года. Ее статьи публиковались в газете «The Gazette» в Мэриленде и в других изданиях.
Сфера ее специализации – здоровье, технологии и благоустройство дома. В настоящее время она является копирайтером для бизнеса, включая частные и государственные школы и онлайн-корпорации. Она имеет степень младшего специалиста по журналистике и истории колледжа Монтгомери.
Фото Кредиты
изображение клавиатуры от vashistha pathak с сайта Fotolia.com
Идентификация кратных чисел | Математика для гуманитарных специальностей
Результаты обучения
- Определить, является ли число кратным заданному числу
- Определить, делится ли заданное число на 2, 3, 5 или 10
Энни считает туфли в шкафу. Туфли подбираются парами, поэтому ей не нужно считать каждую. Она считает двойками: [латекс]2,4,6,8,10,12[/латекс]. У нее в шкафу [латекс]12[/латекс] туфель.
Числа [латекс]2,4,6,8,10,12[/латекс] называются кратными [латекс]2[/латекс]. Кратность [латекс]2[/латекс] может быть записана как произведение счетного числа и [латекс]2[/латекс].
Первые шесть кратных [latex]2[/latex] приведены ниже.
[латекс]\begin{array}{l}1\cdot 2=2\\ 2\cdot 2=4\\ 3\cdot 2=6\\ 4\cdot 2=8\\ 5\cdot 2= 10\\ 6\cdot 2=12\end{массив}[/latex]
Число, кратное числу, является произведением числа на счетное число. Таким образом, число, кратное [латексу]3[/латексу], будет произведением счетного числа и [латекса]3[/латекса]. Ниже приведены первые шесть множителей [latex]3[/latex].
[латекс]\begin{array}{l}1\cdot 3=3\\ 2\cdot 3=6\\ 3\cdot 3=9\\ 4\cdot 3=12\\ 5\cdot 3= 15\\ 6\cdot 3=18\end{массив}[/latex]
Продолжая этот процесс, мы можем найти кратные любого числа. В таблице ниже показаны кратные числа от [латекс]2[/латекс] до [латекс]9[/латекс] для первых двенадцати счетных чисел.
| Счетный номер | [латекс]1[/латекс] | [латекс]2[/латекс] | [латекс]3[/латекс] | [латекс]4[/латекс] | [латекс]5[/латекс] | [латекс]6[/латекс] | [латекс]7[/латекс] | [латекс]8[/латекс] | [латекс]9[/латекс] | [латекс]10[/латекс] | [латекс]11[/латекс] | [латекс]12[/латекс] |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| [латекс]\текст{Количество множителей}2[/латекс] | [латекс]2[/латекс] | [латекс]4[/латекс] | [латекс]6[/латекс] | [латекс]8[/латекс] | [латекс]10[/латекс] | [латекс]12[/латекс] | [латекс]14[/латекс] | [латекс]16[/латекс] | [латекс]18[/латекс] | [латекс]20[/латекс] | [латекс]22[/латекс] | [латекс]24[/латекс] |
| [латекс]\текст{множество на 3[/латекс] | [латекс]3[/латекс] | [латекс]6[/латекс] | [латекс]9[/латекс] | [латекс]12[/латекс] | [латекс]15[/латекс] | [латекс]18[/латекс] | [латекс]21[/латекс] | [латекс]24[/латекс] | [латекс]27[/латекс] | [латекс]30[/латекс] | [латекс]33[/латекс] | [латекс]36[/латекс] |
| [латекс]\текст{множество на 4[/латекс] | [латекс]4[/латекс] | [латекс]8[/латекс] | [латекс]12[/латекс] | [латекс]16[/латекс] | [латекс]20[/латекс] | [латекс]24[/латекс] | [латекс]28[/латекс] | [латекс]32[/латекс] | [латекс]36[/латекс] | [латекс]40[/латекс] | [латекс]44[/латекс] | [латекс]48[/латекс] |
| [латекс]\текст{множество}5[/латекс] | [латекс]5[/латекс] | [латекс]10[/латекс] | [латекс]15[/латекс] | [латекс]20[/латекс] | [латекс]25[/латекс] | [латекс]30[/латекс] | [латекс]35[/латекс] | [латекс]40[/латекс] | [латекс]45[/латекс] | [латекс]50[/латекс] | [латекс]55[/латекс] | [латекс]60[/латекс] |
| [латекс]\текст{Количество кратных}6[/латекс] | [латекс]6[/латекс] | [латекс]12[/латекс] | [латекс]18[/латекс] | [латекс]24[/латекс] | [латекс]30[/латекс] | [латекс]36[/латекс] | [латекс]42[/латекс] | [латекс]48[/латекс] | [латекс]54[/латекс] | [латекс]60[/латекс] | [латекс]66[/латекс] | [латекс]72[/латекс] |
| [латекс]\текст{кратно }7[/латекс] | [латекс]7[/латекс] | [латекс]14[/латекс] | [латекс]21[/латекс] | [латекс]28[/латекс] | [латекс]35[/латекс] | [латекс]42[/латекс] | [латекс]49[/латекс] | [латекс]56[/латекс] | [латекс]63[/латекс] | [латекс]70[/латекс] | [латекс]77[/латекс] | [латекс]84[/латекс] |
| [латекс]\текст{кратно 8[/латекс] | [латекс]8[/латекс] | [латекс]16[/латекс] | [латекс]24[/латекс] | [латекс]32[/латекс] | [латекс]40[/латекс] | [латекс]48[/латекс] | [латекс]56[/латекс] | [латекс]64[/латекс] | [латекс]72[/латекс] | [латекс]80[/латекс] | [латекс]88[/латекс] | [латекс]96[/латекс] |
| [латекс]\текст{множество на 9[/латекс] | [латекс]9[/латекс] | [латекс]18[/латекс] | [латекс]27[/латекс] | [латекс]36[/латекс] | [латекс]45[/латекс] | [латекс]54[/латекс] | [латекс]63[/латекс] | [латекс]72[/латекс] | [латекс]81[/латекс] | [латекс]90[/латекс] | [латекс]99[/латекс] | [латекс]108[/латекс] |
Кратность числа
Число является кратным [latex]n[/latex], если оно является произведением счетного числа и [latex]n[/latex].
Распознавание шаблонов для чисел, кратных [латекс]2, 5, 10, \текст{и }3[/латекс], поможет вам продолжить изучение этого курса.
Выполнение упражнения по манипулятивной математике «Множества» поможет вам лучше понять кратные числа.
В таблице ниже показаны числа от [латекс]1[/латекс] до [латекс]50[/латекс]. Подсвечиваются кратные [латекс]2[/латекс]. Вы замечаете закономерность?
Несколько [латекс]2[/латекс] между [латекс]1[/латекс] и [латекс]50[/латекс]
Последняя цифра каждого выделенного числа в таблице — либо [латекс]0 , 2, 4, 6, \text{или }8[/latex]. Это справедливо для произведения [латекса]2[/латекса] на любое счетное число. Итак, чтобы узнать, является ли какое-либо число кратным [latex]2[/latex], посмотрите на последнюю цифру. Если это [латекс]0, 2, 4, 6, \text{или }8[/латекс], то число кратно [латекс]2[/латекс].
пример
Определите, является ли каждое из следующих чисел кратным [латекс]2\текст{:}[/латекс]
- [латекс]489[/латекс]
- [латекс]3714[/латекс]
Решение:
| 2. | |
| Является ли [латекс]3714[/латекс] кратным [латекс]2[/латекс]? | |
| Последняя цифра [латекс]0, 2, 4, 6, \text{ или } 8[/латекс] ? | Да. |
| [латекс]3,714[/латекс] кратно [латекс]2[/латекс]. |
попробуйте
https://ohm.lumenlearning.com/multiembedq.php?id=145363&theme=oea&iframe_resize_id=mom1
Теперь давайте посмотрим на число, кратное [латексу]5[/латексу]. В таблице ниже показаны все кратные [латекс]5[/латекс] между [латекс]1[/латекс] и [латекс]50[/латекс]. Что вы заметили в кратных [латекс]5?[/латекс]
Кратность [латекс]5[/латекс] между [латекс]1[/латекс] и [латекс]50[/латекс]
Все кратные [латекс]5[/латекс] заканчиваются либо на [латекс]5[/латекс], либо на [латекс]0[/латекс]. Точно так же, как мы идентифицируем числа, кратные [латексу]2[/латексу], глядя на последнюю цифру, мы можем идентифицировать числа, кратные [латексу]5[/латексу], глядя на последнюю цифру.
пример
Определите, является ли каждое из следующих чисел кратным [латекс]5\текст{:}[/латекс]
- [латекс]579[/латекс]
- [латекс]880[/латекс]
Показать решение
попробуйте
https://ohm.lumenlearning.com/multiembedq.php?id=145413&theme=oea&iframe_resize_id=mom2
В приведенной ниже таблице выделены кратные [латекс]10[/латекс] между [латекс] 1[/латекс] и [латекс]50[/латекс]. Все числа, кратные [latex]10[/latex], заканчиваются нулем.
Кратность [латекс]10[/латекс] между [латекс]1[/латекс] и [латекс]50[/латекс]
пример
Определите, кратно ли каждое из следующих чисел [латекс] 10\текст{:}[/латекс]
- [латекс]425[/латекс]
- [латекс]350[/латекс]
Показать решение
попробуйте
https://ohm. lumenlearning.com/multiembedq.php?id=145417&theme=oea&iframe_resize_id=mom3
В таблице ниже выделены числа, кратные [latex]3[/latex]. Паттерн для кратных [латекс]3[/латекс] не так очевиден, как шаблоны для кратных [латекс]2,5,\текст{и }10[/латекс].
Несколько [латекс]3[/латекс] между [латекс]1[/латекс] и [латекс]50[/латекс]
последняя цифра. Шаблон для кратных [латекс]3[/латекс] основан на сумме цифр. Если сумма цифр числа кратна [латекс]3[/латекс], то само число кратно [латекс]3[/латекс]. См. пример ниже.
| [латекс]\mathbf{\text{кратное 3}}[/латекс] | [латекс]3[/латекс] | [латекс]6[/латекс] | [латекс]9[/латекс] | [латекс]12[/латекс] | [латекс]15[/латекс] | [латекс]18[/латекс] | [латекс]21[/латекс] | [латекс]24[/латекс] |
| [латекс]\mathbf{\text{Сумма цифр}}[/латекс] | [латекс]3[/латекс] | [латекс]6[/латекс] | [латекс]9[/латекс] | [латекс]\начало{массив}{c}\hfill 1+2\hfill \\ \hfill 3\hfill \end{массив}[/latex] | [латекс]\начало{массив}{c}\hfill 1+5\hfill \\ \hfill 6\hfill \end{массив}[/latex] | [латекс]\начало{массив}{с}\hfill 1+8\hfill \\ \hfill 9\hfill \end{массив}[/латекс] | [латекс]\начало{массив}{c}\hfill 2+1\hfill \\ \hfill 3\hfill \end{массив}[/latex] | [латекс]\начало{массив}{c}\hfill 2+4\hfill \\ \hfill 6\hfill \end{массив}[/latex] |
Рассмотрим число [латекс]42[/латекс]. Цифры [латекс]4[/латекс] и [латекс]2[/латекс], а их сумма равна [латекс]4+2=6[/латекс]. Поскольку [латекс]6[/латекс] кратен [латекс]3[/латекс], мы знаем, что [латекс]42[/латекс] также кратен [латекс]3[/латекс].
пример
Определить, является ли каждое из заданных чисел кратным [латекс]3\текст{:}[/латекс]
- [латекс]645[/латекс]
- [латекс]10 519[/латекс]
Показать решение
попробуйте
https://ohm.lumenlearning.com/multiembedq.php?id=145418&theme=oea&iframe_resize_id=mom4
Посмотрите на диаграммы, где вы выделили кратные [latex]2[/latex] , [латекс]5[/латекс] и [латекс]10[/латекс]. Обратите внимание, что числа, кратные [латексу]10[/латексу], — это числа, кратные как [латексу]2[/латексу], так и [латексу]5[/латексу]. Это потому, что [латекс]10=2\cdot 5[/латекс]. Аналогичным образом, поскольку [латекс]6=2\cdot 3[/латекс], кратные [латекс]6[/латекс] — это числа, кратные как [латексу]2[/латекс], так и [латексу]3[. /латекс].
В следующем видео показано, как определить первые четыре числа, кратные 6.
Используйте общие критерии делимости
Еще один способ сказать, что [латекс]375[/латекс] кратен [латекс]5[/латекс ] означает, что [латекс]375[/латекс] делится на [латекс]5[/латекс]. Фактически, [латекс]375\div 5[/латекс] — это [латекс]75[/латекс], поэтому [латекс]375[/латекс] — это [латекс]5\cdot 75[/латекс]. Обратите внимание, что в последнем примере [латекс]10 519[/латекс] не является кратным [латекс]3[/латекс]. Когда мы разделили [латекс]10 519[/latex] на [latex]3[/latex] мы не получили счетное число, поэтому [latex]10 519[/latex] не делится на [latex]3[/latex].
Делимость
Если число [латекс]m[/латекс] кратно [латекс]n[/латекс], то говорят, что [латекс]m[/латекс] делится на [латекс]n[/ латекс].
Поскольку умножение и деление являются обратными операциями, найденные нами шаблоны кратных можно использовать в качестве проверки делимости. В таблице ниже приведены тесты на делимость для некоторых счетных чисел от одного до десяти.
| Признаки делимости | |
|---|---|
| Число делится на | |
| [латекс]2[/латекс] | , если последняя цифра [латекс]0,2,4,6,\текст{или }8[/латекс] |
| [латекс]3[/латекс] | , если сумма цифр делится на [латекс]3[/латекс] |
| [латекс]5[/латекс] | , если последняя цифра [латекс]5[/латекс] или [латекс]0[/латекс] |
| [латекс]6[/латекс] | , если делится на [латекс]2[/латекс] и [латекс]3[/латекс] |
| [латекс]10[/латекс] | , если последняя цифра [латекс]0[/латекс] |
пример
Определить, делится ли [латекс]1,290[/латекс] на [латекс]2,3,5,\текст{и }10[/латекс].