Как найти высоту трапеции. Запоминаем и применяем свойства трапеции
Трапецией называется такой четырехугольник, две стороны у которого параллельны (это основания трапеции, обозначенные на рисунке a и b), а другие две — нет (на рисунке АД и CB). Высота трапеции — это отрезок h, проведенный перпендикулярно к основаниям.
Как найти высоту трапеции при известных величинах площади трапеции и длин оснований?
Для вычисления площади S трапеции ABCD, воспользуемся формулой:
S = ((a+b) × h)/2.
Здесь отрезки a и b — это основания трапеции, h — это высота трапеции.
Преобразуя эту формулу, можем записать:
Используя эту формулу, получим значение h, если известны величина площади S и величины длин оснований a и b.
Пример
Если известно, что площадь трапеции S равна 50 см², длина основания a составляет 4 см, длина основания b составляет 6 см, то, чтобы найти высоту h, используем формулу:
Подставляем в формулу известные величины.
h = (2 × 50)/(4+6) = 100/10 = 10 см
Ответ: высота трапеции составляет 10 см.
Как находить высоту трапеции, если даны величины площади трапеции и длина средней линии?
Воспользуемся формулой вычисления площади трапеции:
Здесь m — средняя линия, h — высота трапеции.
Если возникает вопрос, как найти высоту трапеции, формула:
h = S/m, будет ответом.
Таким образом, можем найти величину высоты трапеции h, имея известные величины площади S и отрезка средней линии m.
Пример
Известна длина средней линии трапеции m, которая составляет 20 см, и площадь S, которая равна 200 см². Найдем значение величины высоты трапеции h.
Подставив значения S и m, получим:
h = 200/20 = 10 см
Ответ: высота трапеции составляет 10 см
Как найти высоту прямоугольной трапеции?
Если трапеция — это четырехугольник, с двумя параллельными сторонами (основаниями) трапеции. То диагональ — это отрезок, который соединяющий две противоположные вершины углов трапеции (отрезок АС на рисунке). Если трапеция прямоугольная, с помощью диагонали, найдем величину высоты трапеции h.
Прямоугольной трапецией называется такая трапеция, где одна из боковых сторон перпендикулярна основаниям. В этом случае ее длина (АД) совпадает с высотой h.
Итак, рассмотрим прямоугольную трапецию ABCD, где AD — это высота, DC — это основание, AC — это диагональ. Воспользуемся теоремой Пифагора. Квадрат гипотенузы AC прямоугольного треугольника ADC равен сумме квадратов его катетов AB и BC.
Тогда можно записать:
AC² = AD² + DC².
AD — это катет треугольника, боковая сторона трапеции и, в то же время, ее высота. Ведь отрезок АД перпендикулярен основаниям. Его длина составит:
AD = √(AC² — DC²)
Итак, имеем формулу для вычисления высоты трапеции h = AD
Пример
Если длина основания прямоугольной трапеции(DC) равна 14 см, а диагональ (AC) составляет 15 см, для получения значения высоты(AD -боковой стороны) воспользуемся теоремой Пифагора.
Пусть х — это неизвестный катет прямоугольного треугольника(AD), тогда
AC² = AD² + DC² можно записать
15² = 14² + х²,
х = √(15²-14²) = √(225-196) = √29 см
Ответ: высота прямоугольной трапеции (АВ) составит √29 см, что приблизительно составит, 5. 385 см
385 см
Как найти высоту равнобедренной трапеции?
Равнобедренной трапецией, называют трапецию, у которой длины боковых сторон равны между собой. Прямая, проведенная через середины оснований такой трапеции будет осью симметрии. Частным случаем является трапеция, диагонали которой перпендикулярны друг другу, тогда высота h, будет равна полусумме оснований.
Рассмотрим случай, если диагонали не перпендикулярны друг другу. В равнобочной (равнобедренной) трапеции равны углы при основаниях и длины диагоналей равны. Также известно, что все вершины равнобокой трапеции касаются линии окружности, проведенной вокруг этой трапеции.
Рассмотрим рисунок. ABCD- равнобедренная трапеция. Известно, что основания трапеции параллельны, значит, BC = b параллельно AD = a, сторона AB = CD = c, значит, углы при основаниях соответственно равны, можно записать угол BAQ = CDS = α, и угол ABC = BCD = β. Таким образом, делаем вывод о равенстве треугольника ABQ треугольнику SCD, значит, отрезок
AQ = SD = (AD — BC)/2 = (a — b)/2.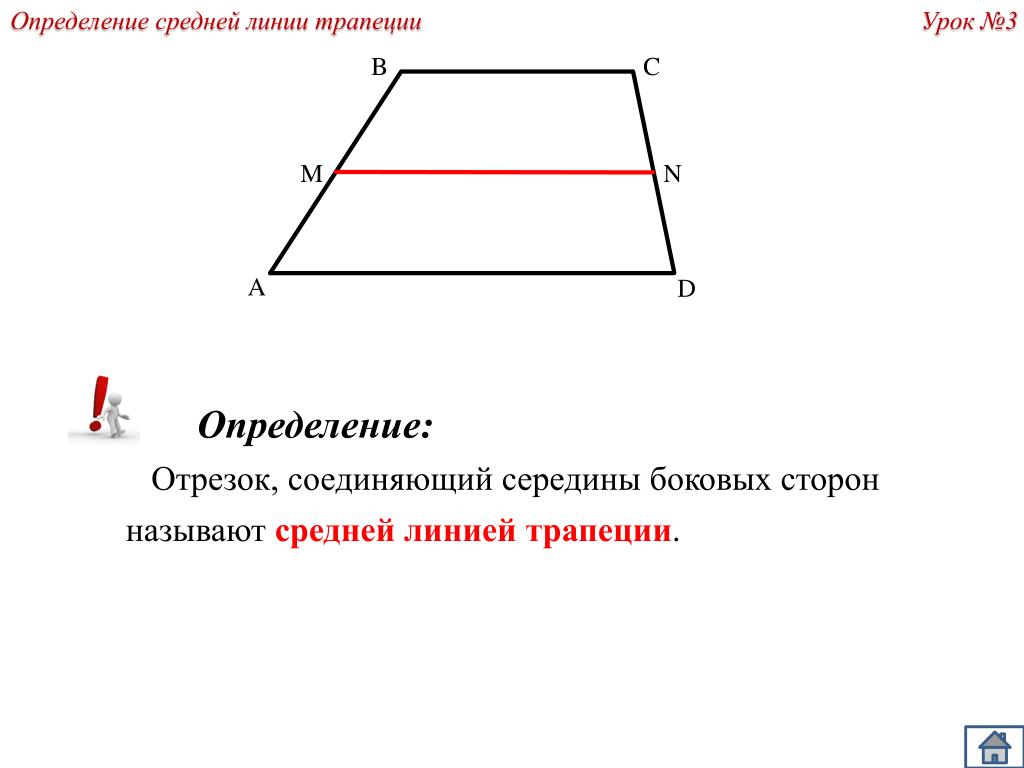
Имея по условию задачи величины оснований a и b, и длину боковой стороны с, найдем высоту трапеции h, равную отрезку BQ.
Рассмотрим прямоугольный треугольник ABQ. ВО — высота трапеции, перпендикулярна основанию AD, значит и отрезку AQ. Сторону AQ треугольника ABQ, найдем, воспользовавшись выведенной нами ранее формулой:
Имея значения двух катетов прямоугольного треугольника, найдем гипотенузу BQ= h. Используем теорему Пифагора.
AB²= AQ² + BQ²
Подставим данные задачи:
c² = AQ² + h².
Получим формулу для нахождения высоты равнобедренной трапеции:
h = √(c²-AQ²).
Пример
Дана равнобедренная трапеция ABCD, где основание AD = a = 10см, основание BC = b = 4см, а боковая сторона AB = c = 12см. При таких условиях, рассмотрим на примере, как найти трапеции высоту, равнобедренной трапеции АВСД.
Найдем сторону AQ треугольника ABQ, подставив известные данные:
AQ = (a — b)/2 = (10-4)/2=3см.
Теперь подставим значения сторон треугольника в формулу теоремы Пифагора.
h = √(c²- AQ²) = √(12²- 3²) = √135 = 11.6см.
Ответ. Высота h равнобедренной трапеции ABCD составляет 11.6 см.
Геометрия – одна из наук, с применением которой на практике человек сталкивается практически ежедневно. Среди многообразия геометрических фигур отдельного внимания заслуживает и трапеция. Она представляет собой выпуклую фигуру с четырьмя сторонами, из которых две параллельны между собой. Последние называются основаниями, а оставшиеся две – боковыми сторонами. Отрезок, перпендикулярный основаниям и определяющий величину промежутка между ними, и будет высотой трапеции. Каким же образом можно вычислить его длину?
Найти высоту произвольной трапеции
Базируясь на исходных данных, определение высоты фигуры возможно несколькими способами.
Известна площадь
Если длина параллельных сторон известна, а также указана площадь фигуры, то для определения искомого перпендикуляра можно воспользоваться следующим соотношением:
S=h*(a+b)/2,
h – искомая величина (высота),
S – площадь фигуры,
a и b – стороны, параллельные друг другу.
Из приведенной формулы следует, что h=2S/(a+b).
Известна величина средней линии
Если среди исходных данных помимо площади трапеции (S) известна, и длина ее линии средины (l), то для вычислений пригодится другая формула. Прежде стоит уточнить, что такое средняя линия для данного вида четырехугольника. Термин определяет часть прямой, соединяющей средины боковых сторон фигуры.
Исходя из свойства трапеции l=(a+b)/2,
l – линия средины,
a, b – стороны-основания четырехугольника.
Поэтому h=2S/(a+b)=S/l.
Известны 4 стороны фигуры
В данном случае поможет теорема Пифагора. Опустив перпендикуляры на большую сторону-основание, воспользуйтесь ею для двух получившихся прямоугольных треугольников. Итоговое выражение будет иметь вид:
h=√c 2 -(((a-b) 2 +c 2 -d 2)/2(a-b)) 2 ,
c и d – 2 другие стороны.
Углы в основании
При наличии данных об углах при основании, воспользуйтесь тригонометрическими функциями.
h = c* sinα = d*sinβ,
α и β – углы в основании четырехугольника,
c и d – его боковые стороны.
Диагонали фигуры и углы, которые пересекаясь они образуют
Длина диагонали – длина отрезка, соединяющего противоположные вершины фигуры. Обозначим данные величины символами d1 и d2, а углы между ними γ и φ. Тогда:
h = (d1*d2)/(a+b) sin γ = (d1*d2)/(a+b) sinφ,
h = (d1*d2)/2l sin γ = (d1*d2)/2l sinφ,
a и b – стороны-основания фигуры,
d1 и d2 – диагонали трапеции,
γ и φ – углы между диагоналями.
Высота фигуры и радиус окружности, которая в нее вписана
Как следует из определения такого рода окружности, она касается каждого основания в 1 точке, которые являются частью одной прямой. Поэтому расстояние между ними – диаметр – искомая высота фигуры. А так как диаметр – удвоенный радиус, то:
h = 2 * r,
r – радиус окружности, которую вписали в данную трапецию.
Найти высоту равнобедренной трапеции
- Как и следует из формулировки, отличительной характеристикой равнобедренной трапеции является равенство ее боковых сторон.
 Поэтому для нахождения высоты фигуры воспользуйтесь формулой для определения данной величины в случае, когда известны стороны трапеции.
Поэтому для нахождения высоты фигуры воспользуйтесь формулой для определения данной величины в случае, когда известны стороны трапеции.
Итак, если с = d, то h=√c 2 -(((a-b) 2 +c 2 -d 2)/2(a-b)) 2 = √c 2 -(a-b) 2 /4,
a, b – стороны-основания четырехугольника,
c = d – его боковые стороны.
- При наличии величины углов, образованных двумя сторонами (основанием и боковой), высоту трапеции определяет следующее соотношение:
h = c* sinα,
h = с * tgα *cosα = с * tgα * (b – a)/2c = tgα * (b-a)/2,
α – угол в основании фигуры,
a, b (a
c = d – его боковые стороны.
- Если даны величины диагоналей фигуры, то выражение для нахождения высоты фигуры видоизменится, т.к. d1 = d2:
h = d1 2 /(a+b)*sinγ = d1 2 /(a+b)*sinφ,
h = d1 2 /2*l*sinγ = d1 2 /2*l*sinφ.
В этой статье мы постараемся насколько возможно полно отразить свойства трапеции. В частности, речь пойдет про общие признаки и свойства трапеции, а также про свойства вписанной трапеции и про окружность, вписанную в трапецию. Затронем мы и свойства равнобедренной и прямоугольной трапеции.
Затронем мы и свойства равнобедренной и прямоугольной трапеции.
Пример решения задачи с использованием рассмотренных свойств поможет вам разложить по местам в голове и лучше запомнить материал.
Трапеция и все-все-все
Для начала коротко вспомним, что такое трапеция и какие еще понятия с ней связаны.
Итак, трапеция – фигура-четырехугольник, две из сторон которой параллельны друг другу (это основания). И две не параллельны – это боковые стороны.
В трапеции может быть опущена высота – перпендикуляр к основаниям. Проведены средняя линия и диагонали. А также из любого угла трапеции возможно провести биссектрису.
Про различные свойства, связанные со всеми эти элементами и их комбинациями, мы сейчас и поговорим.
Свойства диагоналей трапеции
Чтобы было понятнее, пока читаете, набросайте себе на листке трапецию АКМЕ и проведите в ней диагонали.
- Если вы найдете середины каждой из диагоналей (обозначим эти точки Х и Т) и соедините их, получится отрезок.
 Одно из свойств диагоналей трапеции заключается в том, что отрезок ХТ лежит на средней линии. А его длину можно получив, разделив разность оснований на два: ХТ = (a – b)/2 .
Одно из свойств диагоналей трапеции заключается в том, что отрезок ХТ лежит на средней линии. А его длину можно получив, разделив разность оснований на два: ХТ = (a – b)/2 . - Перед нами все та же трапеция АКМЕ. Диагонали пересекаются в точке О. Давайте рассмотрим треугольники АОЕ и МОК, образованные отрезками диагоналей вместе с основаниями трапеции. Эти треугольники – подобные. Коэффициент подобия k треугольников выражается через отношение оснований трапеции: k = АЕ/КМ.
Отношение площадей треугольников АОЕ и МОК описывается коэффициентом k 2 . - Все та же трапеция, те же диагонали, пересекающиеся в точке О. Только в этот раз мы будем рассматривать треугольники, которые отрезки диагоналей образовали совместно с боковыми сторонами трапеции. Площади треугольников АКО и ЕМО являются равновеликими – их площади одинаковые.
- Еще одно свойство трапеции включает в себя построение диагоналей. Так, если продолжить боковые стороны АК и МЕ в направлении меньшего основания, то рано или поздно они пересекутся к некоторой точке.

Если мы теперь продлим прямую ХТ, то она соединит вместе точку пересечения диагоналей трапеции О, точку, в которой пересекаются продолжения боковых сторон и середины оснований Х и Т. - Через точку пересечения диагоналей проведем отрезок, который соединит основания трапеции (Т лежит на меньшем основании КМ, Х – на большем АЕ). Точка пересечения диагоналей делит этот отрезок в следующем соотношении: ТО/ОХ = КМ/АЕ .
- А теперь через точку пересечения диагоналей проведем параллельный основаниям трапеции (a и b) отрезок. Точка пересечения разделит его на две равных части. Найти длину отрезка можно по формуле 2ab/(a + b) .
Свойства средней линии трапеции
Среднюю линию проведите в трапеции параллельно ее основаниям.
- Длину средней линии трапеции можно вычислить, если сложить длины оснований и разделить их пополам: m = (a + b)/2 .

- Если провести через оба основания трапецию любой отрезок (высоту, к примеру), средняя линия разделит его на две равных части.
Свойство биссектрисы трапеции
Выберите любой угол трапеции и проведите биссектрису. Возьмем, например, угол КАЕ нашей трапеции АКМЕ. Выполнив построение самостоятельно, вы легко убедитесь – биссектрисой отсекается от основания (или его продолжения на прямой за пределами самой фигуры) отрезок такой же длины, что и боковая сторона.
Свойства углов трапеции
- Какую бы из двух пар прилежащих к боковой стороне углов вы не выбрали, сумма углов в паре всегда составляет 180 0: α + β = 180 0 и γ + δ = 180 0 .
- Соединим середины оснований трапеции отрезком ТХ. Теперь посмотрим на углы при основаниях трапеции. Если сумма углов при любом из них составляет 90 0 , длину отрезка ТХ легко вычислить исходя из разности длин оснований, разделенной пополам: ТХ = (АЕ – КМ)/2 .
- Если через стороны угла трапеции провести параллельные прямые, те разделят стороны угла на пропорциональные отрезки.

Свойства равнобедренной (равнобокой) трапеции
- В равнобедренной трапеции равны углы при любом из оснований.
- Теперь снова постройте трапецию, чтобы проще было представить, о чем речь. Посмотрите внимательно на основание АЕ – вершина противоположного основания М проецируется в некую точку на прямой, которая содержит АЕ. Расстояние от вершины А до точки проекции вершины М и средняя линия равнобедренной трапеции – равны.
- Пару слов о свойстве диагоналей равнобедренной трапеции – их длины равны. А также одинаковы углы наклона этих диагоналей к основанию трапеции.
- Только около равнобедренной трапеции можно описать окружность, поскольку сумма противолежащих углов четырехугольника 180 0 – обязательное условие для этого.
- Из предыдущего пункта следует свойство равнобедренной трапеции – если возле трапеции можно описать окружность, она является равнобедренной.
- Из особенностей равнобедренной трапеции вытекает свойство высоты трапеции: если ее диагонали пересекаются под прямым углом, то длина высоты равна половине суммы оснований: h = (a + b)/2 .

- Снова проведите отрезок ТХ через середины оснований трапеции – в равнобедренной трапеции он является перпендикуляром к основаниям. И одновременно ТХ – ось симметрии равнобедренной трапеции.
- На этот раз опустите на большее основание (обозначим его a) высоту из противолежащей вершины трапеции. Получится два отрезка. Длину одного можно найти, если длины оснований сложить и разделить пополам: (a + b)/2 . Второй получим, когда из большего основания вычтем меньшее и полученную разность разделим на два: (a – b)/2 .
Свойства трапеции, вписанной в окружность
Раз уже речь зашла о вписанной в окружность трапеции, остановимся на этом вопросе подробней. В частности на том, где находится центр окружности по отношению к трапеции. Тут тоже рекомендуется не полениться взять карандаш в руки и начертить то, о чем пойдет речь ниже. Так и поймете быстрее, и запомните лучше.
- Расположение центра окружности определяется углом наклона диагонали трапеции к ее боковой стороне.
 Например, диагональ может выходить из вершины трапеции под прямым углом к боковой стороне. В таком случае большее основание пересекает центр описанной окружности точно посередине (R = ½АЕ).
Например, диагональ может выходить из вершины трапеции под прямым углом к боковой стороне. В таком случае большее основание пересекает центр описанной окружности точно посередине (R = ½АЕ). - Диагональ и боковая сторона могут встречаться и под острым углом – тогда центр окружности оказывается внутри трапеции.
- Центр описанной окружности может оказаться вне пределов трапеции, за большим ее основанием, если между диагональю трапеции и боковой стороной – тупой угол.
- Угол, образованный диагональю и большим основанием трапеции АКМЕ (вписанный угол) составляет половину того центрального угла, который ему соответствует:МАЕ = ½МОЕ .
- Коротко про два способа найти радиус описанной окружности. Способ первый: посмотрите внимательно на свой чертеж – что вы видите? Вы без труда заметите, что диагональ разбивает трапецию на два треугольника. Радиус можно найти через отношение стороны треугольника к синусу противолежащего угла, умноженному на два. Например, R = АЕ/2*sinАМЕ .
 Аналогичным образом формулу можно расписать для любой из сторон обоих треугольников.
Аналогичным образом формулу можно расписать для любой из сторон обоих треугольников. - Способ второй: находим радиус описанной окружности через площадь треугольника, образованного диагональю, боковой стороной и основанием трапеции: R = АМ*МЕ*АЕ/4*S АМЕ .
Свойства трапеции, описанной около окружности
Вписать окружность в трапецию можно, если соблюдается одно условие. Подробней о нем ниже. И вместе эта комбинация фигур имеет ряд интересных свойств.
- Если в трапецию вписана окружность, длину ее средней линии можно без труда найти, сложив длины боковых сторон и разделив полученную сумму пополам:
- У трапеции АКМЕ, описанной около окружности, сумма длин оснований равна сумме длин боковых сторон: АК + МЕ = КМ + АЕ .
- Из этого свойства оснований трапеции вытекает обратное утверждение: окружность можно вписать в ту трапецию, сумма оснований которой равна сумме боковых сторон.
- Точка касания окружности с радиусом r, вписанной в трапецию, разбивает боковую сторону на два отрезка, назовем их a и b.
 Радиус окружности можно вычислить по формуле: r = √ab .
Радиус окружности можно вычислить по формуле: r = √ab . - И еще одно свойство. Чтобы не запутаться, этот пример тоже начертите сами. У нас есть старая-добрая трапеция АКМЕ, описанная около окружности. В ней проведены диагонали, пересекающиеся в точке О. Образованные отрезками диагоналей и боковыми сторонами треугольники АОК и ЕОМ – прямоугольные.
Высоты этих треугольников, опущенные на гипотенузы (т.е. боковые стороны трапеции), совпадают с радиусами вписанной окружности. А высота трапеции – совпадает с диаметром вписанной окружности.
Свойства прямоугольной трапеции
Прямоугольной называют трапецию, один из углов которой является прямым. И ее свойства проистекают из этого обстоятельства.
- У прямоугольной трапеции одна из боковых сторон перпендикулярна основаниям.
- Высота и боковая сторона трапеции, прилежащая к прямому углу, равны. Это позволяет вычислять площадь прямоугольной трапеции (общая формула S = (a + b) * h/2 ) не только через высоту, но и через боковую сторону, прилежащую к прямому углу.

- Для прямоугольной трапеции актуальны уже описанные выше общие свойства диагоналей трапеции.
Доказательства некоторых свойств трапеции
Равенство углов при основании равнобедренной трапеции:
- Вы уже наверное и сами догадались, что тут нам снова потребуется трапеция АКМЕ – начертите равнобедренную трапецию. Проведите из вершины М прямую МТ, параллельную боковой стороне АК (МТ || АК).
Полученный четырехугольник АКМТ – параллелограмм (АК || МТ, КМ || АТ). Поскольку МЕ = КА = МТ, ∆ МТЕ – равнобедренный и МЕТ = МТЕ.
АК || МТ, следовательно МТЕ = КАЕ, МЕТ = МТЕ = КАЕ.
Откуда АКМ = 180 0 — МЕТ = 180 0 — КАЕ = КМЕ.
Что и требовалось доказать.
Теперь на основании свойства равнобедренной трапеции (равенства диагоналей) докажем, что трапеция АКМЕ является равнобедренной :
- Для начала проведем прямую МХ – МХ || КЕ. Получим параллелограмм КМХЕ (основание – МХ || КЕ и КМ || ЕХ).
∆АМХ – равнобедренный, поскольку АМ = КЕ = МХ, а МАХ = МЕА.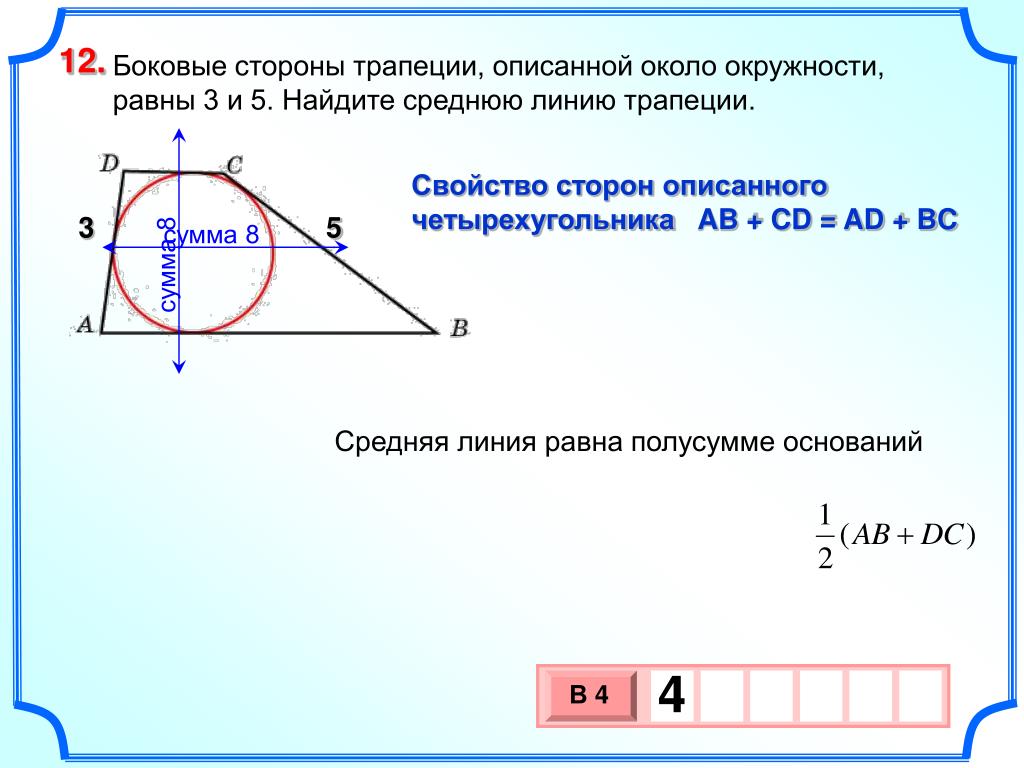
МХ || КЕ, КЕА = МХЕ, поэтому МАЕ = МХЕ.
У нас получилось, что треугольники АКЕ и ЕМА равны между собой, т.к АМ = КЕ и АЕ – общая сторона двух треугольников. А также МАЕ = МХЕ. Можем сделать вывод, что АК = МЕ, а отсюда следует и что трапеция АКМЕ – равнобедренная.
Задача для повторения
Основания трапеции АКМЕ равны 9 см и 21 см, боковая сторона КА, равная 8 см, образует угол 150 0 с меньшим основанием. Требуется найти площадь трапеции.
Решение: Из вершины К опустим высоту к большему основанию трапеции. И начнем рассматривать углы трапеции.
Углы АЕМ и КАН являются односторонними. А это значит, в сумме они дают 180 0 . Поэтому КАН = 30 0 (на основании свойства углов трапеции).
Рассмотрим теперь прямоугольный ∆АНК (полагаю, этот момент очевиден читателям без дополнительных доказательств). Из него найдем высоту трапеции КН – в треугольнике она является катетом, который лежит напротив угла в 30 0 . Поэтому КН = ½АВ = 4 см.
Площадь трапеции находим по формуле: S АКМЕ = (КМ + АЕ) * КН/2 = (9 + 21) * 4/2 = 60 см 2 .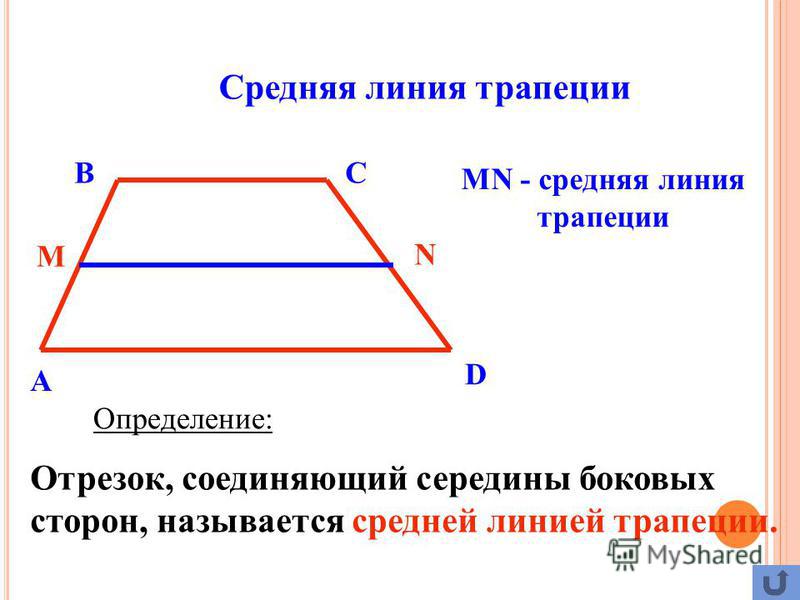
Послесловие
Если вы внимательно и вдумчиво изучили эту статью, не поленились с карандашом в руках начертить трапеции для всех приведенных свойств и разобрать их на практике, материал должен был неплохо вами усвоиться.
Конечно, информации тут много, разнообразной и местами даже запутанной: не так уж сложно перепутать свойства описанной трапеции со свойствами вписанной. Но вы сами убедились, что разница огромна.
Теперь у вас есть подробный конспект всех общих свойств трапеции. А также специфических свойств и признаков трапеций равнобедренной и прямоугольной. Им очень удобно пользоваться, чтобы готовиться к контрольным и экзаменам. Попробуйте сами и поделитесь ссылкой с друзьями!
blog.сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Как найти высоту трапеции
Оглавление
Время чтения: 3 минуты
1 457
Определения
Трапеция — это такой четырехугольник, у которого две стороны параллельны (они являются основаниями трапеции, указанные на рисунках a и b), а две другие — нет.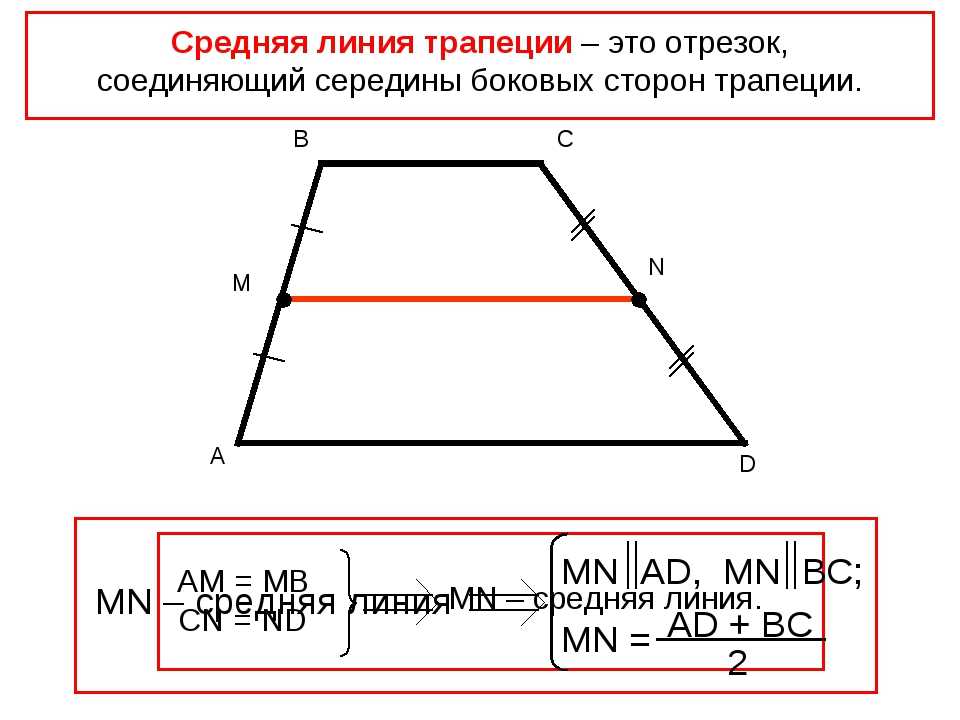
Высота трапеции — это такой отрезок h, который проведен перпендикулярно основаниям.
Нахождение высоты по площади и основаниям
Чтобы вычислить площадь S трапеции мы используем формулу:
\[S=\frac{((a+b) \times h)}{2}\]
Здесь h — высота трапеции, а сегменты a и b являются ее основаниями.
Можем найти h:
\[h=\frac{2 \times S}{(a+b)}\]
Пример 1
Площадь трапеции S составляет 50 см2, длина ее основания a = 4 см, длина второго основания b равна 6 см, то для нахождения высоты h мы используем формулу:
\[h=\frac{2 \times 50}{(4+6)}=10 \mathrm{~cm}\]
Ответ: 10 см.
Нахождение высоты, зная площадь и среднюю линию
Мы используем формулу, с помощью которой можно рассчитать площадь трапеции:
S = m × h,
Здесь h — это высота трапеции, m — ее средняя линия.
Можем найти h:
\[h=\frac{S}{m}\], будет ответом.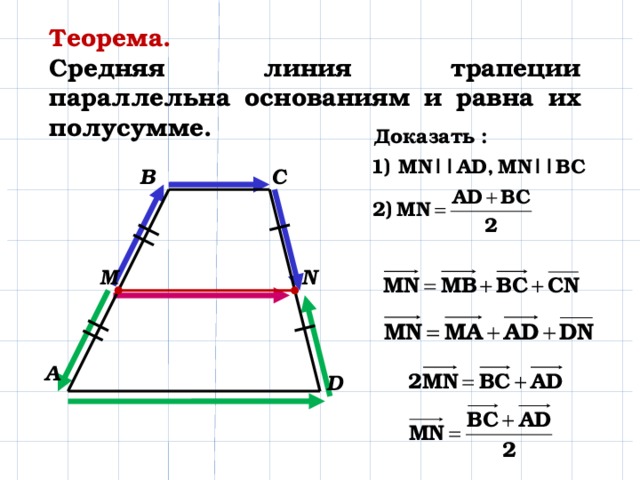
Пример 2
Средняя линия трапеции, обозначенная буквой m, равна 20 см, а площадь S, которая составляет 200 см2. Давайте найдем значение высоты трапеции h.
\[h=\frac{200}{20}=10 \mathrm{~cm}\]
Ответ: 10 см
Высота прямоугольной трапеции
Определение
Диагональ — это сегмент, соединяющий пару противоположных вершин трапеции. Когда трапеция прямоугольная, используя диагональ, мы находим высоту данной фигуры.
Трапецию, одна из боковых сторон которой перпендикулярна основаниям, называют прямоугольной трапецией.
Таким образом, рассмотрим подобную трапецию ABCD, где AD — высота, AC — диагональ, DC-основание. Мы используем теорему Пифагора, которая говорит, что в прямоугольном треугольнике ADC квадрат гипотенузы AC равен сумме квадратов его сторон — катетов AB и BC.
Тогда мы сможем написать:
AC² = AD² + DC².
AD — это катет треугольника, сторона трапеции и, одновременно, ее высота. {2}}=\sqrt{4}=2 см\]
{2}}=\sqrt{4}=2 см\]
Ответ: h=2 см.
Оценить статью (55 оценок):
Поделиться
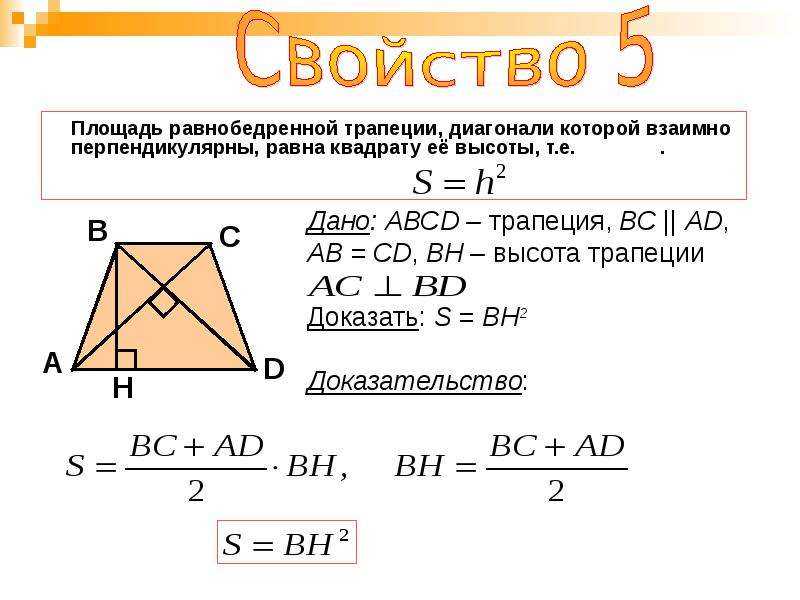
Длинное основание трапеции с учетом центральной медианы и калькулятора короткого основания
✖Центральная медиана трапеции — это длина линии, соединяющей середины обеих сторон или непараллельной пары противоположных сторон трапеции.ⓘ Центральная медиана трапеции [M] | AlnАнгстремArpentАстрономическая единица АттометрAU длиныЯчменное зерноМиллиард световых летБор РадиусКабель (международный)Кабель (Великобритания)Кабель (США)КалибрСантиметрЦепьКубит (греческий)Кубит (длинный)Кубит (Великобритания)ДекаметрЗемляДиметрЗемное Экваториальное расстояние от Луны RadiusElectron Radius (Classical)EllExameterFamnFathomFemtometerFermiFinger (Cloth)FingerbreadthFootFoot (US Survey)FurlongGigameterHandHandbreadthHectometerInchKenKilometerKiloparsecKiloyardLeagueLeague (Statute)Light YearLinkMegameterMegaparsecMeterMicroinchMicrometerMicronMilMileMile (Roman)Mile (US Survey)MillimeterMillion Light YearNail (Cloth)NanometerNautical Leag ue (int)Nautical League UKNautical Mile (International)Nautical Mile (UK)ParsecPetameterPicaPicometerPlanck LengthPointPoleQuarterReedReed (Long)RodRoman ActusRopeRussian ArchinSpan (ткань)Sun RadiusTerameterTwipVara CastellanaVara ConuqueraVara De TareaYardYardYardYottameterZeptometerZettameter | +10% -10% | |
✖Короткое основание трапеции — это более короткая сторона среди пары параллельных сторон трапеции. AlnAngstromArpentAstronomical UnitAttometerAU of LengthBarleycornBillion Light YearBohr RadiusCable (International)Cable (UK)Cable (US)CaliberCentimeterChainCubit (Greek)Cubit (Long)Cubit (UK)DecameterDecimeterEarth Distance from MoonEarth Distance from SunEarth Equatorial RadiusEarth Polar RadiusElectron Radius (Classical)EllExameterFamnFathomFemtometerFermiFinger ( Ткань)FingerbreadthFootFoot (US Survey)FurlongGigameterHandHandbreadthHectometerInchKilometerKiloparsekKiloyardLeagueLeague (Statute)Light YearLinkMegameterMegaparsecMeterMicroinchMicrometerMicronMilMileMile (Roman)Mile (US Survey)MillimeterMillion Light YearNail (Cloth)NanometerMileNauticalNautical League UK (int)Nauile le (Великобритания)ПарсекОкуньПетаметрПикаПикометрПланк ДлинаТочкаПолюсКварталТростник (Длинный)РодРоман АктусВеревкаРусский АрчинПротяженность (Ткань)Солнце РадиусТераметрТвипВара КастелланаВара КонукераВара Де ТареаЯрдЙоктометрЙоттаметрЗептометрЗеттаметр +10% -10% |
✖Длинное основание трапеции — это более длинная сторона среди пары параллельных сторон трапеции. | AlnAngstromArpentAstronomical UnitAttometerAU of LengthBarleycornBillion Light YearBohr RadiusCable (International)Cable (UK)Cable (US)CaliberCentimeterChainCubit (Greek)Cubit (Long)Cubit (UK)DecameterDecimeterEarth Distance from MoonEarth Distance from SunEarth Equatorial RadiusEarth Polar RadiusElectron Radius (Classical)EllExameterFamnFathomFemtometerFermiFinger (Cloth)FingerbreadthFootFoot (US Survey)FurlongGigameterHandHandbreadthHectometerInchKenKilometerKiloparsecKiloyardLeagueLeague (Statute)Light YearLinkMegameterMegaparsecMeterMicroinchMicrometerMicronMilMileMile (Roman)Mile (US Survey)MillimeterMillion Light YearNail (Cloth)NanometerNautical League (int)Nautical League UKNautical Mile (International)Nautical Mile (UK)ParsecPerchPetameterPicaPicometerPlanck LengthPointPoleQuarterReedReed (Long)RodRoman ActusRopeRussian ArchinSpan ( Ткань)Sun RadiusTerameterTwipVara CastellanaVara ConuqueraVara De TareaYardYoctometerYottameterZeptometerZettameter | ⎘ Копировать |
👎
Формула
Перезагрузить
👍
Длинное основание трапеции с учетом центральной медианы и решения с коротким основанием
ШАГ 0: Итоги предварительного расчета
ШАГ 1: Преобразование входных данных в базовые единицы
Центральная медиана трапеции: 10 метров —> 10 метров Преобразование не требуется
Короткое основание трапеции: 5 метров —> 5 Метр Преобразование не требуется
ШАГ 2: Вычисление формулы
ШАГ 3: Преобразование результата в единицу измерения
15 Метр —> Преобразование не требуется
< 6 Калькулятор длинного основания трапецииДлинное основание трапеции с учетом центральной медианы и формулы короткого основания
Длинное основание трапеции = (2 * центральная медиана трапеции) — короткое основание трапеции
B Длинный = (2*M)-B Короткий
Что такое Трапеция?
Трапеция – это четырехугольник с одной парой противоположных и параллельных сторон. Пару параллельных сторон называют основаниями трапеции, а пару непараллельных ребер — катетами трапеции. Из четырех углов трапеция обычно имеет 2 острых угла и 2 тупых угла, которые являются попарно дополнительными углами.
Пару параллельных сторон называют основаниями трапеции, а пару непараллельных ребер — катетами трапеции. Из четырех углов трапеция обычно имеет 2 острых угла и 2 тупых угла, которые являются попарно дополнительными углами.
Как рассчитать длинное основание трапеции, учитывая центральную медиану и короткое основание?
Длинное основание трапеции с учетом центральной медианы и короткого основания калькулятор использует длинное основание трапеции = (2 * центральная медиана трапеции)-короткое основание трапеции для расчета длинного основания трапеции, длинного основания трапеции с учетом центральной медианы и короткого основания формула определяется как более длинная сторона среди пары параллельных сторон трапеции и рассчитывается с использованием центральной медианы и короткого основания трапеции. Длинное основание трапеции обозначается цифрой 9.0105 B Длинный символ .
Как рассчитать длинное основание трапеции, зная центральную медиану и короткое основание, используя этот онлайн-калькулятор? Чтобы использовать этот онлайн-калькулятор для расчета длинного основания трапеции с учетом центральной медианы и короткого основания, введите центральную медиану трапеции (M) и короткое основание трапеции (B короткое ) и нажмите кнопку расчета.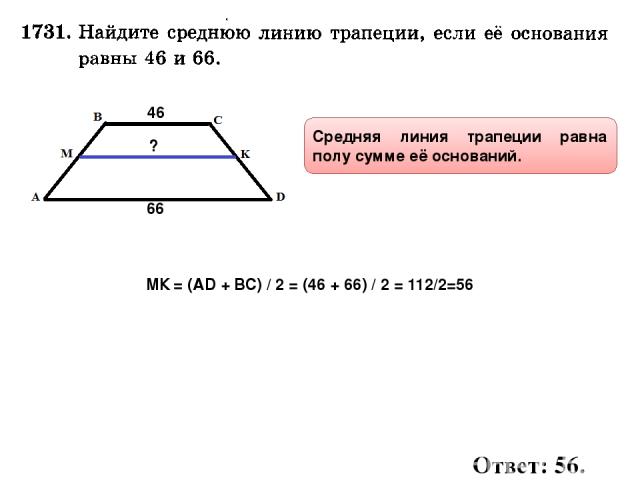 Вот как длинное основание трапеции с учетом расчета центральной медианы и короткого основания можно объяснить с заданными входными значениями -> 15 = (2*10)-5 .
Вот как длинное основание трапеции с учетом расчета центральной медианы и короткого основания можно объяснить с заданными входными значениями -> 15 = (2*10)-5 .
Часто задаваемые вопросы
Что такое длинное основание трапеции с учетом центральной медианы и короткого основания?
Длинное основание трапеции с учетом центральной медианы и короткого основания Формула определяется как более длинная сторона среди пары параллельных сторон трапеции и рассчитывается с использованием центральной медианы и короткого основания трапеции и представляется как B Long = (2*M)-B Короткий или Длинное основание трапеции = (2*центральная медиана трапеции)-короткое основание трапеции . Центральная медиана трапеции — это длина линии, соединяющей середины обеих сторон или непараллельной пары противоположных сторон трапеции, а короткое основание трапеции — это более короткая сторона среди пары параллельных сторон трапеции.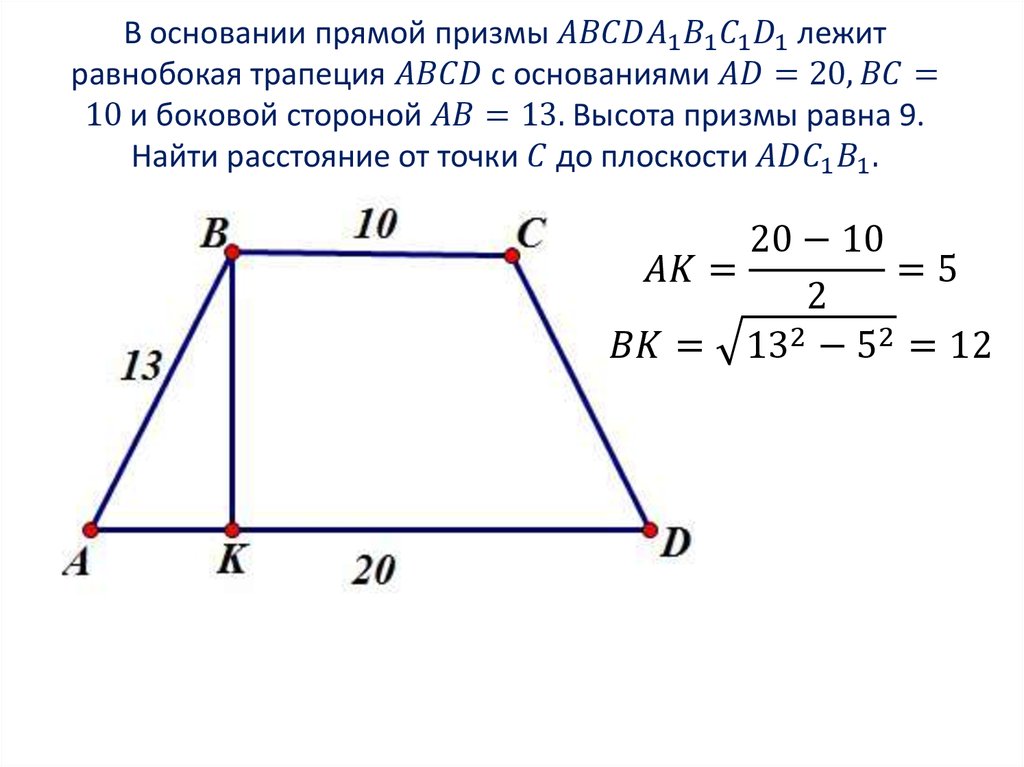
Как рассчитать длинное основание трапеции, зная центральную медиану и короткое основание?
Длинное основание трапеции с учетом центральной медианы и формулы короткого основания определяется как более длинная сторона среди пары параллельных сторон трапеции и рассчитывается с использованием центральной медианы, а короткое основание трапеции рассчитывается с использованием Длинное основание трапеции = (2*центральная медиана трапеции)-короткое основание трапеции . Чтобы рассчитать длинное основание трапеции с учетом центральной медианы и короткого основания, вам потребуется центральная медиана трапеции (M) и короткое основание трапеции (B короткое ) . С помощью нашего инструмента вам нужно ввести соответствующее значение для центральной медианы трапеции и короткого основания трапеции и нажать кнопку расчета. Вы также можете выбрать единицы измерения (если есть) для ввода (ов) и вывода.
Сколько существует способов вычисления длинного основания трапеции?
В этой формуле длинное основание трапеции использует центральную медиану трапеции и короткое основание трапеции. Мы можем использовать 5 других способов для вычисления того же самого, которые заключаются в следующем:
Мы можем использовать 5 других способов для вычисления того же самого, которые заключаются в следующем:
- длинное основание трапеции = (2 * (площадь трапеции / высота трапеции)) — короткое основание трапеции
- длинное Основание трапеции = короткое основание трапеции + (высота трапеции * (больший острый угол трапеции) + кроватка (меньший острый угол трапеции)))
- Длинное основание трапеции = короткое основание трапеции+(длинная сторона трапеции*((sin(меньший острый угол трапеции+больший острый угол трапеции))/(sin(больший острый угол трапеции))))
- Длинная Основание трапеции = Короткое основание трапеции+(Короткое плечо трапеции*((sin(Меньший острый угол трапеции+Большой острый угол трапеции))/(sin(Меньший острый угол трапеции))))
- Длинное основание трапеции = (((Длинная диагональ трапеции*Короткая диагональ трапеции)/Высота трапеции)*(sin(Угол катета между диагоналями трапеции)))-Короткое основание трапеции
Поделиться
Скопировано!
все формулы и примеры задач.
 Видео «Квадрат трапеции»
Видео «Квадрат трапеции»Задачи о трапециях не кажутся сложными на ряде фигур, изученных ранее. Прямоугольная трапеция рассматривается как частный случай. А при поиске его площади иногда удобнее разбить его на два уже привычных: прямоугольник и треугольник. Нужно просто немного подумать, и решение обязательно найдется.
Определение прямоугольной трапеции и ее свойства
У произвольной трапеции основания параллельны, а стороны могут иметь к ним произвольный угол. Если рассматривается прямоугольная трапеция, то одна из ее сторон всегда перпендикулярна основаниям. То есть два угла в нем будут равны 90 градусам. При этом они всегда принадлежат смежным вершинам или, другими словами, одной боковой стороне.
Остальные углы прямоугольной трапеции всегда острые и тупые. При этом их сумма всегда будет равна 180 градусам.
Каждая диагональ образует прямоугольный треугольник с меньшей боковой стороной. А высота, проведенная из вершины под тупым углом, делит фигуру на две части.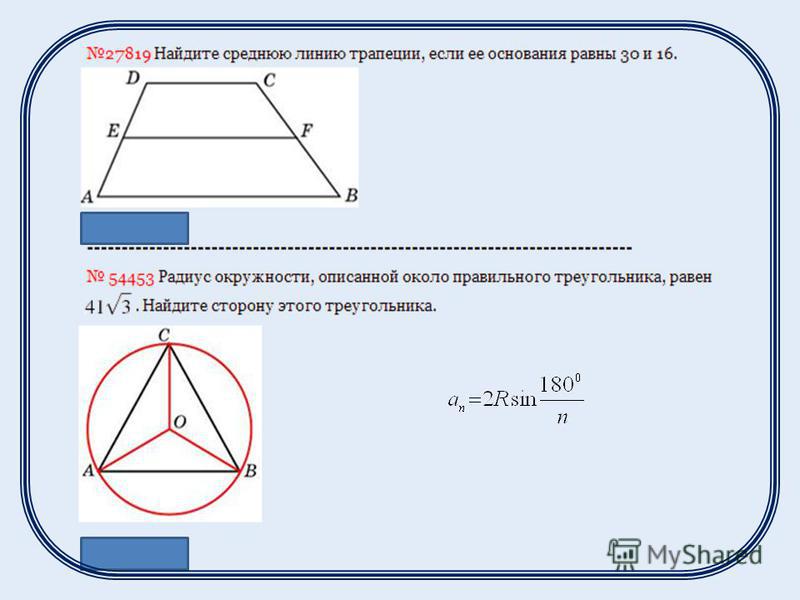 Один прямоугольник, а другой прямоугольный треугольник. Кстати, эта сторона всегда равна высоте трапеции.
Один прямоугольник, а другой прямоугольный треугольник. Кстати, эта сторона всегда равна высоте трапеции.
Какие обозначения используются в представленных формулах?
Все величины, используемые в разных выражениях, описывающих трапецию, удобно сразу указать и представить в виде таблицы:
Формулы, описывающие элементы прямоугольной трапеции
Простейшая из них связывает высоту и меньшую сторону:
Еще несколько формул для этой стороны прямоугольной трапеции:
c = d*sinα;
c = (a — b) * tan α;
с = √ (d 2 — (а — б) 2).
Первый следует из прямоугольного треугольника. И он говорит, что катет к гипотенузе дает синус противоположного угла.
В том же треугольнике второй катет равен разности двух оснований. Следовательно, верно утверждение, приравнивающее тангенс угла к отношению катетов.
Из того же треугольника можно вывести формулу, основанную на знании теоремы Пифагора.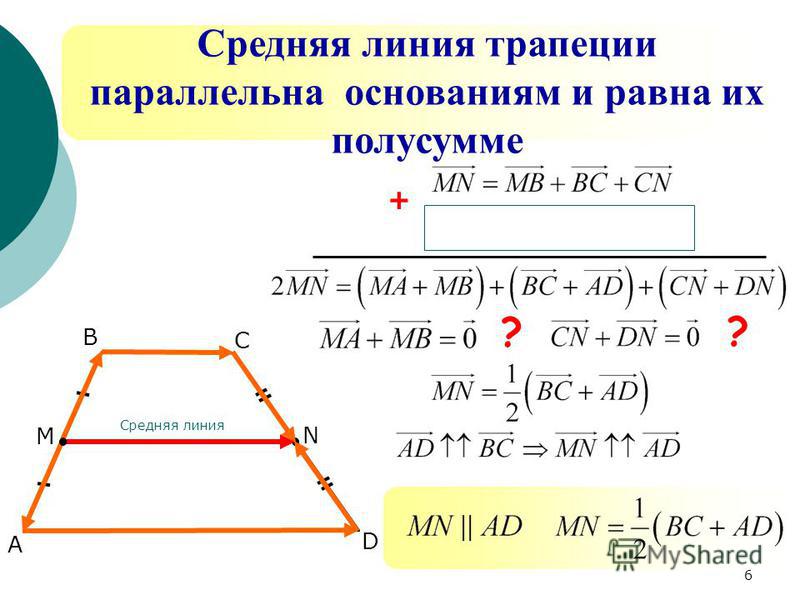 Это третье записанное выражение.
Это третье записанное выражение.
Вы можете написать формулы для другой стороны. Их тоже три:
d = (a — b) /cosα;
д = с/sinα;
d = √ (c 2 + (a — b) 2).
Первые два снова получены из пропорций того же прямоугольного треугольника, а второй выведен из теоремы Пифагора.
По какой формуле можно вычислить площадь?
Тот, что дан для произвольной трапеции. Только учтите, что высота – это сторона, перпендикулярная основаниям.
S = (a + b) * h/2.
Эти значения не всегда указываются явно. Поэтому для вычисления площади прямоугольной трапеции потребуется произвести некоторые математические расчеты.
Что делать, если вам нужно вычислить диагонали?
В этом случае нужно следить, чтобы они образовывали два прямоугольных треугольника. Так что всегда можно воспользоваться теоремой Пифагора. Тогда первая диагональ будет выражена так:
d1 = √ (c 2 + b 2)
или по-другому, заменив «c» на «h»:
d1 = √ (h 2 + Би 2).
Аналогично получаются формулы для второй диагонали:
d2 = √ (c 2 + b 2) или d 2 = √(ч 2 + а 2).
Задача №1
Условие . Площадь прямоугольной трапеции известна и равна 120 дм 2 . Его высота имеет длину 8 дм. Необходимо вычислить все стороны трапеции. Дополнительным условием является то, что одно основание меньше другого на 6 дм.
Раствор. Так как дана прямоугольная трапеция, у которой известна высота, то сразу можно сказать, что одна из сторон равна 8 дм, то есть меньшая сторона.
Теперь можно посчитать еще: d = √ (c 2 + (a — b) 2). А тут сразу дана и сторона с, и разность оснований. Последняя равна 6 дм, это известно из условия. Тогда d будет равно квадратному корню из (64 + 36), то есть из 100. Таким образом, находится еще одна сторона, равная 10 дм.
Сумму оснований можно найти по формуле площади. Она будет равна удвоенной площади, деленной на высоту. Если посчитать, то получается 240/8. Значит, сумма оснований равна 30 дм. С другой стороны, их разница составляет 6 дм. Комбинируя эти уравнения, вы можете вычислить оба основания:
Значит, сумма оснований равна 30 дм. С другой стороны, их разница составляет 6 дм. Комбинируя эти уравнения, вы можете вычислить оба основания:
a + b = 30 и a — b = 6.
Вы можете выразить a как (b + 6), подставив его в первое уравнение. Тогда получается, что 2b будет равно 24. Следовательно, просто b будет 12 дм.
Тогда последняя сторона а равна 18 дм.
Ответ. Стороны прямоугольной трапеции: а = 18 дм, b = 12 дм, с = 8 дм, d = 10 дм.
Задача №2
Условие. Дана прямоугольная трапеция. Его длинная сторона равна сумме оснований. Его высота имеет длину 12 см. Строится прямоугольник, стороны которого равны основаниям трапеции. Вам нужно вычислить площадь этого прямоугольника.
Раствор. Вам нужно начать с того, что вы ищете. Требуемая площадь определяется как произведение a и b. Обе эти величины неизвестны.
Вам нужно будет использовать дополнительные равенства. Один из них основан на утверждении из условия: d = a + b.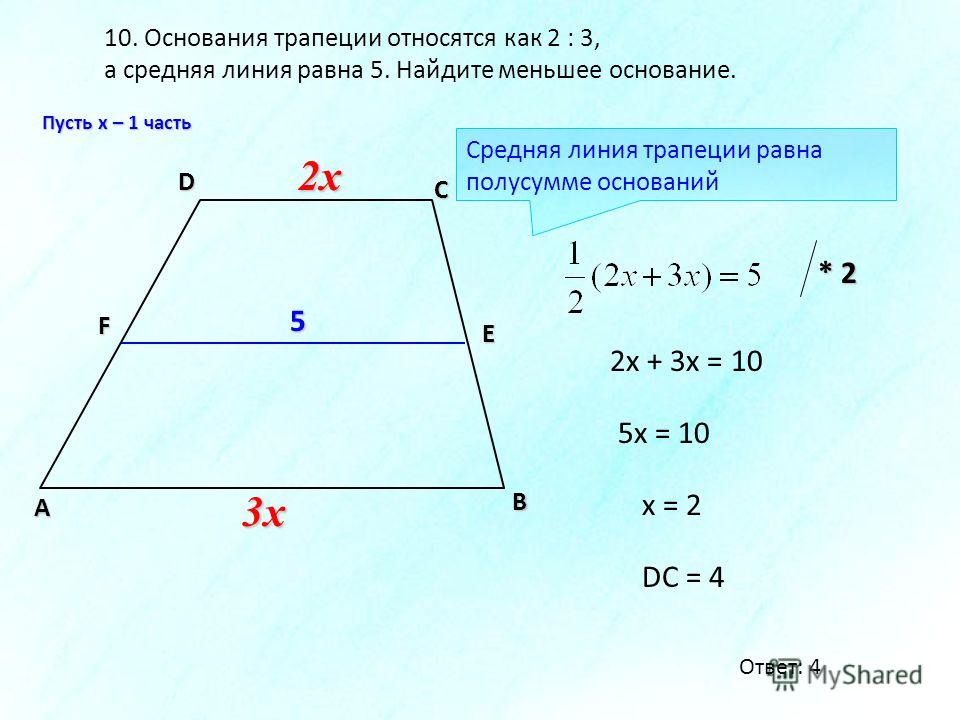 Для этой стороны необходимо использовать третью формулу, приведенную выше. Получается: d 2 = c 2 + (a — b) 2 или (a + b) 2 = c 2 + (a — b) 2.
Для этой стороны необходимо использовать третью формулу, приведенную выше. Получается: d 2 = c 2 + (a — b) 2 или (a + b) 2 = c 2 + (a — b) 2.
Необходимо произвести преобразования подстановкой вместо с его значение из условия — 12. После раскрытия скобок и приведения подобных слагаемых получается, что 144 = 4 аб.
В начале решения было сказано, что a * b дает нужную площадь. Поэтому в последнем выражении можно заменить это произведение на S. Простой расчет даст значение площади. S = 36 см 2 .
Ответ. Требуемая площадь 36 см 2 .
Задание №3
Условие. Площадь прямоугольной трапеции равна 150√3 см². Острый угол равен 60 градусов. То же значение имеет угол между малым основанием и меньшей диагональю. Вам нужно рассчитать меньшую диагональ.
Раствор. Из свойства углов трапеции получается, что ее тупой угол равен 120º. Потом диагональ делит его на равные части, потому что одна его часть уже 60 градусов. Тогда угол между этой диагональю и вторым основанием также равен 60 градусов.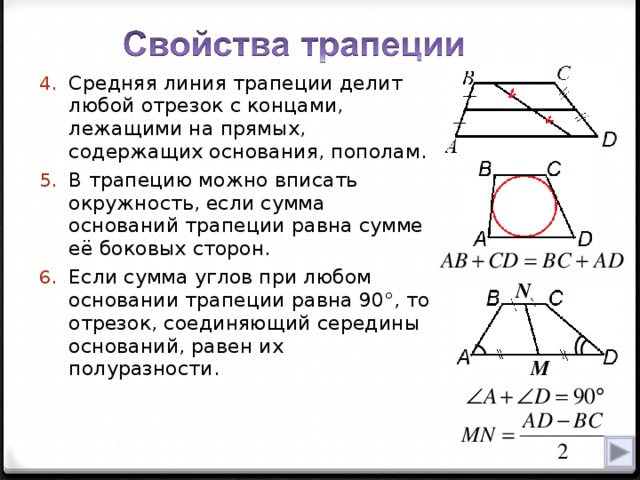 То есть треугольник, образованный большим основанием, наклонной стороной и меньшей диагональю, равносторонний. Таким образом, искомая диагональ будет равна а, как и боковая сторона d = а.
То есть треугольник, образованный большим основанием, наклонной стороной и меньшей диагональю, равносторонний. Таким образом, искомая диагональ будет равна а, как и боковая сторона d = а.
Теперь нам нужно рассмотреть прямоугольный треугольник. Третий угол равен 30 градусов. Следовательно, катет, противолежащий ему, равен половине гипотенузы. То есть меньшее основание трапеции равно половине искомой диагонали: b = a/2. От нее нужно найти высоту, равную стороне, перпендикулярной основаниям. Сторона с этой ногой. Из теоремы Пифагора:
с = (а/2) * √3.
Теперь осталось только подставить все величины в формулу площади:
150√3 = (a + a/2) * (a/2 * √3) / 2.
Решение этого уравнения дает корень 20
Ответ. Меньшая диагональ имеет длину 20 см.
Добрый день дорогие друзья! Сегодня у нас тема — решение задачи о трапеции по геометрии. Прежде чем приступить к разбору заданий, давайте вспомним, что такое трапеция и какие у нее элементы.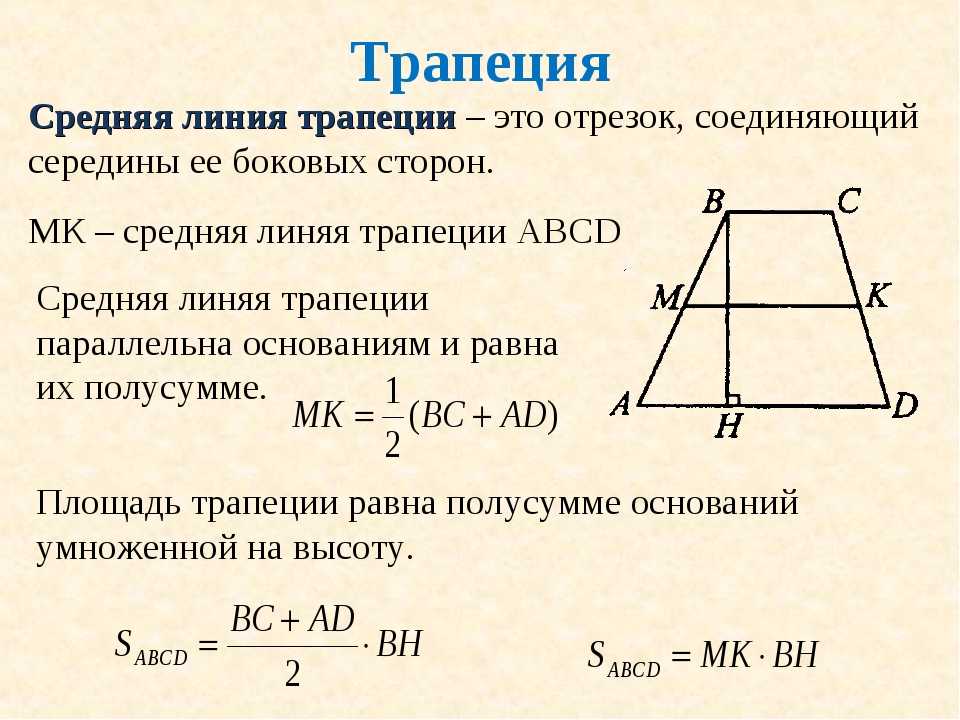
Трапеция – это выпуклый четырехугольник, у которого две стороны параллельны, а две другие не параллельны.
Параллельные стороны называются основаниями, а непараллельные стороны называются сторонами.
Трапеции прямоугольные, равнобедренные и простые.
Прямоугольные трапеции имеют 2 прямых угла.
В равнобедренных трапециях, как и в равнобедренных треугольниках, углы при основании равны, равны и стороны.
Трапеция имеет среднюю линию, соединяющую середины сторон.
А теперь задачи.
Острый угол равнобедренной трапеции равен 60°. Докажите, что основание BC = AD — AB.
Доказательство. Опустим высоты BM и CN из вершин трапеции на нижнее основание AD.
Получаем два прямоугольных треугольника ABM и DCN, а также прямоугольник BCNM.
Так как в прямоугольных треугольниках один угол равен 60°, то другой по следствию теоремы о сумме внутренних углов треугольника равен 30°.
А мы знаем, что катет против угла 30° равен половине гипотенузы.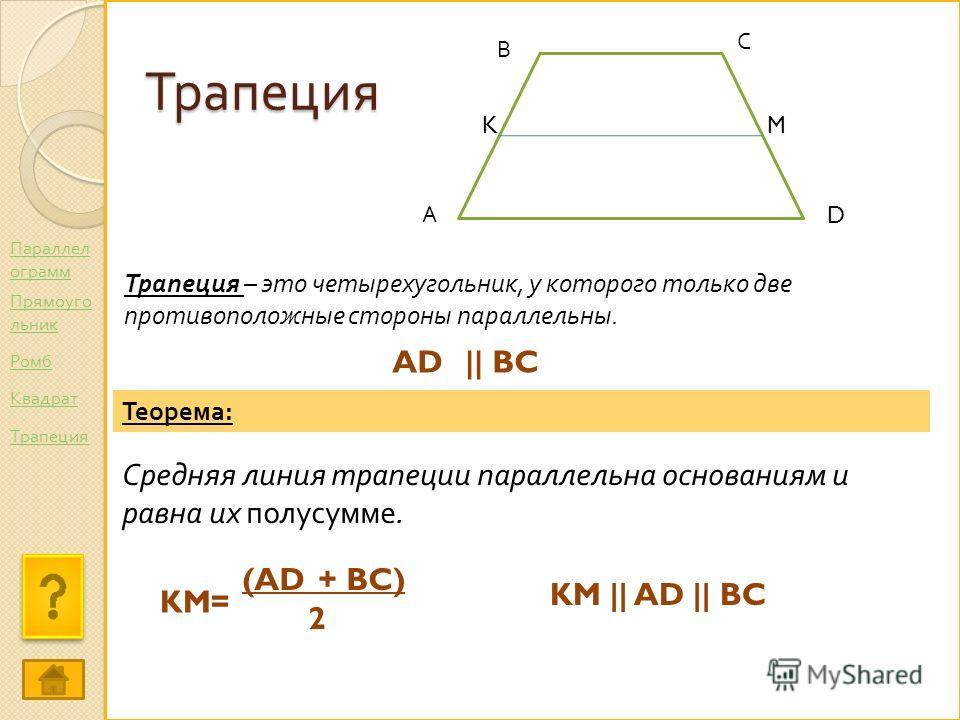 Те. АМ=с/2.
Те. АМ=с/2.
То же самое и в прямоугольном треугольнике — ND = c/2.
Получается, что нижнее основание можно представить в виде суммы трех отрезков, а именно AM, MN, ND, где AM=ND=c/2.
MN=BC или верхнее основание.
Отсюда можно написать MN=BC=AD — AM — ND = AD — c/2 — c/2 = AD — AB.
Мы доказали, что верхнее основание равно разнице между нижним основанием и стороной.
Основания трапеции равны AD и BC. Найдите длину отрезка КР, соединяющего середины диагоналей трапеции.
Решение: По теореме Фалеса отрезок KP принадлежит большему отрезку MN, являющемуся средней линией трапеции.
Срединная линия трапеции, как известно, равна половине суммы оснований трапеции, или (AD+BC)/2.
В то же время, рассматривая треугольник ACD и его среднюю линию KN, мы можем понять, что KN=AD/2.
Рассматривая другой треугольник BCD и его среднюю линию PN, можно увидеть, что PN=BC/2.
Следовательно, KP=KN-PN = AD/2 — BC/2 = (AD-BC)/2.
Мы доказали, что отрезок, соединяющий середины диагоналей трапеции, равен полуразности оснований этой трапеции.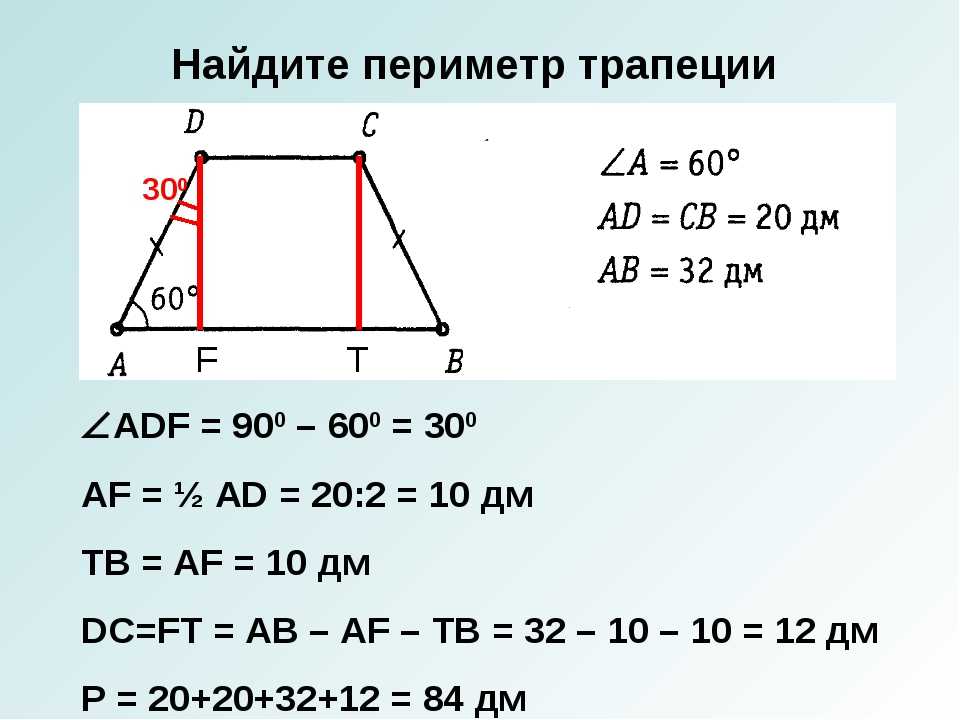
Задача 3. Найдите меньшее основание ВС равнобедренной трапеции, если высота СК, проведенная от конца С меньшего основания, делит большее основание на отрезки АК и КD, разница которых составляет 8 см.
Решение: Сделаем дополнительную конструкцию. Нарисуем высоту ВМ.
Рассмотрим треугольники ABM и DCK. Они равны по гипотенузе и катету — AB=CD, как стороны равнобедренной трапеции.
Высоты трапеций BM и CK слишком равны, так как они являются перпендикулярами между двумя параллельными прямыми.
Следовательно, AM=KD. Получается, что разница между АК и КД равна разнице между АК и АМ.
А это сегмент МК. Но MK равно BC, потому что BCKM — прямоугольник.
Отсюда меньшее основание трапеции равно 8 см.
Задача 4. Найдите отношение оснований трапеции, если ее средняя линия разделена диагоналями на 3 равные части.
Решение: Так как MN — средняя линия трапеции, то она параллельна основаниям и делит стороны пополам.
По теореме Фалеса MN также делит пополам стороны AC и BD.
Рассматривая треугольник ABC, можно увидеть, что МО в нем является срединной линией. НО средняя линия треугольника параллельна основанию и равна его половине. Те. если МО=Х, то ВС=2Х.
Из треугольника ACD имеем ON — среднюю линию.
Он также параллелен основанию и равен его половине.
Но так как OP+PN=X+X=2X, то AD=4X.
Получается, что верхнее основание трапеции 2Х, а нижнее 4Х.
Ответ: Соотношение оснований трапеции равно 1:2.
В этой статье для вас сделана очередная подборка заданий с трапецией. Условия так или иначе связаны с его средней линией. Типы задач взяты из открытого банка типовых задач. При желании вы можете освежить свои теоретические знания. В блоге уже освещались задачи, условия которых связаны с , а также . Кратко о средней линии:
Средняя линия трапеции соединяет середины сторон. Он параллелен основаниям и равен их полусумме.
Прежде чем решать задачи, рассмотрим теоретический пример.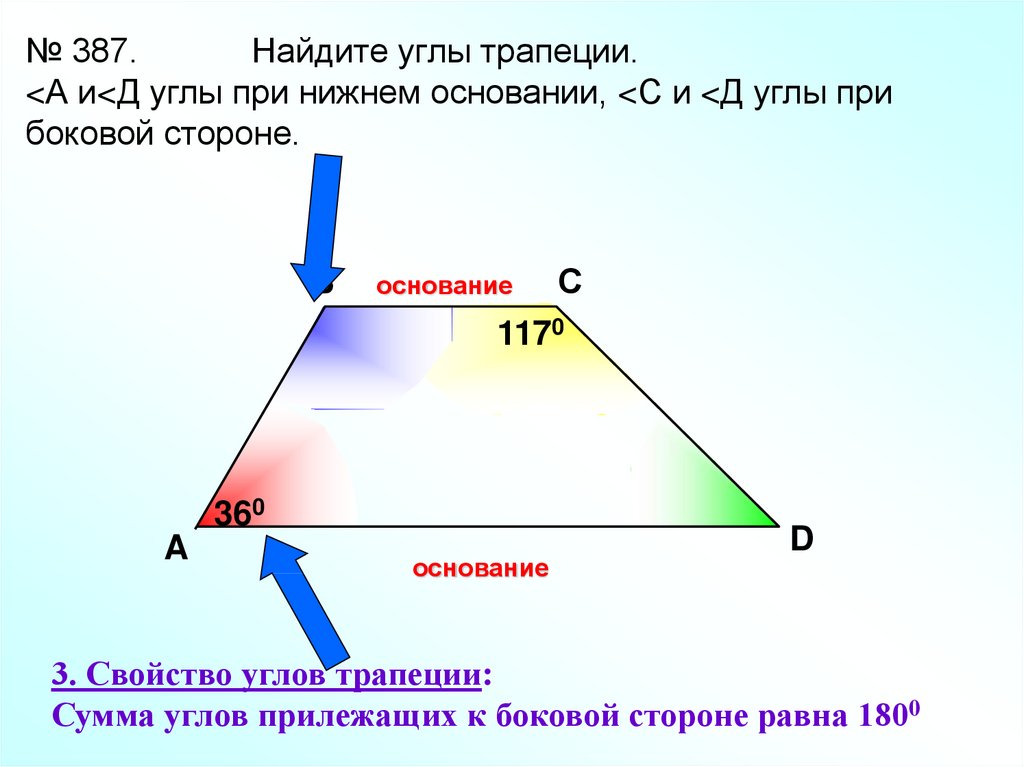
Дана трапеция ABCD. Диагональ AC, пересекающаяся со средней линией, образует точку K, диагональ BD образует точку L. Докажите, что отрезок KL равен половине разности оснований.
Прежде всего отметим тот факт, что средняя линия трапеции делит пополам любой отрезок, концы которого лежат на ее основаниях. Этот вывод напрашивается сам собой. Представьте себе отрезок, соединяющий две точки оснований, он разделит эту трапецию на две другие. Получается, что отрезок, параллельный основаниям трапеции и проходящий через середину стороны другой стороны, пройдет через ее середину.
Основан также на теореме Фалеса:
Если на одной из двух прямых отложить последовательно несколько равных отрезков и провести через их концы параллельные линии, пересекающие вторую прямую, то они будут отсекать равные отрезки на второй прямой.
То есть в данном случае К — середина АС, а L — середина BD. Следовательно, EK — средняя линия треугольника ABC, LF — средняя линия треугольника DCB. По свойству средней линии треугольника:
По свойству средней линии треугольника:
Теперь мы можем выразить отрезок KL в терминах оснований:
Доказано!
Этот пример приведен не просто так. В задачах для самостоятельного решения есть именно такая задача. Только не сказано, что отрезок, соединяющий середины диагоналей, лежит на средней линии. Рассмотрим задачи:
27819. Найдите среднюю линию трапеции, если ее основания 30 и 16.
Рассчитаем по формуле:
27820. Средняя линия трапеции равна 28, а меньшее основание равно 28. равно 18. Найдите большее основание трапеции.
Выразим большее основание:
Таким образом:
27836. Перпендикуляр, опущенный из вершины тупого угла на большее основание равнобедренной трапеции, делит ее на части, имеющие длины 10 и 4. Найти средней линии этой трапеции.
Чтобы найти среднюю линию, нужно знать основания. Основание АВ найти легко: 10+4=14. Найдите ДК.
Построим второй перпендикуляр DF:
Сегменты AF, FE и EB будут равны 4, 6 и 4 соответственно. Почему?
Почему?
В равнобедренной трапеции перпендикуляры, опущенные на большее основание, делят ее на три сегмента. Две из них, являющиеся катетами отсеченных прямоугольных треугольников, равны друг другу. Третий отрезок равен меньшему основанию, так как при построении указанных высот образуется прямоугольник, а у прямоугольника противоположные стороны равны. В этой задаче:
Таким образом, DC=6. Рассчитаем:
27839. Основания трапеции относятся как 2:3, а средняя линия равна 5. Найдите меньшее основание.
Введем коэффициент пропорциональности x. Тогда AB=3x, DC=2x. Мы можем написать:
Следовательно, меньшее основание равно 2∙2=4.
27840. Периметр равнобедренной трапеции равен 80, ее средняя линия равна боковой стороне. Найдите сторону трапеции.
Исходя из условия можно написать:
Если обозначить среднюю линию через x, то получим:
Второе уравнение уже можно записать так:
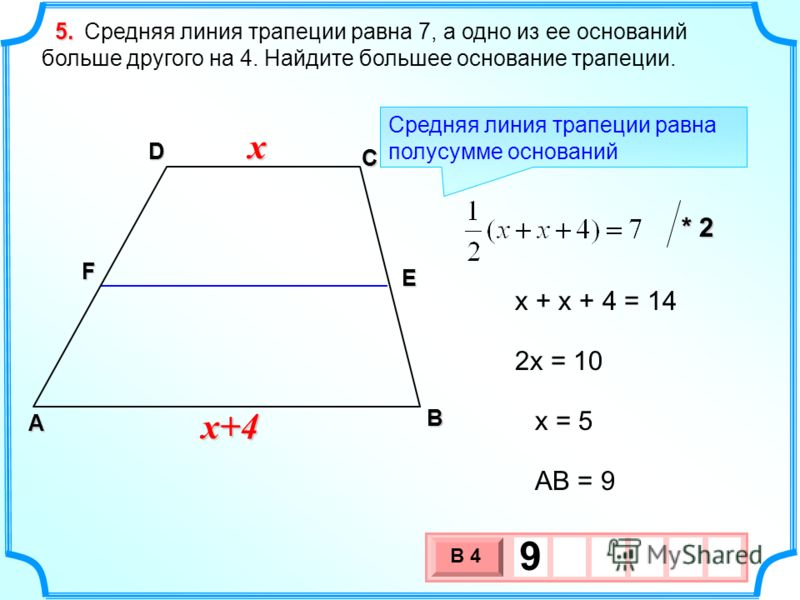
27841.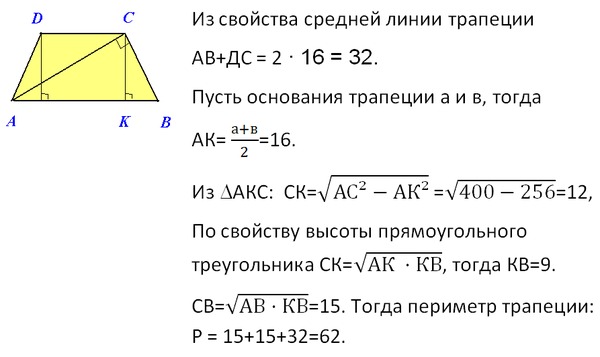 Средняя линия трапеции равна 7, а одно из ее оснований на 4 больше, чем другой. Найдите большее основание трапеции.
Средняя линия трапеции равна 7, а одно из ее оснований на 4 больше, чем другой. Найдите большее основание трапеции.
Обозначим меньшее основание (DC) за x, тогда большее (AB) будет равно x + 4. Запишем
Получили, что меньшее основание раньше пяти, а значит, что большая равна 9.
27842. Средняя линия трапеции равна 12. Одна из диагоналей делит ее на два отрезка, разница которых равна 2. Найдите большее основание трапеции.
Мы можем легко найти большее основание трапеции, если вычислим отрезок EO. Это средняя линия в треугольнике ADB, а AB=2∙EO.
Что у нас есть? Говорят, что средняя линия равна 12, а разница между отрезками EO и OF равна 2. Мы можем написать два уравнения и решить систему:
Понятно, что в данном случае можно без вычислений выбрать пару чисел, это 5 и 7. Но, тем не менее, решим систему:
Значит EO=12–5 =7. Таким образом, большее основание равно AB=2∙EO=14.
27844.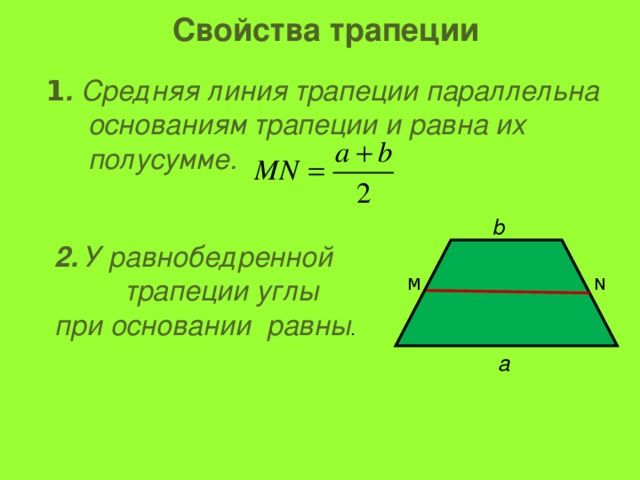 В равнобедренной трапеции диагонали перпендикулярны. Высота трапеции равна 12. Найдите ее среднюю линию.
В равнобедренной трапеции диагонали перпендикулярны. Высота трапеции равна 12. Найдите ее среднюю линию.
Сразу отметим, что высота, проведенная через точку пересечения диагоналей в равнобедренной трапеции, лежит на оси симметрии и делит трапецию на две равные прямоугольные трапеции, то есть основания этой высоты делятся на половина.
Казалось бы, чтобы вычислить среднюю линию, надо найти основания. Тут возникает небольшой тупик… Как, зная высоту, в таком случае вычислить основания? И ни как! Таких трапеций с фиксированной высотой и диагоналями, пересекающимися под углом 90 градусов, можно построить много. Как быть?
Посмотрите на формулу средней линии трапеции. Ведь нам не нужно знать сами основания, достаточно знать их сумму (или полусумму). Это мы можем сделать.
Поскольку диагонали пересекаются под прямым углом, образуются равнобедренные прямоугольные треугольники с высотой EF:
Из сказанного выше следует, что FO=DF=FC, а OE=AE=EB. Теперь запишем, чему равна высота, выраженная через отрезки DF и AE:
Теперь запишем, чему равна высота, выраженная через отрезки DF и AE:
Значит, средняя линия равна 12.
* В общем, это задача, как вы понимаете, для устного счета. Но я уверен, что подробное объяснение необходимо. И так… Если посмотреть на рисунок (при условии соблюдения угла между диагоналями при построении), сразу бросается в глаза равенство FO=DF=FC, и OE=AE=EB.
В составе прототипов также есть виды заданий с трапециями. Он построен на листе в ячейке и требуется найти среднюю линию, сторона клетки обычно равна 1, но может быть и другое значение.
27848. Найдите среднюю линию трапеции ABCD , если стороны квадратных клеток равны 1.
Все просто, посчитаем основания по ячейкам и воспользуемся формулой: (2+4)/2=3
Если базы строятся под углом к ячейке сетки, то есть два пути. Например!
Всем выпускникам, готовящимся к сдаче ЕГЭ по математике, будет полезно освежить в памяти тему «Произвольная трапеция».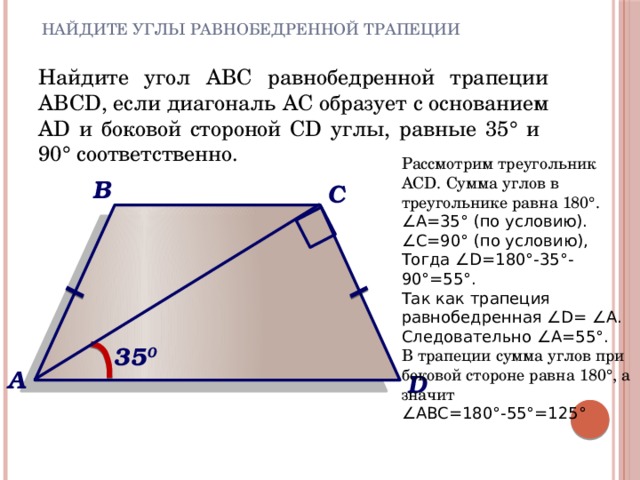 Как показывает многолетняя практика, контурные задания из этого раздела вызывают у многих старшеклассников определенные трудности. При этом требуется решить задания ЕГЭ по теме «Произвольная трапеция» при сдаче как базового, так и профильного уровня аттестационного испытания. Поэтому все выпускники должны уметь справляться с такими упражнениями.
Как показывает многолетняя практика, контурные задания из этого раздела вызывают у многих старшеклассников определенные трудности. При этом требуется решить задания ЕГЭ по теме «Произвольная трапеция» при сдаче как базового, так и профильного уровня аттестационного испытания. Поэтому все выпускники должны уметь справляться с такими упражнениями.
Как подготовиться к экзамену?
Большинство планиметрических задач решаются классическими построениями. Если в задании ЕГЭ требуется найти, например, площадь трапеции, изображенной на рисунке, стоит отметить на чертеже все известные параметры. После этого вспомните основные теоремы, связанные с ними. Применив их, вы сможете найти правильный ответ.
Чтобы подготовка к ЕГЭ была действительно эффективной, обращайтесь на образовательный портал Школково. Здесь вы найдете весь базовый материал по теме «Произвольная трапеция или которая поможет вам успешно сдать экзамен. Основные свойства рисунка, формулы и теоремы собраны в разделе «Теоретический справочник».

 Поэтому для нахождения высоты фигуры воспользуйтесь формулой для определения данной величины в случае, когда известны стороны трапеции.
Поэтому для нахождения высоты фигуры воспользуйтесь формулой для определения данной величины в случае, когда известны стороны трапеции. Одно из свойств диагоналей трапеции заключается в том, что отрезок ХТ лежит на средней линии. А его длину можно получив, разделив разность оснований на два: ХТ = (a – b)/2 .
Одно из свойств диагоналей трапеции заключается в том, что отрезок ХТ лежит на средней линии. А его длину можно получив, разделив разность оснований на два: ХТ = (a – b)/2 .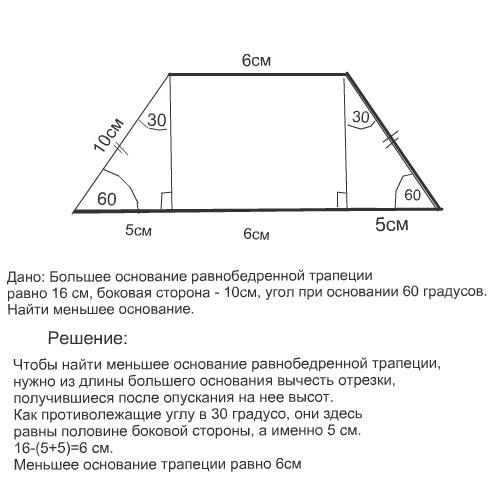



 Например, диагональ может выходить из вершины трапеции под прямым углом к боковой стороне. В таком случае большее основание пересекает центр описанной окружности точно посередине (R = ½АЕ).
Например, диагональ может выходить из вершины трапеции под прямым углом к боковой стороне. В таком случае большее основание пересекает центр описанной окружности точно посередине (R = ½АЕ). Аналогичным образом формулу можно расписать для любой из сторон обоих треугольников.
Аналогичным образом формулу можно расписать для любой из сторон обоих треугольников. Радиус окружности можно вычислить по формуле: r = √ab .
Радиус окружности можно вычислить по формуле: r = √ab .
 ⓘ Короткое основание трапеции [B ]
ⓘ Короткое основание трапеции [B ] ⓘ Длинное основание трапеции с учетом центральной медианы и короткого основания [B Long ]
ⓘ Длинное основание трапеции с учетом центральной медианы и короткого основания [B Long ]