Деление окружности на любое количество равных частей
Деление окружности на любое количество равных частей
Окружность является одним из основных элементов изонити и на ней нужно разметить большое количество точек проколов. Как это сделать? Об этом сегодняшний пост.
Для деления окружности на любое количество равных частей можно воспользоваться коэффициентами (см. таблицу 1.). Зная на какое число n следует разделить окружность, находят коэффициент k. При умножении коэффициента k на диаметр D этой окружности, получают длину хорды, которую циркулем откладывают на заданной окружности n раз.
n | k | n | k |
| 3 | 0,86603 | 20 | 0,15643 |
| 4 | 0,70711 | 21 | 0,14904 |
| 5 | 0,58779 | 22 | 0,14231 |
| 6 | 0,5 | 23 | 0,13617 |
| 7 | 0,43388 | 24 | 0,13053 |
| 8 | 0,38268 | 25 | 0,12533 |
| 9 | 0,34202 | 26 | 0,12054 |
| 10 | 0,30902 | 27 | 0,11609 |
| 11 | 0,28173 | 28 | 0,11196 |
| 12 | 0,25782 | 29 | 0,10812 |
| 13 | 0,23932 | 30 | 0,10453 |
| 14 | 0,22252 | 31 | 0,10117 |
| 15 | 0,20791 | 32 | 0,09802 |
| 16 | 0,19509 | 33 | 0,09506 |
| 17 | 0,18375 | 34 | 0,09227 |
| 18 | 0,17365 | 35 | 0,08964 |
| 19 | 0,16459 | 36 | 0,08716 |
Если требуется большее количество, то коэффициент можно рассчитать самостоятельно.
Для этого делим 360 на нужное количество частей и берем синус этого числа. Полученный результат делим на два — это и есть наш коэффициент.
Понятно, что все вышеописанное применимо только к правильной, “круглой” окружности, а не к любому замкнутому контуру, который также прошивается по правилу заполнения окружности. И только если нужно получить на контуре окружности равные отрезки. Иначе все придется делать вручную, без применения математики и прочих геометрических построений.
Популярные сообщения из этого блога
Перепись населения — Опрос
В декабре, через пару недель, блогу исполняется год. Страшно подумать – уже целый год! Когда я начинал писать в блог, у меня в запасе хорошо если набралось десяток тем будущих постов, а написанных постов в черновиках не было и вовсе, что, с точки зрения серъезного блоггинга, никуда не годилось.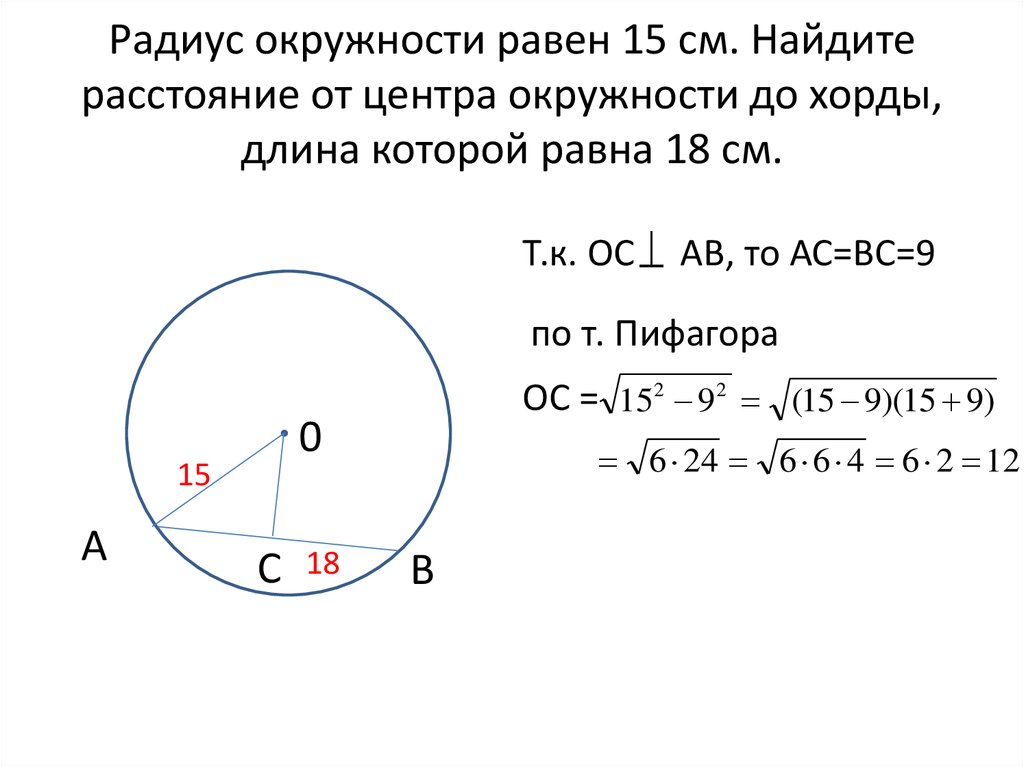
Получилось, я действовал по принципу – Сначала ввяжемся, а потом посмотрим. И вот что получилось. На сегодняшний день моя читательская аудитория представлена 58 странами. Но мне очень хотелось бы узнать больше о том, кто приходит ко мне в блог и с какой целью, как используюся материалы блога. Это очень важно, чтобы я мог оценить полезность наполнения страниц и в будущем году, на новом витке развития, учесть пожелания уважаемой аудитории (во загнулJ). Я разработал опросник, состоящий из 10 вопросов с мульти-выбором, т.е. нужно выбрать один из предлагаемых ответов. Если есть что-то, что Вам хотелось бы высказать, но это не вошло в список вопросов, пишите мне на e-mail или в комментриях к этому
Далее…
Материалы для работы в технике “изонить”. Часть 2: Нитки
В предыдущем посте мы рассматривали что можно использовать как фон для картинки, вышитой изонитью. Сегодня рассмотрим какие нитки лучше брать. Правильно подобранные нитки являются основой восприятия картины.
Вышивать можно любыми не очень толстыми нитками. Работы выглядят лучше, если вышиты блестящими нитками, а не матовыми. Лучше вышивать кручеными нитями, чем в несколько рассыпающихся нитей. Например, сердцевина ромашки (смотри ниже) вышита металлизированной нитью. В исходной нити было 9 ниточек, Я вышивал, беря по 3. Оказалось очень неудобно. Наиболее часто используется мулине, поскольку с ним работать наиболее легко. Хорошие нити мулине должны обладать блеском и иметь равномерную прокраску. Обычно мулине поступает в продажу пасмами, состоящими из 6 ниточек. Если ниточки разделить, то каждая из них должна быть ровной по толщине и не должна лохматиться. (Я предпочитаю разделять пасма на отдельные ниточки и вышивать по одной. Пробовал брать больше ниток – работа выглядела грубов
Далее…
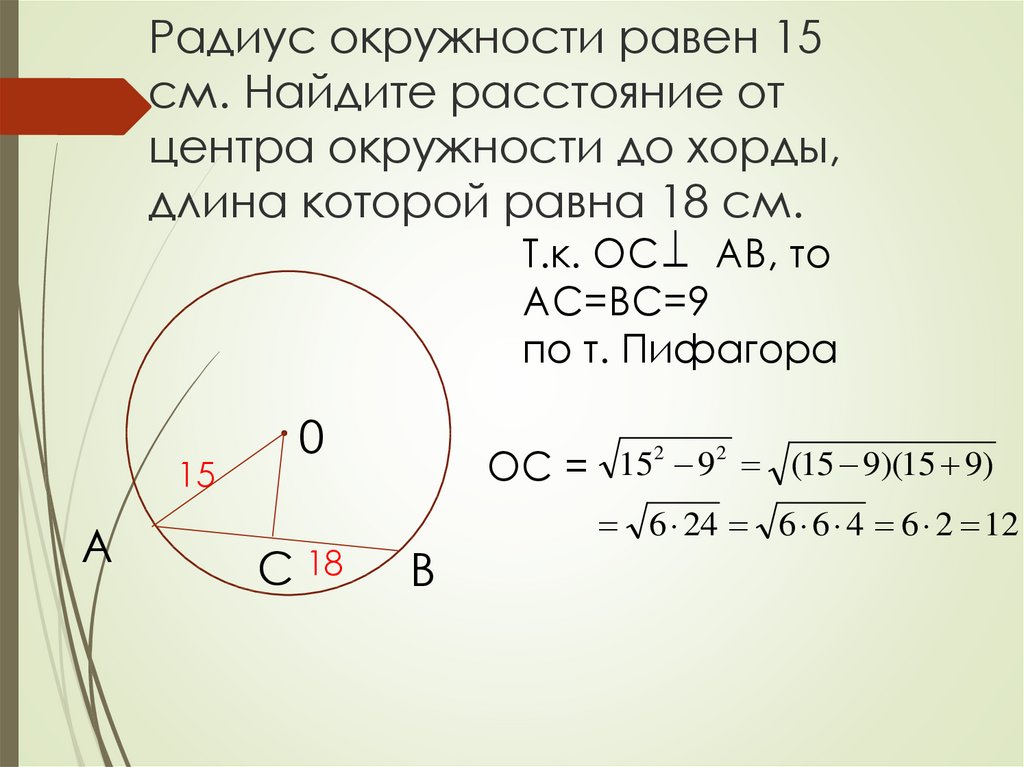
Математическая задача: Хорда окружности — вопрос № 972, алгебра, квадратное уравнение
Определите радиус окружности, в которой хорда, удаленная от центра на 6 см, на 12 см длиннее радиуса окружности.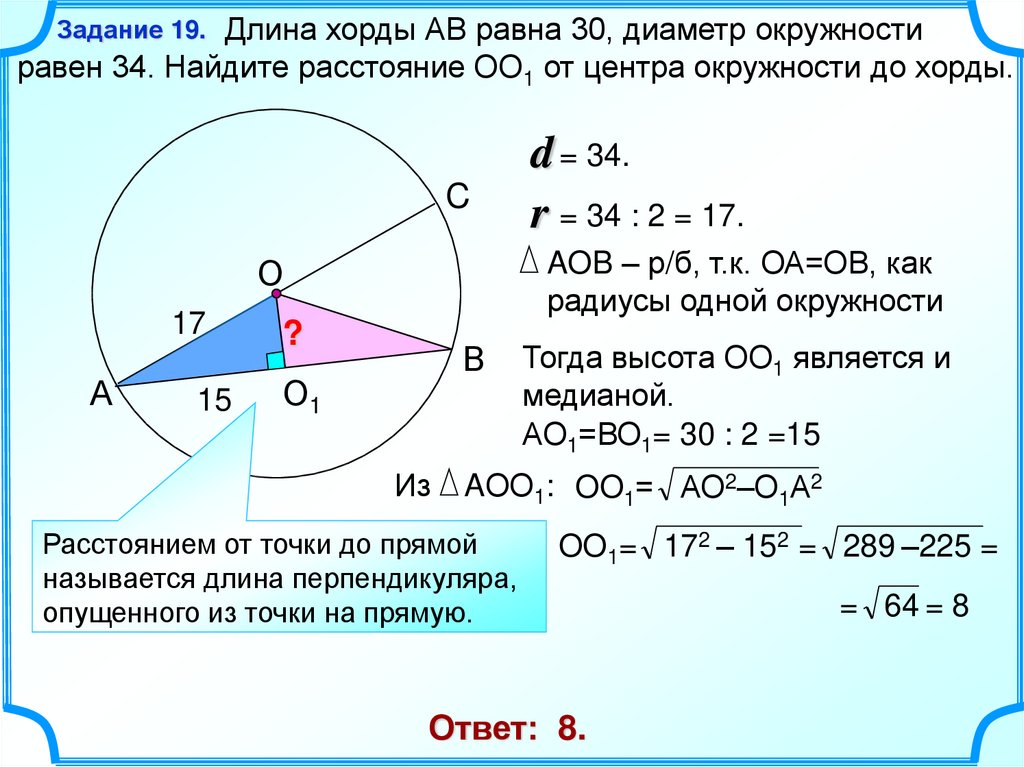
Правильный ответ:
r = 14,58 смПошаговое объяснение:
r2=62+(2r+12)2 3r2−24r−288=0 a=3;b=−24;c =−288 D=b2−4ac=242−4⋅3⋅(−288)=4032 D>0 r1,2=2a−b±D
=624±4032
=624±247
r1,2=4±10,583005 r1=14,583005244 r2=−6,583005244 Факторизованная форма уравнения: 3(r−14,583005244)(r+6,583005244)=0 r=9,5 r=9,5 r=9,8 r0003
Нашли ошибку или неточность? Не стесняйтесь
пишите нам. Спасибо!
Советы для связанных онлайн-калькуляторов
Вам нужна помощь в вычислении корней квадратного уравнения?
Теорема Пифагора является основой для калькулятора прямоугольного треугольника.
Для решения этой задачи по математике вам необходимо знать следующие знания:
- алгебра
- квадратное уравнение
- Неравенство
- Planimetrics
- Pythagorean Теорема
- Circle
- Аккорд
Оценка слов Проблема:
- СРЕДНА
video1 video2- Вычислить 2577
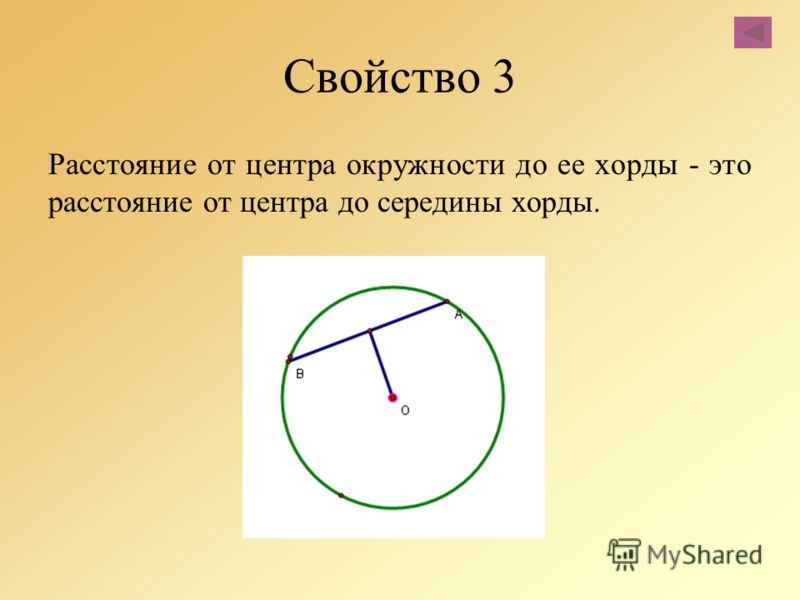
Вычислить длину хорды окружности, которая находится на расстоянии 2,5 см от центра окружности. Радиус 6,5 см. - Хорда окружности
Вычислите длину хорды окружности радиусом r = 10 см, длина которой равна расстоянию от центра окружности. - Хорды круга
Хорды круга имеют две длины: 30 и 34 см. Более короткая хорда идет от центра в два раза длиннее хорды. Определить радиус окружности. - Хорда 3
Хорда составляет 2/3 радиуса окружности от центра и имеет длину 10 см. Какова длина радиуса окружности? - Хорда
В окружности радиусом r=60 см проходит хорда, длина которой в 4 раза больше ее расстояния от центра. Какова длина хорды? - Рассчитать 79144
Радиус окружности r=8,9 см, хорда AB этой окружности имеет длину 16 см. Вычислите расстояние хорды АВ от центра окружности. - Хорда
Рассчитайте длину хорды, если расстояние от центра окружности (S, 6 см) равно 3 см.
- Хорда 2
Точка А находится на расстоянии 13 см от центра окружности с радиусом r = 5 см. Вычислите длину хорды, соединяющей точки Т1 и Т2 касательных, проведенных из точки А к окружности. - Вычислить 3562
Нить длиной 16 см проходит на расстоянии 6 см от центра круга. Вычислите длину окружности. - Хорда MN
Хорда MN окружности на расстоянии от центра окружности S 120 см. Угол MSN равен 64°. Определить радиус окружности. - Хорда 5
Дан круг к/с; 5 см/. Его хорда MN находится на расстоянии 3 см от центра окружности. Вычислите его длину. - Концентрические окружности и хорда
В окружности диаметром d = 10 см построена хорда длиной 6 см. Какой радиус имеет концентрическая окружность при касании этой хорды? - Два кольца
Площадь кольцевой окружности, образованной двумя окружностями с общим центром, составляет 100 см². Радиус внешней окружности равен удвоенному радиусу внутренней окружности. Определить радиус внешней окружности в сантиметрах. - Вычислить 3561
В окружности есть хорда длиной 12 см и радиусом 10 см. Вычислите расстояние хорды от центра окружности. - Две хорды
Рассчитайте длину хорды AB и хорды, перпендикулярной BC к окружности, если AB находится на расстоянии 4 см от центра окружности, а BC — на 8 см от центра. - Две хорды
Дана окружность k (центр S, радиус r). Из точки А, лежащей на окружности k, начинаются две хорды длины r. Какой угол составляют хорды? Нарисуй и измерь. - Хорда
В окружности радиусом 6 см проведена хорда на расстоянии 3 см от центра. Вычислите угол, образуемый шнуром в центре окружности. Отсюда найдите длину малой дуги, отсекаемой хордой.
Вычислите длину хорды, проходящей на расстоянии 6 см от центра окружности диам…
Перейти к
- Круговое упражнение 15.1
- Круговое упражнение 15.2
- Рациональные и иррациональные числа
- Сложные проценты
- Расширения
- Факторизация
- Одновременные линейные уравнения
- Задачи на одновременные линейные уравнения
- Квадратные уравнения
- Индексы
- Логарифмы
- Треугольники
- Теорема о средней точке
- Прямолинейные фигуры
- Теоремы о площади
- Круг
- Измерение
- Тригонометрические отношения
- Тригонометрические отношения и стандартные углы
- Координатная геометрия
- Статистика
Главная >
ML Aggarwal Solutions
Класс 9
Математика
>
Глава 15 — Круг
>
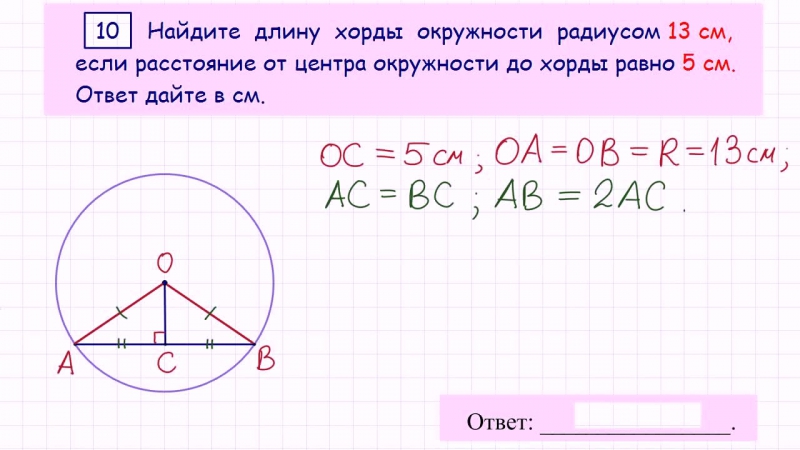
Круговое упражнение 15.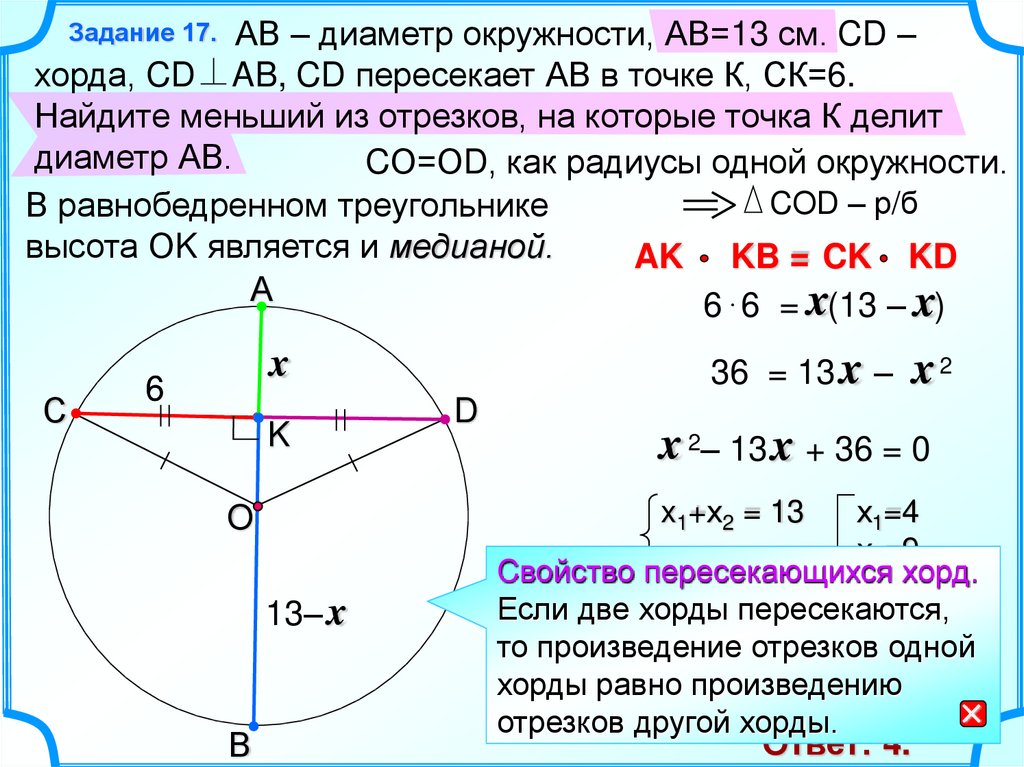
{2}
\end{выровнено}
AM = 8 см
OM ⊥ AB
M — середина AB.
АВ = 2 АМ = 2 × 8 = 16 см.
Стенограмма видео
«Здравствуйте и добро пожаловать, мои дорогие студенты
Я Ришаб, репетитор по математике на Лидо
и я здесь новый вопрос он говорит
рассчитать длину кода, который
находится на расстоянии
6 см от центра
круг
для диаметра 20 см так без
потеряем много времени давайте посмотрим на
решение
поэтому нам дали этот аккорд abc
тогда как oa — радиус
а также из рисунка замечаем, что
om перпендикулярен a b
теперь, поскольку нам известно, что диаметр
20
поэтому я пишу d для диаметра
быть 20 сантиметров
что означает, что радиус r
не что иное, как 20 на 2, что равно 10
сантиметр
разделит этот сегмент
так что мы наблюдаем сейчас
что oa составляет 10 сантиметров
ома6
теперь в прямоугольном треугольнике
4 утра, будь осторожен, мой ученик, это стоит rt
за право
так что это читается как прямоугольный треугольник
мы видим, что квадрат oa равен
ом квадрат
плюс я квадратный
o дается на 10 больше
м равно 6
и сейчас я квадратный
упрощая его, мы получаем am квадрат
равно
100 минус 36, что равно 64.
значит am равен 8 сантиметрам
будьте осторожны, что мы обязаны найти
длина
шнур
это означает
у нас есть до сих пор
имея в виду, что ом
перпендикулярно а б
мы замечаем, что m является серединой a b
что означает, что a b в два раза больше
я что значит
2 в 8, что равно 16
сантиметр
значит a b равно 16 сантиметрам
Я надеюсь, что мои ученики получили этот вопрос
ну не забудь подписаться
кнопка
Вы также можете поделиться своими сомнениями в
раздел комментариев, увидимся в следующий раз, пока»
Связанные вопросы
Вычислите длину хорды, которая находится на расстоянии 12 см от центра окружности радиуса…
Хорда длиной 8 см проходит на расстоянии 3 см от центра окружности. Вычислите радиус…
Хорда длиной 16 см проходит на расстоянии 6 см от центра окружности. Найдите длину т…
В окружности радиусом 5 см AB и CD проходят две параллельные хорды длиной 8 см и 6 см соответственно.