Как найти координаты отрезка: Середина отрезка. Координаты середины отрезка

примеры, решения, как найти середину отрезка по координатам

В статье ниже будут освещены вопросы нахождения координат середины отрезка при наличии в качестве исходных данных координат его крайних точек. Но, прежде чем приступить к изучению вопроса, введем ряд определений.

Определение 1

Отрезок – прямая линия, соединяющая две произвольные точки, называемые концами отрезка. В качестве примера пусть это будут точки A и B и соответственно отрезок AB.

Если отрезок AB продолжить в обе стороны от точек A и B, мы получим прямую AB. Тогда отрезок AB – часть полученной прямой, ограниченный точками A и B. Отрезок AB объединяет точки A и B, являющиеся его концами, а также множество точек, лежащих между. Если, к примеру, взять любую произвольную точку K, лежащую между точками A и B, можно сказать, что точка K лежит на отрезке AB.

Определение 2

Длина отрезка – расстояние между концами отрезка при заданном масштабе (отрезке единичной длины). Длину отрезка AB обозначим следующим образом: AB.

Определение 3

Середина отрезка – точка, лежащая на отрезке и равноудаленная от его концов. Если середину отрезка AB обозначить точкой C, то верным будет равенство: AC=CB

И далее мы рассмотрим, как же определять координаты середины отрезка (точки C) при заданных координатах концов отрезка (A и B), расположенных на координатной прямой или в прямоугольной системе координат.

Середина отрезка на координатной прямой

Исходные данные: координатная прямая Ox и несовпадающие точки на ней: A и B. Этим точкам соответствуют действительные числа xA и xB. Точка C – середина отрезка AB: необходимо определить координату xC.

Поскольку точка C является серединой отрезка АВ, верным будет являться равенство: |АС| = |СВ|. Расстояние между точками определяется модулем разницы их координат, т.е.

|АС| = |СВ|⇔xC-xA=xB-xC

Тогда возможно два равенства: xC-xA=xB-xC и xC-xA=-(xB-xC)

Из первого равенства выведем формулу для координаты точки C : xC=xA+xB2 (полусумма координат концов отрезка).

Из второго равенста получим: xA=xB , что невозможно, т.к. в исходных данных — несовпадающие точки. Таким образом, формула для определения координат середины отрезка AB с концами A(xA) и B(xB):

xA+xB2

Полученная формула будет основой для определения координат середины отрезка на плоскости или в пространстве.

Середина отрезка на плоскости

Исходные данные: прямоугольная система координат на плоскости Оxy, две произвольные несовпадающие точки с заданными координатами AxA, yA и  BxB, yB . Точка C – середина отрезка AB. Необходимо определить координаты xC и yC для точки C.

Возьмем для анализа случай, когда точки A и B не совпадают и не лежат на одной координатной прямой или прямой, перпендикулярной одной из осей.Ax, Ay ; Bx, By и Cx ,Cy — проекции точек A, B и C на оси координат (прямые Ох и Оy).

Согласно построению прямые AAx, BBx, CCx параллельны; прямые также параллельны между собой. Совокупно с этим по теореме Фалеса из равенства АС = СВ следуют равенства: АxСx = СxВx и АyСy = СyВy, и они в свою очередь свидетельствуют о том, что точка Сx – середина отрезка АxВx, а Сy – середина отрезка АyВy. И тогда, опираясь на полученную ранее формулу, получим:

xC=xA+xB2 и yC=yA+yB2

Этими же формулами можно воспользоваться в случае, когда точки A и B лежат на одной координатной прямой или прямой, перпендикулярной одной из осей. Проводить детальный анализ этого случая не будем, рассмотрим его лишь графически:

Резюмируя все выше сказанное, координаты середины отрезка AB на плоскости с координатами концов A (xA,yA) и B (xB, yB) определяются как:

(xA+xB2, yA+yB2)

Середина отрезка в пространстве

Исходные данные: система координат Оxyz и две произвольные точки с заданными координатами A(xA, yA, zA) и B (xB, yB, zB). Необходимо определить координаты точки C, являющейся серединой отрезка AB.

Ax, Ay, Az ; Bx, By,Bz и Cx, Cy, Cz — проекции всех заданных точек на оси системы координат.

Согласно теореме Фалеса верны равенства: AxCx=CxBx, AyCy=CyBy,AzCz=CzBz

Следовательно, точки Cx, Cy,Cz являются серединами отрезков AxBx, AyBy, AzBz соответственно. Тогда, для определения координат середины отрезка в пространстве верны формулы:

xC=xA+xB2, yc=yA+yB2, zc=zA+ZB2

Полученные формулы применимы также в случаях, когда точки A и B лежат на одной из координатных прямых; на прямой, перпендикулярной одной из осей; в одной координатной плоскости или плоскости, перпендикулярной одной из координатных плоскостей.

Определение координат середины отрезка через координаты радиус-векторов его концов

Формулу для нахождения координат середины отрезка также можно вывести согласно алгебраическому толкованию векторов.

Исходные данные: прямоугольная декартова система координат Oxy, точки с заданными координатами A(xA,yA) и B(xB, xB) . Точка C – середина отрезка AB.

Согласно геометрическому определению действий над векторами верным будет равенство: OC→=12·OA→+OB→ . Точка C в данном случае – точка пересечения диагоналей параллелограмма, построенного на основе векторов OA→ и OB→ , т.е. точка середины диагоналей.Координаты радиус-вектора точки равны координатам точки, тогда верны равенства: OA→=(xA, yA), OB→=(xB,yB) . Выполним некоторые операции над векторами в координатах  и получим: 

OC→=12·OA→+OB→=xA+xB2, yA+yB2

Следовательно, точка C имеет координаты:

xA+xB2, yA+yB2

По аналогии определяется формула для нахождения координат середины отрезка в пространстве:

C(xA+xB2, yA+yB2, zA+zB2)

Примеры решения задач на нахождение координат середины отрезка

Среди задач, предполагающих использование полученных выше формул, встречаются, как и те, в которых напрямую стоит вопрос рассчитать координаты середины отрезка, так и такие, что предполагают приведение заданных условий к этому вопросу: зачастую используется термин «медиана», ставится целью нахождение координат одного из концов отрезка, а также распространены задачи на симметрию, решение которых в общем также не должно вызывать затруднений после изучения настоящей темы. Рассмотрим характерные примеры.

Пример 1

Исходные данные: на плоскости – точки с заданными координатами А (-7,3) и В (2,4). Необходимо найти координаты середины отрезка АВ.

Решение 

Обозначим середину отрезка AB точкой C. Координаты ее буду определяться как полусумма координат концов отрезка, т.е. точек A и B.

xC=xA+xB2=-7+22=-52yC=yA+yB2=3+42=72

Ответ: координаты середины отрезка АВ-52, 72.

Пример 2

Исходные данные: известны координаты треугольника АВС: А (-1,0), В (3,2), С (9,-8). Необходимо найти длину медианы АМ.

Решение

1. По условию задачи AM – медиана, а значит M является точкой середины отрезка BC. В первую очередь найдем координаты середины отрезка BC, т.е. точки M:

xM=xB+xC2=3+92=6yM=yB+yC2=2+(-8)2=-3

2. Поскольку теперь нам известны координаты обоих концов медианы (точки A и М), можем воспользоваться формулой для определения расстояния между точками и посчитать длину медианы АМ:

AM=(6-(-1))2+(-3-0)2=58

Ответ: 58

Пример 3

Исходные данные: в прямоугольной системе координат трехмерного пространства задан параллелепипед ABCDA1B1C1D1 . Заданы координаты точки C1(1, 1, 0), а также определена точка M, являющаяся серединой диагонали BD1 и имеющая координаты M (4, 2, -4) . Необходимо рассчитать координаты точки А.

Решение

Диагонали параллелепипеда имеют пересечение в одной точке, которая при этом является серединой всех диагоналей. Исходя из этого утверждения, можно иметь в виду, что известная по условиям задачи точка М является серединой отрезка АС1. Опираясь на формулу для нахождения координат середины отрезка в пространстве, найдем координаты точки А: xM=xA+xC12 ⇒xA=2·xM-xC1=2·4-1+7yM=yA+yC12⇒yA=2·yM-yC1=2·2-1=3zM=zA+zC12⇒zA=2·zM-zC1=2·(-4)-0=-8

Ответ: координаты точки А (7,3,-8).

Как найти координаты середины отрезка

Основное определение отрезка

Определение

Отрезок — это прямая линия, которая соединяет две произвольно расположенные точки, именуемые окончанием отрезка. В качестве конкретного примера можно назвать точки A и B и соответственно отрезок AB.

Прямую АВ можно получить путем удлинения отрезка, который состоит из двух точек. Вследствие чего, можно сказать, что полученный отрезок АВ — это часть прямой, которая ограничена точками А и В. Отрезок объединяет обе точки, которые являются концами прямой, а также множество других точек, лежащих на отрезке.  

Например: дана точка К которая расположена между заданными отметками, следовательно, можно сказать, что данная точка лежит на этом отрезке.

Определения

Длина прямой – конкретное отмеренное расстояние, которое задано в масштабе. Чаще всего данный параметр задается как АВ.

Середина отрезка – это некая определенная отметка, которая лежит на прямой и удалена от концов на одинаковом расстоянии друг от друга. Ее можно обозначить как координата С.

Середина отрезка на координатной прямой

Заданы следующие параметры: координатная прямая Ox; точки А и В, которые не совпадают с данной прямой.

Заданным точкам соответствуют действительные числовые значения \[x_{A}\] и \[x_{B}\].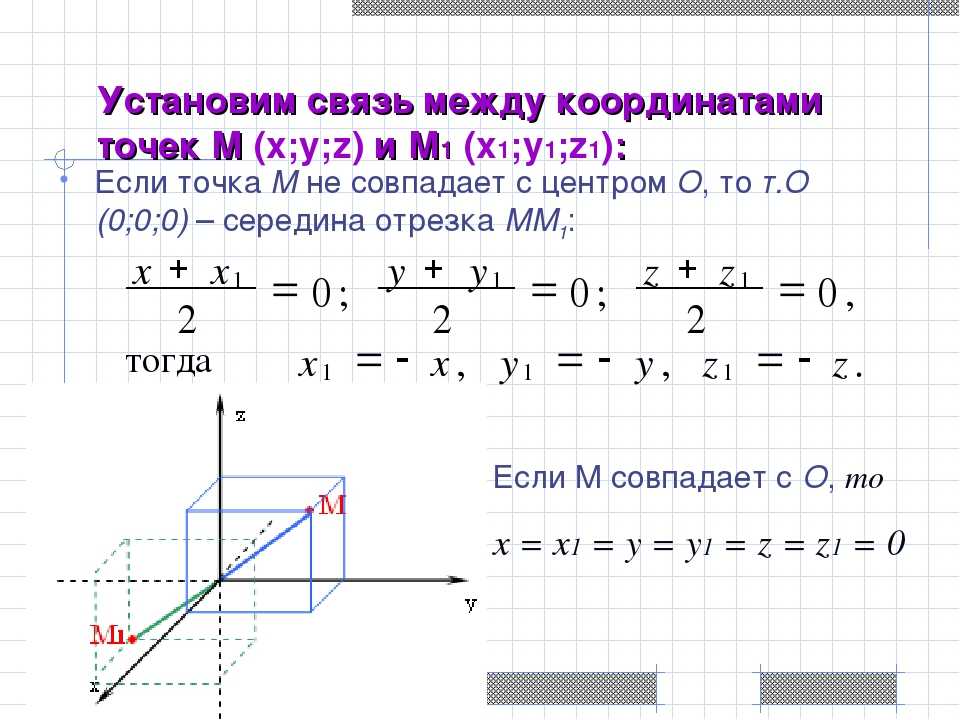 Координата С — это середина отрезка А и В. Исходя из этого нужно определить значение координаты \[x_{C}\] .

Рисунок 1. Координатная прямая с заданными точками.

AB = |a — b|, где A и B — это произвольные точки, расстояние между которыми надо найти, то есть, найти длину отрезка AB, a и b — координаты точек.
Выражение |a — b| можно заменить выражением |b — a|, так как a — b и b — a являются противоположными числами и их модули равны.
Следовательно, чтобы найти расстояние между точками координатной прямой надо из координаты одной точки вычесть координату другой точки.

Середина отрезка на плоскости

Зададим следующие параметры: прямоугольная система координат относительно заданной плоскости Oxy; две произвольно расположенные несовпадающие точки, для которых заданы координаты \[\mathrm{A}\left(x_{A} y_{A}\right)\] и \[B\left(\chi_{B} \chi_{B}\right)\]. Точка C — это заданная середина отрезка АВ. Нужно вычислить координаты \[x_{C}\] и \[y_{C}\] относительно точки С.

Чтобы правильно проанализировать задачу, возьмем случай, когда точки A и В между собой не совпадают и расположены на одной координатной плоскости.

В свою очередь координатная плоскость является перпендикулярной относительной одной из осей.

Координаты отметок \[A_{x} A_{y} B_{x} B_{y} C_{x} C_{y}\] — это проекции точек А, В, С.

Рисунок 2. Координатная плоскость с заданным отрезком.

Согласно построению, все прямые можно назвать параллельными; прямые также параллельны между собой. Принимая во внимание данное свойство и теорему Фалеса из равенства А С   =   С В следуют, что все  равенства между собой равны. Также они в свою очередь свидетельствуют о том, что точка \[C_{x}\] – это середина отрезка \[A_{x}\] и \[B_{x}\], \[C_{y}\] а – середина отрезка \[A_{y}\] и \[B_{y}\].

Опираясь на полученное выражение получаем основное уравнение середины отрезка на координатной плоскости. 

\[x_{c}=\frac{x_{A}+x_{B}}{2}\text { и } y_{c}=\frac{y_{A}+y_{B}}{2}\]

Данным набором формул можно использовать, когда точки А и B лежат на одной координатной плоскости или прямой. Которая соответственно перпендикулярна относительной одной из осей.

Рисунок 3. Графическое изображение решения задач при условии нахождения точек на одной плоскости.

В данном случае координаты отрезка будут определяться по следующей формуле:

\[x_{C}=\frac{x_{A}+x_{B}}{2} \text{ и } y_{c}=\frac{y_{A}+y_{B}}{2}\]

Параметры середины отрезка в пространстве

Для выведения основной формулы для решения подобного рода задач, нужно рассмотреть конкретный пример.

Дана система координат, две произвольные координатные точки с конкретными координатами \[\mathrm{A}\left(A_{x} A_{y} A_{z}\right)\] и \[\mathrm{B}\left(B_{\chi} B_{y} B_{z}\right)\]. Нужно определить отметку точки C, которая в свою очередь будет являться серединой отрезка.

Рисунок 4. Система координат с тремя координатными осями.

Согласно основной теоремы Фалеса, все равенства между собой являются равными. Следовательно, значение точек С будут являться серединами отрезков, каждой координатной плоскости, коих имеется три.

Можно составить и записать окончательную формулу для определения середины прямой при координатной плоскости, состоящей более чем двух осей.

\[x_{c}=\frac{x_{A}+x_{B}}{2} \text{ и } y_{C}=\frac{y_{A}+y_{B}}{2}, z_{c}=\frac{z_{A}+z_{B}}{2}\]

Данные формулы также можно применять в случаях, когда точки A и B расположены на одной из координатных прямых. Либо на прямой, которая перпендикулярна относительно одной из осей. Есть еще случай, когда точки расположены в одной координатной плоскости, которая перпендикулярна одной из координатных плоскостей.

Нет времени решать самому?

Наши эксперты помогут!

Контрольная

| от 300 ₽ |

Реферат

| от 500 ₽ |

Курсовая

| от 1 000 ₽ |

Определение координат середины отрезка через координаты радиус-векторов его концов

Формулу для определения отметок середины отрезка, можно определить применяя алгебраическое правило решения векторных выражений.

Исходные данные: прямоугольная декартова система координат Oxy, точки с конкретно заданными координатами \[\mathrm{A}\left(A_{x} A_{y}\right)\] и \[\text { B }\left(B_{x} B_{y}\right)\].

Точка  C – это середина отрезка с точками А и В.

Согласно геометрическому правилу и определению, действия над векторами будет выглядеть следующим образом:

\[\overline{O C}=\frac{1}{2} \cdot(\overline{O A}+\overline{O B}).\]

Координата С в данной ситуации — это значение, в которой пересекаются диагонали геометрической фигуры параллелограмм. Данная фигура построена на основании следующих векторов  \[\overline{O A}\] и \[\overline{O B}\], иными словами — это точка середины диагоналей.

Координатные показатели радиуса — это векторные показатели, которые  равны координатам, тогда будут верны и равенства: \[\overline{O A}\left(x_{A} y_{A}\right)\] и \[\overline{O B}\left(x_{B} y_{B}\right)\].

Выполним следующие действия над векторными значениями и получим следующие формулы:

\[\overline{O C}=\frac{1}{2} \cdot(\overline{O A}+\overline{O B})=\left(\frac{x_{A}+y_{B}}{2}, \frac{y_{A}+y_{B}}{2}\right).\]

Следовательно, заданная координата С обладает данными:

\[\left(\frac{x_{A}+y_{B}}{2}, \frac{y_{A}+y_{B}}{2}\right). \]

Аналогичным образом определяется нахождение координат середины заданного отрезка в пространстве.

\[C\left(\frac{x_{A}+y_{B}}{2}, \frac{y_{A}+y_{B}}{2}, \frac{z_{A}+z_{B}}{2}\right)\]

Примеры решения задачи, при нахождении точки середины отрезка

Примеры

Пример №1:

Заданы координатные данные. Точка А с показателями (-7,3) и В (2,4).
Нужно определить точку с отметками, которая является серединой отрезка А и В.

Решение:

Середину отрезка можно обозначить любой точкой. В данном примере возьмем наименование точки — С.

Координатные значения ее будут вычисляться как половина суммы координат концов заданного отрезка с точками А
и В.

Составим и запишем следующие формулы:

\[x_{C}=\frac{x_{A}+x_{B}}{2}=\frac{-7+2}{2}=-\frac{5}{2}\\y_{C}=\frac{y_{A}+y_{B}}{2}=\frac{3+4}{2}=\frac{7}{2}\]

Ответ: искомые координатные значения середины отрезка будут равны следующим данным:
\[\mathrm{AB}\left(-\frac{5}{2}, \frac{7}{2}\right)\]

---

Пример №2:

Заданы координатные отметки геометрической фигуры треугольника: АВС А(-1,0), В (3,2), С (9,-8). {2}}=\sqrt{58}\]

Ответ: \[\sqrt{58}\].

Как найти концы отрезка

Все математические ресурсы SAT

16 диагностических тестов 660 практических тестов Вопрос дня Карточки Learn by Concept

SAT Math Help » Геометрия » Координатная геометрия » Линии » Формула середины » Как найти концы отрезка

Середина отрезка AB равна (2, -5). Если координаты точки А равны (4, 4), то каковы координаты точки В?

Возможные ответы:

(0, -14)

(0, -13)

(6, 14)

(6, 13)

(3, -0,5)

1 Правильный ответ :

(0, -14)

Объяснение:

Самый быстрый способ найти отсутствующую конечную точку — определить расстояние от известной конечной точки до средней точки, а затем выполнить такое же преобразование для средней точки.

В этом случае координата x перемещается с 4 на 2 или вниз на 2, поэтому новая координата x должна быть 2-2 = 0. Координата y перемещается с 4 на -5 или вниз на 9., поэтому новая координата y должна быть -5-9 = -14.

 

Альтернативным решением может быть замена (4,4) вместо (x ₁ ,y ₁ ) и (2,-5) вместо (x,y) в формуле средней точки:

x= (x ₁ +x ₂ )/2

y=(y ₁ +y ₂ )/2

Решение каждого уравнения для (x ₂ ,y 2900s дает решение) 3 8 ,y 900s (0,-14).

Сообщить об ошибке

Точка A (5, 7). Точка B равна (x, y). Середина AB равна (17, –4). Какова ценность Б?

 

Возможные ответы:

Ни один из других ответов

(8.5, –2)

(22, –9)

(29, –15) 90, –05

Правильный ответ:

(29, –15)

Пояснение:

Точка А (5, 7).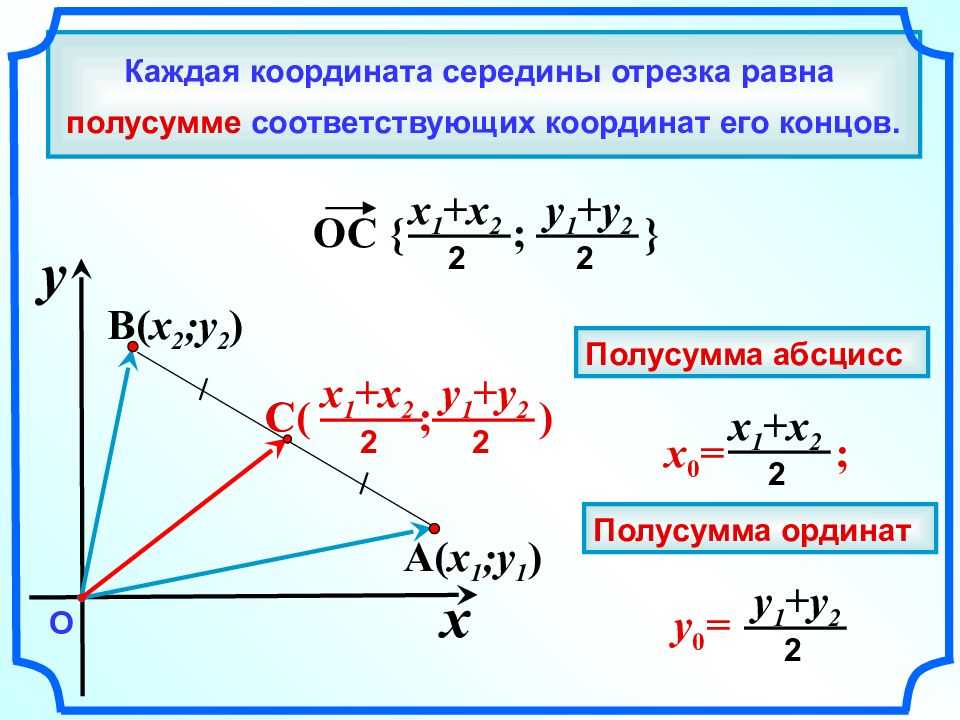 Точка B равна (x, y). Середина AB равна (17, –4). Какова ценность Б?

Нам нужно использовать нашу обобщенную формулу средней точки:

MP = ((5 + x)/2, (7 + y)/2)

Решить каждое по отдельности:

(5 + x)/2 = 17 → 5 + x = 34 → x = 29

(7 + y)/2 = –4 → 7 + y = –8 → y = – 15

Следовательно, B равно (29, –15).

Сообщить об ошибке

Отрезок AB имеет конечную точку A, расположенную в точке , и среднюю точку в точке . Каковы координаты точки B отрезка AB?

Возможные ответы:

Вторая конечная точка не может существовать

Правильный ответ:

Объяснение:

С конечной точкой A, расположенной в (10,-1), и средней точкой в ​​​​(10,0), мы хотим добавить длину от A до середины на другой стороне сегмента, чтобы найти точку B.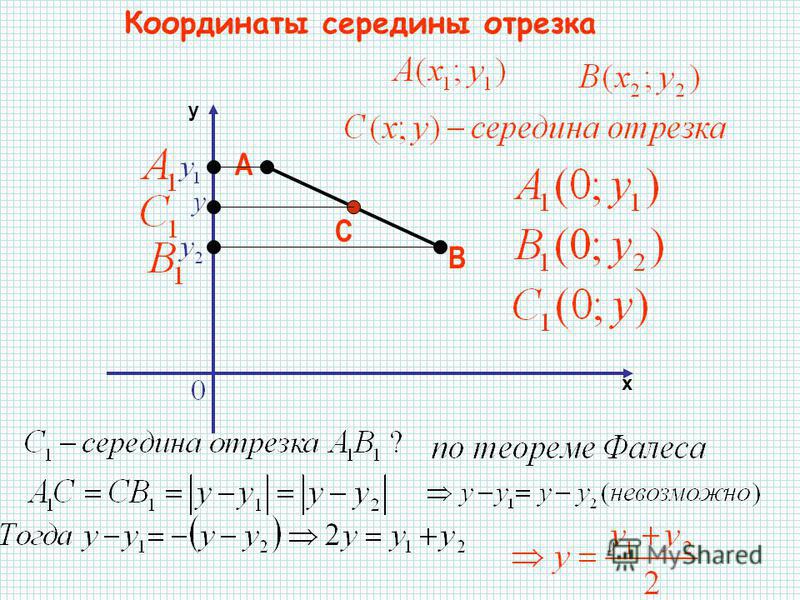 Общая длина отрезка должна быть в два раза больше расстояния от точки А до середины.

A расположен ровно на одну единицу ниже средней точки по оси y для полного смещения (0,1). Чтобы найти точку B, мы добавляем (10+0, 0+1) и получаем координаты для B: (10,1).

Сообщить об ошибке

Решите каждую проблему и выберите лучший из предложенных вариантов.

 

Какое расстояние между точками  и  на стандартной координатной плоскости?

Возможные ответы:

Правильный ответ:

Пояснение:

Сделай треугольник. Точки отстоят друг от друга на 8 единиц по -оси и на  единиц друг от друга по -оси. Затем используйте теорему Пифагора, чтобы найти расстояние до гипотенузы, которое в конечном итоге равно .

Другой способ решить эту задачу — использовать формулу расстояния,

Подставив две полученные точки,

Сообщить об ошибке

4 002 Все математические ресурсы SAT

16 диагностических тестов 660 практических тестов Вопрос дня Карточки Learn by Concept

Основы координатной геометрии — Раздел Формула

В этом уроке мы установим формулу для нахождения координат точки, которая делит отрезок, соединяющий две заданные точки в заданном отношении. Формула известна как формула раздела . Начнем!

Рассмотрим две точки P(x ₁ , y ₁ )  и Q(x ₂ , y ₂ ) . Нам нужно найти координаты точки R , которая делит PQ в отношении m : n , т.е. PR/RQ = m/n .

Учитывая соотношение, точка R может либо лежать между P и Q , либо вне отрезка PQ . Взгляни.

(Обратите внимание, что на приведенном выше рисунке m и n не обозначают длины PR и QR . Они просто указывают соотношение.)

Рассмотрим эти случаи по одному. .

Случай I — R лежит между P и Q

Сначала я проиллюстрирую уродливый (но действующий) метод вычисления координат R , используя то, что мы уже знаем — формулу расстояния.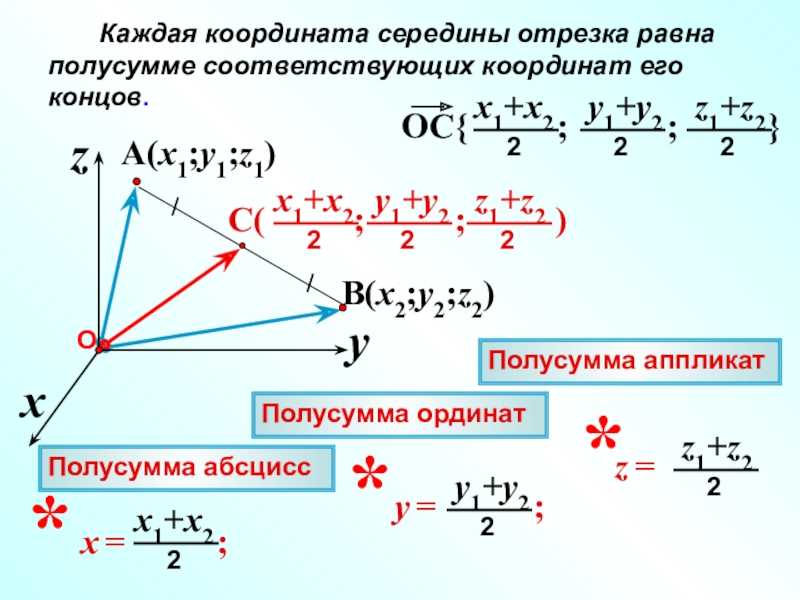 Как я упоминал ранее, существует (в общем) несколько методов решения задачи координатной геометрии. Это один из таких случаев. Идея состоит в том, чтобы развить ваш уровень мышления и дать вам представление о том, какие методы хороши, а какие нет.

Вот как можно подумать: «Поскольку есть два неизвестных 92}\)

На этом я остановлюсь. Возможно, вы поняли, почему это не лучший метод. На самом деле, как мы увидим позже, методы, использующие формулу расстояния, обычно становятся довольно сложными и трудными для решения.

Итак, какова наша альтернатива? Немного геометрии — давайте сделаем некоторые построения.

Я начертил RA и QB параллельно оси Y и PA и RB параллельно оси X ось. Тогда треугольники RPA и QRB подобны по АА-подобию.

Как это поможет? Нам дано PR/QR , что с помощью подобия равно RA/QB и PA/RB .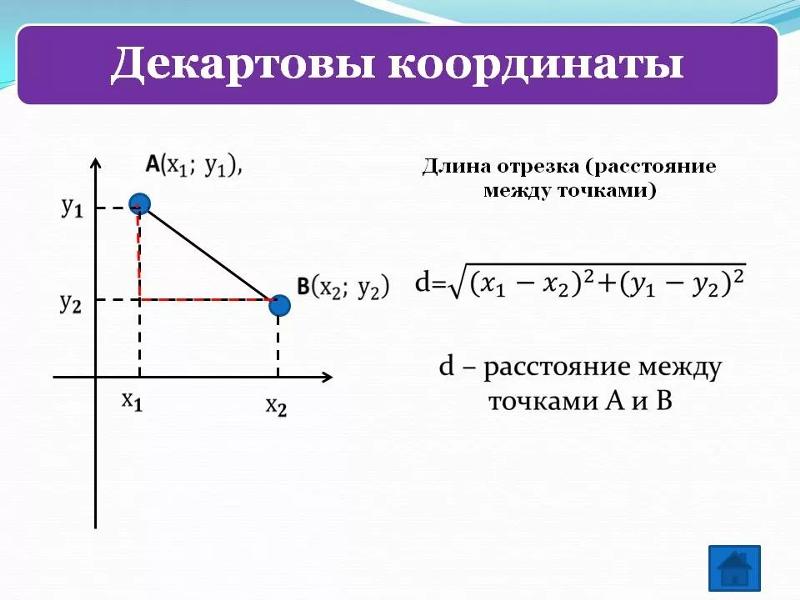 Позвольте мне написать это лучше:

\(\frac{PR}{QR} = \frac{RA}{QB} = \frac{PA}{RB} = \frac{m}{n}\)

Теперь PA = x – x ₁  и RB = x ₂ – x (объяснение этому я дал в предыдущем уроке.)

Следовательно, мы можем написать

\(\frac{PA}{RB}=\frac{x-x_1}{x_2-x}=\frac{m}{n}\)

x , мы получаем

x = \(\frac{mx_2+nx_1}{m+n}\)

А как насчет y ?

На рисунке выше RA = y – y ₁ и QB = y ₂ – y .

Теперь мы можем использовать тот же процесс, чтобы получить

y = \(\frac{my_2+ny_1}{m+n}\)

Итак у нас есть координаты точки R , которая делит PQ в отношении m : n .

Когда R лежит между P и Q , мы говорим, что R делит PQ в отношении m : n внутри . Вот симуляция, которая показывает две точки A и B , а также точку C , разделяющую соединяющий их отрезок в некотором отношении.

Попробуйте изменить значения м и n и обратите внимание на координаты C . Вы получаете те же координаты, используя формулу сечения?

Посмотрим, что произойдет, если R окажется за пределами PQ .

Случай II – R лежит вне PQ

Данное условие то же самое, т.е. PR / RQ = m / n , но цифра будет немного другой.

В этом случае мы говорим, что R делит PQ внешне в отношении m : n .

Я не буду его выводить. Пожалуйста, попробуйте сделать это сами. Метод тот же, что и в первом случае – найти подобные треугольники, выразить данное отношение через х ₁ , х ₂ , у ₁ и 11 71 2 у 1 2 .