Как найти критические точки: Отыскание точек экстремума — урок. Алгебра, 11 класс.

Критические точки функции: максимумы и минимумы

• Лаврова Наталья Григорьевна

Разделы: Математика

---

Цели урока:

Обучающая:

• способствовать выработке навыка отыскания экстремумов функции

Воспитывающая:

• воспитывать чувство уважения  между учащимися для максимального раскрытия их способностей
• воспитывать аккуратность выполнения записей в тетради и на доске

Развивающая

• способствовать развитию внимания
• совершенствовать умения вычислять производные.

Тип урока: комбинированный

Методы обучения: объяснительно-иллюстративный, репродуктивный.

Структура урока

1. Организационный момент. (1-2 мин.)

Учитель здоровается с ребятами и предлагает, посмотрев на экран, догадаться какая тема будет на сегодняшнем уроке.
Далее сообщает цель урока.

2. Актуализация знаний.

 Устная работа(1-2 мин.) Заполнение схемы (Учащимся необходимо  правильно соединить части правил).

• Какие точки называются критическими?
• Необходимое условие экстремума
• Признак максимума функции.
• Признак минимума функции

(За правильный ответ ученик получает бонус)

Достаточный признак возрастания функции: Если  f′(х)> 0  в каждой точке интервала  I, то функция возрастает на  I.

Достаточный признак убывания функции:  Если  f′(х)<  0  в каждой точке интервала  I, то функция убывает на  I.     .

Необходимое условие экстремума: Если точка х  является точкой экстремума функции f   и в этой  точке существует производная  f ′ , то она равна нулю:   f′(х°) =0.

Признак максимума функции: Если функция f непрерывна в точке х, а   f ′ (х)> 0  на интервале  (а;х°) и  f ′ (х)<  0  на интервале (х°; в) , то точка х является точкой максимума функции f  .

Признак минимума функции: Если функция f непрерывна в точке х°, а   f ′ (х)<  0   на интервале  (а;х°) и f ′ (х)> 0  на интервале (х°; в) , то точка х° является точкой максимума функции f  .

Теперь коснемся вопроса последовательности операций, которые нужно выполнить при отыскании экстремумов функции.(3-4 минуты)

• 1. найти область определения функции
• 2. найти производную функции
• 3. найти точки, в которых выполняется равенство f(х)=0
• 4. найти точки, в которых производная не существует
• Отметить на координатной прямой все критические точки и область определения
• 5. определить знак производной на каждом из промежутков
• 6. сделать вывод о наличии или отсутствии экстремумов

Выполнение теста.

Учитель: Ребята, сейчас вам необходимо выполнить тест, который вам поможет  разделить понятия максимума и минимума с помощью графиков функции (на тест отводится  3-4 минуты)

Ответы к тесту:

• Задание 1. -3
• Задание 2. -1
• Задание 3. -4
• Задание 4. -4
• Задание 5. -4
• Задание 6. -4

За каждый правильный ответ ученик получает  один бонус.

4.Совместное выполнение задания. (10 мин.)
Следующим этапом нашего урока является выполнение задания               (один ученик выходит к доске, остальные решают на месте)
 Необходимо исследовать на экстремум функцию и построить ее график.

1. Д(у)=R, т.к. у- многочлен
   
2. у′ = 3х(х-2)
   
3. у′ = 0 при х=0 , х=2
   
5. х=0 – точка максимума
   Х=2- точка минимума
   
6. Экстремумы функции у(0)=0
   У(2)=4
   
7. Точки пересечения с осями.
   С осью ОХ: у=0 при х=0; х=3 т.е. (0;0) , (3;0)
   С осью оу: х=0,у=0 т.е. (0;0)
8. функция возрастает на (-∞;0] и [2; ∞)
   Функция убывает [0;2]
   
9. график функции

5.Самостоятельная работа. .(5 мин.)

Учащиеся выполняют на месте

Далее на экране появляются правильные ответы, и каждый учащийся дает оценку  своему решению.

Критерии оценок:

5 бонусов — верно выполненное задание
4 бонуса – в работе имеются небольшие недочеты
3 бонуса – работа выполнена  на 50%

7. Домашнее задание. (2 минуты)

— составить слайды о жизни и деятельности  Пьера Ферма
— Найти промежутки возрастания и убывания функции  (функции у каждого учащегося на столе)

8.

9. Рефлексия.(2 минуты)

 — С каким настроением уходите с урока?
— С чем ассоциируется математические понятия  максимума и минимума?

10.

Приложение

19.02.2009

Как найти критические точки первого рода функции f(x)

Как найти критические точки первого рода функции f(x)

Общую схему исследования функции удобно делить на этапы.

Первый этап исследования функции, который не требует привлечения производной, уже рассмотрен нами выше. Этот этап включает выполнение семи основных заданий:

1. Найти область определения функции f(x), точки ее разрыва. 
2. Найти множество значений функции f(x). 
3. Найти точки пересечения графика функции f(x) с осью Ox (нули функции f(x)). 
4. Найти точку пересечения графика функции f(x) с осью Oy. 
5. Найти асимптоты графика функции f(x). 
6. Исследовать поведение функции f(x) возле ее вертикальных асимптот. 
7. Найти координаты точек пересечения графика функции f(x) с ее асимптотами

На втором этапе для исследования функции уже применяется производная. Цель второго этапа — найти критические точки первого рода, интервалы возрастания и убывания функции, точки экстремума и экстремальные значения функции, угловые точки графика функции (используется первая производная).

Рассмотрим первое задание второго этапа (оно восьмое по счету в общей схеме исследования функции): найти критические точки первого рода (точки, где производная функции f(x) равна нулю или не существует).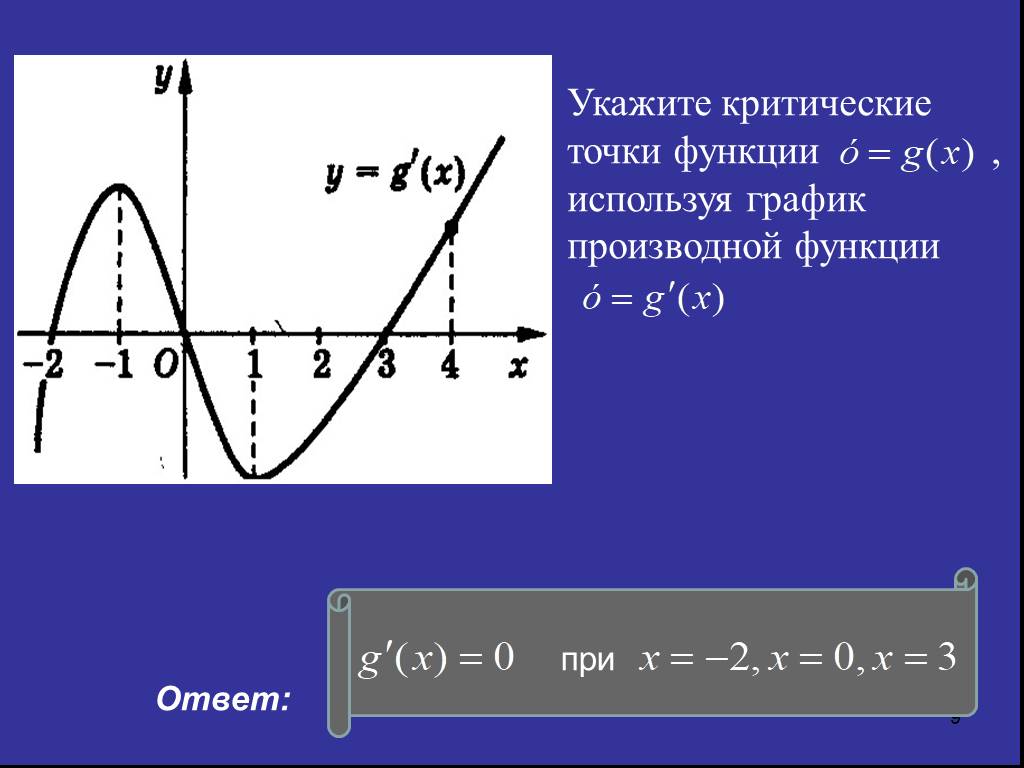 4))

Итак, восьмое задание в общей семе исследования функции решено. На очереди 9-е задание: Определить интервалы монотонности функции f(x). Как его решить? Об этом — в следующем посте.

Следующее Предыдущее Главная страница

Критическая точка — определение, график, как найти критические точки?

Концепция критической точки очень важна в исчислении, так как она широко используется при решении задач оптимизации. График функции имеет либо горизонтальную касательную, либо вертикальную касательную в критической точке. На основании этого выведем еще несколько фактов о критических точках.

Давайте узнаем больше о критических точках вместе с их определением и тем, как найти их из функции и из графика, а также несколько примеров.

1.	Что такое критическая точка функции?
2.	Поиск критических точек
3.	Критические точки на графике
4.	Критические точки многомерных функций
5.	Часто задаваемые вопросы о критических точках

Что такое критическая точка функции?

Критическая точка функции y = f(x) — это точка (c, f(c)) на графике f(x), в которой либо производная равна 0, либо производная не определена. Но как критическая точка связана с производной? Мы знаем, что наклон касательной к y = f(x) в точке есть не что иное, как производная f'(x) в этой точке. Мы уже видели, что функция имеет либо горизонтальную, либо вертикальную касательную в критической точке.

• Горизонтальная касательная в точке (c, f(c)) ⇒ Наклон = 0 ⇒ f ‘(c) = 0
• Касательная по вертикали в точке (c, f(c)) ⇒ Наклон = не определено ⇒ f'(c) НЕ определено

Критическая точка функции Определение

На основании вышеизложенного критическая точка функции математически определяется следующим образом.

Точка (c, f(c)) является критической точкой непрерывной функции y = f(x) тогда и только тогда, когда

• c находится в области определения f(x).
• Либо f ‘(c) = 0, либо f'(c) НЕ определено.

Критические значения функции

Критические значения функции — это значения функции в критических точках. Например, если (c, f(c)) является критической точкой y = f(x), то f(c) называется критическим значением функции, соответствующей критической точке (c, f(c)).

Поиск критических точек

Ниже приведены шаги для нахождения критической точки (точек) функции на основе определения. Чтобы найти критическую точку (точки) функции y = f (x):

• Шаг — 1: Найдите производную f'(x).
• Шаг — 2: Установите f ‘(x) = 0 и решите его, чтобы найти все значения x (если они есть), удовлетворяющие ему.
• Шаг — 3: Найдите все значения x (если есть), где f'(x) НЕ определено.
• Шаг — 4: Все значения x (только те, которые находятся в области определения f(x)) из Шаг — 2 и Шаг — 3 являются x-координатами критических точек. Чтобы найти соответствующие y-координаты, просто подставьте каждую из них в функцию y = f(x). Запись всех таких пар (x, y) даст нам все критические точки.

Пример поиска критических точек

Найдем критические точки функции f(x) = x ^1/3 — x. Для этого сначала нужно найти производную.

Шаг — 1: f'(x) = (1/3) x ^-2/3 — 1 = 1 / (3x ^2/3) ) — 1

Шаг — 2: f'(х) = 0
1 / (3x ^2/3) ) — 1 = 0
1 / (3x ^2/3) ) = 1
1 = 3x ^2/3
1/3 = х ^2/3
Кубирование с обеих сторон,
1/27 = х ²
Извлекая квадратный корень с обеих сторон,
± 1/(3√3) = х (или) х = ± √3 / 9
Таким образом, x = √3/9 и x = — √3/9

Шаг — 3: f'(x) НЕ определен при x = 0.

Шаг — 4: Область определения f(x ) представляет собой набор всех действительных чисел и, следовательно, все значения x из Step — 2 и Step — 3 присутствуют в области f (x) и, следовательно, все они являются x-координатами критических точек. Найдем их соответствующие y-координаты:

• Когда x = √3/9, y = (√3/9) ^1/3 — (√3/9) = 2√3/9
• Когда x = -√3/9, y = (-√3/9) ^1/3 — (-√3/9) = -2√3/9
• Когда x = 0, y = 0 ^1/3 — 0 = 0

Следовательно, критическими точками f(x) являются (√3/9, 2√3/9), (-√3/9, -2√3/9) и (0, 0). В этом примере координаты y критических точек, равные 2√3/9, -2√3/9 и 0, являются критическими значениями функции.

Критические точки на графике

Мы уже видели, как найти критические точки, когда задана функция. Теперь мы увидим, как найти критические точки на графике функции. Следующие пункты помогут нам определить критические точки на данном графике.

• Мы знаем, что точки, в которых касательные горизонтальны, являются критическими точками. Так что во всех таких критических точках график либо меняется от «возрастания к убыванию», либо от «убывания к возрастанию». это значит кривая может иметь (но не обязательно) локальный максимум или локальный минимум в критических точках. Вот пример.

  
  На приведенном выше рисунке (0, 0) и (2, 4) являются критическими точками, поскольку в этих точках мы имеем соответственно локальный минимум и локальный максимум. Обратите внимание, что мы можем провести горизонтальные касательные и в этих точках.

• Точки на кривой, где мы можем провести вертикальную касательную, также являются критическими точками.

  
  На приведенном выше рисунке (0, 0) является критической точкой.

• Острые поворотные точки (каспы) также являются критическими точками.

  
  На приведенном выше рисунке (0, 0) является критической точкой.

Критические точки многомерных функций

Для нахождения критических точек функции с одной переменной y = f(x) мы установили ее производную равной нулю и решили. Но чтобы найти критические точки функций с несколькими переменными (функций с более чем одной переменной), мы просто установим каждую первую частную производную по каждой переменной равной нулю и решим полученные одновременные уравнения. Например:

• Чтобы найти критические точки функции двух переменных f(x, y), положим ∂f / ∂x = 0 и ∂f / ∂y = 0 и решим систему уравнений.
• Чтобы найти критические точки функции трех переменных f(x, y, z), положим ∂f / ∂x = 0, ∂f / ∂y = 0 и ∂f / ∂z = 0, и решим результат система уравнений.

Пример нахождения критических точек функции двух переменных

Найдем критические точки функции f(x, y) = x ² + y ² + 2x + 2y. Для этого мы должны сначала найти частные производные, а затем приравнять каждую из них к нулю.

∂f / ∂x = 2x + 2 и ∂f / ∂y = 2y + 2

Если мы установим их равными нулю,

• 2x + 2 = 0 ⇒ x = -1
• 2у + 2 = 0 ⇒ у = -1

Итак, критическая точка (-1, -1).

Важные моменты в критических точках:

• Точки, в которых можно провести касательную по горизонтали, являются критическими точками.
• Точки, в которых можно провести вертикальную касательную, являются критическими точками.
• Все острые поворотные точки являются критическими.
• Точки локального минимума и локального максимума являются критическими точками, но функция не обязана иметь локальный минимум или локальный максимум в критической точке. Например, f(x) = 3x ⁴ — 4x ³ имеет критическую точку в точке (0, 0), но она не является ни минимумом, ни максимумом.
• Критическая точка линейной функции не существует.
• Критическая точка квадратичной функции всегда является ее вершиной.

Связанные темы:

• Калькулятор производных
• Применение деривативов
• Максимум и минимум
• Тест первой производной
• Тест второй производной

Часто задаваемые вопросы о критических точках

Что такое критическая точка в исчислении?

Критическая точка функции y = f(x) — это точка, в которой график функции имеет либо вертикальную, либо горизонтальную касательную. Для нахождения критических точек видим:

• Точки, в которых f'(x) = 0.
• Точки, в которых f'(x) НЕ определено.

Как найти критические точки функции?

Чтобы найти критические точки функции y = f(x), просто найдите значения x, где производная f'(x) = 0, а также значения x, где f'(x) не определено. Они дадут значения x критических точек, а подстановка каждого из них в y = f (x) даст значения y критических точек.

Как найти критические точки на графике?

Чтобы найти критические точки на графике:

• Проверьте минимальные и максимальные точки.
• Проверьте точки, в которых возможно проведение горизонтальной или вертикальной касательной.
• Проверьте наличие острых поворотных точек (выступов).

Как найти критические точки функций многих переменных?

Чтобы найти критические точки функции многих переменных, скажем, f(x, y), мы просто устанавливаем частные производные по каждой переменной равными 0 и решаем уравнения. т. е. решаем f\(_x\)=0 и f\(_y\)=0 и решаем их.

Является ли критическая точка всегда локальным минимумом или локальным максимумом?

Нет, критическая точка не всегда должна быть локальным минимумом или локальным максимумом. Например, критическая точка f(x) = x ³ равна (0, 0), но f(x) не имеет ни минимума, ни максимума в точке (0, 0).

Для чего нужна критическая точка?

Критическая точка используется для:

• Нахождения максимумов и минимумов.
• Нахождение возрастающих и убывающих интервалов.
• Используется в задачах оптимизации.

Какие бывают типы критических точек?

Может быть три типа критических точек:

• Критические точки, в которых функция имеет максимумы/минимумы.
• Критические точки, в которых может быть вертикальная касательная.
• Критические точки, в которых график делает резкий поворот.

Исчисление I – критические точки

Онлайн-заметки Пола
Главная / Исчисление I / Применение производных / Критические точки

Показать мобильное уведомление Показать все примечания Скрыть все примечания

Уведомление для мобильных устройств

Похоже, вы используете устройство с «узкой» шириной экрана ( т. е. вы наверное на мобильном телефоне). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.

Раздел 4.2: Критические точки

Критические точки будут появляться на протяжении большей части этой главы, поэтому нам сначала нужно определить их и поработать с несколькими примерами, прежде чем переходить к разделам, в которых они используются.

Определение

Мы говорим, что \(x = c\) является критической точкой функции \(f\left( x \right)\), если \(f\left( c \right)\) существует и если верно любое из следующих утверждений.

\[f’\влево(c\вправо) = 0\hspace{0,5 дюйма}{\mbox{OR}}\hspace{0,5in}f’\влево(c\вправо)\,\,\,{\mbox {не существует}}\]

Обратите внимание, что мы требуем, чтобы \(f\left( c \right)\) существовало, чтобы \(x = c\) действительно было критической точкой. Это важный момент, которым часто пренебрегают. На самом деле это говорит о том, что все критические точки должны находиться в области определения функции. Если точка не находится в области определения функции, то она не является критической точкой.

Также обратите внимание, что на данный момент мы работаем только с действительными числами, поэтому любые комплексные числа, которые могут возникнуть при нахождении критических точек (а они иногда будут возникать), будут игнорироваться. Есть части исчисления, которые работают немного по-другому при работе с комплексными числами, поэтому в первом классе исчисления, таком как этот, мы игнорируем комплексные числа и работаем только с действительными числами. Расчет с комплексными числами выходит за рамки этого курса и обычно преподается на курсах математики более высокого уровня. 92}\влево({5x — 3}\вправо)\влево({x+5}\вправо) = 0\]

Поскольку это факторизованная форма производной, довольно легко определить три критические точки. Они есть,

\[x = — 5,\,\,\,\,\,\,x = 0,\,\,\,\,\,\,x = \frac{3}{5}\]

Полиномы обычно представляют собой довольно простые функции для нахождения критических точек при условии, что степень не становится настолько большой, что возникают проблемы с поиском корней производной. 9{\ гидроразрыва {1} {3}}}}} \]

Нам нужно быть осторожными с этой проблемой. Столкнувшись с отрицательным показателем степени, часто лучше исключить знак минус в показателе степени, как мы сделали выше. На самом деле это не обязательно, но иногда это может облегчить нашу жизнь, если мы это сделаем.

Заметим также, что устранение отрицательного показателя степени во втором члене позволяет нам правильно определить, почему \(t = 0\) является критической точкой для этой функции. Как только мы переместим второй член в знаменатель, мы ясно увидим, что производная не существует в \(t = 0\), и поэтому это будет критическая точка. Если вы не избавитесь от отрицательного показателя степени во втором члене, многие люди неправильно заявят, что \(t = 0\) является критической точкой, потому что производная равна нулю в \(t = 0\). Хотя это может показаться глупой точкой, в конце концов, в каждом случае \(t = 0\) идентифицируется как критическая точка, это иногда важно знать, почему точка является критической точкой. Фактически, через пару разделов мы увидим факт, который работает только для критических точек, в которых производная равна нулю. 9{\ гидроразрыва {1} {3}}}}} \]

Обратите внимание, что у нас все еще есть \(t = 0\) в качестве критической точки. Выполнение такого объединения никогда не должно терять критические точки, это делается только для того, чтобы помочь нам их найти. Как мы видим, теперь стало намного проще быстро определить, где производная будет равна нулю. Напомним, что рациональное выражение будет равно нулю только в том случае, если его числитель равен нулю (и, конечно, при условии, что знаменатель в этот момент не равен нулю). 2} — w — 6 = \left( {w — 3} \right)\left( {w + 2} \right) = 0\]

Мы не стали возводить это в квадрат, так как если это ноль, то ноль в квадрате по-прежнему будет нулем, а если он не равен нулю, то возведение в квадрат не сделает его равным нулю.

Отсюда видно, что производная не будет существовать при \(w = 3\) и \(w = — 2\). Однако это НЕ критические точки, так как в этих точках функция также не будет существовать. Напомним, что для того, чтобы точка была критической, функция должна действительно существовать в этой точке.

В этот момент мы должны быть осторожны. Числитель не учитывается, но это не означает, что нет критических точек, в которых производная равна нулю. Мы можем использовать формулу квадрата для числителя, чтобы определить, равна ли дробь в целом нулю. 92} — 4\влево( 1 \вправо)\влево( { — 1} \вправо)} }}{{2\влево( 1 \вправо)}} = \frac{{ — 14 \pm \sqrt {200} }}{2} = \frac{{ — 14 \pm 10\sqrt 2 }}{2} = — 7 \pm 5\sqrt 2 \]

Итак, мы получаем две критические точки. Кроме того, это не «хорошие» целые числа или дроби. Это будет происходить при случае. Не зацикливайтесь на ответах, которые всегда должны быть «хорошими». Часто это не так.

Обратите внимание, что мы используем только действительные числа для критических точек. Итак, если бы при решении квадратного числа в числителе мы получили комплексное число, эти точки не считались бы критическими.

Подводя итог, у нас есть две критические точки. Они есть,

\[w = — 7 + 5\sqrt 2 ,\,\,\,\,w = — 7 — 5\sqrt 2 \]

Опять же, помните, что, хотя производная не существует в точках \(w = 3\) и \(w = — 2\), не существует и функции, поэтому эти две точки не являются критическими для этой функции.

В предыдущем примере нам пришлось использовать квадратичную формулу для определения некоторых потенциальных критических точек. Мы знаем, что иногда мы получаем комплексные числа из квадратичной формулы. Просто помните, что, как упоминалось в начале этого раздела, когда это происходит, мы игнорируем возникающие комплексные числа.

До сих пор во всех примерах не было триггерных функций, экспоненциальных функций, и т. д. . в них. Мы не должны ожидать, что так будет всегда. Итак, давайте взглянем на некоторые примеры, в которых используются не только степени \(x\).

Пример 4. Определить все критические точки функции. \[y = 6x — 4\cos \left( {3x} \right)\]

Показать решение

Сначала получите производную и не забудьте использовать цепное правило для второго члена.

\[y’ = 6 + 12\sin\left( {3x} \right)\]

Теперь это будет существовать везде, поэтому не будет критических точек, для которых производная не существует. Единственными критическими точками будут точки, в которых производная равна нулю. Нам нужно будет решить,

\[\begin{align*}6 + 12\sin \left( {3x} \right) & = 0\\ \sin \left( {3x} \right) & = — \frac{1}{2}\ конец {выравнивание *} \]

Решение этого уравнения дает следующее.

\[\begin{align*}3x & = 3,6652 + 2\pi n,\hspace{0,25in}n = 0, \pm 1, \pm 2, \ldots \\ 3x & = 5,7596 + 2\pi n, \hspace{0.25in}n = 0, \pm 1, \pm 2, \ldots \end{align*}\]

Не забудьте \(2 \pi n\) на них! В будущем будут проблемы, в которых мы упустим решения без этого! Также убедитесь, что он надет на этом этапе! Теперь разделите на 3, чтобы получить все критические точки для этой функции.

\[\begin{align*}x &= 1,2217 + \frac{{2\pi n}}{3},\hspace{0.5in}n = 0, \pm 1, \pm 2, \ldots \\ x &= 1,9199 + \frac{{2\pi n}}{3},\hspace{0.5in}n = 0, \pm 1, \pm 2, \ldots \end{align*}\]

Обратите внимание, что в предыдущем примере мы получили бесконечное количество критических точек. 2}}}\] 92}\left( {\frac{3}{{3x}}} \right)\\ & = 2x\ln \left( {3x} \right) + x\\ & = x\left( {2\ln \left( {3x} \right) + 1} \right)\end{align*}\]

Теперь этой производной не будет, если \(x\) является отрицательным числом или если \(x = 0\), но опять же не будет и функции, так что это не критические точки. Помните, что функция будет существовать только в том случае, если \(x > 0\), и достаточно хорошо, что производная также будет существовать только в том случае, если \(x > 0\), поэтому единственное, о чем нам нужно беспокоиться, это где производная равна нулю.

Во-первых, обратите внимание, что, несмотря на внешний вид, производная не будет равна нулю для \(x = 0\). Как отмечалось выше, производная не существует в \(x = 0\) из-за натурального логарифма, и поэтому производная не может быть там равна нулю!

Таким образом, производная будет равна нулю, только если

\[\begin{align*}2\ln \left( {3x} \right) + 1 & = 0\\ \ln \left( {3x} \right) & = — \frac{1}{2}\ конец {выравнивание *} \]

Напомним, что мы можем решить эту задачу, возведя обе части в степень.