Как найти определитель матрицы 3х3 треугольником: Определитель матрицы методом треугольника | Мозган калькулятор онлайн

Теоретические вопросы

1. Матрицы. Различные виды матриц.

2. Определители. Основные свойства определителей.

3. Миноры. Алгебраические дополнения.

4. Разложение определителей по строке или столбцу.

5. Метод обращения в нуль всех, кроме одного, элементов столбца или строки.

6. Действия над матрицами:

• сложение матриц;

• умножение матрицы на число;

• произведение матриц.

• транспонирование матриц.

7. Равенство матриц.

8. Обратная матрица.

9. Ранг матрицы. Свойства, вычисление. Метод окаймляющих миноров.

10. Элементарные преобразования.

    Вычисление ранга матрицы с помощью элементарных преобразований.

11. Система линейных уравнений. Матрицы системы. Матричная форма записи системы.

12. Исследование систем линейных уравнений, теорема Кронекера-Капелли.

13. Решение систем линейных уравнений по правилу Крамера.

14. Матричный метод решения систем линейных уравнений.

15. Метод Жордана – Гаусса для решения систем линейных уравнений.

16. Однородная система линейных уравнений. Совместность системы. Фундаментальная система решений. Общее решение.

17. Линейные операторы. Собственные значения и собственные векторы линейного оператора.

Задание №1

Пример 1. Найти 4А + 2В, если , .

Решение.

.

Пример 2. Определить АВ, если , .

Решение.

Примеры для самостоятельной работы

Составить матрицы А=(а_ij), В=(в_ij) и вычислить:

1. 2А +3В, где А и В матрицы размера 4х6;

2. матрицу С, если 4С – 3В = 2А;

3. А², А³, А⁴, если А_2х2;

4. произведение матриц:

а) А_1х4∙В_4х2; б) А_1х3∙В_3х3; в) А_3х5∙В_5х1; г) А_3х3

∙В_3х6.

Задание №2

Пример 3. Вычислить определитель .

Решение. Вычислим определитель, используя правило треугольника

Пример 4. Вычислить определитель .

Решение. Разложим определитель по элементам второй строки:

Пример 5. Вычислить определитель .

Решение. Обозначим данный определитель через . Общий множитель элементов первого столбца (2) вынесем за знак определителя, затем элементы второго столбца прибавим к элементам третьего столбца, наконец, элементы третьей строки, умноженные на (-3), прибавим к элементам четвертой строки.

.

Разложим определитель по элементам третьего столбца:

.

Преобразуем полученный определитель. Вторую строку, умноженную на (-2), прибавим к первой строке.

.

Разложим определитель по элементам первого столбца:

.

Примеры для самостоятельной работы

а) Вычислить определители третьего порядка:

1. 2. 3.

4. 6.

7. 8. 9.

10. 11. 12.

13. 14. 15.

16. 17. 18.

19. 20. 21.

22. 23. 24.

26. 27.

28. 29. 30.

б) Вычислить определители четвертого порядка:

1. 2. 3.

4. 5. 6.

7. 8. 9.

10. 11. 12.

13. 14. 15.

16. 17. 18.

19. 20. 21.

22. 23. 24.

25. 26. 27.

28. 29. 30.

Задание №4

Пример 6. Пользуясь правилом умножения матриц, представить в виде определителя произведение определителей .

Решение.

Примеры для самостоятельной работы

Пользуясь правилом умножения матриц, представить в виде определителя произведение определителей:

1. 2.

3. 4.

5. 6.

7. 8.

9. 10.

11. 12.

13. 14.

15. 16.

17. 18.

19. 20.

21. 22.

23. 24.

25. 26.

27. 28.

29. 30.

Задание №5

Пример 7. Найти обратную матрицу для матрицы .

Решение. Вычислим определитель матрицы

.

Определитель detА0, следовательно, матрица А имеет обратную.

Составим транспонированную матрицу А^Т для матрицы А:

.

Найдем алгебраические дополнения элементов матрицы А^Т:

Тогда матрица, составленная из алгебраических дополнений матрицы А^Т, запишется в виде: .

Запишем обратную матрицу:

.

Покажем, что АА^-1=Е.

Действительно,

.

Площадь треугольника в детерминантной форме

Площадь треугольника в детерминантной форме вычисляется в координатной геометрии, когда заданы координаты вершин треугольника. Нахождение площади треугольника в виде определителя является одним из важных приложений определителей. Как правило, мы определяем площадь треугольника, используя формулу половины произведения основания и высоты треугольника. Но если высота треугольника неизвестна и известны его вершины, то площадь треугольника можно найти по формуле определителя.

В этой статье мы вычислим площадь треугольника в форме определителя, используя его формулу. Мы решим несколько примеров, основанных на понятии площади треугольника в детерминантной форме, чтобы лучше понять его применение.

1.	Чему равна площадь треугольника в определяющей форме?
2.	Формула площади треугольника в определителе
3.	Как определить площадь треугольника в форме определителя?
4.	Часто задаваемые вопросы о площади треугольника в форме определителя

Чему равна площадь треугольника в определяющей форме?

Площадь треугольника в детерминантной форме можно вычислить, если известны вершины треугольника. Если у нас есть треугольник ABC с вершинами A(x ₁ , y ₁ ), B(x ₂ , y ₂ ) и C(x ₃ , y ₃ ), то его площадь можно вычислить как (1/2) [x ₁ (y ₂ — y ₃ ) + х ₂ (у ₃ — у ₁ ) + х ₃ (у ₁ — у ₂ )]. Общая формула площади треугольника равна половине произведения его основания на высоту.

Но в координатной геометрии, если даны координаты вершин треугольника, мы можем вычислить площадь треугольника в детерминантной форме. Давайте теперь пройдемся по его формуле в форме определителя в следующем разделе.

Формула площади треугольника в определителе

Формула площади треугольника в форме определителя дает скалярное значение, которое может быть положительным или отрицательным. Но так как площадь треугольника никогда не может быть отрицательной, мы рассматриваем абсолютное значение определителя как площадь треугольника. Теперь, если вершины треугольника ABC равны A(x ₁ , y ₁ ), B(x ₂ , y ₂ ) и C(x ₃ , y ₃ ) в декартовой плоскости, то площадь треугольника в формуле детерминанта определяется как end{vmatrix}\)

После упрощения эту формулу площади треугольника в детерминантной форме можно также записать как:

Площадь треугольника ABC = (1/2) | [х ₁ (у ₂ — у ₃ ) + х ₂ (у ₃ — у ₁ ) + х ₃ (у ₁ — у ₂ )] |

Как определить площадь треугольника в форме определителя?

Теперь, когда мы знаем формулу для вычисления площади треугольника в форме определителя, мы решим несколько примеров, чтобы понять ее применение. Рассмотрим треугольник ABC, вершины которого заданы с координатами.

Пример 1: Найдите площадь треугольника в детерминантной форме с вершинами A(0, 0), B(0, -5) и C(8, 0).

Решение: Чтобы найти площадь треугольника ABC, воспользуемся формулой Площадь треугольника ABC = \(\dfrac{1}{2}\begin{vmatrix}x_1&y_1&1\\x_2&y_2&1\\x_3&y_3&1\end{ vmatrix}\)

Здесь х ₁

= 0, х ₂ = 0, х ₃ = 8, у ₁ = 0, у ₂ = -5, у 3 Следовательно, площадь определяется как

Площадь = \(\dfrac{1}{2}\begin{vmatrix}x_1&y_1&1\\x_2&y_2&1\\x_3&y_3&1\end{vmatrix}\)

= \(\dfrac{1}{2}\begin{vmatrix}0&0&1\\0&-5&1\\8&0&1\end{vmatrix}\)

= (1/2) | [0 _{(-5 — 0) + 0 (0 — 0) + 8 (0 — (-5))] |}

= (1/2) | 0 + 0 + 8 × 5 |

= (1/2) × 40

= 20 квадратных единиц

Ответ: Следовательно, площадь треугольника ABC с вершинами A(0, 0), B(0, -5) и C(8 , 0) составляет 20 квадратных единиц.

Пример 2: Вычислите площадь треугольника PQR методом определителя, вершинами которого являются P(-3, -5), Q(-8, 5) и R(1, 2).

Решение: Чтобы найти площадь треугольника PQR, воспользуемся формулой Площадь треугольника PQR = \(\dfrac{1}{2}\begin{vmatrix}x_1&y_1&1\\x_2&y_2&1\\x_3&y_3&1\end{ vmatrix}\)

Здесь х ₁ = -3, х ₂ = -8, х ₃ = 1, у ₁ = -5, у ₂ = 5, у 3 = 3 2. Следовательно, площадь определяется как

Площадь = (1/2) | [х ₁ (у ₂ — у ₃ ) + х ₂ (у ₃ — у ₁ ) + х ₃ (у ₁ — у ₂ )] |

= (1/2) | [-3 _{(5 — 2) + (-8) (2 — (-5)) + 1 (-5 — 5)] |}

= (1/2) | [-3 _{(3) — 8 (7) + 1 (-10)] |}

= (1/2) |- 9 — 56 — 10|

= (1/2) |-75|

= (1/2) × 75

= 37,5 квадратных единиц

Ответ: Следовательно, площадь треугольника PQR равна 37,5 квадратных единиц.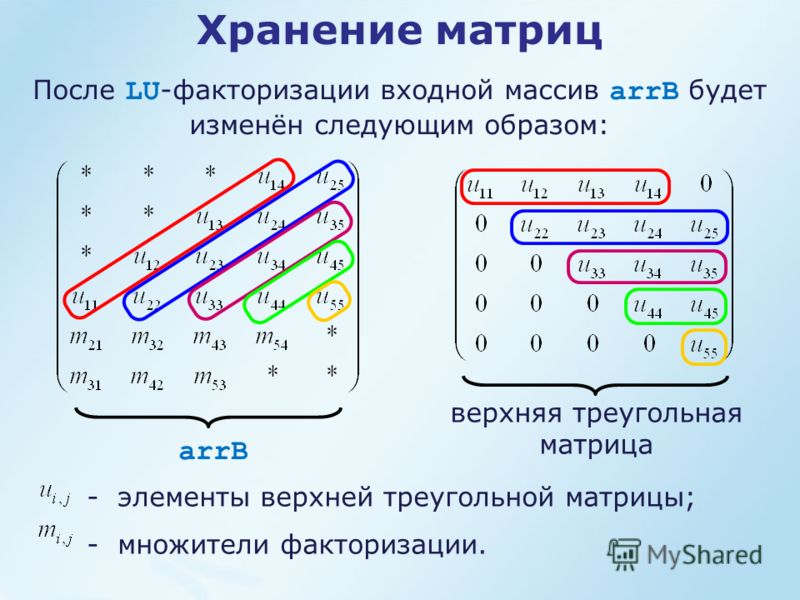

Важные примечания о площади треугольника в форме определителя

• При упрощении формула площади треугольника ABC с вершинами A(x ₁ , y ₁ ), B(x ₂ , y ₂ ), и C(x _{4 ) , y 3 ) в форме определителя равно (1/2) | [x 1 (Y 2 — Y 3 ) + x 2 (Y 3 — Y 1 ) + x 3 (Y 1 — Y 2 )] | .}
• Вычисление площади треугольника в форме определителя является применением определителей.

☛ Похожие темы:

• Инволютивная матрица
• Равенство матриц
• Треугольная матрица

Часто задаваемые вопросы о площади треугольника в форме определителя

Что такое площадь треугольника в детерминантной форме?

Площадь треугольника в детерминантной форме можно вычислить, если известны вершины треугольника. Если у нас есть треугольник ABC с вершинами A(x ₁ , y ₁ ), B(x ₂ , y ₂ ) и C(x ₃ , y ₃ ), то его площадь можно вычислить как (1/2) [x ₁ ( у ₂ — у ₃ ) + х ₂ (у ₃ — у ₁ ) + х ₃ (у ₁ — у 2 _].

Как найти площадь треугольника с тремя координатами?

Мы можем найти площадь треугольника с 3 координатами, используя формулу определителя. Для треугольника ABC с вершинами A(x ₁ , y ₁ ), B(x ₂ , y ₂ ) и C(x ₃ , y ₃ ), мы можем использовать формулу \(\dfrac{1}{ 2}\begin{vmatrix}x_1&y_1&1\\x_2&y_2&1\\x_3&y_3&1\end{vmatrix}\).

Какая формула площади треугольника в форме определителя?

Формула для нахождения площади треугольника в форме определителя с использованием формулы \(\dfrac{1}{2}\begin{vmatrix}x_1&y_1&1\\x_2&y_2&1\\x_3&y_3&1\end{vmatrix}\), где A(x ₁ , y ₁ ), B(x ₂ , y ₂ ) и C(x ₃ , y ₃ ) — вершины треугольника ABC. При упрощении формулы определителя имеем формулу вида (1/2) [x ₁ (y ₂ — y ₃ ) + x ₂ (y ₃ — y ₁ ) + х ₃ (у ₁ — у ₂ )].

Как найти площадь треугольника в форме определителя?

Площадь треугольника в детерминантной форме можно определить по формуле (1/2) [x ₁ (Y ₂ — Y ₃ ) + x ₂ (Y ₃ — Y ₁ ) + x ₃ (Y ₁ — Y ₂ )], где A ₁ — Y ₂ )], где A ₁ — Y (x ₁ , y ₁ ), B(x ₂ , y ₂ ) и C(x ₃ , y ₃ ) — вершины треугольника ABC.

12.8: Основные методы определения определителей

Кофакторы и определители 2 x 2

Результаты

1. Вычислить определитель квадратной матрицы, используя разложение Лапласа или операции со строками.
2. Продемонстрируйте влияние операций со строками на определители.
3. Проверьте следующее:
   1. Определитель произведения матриц является произведением определителей.
   2. Определитель матрицы равен определителю ее транспонирования.

Пусть \(A\) — матрица \(n\times n\). То есть пусть \(A\) — квадратная матрица. Определитель числа \(A\), обозначаемый \(\det \left(A\right)\), является очень важным числом, которое мы будем исследовать в этом разделе.

Если \(A\) является 2\(\×2\) матрицей, определитель определяется следующей формулой.

Определение \(\PageIndex{1}\): определитель матрицы два на два

Пусть \(A=\left[ \begin{array}{rr} a & b \\ c & d \end{array } \right].\) Тогда \[\det \left( A\right) = ad-cb\nonumber \]

Определитель также часто обозначают, заключая матрицу в две вертикальные линии. Таким образом, \[\det \left[ \begin{array}{rr} a & b \\ c & d \end{array} \right] =\left| \begin{array}{rr} a & b \\ c & d \end{array} \right| =ad — bc\номер \]

Ниже приведен пример нахождения определителя матрицы \(2 \times 2\).

Пример \(\PageIndex{1}\): Определитель два на два

Найдите \(\det\left(A\right)\) для матрицы \(A = \left[ \begin{array}{ rr} 2 & 4 \\ -1 & 6 \end{массив} \right].\)

Решение

Из определения \(\PageIndex{1}\), \[\det \left( A\right) = \left( 2\right) \left( 6\right) -\left( -1\right) \left( 4\right) = 12 + 4 = 16\nonnumber \]

\(2 \times 2 \) определитель можно использовать для нахождения определителя больших матриц. Теперь мы рассмотрим, как найти определитель матрицы \(3 \times 3\), используя несколько инструментов, включая определитель \(2 \times 2\). 9{th}\) столбец \(A\).

Следовательно, с каждой записью \(A\) связан минор. Рассмотрим следующий пример, демонстрирующий это определение.

Пример \(\PageIndex{2}\): поиск миноров матрицы

Пусть \[A = \left[ \begin{array}{rrr} 1 & 2 & 3 \\ 4 & 3 & 2 \\ 3 & 2 & 1 \end{массив} \right]\nonumber \] Найти \(второстепенный\левый(A\правый) _{12}\) и \(второстепенный\левый(A\правый) _{23}\ ).

Решение

Сначала найдем \(второстепенный\левый( A\правый) _{12}\). По определению \(\PageIndex{2}\) это определитель матрицы \(2\times 2\), которая получается при удалении первой строки и второго столбца. Этот минор задается \[минор \left(A\right)_{12} = \det \left[ \begin{array}{rr} 4 & 2 \\ 3 & 1 \end{array} \right]\ nonumber \] Используя определение \(\PageIndex{1}\), мы видим, что \[\det \left[ \begin{array}{rr} 4 & 2 \\ 3 & 1 \end{array} \right] = \влево(4\вправо)\влево(1\вправо) — \влево(3\вправо)\влево(2\вправо) = 4 — 6 = -2\не число\] 9{th}\) элемент матрицы, то его сомножитель равен просто \(\mathrm{cof}\left( A\right) _{ij}.\)

Пример \(\PageIndex{3}\): Поиск Сомножители матрицы

Рассмотрим матрицу \[A=\left[ \begin{array}{rrr} 1 & 2 & 3 \\ 4 & 3 & 2 \\ 3 & 2 & 1 \end{array} \right ]\nonumber \] Найдите \(\mathrm{cof}\left(A\right) _{12}\) и \(\mathrm{cof}\left(A\right) _{23}\).

Решение

Мы будем использовать определение \(\PageIndex{3}\) для вычисления этих кофакторов.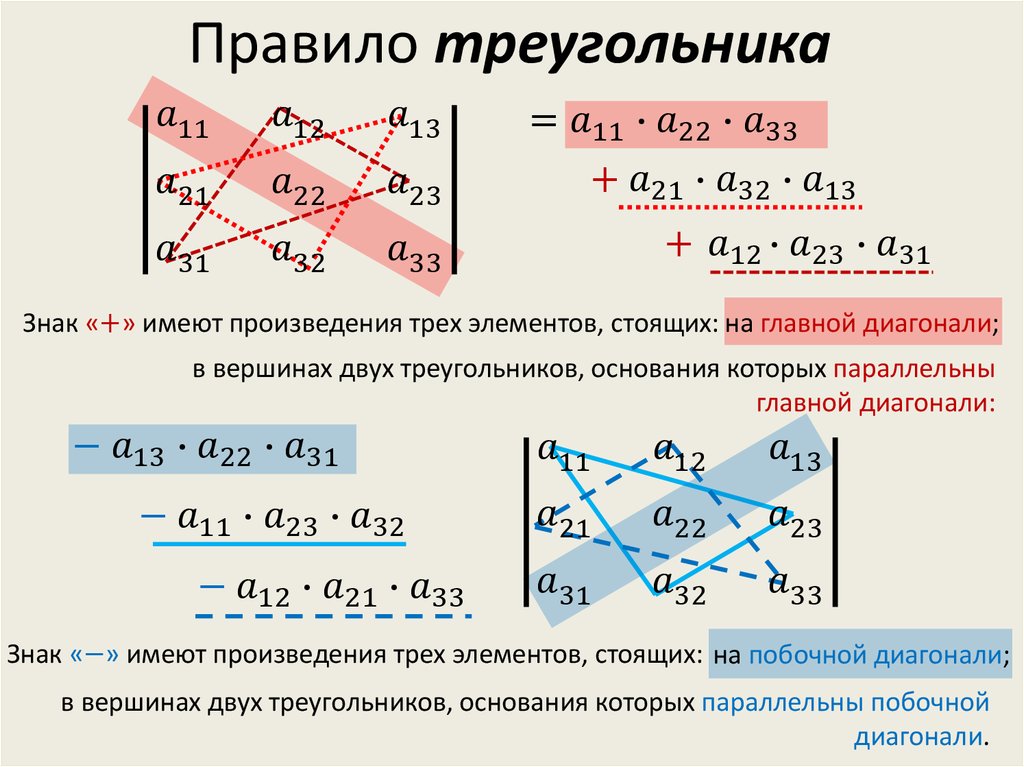 9{2+3}\left( -4\right) =4\nonnumber \]

Вы можете найти оставшиеся сомножители для приведенной выше матрицы. Помните, что для каждой записи в матрице есть кофактор.

Теперь мы установили инструменты, необходимые для нахождения определителя матрицы \(3 \times3\).

Определение \(\PageIndex{4}\): определитель матрицы три на три

Пусть \(A\) — матрица \(3\x 3\). Затем \(\det \left(A\right)\) вычисляется путем выбора строки (или столбца) и произведения каждой записи в этой строке (столбце) с ее кофактором и сложения этих продуктов вместе. 9{th}\) строка (столбец) , как указано \[\det \left(A\right) = a_{i1}\mathrm{cof}(A)_{i1} + a_{i2}\mathrm{ cof}(A)_{i2} + a_{i3}\mathrm{cof}(A)_{i3}\nonumber \]

При вычислении определителя вы можете расширить любую строку или любой столбец. Независимо от вашего выбора, вы всегда получите одно и то же число, которое является определителем матрицы \(A.\). Этот метод вычисления определителя путем расширения по строке или столбцу называется Расширение Лапласа или Расширение кофактора . {3+1}\left| \begin{массив}{rr} 2 и 3 \\ 3 и 2 \end{массив} \right| }}\nonumber \] Вычисляя каждое из них, получаем \[\det \left(A\right) = 1 \left(1\right)\left(-1\right) + 4 \left(-1\right) )\left(-4\right) + 3 \left(1\right)\left(-5\right) = -1 + 16 + -15 = 0\nonnumber \] Следовательно, \(\det\left(A \справа) = 0\). 9{2+3}\влево| \begin{массив}{rr} 1 и 2 \\ 3 и 2 \end{массив} \right| }}\nonumber \]

Вычисляя каждое из этих произведений, получаем \[\det \left(A\right) = 4\left(-1\right)\left(-2\right) + 3\left( 1\right)\left(-8\right) + 2 \left(-1\right)\left(-4\right) = 0\nonnumber \]

Как видите, для обоих методов мы получили \( \det \влево(А\вправо) = 0\).

Как упоминалось выше, мы всегда будем получать одно и то же значение для \(\det \left(A\right)\) независимо от строки или столбца, которые мы выбираем для расширения. Вы должны попытаться вычислить указанный выше определитель, развернув его по другим строкам и столбцам. Это хороший способ проверить свою работу, потому что вы должны каждый раз придумывать одно и то же число!

Мы формально представим эту идею в следующей теореме.

Теорема \(\PageIndex{1}\): определитель правильно определен

Разложение матрицы \(n\times n\) по любой строке или столбцу всегда дает один и тот же ответ, который является определителем.

Теперь мы рассмотрели определитель матриц \(2 \times 2\) и \(3 \times 3\). Оказывается, что метод, используемый для вычисления определителя матрицы \(3 \times 3\), может быть использован для вычисления определителя матрицы любого размера. Обратите внимание, что определение \(\PageIndex{2}\), определение \(\PageIndex{3}\) и определение \(\PageIndex{4}\) можно применять к матрице любого размера. 9{й}\) столбец. Как и в случае с определителем \(3 \times 3\), мы можем вычислить определитель матрицы \(4 \times 4\) с помощью разложения Лапласа по любой строке или столбцу

Рассмотрим следующий пример.

Пример \(\PageIndex{5}\): определитель матрицы четыре на четыре

Найдите \(\det \left( A\right)\), где \[A=\left[ \begin{array}{ rrrr} 1 & 2 & 3 & 4 \\ 5 & 4 & 2 & 3 \\ 1 & 3 & 4 & 5 \\ 3 & 4 & 3 & 2 \end{array} \right]\nonumber \] 9{4+3}\left\vert \begin{array}{rrr} 1 & 2 & 4 \\ 5 & 4 & 3 \\ 1 & 3 & 5 \end{array} \right\vert\nonumber \]

Теперь вы можете вычислить каждый \(3 \times 3\) определитель, используя разложение Лапласа, как мы сделали выше. Вы должны выполнить их в качестве упражнения и убедиться, что \(\det \left( A \right)= -12\).

Ниже приводится формальное определение определителя матрицы \(n \times n\). Вы можете воспользоваться моментом и рассмотреть приведенные выше определения для детерминантов \(2 \times 2\) и \(3 \times 3\) в контексте этого определения. 9{й}\) столбец.

В следующих разделах мы рассмотрим некоторые важные свойства и характеристики определителя.

Определитель треугольной матрицы

Существует определенный тип матрицы, для которого нахождение определителя является очень простой процедурой. Рассмотрим следующее определение.

Определение \(\PageIndex{6}\): треугольные матрицы

Матрица \(A\) является верхнетреугольной, если \(a_{ij}=0\) при \(i>j\). Таким образом, элементы такой матрицы ниже главной диагонали равны \(0\), как показано. Здесь \(\ast\) относится к любому ненулевому числу. \[ \left[ \begin{array}{cccc} \ast & \ast & \cdots & \ast \\ 0 & \ast & \cdots & \vdots \\ \vdots & \vdots & \ddots & \ast \ \ 0 & \cdots & 0 & \ast \end{array} \right]\nonumber \] Аналогично определяется нижняя треугольная матрица как матрица, у которой все элементы выше главной диагонали равны нулю.

Следующая теорема дает полезный способ вычисления определителя треугольной матрицы.

Теорема \(\PageIndex{2}\): определитель треугольной матрицы

Пусть \(A\) — верхняя или нижняя треугольная матрица. Тогда \(\det \left( A\right)\) получается произведением элементов на главной диагонали.

Проверить эту теорему можно, вычислив определитель с помощью разложения Лапласа по первой строке или столбцу.

Рассмотрим следующий пример.

Пример \(\PageIndex{6}\): определитель треугольной матрицы

Пусть \[A=\left[ \begin{array}{rrrr} 1 & 2 & 3 & 77 \\ 0 & 2 & 6 & 7 \\ 0 & 0 & 3 & 33,7 \\ 0 & 0 & 0 & -1 \end{массив} \right]\nonumber \] Найти \(\det \left( A\right).\)

Решение

Из теоремы \(\PageIndex{2}\) достаточно взять произведение элементов на главной диагонали. Таким образом, \(\det \left( A\right) =1\times 2\times 3\times \left(-1\right) =-6.\) 9{4+1}\влево| \begin{array}{rrr} 2 & 3 & 77 \\ 2 & 6 & 7 \\ 0 & 3 & 33.7 \end{array} \right|\end{aligned}\] и единственный ненулевой член в расширении это \[1\левый| \begin{array}{rrr} 2 & 6 & 7 \\ 0 & 3 & 33.