Как найти периметр сечения: Как найти периметр сечения. Как найти сечение параллелепипеда

Как найти периметр сечения. Как найти сечение параллелепипеда

Сечения геометрических фигур имеют различные формы. У параллелепипеда сечение всегда представляет собой прямоугольник или квадрат. Оно имеет ряд параметров, которые могут быть найдены аналитическим способом.

Через параллелепипед можно провести четыре сечения, которые представляют собой квадраты или прямоугольники. Всего он имеет два диагональных и два поперечных сечения. Как правило, они имеют разные размеры. Исключением является куб, у которого они одинаковы.
Перед тем как строить сечение параллелепипеда, составьте представление о том, что представляет собой эта фигура. Существует два вида параллелепипедов — обычный и прямоугольный. У обычного параллелепипеда грани располагаются под некоторым углом к основанию, а у прямоугольного они перпендикулярны ему. Все грани прямоугольного параллелепипеда представляют собой прямоугольники или квадраты. Из этого следует,что куб — это частный случай прямоугольного параллелепипеда. 2.
Найдя диагональ и зная высоту параллелепипеда, вычислите площадь сечения параллелепипеда:

S=d*h.

Периметр диагонального сечения тоже можно вычислять по двум величинам — диагонали основания и высоте параллелепипеда. В этом случае вначале найдите две диагонали (верхнего и нижнего оснований) по теореме Пифагора, а затем сложите с удвоенным значением высоты.

Если провести плоскость, параллельную ребрам параллелепипеда, можно получить сечение-прямоугольник, сторонами которого являются одна из сторон основания параллелепипеда и высота. Площадь этого сечения найдите следующим образом:
S=a*h.
Периметр этого сечения найдите аналогичным образом по следующей формуле:
p=2*(a+h).

Последний случай возникает, когда сечение проходит параллельно двум основаниям параллелепипеда. Тогда его площадь и периметр равны значению площади и периметра оснований, т.е.:
S=a*b — площадь сечения;

Разделы: Математика

Класс: 10

Цели урока

• Формирование у учащихся навыков решения задач на построение сечений.
• Формирование и развитие у учащихся пространственного воображения.
• Развитие графической культуры и математической речи.
• Формирование умения работать индивидуально и в коллективе.

Тип урока: урок формирования и совершенствования знаний.

Формы организации учебной деятельности: групповая, индивидуальная, коллективная.

Техническое обеспечение урока: компьютер, мультимедийный проектор, экран, набор геометрических тел (куб, параллелепипед, тетраэдр).

ХОД УРОКА

1. Организационный момент

Класс разбивается на 3 группы по 5-6 человек. На каждом столе – индивидуальные и групповые задания по построению сечения, набор тел. Знакомство учащихся с темой и целями урока.

2. Актуализация опорных знаний

Опрос теории:

– Аксиомы стереометрии.
– Понятие параллельных прямых в пространстве.
– Теорема о параллельных прямых.
– Параллельность трех прямых.
– Взаимное расположение прямой и плоскости в пространстве.
– Признак параллельности прямой и плоскости.
– Определение параллельности плоскостей.
– Признак параллельности двух плоскостей.
– Свойства параллельных плоскостей.
– Тетраэдр. Параллелепипед. Свойства параллелепипеда.

3. Изучение нового материала

Слово учителя: При решении многих стереометрических задач используется сечение многогранника плоскостью. Назовем секущей плоскостью многогранника любую плоскость, по обе стороны от которой имеются точки данного многогранника.
Секущая плоскость пересекает грани по отрезкам. Многоугольник, сторонами которого являются эти отрезки, называется сечением многогранника.
С помощью рисунков 38-39 давайте выясним: Какое количество сторон может иметь сечение тетраэдра и параллелепипеда?

Учащиеся анализируют рисунки и делают выводы. Учитель корректирует ответы учащихся, указывая на тот факт, что если секущая плоскость пересекает две противоположные грани параллелепипеда по каким-то отрезкам, то эти отрезки параллельны.

Анализ решения задач 1, 2, 3, приведенных в учебнике (устная коллективная работа).

4. Закрепление изученного материала (по группам)

1 группе: объясните, как построить сечение тетраэдра плоскостью, проходящей через данные точки М, N, К и в задачах 1-3 найти периметр сечения, если М, N, К – середины ребер и каждое ребро тетраэдра равно а .

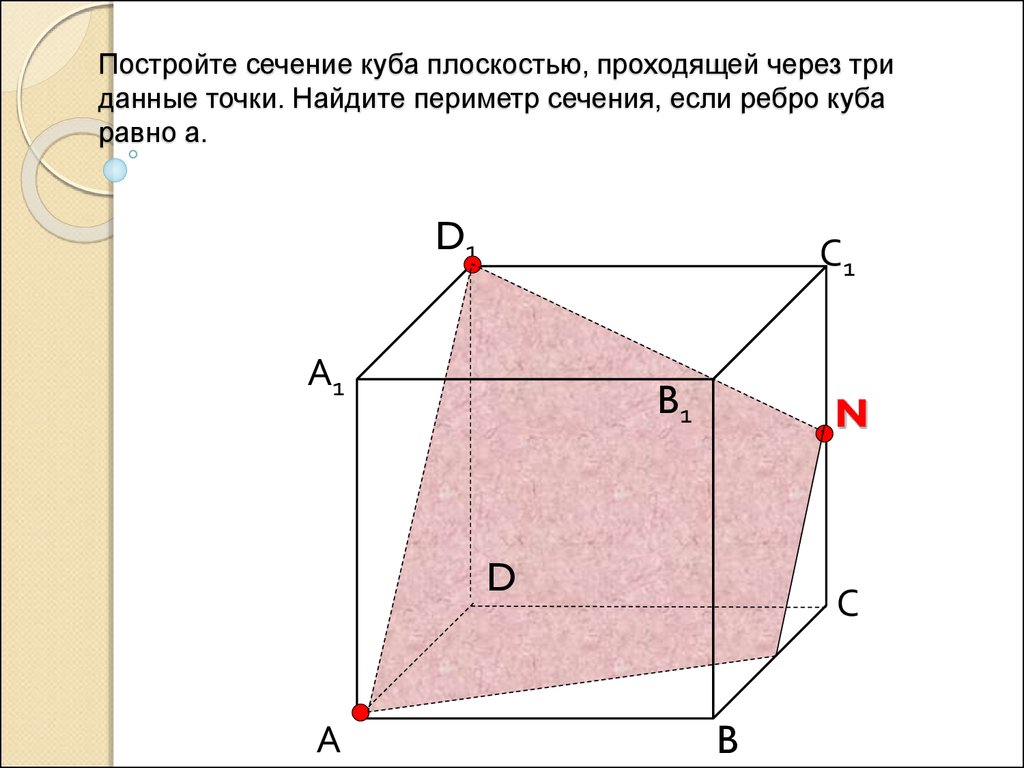
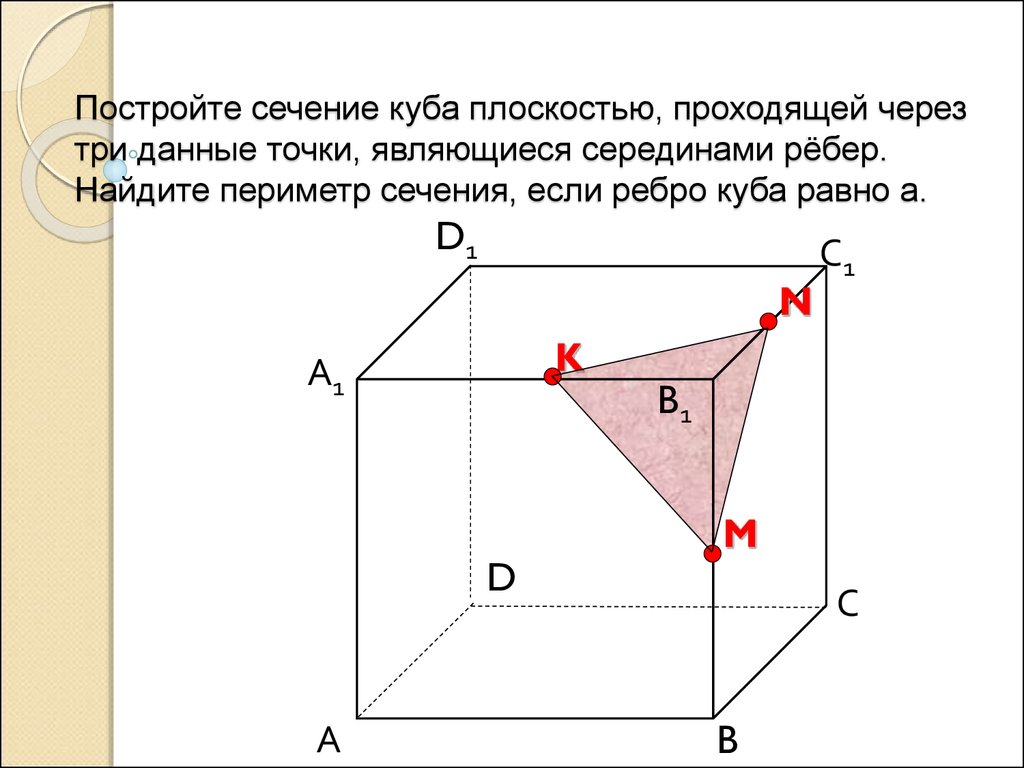
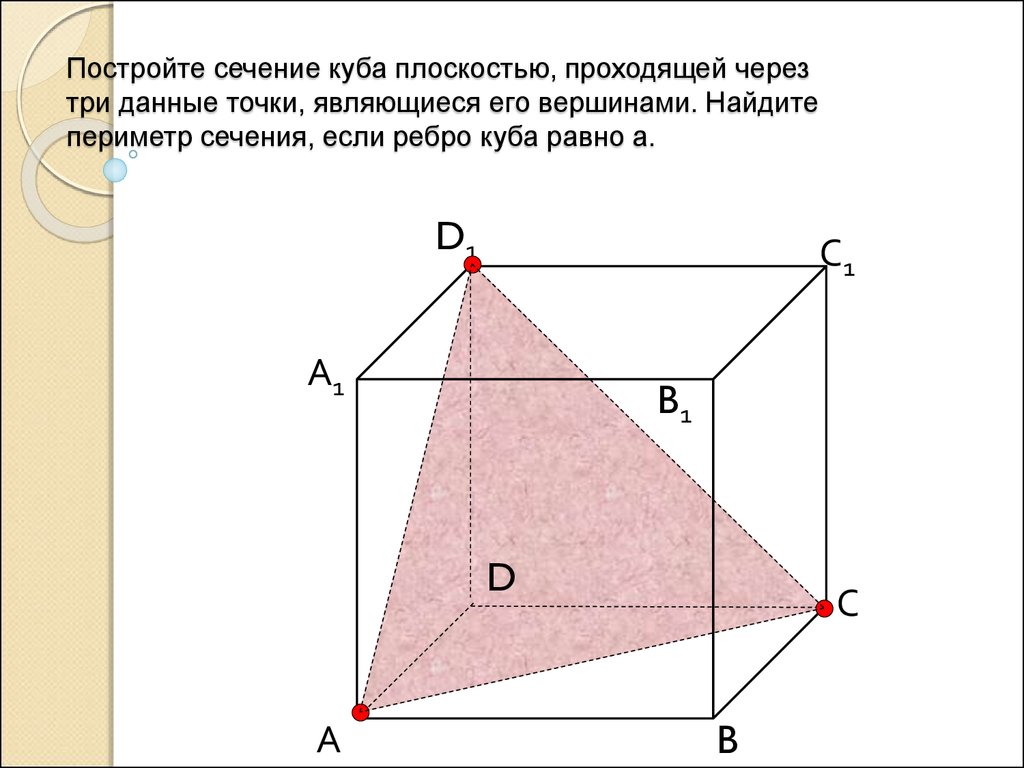
2 группе: объясните, как построить сечение куба плоскостью, проходящей через три данные точки, являющиеся либо вершинами куба, либо серединами его ребер (три данные точки на рисунках выделены), в задачах 1-4 и 6 найдите периметр сечения, если ребро куба равно

а. в задаче 5докажите, что АЕ = а /3

3 группе: построить сечение параллелепипеда АВСDА 1 В 1 С 1 D 1 плоскостью, проходящей через точки:

Все выполненные задания группа защищает у доски, с использованием слайдов.

5. Самостоятельная работа № 85, № 105.

6. Подведение итогов урока

Оценка работы учащихся на уроке.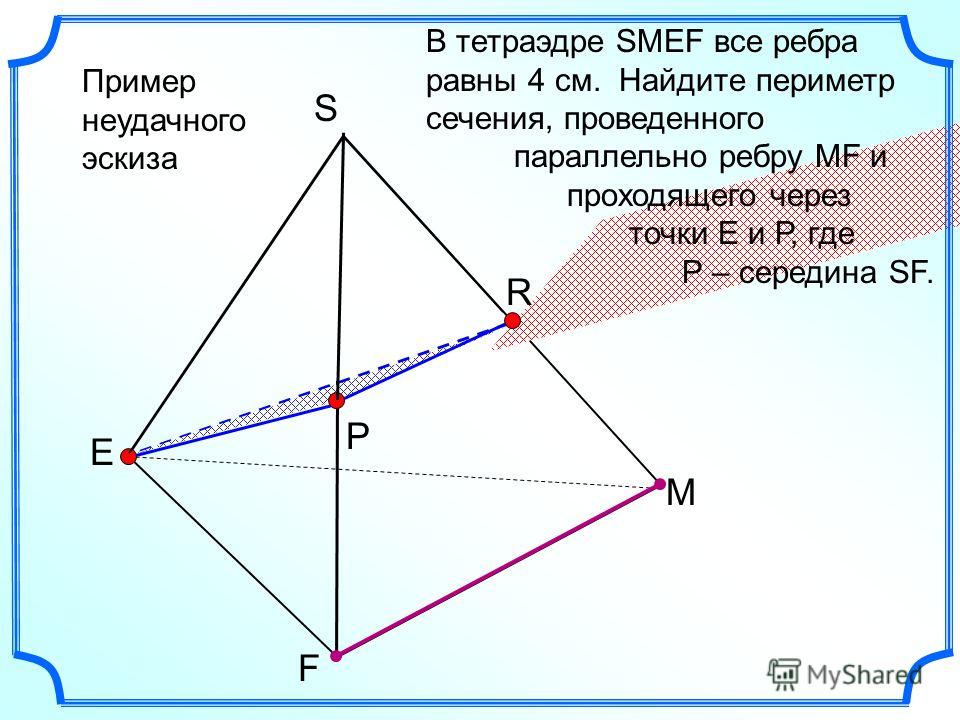

7. Домашнее задание: индивидуальные карточки.

Сечения геометрических фигур имеют разные формы. У параллелепипеда сечение неизменно представляет собой прямоугольник либо квадрат. Оно имеет ряд параметров, которые могут быть обнаружены аналитическим методом.

Инструкция

1. Через параллелепипед дозволено провести четыре сечения, которые представляют собой квадраты либо прямоугольники. Каждого он имеет два диагональных и два поперечных сечения. Как водится, они имеют различные размеры. Исключением является куб, у которого они идентичны.Перед тем как строить сечение параллелепипеда, составьте представление о том, что представляет собой эта фигура. Существует два вида параллелепипедов – обыкновенный и прямоугольный. У обыкновенного параллелепипеда грани располагаются под некоторым углом к основанию, а у прямоугольного они перпендикулярны ему. Все грани прямоугольного параллелепипеда представляют собой прямоугольники либо квадраты. Из этого следует,что куб – это частный случай прямоугольного параллелепипеда.

2.Обнаружив диагональ и зная высоту параллелепипеда, вычислите площадь сечения параллелепипеда:S=d*h.

3. Периметр диагонального сечения тоже дозволено вычислять по двум величинам – диагонали основания и высоте параллелепипеда. В этом случае сначала обнаружьте две диагонали (верхнего и нижнего оснований) по теореме Пифагора, а после этого сложите с удвоенным значением высоты.

4. Если провести плоскость, параллельную ребрам параллелепипеда, дозволено получить сечение-прямоугольник, сторонами которого являются одна из сторон основания параллелепипеда и высота. Площадь этого сечения обнаружьте дальнейшим образом:S=a*h.Периметр этого сечения обнаружьте аналогичным образом по дальнейшей формуле:p=2*(a+h).

5. Конечный случай появляется, когда сечение проходит параллельно двум основаниям параллелепипеда. Тогда его площадь и периметр равны значению площади и периметра оснований, т.е.:S=a*b – площадь сечения;p=2*(a+b).

Раньше, чем перейти к нахождению высоты параллелепипеда, необходимо прояснить, что есть высота и что есть параллелепипед. В геометрии, высотой называют перпендикуляр, от вершины фигуры до ее основания либо отрезок, кратчайшим методом соединяющий верхнее и нижнее основания. Параллелепипед – это многогранник, имеющий два параллельных и равных многоугольника в качестве оснований, углы которых объединены отрезками. Параллелепипед составлен из шести параллелограммов, попарно параллельных и равных друг другу.

Инструкция

1. Высоты в параллелограмме может быть три, в зависимости от расположения фигуры в пространстве, чай повернув параллелепипед на бок, вы поменяете местами его основания и грани. Верхний и нижний параллелограммы – неизменно основания. Если боковые ребра фигуры перпендикулярны основаниям, то параллелепипед прямой, и всякое его ребро – готовая высота. Дозволено измерить.

2. Дабы из наклонного параллелепипеда получить прямой, того же размера, нужно продолжить боковые грани в одном направлении. После этого, возвести перпендикулярное сечение, от углов которого, отложить длину ребра параллелепипеда, и на этом расстоянии возвести второе перпендикулярное сечение.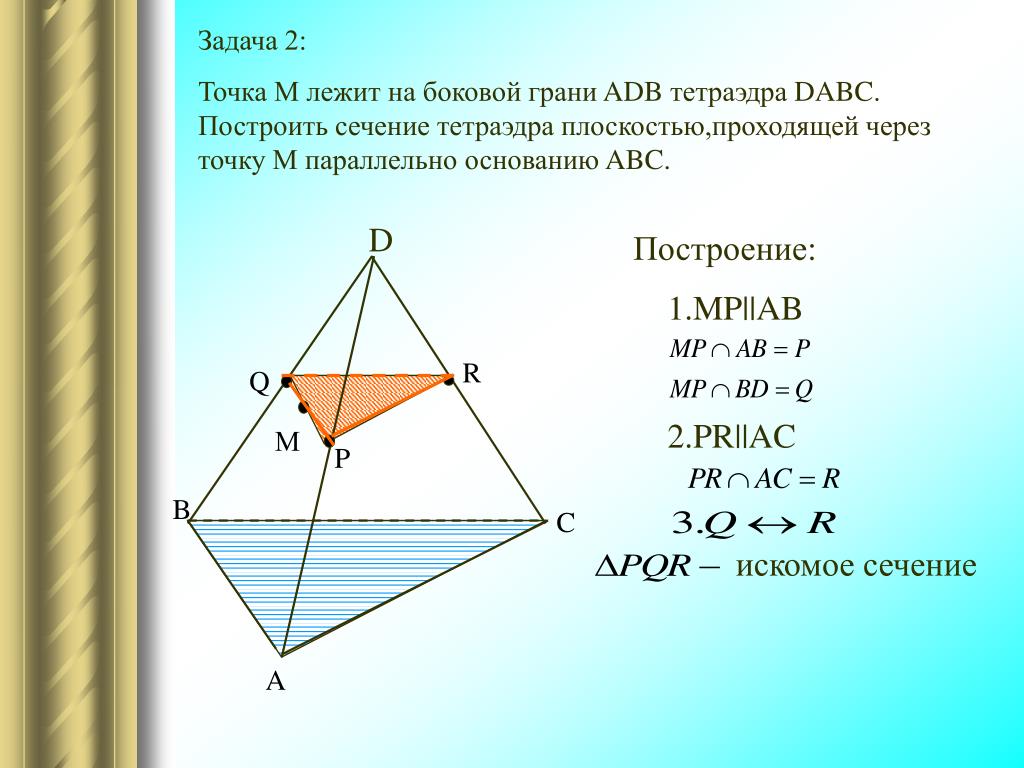

Два построенных вами параллелограмма, ограничат новейший параллелепипед, равновеликий первому. На грядущее следует подметить, что объемы равновеликих фигур идентичны.

3. Почаще вопрос о высоте нам встречается в задачах. Неизменно нам даны данные, дозволяющие вычислить её. Это может быть объем, линейные размеры параллелепипеда, длины его диагоналей.Так объем параллелепипеда равен произведению его основания на высоту, то есть, зная объем и размер основания, легко узнать высоту путем деления первого на второе. Если вы имеете дело с прямоугольным параллелепипедом, то есть такие, основание которого прямоугольник, вам могут попытаться усложнить задачу, в связи с его особенными качествами. Так в прямоугольном параллелепипеде, квадрат всякий его диагонали равен сумме квадратов 3 измерений параллелепипеда. Если в «дано» к задаче о прямоугольном параллелепипеде указаны длина его диагонали и длины сторон основания, то этих сведений довольно, дабы узнать размер желанной высоты.

Параллелепипед – частный случай призмы, у которой все шесть граней являются параллелограммами либо прямоугольниками. Параллелепипед с прямоугольными гранями называют также прямоугольным. У параллелепипеда имеется четыре пересекающиеся диагонали. Если даны три ребра а, b, с, обнаружить все диагонали прямоугольного параллелепипеда дозволено, исполняя добавочные построения.

Инструкция

1. Нарисуйте прямоугольный параллелепипед. Запишите вестимые данные: три ребра а, b, с. Сначала постройте одну диагональ m. Для ее определения используем качество прямоугольного параллелепипеда, согласно которому все его углы являются прямыми.

2. Постройте диагональ n одной из граней параллелепипеда. Построение проведите так, дабы вестимое ребро, желанная диагональ параллелепипеда и диагональ грани совместно образовывали прямоугольный треугольник а, n, m.

3. Обнаружьте построенную диагональ грани. Она является гипотенузой иного прямоугольного треугольника b, с, n. Согласно теореме Пифагора n² = с² + b². Вычислите данное выражение и возьмите корень квадратный из полученного значения – это будет диагональ грани n.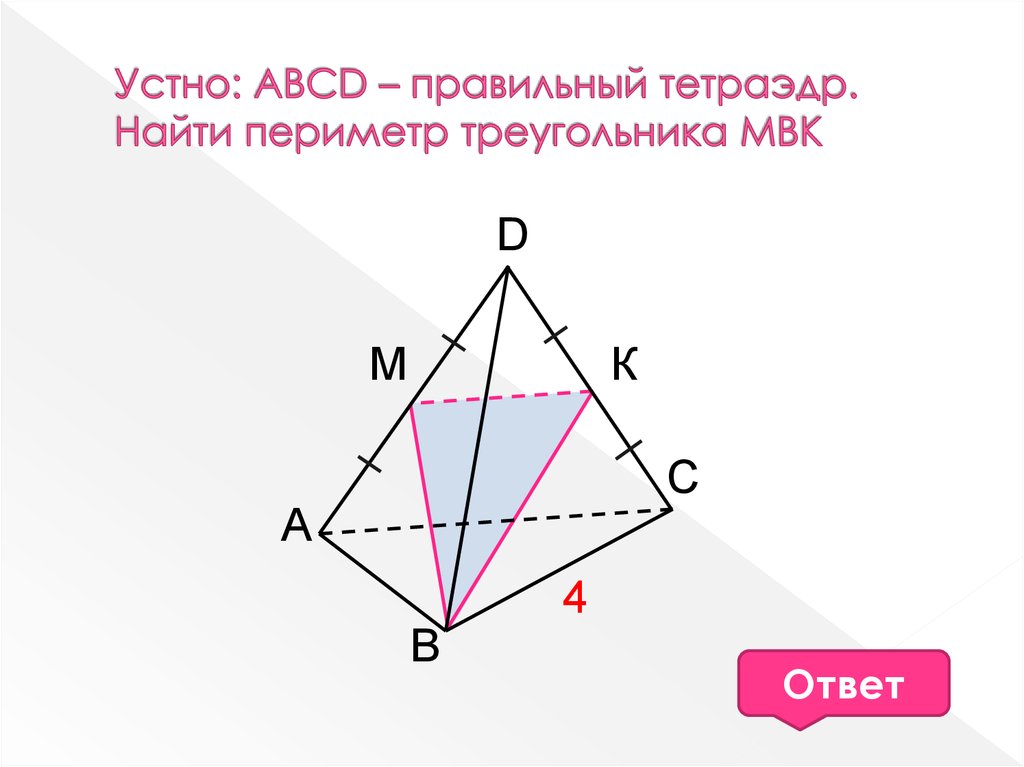

4. Обнаружьте диагональ параллелепипеда m. Для этого в прямоугольном треугольнике а, n, m обнаружьте неведомую гипотенузу: m² = n² + a². Подставьте вестимые значения, после этого вычислите корень квадратный. Полученный итог и будет первой диагональю параллелепипеда m.

5. Аналогичным образом проведите ступенчато все остальные три диагонали параллелепипеда. Также для всей из них исполните добавочные построения диагоналей прилегающих граней. Рассматривая образуемые прямоугольные треугольники и применяя теорему Пифагора, обнаружьте значения остальных диагоналей прямоугольного параллелепипеда.

Видео по теме

Форму параллелепипеда имеют многие настоящие объекты. Примерами являются комната и бассейн. Детали, имеющие такую форму – не редкость и в промышленности. По этой причине зачастую появляется задача нахождения объема данной фигуры.

Инструкция

1. Параллелепипед представляет собой призму, основанием которой является параллелограмм.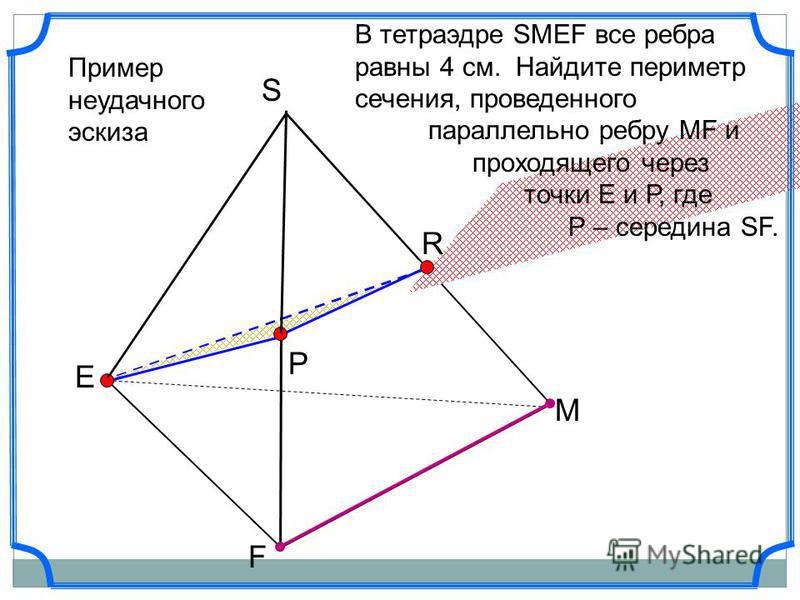 У параллелепипеда имеются грани – все плоскости, формирующие данную фигуру. Каждого у него насчитывается шесть граней, причем, все они являются параллелограммами. Его противоположные грани между собой равны и параллельны. Помимо того, он имеет диагонали, которые пересекаются в одной точке и в ней делятся напополам.

2. Параллелепипед бывает 2-х видов. У первого все грани являются параллелограммами, а у второго – прямоугольниками. Конечный из них именуется прямоугольным параллелепипедом. У него все грани прямоугольные, а боковые грани перпендикулярны к основанию. Если прямоугольный параллелепипед имеет грани, основы которых – квадраты, то он именуется кубом. В этом случае, его грани и ребра равны. Ребром именуется сторона всякого многогранника, к числу которых относится и параллелепипед.

3. Для того, дабы обнаружить объем параллелепипеда, нужно знать площадь его основания и высоту. Объем находится исходя из того, какой именно параллелепипед фигурирует в условиях задачи.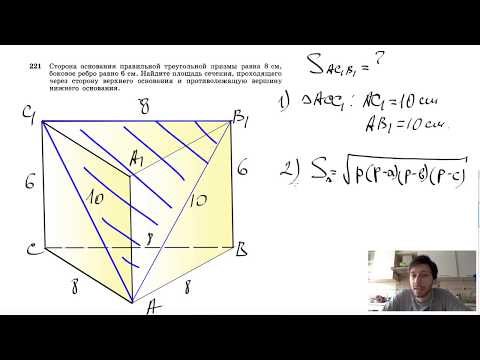 У обычного параллелепипеда в основании находится параллелограмм, а у прямоугольного – прямоугольник либо квадрат, у которого неизменно углы прямые. Если в основании параллелепипеда лежит параллелограмм, то его объем находится дальнейшим образом:V=S*H, где S – площадь основания, H -высота параллелепипедаВысотой параллелепипеда обыкновенно выступает его боковое ребро. В основании параллелепипеда может лежать и параллелограмм, не являющийся прямоугольником. Из курса планиметрии знаменито, что площадь параллелограмма равна:S=a*h, где h – высота параллелограмма, a – длина основания, т.е. :V=a*hp*H

4. Если имеет место 2-й случай, когда основание параллелепипеда – прямоугольник, то объем вычисляется по той же формуле, но площадь основания находится несколько другим образом:V=S*H,S=a*b, где a и b – соответственно, стороны прямоугольника и ребра параллелепипеда.V=a*b*H

5. Для нахождения объема куба следует руководствоваться примитивными логическими методами. От того что все грани и ребра куба равны, а в основании куба – квадрат, руководствуясь формулами, указанными выше, дозволено вывести следующую формулу:V=a^3

Во многих учебниках встречаются задания, связанные с построением сечений разных геометрических фигур, в том числе параллелепипедов.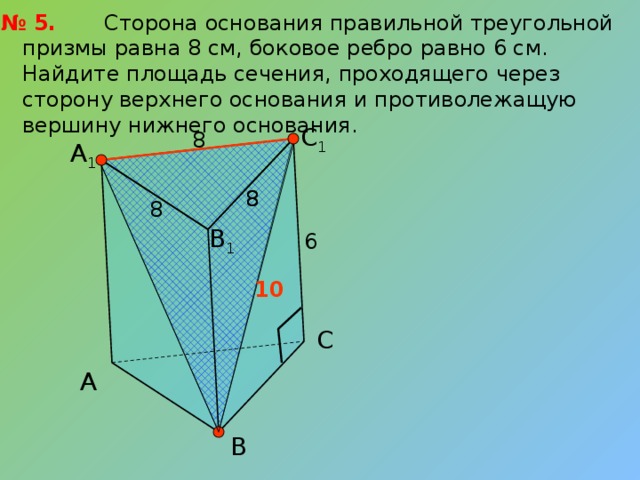 Для того дабы совладать с такой задачей, следует вооружиться некоторыми познаниями.

Вам понадобится

• – бумага;
• – ручка;
• – линейка.

Инструкция

1. На листе бумаге начертите параллелепипед. Если в вашей задаче сказано, что параллелепипед должен быть прямоугольным, то сделайте его углы прямыми. Помните, что противоположные ребра обязаны быть параллельны друг другу. Назовите его вершины, скажем, S1, T1, T, R, P, R1, P1 (как показано на рисунке).

2. На краю SS1TT1 поставьте 2 точки: А и С, пускай точка А будет на отрезке S1T1, а точка С на отрезке S1S. Если в вашей задаче не сказано, где именно обязаны стоять эти точки, и не указано расстояние от вершин, поставьте их произвольно. Проведите прямую линию через точки А и С. Продолжите эту линию до пересечения с отрезком ST. Обозначьте место пересечения, пускай это будет точка М.

3. Поставьте точку на отрезке RT, обозначьте ее как точку В. Проведите прямую линию через точки М и В. Точку пересечения этой линии с ребром SP обозначьте как точку К.

4. Объедините точки К и С. Они обязаны лежать на одной грани PP1SS1. Позже этого через точку B проведите прямую линию, параллельную отрезку КС, продолжите линию до пересечения с ребром R1T1. Точку пересечения обозначьте как точку Е.

5. Объедините точки А и Е. Позже этого выделите получившийся многоугольник ACKBE иным цветом – это будет сечение заданного параллелепипеда.

Обратите внимание!
Помните, что при построении сечения параллелепипеда дозволено соединять между собой только те точки, которые лежат в одной плоскости, если имеющихся у вас точек неудовлетворительно для построения сечения, достраивайте их, путем продолжения отрезков до пересечения с гранью, на которой надобна точка.

Полезный совет
Каждого в параллелепипеде может быть построено 4 сечения: 2 диагональных и 2 поперечных. Для большей наглядности, выделите получившийся многоугольник-сечение, для этого можете примитивно обвести либо заштриховать его иным цветом.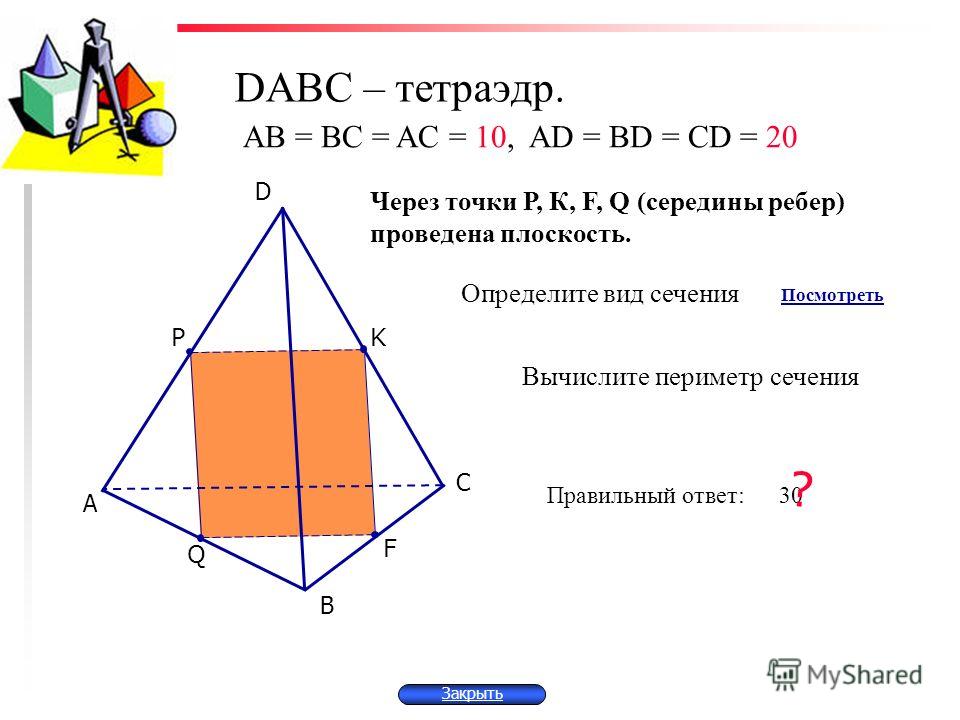

Параллелепипедом именуется призма, основанием которой служит параллелограмм. Параллелограммы, из которых составлен параллелепипед, именуются его гранями, их стороны — ребрами, а вершины параллелограммов — вершинами параллелепипеда.

Инструкция

1. У параллелепипеда дозволено возвести четыре пересекающиеся диагонали. Если знамениты данные 3 ребер а, b и с, обнаружить длины диагоналей прямоугольного параллелепипеда не составит труда, исполняя добавочные построения.

2. Вначале нарисуйте прямоугольный параллелепипед. Подпишите все вестимые вам данные, их должно быть три: ребра а, b и с. Начертите первую диагональ m. Для ее построения воспользуйтесь свойством прямоугольных параллелепипедов, согласно которому все углы сходственных фигур являются прямыми.

3. Постройте диагональ n одной из граней параллелепипеда . Построение сделайте таким образом, дабы знаменитое ребро (а), незнакомая диагональ параллелепипеда и диагональ прилегающей грани (n) образовывали прямоугольный треугольник а, n, m.

4. Посмотрите на построенную диагональ грани (n). Она является гипотенузой иного прямоугольного треугольника b, с, n. Следуя теореме Пифагора, которая гласит, что квадрат гипотенузы равен сумме квадратов катетов (n? = с? + b?), обнаружьте квадрат гипотенузы, после этого извлеките корень квадратный из полученного значения – это и будет длина диагонали грани n.

5. Обнаружьте диагональ самого параллелепипеда m. Для того, дабы обнаружить ее значение, в прямоугольном треугольнике а, n, m вычислите по той же формуле гипотенузу: m? = n? + a?. Вычислите корень квадратный. Обнаруженный итог будет первой диагональю вашего параллелепипеда . Диагональ m.

6. Верно так же проведите ступенчато все остальные диагонали параллелепипеда , для всей из которых исполняйте добавочные построения диагоналей прилегающих граней. Применяя теорему Пифагора, обнаружьте значения остальных диагоналей данного параллелепипеда .

7. Есть еще один метод, с поддержкой которого дозволено обнаружить длину диагонали. Согласно одному из свойств параллелограмма, квадрат диагонали равен сумме квадратов 3 его сторон. Из этого следует, что длину дозволено обнаружить сложив квадраты сторон параллелепипеда и из получившегося значения извлечь квадрат.

Полезный совет
Свойства параллелепипеда:- параллелепипед симметричен касательно середины его диагонали;- всякий отрезок с концами, принадлежащими поверхности параллелепипеда и проходящий через середину его диагонали, делится ею напополам, в частности, все диагонали параллелепипеда пересекаются в одной точке и делятся ею напополам;- противолежащие грани параллелепипеда параллельны и равны;- квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадратов трёх его измерений.

Параллелепипед – объемная геометрическая фигура с тремя измерительными колляциями: длиной, шириной и высотой. Все они участвуют в нахождении площади обеих поверхностей параллелепипеда : полной и боковой.

Инструкция

1. Параллелепипед – многогранник, построенный на основе параллелограмма. У него шесть граней, также являющихся этими двухмерными фигурами. В зависимости от того, как они расположены в пространстве, различают прямой и наклонный параллелепипед. Эта разница выражается в равенстве угла между основанием и боковым ребром 90°.

2. По тому, к какому частному случаю параллелограмма относится основание, дозволено выделить прямоугольный параллелепипед и особенно распространенную его разновидность – куб. Эти формы особенно зачастую встречаются в повседневной жизни и носят наименование стандартных. Они присущи бытовой технике, предметам мебели, электронным приборам и др., а также самим человеческим жилищам, размеры которых имеют весомое значение для обитателей и риелторов.

3. Обыкновенно считают площадь обеих поверхностей параллелепипеда , боковой и полной. Первая числовая колляция представляет собой общность площадей его граней, вторая – та же величина плюс площади обоих оснований, т. е. сумма всех двухмерных фигур, из которых состоит параллелепипед. Следующие формулы носят наименование основных наравне с объемом:Sб = Р h, где Р – пeримeтр основания, h – высота;Sп = Sб + 2 S, где So – площадь основания.

4. Для частных случаев, куба и фигуры с прямоугольными основаниями, формулы упрощаются. Сейчас теснее не надобно определять высоту, которая равна длине вертикального ребра, а площадь и периметр обнаружить значительно легче вследствие наличию прямых углов, в их определении участвуют только длина и ширина. Выходит, для прямоугольного параллелепипеда :Sб = 2 с (a + b), где 2 (а + b) – удвоенная сумма сторон основания (периметр), с – длина бокового ребра;Sп = Sб + 2 а b = 2 а с + 2 b с + 2 a b = 2 (а с + b с + а b).

5. У куба все ребра имеют идентичную длину, следственно:Sб = 4 а а = 4 а?;Sп = Sб + 2 а? = 6 а?.

Вопрос относится к аналитической геометрии. Он решается с привлечением уравнений пространственных прямых и плоскостей, представления куба и его геометрических свойств, а также с применением векторной алгебры.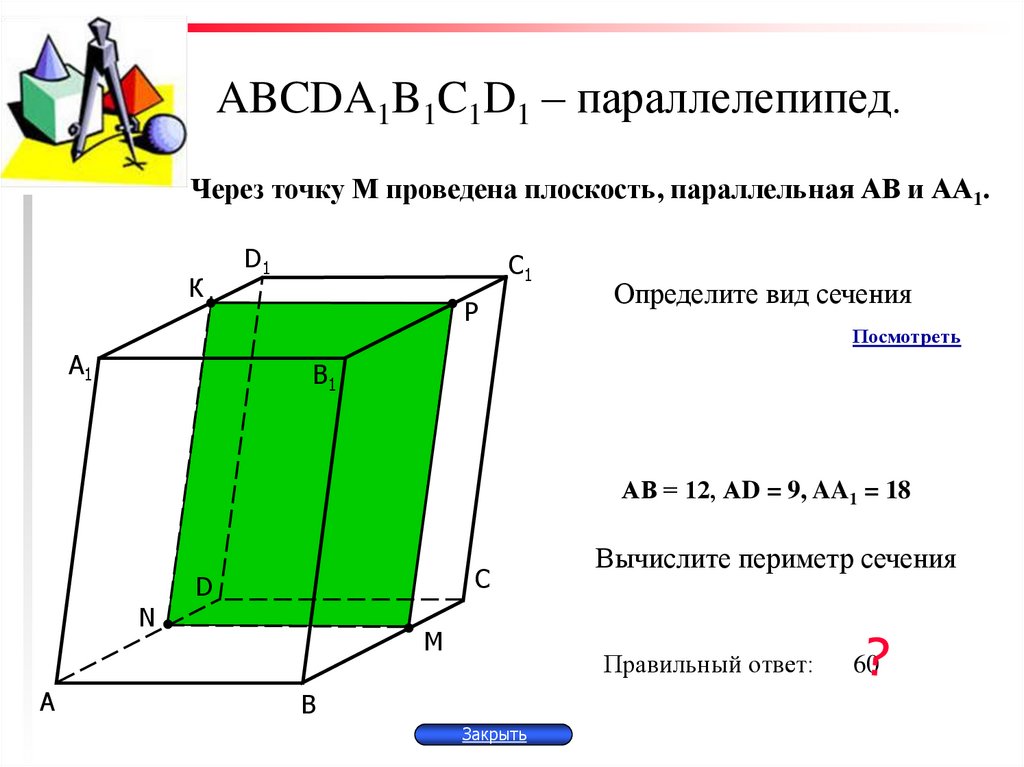 Могут потребоваться методы рения систем линейных уравнений.

Инструкция

1. Выберите данные задачи так, дабы они были исчерпывающими, но не избыточными. Секущую плоскость? следует задать всеобщим уравнением вида Ax+By+Cz+D=0, что наилучшим образом согласуется с произвольным его выбором. Для задания куба абсолютно хватит координат всяких 3 его вершин. Возьмите, скажем, точки M1(x1,y1,z1), M2(x2,y2,z2), M3(x3,y3,z3), в соответствии с рисунком 1. На этом рисунке проиллюстрировано сечение куба. Оно пересекает два боковых ребра и три ребра оснований.

2. Определитесь с планом последующей работы. Предстоит искать координаты точек Q, L, N, W, R пересечения сечения с соответствующими ребрами куба. Для этого придется находить уравнения прямых, содержащих эти ребра, и искать точки пересечения ребер с плоскостью?. Позже этого последует разбиение пятиугольника QLNWR на треугольники (см. рис. 2) и вычисление пощади всего из них с подмогой свойств векторного произведения.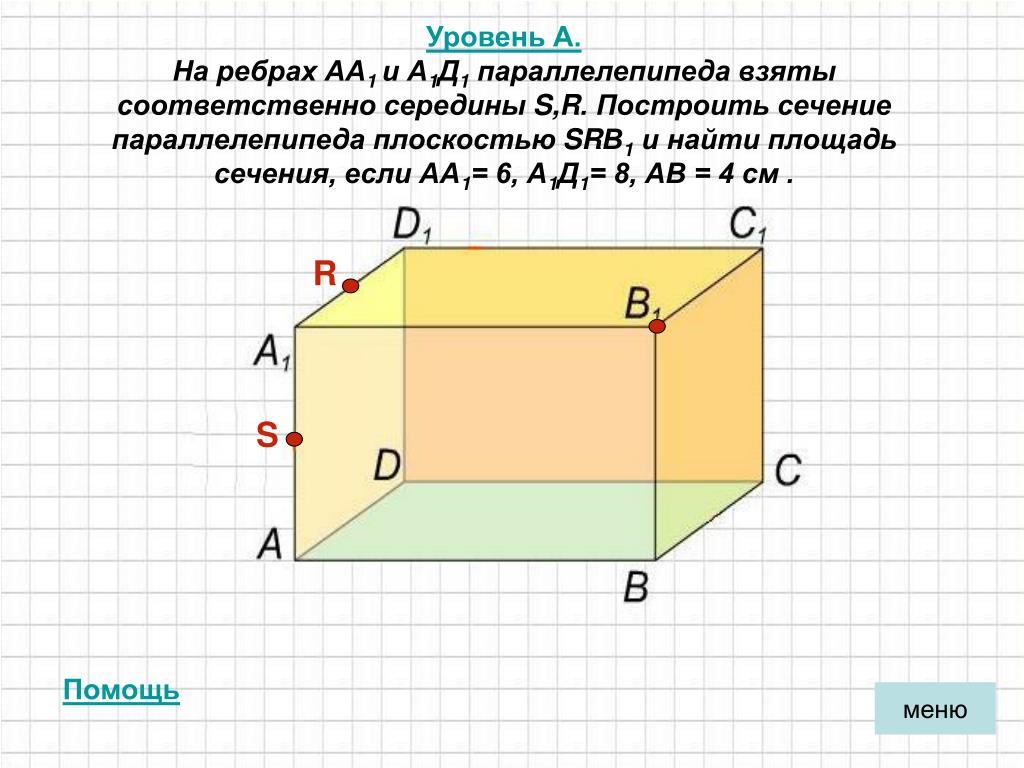 2). Если модуль вектора h |h|??, то замените его соответствующим коллинеарным вектором s={m, n, p}=(h/|h|)?. Сейчас запишите уравнение прямой, содержащей М1М5 параметрически (см. рис. 3). Позже подстановки соответствующих выражений в уравнение секущей плоскости получите А(x1+mt)+B(y1+nt)+C(z1+pt)+D=0. Определите t, подставьте в уравнения для М1М5 и запишите координаты точки Q(qx, qy, qz) (рис. 3).

4. Видимо, что точка М5 имеет координаты М5(x1+m, y1+n, z1+p). Направляющий вектор для прямой, содержащей ребро М5М8 совпадает с М2М3={x3-x2, y3-y2,z3-z2}. После этого повторите предыдущие рассуждения касательно точки L(lx, ly, lz) (см. рис. 4). Все последующее, для N(nx, ny, nz) – точная копия это шага.

5. Запишите векторы QL={lx-qx, ly-qy, lz-qz} и QN={nx-qx, ny-qy, nz-qz}. Геометрический толк их векторного произведения состоит в том, что его модуль равен площади параллелограмма построенного на векторах. Следственно площадь?QLN S1=(1/2)||. Следуйте предложенной методике и вычислите площади треугольников?QNW и?QWR – S1 и S2. Векторное произведение комфортнее каждого находить с поддержкой вектора-определителя (см. рис. 5). Запишите окончательный результат S=S1+S2+S3.

Призма — это многогранник с двумя параллельными основаниями и боковыми гранями в форме параллелограмма и в числе, равном числу сторон многоугольника основания.

Инструкция

1. В произвольной призме боковые ребра расположены под углом к плоскости основания. Частным случаем является прямая призма. В ней боковые стороны лежат в плоскостях, перпендикулярных основаниям. В прямой призме боковые грани — прямоугольники, а боковые ребра равны высоте призмы.

2. Диагональное сечение призмы — часть плоскости, всецело заключенная во внутреннем пространстве многогранника. Диагональное сечение может быть ограничено двумя боковыми ребрами геометрического тела и диагоналями оснований. Видимо, что число допустимых диагональных сечений при этом определяется числом диагоналей в многоугольнике основания.

3.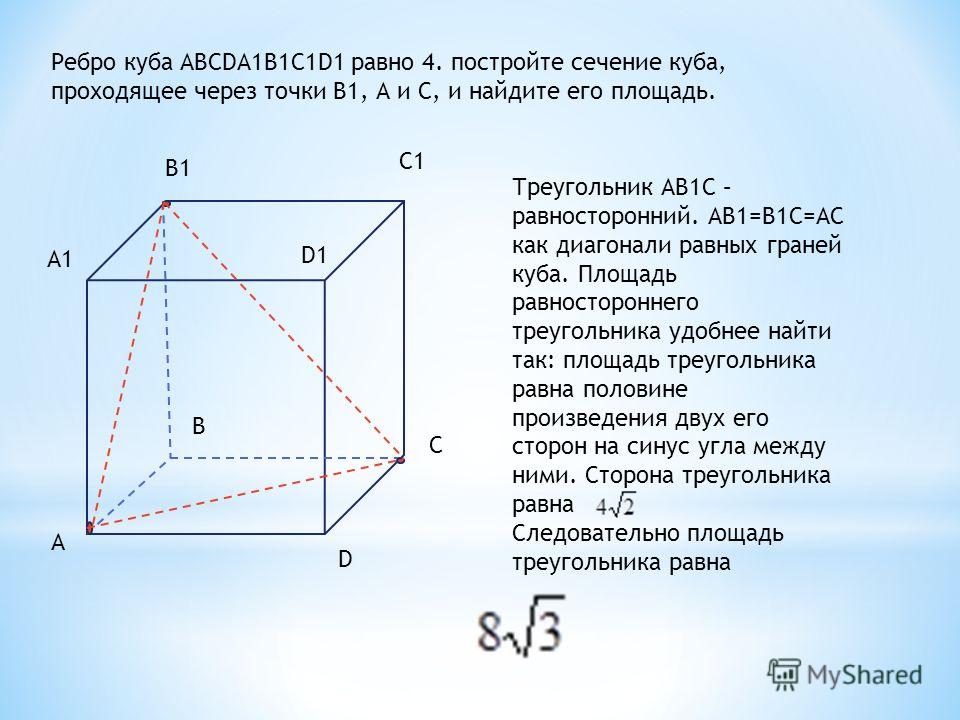 Либо границами диагонального сечения могут служить диагонали боковых граней и противоположные стороны оснований призмы. Диагональное сечение прямоугольной призмы имеет форму прямоугольника. В всеобщем случае произвольной призмы форма диагонального сечения – параллелограмм.

4. В прямоугольной призме площадь диагонального сечения S определяется по формулам:S=d*Hгде d — диагональ основания, H — высота призмы.Либо S=a*Dгде а — сторона основания, принадлежащая единовременно плоскости сечения, D — диагональ боковой грани.

5. В произвольной непрямой призме диагональное сечение — параллелограмм, одна сторона которого равна боковому ребру призмы, иная – диагонали основания. Либо сторонами диагонального сечения могут быть диагонали боковых граней и стороны оснований между вершинами призмы, откуда проведены диагонали боковых поверхностей. Площадь параллелограмма S определяется формулой: S=d*hгде d — диагональ основания призмы, h — высота параллелограмма — диагонального сечения призмы.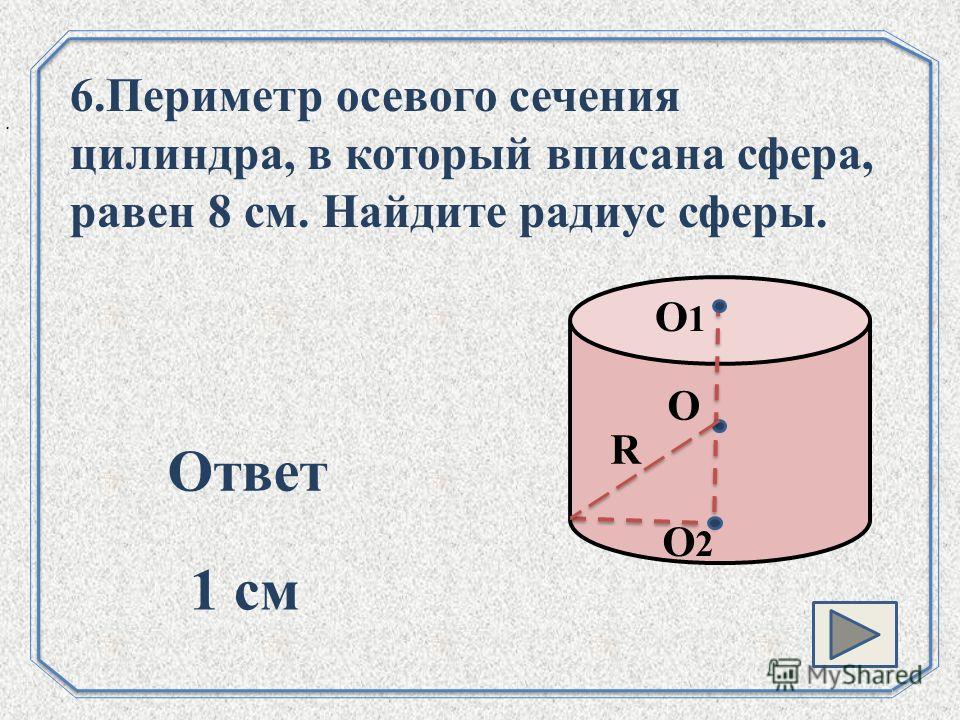 Либо S=a*hгде а — сторона основания призмы, являющаяся и рубежом диагонального сечения, h — высота параллелограмма.

6. Для определения высоты диагонального сечения неудовлетворительно знать линейные размеры призмы. Нужны данные о наклоне призмы к плоскости основания. Последующая задача сводится к ступенчатому решению нескольких треугольников в зависимости от начальных данных об углах между элементами призмы.

315.3. В правильной треугольной призме ABCA 1 B 1 C 1 проведено сечение через вершину С 1 и ребро АB. Найдите периметр сечения. Если сторона основании равна 24 см, а боковое ребро = 10 см.

Сечение ABC 1 — равнобедренный треугольник, так как

как диагонали боковых граней (рис. 92). В правильной треугольной призме боковые ребра перпендикулярны основанию. Поэтому треугольник BCC 1 — прямоугольный и по теореме Пифагора

Таким образом, периметр сечения равен

Ответ. 76 см.

315.4. Докажите, что если точка X равноудалена от концов данного отрезка AB то она лежит па плоскости, проходящей через середину отрезка АB и перпендикулярной прямой AB.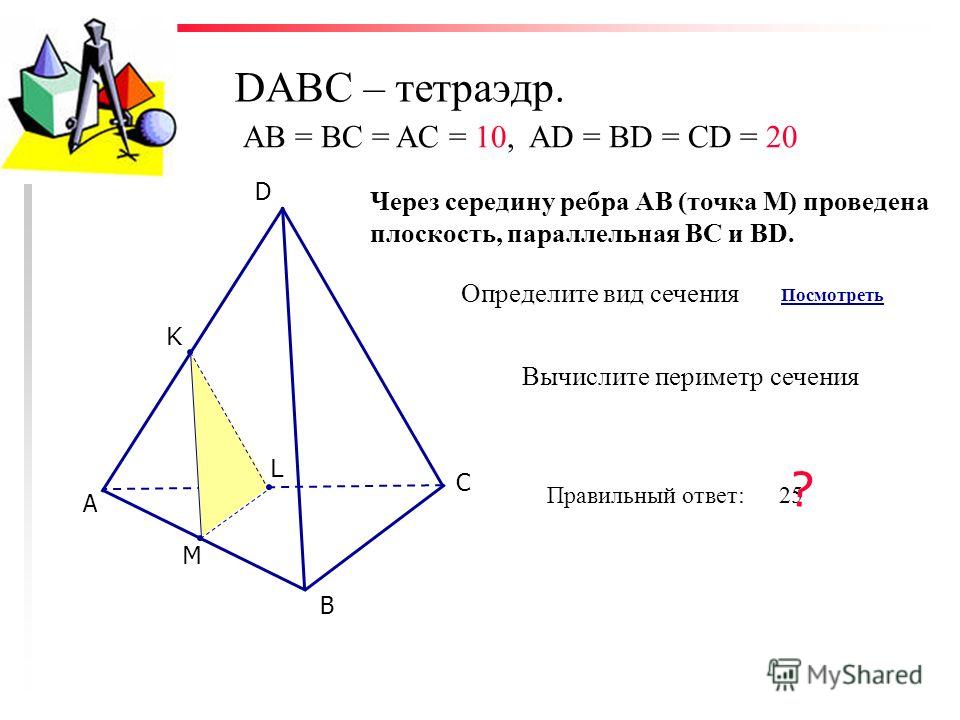

Пусть X — некоторая точка пространства такая, что

Через точку X п прямую Alt можно принести плоскость а (рис. 93). Известно, что мпожество точек плоскости а, равноудаленных от концов A и B отрезка AB, представляет собой серединный перпендикуляр ОX к oтрезку АB (О — середина АB), т.е.

Пусть теперь Y — другая точка (не лежащая на ОX) такая, что

Тогда все точки прямой OY также равноудалены от А и B. Через прямые ОX и OY проходит единственая плоскость . Для каждой точки Z, плоскости имеем

Найдите периметр и площадь сечения тетраэдра. Дополнительные задачи 102, Геометрия, 10-11 класс, Атанасян Л.С. – Рамблер/класс

Найдите периметр и площадь сечения тетраэдра. Дополнительные задачи 102, Геометрия, 10-11 класс, Атанасян Л.С. – Рамблер/класс

Интересные вопросы

Школа

Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?

Новости

Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?

Школа

Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?

Школа

Когда в 2018 году намечено проведение основного периода ЕГЭ?

Новости

Будет ли как-то улучшаться система проверки и организации итоговых сочинений?

Вузы

Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?

Дочка просит помочь, а я уже и не помню геометрию(
 
Докажите, что плоскость α, проходящая через середины двух ребер основания тетраэдра и вершину, не принадлежащую основанию, параллельна третьему ребру основания. Найдите периметр и площадь сечения тетраэдра плоскостью а, если длины всех ребер тетраэдра равны 20 см.
 

Лучший ответ

Здравствуйте. Могу поделиться)
По теореме I пл. DNM || DC (MN — средняя линия ААВС, поэтому МН || ВС ).
Если все ребра тетраэдра равны, тогда в ΔADC отрезок DM — ме­ диана, а значит и высота и биссектриса. Из ΔADM:

ΔAND — ΔAMD (они — прямоугольные, AD — общая гипотенуза,
AM=AN)\ из равенства треугольников DM= DN;


Рассмотрим ΔMDN.

Проведем в равнобедренном ΔМDN высоту DK.

еще ответы

ваш ответ

Можно ввести 4000 cимволов

отправить

дежурный

Нажимая кнопку «отправить», вы принимаете условия  пользовательского соглашения

похожие темы

Юмор

Олимпиады

ЕГЭ

Компьютерные игры

похожие вопросы 5

Докажите, что треугольники подобны. Вопросы и задачи 64, Геометрия, 10-11 класс, Атанасян Л.С.

Привет. Запуталась при решении, нужна помощь знатоков!!!
 
Три прямые, проходящие через одну точку и не лежащие в одной (Подробнее…)

ГДЗГеометрия11 класс10 классАтанасян Л.С.

Самостоятельная работа 19. Вариант 2. № 2 ГДЗ Геометрия 9 класс Зив Б.Г. Помогите доказать, используя параллельный перенос

Используя параллельный перенос, докажите, что углы при основании равнобедренной трапеции равны между собой.
 

ГДЗЭкзаменыГеометрия9 классЗив Б. Г.

Почему сейчас школьники такие агрессивные ?

Читали новость про 10 классника который растрелял ? как вы к этому относитесь 

Новости10 классБезопасность

Какой был проходной балл в вузы в 2017 году?

Какой был средний балл ЕГЭ поступивших в российские вузы на бюджет в этом году? (Подробнее…)

Поступление11 классЕГЭНовости

ЕГЭ-2017 Цыбулько И. П. Русский язык ГДЗ. Вариант 13. 18. Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)…

18.
Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)
в предложении должна(-ы) стоять запятая(-ые). (Подробнее…)

ГДЗЕГЭРусский языкЦыбулько И.П.

Периметр сектора – формула, определение, примеры

Периметр сектора – это общая граница сектора. Сектор – это часть окружности, образованная двумя радиусами и соединяющей их дугой. Следовательно, периметр сектора круга можно рассчитать, добавив длину двух радиусов и длину дуги, образующей сектор. Давайте узнаем больше о периметре сектора круга в этой статье.

1.	Что такое периметр сектора?
2.	Периметр сектора круга
3.	Периметр сектора, использующего Зону
4.	Часто задаваемые вопросы о периметре сектора

Что такое периметр сектора?

Периметр сектора — это длина границы сектора круга. Эта граница включает в себя длину двух радиусов и дуги, образующей конкретный сектор. Обратите внимание на приведенный ниже рисунок, чтобы понять, что означает периметр сектора.

Периметр сектора круга

Периметр сектора круга включает длину двух радиусов и длину дуги, образующей сектор. Хотя мы можем легко получить длину радиуса сектора, длину дуги необходимо рассчитать по формуле. Длина дуги = r × θ , где r — радиус, а θ — угол сектора в радианах. Следует отметить, что этот угол θ должен быть выражен в радианах. После того, как длина дуги рассчитана, можно вычислить периметр сектора, найдя сумму двух радиусов и длины дуги.

Как найти периметр сектора?

Периметр сектора можно рассчитать, зная радиус и длину дуги. Если угол сектора задан в градусах, нам нужно преобразовать его в радианы, а затем можно рассчитать длину дуги, чтобы получить периметр сектора. Давайте разберемся в этом на примере.

Пример: Найдите периметр сектора круга, радиус которого равен 11 единицам, а угол сектора, опирающегося на дугу, равен 10°.

Решение: Длина радиуса = 11 единиц, Угол сектора = 10°, который необходимо преобразовать в радианы. Давайте выполним шаги, указанные ниже, чтобы найти периметр сектора.

• Чтобы преобразовать угол из градусов в радианы, мы используем формулу Радианы = Градусы × π /180
• Это означает, что нам нужно умножить данное значение градусов на π /180. Это составит (10 × π)/180 = π/18 
.
• Теперь мы можем найти длину дуги по формуле Длина дуги = r × θ ; (где r = радиус = 11 единиц, θ = угол сектора в радианах = π/18)
• Длина дуги = 11 × π/18, длина дуги = (11 × 3,14)/18 = 1,92 единицы
• Теперь, когда мы знаем длину дуги, мы можем найти периметр сектора, сложив значения, потому что мы знаем, что длина дуги = 1,92 единицы, радиус = 11 единиц
• Периметр сектора = Радиус + Радиус + Длина дуги , Периметр сектора = (2 × радиус) + длина дуги, Периметр сектора = (2 × 11) + 1,92 ⇒ 22 + 1,92 = 23,92 единицы.
• Следовательно, периметр сектора равен 23,92 единицы.

Периметр сектора, использующего Зону

Периметр сектора можно рассчитать, если известна площадь сектора. Мы знаем, что площадь сектора можно рассчитать по следующей формуле:

• Площадь сектора круга = (θ/360º) × πr ² , где θ — угол сектора, образуемый дугой в центре, в градусах, а «r» — радиус окружности.
• Площадь сектора круга = 1/2 × r ² θ, где θ — угол сектора, образуемый дугой в центре, в радианах, а «r» — радиус круга.

Таким образом, если площадь сектора и радиус заданы, то мы можем найти угол сектора, используя следующие шаги.

• Шаг 1: Мы можем найти угол сектора, используя соответствующую формулу для площади сектора (данную выше).
• Шаг 2: Когда угол известен, длину дуги можно рассчитать по формуле Длина дуги = r × θ ; (где r = радиус и θ = угол сектора в радианах)
• Шаг 3: После расчета длины дуги периметр сектора можно рассчитать по формуле Периметр сектора = Радиус + Радиус + Длина дуги

Давайте разберемся с этим на примере.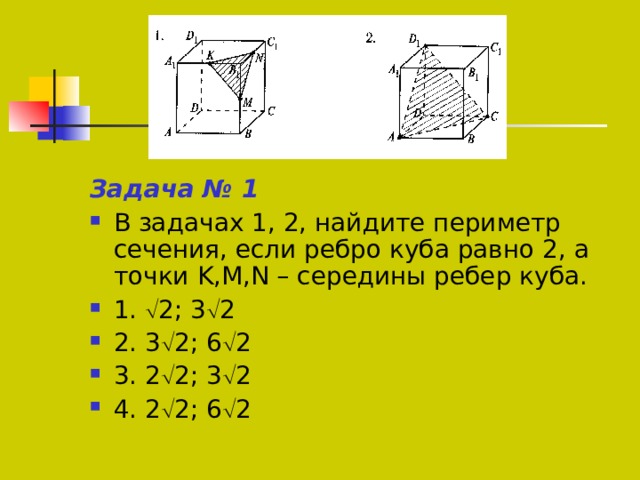

Пример: Найдите периметр сектора, площадь которого равна 324 квадратных единиц, а радиус равен 27 единицам.

Решение: Найдем периметр сектора, используя следующие шаги:

• Мы знаем, что площадь сектора круга = 1/2 × r ² θ, где θ – угол сектора стягиваемой дугой в центре, в радианах, а «r» — радиус окружности.
• После подстановки значения площади сектора = 324 и радиуса = 27 единиц, мы можем вычислить угол сектора.
• Это будет Площадь сектора круга = 1/2 × r ² θ ⇒ 324 = 1/2 × 27 ² × θ. После решения этого уравнения получаем значение θ = 0,89
• Теперь мы можем найти длину дуги по формуле Длина дуги = r × θ ⇒ 27 × 0,89 = 24 единицы.
• Наконец, можно вычислить периметр сектора, поскольку мы знаем, что длина дуги = 24 единицы, радиус = 27 единиц. Итак, подставив эти значения в формулу Периметр сектора = Радиус + Радиус + Длина дуги, получим, Периметр сектора = 27 + 27 + 24 = 78 единиц.

☛ Похожие темы

• Формулы периметра
• Периметр прямоугольника
• Периметр квадрата
• Периметр треугольника
• Периметр круга Формула
• Разница между площадью и периметром

 

Периметр сектора Примеры

1. Пример 1: Найдите периметр сектора круга радиусом 5,2 единицы и длиной дуги 2 единицы.

   Решение: Радиус сектора круга = 5,2 единицы, Длина дуги = 2 единицы.

   Периметр сектора можно найти по формуле

   Периметр сектора = радиус + радиус + длина дуги

   Периметр сектора = 5,2 + 5,2 + 2 = 12,4 единицы

2. Пример 2: Найдите периметр сектора круга, угол которого равен 90°, а радиус равен 7 см.

   Решение:

   Радиус сектора круга = 7 см, угол сектора = 90°

   Нам нужно перевести угол из градусов в радианы по формуле Радианы = Градусы × π /180

   Радианы = 90° × π /180 = π/2

   Теперь мы можем найти длину дуги по формуле Длина дуги = r × θ ; (где r = радиус = 7, а θ = угол сектора в радианах = π/2)

   Длина дуги = r × θ

   Длина дуги = 7 × π/2 = (7 × 3,14)/2 = 10,99 ⇒ 11 см

   Теперь мы можем найти периметр сектора по формуле

   Периметр сектора = радиус + радиус + длина дуги

   Периметр сектора = 7 + 7 + 11 = 25 см

3. Пример 3: Найдите периметр сектора круга с центральным углом θ = π/2 и радиусом = 8 футов.

   Решение:

   Радиус сектора круга = 8 футов, угол сектора θ = π/2

   Итак, мы можем найти длину дуги по формуле Длина дуги = r × θ ; (где r = радиус = 8, а θ = угол сектора в радианах = π/2)

   Длина дуги = r × θ

   Длина дуги = 8 × π/2 = (8 × 3,14)/2 = 12,56 футов

   Теперь мы можем найти периметр сектора по формуле

   Периметр сектора = радиус + радиус + длина дуги

   Периметр сектора = 8 + 8 + 12,56 = 28,56 футов

перейти к слайду перейти к слайду перейти к слайду

Отличное обучение в старшей школе с использованием простых подсказок

Увлекаясь зубрежкой, вы, скорее всего, забудете понятия. С Cuemath вы будете учиться визуально и будете удивлены результатами.

Записаться на бесплатный пробный урок

Практические вопросы по периметру сектора

 

перейти к слайдуперейти к слайду

Часто задаваемые вопросы по периметру сектора

Что такое периметр сектора?

Периметр сектора круга — это общая длина его границы, которая включает 2 радиуса и длину дуги, образующей сектор. Его можно рассчитать, если известны длина дуги и радиус.

Какая формула для периметра сектора?

Для определения периметра сектора используется следующая формула: Периметр сектора = Радиус + Радиус + Длина дуги. Здесь, если длина дуги неизвестна, ее можно рассчитать по формуле Длина дуги = r × θ ; (где r = радиус и θ = угол сектора в радианах). Если угол сектора не указан в радианах, его можно преобразовать из градусов в радианы, используя формулу радиана = градусы × π /180

Как найти периметр сектора круга?

Периметр сектора можно рассчитать, выполнив следующие действия. Найдем периметр сектора круга, радиус которого равен 9 единицам, а угол, образуемый дугой, равен 10°.

Решение: Длина радиуса = 9 единиц. Угол сектора = 10 °, который необходимо преобразовать в радианы. Давайте выполним шаги, указанные ниже, чтобы найти периметр сектора.

• Чтобы преобразовать угол из градусов в радианы, мы используем формулу Радианы = Градусы × π /180
• Это означает, что нам нужно умножить данное значение градусов на π /180. Это будет (10 × π)/180 = π/18
• Теперь мы можем найти длину дуги по формуле Длина дуги = r × θ ; (где r = радиус = 9 единиц, θ = угол сектора в радианах = π/18)
• Длина дуги = 9 × π/18, длина дуги = (9 × 3,14)/18 = 1,57 единицы
• Теперь, когда мы знаем длину дуги, мы можем найти периметр сектора, сложив значения, потому что мы знаем, что длина дуги = 1,57 единицы, радиус = 9 единиц
• Периметр сектора = Радиус + Радиус + Длина дуги , Периметр сектора = (2 × радиус) + Длина дуги, Периметр сектора = (2 × 9) + 1,57 ⇒ 18 + 1,57 = 19,57 ед.
• Следовательно, периметр сектора равен 19,57 единиц.

Чему равен периметр сектора с радиусом 10,5 см и углом сектора 60°?

Периметр сектора радиусом 10,5 см и углом сектора 60° можно рассчитать с помощью следующих шагов.

• Прежде всего, нам нужно преобразовать угол сектора из градусов в радианы. Дано, радиус сектора = 10,5 см, Угол сектора = 60°. Таким образом, значение угла в радианах можно рассчитать по формуле Радианы = Градусы × π/180 ⇒ Радианы = 60 × π/180 = π/3
• Теперь длину дуги можно рассчитать по формуле Длина дуги = r × θ ; (где r = радиус = 10,5 см, θ = угол сектора в радианах = π/3). Итак, длина дуги = 10,5 × π/3 = 10,99 = 11 см
• Теперь периметр сектора можно рассчитать по формуле Периметр сектора = Радиус + Радиус + Длина дуги , Периметр сектора = 10,5 + 10,5 + 11 ⇒ 32 см

Как найти периметр сектора по формуле длины дуги?

Периметр сектора можно рассчитать, если задана длина дуги, потому что формула для периметра сектора: Периметр сектора = радиус + радиус + длина дуги. Теперь, если длина дуги не задана, мы можем вычислить ее, используя формулу длины дуги, Длина дуги = r × θ ; (где r = радиус сектора, а θ = угол сектора в радианах). Зная длину дуги, можно вычислить периметр сектора.

Как найти периметр сектора круга с радиусом?

Периметр сектора круга можно рассчитать, если известны радиус и длина дуги сектора. Формула, которая используется для нахождения периметра сектора с использованием радиуса: Периметр сектора = Радиус + Радиус + Длина дуги .

Калькулятор периметра сектора

Создано Komal Rafay

Отзыв от Anna Szczepanek, PhD

Последнее обновление: 23 сентября 2022 г.

Содержание:

• Калькулятор периметра сектора
• Формула периметра сектора
• Подробнее о секторах
• Часто задаваемые вопросы

Калькулятор периметра сектора — это инструмент, созданный для того, чтобы избавить вас от проблем, возникающих в геометрии. Да, сектор круга может стать головной болью, но только не тогда, когда на вашей стороне Омни! Здесь мы должны обсудить многие аспекты периметра сектора круга:

• Что такое периметр сектора?
• Какова формула периметра сектора?
• Как рассчитать периметр сектора?

Калькулятор периметра сектора

Калькулятор периметра сектора — это инструмент, созданный для того, чтобы сделать вашу жизнь, по крайней мере ее математический аспект, легкой и удобной. Излишне говорить, что с помощью нашего калькулятора проще простого. На самом деле, кусочек торта — как раз подходящий пример для визуализации сектора круга 9.0004 . Увлекательно, не так ли?

Шаги для использования нашего инструмента:

1. Введите центральный угол сектора. У вас есть возможность выбирать между такими единицами, как градусы и радианы.
2. Введите радиус окружности. У вас снова есть список опций для выбора устройства. Сантиметр является единицей измерения по умолчанию.
3. Инструмент оценит длину дуги , а затем использует ее для быстрого получения периметра сектора 9.0004 .

Например, вы вводите 2 радиана в качестве центрального угла и 7 см в качестве радиуса. Получится 28 см, периметр сектора.

Периметр сектора формула

Периметр сектора — это мера границы сечения круга , поэтому он называется сектором. Формула использует радиус сектора rrr и длину дуги LLL для определения рассматриваемого периметра сектора PPP:

P=2×r + LP = 2 \times r\ +\ LP=2×r + L

Эта формула периметра сектора проста, но предполагает, что вы знаете длину дуги.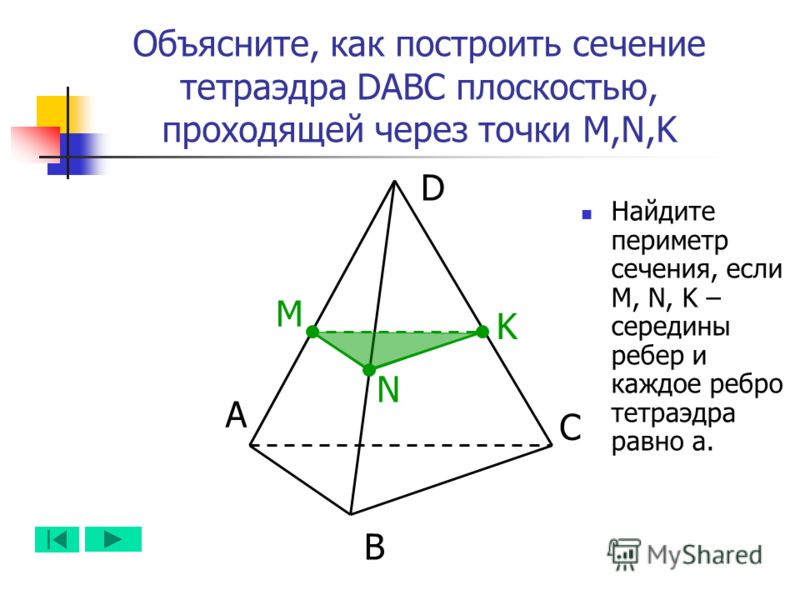 На самом деле длину дуги не так просто измерить напрямую, и ее лучше вычислить по центральному углу α\alpha α:

L=α×rL = \alpha \times rL=α×r

Заглушка эту формулу для LLL в нашу исходную формулу для PPP, мы приходим к следующей формуле периметра: г

где:

• ППС — Периметр сектора;
• α\alpha α — Центральный угол;
• ррр — Радиус; и
• LLL — Длина дуги.

Подробнее об секторах

Никакие знания не могут считаться достаточными! Вот почему мы продолжаем добавлять новые инструменты в нашу коллекцию для вас.

Когда вы закончите с нахождением периметра секторов, взгляните на некоторые другие инструменты Omni, связанные с сектором круга.

• Калькулятор площади сектора;
• Калькулятор четверти окружности;
• Калькулятор площади четверти круга; и
• Калькулятор периметра четверти круга.

Часто задаваемые вопросы

Как рассчитать периметр сектора?

Найти периметр сектора легко! Используйте формулу:

Периметр = (2 × радиус) + длина дуги

Все, что вам нужно сделать, это:

1. Умножить радиус на два, что дает диаметр окружности.

   No related posts.