Как найти площадь прямоугольного треугольника 3 класс формула пример: Составить алгоритм площади прямоугольного треугольника если известна гипотенуза и катет

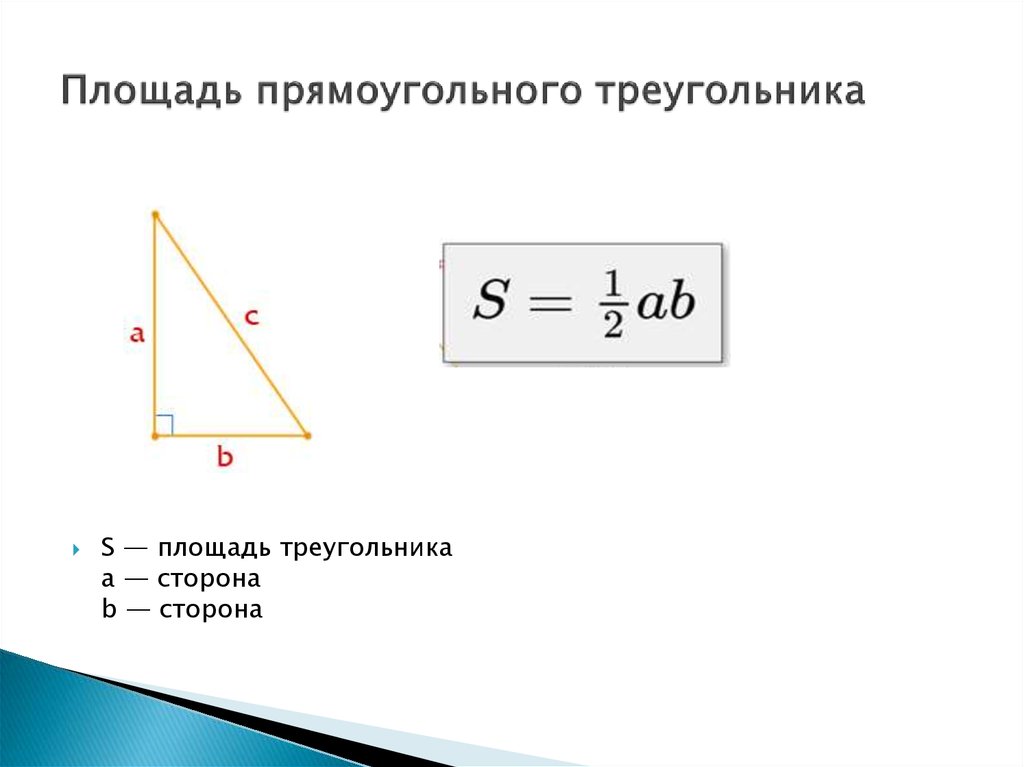
Формула нахождения площади прямоугольного треугольника через синус.

Площадь треугольника равна половине произведения его сторон на синус угла между ними.

Доказательство:

Рассмотрим произвольный треугольник ABC. Пусть в нем сторона BC = a, сторона CA = b и S — площадь этого треугольника. Необходимо доказать, что S = (1/2)*a*b*sin(C) .

Для начала введем прямоугольную систему координат и поместим начало координат в точку С. Расположим нашу систему координат так, чтобы точка B лежала на положительном направлении оси Сх, а точка А имела бы положительную ординату.

Если все выполнить правильно, то должен получится следующий рисунок.

Площадь данного треугольника можно вычислить по следующей формуле: S = (1/2)*a*h , где h — это высота треугольника. В нашем случае высота треугольника h равна ординате точки А, то есть h = b*sin(C).

Учитывая полученные результат, формулу площади треугольника можно переписать следующим образом: S = (1/2)*a*b*sin(C). 2. Найдите сторону AB, если AC = 15 см, угол А = 30˚.

Положим S — площадь треугольника ABC. По теореме о площади треугольника имеем:

S = (1/2)*AB*AC*sin(A).

Подставим в неё имеющиеся у нас значения:

60 = (1/2)*AB*15*sin30˚ = (1/2)*15*(1/2)*AB=(15/4)*AB.

Отсюда выражаем длину стороны AB: AB = (60*4)/15 = 16.

Если в задаче даны длины двух сторон треугольника и угол между ними, то можно применить формулу площади треугольника через синус.

Пример расчета площади треугольника через синус. Даны стороны a = 3, b = 4, и угол γ= 30°. По синус угла в 30° равен 0.5

Площадь треугольника будет равна 3 кв. см.

Также могут быть и другие условия. Если дана длина одной стороны и углы, то для начала нужно вычислить недостающий угол. Т.к. сумма всех углов треугольника равняется 180°, то:

Площадь будет равна половине квадрата стороны, умноженной на дробь. В ее числителе находится произведение синусов прилегающих углов, а в знаменателе синус противолежащего угла.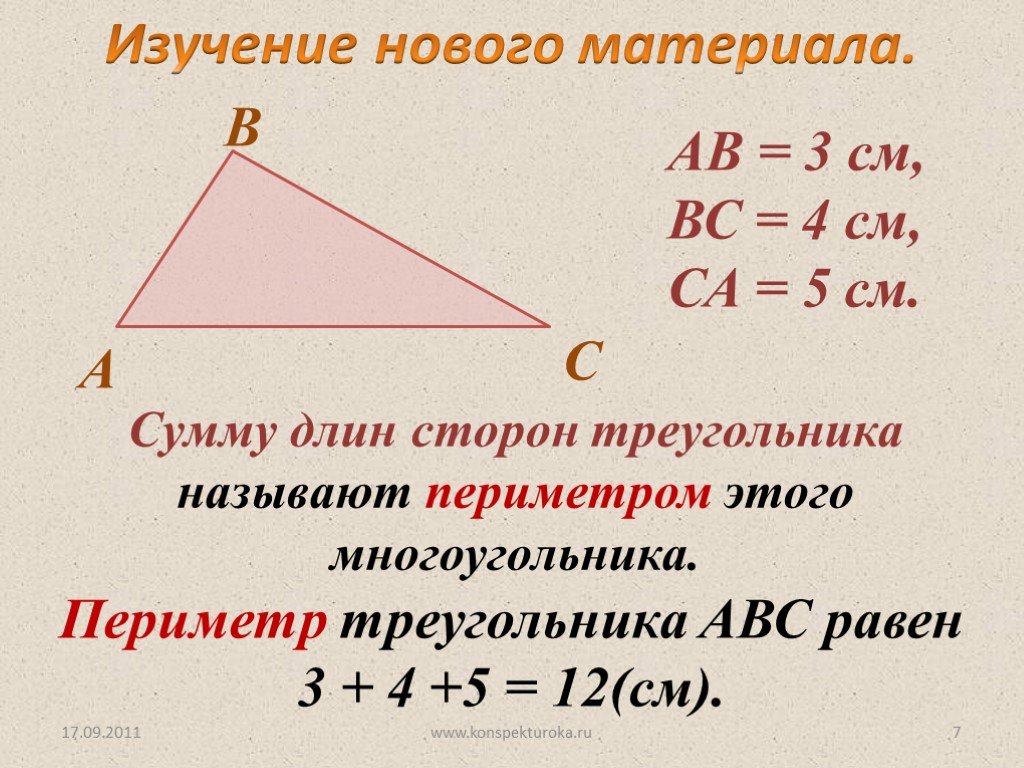

Теперь рассчитываем площадь по следующим формулам:

Например, дан треугольник со стороной a=3 и углами γ=60°, β=60°. Вычисляем третий угол:
Подставляем данные в формулу
Получаем, что площадь треугольника равняется 3,87 кв. см.

II. Площадь треугольника через косинус

Чтобы найти площадь треугольника, нужно знать длины всех сторон. По теореме косинусов можно найти не известные стороны, а уже потом использовать .
По теореме косинусов квадрат неизвестной стороны треугольника равняется сумме квадратов остальных сторон минус удвоенное произведение этих сторон на косинус угла, находящегося между ними.

Из теоремы выводим формулы для поиска длины неизвестной стороны:

Зная как найти недостающую сторону, имея две стороны и угол между ними можно легко посчитать площадь. Формула площади треугольника через косинус помогает легко и быстро найти решение различных задач.

Пример расчета формулы площади треугольника через косинус
Дан треугольник с известными сторонами a = 3, b = 4, и углом γ= 45°.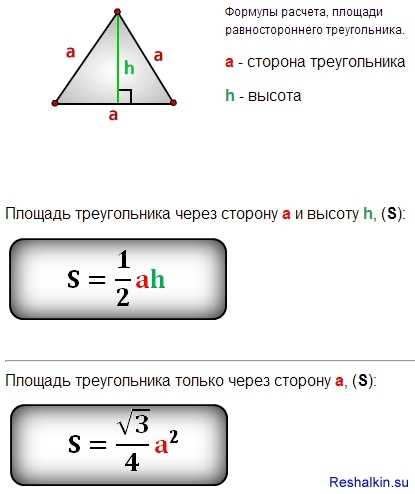 Для начала найдем недостающую сторону с . По косинус 45°=0,7. Для этого подставим данные в уравнение, выведенное из теоремы косинусов.
Теперь используя формулу, найдем

В жизни нам часто придется сталкиваться с математическими задачами: в школе, в университете, а затем помогая своему ребенку с выполнением домашнего задания. Люди определенных профессий будут сталкиваться с математикой ежедневно. Поэтому полезно запоминать или вспоминать математические правила. В этой статье мы разберем одно из них: нахождение катета прямоугольного треугольника.

Что такое прямоугольный треугольник

Для начала вспомним, что такое прямоугольный треугольник. Прямоугольный треугольник – это геометрическая фигура из трех отрезков, которые соединяют точки, не лежащие на одной прямой, и один из углов этой фигуры равен 90 градусам. Стороны, образующие прямой угол, называются катетами, а сторона, которая лежит напротив прямого угла – гипотенузой.

Находим катет прямоугольного треугольника

Существует несколько способов, позволяющих узнать длину катета. Хотелось бы рассмотреть бы их подробнее.

Теорема Пифагора, чтобы найти катет прямоугольного треугольника

Если нам известны гипотенуза и катет, то мы можем найти длину неизвестного катета по теореме Пифагора. Звучит она так: “Квадрат гипотенузы равен сумме квадратов катетов”. Формула: c²=a²+b², где c – гипотенуза, a и b – катеты. Преобразовываем формулу и получаем: a²=c²-b².

Пример. Гипотенуза равна 5 см, а катет – 3 см. Преобразовываем формулу: c²=a²+b² → a²=c²-b². Далее решаем: a²=5²-3²; a²=25-9; a²=16; a=√16; a=4 (см).

Тригонометрические соотношения, чтобы найти катет прямоугольного треугольника

Также можно найти неизвестный катет, если известны любая другая сторона и любой острый угол прямоугольного треугольника. Есть четыре варианта нахождения катета при помощи тригонометрических функций: по синусу, косинусу, тангенсу, котангенсу. Для решения задач нам поможет таблица, которая находится чуть ниже. Рассмотрим эти варианты.

Найти катет прямоугольного треугольника при помощи синуса

Синус угла (sin) – это отношение противолежащего катета к гипотенузе.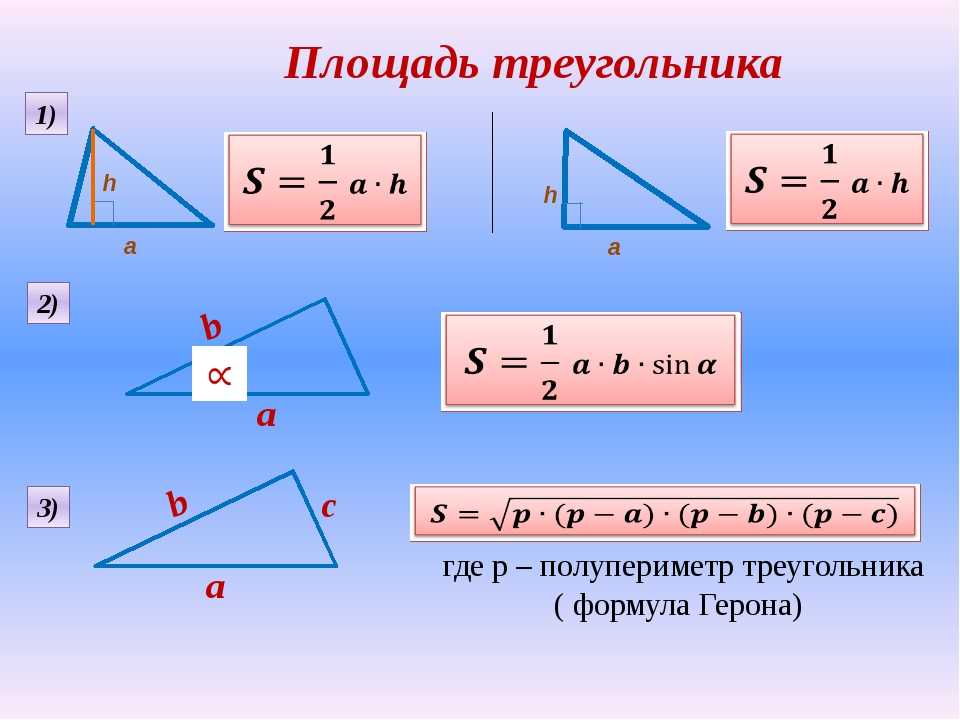 Формула: sin=a/c, где а – катет, лежащий против данного угла, а с – гипотенуза. Далее преобразуем формулу и получаем: a=sin*c.

Пример. Гипотенуза равна 10 см, угол А равен 30 градусов. По таблице вычисляем синус угла А, он равен 1/2. Затем по преобразованной формуле решаем: a=sin∠А*c; a=1/2*10; a=5 (см).

Найти катет прямоугольного треугольника при помощи косинуса

Косинус угла (cos) – это отношение прилежащего катета к гипотенузе. Формула: cos=b/c, где b – катет, прилежащий к данному углу, а с – гипотенуза. Преобразуем формулу и получим: b=cos*c.

Пример. Угол А равен 60 градусов, гипотенуза равна 10 см. По таблице вычисляем косинус угла А, он равен 1/2. Далее решаем: b=cos∠A*c; b=1/2*10, b=5 (см).

Найти катет прямоугольного треугольника при помощи тангенса

Тангенс угла (tg) – это отношение противолежащего катета к прилежащему. Формула: tg=a/b, где а – противолежащий к углу катет, а b – прилежащий. Преобразуем формулу и получаем: a=tg*b.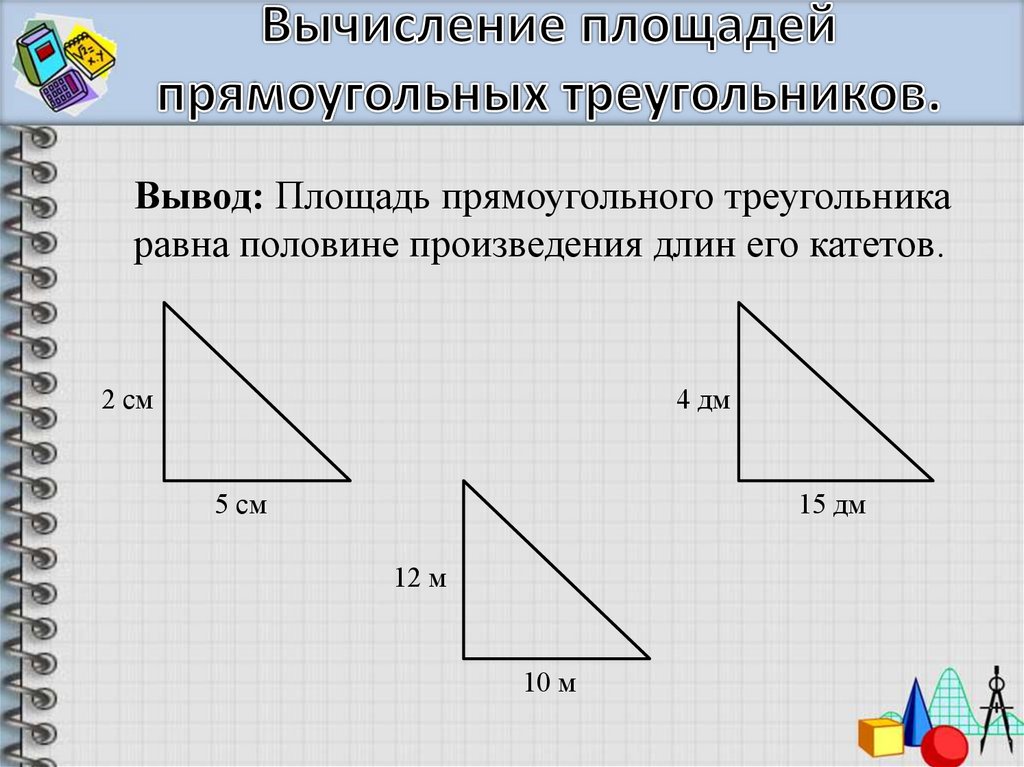

Пример. Угол А равен 45 градусов, гипотенуза равна 10 см. По таблице вычисляем тангенс угла А, он равен Решаем: a=tg∠A*b; a=1*10; a=10 (см).

Найти катет прямоугольного треугольника при помощи котангенса

Котангенс угла (ctg) – это отношение прилежащего катета к противолежащему. Формула: ctg=b/a, где b – прилежащий к углу катет, а – противолежащий. Иначе говоря, котангенс – это “перевернутый тангенс”. Получаем: b=ctg*a.

Пример. Угол А равен 30 градусов, противолежащий катет равен 5 см. По таблице тангенс угла А равен √3. Вычисляем: b=ctg∠A*a; b=√3*5; b=5√3 (см).

Итак, теперь вы знаете, как находить катет в прямоугольном треугольнике. Как видите, это не так уж и сложно, главное – запомнить формулы.

Синус является одной из основных тригонометрических функций, применение которой не ограничено одной лишь геометрией. Таблицы вычисления тригонометрических функций, как и инженерные калькуляторы, не всегда под рукой, а вычисление синуса порой нужно для решения различных задач. Вообще, вычисление синуса поможет закрепить чертёжные навыки и знание тригонометрических тождеств.

Игры с линейкой и карандашом

Простая задача: как найти синус угла, нарисованного на бумаге? Для решения понадобится обычная линейка, треугольник (или циркуль) и карандаш. Простейшим способом вычислить синус угла можно, разделив дальний катет треугольника с прямым углом на длинную сторону — гипотенузу. Таким образом, сначала нужно дополнить острый угол до фигуры прямоугольного треугольника, прочертив перпендикулярную одному из лучей линию на произвольном расстоянии от вершины угла. Потребуется соблюсти угол именно 90°, для чего нам и понадобится канцелярский треугольник.

Использование циркуля немного точнее, но займёт больше времени. На одном из лучей нужно отметить 2 точки на некотором расстоянии, настроить на циркуле радиус, примерно равный расстоянию между точками, и прочертить полуокружности с центрами в этих точках до получения пересечений этих линий. Соединив точки пересечения наших окружностей между собой, мы получим строгий перпендикуляр к лучу нашего угла, остаётся лишь продлить линию до пересечения с другим лучом.

В полученном треугольнике нужно линейкой измерить сторону напротив угла и длинную сторону на одном из лучей. Отношение первого измерения ко второму и будет искомой величиной синуса острого угла.

Найти синус для угла больше 90°

Для тупого угла задача не намного сложнее. Нужно прочертить луч из вершины в противоположную сторону с помощью линейки для образования прямой с одним из лучей интересующего нас угла. С полученным острым углом следует поступать как описано выше, синусы смежных углов, образующих вместе развёрнутый угол 180°, равны.

Вычисление синуса по другим тригонометрическим функциям

Также вычисление синуса возможно, если известны значения других тригонометрических функций угла или хотя бы длины сторон треугольника. В этом нам помогут тригонометрические тождества. Разберём распространённые примеры.

Как находить синус при известном косинусе угла? Первое тригонометрическое тождество, исходящее из теоремы Пифагора, гласит, что сумма квадратов синуса и косинуса одного и того же угла равна единице.

Как находить синус при известном тангенсе угла? Тангенс получают делением дальнего катета на ближний или делением синуса на косинус. Таким образом, синусом будет произведение косинуса на тангенс, а квадратом синуса будет квадрат этого произведения. Заменяем косинус в квадрате на разность между единицей и квадратным синусом согласно первому тригонометрическому тождеству и путём нехитрых манипуляций приводим уравнение к вычислению квадратного синуса через тангенс, соответственно, для вычисления синуса придётся извлечь корень из полученного результата.

Как находить синус при известном котангенсе угла? Значение котангенса можно вычислить, разделив длину ближнего от угла катета на длину дальнего, а также поделив косинус на синус, то есть котангенс — функция, обратная тангенсу относительно числа 1. Для расчёта синуса можно вычислить тангенс по формуле tg α = 1 / ctg α и воспользоваться формулой во втором варианте. Также можно вывести прямую формулу по аналогии с тангенсом, которая будет выглядеть следующим образом.

Как находить синус по трём сторонам треугольника

Существует формула для нахождения длины неизвестной стороны любого треугольника, не только прямоугольного, по двум известным сторонам с использованием тригонометрической функции косинуса противолежащего угла. Выглядит она так.

Ну, а синус можно далее рассчитать по косинусу согласно формулам выше.

Сторону треугольника дозволено обнаружить не только по периметру и площади, но и по заданной стороне и углам. Для этого применяются тригонометрические функции –

синус и косинус . Задачи с их применением встречаются в школьном курсе геометрии, а также в вузовском курсе аналитической геометрии и линейной алгебры.

Инструкция

1. Если знаменита одна из сторон треугольника и угол между ней и иной его стороной, воспользуйтесь тригонометрическими функциями – синус ом и косинус ом. Представьте себе прямоугольный треугольник НBC , у которого угол? равен 60 градусам.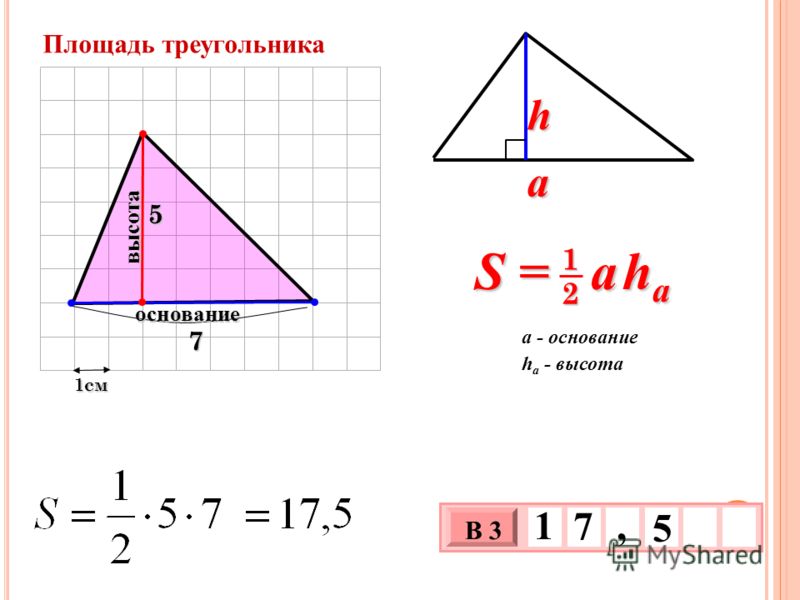 Треугольник НBC показан на рисунке. От того что синус , как знаменито, представляет собой отношение противолежащего катета к гипотенузе, а косинус – отношение прилежащего катета к гипотенузе, для решения поставленной задачи воспользуйтесь дальнейшим соотношением между этими параметрами:sin ?=НB/BCСоответственно, если вы хотите узнать катет прямоугольного треугольника, выразите его через гипотенузу дальнейшим образом:НB=BC*sin ?

2. Если в условии задачи, напротив, дан катет треугольника, обнаружьте его гипотенузу, руководствуясь дальнейшим соотношением между заданными величинами:BC=НB/sin ?По аналогии обнаружьте стороны треугольника и с применением косинус а, изменив предыдущее выражение дальнейшим образом:cos ?=НC/BC

3. В элементарной математике существует представление теоремы синус ов. Руководствуясь фактами, которые описывает данная теорема, также дозволено обнаружить стороны треугольника. Помимо этого, она разрешает обнаружить стороны треугольника, вписанного в окружность, если знаменит вестим радиус последней. 2-2ab*cos ?

Геометрическая фигура, состоящая из трёх точек, не принадлежащих одной прямой называемых вершинами, и трёх попарно соединяющих их отрезков, называемых сторонами, именуется треугольником. Существует уйма задач на нахождение сторон и углов треугольника по ограниченному числу начальных данных, одна из таких задач – нахождение стороны треугольника по одной из его сторон и двум

углам .

Инструкция

1. Пускай построен треугольник?ABC и знамениты – сторона BC и углы?? и??.Знаменито, что сумма углов всякого треугольника равна 180?, следственно в треугольнике?ABC угол?? будет равен?? = 180? – (?? + ??).Обнаружить стороны AC и AB дозволено применяя теорему синусов, которая гласитAB/sin?? = BC/sin?? = AC/sin?? = 2 * R, где R – радиус описанной около треугольника?ABC окружности,тогда получаемR = BC/sin??,AB = 2 * R * sin??,AC = 2 * R * sin??.Теорему синусов дозволено использовать при всяких данных 2-х углах и стороне.

2. Стороны заданно треугольника дозволено обнаружить, вычислив его площадь по формулеS = 2 * R? * sin?? * sin?? * sin??,где R вычисляется по формулеR = BC/sin??, R – радиус описанной около треугольника?ABC отсюдаТогда сторону AB дозволено обнаружить, вычислив высоту, опущенную на неёh = BC * sin??,отсель по формуле S = 1/2 * h * AB имеемAB = 2 * S/hАналогичным образом дозволено вычислить

сторону AC.

3. Если в качестве углов даны внешние углы треугольника?? и??, то обнаружить внутренние углы дозволено с поддержкой соответствующих соотношений?? = 180? – ??,?? = 180? – ??,?? = 180? – (?? + ??).Дальше действуем подобно первым двум пунктам.

Постижение треугольников ведется математиками на протяжении нескольких тысячелетий. Наука о треугольниках – тригонометрия – использует особые величины: синус и косинус.

Прямоугольный треугольник

Изначально синус и косинус появились из-за необходимости рассчитывать величины в прямоугольных треугольниках. Было подмечено, что если значение градусной меры углов в прямоугольном треугольнике не менять, то соотношение сторон, насколько бы эти стороны ни изменялись в длине, остается неизменно идентичным.Именно так и были введены представления синуса и косинуса. Синус острого угла в прямоугольном треугольнике – это отношение противолежащего катета к гипотенузе, а косинус – прилежащего к гипотенузе.

Теоремы косинусов и синусов

Но косинусы и синусы могут использоваться не только в прямоугольных треугольниках.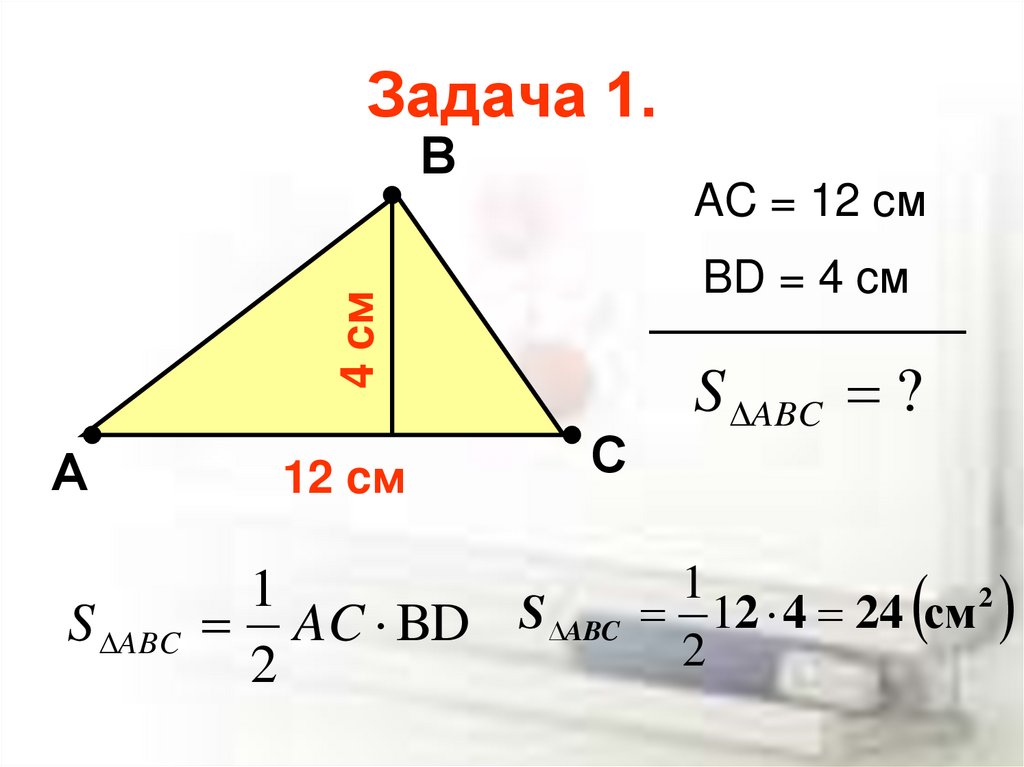 Дабы обнаружить значение тупого либо острого угла, стороны всякого треугольника, довольно применить теорему косинусов и синусов.Теорема косинусов достаточно примитивна: «Квадрат стороны треугольника равен сумме квадратов 2-х других сторон за вычетом удвоенного произведения этих сторон на косинус угла между ними». Существует две трактовки теоремы синусов: малая и расширенная. Согласно малой: «В треугольнике углы пропорциональны противолежащим сторонам». Данную теорему зачастую расширяют за счет свойства описанной около треугольника окружности: «В треугольнике углы пропорциональны противолежащим сторонам, а их отношение равно диаметру описанной окружности».

Производные

Производная – математический инструмент, показывающий, как стремительно меняется функция касательно метаморфозы ее довода. Производные применяются в алгебре, геометрии, экономике и физике, ряде технических дисциплин. При решении задач требуется знать табличные значения производных тригонометрических функций: синуса и косинуса. Производной синуса является косинус, а косинуса – синус, но со знаком «минус».

Применение в математике

Особенно зачастую синусы и косинусы применяются при решении прямоугольных треугольников и задач, связанных с ними. Удобство синусов и косинусов обнаружило свое отражение и в технике. Углы и стороны было примитивно оценивать по теоремам косинусов и синусов, разбивая трудные фигуры и объекты на «примитивные» треугольники. Инженеры и архитекторы, зачастую имеющие дело с расчетами соотношения сторон и градусных мер, тратили много времени и усилий для вычисления косинусов и синусов не табличных углов. Тогда «на подмогу» пришли таблицы Брадиса, содержащие тысячи значений синусов, косинусов, тангенсов и котангенсов различных углов. В советское время некоторые преподаватели принуждали своих подопечных учить страницы таблиц Брадиса назубок.

формулы и алгоритмы решения задач

Математика

12.11.21

11 мин.

При решении задач по геометрии очень часто возникает необходимость вычислить площадь прямоугольного треугольника через катеты.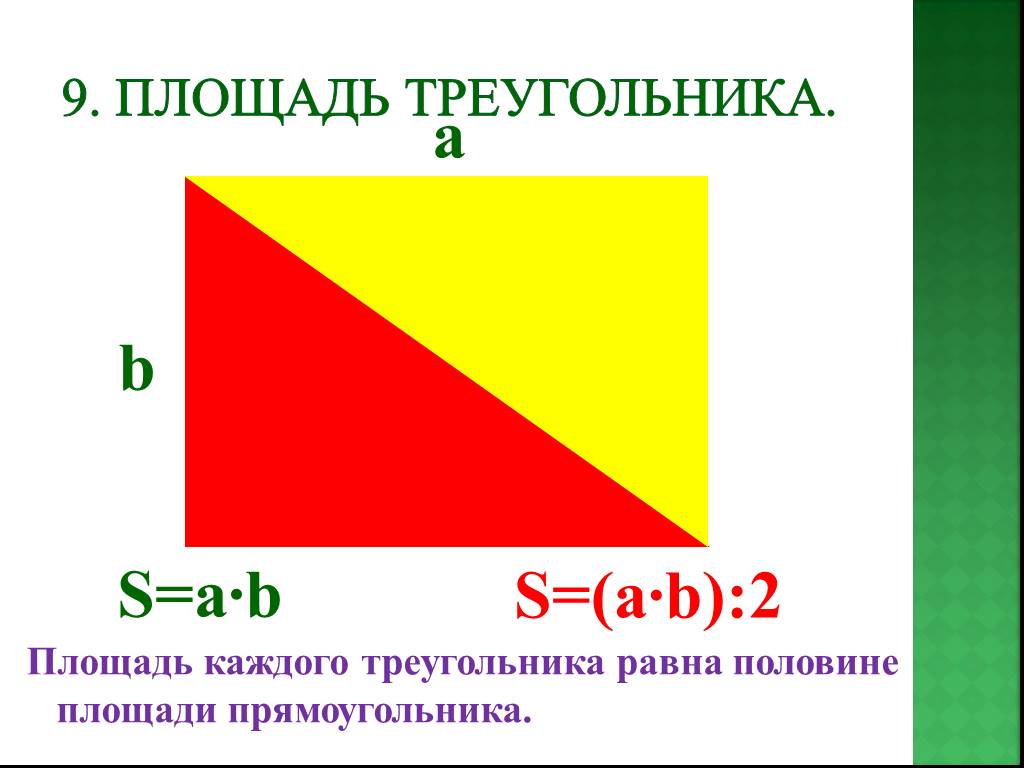

В интернете можно найти много информации на эту тему, но не всегда она соответствует действительности, поскольку некоторые авторы не являются экспертами в физико-математическом направлении. Они упускают алгоритмы правильного выполнения заданий, что приводит к некачественному обучению.

Оглавление:

• Теорема Пифагора
• Нахождение площади
• Простая задача
• Сложное задание

Общая информация

Прямоугольный треугольник — разновидность фигуры, один из углов которой эквивалентен градусной мере в 90 градусов. У него, как и другого вида, есть 3 стороны, имеющие названия катеты и гипотенуза. Именно 2 катета образуют прямой угол. Их соединяет гипотенуза. Последняя всегда больше любого катета.

Сумма углов фигуры эквивалентна 180 градусам. Из этого утверждения следует, что сумма углов между гипотенузой и катетами всегда будет равна 90, поскольку 180 — 90 = 90.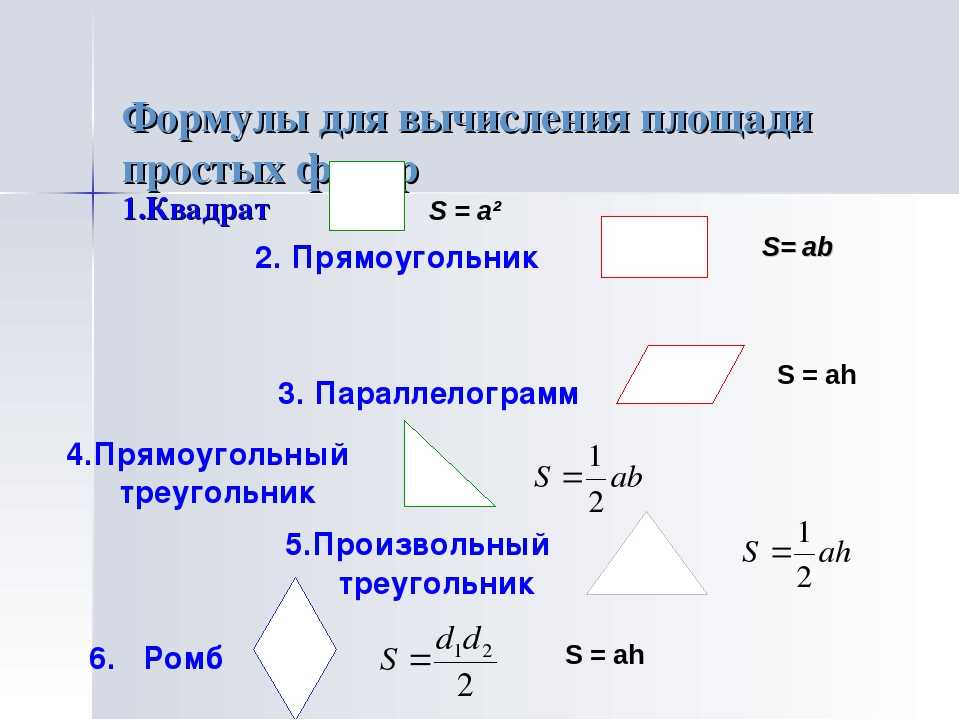

Фигура обладает некоторыми параметрами:

1. P: периметром.
2. S: площадью.
3. H: высотой.
4. M: медианой.
5. B: биссектрисой.

Первая величина (P) — алгебраическая сумма всех сторон фигуры. Площадь — величина фигуры, определяющая ее размерность. При нахождении S в литературе по геометрии можно встретить понятие «полупериметр», которое обозначает половину значения Р. Высота фигуры — перпендикуляр, опускающийся всегда из некоторой вершины на противоположную сторону. У него существует и другое название — проекция. Она всегда опускается из прямого угла на гипотенузу, поскольку из других вершин треугольника нет смысла ее опускать, т. к. отрезок совпадает с катетами.

Медиана — отрезок, проведенный из любой вершины к середине противоположной стороны. Биссектриса — прямая, проходящая через заданную вершину и делящая угол при ней на 2 равных значения. Биссектриса может быть и отрезком, проведенным к противоположной стороне. 2 * tg(∠F)) / 2.

В прямоугольный треугольник вписана окружность с радиусом R, которая делит гипотенузу t на отрезки t1 и t2: S = R(R + t) = t1 * t2.

Необходимо отметить, что тригонометрическая функция sin называется синусом угла. Она равна отношению противоположного катета к линейной мере гипотенузы (длине).

Косинус (cos) — величина, которая может находиться из отношения прилежащего катета к t.

Первая формула используется также и при определении площади прямоугольника или квадрата. Как известно, эти фигуры имеют прямые углы. Диагональ делит квадрат (прямоугольник) на 2 «Δ» с прямыми углами. Следовательно, результирующее значение площади состоит из численных значений «Δ», т. е. S = S1 + S2 = (vt / 2) + (vt / 2) = 2vt / 2 = vt.

Пример решения

При решении задач по геометрии необходимо руководствоваться алгоритмом, рекомендуемым специалистами. Суть его состоит в следующем:

1. Внимательно несколько раз прочитать условие и кратко его записать.
2. Записать основную формулу нахождения S.
3. Схематически изобразить фигуру (если есть в этом необходимость).
4. Определить недостающие величины посредством формул.
5. Подставить соотношения из 4 пункта во 2. Можно вычислить отдельно каждую величину.
6. Найти искомый результат.

Далее нужно разобрать решение задач при помощи алгоритма, которые делятся на простые и сложные.

К первому типу относятся задания на одно или два действия, а ко второму — несколько действий. В условиях последних указано минимальное количество известных параметров.

Простая задача

Необходимо найти S прямоугольника с исходными данными: большая сторона 4, а диагональ 5. Решать следует по алгоритму. 2).

Значение f1 = -1 не подходит, поскольку сторона не может иметь отрицательное значение. Второе значение является истинным.

Таким образом, необходимо уметь находить S прямоугольного треугольника, поскольку формулы помогут решать не только простые задачи, но и более сложные.

Площадь прямоугольного треугольника

Введение

Что такое прямоугольный треугольник?

Как назвать треугольник

Как мы находим площадь треугольника?

формула прямоугольного треугольника

Как найти площадь прямоугольного треугольника

Рабочий лист площади прямоугольного треугольника

Как найти недостающую длину стороны, зная площадь

Распространенные заблуждения

Практические вопросы по прямоугольным треугольникам

Площадь прямоугольного треугольника Вопросы GCSE

Контрольный список обучения

Следующие уроки

Все еще застряли?

Индивидуальные занятия по математике, созданные для успеха KS4

Теперь доступны еженедельные онлайн-уроки повторения математики GCSE

Узнать больше

Введение

Что такое прямоугольный треугольник?

Как назвать треугольник

Как мы находим площадь треугольника?

формула прямоугольного треугольника

Как найти площадь прямоугольного треугольника

Рабочий лист площади прямоугольного треугольника

Как найти недостающую длину стороны, зная площадь

Распространенные заблуждения

Практические вопросы по прямоугольным треугольникам

Площадь прямоугольного треугольника Вопросы GCSE

Контрольный список обучения

Следующие уроки

Все еще застряли?

Здесь мы узнаем о площади прямоугольного треугольника , в том числе о том, как найти площадь прямоугольного треугольника с заданными длинами и как вычислить эти длины, если они не заданы.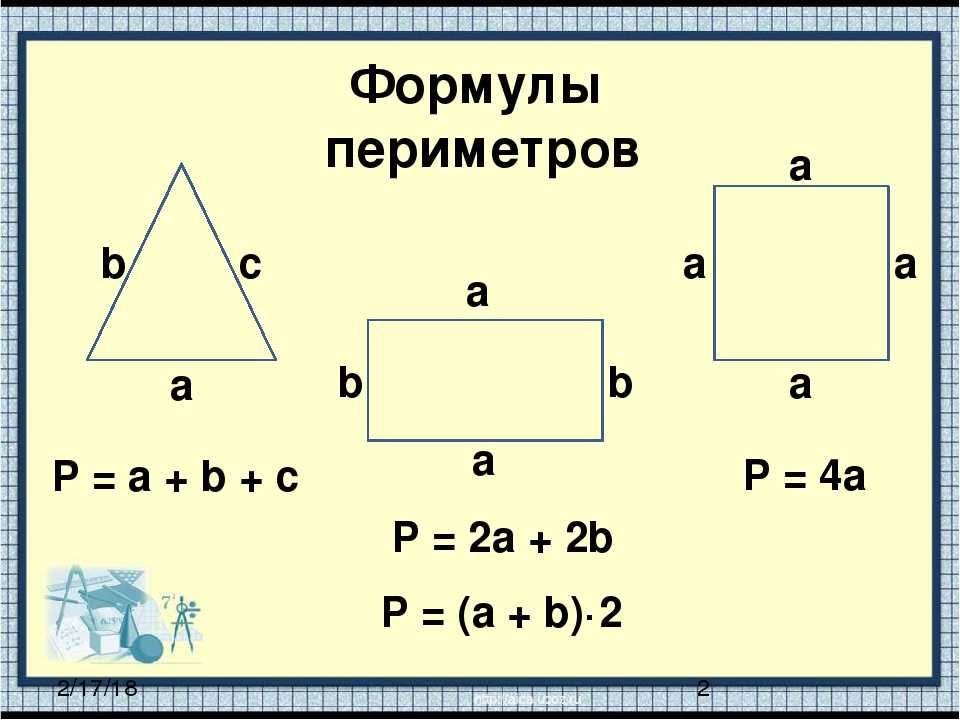

Существуют также рабочие листы в виде треугольника, основанные на экзаменационных вопросах Edexcel, AQA и OCR, а также дополнительные указания о том, что делать дальше, если вы все еще застряли.

Что такое прямоугольный треугольник?

Прямоугольный треугольник — это треугольник с одним прямым углом (угол 90°). Маленький квадрат в углу говорит нам, что это прямоугольный треугольник.

Прямоугольные треугольники бывают двух типов:

Прямоугольный равнобедренный треугольник

-два равных угла (по 45° каждый)

-две стороны равны по длине

Разносторонний прямоугольный треугольник 

-все углы3 разных размеров

0002 — все стороны разной длины

• Соотношение между углами и длинами сторон треугольника составляют основу тригонометрических функций синуса, косинуса и тангенса.

Пошаговое руководство: тригонометрия

• Сторона треугольника, противоположная прямому углу, является наибольшей стороной треугольника и называется гипотенузой .

Пошаговое руководство: Гипотенуза (скоро) 9{2}\]

Пошаговое руководство: Теорема Пифагора (скоро)

Что такое прямоугольный треугольник?

Как назвать треугольник

Мы можем определить треугольник, поставив заглавную букву на каждую вершину (угол).

Затем мы можем обратиться к каждой из сторон треугольника, используя две буквы, чтобы описать, где линия начинается и заканчивается.

Мы можем обозначить весь треугольник, используя все три буквы.

Напр.

Название сторон:
сторона AB , сторона AC , сторона BC

Название треугольника:
треугольник ABC

Как найти площадь треугольника?

Чтобы найти площадь треугольника, нам нужно начать с площади прямоугольника.

Чтобы найти площадь прямоугольника, нужно умножить смежных сторон.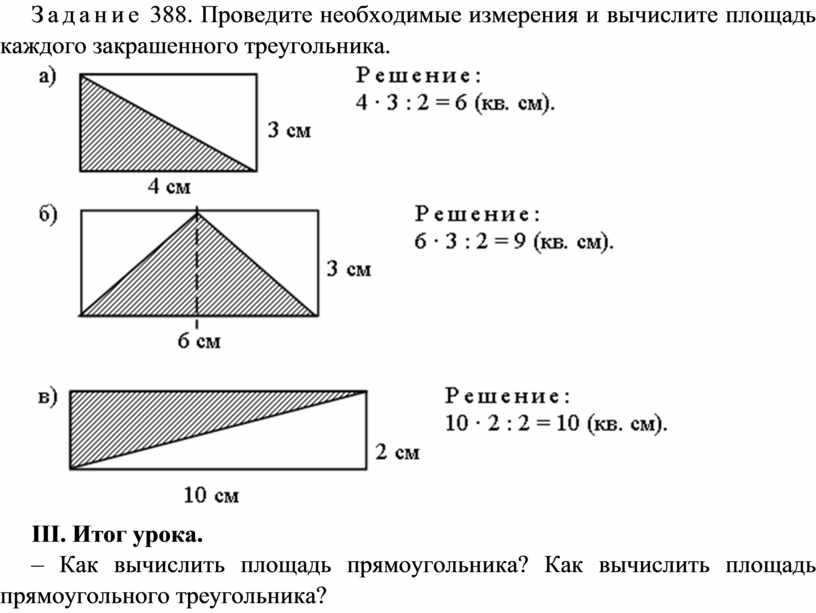

Площадь прямоугольника ниже будет рассчитана путем умножения основания на высоту
(б х ч).

Прямоугольник можно разделить на 2 конгруэнтных (идентичных) прямоугольных треугольников.

Итак, площадь каждого из прямоугольных треугольников равна половине площади прямоугольника.

Формула площади прямоугольного треугольника

\[\text { Площадь треугольника }=\frac{\text { основание } \times \text { высота }}{2}\]

Это можно сократить до

\[A=\frac{1}{2} b h\]

где b — длина основания, а h — высота треугольника.

Ваш окончательный ответ должен быть дан в единицах ² (например, см ² , м ² , мм ² ).

Как найти площадь прямоугольного треугольника

Чтобы найти площадь прямоугольного треугольника:

1Определите высоту и длину основания треугольника (возможно, вам потребуется рассчитать эти значения)

2 Напишите формулу

\[A=\frac{1}{2} b h\]

3 Подставьте значения основания и высоты

4 Вычислить

Как найти площадь прямоугольного треугольника

Рабочий лист с прямоугольным треугольником

Получите свободную область рабочего листа с прямоугольным треугольником из 20+ вопросов и ответов. Включает рассуждения и прикладные вопросы.

СКАЧАТЬ

Икс

Рабочий лист с прямоугольным треугольником

Получите свободную область рабочего листа с прямоугольным треугольником из 20+ вопросов и ответов. Включает рассуждения и прикладные вопросы.

СКАЧАТЬ

Примеры площади прямоугольного треугольника

Пример 1: данные длины основания и высоты

Найдите площадь треугольника ниже:

1. Определите высоту и длину основания треугольника

9 h0 = 7 3

b = 8см

2 Запишите формулу

\[A=\frac{1}{2} b h\]

3 Подставьте значения основания и высоты выровнено} A &=\frac{1}{2} b h \\ &=\фракция{1}{2}(8)(7) \конец{выровнено}\] 92 \end{aligned}\]

Помните: ваш окончательный ответ должен быть выражен в единицах, возведенных в квадрат.

Пример 2: заданы длина и высота основания

Найдите площадь треугольника:

Определите высоту и длину основания треугольника

h = 200 см

b = 6 м Вы

6 Примечание: здесь есть 2 разных блока.

Вы должны перевести их в общую единицу измерения 200см = 2м .

h = 2 м

b = 6 м

Запишите формулу 92 \end{aligned}\]

Помните: ваш окончательный ответ должен быть выражен в единицах, возведенных в квадрат.

Пример 4: составная форма

Ниже приведен план новой палубы, которую необходимо покрасить. Одна банка краски стоит 12 фунтов стерлингов и покрывает площадь 2,5 м ² . Сколько будет стоить покрасить всю колоду?

Определите высоту и длину основания треугольника

Разделите план на 2 фигуры. У вас есть прямоугольник и прямоугольный треугольник. 9{2} \\ \end{aligned}\]

Общая площадь = 4,375 + 7,5 = 11,875 м ²

Теперь нам нужно разделить 11,875 на 2,5, так как одна банка краски покрывает только площадь 2,5 м ^{2 :}

0

11,875 ÷ 2,5 = 4,75

Это означает, что вам нужно купить 5 банок краски, так как мы можем купить только целые банки краски.

Теперь подсчитаем стоимость: 5 банок краски x 12 фунтов стерлингов = 60 фунтов стерлингов

Общая стоимость покраски палубы составляет 60 фунтов стерлингов .

Как найти недостающую длину стороны по площади

Иногда вопрос может дать вам площадь и попросить определить высоту или недостающую длину. Для этого нужно изменить формулу.

Чтобы найти недостающую длину по площади:

1 Измените формулу

2 Подставьте известные значения

3 Вычислите

Пример 5: расчет длины основания

Треугольник XYZ является прямоугольным треугольником с площадью 90 27 15 см . Высота треугольника 5 см. Найдите длину основания треугольника.

Измените формулу

\[A = \frac{1}{2}bh\]

, чтобы сделать b подлежащим, начните с умножения обеих частей формулы на 2

\[2A = bh\ ]

Затем нам нужно разделить обе части формулы на h

\[\frac{2(A)}{h}=b\]

Теперь подставляем данные значения

Площадь = 15

Высота = 5

\[b=\frac{2(15)}{5}\]

Вычислить

\[\begin{align} b&=\frac{2(15)}{5} \\ b&=\frac{30}{5} \\ b&=6 \mathrm{~см} \конец{выровнено}\] 9{2}

Начиная с формулы для площади треугольника: Площадь=\доля{1}{2} \умножить на основание \умножить на высоту

 

Подставляем известную информацию (преобразуем длины в те же единицы) , Таким образом,

40 = \ frac {1} {2} \ Times 10 \ Times Height

40 = 5 \ Times Height

Следовательно:

Высота = 8см

Площадь прямоугольного треугольника

Вопросы GCSE 9{2}

(1)

Переставить площадь треугольника:

 

\begin{выровнено} A &= \frac{1}{2} bh \\ 2А &= чч\\ ч &= \ гидроразрыва {2A} {b} \end{выровнено}

(1)

Замените значения:

h= \frac{2 \times 36}{9} \начать{массив}{л} h= \frac{72}{9}\end{массив}\begin{массив}{l} ч=8см \конец{массив}

(1)

Контрольный список для обучения

Теперь вы знаете, как:

•  Применить формулу для расчета и решения задач, связанных с площадью треугольников
•  Использовать теорему Пифагора для решения задач, связанных с треугольниками

Все еще застряли?

Подготовьте своих учеников KS4 к успешной сдаче выпускных экзаменов по математике с помощью программы Third Space Learning. Еженедельные онлайн-уроки повторения GCSE по математике, которые проводят опытные преподаватели математики.

Узнайте больше о нашей программе повторения GCSE по математике.

Узнайте, как найти площадь неправильного треугольника

Learn How To Find the Area of ​​a Non-Right Triangle

Charlotte Taylor

January 27, 2021

Online Tutoring

,

Study Tips

,

Mathematics

,

Trigonometry

Чтобы найти площадь непрямоугольного треугольника, давайте сначала рассмотрим стандартную формулу площади прямоугольного треугольника. Прямоугольный треугольник состоит из трех сторон: основания, высоты и гипотенузы. Чтобы получить площадь треугольника, нужно умножить длины двух соседних сторон 90° угол, который является основанием и высотой треугольника, и разделить эту величину пополам.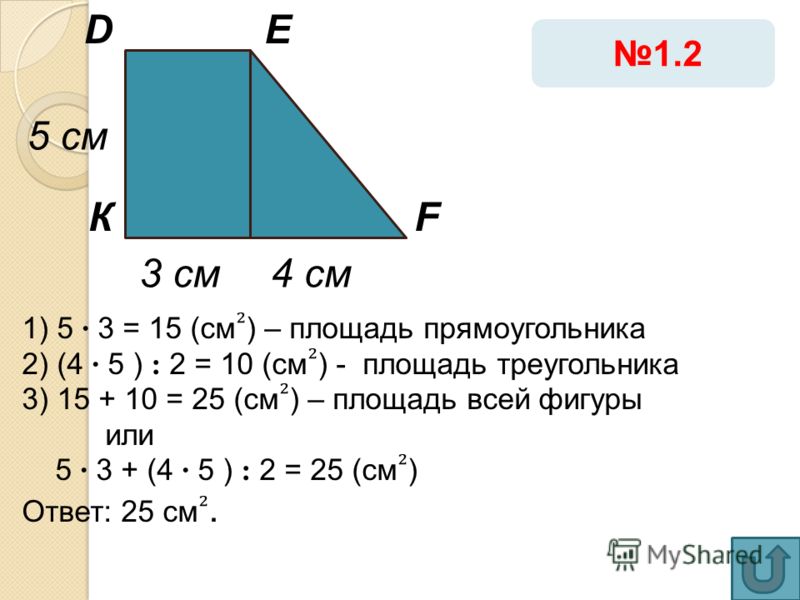 Это формула площади прямоугольного треугольника:

Однако эта формула не так эффективна для острых и тупых углов. Итак, как найти площадь непрямоугольного треугольника.

Формулы площади непрямого треугольника

При использовании тригонометрии есть еще одна группа формул, которые можно использовать для нахождения площади треугольника без прямых углов. Используя эти формулы, вы можете найти площадь непрямоугольного треугольника, даже если отсутствует длина стороны. Существуют разные способы нахождения площадей тупоугольного и остроугольного треугольников.

Нахождение площади остроугольного треугольника

Когда вам нужно найти площадь остроугольного треугольника, вы должны использовать закон синусов вместо отсутствующей длины стороны. В зависимости от того, какие стороны или углы известны, для нахождения площади остроугольного непрямоугольного треугольника можно использовать одну из следующих формул:

См. ниже остроугольный треугольник ΔABC.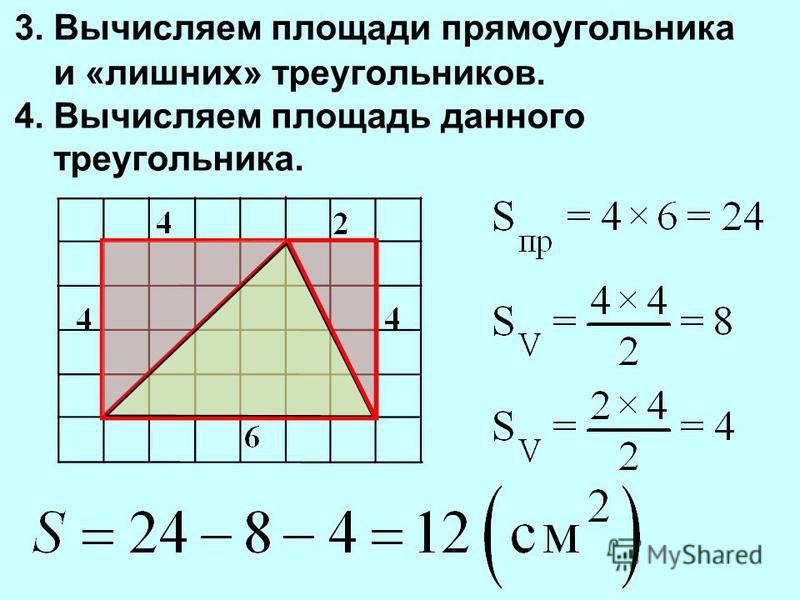 Вы можете видеть, что мы не знаем длины всех сторон треугольника, но мы знаем, что острый угол равен 56°, а длины двух соседних сторон равны 18 и 12. Мы воспользуемся функцией синуса на калькуляторе. чтобы включить это в формулу , где ab представляет известную длину сторон треугольника. Площадь треугольника 88,47.

При использовании тригонометрической формулы для нахождения площади остроугольного непрямоугольного треугольника заглавная буква «С» используется для обозначения известного угла, лежащего напротив длины противоположной стороны, представленной строчной буквой «с».

Нахождение площади тупоугольного треугольника

Функции синуса, косинуса и тангенса можно использовать только для нахождения площади треугольника с острым углом. Таким образом, вы должны использовать другой метод, чтобы найти площадь треугольника с тупым углом. Чтобы найти площадь нижеприведенного треугольника, вы должны провести прямую линию из точки С и точки А, создав прямоугольный треугольник в месте пересечения двух линий.

No related posts.