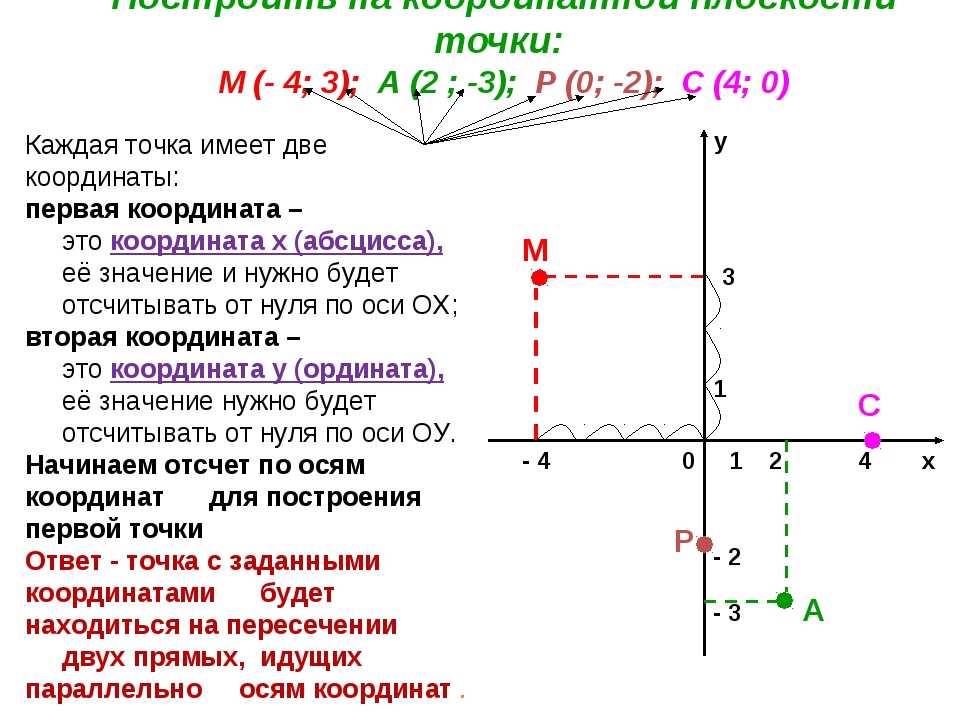
Как найти расстояние на координатной плоскости
В математике как алгебра, так и геометрия ставят задачи по нахождению расстояния до точки или прямой от заданного объекта. Оно находится совершенно разными способами, выбор которых зависит от исходных данных. Рассмотрим, как найти расстояние между заданными объектами в разных условиях.
Использование измерительных инструментов
На начальном этапе освоения математической науки учат, как пользоваться элементарными инструментами (такими, как линейка, транспортир, циркуль, треугольник и другие). Найти расстояние между точками или прямыми при их помощи совсем несложно. Достаточно приложить шкалу делений и записать ответ. Стоит лишь знать, что расстояние будет равным длине прямой, которую можно провести между точками, а в случае с параллельными линиями – перпендикуляру между ними.
Использование теорем и аксиом геометрии
В старших классах учатся измерять расстояние без помощи специальных приспособлений или миллиметровой бумаги. Для этого нужны многочисленные теоремы, аксиомы и их доказательства. Зачастую задачи о том, как найти расстояние, сводятся к образованию прямоугольного треугольника и поиску его сторон. Для решения таких задач достаточно знать теорему Пифагора, свойства треугольников и способы их преобразования.
Для этого нужны многочисленные теоремы, аксиомы и их доказательства. Зачастую задачи о том, как найти расстояние, сводятся к образованию прямоугольного треугольника и поиску его сторон. Для решения таких задач достаточно знать теорему Пифагора, свойства треугольников и способы их преобразования.
Точки на координатной плоскости
Если есть две точки и задано их положение на координатной оси, то как найти расстояние от одной до другой? Решение будет включать несколько этапов:
- Соединяем точки прямой, длина которой и будет являться расстоянием между ними.
- Находим разность значений координат точек (к;р) каждой оси: |к1 — к2|= д1 и |р1 — р2|= д2 (значения берем по модулю, т.к. расстояние не может быть отрицательным).
- После этого возводим получившиеся числа в квадрат и находим их сумму: д12 + д22
- Заключительным этапом будет извлечение квадратного корня из получившегося числа.
 Это и будет расстоянием между точками: д=V (д12 + д22).
Это и будет расстоянием между точками: д=V (д12 + д22).
В итоге все решение осуществляется по одной формуле, где расстояние равно квадратному корню от суммы квадратов разности координат:
д =V(|к1 — к2|2+|р1 — р2|2)
Если возникнет вопрос о том, как найти расстояние от одной точки до другой в трехмерном пространстве, то поиск ответа на него не будет особо отличаться от приведенного выше. Решение будет осуществляться по следующей формуле:
д=V(|к1 — к2|2+|р1 — р2|2+|е1 — е2|2)
Параллельные прямые
Перпендикуляр, проведенный из любой точки, лежащей на одной прямой, к параллели, и будет расстоянием. При решении задач в плоскости необходимо найти координаты любой точки одной из прямых. А затем вычислить расстояние от нее до второй прямой.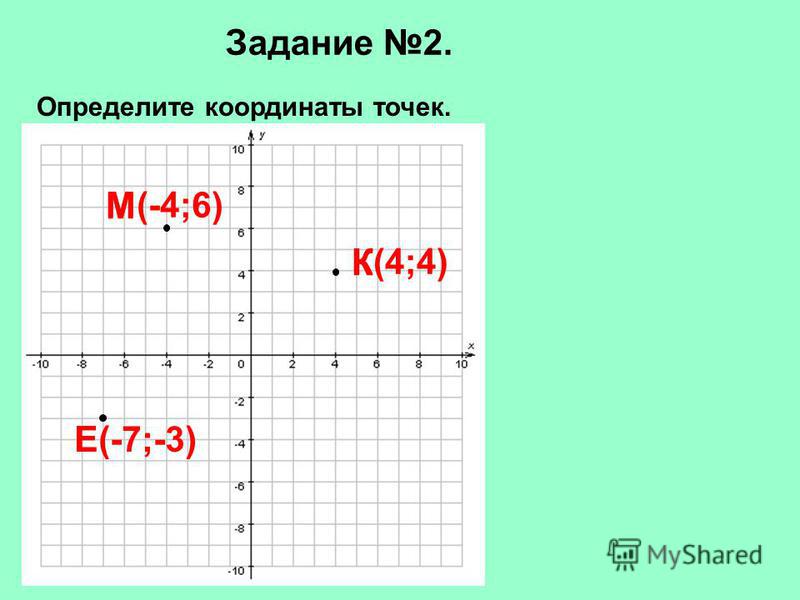 Для этого приводим их к общему уравнению прямой вида Ах+Ву+С=0. Из свойств параллельных прямых известно, что их коэффициенты А и В будут равны. В таком случае найти расстояние между параллельными прямыми можно по формуле:
Для этого приводим их к общему уравнению прямой вида Ах+Ву+С=0. Из свойств параллельных прямых известно, что их коэффициенты А и В будут равны. В таком случае найти расстояние между параллельными прямыми можно по формуле:
д = |C1 — C2|/V(A2 + B2)
Таким образом, при ответе на вопрос о том, как найти расстояние от заданного объекта, необходимо руководствоваться условием задачи и предоставляемыми инструментами ее решения. Ими могут быть как измерительные приспособления, так и теоремы и формулы.
Узнаем как найти расстояние на координатной плоскости
В математике как алгебра, так и геометрия ставят задачи по нахождению расстояния до точки или прямой от заданного объекта. Оно находится совершенно разными способами, выбор которых зависит от исходных данных. Рассмотрим, как найти расстояние между заданными объектами в разных условиях.
Использование измерительных инструментов
На начальном этапе освоения математической науки учат, как пользоваться элементарными инструментами (такими, как линейка, транспортир, циркуль, треугольник и другие). Найти расстояние между точками или прямыми при их помощи совсем несложно. Достаточно приложить шкалу делений и записать ответ. Стоит лишь знать, что расстояние будет равным длине прямой, которую можно провести между точками, а в случае с параллельными линиями – перпендикуляру между ними.
Найти расстояние между точками или прямыми при их помощи совсем несложно. Достаточно приложить шкалу делений и записать ответ. Стоит лишь знать, что расстояние будет равным длине прямой, которую можно провести между точками, а в случае с параллельными линиями – перпендикуляру между ними.
Использование теорем и аксиом геометрии
В старших классах учатся измерять расстояние без помощи специальных приспособлений или миллиметровой бумаги. Для этого нужны многочисленные теоремы, аксиомы и их доказательства. Зачастую задачи о том, как найти расстояние, сводятся к образованию прямоугольного треугольника и поиску его сторон. Для решения таких задач достаточно знать теорему Пифагора, свойства треугольников и способы их преобразования.
Точки на координатной плоскости
Если есть две точки и задано их положение на координатной оси, то как найти расстояние от одной до другой? Решение будет включать несколько этапов:
- Соединяем точки прямой, длина которой и будет являться расстоянием между ними.

- Находим разность значений координат точек (к;р) каждой оси: |к1 — к2|= д1 и |р1 — р2|= д2 (значения берем по модулю, т.к. расстояние не может быть отрицательным).
- После этого возводим получившиеся числа в квадрат и находим их сумму: д12 + д22
- Заключительным этапом будет извлечение квадратного корня из получившегося числа. Это и будет расстоянием между точками: д=V (д12 + д22).
В итоге все решение осуществляется по одной формуле, где расстояние равно квадратному корню от суммы квадратов разности координат:
д =V(|к1 — к2|2+|р1 — р2|2)
Если возникнет вопрос о том, как найти расстояние от одной точки до другой в трехмерном пространстве, то поиск ответа на него не будет особо отличаться от приведенного выше. Решение будет осуществляться по следующей формуле:
д=V(|к1 — к2|2+|р1 — р2|2+|е1 — е2|2)
Параллельные прямые
Перпендикуляр, проведенный из любой точки, лежащей на одной прямой, к параллели, и будет расстоянием.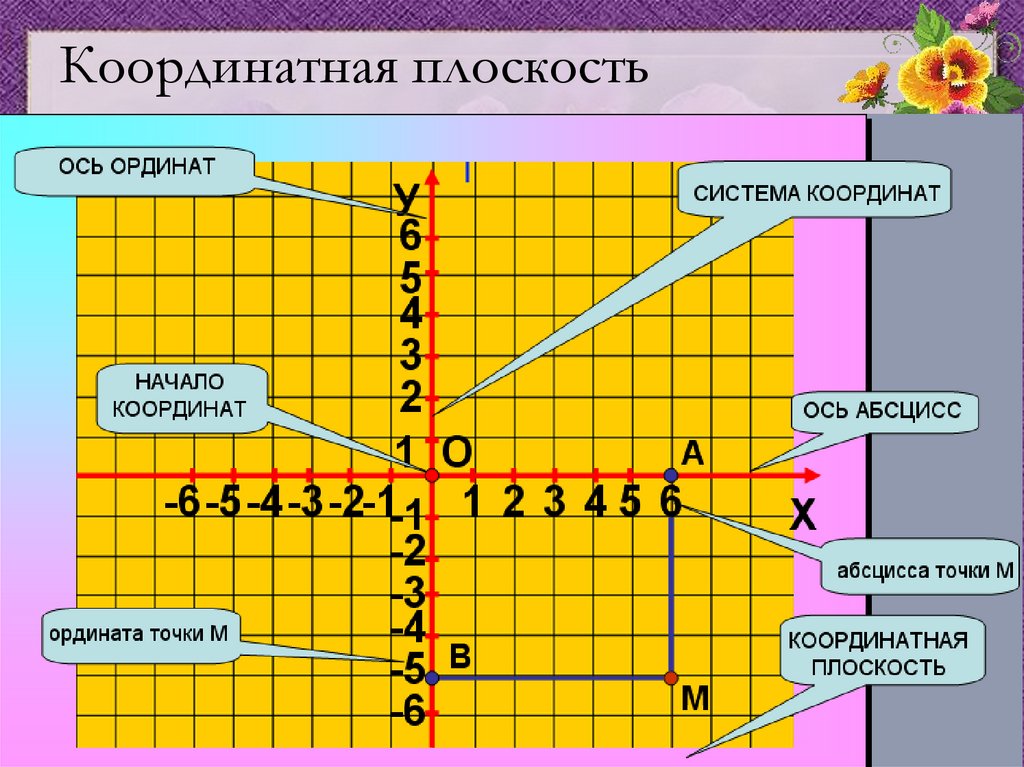 При решении задач в плоскости необходимо найти координаты любой точки одной из прямых. А затем вычислить расстояние от нее до второй прямой. Для этого приводим их к общему уравнению прямой вида Ах+Ву+С=0. Из свойств параллельных прямых известно, что их коэффициенты А и В будут равны. В таком случае найти расстояние между параллельными прямыми можно по формуле:
При решении задач в плоскости необходимо найти координаты любой точки одной из прямых. А затем вычислить расстояние от нее до второй прямой. Для этого приводим их к общему уравнению прямой вида Ах+Ву+С=0. Из свойств параллельных прямых известно, что их коэффициенты А и В будут равны. В таком случае найти расстояние между параллельными прямыми можно по формуле:
д = |C1 — C2|/V(A2 + B2)
Таким образом, при ответе на вопрос о том, как найти расстояние от заданного объекта, необходимо руководствоваться условием задачи и предоставляемыми инструментами ее решения. Ими могут быть как измерительные приспособления, так и теоремы и формулы.
Нахождение расстояний на координатной плоскости
Ключевые понятия
- Нахождение вертикального расстояния.
- Найти горизонтальное расстояние.
- Решайте задачи, используя расстояние.
Когда две точки находятся в одном квадранте, мы вычитаем, чтобы найти разницу их абсолютных значений, чтобы найти расстояние между ними.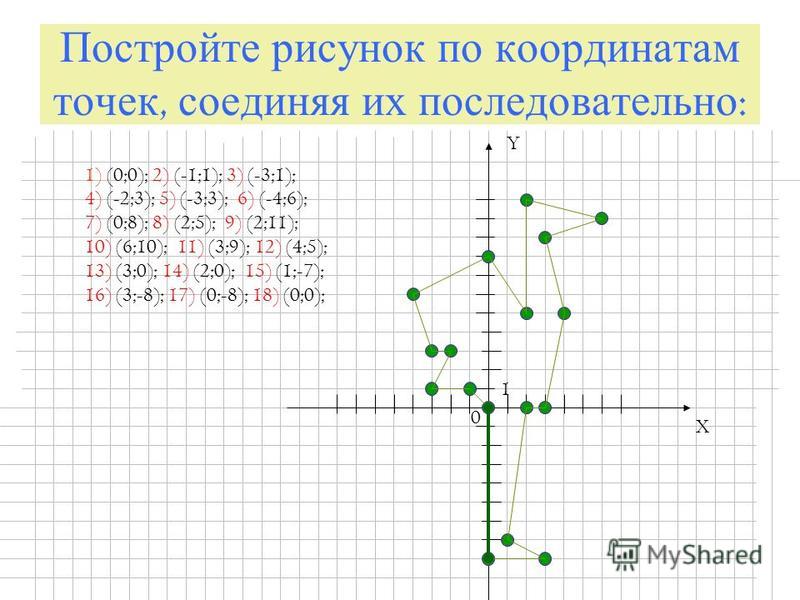
Когда две точки находятся в разных квадрантах, мы добавляем, чтобы найти разницу их абсолютных значений, чтобы найти расстояние между ними.
- Если координаты x совпадают, мы используем координаты y для определения расстояния.
- Если координаты y совпадают, мы используем координаты x для определения расстояния.
Например, если координаты (3, 5) и (3, -2), используйте координаты y.
Если координаты (-1, 4) и (6, 4), используйте координаты x.
2.5.1 Найти вертикальное расстояниеПример 1:
Найти расстояние между (-4, –1) и (-4, –6).
Решение:
Использовать абсолютное значение. Посмотрите на координаты y. Поскольку точки находятся в одном квадранте, вычтите абсолютные значения.
|-6| – |-1| = 6 – 1 = 5.
Пример 2:
Найдите расстояние от колеса обозрения до американских горок 3.
Решение:
Найдите координаты колеса обозрения и американских горок 90 0 3.
- Координаты колеса обозрения (-6, 2).
- Координаты американских горок 3 (-6, -8).
Абсолютное значение координаты Y говорит вам о расстоянии между каждой точкой и осью X.
Расстояние от колеса обозрения до американских горок 3 составляет
|2|+|-8| = 2 + 8 = 10 миль.
2.5.2 Найти расстояние по горизонтали
Пример 3:
Найти расстояние между (-3, 5) и (4, 5).
Решение:
Использовать абсолютное значение. Посмотрите на координаты x . Поскольку точки находятся в разных квадрантах, добавьте абсолютные значения.
|-3| + |4| = 3 + 4 = 7.
Пример 4:
Найдите расстояние от американских горок 1 до качелей.
Решение:
Найдите координаты американских горок 1 и качелей.
- Координаты американских горок 1 (-6, 7).
- Координаты качания ролика (1, 7).

Расстояние от американских горок 1 до качелей
|-6|+|1| = 6 + 1 = 7 миль.
2.5.3 Решение задач с использованием расстоянияПример 5:
На графике показано расположение точки G и точки H . Точка J обозначена на графике как (n, -3). Расстояние от точки H до точки J равно расстоянию от точки H до точки G .
- Какое расстояние от точки H до точки J ?
- Каково значение n ?
Решение:
Шаг 1:
Найдите расстояние от точки H до точки J .
Координаты x совпадают.
|-6|-|-3| = 6 – 3 = 3 единицы.
Шаг 2:
Расстояние от точки H до точки G равно 3 единицам.
н – 0 =3
n = 3
- Чтобы найти расстояния между точками на координатной плоскости, нам нужно использовать _______________.

- Нам нужно ___________ абсолютных значений, чтобы найти расстояние между двумя точками, используя их координаты, если они лежат в разных квадрантах.
- Нам нужно _____________ абсолютных значений, чтобы найти расстояние между двумя точками, используя их координаты, если они лежат в одном квадранте.
- Найти расстояние между точками (5, —6) и (2, —6)
- Найти расстояние между каждой парой точек (-6, -4,7) и (-6, 4,1)
- Найти расстояние между точками (-2, 1) и (-1, 1)
- Найти расстояние между точки (-7, -4) и (-7, 9)
- Найдите расстояние от американских горок 1 до колеса обозрения.
9. Найдите расстояние между аквапарком и домом Коултера.
10. Найдите расстояние между школой и магазином.
Концептуальная карта
Чему мы научились:
- Найти расстояние по вертикали между двумя точками на плане координат.
- Найти расстояние по горизонтали между двумя точками на плане координат.

- Решайте задачи, используя расстояние на плане координат.
как найти расстояние между двумя точками, если график не указан
Справка по математике
Ник С.
спросил 20.12.16например, если бы мне дали найти точки между (10, 10) и (4,4), как мне их найти, если нет графика с ними
Подписаться І 3
Подробнее
Отчет
2 ответа от опытных наставников
Лучший Новейшие Самый старыйАвтор: Лучшие новыеСамые старые
Стивен М. ответил 20.12.16
Репетитор
4.9(679)
Выпускник Военно-морской академии по математике и естественным наукам
См. таких репетиторов
Смотрите таких репетиторов
Формула расстояния на самом деле является просто переформулировкой теоремы Пифагора.
(изменение x) 2 + (изменение y) 2 = (расстояние) 2
Δx 2 +ΔY 2 = D 2
. Δx 2 + Δy 2 )
Если у вас есть дополнительные вопросы, пожалуйста, дайте мне знать.
Голосовать за 1 Понизить
Подробнее
Отчет
Кеннет С. ответил 20.12.16
Репетитор
4,8 (62)
Экспертная помощь по алгебре/тригонометрии/(пред)исчислению для гарантии успеха в 2018 году
См.

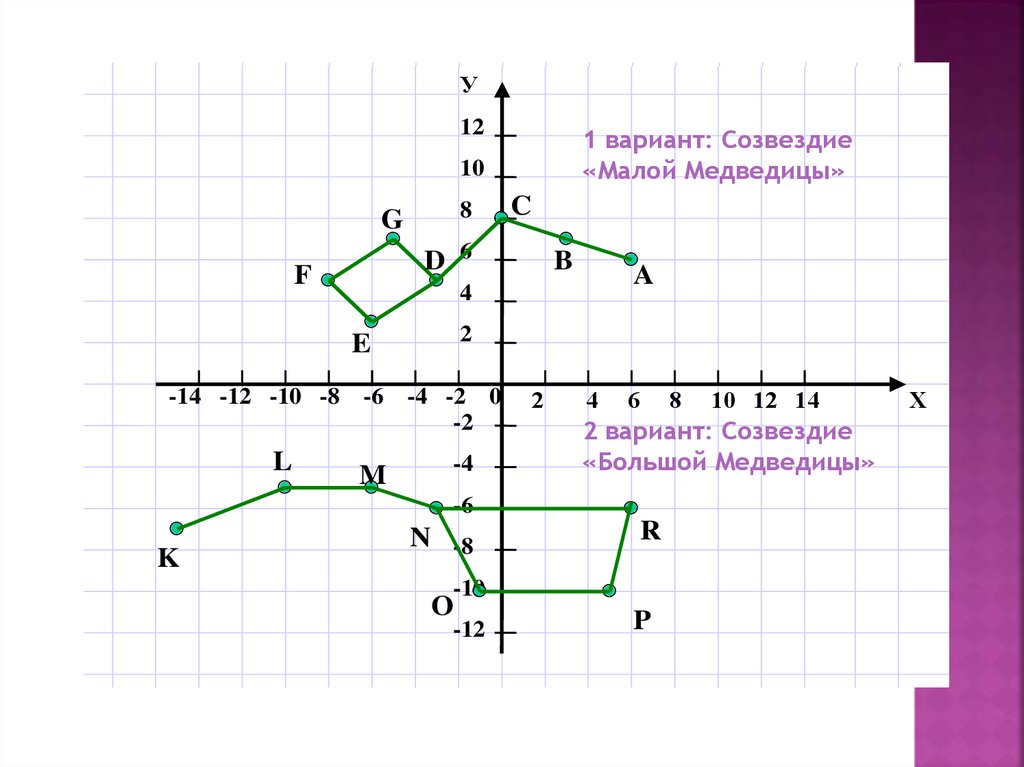 Это и будет расстоянием между точками: д=V (д12 + д22).
Это и будет расстоянием между точками: д=V (д12 + д22).