Как найти разность векторов — интернет энциклопедия для студентов
ФОРМУЛА
Чтобы найти разность векторов\(\ \overline{a}-\overline{b} \), заданных на плоскости координатами \(\ \overline{a}=\left(a_{x} ; a_{y}\right)\quad{и}\quad \overline{b}=\left(b_{x} ; b_{y}\right) \) , необходимо вычесть из координат первого вектора соответствующие координаты второго, т.е.
\(\ \overline{a}-\overline{b}=\left(a_{x}-b_{x} ; a_{y}-b_{y}\right) \)
Если векторы заданы в пространстве, то есть \(\ \tilde{a}=\left(a_{x} ; a_{y} ; a_{z}\right)\quad{и}\quad \overline{b}=\left(b_{x} ; b_{y} ; b_{z}\right) \)тогда их различие
\(\ \overline{a}-\overline{b}=\left(a_{x}-b_{x} ; a_{y}-b_{y} ; a_{z}-b_{z}\right) \)
ПРИМЕР
ПРИМЕР
\(\ \overline{a}-\overline{b}-\overline{c}=(2 ;-3 ; 1)-(1 ; 0 ;-2)-(-1 ; 2 ; 3)= \)
\(\ =(2-1-(-1) ;-3-0-2 ; 1-(-2)-3)=(2 ;-5 ; 0) \)
Физика
166
Реклама и PR
31
Педагогика
80
Психология
72
Социология
7
Астрономия9
Биология
30
Культурология
86
Экология
8
Право и юриспруденция
36
Политология
13
Экономика
49
Финансы
9
История
16
Философия
8
Информатика
20
Право
35
Информационные технологии
6
Экономическая теория
7
Менеджент
719
Математика
338
Химия
20
Микро- и макроэкономика
1
Медицина
5
Государственное и муниципальное управление
2
География
542
Информационная безопасность
2
Аудит
11
Безопасность жизнедеятельности
3
Архитектура и строительство
1
Банковское дело
1
Рынок ценных бумаг
6
Менеджмент организации
2
Маркетинг
238
Кредит
3
Инвестиции
2
Журналистика
1
Конфликтология
15
Этика9
Формулы дифференцирования Как найти сумму векторов Как найти вектор по точкам Периодические десятичные дроби Понятие десятичной дроби
Узнать цену работы
Узнай цену
своей работы
Имя
Выбрать тип работыЧасть дипломаДипломнаяКурсоваяКонтрольнаяРешение задачРефератНаучно — исследовательскаяОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерскаяНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация в ВАКПубликация в ScopusДиплом MBAПовышение оригинальностиКопирайтингДругоеПринимаю Политику конфиденциальности
Подпишись на рассылку, чтобы не пропустить информацию об акциях
Разность векторов: определение, формула для нахождения, аналитический метод и графическое построение
В математике и физике студентам и школьникам зачастую попадаются задачи на векторные величины и на выполнение различных операций над ними. В чём же отличие векторных величин от привычных нам скалярных, единственная характеристика которых — это численное значение? В том, что они обладают направлением.
В чём же отличие векторных величин от привычных нам скалярных, единственная характеристика которых — это численное значение? В том, что они обладают направлением.
Оглавление:
- Определения векторной математики
- Аналитический метод
- Вычисление разности графически
- Решение задач
Максимально наглядно применение векторных величин объясняется в физике. Самыми простыми примерами являются силы (сила трения, сила упругости, вес), скорость и ускорение, поскольку помимо численных значений они также обладают направлением действия. Для сравнения приведём пример скалярных величин: это может быть расстояние между двумя точками или масса тела. Для чего же необходимо выполнять действия над векторными величинами такие как сложение или вычитание? Это нужно, чтобы было возможно определить результат действия системы векторов, состоящей из 2 или более элементов.
Содержание
Определения векторной математики
Введём главные определения, используемые при выполнении линейных операций.
- Вектором называют направленный (имеющий точку начала и точку конца) отрезок.
- Длина (модуль) — это длина направленного отрезка.
- Коллинеарными называют такие два вектора, которые либо параллельны одной и той же прямой, либо одновременно лежат на ней.
- Противоположно направленными векторами называют коллинеарные и при этом направленные в разные стороны. Если же их направление совпадает, то они являются сонаправленными.
- Вектора являются равными, когда они сонаправлены и одинаковы по модулю.
- Суммой двух векторов a и b является такой вектор c, начало которого совпадает с началом первого, а конец — с концом второго при условии, что b начинается в той же точке, в которой заканчивается a.
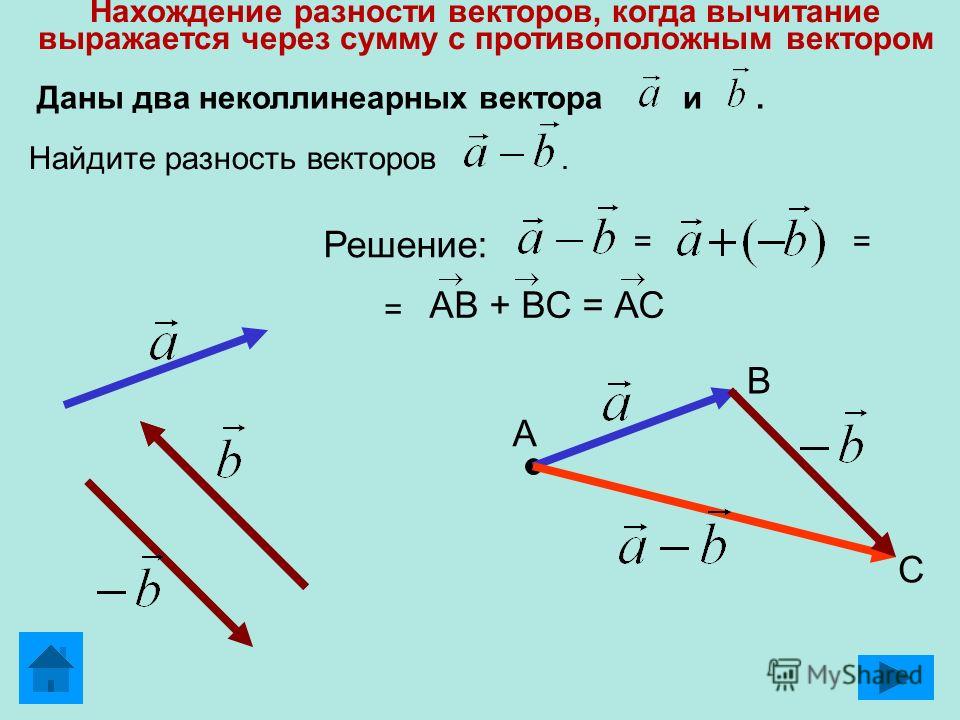
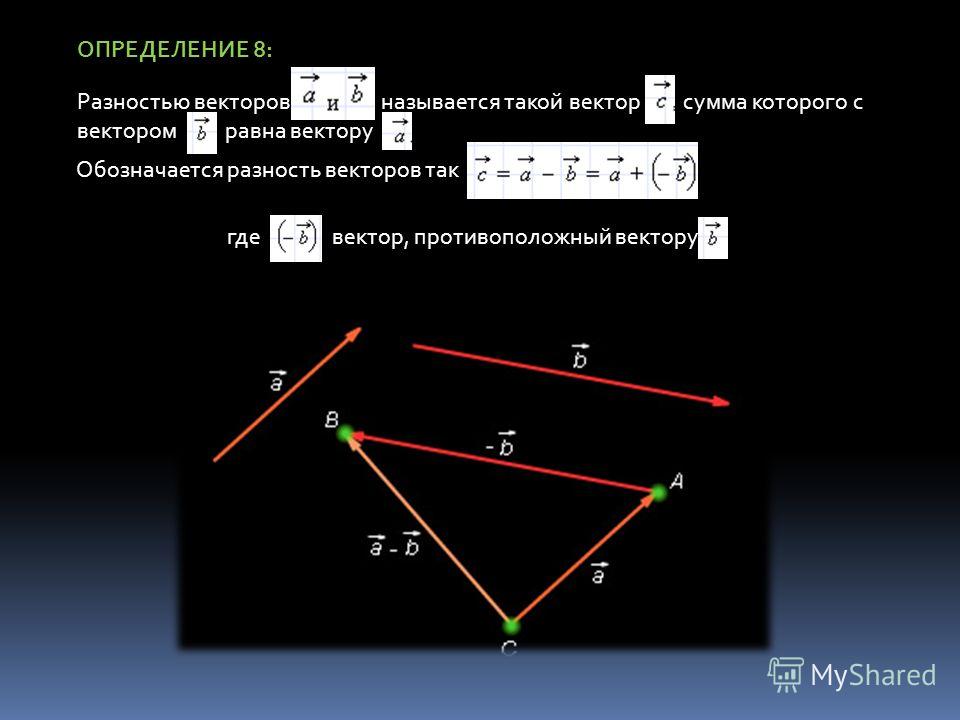
- Разностью векторов a и b называют сумму a и (— b), где (— b) — противоположно направленный к вектору b. Также определение разности двух векторов может быть дано следующее: разностью c пары векторов a и b называют такой c, который при сложении с вычитаемым b образует уменьшаемое a.

Аналитический метод
Аналитический способ подразумевает получение координат разности по формуле без построения. Возможно выполнить вычисление для плоского (двухмерного), объёмного (трёхмерного) или же n-мерного пространства.
Для двухмерного пространства и векторных величин a {a₁, a₂} и b {b₁, b₂} расчёты будут иметь следующий вид: c {c₁, c₂} = {a₁ b₁, a₂ b₂}.
В случае с добавлением третьей координаты расчёт будет проводиться аналогично, и для a {a₁, a₂, a₃} и b {b₁, b₂, b₃} координаты разности будут также получены попарным вычитанием: c {c₁, c₂, c₃} = {a₁ b₁, a₂ b₂, a₃ b₃}.
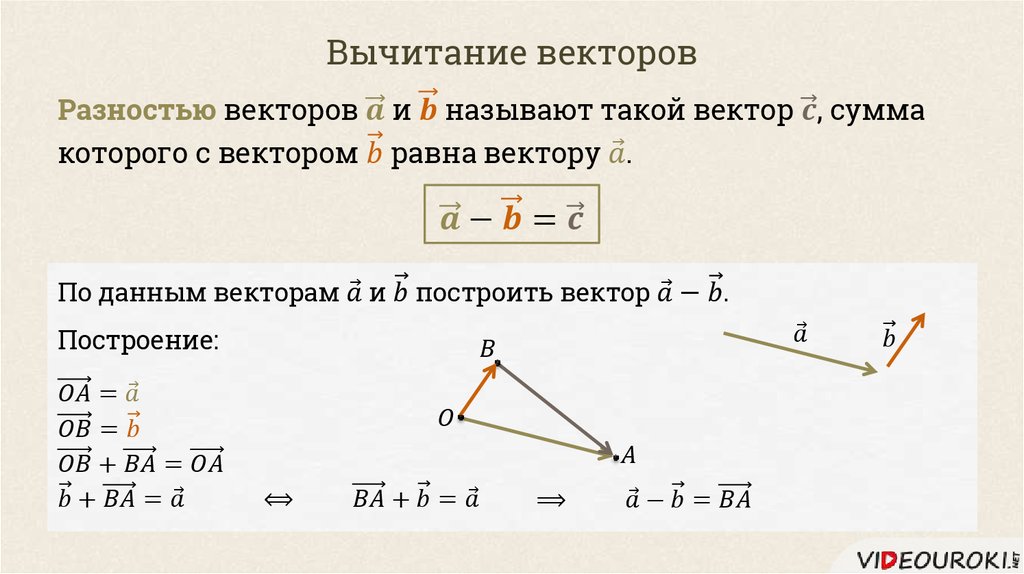
Вычисление разности графически
Для того чтобы построить разность графическим способом, следует воспользоваться правилом треугольника. Для этого необходимо выполнить следующую последовательность действий:
- По заданным координатам построить векторы, для которых нужно найти разность.

- Совместить их концы (т. е. построить два направленных отрезка, равных заданным, которые будут оканчиваться в одной и той же точке).
- Соединить начала обоих направленных отрезков и указать направление, результирующий будет начинаться в той же точке, где начинался вектор, являющийся уменьшаемым, и заканчиваться в точке начала вычитаемого.
Результат операции вычитания показан на рисунке ниже.
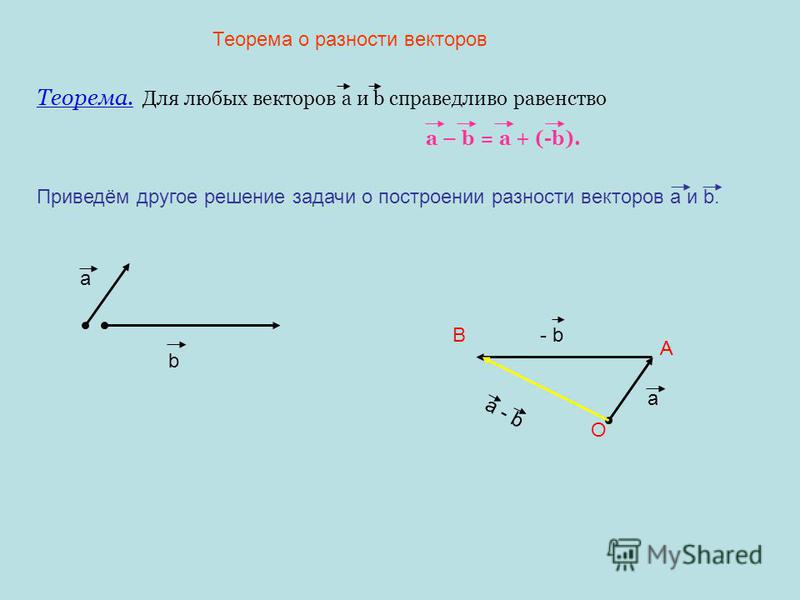
Также существует метод построения разности, незначительно отличающийся от предыдущего. Его суть заключается в применении теоремы о разности векторов, которая формулируется следующим образом: для того чтобы найти разность пары направленных отрезков, достаточно найти сумму первого из них с отрезком, противоположно направленным ко второму. Алгоритм построения будет иметь следующий вид:
- Построить исходные направленные отрезки.
- Тот, что является вычитаемым, необходимо отразить, т. е. построить противоположно направленный и равный ему отрезок, затем совместить его начало с уменьшаемым.

- Построить сумму: соединить начало первого отрезка с концом второго.
Результат такого решения изображён на рисунке:
Решение задач
Для закрепления навыка разберём несколько заданий, в которых требуется рассчитать разность аналитически или графически.
Задача 1. На плоскости заданы 4 точки: A (1, —3), B (0, 4), C (5, 8), D (—3, 2). Определить координаты вектора q = AB — CD, а также рассчитать его длину.
Решение. Вначале следует найти координаты AB и CD. Для этого из координат конечных точек вычтем координаты начальных. Для AB началом является A (1, —3), а концом B (0, 4). Рассчитаем координаты направленного отрезка:
AB {0 — 1, 4 — (— 3)} = {— 1, 7}
Аналогичный расчёт выполняется для CD:
CD {— 3 — 5, 2 — 8} = {— 8, — 6}
Теперь, зная координаты, можно найти разность векторов. Формула для аналитического решения плоских задач была рассмотрена ранее: для c = a — b координаты имеют вид {c₁, c₂} = {a₁ b₁, a₂ b₂}. Для конкретного случая можно записать:
Для конкретного случая можно записать:
q = {— 1 — 8, 7 — ( — 6)} = { — 9, — 1}
Чтобы найти длину q, воспользуемся формулой | q | = √(q₁² + q₂²) = √((— 9)² + (— 1)²) = √(81 + 1) = √82 ≈ 9,06.
Задача 2. На рисунке изображены векторы m, n и p.
Необходимо построить для них разности: p — n, m — n, m — n — p. Выяснить, какая из них обладает наименьшим модулем.
Решение. В задаче требуется выполнить три построения. Рассмотрим каждую часть задания более подробно.
Часть 1. Для того чтобы изобразить p — n, воспользуемся правилом треугольника. Для этого при помощи параллельного переноса соединим отрезки так, чтобы совпала их конечная точка. Теперь соединим начальные точки и определим направление. В нашем случае вектор разности начинается там же, где и вычитаемый n.
Часть 2. Изобразим m — n. Теперь для решения воспользуемся теоремой о разности векторов. Для этого следует построить вектор, противоположный n, а затем найти его сумму с m.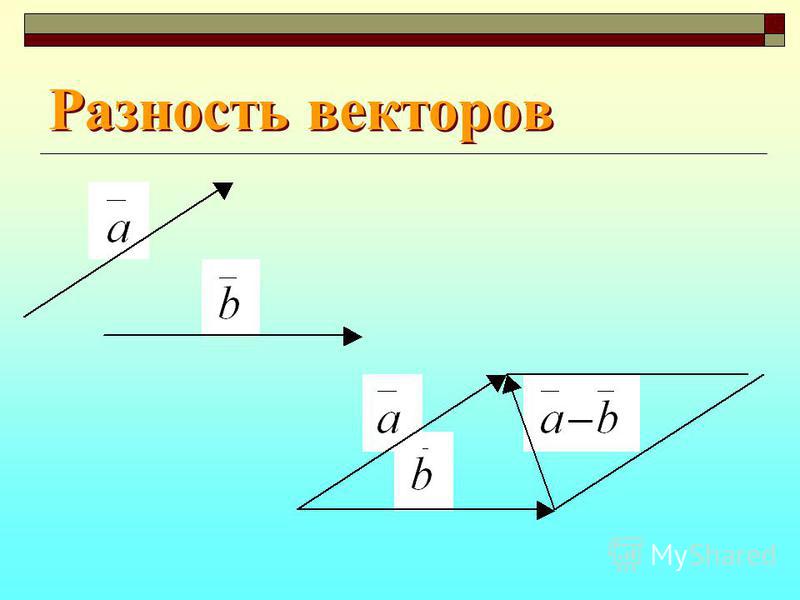 Полученный результат будет выглядеть так:
Полученный результат будет выглядеть так:
Часть 3. Для того чтобы найти разность m — n — p, следует разбить выражение на два действия. Поскольку в векторной алгебре действуют законы аналогичные законам арифметики, то возможны варианты:
- m — (n + p): в этом случае вначале строится сумма n + p, которая затем вычитается из m,
- (m — n) — p: здесь сначала нужно найти m — n, а затем отнять от этой разности p,
- (m — p) — n: первым действием определяется m — p, после чего из полученного результата нужно вычесть n.
Так как в предыдущей части задачи мы уже нашли разность m — n, нам остаётся лишь вычесть из неё p. Построим разность двух данных векторов при помощи теоремы о разности. Ответ показан на изображении ниже (красным цветом обозначен промежуточный результат, а зелёным — окончательный).
Остаётся определить, модуль какого из отрезков является наименьшим. Вспомним, что понятия длины и модуля в векторной математике являются идентичными. Оценим визуально длины p — n, m — n и m — n — p. Очевидно, что самым коротким и обладающим наименьшим модулем является ответ в последней части задачи, а именно m — n — p.
Оценим визуально длины p — n, m — n и m — n — p. Очевидно, что самым коротким и обладающим наименьшим модулем является ответ в последней части задачи, а именно m — n — p.
Разность векторов.
Вектор, коллинеарный данному вектору , равный ему по длине и противоположно направленный, называется противоположнымвектором для вектора и обозначается . Противоположный вектор можно рассматривать как результат умножения вектора на число λ = –1: .
Разностью двух векторов и называется вектор , равный сумме векторов и , т.е. .
Очевидно, что , для любого вектора .
Легко показать, что .
Действительно,
Таким образом, если .
Из
определения суммы двух векторов вытекает
правило построения вектора разности. Откладываем векторы и из
общей точки O.
Чтобы найти вектор-разность, нужно
к добавить
вектор или .
Тогда .
Вектор ,
соединяющий концы векторов и и
направленный от «вычитаемого» к
«уменьшаемому» (т.е. от второго
вектора к первому), и будет разностью .
Действительно, по правилу сложения
векторов или .
Откладываем векторы и из
общей точки O.
Чтобы найти вектор-разность, нужно
к добавить
вектор или .
Тогда .
Вектор ,
соединяющий концы векторов и и
направленный от «вычитаемого» к
«уменьшаемому» (т.е. от второго
вектора к первому), и будет разностью .
Действительно, по правилу сложения
векторов или .
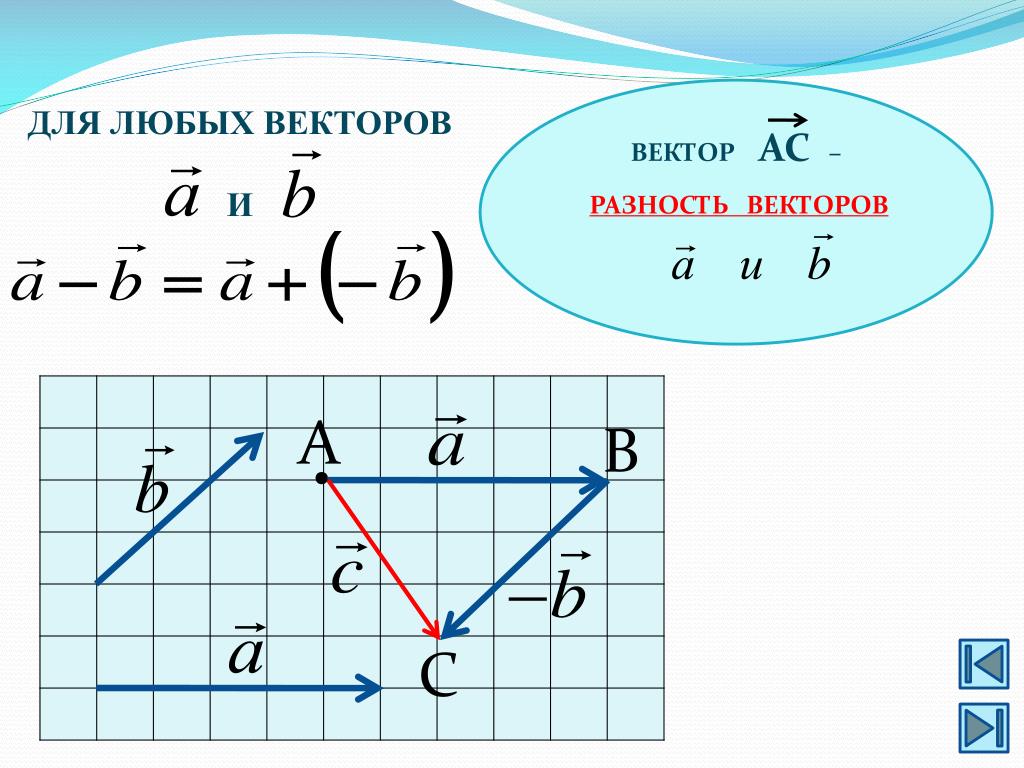
Таким образом, если на векторах и , отложенных из общей точки O, построить параллелограмм OACB, то вектор , совпадающий с одной диагональю параллелограмма, равен сумме , а вектор , совпадающий с другой диагональю, равен разности .
Проекция вектора на ось
усть в пространстве даны два вектора и . Отложим от произвольной точки O векторы и . Углом между векторами и называется наименьший из углов . Обозначается . Рассмотрим
ось l и
отложим на ней единичный вектор (т. Под углом между вектором и осью l понимают угол между векторами и . Итак, пусть l – некоторая ось и – вектор. Обозначим через A1 и B1 проекции на ось lсоответственно точек A и B. Предположим, что A1 имеет координату x1, а B1 – координату x2 на оси l. Тогда проекцией вектора на ось l называется разность x1 – x2 между координатами проекций конца и начала вектора на эту ось. Проекцию вектора на ось l будем обозначать . Ясно, что если
угол между вектором и
осью l острый,
то x2> x1,
и проекция x2 – x1>
0; если этот угол тупой, то x2< x1 и
проекция x2 – x1<
0. Таким образом, проекция вектора на ось l – это длина отрезка A1B1, взятая с определённым знаком. Следовательно, проекция вектора на ось это число или скаляр. Аналогично определяется проекция одного вектора на другой. В этом случае находятся проекции концов даного вектора на ту прямую, на которой лежит 2-ой вектор. Рассмотрим некоторые основные свойства проекций.
Доказательство.
Ясно, что проекция вектора не изменится
при его параллельном переносе, поэтому
достаточно рассмотреть случай, когда
начало вектора совпадает с началом
отсчёта O оси l.
Доказательство. Пусть . Обозначим через x1, x2 и x3 координаты проекций A1, B1, C1 на ось l точек A, B и C. Тогда . Но . Это свойство можно обобщить на случай любого числа слагаемых.
. Доказательство. Пусть угол между вектором и осью . Если λ > 0, то вектор имеет то же направление, что и , и составляет с осью такой же угол . При λ > 0 . Если же λ < 0, то и имеют противоположные направления и вектор составляет с осью угол π – φ и . Следствие. Проекция разности двух векторов на ось равна разности проекций этих векторов на ту же ось. |
ЛИНЕЙНО ЗАВИСИМЫЕ И ЛИНЕЙНО НЕЗАВИСИМЫЕ СИСТЕМЫ ВЕКТОРОВ
Рассмотрим несколько векторов .
Линейной
комбинацией данных
векторов называется любой вектор вида ,
где —
некоторые числа. Числа называются
коэффициентами линейной комбинации.
Говорят также, что в этом случае линейно
выражается через данные векторы ,
т.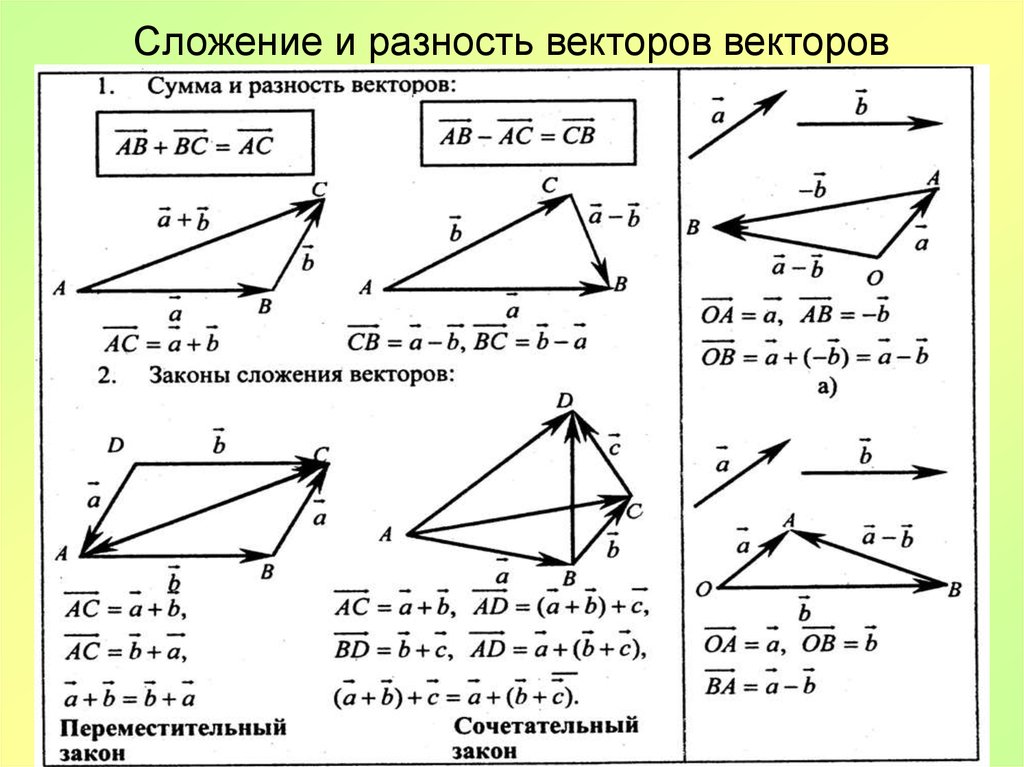 е. получается из них с помощью линейных
действий.
е. получается из них с помощью линейных
действий.
Например, если даны три вектора то в качестве их линейной комбинации можно рассматривать векторы:
Если вектор представлен как линейная комбинация каких-то векторов, то говорят, что он разложен по этим векторам.
Векторы называются линейно зависимыми, если существуют такие числа, не все равные нулю, что . Ясно, что заданные векторы будут линейно зависимыми, если какой-либо из этих векторов линейно выражается через остальные.
В противном случае, т.е. когда соотношение выполняется только при , эти векторы называются линейно независимыми.
Теорема 1. Любые два вектора линейно зависимы тогда и только тогда, когда они коллинеарны.
Доказательство:
Действительно, пусть имеем два коллинеарных вектора и . Тогда либо оба они равны нулю, и следовательно, любая их линейная комбинация при любых λ1 и λ2, либо один из них не нуль, тогда другой отличается от него на числовой множитель, например, .
 Но отсюда ,
а это и означает линейную зависимость
векторов и .
Но отсюда ,
а это и означает линейную зависимость
векторов и .Докажем обратное, т.е. если два вектора линейно зависимы, то они коллинеарны. Пусть векторы и линейно зависимы. Тогда найдутся числа λ1 и λ2 такие, что , причём, например, λ2 ≠ 0. Тогда , т.е. векторы коллинеарны.
Таким образом, теорема утверждает, что линейно независимыми на плоскости могут быть только те векторы, которые неколлинеарны.
Аналогично можно доказать следующую теорему.
Теорема 2. Три вектора линейно зависимы тогда и только тогда, когда они компланарны.
Доказательство.
Пусть три вектора линейно зависимы, т.е. , где, например, λ3 ≠ 0. Тогда .
Отнесём
векторы и к
одному началу и проведём через них
плоскость. Тогда и будут
лежать в той же плоскости, а потому и их
сумма, т. е. будет
лежать в той же плоскости, т.е. –
компланарны.
е. будет
лежать в той же плоскости, т.е. –
компланарны.
Пусть теперь векторы – компланарны. Тогда они будут лежать в одной плоскости. Отнесём все три вектора к одному началу.
Если векторы и не коллинеарны, то очевидно, вектор можно предствить в виде . Действительно из рисунка видно, что , где и , а значит найдутся числа и такие, что .
Если же вектор коллинеарен вектору , то один из них линейно выражен через другой, т.е. . Что и требовалось доказать.
Таким образом, три некомпланарных вектора всегда линейно независимы. Кроме того, можно показать, что каждые четыре вектора линейно зависимы.
БАЗИС
Базисом называется совокупность отличных от нулей линейно независимых векторов. Элементы базиса будем обозначать .
В
предыдущем пункте мы видели, что два
неколлинеарных вектора на плоскости
линейно независимы. Поэтому согласно
теореме 1, из предыдущего пункта, базисом
на плоскости являются любые два
неколлинеарных вектора на этой плоскости.
Поэтому согласно
теореме 1, из предыдущего пункта, базисом
на плоскости являются любые два
неколлинеарных вектора на этой плоскости.
Аналогично в пространстве линейно независимы любые три некомпланарных вектора. Следовательно, базисом в пространстве назовём три некомпланарных вектора.
Справедливо следующее утверждение.
Теорема. Пусть в пространстве задан базис . Тогда любой вектор можно представить в виде линейной комбинации , где x, y, z – некоторые числа. Такое разложение единственно.
Доказательство.
Докажем сначала существование такого представления.
Предположим, что коллинеарен какому-либо из векторов базиса, например, . Тогда по доказанному выше . Следовательно, , где x = l, y = z = 0.
Пусть компланарен с какой-либо парой базисных векторов, например, с и .
 Отложим три вектора от одной точки O.
Через точку Aпроведём
прямые, параллельные векторам и .
Тогда ,
причём векторы и коллинеарны
соответственно векторам и .
Поэтому найдутся числа x и y такие,
что ,
а значит .
Отложим три вектора от одной точки O.
Через точку Aпроведём
прямые, параллельные векторам и .
Тогда ,
причём векторы и коллинеарны
соответственно векторам и .
Поэтому найдутся числа x и y такие,
что ,
а значит .Пусть некомпланарен ни с одной парой базисных векторов. Отложим от одной точки и проведём через конец вектора прямую, параллельную вектору . Она пересечёт плоскость в точке A1. Очевидно, что . Но вектор компланарен векторам и , следовательно, по доказанному выше, , а вектор коллинеарен , поэтому . Таким образом, .
Докажем теперь единственность такого представления.
Допустим,
что возможны два представления
вектора и .
Причём, например, .
Тогда должны иметь ,
т.к. иначе мы имели бы две прямые,
проходящие через точку A1 параллельно .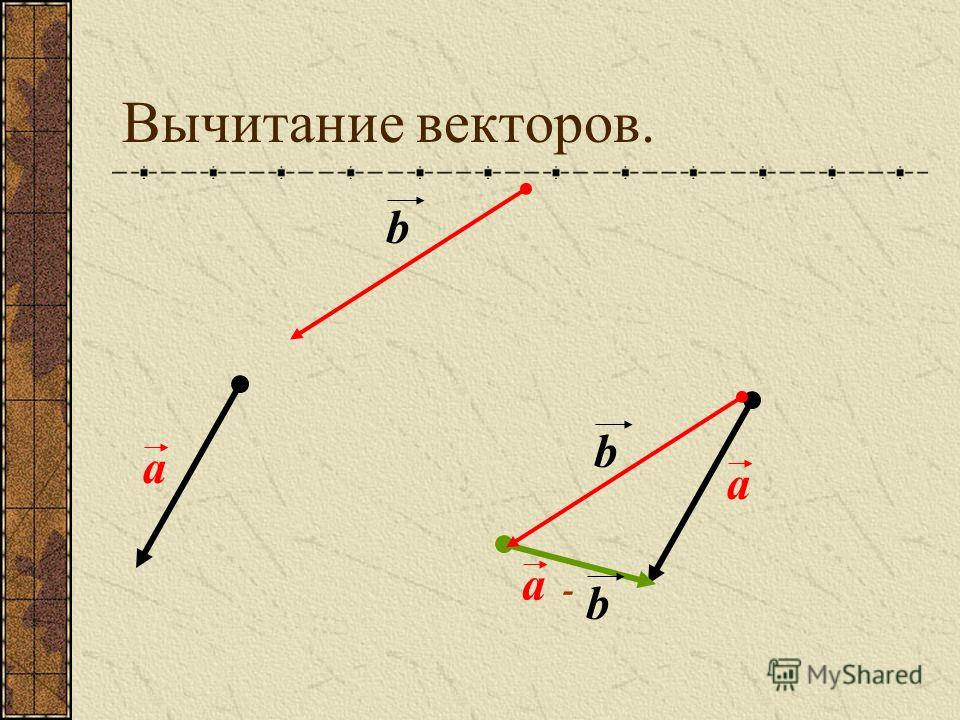 Из последнего равенства вытекает, что .
Получили противоречие с нашим
предположением, что и доказывает теорему.
Из последнего равенства вытекает, что .
Получили противоречие с нашим
предположением, что и доказывает теорему.
В качестве частного случая из этой же теоремы можно сформировать следующее утверждение:
Если задан базис на плоскости, то любой вектор, компланарный с векторами можно представить в виде , причём такое разложение единственно.
Таким образом, базис позволяет однозначно сопоставить каждому вектору тройку чисел – коэффициенты разложения этого вектора по векторам базиса: . Верно и обратное, каждой тройке чисел x, y, z при помощи базиса можно сопоставить вектор, если составить линейную комбинацию .
Если базис и , то числа x, y, z называются координатами вектора в данном базисе. Координаты вектора обозначают .
ДЕКАРТОВА СИСТЕМА КООРДИНАТ
Пусть в пространстве
задана точка O и
три некомпланарных вектора . Декартовой системой координат в пространстве (на плоскости) называется совокупность точки и базиса, т.е. совокупность точки и трёх некомпланарных векторов (2-х неколлинеарных векторов), выходящих из этой точки. Точка O называется началом координат; прямые, проходящие через начало координат в направлении базисных векторов, называются осями координат – осью абсцисс, ординат и аппликат. Плоскости, проходящие через оси координат, называют координатными плоскостями. Рассмотрим в выбранной системе координат произвольную точку M. Введём понятие координаты точки M. Вектор , соединяющий начало координат с точкой M. называется радиус-вектором точки M. Вектору в выбранном базисе можно сопоставить тройку чисел – его координаты: . Координаты
радиус-вектора точки M. Аналогично определяются декартовы координаты на плоскости. Здесь точка имеет только две координаты – абсциссу и ординату. Легко видеть, что при заданной системе координат каждая точка имеет определённые координаты. С другой стороны, для каждой тройки чисел найдётся единственная точка, имеющая эти числа в качестве координат. Если векторы, взятые в качестве базиса, в выбранной системе координат, имеют единичную длину и попарно перпендикулярны, то система координат называется декартовой прямоугольной системой координат. В этом случае основные векторы принято обозначать буквами , а оси координат Ox, Oy и Oz. Таким образом,
любой вектор в декартовой прямоугольной
системе координат можно записать в
виде: . Примеры.
М(-1;3).
В дальнейшем мы в основном будем использовать только декартову прямоугольную систему координат. |
НАПРАВЛЯЮЩИЕ КОСИНУСЫ ВЕКТОРА
Пусть в декартовой прямоугольной системе координат задан вектор . Направление вектора в пространстве определяется углами α, β, γ которые вектор составляет с осями координат. Косинусы этих углов cos α, cos β, cos γ называются направляющими косинусами вектора.
Найдем
выражение для направляющих косинусов
вектора.
Пусть вектор задан в координатной форме .
Тогда , откуда.
Несложно показать, что .
Направляющие косинусы вектора полностью определяют его направление, но ничего не говорят о его длине.
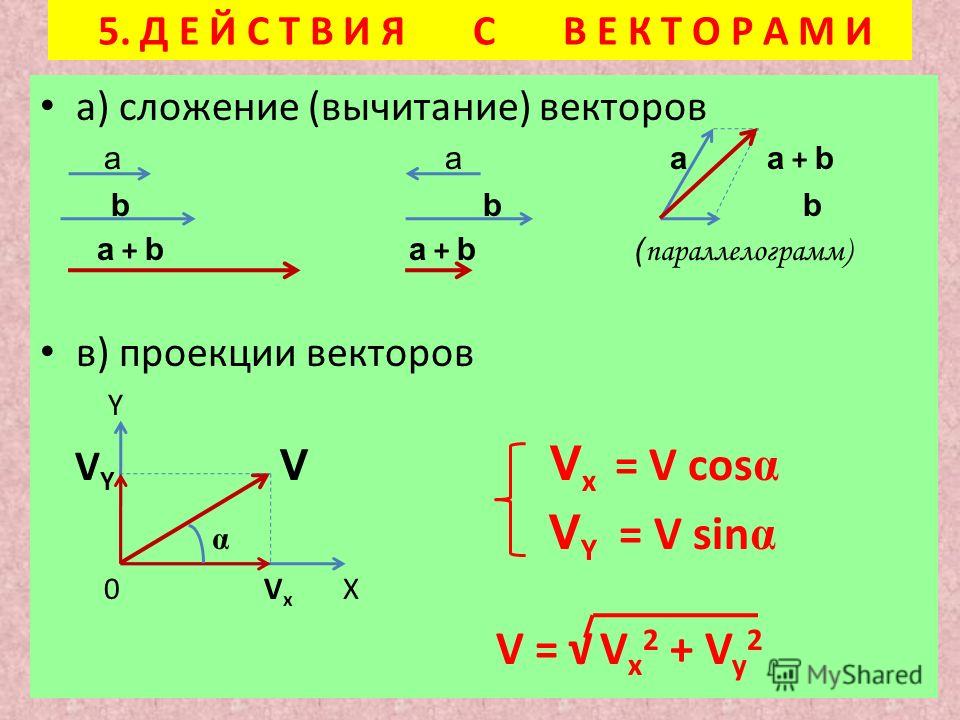
ЛИНЕЙНЫЕ ОПЕРАЦИИ НАД ВЕКТОРАМИ В КООРДИНАТНОЙ ФОРМЕ
При умножении вектора на число все его координаты умножаются на это число, т.е. если .
Действительно, используя свойства операций умножения вектора на число и сложении векторов будем иметь
.
При сложении векторов их соответствующие координаты складываются, т.е. если .
Доказательство очевидно.
Условие коллинеарности двух векторов в коорднинатной форме.
Два
вектора коллинеарны тогда и только
тогда, когда их соответствующие координаты
пропорциональны. Т.е. если ,
то.
Т.е. если ,
то.
Доказательство:
Пусть вектор коллинеарен , тогда найдется λ такое, что . Значит, и . Поскольку разложение вектора по элементам базиса единственно, то .
Пусть выполняется равенство . Обозначим коэффициент пропорциональности через λ. Тогда и, следовательно, , т.е. . Теорема доказана.
Пример.
Даны векторы . Найти вектор .
.
Найти координаты вектора в базисе, образованном векторами , , .
Обозначим координаты вектора в новом базисе . Тогда в новом базисе будем иметь:
Итак, .
Рассмотрим
две произвольные функцию y=
x3. Будем рассматривать равенство y= x3 как
уравнение относительно x.
Это уравнение для каждого значения у определяет
единственное значение x: .
Геометрически это значит, что всякая
прямая параллельная оси Oxпересекает
график функции y=
x3 только
в одной точке. Поэтому мы можем
рассматривать x как
функцию от y.
Функция называется
обратной по отношению к функции y=
x3.
Будем рассматривать равенство y= x3 как
уравнение относительно x.
Это уравнение для каждого значения у определяет
единственное значение x: .
Геометрически это значит, что всякая
прямая параллельная оси Oxпересекает
график функции y=
x3 только
в одной точке. Поэтому мы можем
рассматривать x как
функцию от y.
Функция называется
обратной по отношению к функции y=
x3.
Прежде чем перейти к общему случаю, введем определения.
Функция y = f(x) называется возрастающей на некотором отрезке, если большему значению аргумента x из этого отрезка соответствует большее значение функции, т.е. если x2>x1, вектора .
Очевидно, что . Но по определению координат вектора и . Следовательно,
Таким
образом, чтобы найти координаты вектора ,
нужно из координат его конца вычесть
соответствующие координаты начала.
Примеры.
Заданы точкиA(1; -2; 3), B(2; 0; -1). Найти вектор .
Даны A(-2; 3; 1), В(-1; 2; 0), С(0; 1; 1). Найти .
Известно, что. Найти координаты точки D, если
А(3; -4; -1), В(-4; 4; 1), С(-3; -5; 4).
Пусть тогда
. С другой стороны . Следовательно, должно выполняться равенство (x+3; y+5; z-4)=(5;10;-8). Отсюда
x=2, y=5, z=-4, т.е. точка D имеет координаты D(2; 5; -4).
СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ И ЕГО СВОЙСТВА
Мы
рассмотрели умножение вектора на число. Однако во многих задачах механики и
физики встречается операция умножения
вектора на вектор. Но при этом результат
может быть как числом, так и вектором.
Поэтому рассматривают два вида умножения
векторов: скалярное и векторное.
Однако во многих задачах механики и
физики встречается операция умножения
вектора на вектор. Но при этом результат
может быть как числом, так и вектором.
Поэтому рассматривают два вида умножения
векторов: скалярное и векторное.
Пусть даны два вектора и , угол между, которыми равен .
Скалярным произведением векторов и называется число, равное произведению длин этих векторов на косинус угла между ними. Скалярное произведение обозначается . Итак, .
Если один из векторов нулевой, то угол не определен, и скалярное произведение по определения считается равным нулю.
Рассмотрим свойства скалярного произведения.
Скалярное произведение двух векторов подчиняется коммутативному закону, т.е. для любых векторов и .
Очевидно, из определения скалярного произведения:
.
Для любого числа λ и любых векторов имеем:
.
Доказательство. Ограничимся случаем, когда λ > 0. В этом случае угол между векторами и совпадает с углом между векторами и , .
Поэтому . Откуда
Аналогично доказывается и равенство .
Случай λ <0 рассмотреть самостоятельно.
Для любых векторов выполняется равенство .
Доказательство. Используя определение скалярного произведения и свойства проекций вектора на ось, будем иметь
Для любого вектора выполняется соотношение.
Действительно, так как , то .
Из этого свойства в частности следует .
Скалярное произведение двух векторов равно нулю тогда и только тогда,когда равен нулю один из сомножителей или векторы перпендикулярны.
Это
свойство очевидно из определения
скалярного произведения.
Таким образом, необходимым и достаточным условием ортогональности двух векторов является равенство нулю их скалярного произведения.
Пример. Дан вектор . Известно, что
Найти .
Имеем, т.е. .
Найдем:
Следовательно, .
Рассмотрим, как находится скалярное произведение векторов, если они заданы в координатной форме. Пусть даны два вектора и .
Рассмотрим сначала все возможные скалярные произведения векторов друг на друга.
Поэтому
Итак, скалярное произведение векторов равно сумме произведений соответствующих координат: .
Это соотношение позволяет вычислить длину вектора через его координаты:
.
Далее из определения скалярного произведения находим
.
Выражая скалярное произведение и длины векторов через их координаты,получим формулу для нахождения косинуса угла между векторами
.
Условие ортогональности двух векторов:
или .
Т.о., для того чтобы два вектора были перпендикулярны необходимо и достаточно, чтобы сумма произведений соответствующих координат этих векторов была равна нулю.
Примеры.
Пусть А(-1; 1; 0), B(3; 1; -2), . Найти:
;
и ;
.
.
.
.
Найти в , если известны координаты его вершин A(1; 5; 6),
B(5;
3; 10), C(2;
1; 14).
При каком значении m векторы и перпендикулярны?
Условие ортогональности двух векторов .
. Следовательно, m = 15.
ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ И ЕГО СВОЙСТВА
Введем сначала понятие ориентации тройки векторов.
Пусть даны три некомпланарных вектора с общим началом, перечисленных в определенном порядке: первый – , второй – , третий – .
Тройка некомпланарных векторов называется правоориентированной или просто правой, если из конца третьего вектора кратчайший поворот от первого ко второму виден против часовой стрелки. В противном случае тройку векторов называют левой, в этом случае если мы будем смотреть с конца вектора , то кратчайший поворот от к осуществляется по часовой стрелке.
Векторным произведением векторов и называется новый вектор , удовлетворяющий условиям:
Длина вектора равна площади параллелограмма, построенного на векторах и .

Вектор перпендикулярен плоскости этого параллелограмма.
Он направлен так, что векторы и образуют правую тройку векторов.
Векторное произведение векторов и обозначается символом . Если хотя бы один из сомножителей равен нулю, то векторное произведение по определению считают равным нулю
Векторное произведение обладает следующими свойствами:
Из определения следует, что длина векторного произведения численно равна площади параллелограмма, построенного на векторах, и, следовательно, находится по формуле:
.
Таким образом, и .
При перестановке сомножителей векторное произведение меняет свой знак .
Действительно
из определения векторного произведения
следует, что векторы и имеют
одинаковые модули, расположены на одной
прямой, но направлены в противоположные
стороны. Поэтому, векторы и являются
противоположными векторами и поэтому .
Поэтому, векторы и являются
противоположными векторами и поэтому .
Скалярный множитель можно выносить за знак векторного произведения, т.е. для любого числа λ и любых векторов
.
Доказательство этого свойства непосредственно следует из определения векторного произведения. Докажем для λ > 0. В этом случае . Тогда по определению векторного произведения
Вектор перпендикулярен векторам и . Вектор также векторам и , т.к. векторы и , и лежат в одной плоскости. Следовательно, векторы и коллинеарны. Очевидно, что направления их также совпадают. Т. к. , и следовательно, , то .
Поэтому .
Аналогично проводится доказательство для случая λ < 0.
Для любых векторов имеет место равенство
.
Примем
без доказательства.
Векторное произведение двух векторов равно нулевому вектору тогда и только тогда, когда один из сомножителей равен нулю или векторы коллинеарны.
Действительно, если векторы коллинеарны, то , т.е. площадь параллелограмма, построенного на данных векторах,равна нулю.
Таким образом, для того чтобы два ненулевых вектора были коллинеарны, необходимо и достаточно, чтобы их векторное произведение равнялось нулевому вектору.
В частности .
Примеры.
Раскрыть скобки
.
Найти площадь треугольника, построенного на векторах и , если известно, что и .
.
Найдем .
.
Можно показать, что если и , то координаты векторного произведения векторов и находятся по формуле:
.
Примеры.
Найти векторное произведение векторов и .
.
Найти площадь , если A(2; 3; 1), B(-1; -2; 0), C(-3; 0; 1).
Даны векторы . Найти параметры n, p, q если известно, что векторы и коллинеарны, а векторы и ортогональны.
Так как векторы и коллинеарны, то . Векторы и ортогональны, поэтому . Итак, получили систему уравнений
Объяснение урока: Сложение и вычитание векторов в 2D
В этом объяснении мы узнаем, как складывать и вычитать векторы в 2D.
Мы знаем, что векторы могут быть представлены отрезками определенной длины (величина) и направление. Мы будем использовать их, чтобы помочь визуализировать сложение векторов и вычитание.
В рамках этого объяснения будут рассматриваться только векторы в двух измерениях;
однако описанная методология может быть распространена на переносчиков в трех или более
Габаритные размеры.
Напомним, что единичный вектор — это вектор с величиной, равной 1, и что единичные векторы в 𝑥- и 𝑦-направлениях обозначаются ⃑𝑖 и ⃑𝑗 соответственно.
Любой двумерный вектор можно записать в виде 𝑥⃑𝑖+𝑦⃑𝑗. Они могут альтернативно быть представлено в компонентной форме как (𝑥,𝑦) или 𝑥𝑦.
Определение: Сложение векторов
Сложение векторов — это операция сложения двух или более векторов для нахождения их сумма.
Имея два (или более) вектора в компонентной форме, мы можем найти их сумму по формуле добавление соответствующих компонентов векторов.
Например, если ⃑𝑢=(𝑥,𝑦) и ⃑𝑣=(𝑥,𝑦), тогда ⃑𝑢+⃑𝑣=(𝑥+𝑥,𝑦+𝑦).
Сложение векторов — это операция сложения двух или более векторов вместе в векторная сумма. Сумма двух и более векторов называется равнодействующей.
Сейчас мы рассмотрим пару примеров, где нам нужно сложить векторы в два
Габаритные размеры.
Пример 1. Нахождение суммы двух векторов
Если ⃑𝑎=(3,2) и ⃑𝑏=(4,−1), найти ⃑𝑎+⃑𝑏.
Ответ
Напомним, что в декартовых координатах сложение векторов можно выполнить с помощью добавление соответствующих компонентов векторов.
Если ⃑𝑎=(𝑥,𝑦) и ⃑𝑏=(𝑥,𝑦), тогда ⃑𝑎+⃑𝑏=(𝑥+𝑥,𝑦+𝑦).
В этом вопросе ⃑𝑎=(3,2) и ⃑𝑏=(4,−1).
Итак, ⃑𝑎+⃑𝑏=(3+4,2+(−1))=(7,1).
Таким образом, ⃑𝑎+⃑𝑏=(7,1).
Пример 2. Нахождение компонентов двух векторов и их суммы по диаграмме
На сетке единичных квадратов показаны векторы ⃑𝑢, ⃑𝑣, и ⃑𝑢+⃑𝑣.
- Из каких компонентов состоит ⃑𝑢?
- Из каких компонентов состоит ⃑𝑣?
- Какие компоненты ⃑𝑢+⃑𝑣?
Ответ
Любой двумерный вектор можно записать через его 𝑥- и
𝑦-компоненты вида (𝑥,𝑦),
где 𝑥 — количество единиц в
положительное 𝑥-направление, а 𝑦 — количество единиц в положительном
𝑦-направление.
От начальной точки до конечной точки ⃑𝑢 идем на 2 единицы вправо и 1 единица вверх. Это соответствует 2 единицам в 𝑥-направлении и 1 единице в 𝑦-направление.
Итак, ⃑𝑢=(2,1).
От начальной точки до конечной точки ⃑𝑣, проходим 3 единицы осталось и 4 единицы вниз. Это соответствует −3 единицам в 𝑥-направление и −4 единиц в 𝑦-направлении.
Итак, ⃑𝑣=(−3,−4).
Мы знаем, что сумма двух векторов называется равнодействующей и что в Декартовы координаты, сложение векторов можно выполнить, добавив соответствующие компоненты векторов.
Если ⃑𝑢=(𝑥,𝑦) и ⃑𝑣=(𝑥,𝑦), тогда ⃑𝑢+⃑𝑣=(𝑥+𝑥,𝑦+𝑦).
С ⃑𝑢=(2,1)⃑𝑣=(−3,−4) и тогда ⃑𝑢+⃑𝑣=(2+(−3),1+(−4))=(−1,−3).
Мы также можем прочитать эту информацию прямо из векторной диаграммы.
Из начальной точки ⃑𝑢
в конечную точку вектора ⃑𝑣,
мы перемещаемся на 1 единицу влево и на 3 единицы вниз. Это соответствует -1 единице
в 𝑥-направлении и −3 единицы в
𝑦-направление.
Это соответствует -1 единице
в 𝑥-направлении и −3 единицы в
𝑦-направление.
Итак, ⃑𝑢+⃑𝑣=(−1,−3).
Таким образом, ⃑𝑢=(2,1), ⃑𝑣=(−3,−4), и ⃑𝑢+⃑𝑣=(−1,−3).
Вычитание векторов — это процесс нахождения разности векторов; это операция, обратная сложению векторов. Это означает, что ⃑𝑢−⃑𝑣=⃑𝑢+−⃑𝑣. При вычитании ⃑𝑣 из ⃑𝑢, находим равнодействующую ⃑𝑢 и −⃑𝑣.
Определение: вычитание векторов
Вычитание векторов — это операция вычитания двух векторов для нахождения их разница.
Имея два вектора в компонентной форме, мы можем найти их разность по формуле вычитая соответствующие компоненты векторов.
Например, если ⃑𝑢=(𝑥,𝑦) и ⃑𝑣=(𝑥,𝑦), тогда ⃑𝑢−⃑𝑣=(𝑥−𝑥,𝑦−𝑦).
Стоит отметить, что эффект отрицания ⃑𝑣 является изменением направления. Например, если бы у нас был вектор ⃑𝑣=(5,0),
это будет вектор длины 5, параллельный оси 𝑥, указывающей слева
направо.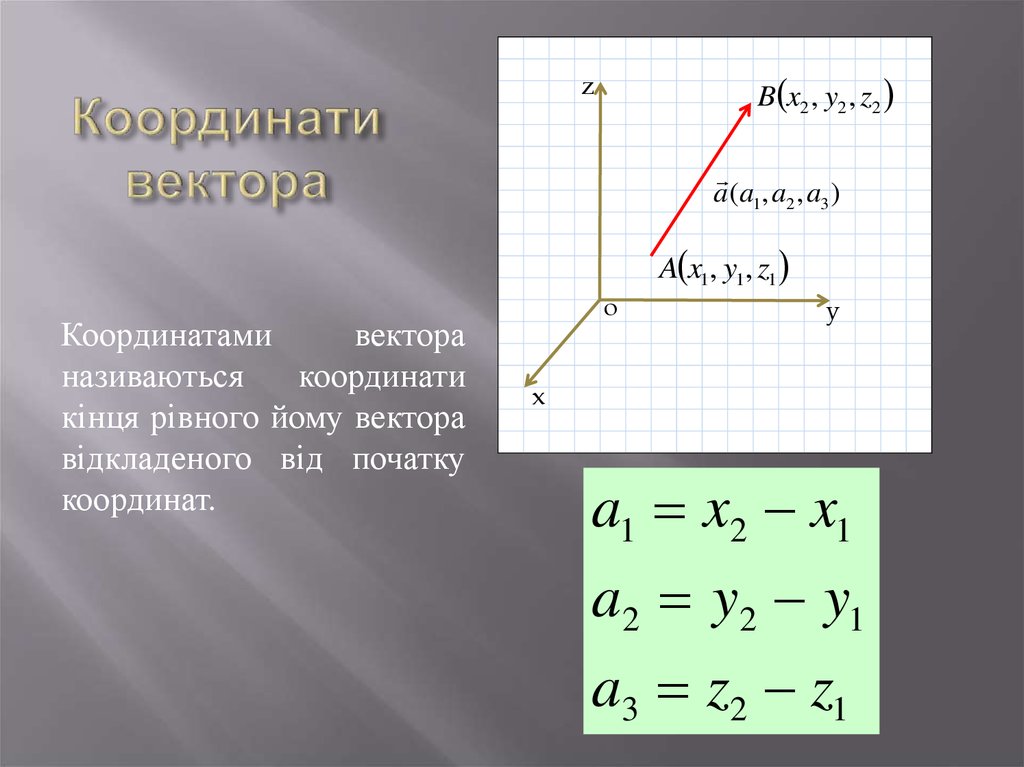 Если мы отрицаем ⃑𝑣,
мы получаем −⃑𝑣=(−5,0). Величина вектора
без изменений; он по-прежнему параллелен оси 𝑥, но его направление изменилось
перевернутый; теперь он указывает справа налево.
Если мы отрицаем ⃑𝑣,
мы получаем −⃑𝑣=(−5,0). Величина вектора
без изменений; он по-прежнему параллелен оси 𝑥, но его направление изменилось
перевернутый; теперь он указывает справа налево.
Теперь мы рассмотрим еще несколько примеров, где мы будем складывать и вычитать векторы в двух измерениях.
Пример 3. Вычитание векторов, выраженных в терминах единичных векторов
При заданных векторах 𝐴𝐵=3⃑𝑖−4⃑𝑗 и 𝐶𝐷=−5⃑𝑖−5⃑𝑗, рассчитать 𝐴𝐵−𝐶𝐷.
Ответ
Начнем с того, что вспомним, что в декартовых координатах вычитание векторов можно выполнить, вычитая соответствующие компоненты из векторы.
Если ⃑𝑢=𝑎⃑𝑖+𝑏⃑𝑗 и ⃑𝑣=𝑐⃑𝑖+𝑑⃑𝑗, тогда ⃑𝑢−⃑𝑣=(𝑎−𝑐)⃑𝑖+(𝑏−𝑑)⃑𝑗.
Итак, 𝐴𝐵−𝐶𝐷=3⃑𝑖−4⃑𝑗−−5⃑𝑖−5⃑𝑗=(3−(−5))⃑𝑖+(−4−(−5))⃑𝑗=8⃑𝑖+⃑𝑗.
Таким образом, 𝐴𝐵−𝐶𝐷=8⃑𝑖+⃑𝑗.
Пример 4. Сложение и вычитание векторов
Учитывая, что ⃑𝐴=(−2,2),
⃑𝐵=(5,2) и
⃑𝐶=(−3,−2), найти
−⃑𝐴+⃑𝐵−⃑𝐶.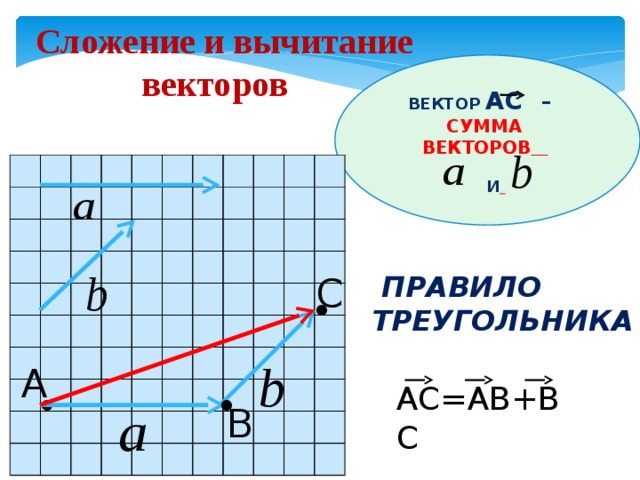
Ответ
Начнем с того, что вспомним, что в декартовых координатах сложение векторов и вычитание может быть выполнено путем добавления или вычитания соответствующего компоненты векторов.
Итак, −⃑𝐴+⃑𝐵−⃑𝐶=(−(−2)+5−(−3),−2+2−(−2))=(2+5+3,−2+2+2)=(10, 2).
Таким образом, −⃑𝐴+⃑𝐵−⃑𝐶=(10,2).
Пример 5. Поиск пропущенного вектора по заданному другому вектору и сумме двух векторов
Учитывая, что ⃑𝐴=(−4,5), и ⃑𝐴+⃑𝐵=(2,7), найти ⃑𝐵.
Ответ
Начнем с того, что вспомним, что в декартовых координатах сложение векторов и вычитание может быть выполнено путем добавления или вычитания соответствующего компоненты векторов.
Если ⃑𝐴=(𝑥,𝑦) и ⃑𝐵=(𝑥,𝑦), тогда ⃑𝐴+⃑𝐵=(𝑥+𝑥,𝑦+𝑦).
Поскольку ⃑𝐴=(−4,5) и ⃑𝐴+⃑𝐵=(2,7), тогда (−4,5)+⃑𝐵=(2,7)((−4,5))⃑𝐵=(2,7)−(−4,5)⃑𝐵=(2−(−4),7−5) ⃑𝐵=(6,2).вычитание из обеих сторон
Итак, ⃑𝐵=(6,2).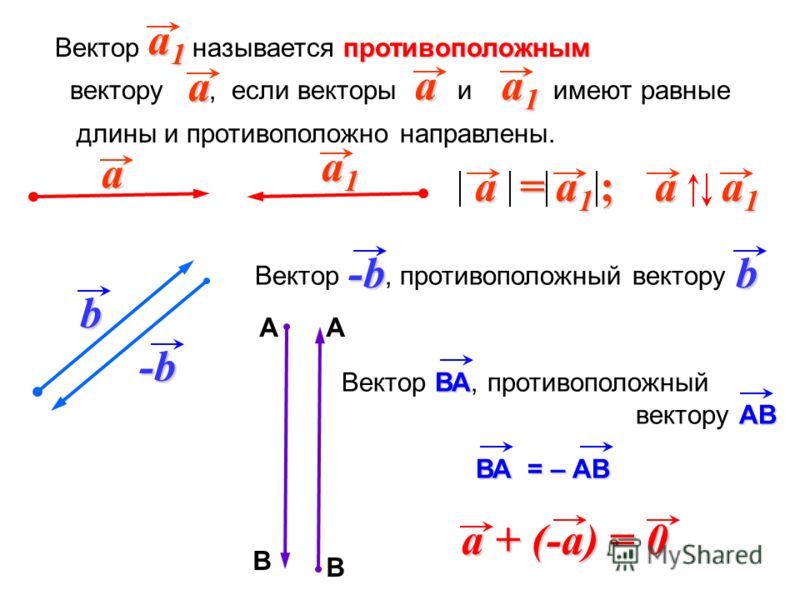
Пример 6. Нахождение суммы двух векторов по одному из них и разности между ними
Учитывая, что ⃑𝐴=(7,−1) и ⃑𝐴−⃑𝐵=(3,−2), найти ⃑𝐴+⃑𝐵.
Ответ
Начнем с того, что вспомним, что в декартовых координатах сложение векторов и вычитание может быть выполнено путем добавления или вычитания соответствующего компоненты векторов.
Если ⃑𝐴=(𝑥,𝑦) и ⃑𝐵=(𝑥,𝑦), тогда ⃑𝐴−⃑𝐵=(𝑥−𝑥,𝑦−𝑦).
Так как ⃑𝐴=(7,−1) и ⃑𝐴−⃑𝐵=(3,−2), то (7,−1)−⃑𝐵=(3,−2)⃑𝐵(3,−2)⃑𝐵=(7,−1)−(3,−2)⃑𝐵=(7−3,−1−( −2))⃑𝐵=(4,1).сложение и вычитание из обеих сторон
Теперь мы вычисляем ⃑𝐴+⃑𝐵.
Если ⃑𝐴=(𝑥,𝑦) и ⃑𝐵=(𝑥,𝑦), тогда ⃑𝐴+⃑𝐵=(𝑥+𝑥,𝑦+𝑦).
Так как ⃑𝐴=(7,−1) и ⃑𝐵=(4,1), тогда ⃑𝐴+⃑𝐵=(7,−1)+(4,1)=(7+4,−1+1)=(11,0).
Итак, ⃑𝐴+⃑𝐵=(11,0).
Пример 7. Нахождение вектора по двум другим векторам и выражению между тремя векторами
Учитывая, что ⃑𝐴=(3,−2),
⃑𝐵=(−5,4),
и ⃑𝐴−⃑𝐵+⃑𝐶=(6,−1),
найти ⃑𝐶.
Ответ
Начнем с того, что вспомним, что в декартовых координатах сложение векторов и вычитание может быть выполнено путем добавления или вычитания соответствующего компоненты векторов.
Если ⃑𝐴=(𝑥,𝑦), ⃑𝐵=(𝑥,𝑦), и ⃑𝐶=(𝑥,𝑦), тогда ⃑𝐴−⃑𝐵+⃑𝐶=(𝑥−𝑥+𝑥,𝑦−𝑦+𝑦).
Так как ⃑𝐴=(3,−2), ⃑𝐵=(−5,4), и ⃑𝐴−⃑𝐵+⃑𝐶=(6,−1), то (3,−2)−(−5,4)+⃑𝐶=(6,−1)(8,−6)+⃑𝐶=(6,−1)((8,−6))⃑𝐶=(6, −1)−(8,−6)⃑𝐶=(6−8,−1−(−6))⃑𝐶=(−2,5).вычитая из обеих сторон
Итак, ⃑𝐶=(−2,5).
Хотя это выходит за рамки этого объяснения, мы можем представить вектор сложение и вычитание графически с помощью метод параллелограмма или метод метод треугольника .
Мы закончим это объяснение повторением некоторых ключевых моментов.
Ключевые точки
- В декартовых координатах возможно сложение и вычитание векторов.
выполняется сложением или вычитанием соответствующих компонент векторов.

- Если ⃑𝑢=(𝑥,𝑦) и ⃑𝑣=(𝑥,𝑦), тогда ⃑𝑢+⃑𝑣=(𝑥+𝑥,𝑦+𝑦).
- Если ⃑𝑢=(𝑥,𝑦) и ⃑𝑣=(𝑥,𝑦), тогда ⃑𝑢−⃑𝑣=(𝑥−𝑥,𝑦−𝑦).
Вычисление разности двух векторов
Разность векторов, расчет онлайн
Резюме:
Функция vector_difference используется для вычисления разницы двух векторов в режиме онлайн.
vector_difference онлайн
Описание:
векторный калькулятор позволяет определить разность двух векторов самолета или космоса.
- Вычислить разность двух векторов плана
- Вычислить разность двух векторов в пространстве
- Вычислить разность двух векторов в пространстве любой размерности Векторный калькулятор используется по тому же принципу для любой размерности пространств.
Пусть (O,`vec(i)`,`vec(j)`) — каркас плана, `vec(u)` и `vec(v)` — два вектора, имеющие соответствующие координаты (`x_u`,`y_(u)`) и (`x_(v)`,`y_(v)`) в кадре (O,`vec(i)`,`vec(j)`) .
Вектор `vec(u)-vec(v)` имеет координаты (`x_(u)`-`x_(v)`,`y_(u)`-`y_(v)`) в системе (` vec(i)`,`vec(j)`).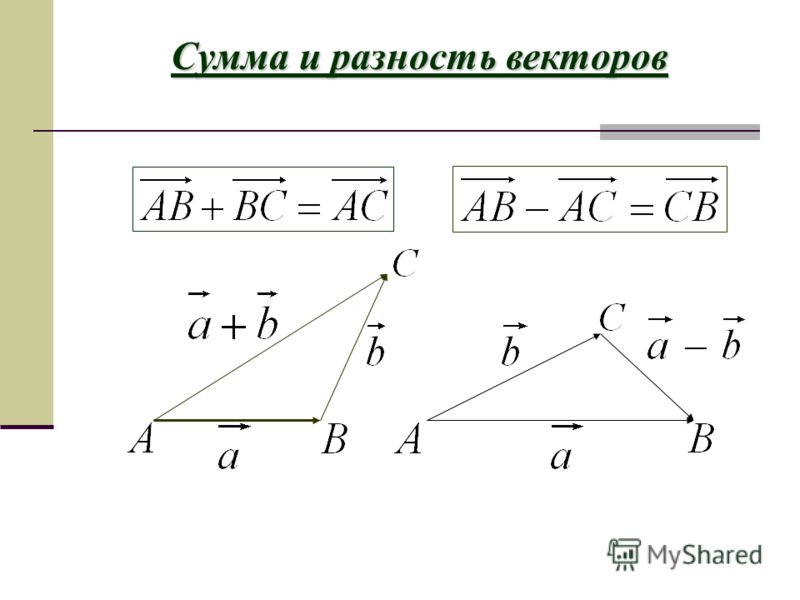
Векторный калькулятор может вычитать векторы, имеющие числовые или буквенные координаты.
Пусть `vec(u)`(1;2) `vec(v)`(3;5) для вычисления разницы `vec(u)`-`vec(v)`, введите vector_difference(`[1;2];[3;5]`) , после вычисления возвращается вектор [-2;-3].
Пусть `vec(u)`(a;b) `vec(v)`(2*a;`b`) для вычисления разницы `vec(u)`-`vec(v)`, введите vector_difference(`[a;b];[2*a;b]`)
Пусть (O,`vec(i)`,`vec(j)`,`vec(k)`) пространственная система отсчета, `vec(u)` и `vec(v)` два вектора, которые имеют соответствующие координаты (`x_u`,`y_(u)`,`z_(u)`) и (`x_(v)`,`y_(v)`,`z_(v)`) в кадре (O,`vec (i)`,`vec(j)`,`vec(k)`) .
Вектор `vec(u)-vec(v)` имеет координаты (`x_(u)`-`x_(v)`,`y_(u)`-`y_(v)`,`z_(u) `-`z_(v)`) в системе (`vec(i)`,`vec(j)`,`vec(k)`).
Векторный калькулятор может вычитать векторы, имеющие числовые или буквенные координаты.
Пусть `vec(u)`(1;2;1) `vec(v)`(3;5;2) для вычисления разницы `vec(u)`-`vec(v)`, введите vector_difference(`[3;5;2];[1;2;1]`) после вычисления возвращается результат [2;3;1].
Пусть `vec(u)`(a;b,c) `vec(v)`(2*a;2-b,c+1) для вычисления разницы `vec(u)`-`vec(v) `, введите vector_difference(`[a;b;c];[3*a;2;2*c+1]`) , после расчета возвращается результат.
Синтаксис:
vector_difference(vector;vector)
Примеры:
vector_difference(`[1;1;1];[5;5;6]`) возвращает [-4;-4;-5]
Расчет онлайн с помощью vector_difference (вычисление разности двух векторов)
См. также
Список связанных калькуляторов:
- Векторный калькулятор : vector_calculator.
 Векторный калькулятор позволяет производить вычисления с векторами, используя координаты.
Векторный калькулятор позволяет производить вычисления с векторами, используя координаты. - Вычисление координат вектора по двум точкам. : вектор_координаты. Векторный калькулятор позволяет вычислить координаты вектора по координатам двух точек в режиме онлайн.
- Калькулятор определителя: определитель. Функция определителя вычисляет онлайн определитель векторов или определитель матрицы.
- Вычисление разности двух векторов: vector_difference. Функция vector_difference используется для вычисления разницы двух векторов в режиме онлайн.
- Вычисление нормы вектора: vector_norm. Векторный калькулятор позволяет рассчитать норму вектора онлайн.
- Исчисление скалярного тройного произведения: scalar_triple_product. Калькулятор скалярного тройного произведения позволяет онлайн рассчитать скалярное тройное произведение.
- Калькулятор скалярного произведения: dot_product. Калькулятор скалярного произведения позволяет вычислить скалярное произведение двух векторов онлайн по их координатам.

- Произведение вектора на число: product_vector_number. Векторный калькулятор позволяет вычислить произведение вектора на число онлайн.
- Калькулятор перекрестного произведения: перекрестное_произведение. Векторный калькулятор позволяет вычислить векторное произведение двух векторов онлайн по их координатам.
- Вычисление суммы двух векторов: vector_sum. Векторный калькулятор позволяет вычислить сумму двух векторов онлайн.
Напоминания о курсах, калькуляторы, упражнения и игры: Векторы
Графические методы – Главы физики колледжа 1–17
3 Двумерная кинематика
Резюме
- Понимание правил сложения, вычитания и умножения векторов.
- Применять графические методы сложения и вычитания векторов для определения перемещения движущихся объектов.
 Путешествие с Гавайев на Молокаи состоит из нескольких этапов или сегментов пути. Эти сегменты могут быть добавлены графически с помощью линейки, чтобы определить общее двухмерное перемещение пути. (кредит: Геологическая служба США).
Путешествие с Гавайев на Молокаи состоит из нескольких этапов или сегментов пути. Эти сегменты могут быть добавлены графически с помощью линейки, чтобы определить общее двухмерное перемещение пути. (кредит: Геологическая служба США).Вектор — это величина, которая имеет величину и направление. Например, перемещение, скорость, ускорение и сила — все это векторы. В одномерном или прямолинейном движении направление вектора может быть задано просто знаком плюс или минус. Однако в двух измерениях (2-d) мы указываем направление вектора относительно некоторой системы отсчета (т. е. системы координат), используя стрелку, длина которой пропорциональна величине вектора и указывает направление вектора.
На рис. 2 показано такое графическое представление вектора на примере полного перемещения человека, идущего по городу, рассмотренного в главе 3.1 «Кинематика в двух измерениях: введение». Мы будем использовать обозначение, что жирный шрифт, такой как [latex]\textbf{D}[/latex], обозначает вектор.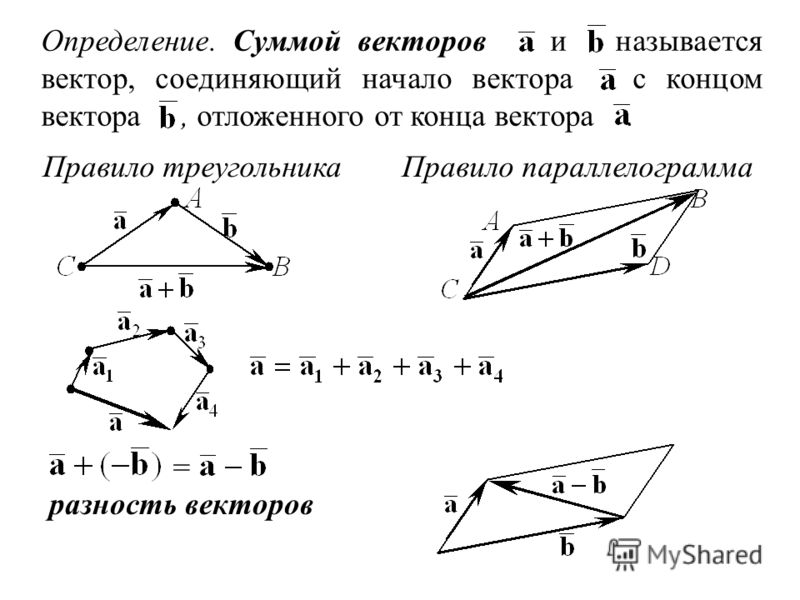 Его величина представлена символом, выделенным курсивом, [латекс]\жирныйсимвол{D},[/латекс], а его направление – [латекс]\жирныйсимвол{\тета}.[/латекс]
Его величина представлена символом, выделенным курсивом, [латекс]\жирныйсимвол{D},[/латекс], а его направление – [латекс]\жирныйсимвол{\тета}.[/латекс]
ВЕКТОРОВ В ЭТОМ ТЕКСТЕ
В этом тексте мы будем представлять вектор переменной, выделенной жирным шрифтом. Например, мы представим количественную силу вектором[latex]\textbf{F},[/latex], который имеет как величину, так и направление. Величина вектора будет представлена переменной, выделенной курсивом, например [латекс]\жирныйсимвол{F},[/латекс], а направление переменной будет задано углом[латекс]\жирныйсимвол{\тета} .[/латекс]
Рисунок 2. Человек проходит 9 кварталов на восток и 5 кварталов на север. Водоизмещение 10,3 блока под углом 29.1 o к северу от востока. Рисунок 3. Чтобы графически описать результирующий вектор для человека, идущего по городу, показанному на рисунке 2, нарисуйте стрелку, представляющую общий вектор смещения D .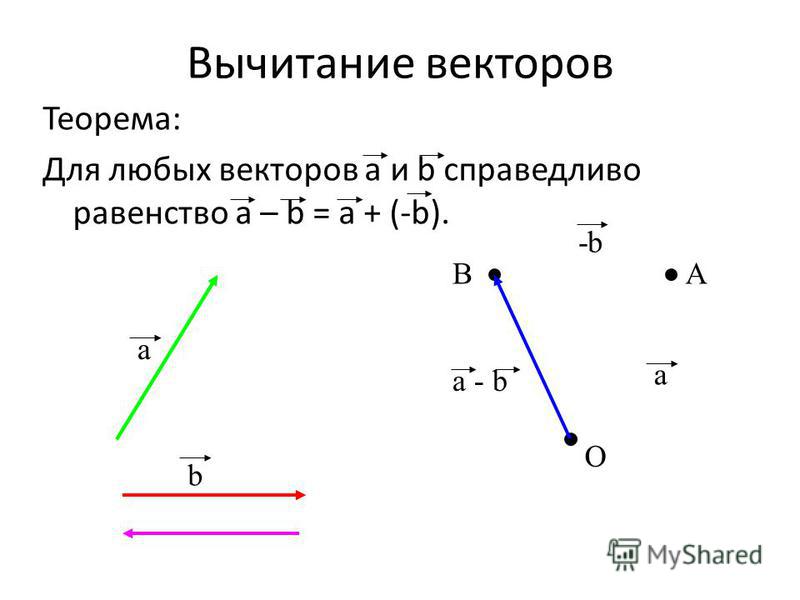 С помощью транспортира начертите линию под углом 90 200 θ 90 201 относительно оси восток-запад. Длина D стрелки пропорциональна модулю вектора и измеряется линейкой вдоль линии. В этом примере магнитуда D вектора составляет 10,3 единицы, а направление θ равно 29,1 o к северу от востока.
С помощью транспортира начертите линию под углом 90 200 θ 90 201 относительно оси восток-запад. Длина D стрелки пропорциональна модулю вектора и измеряется линейкой вдоль линии. В этом примере магнитуда D вектора составляет 10,3 единицы, а направление θ равно 29,1 o к северу от востока.Метод «голова к хвосту» представляет собой графический способ добавления векторов, описанный на рис. 4 ниже и в следующих шагах. Конец вектора является начальной точкой вектора, а конец (или кончик) вектора является конечным заостренным концом стрелки.
Рисунок 4. Метод «голова к хвосту»: метод «голова к хвосту» графического сложения векторов проиллюстрирован для двух перемещений человека, идущего по городу, рассмотренного на рисунке 2. (a) Нарисуйте вектор, представляющий перемещение на восток. (b) Нарисуйте вектор, представляющий смещение на север. Хвост этого вектора должен исходить из головы первого вектора, указывающего на восток. (c) Проведите линию от хвоста вектора, указывающего на восток, до начала вектора, указывающего на север, чтобы получить сумму или результирующий вектор D . Длина стрелки D пропорциональна модулю вектора и составляет 10,3 единицы. Его направление, описываемое как угол относительно востока (или горизонтальной оси) θ , измеренное с помощью транспортира, равно 29,1 0 .
Хвост этого вектора должен исходить из головы первого вектора, указывающего на восток. (c) Проведите линию от хвоста вектора, указывающего на восток, до начала вектора, указывающего на север, чтобы получить сумму или результирующий вектор D . Длина стрелки D пропорциональна модулю вектора и составляет 10,3 единицы. Его направление, описываемое как угол относительно востока (или горизонтальной оси) θ , измеренное с помощью транспортира, равно 29,1 0 .Шаг 1. Нарисуйте стрелку, представляющую первый вектор (9 блоков на восток), используя линейку и транспортир .
Рисунок 5.Шаг 2. Теперь нарисуйте стрелку, представляющую второй вектор (5 кварталов на север). Поместите конец второго вектора в начало первого вектора .
Рисунок 6. Шаг 3. Если имеется более двух векторов, продолжайте этот процесс для каждого добавляемого вектора. Обратите внимание, что в нашем примере у нас есть только два вектора, поэтому мы закончили размещать стрелки от начала до конца .
Обратите внимание, что в нашем примере у нас есть только два вектора, поэтому мы закончили размещать стрелки от начала до конца .
Шаг 4. Проведите стрелку от конца первого вектора к началу последнего вектора . Это результат или сумма других векторов.
Рисунок 7.Шаг 5. Чтобы получить величину равнодействующей, измерьте ее длину линейкой. (Обратите внимание, что в большинстве вычислений мы будем использовать теорему Пифагора для определения этой длины.)
Шаг 6. Чтобы получить направление равнодействующей, измерьте угол, который она образует с системой отсчета, используя транспортир. (Обратите внимание, что в большинстве расчетов мы будем использовать тригонометрические отношения для определения этого угла.)
Точность графического сложения векторов ограничена только точностью, с которой могут быть выполнены чертежи, и точностью измерительных инструментов. Это справедливо для любого количества векторов.
Это справедливо для любого количества векторов.
Пример 1. Графическое добавление векторов методом «голова к хвосту»: женщина на прогулке 9о}[/latex]северо-восток. Наконец, она поворачивается и проходит 32,0 м в направлении 68,0° к югу от востока.
Стратегия
Представьте каждый вектор смещения графически со стрелкой, пометив первый[latex]\textbf{A},[/latex]второй[latex]\textbf{B},[/latex]и третий [latex]\textbf{C},[/latex] делая длины пропорциональными расстоянию и направлениям, указанным относительно линии восток-запад. Описанный выше метод «голова к хвосту» позволяет определить величину и направление результирующего смещения, обозначаемого[latex]\textbf{R}.[/latex]
Решение
(1) Нарисуйте три вектора смещения.
Рис. 8.(2) Разместите векторы от начала до конца, сохранив их первоначальную величину и направление.
Рисунок 9. (3) Нарисуйте результирующий вектор,[latex]\textbf{R}. [/latex]
[/latex]
(4) Используйте линейку для измерения величины[latex]\ textbf{R},[/latex]и транспортир для измерения направления[latex]\textbf{R}.[/latex]Хотя направление вектора можно задать разными способами, проще всего измерить угол между вектором и ближайшей горизонтальной или вертикальной осью. Поскольку результирующий вектор находится к югу от оси, направленной на восток, мы переворачиваем транспортир вверх ногами и измеряем угол между осью, направленной на восток, и вектором. 9о}[/latex]юго-восток.
Обсуждение
Графический метод сложения векторов «голова к хвосту» работает для любого количества векторов. Также важно отметить, что результирующая не зависит от порядка добавления векторов. Следовательно, мы можем добавлять векторы в любом порядке, как показано на рис. 12, и все равно получим то же решение.
Рисунок 12. Здесь мы видим, что при сложении одних и тех же векторов в другом порядке результат будет тот же.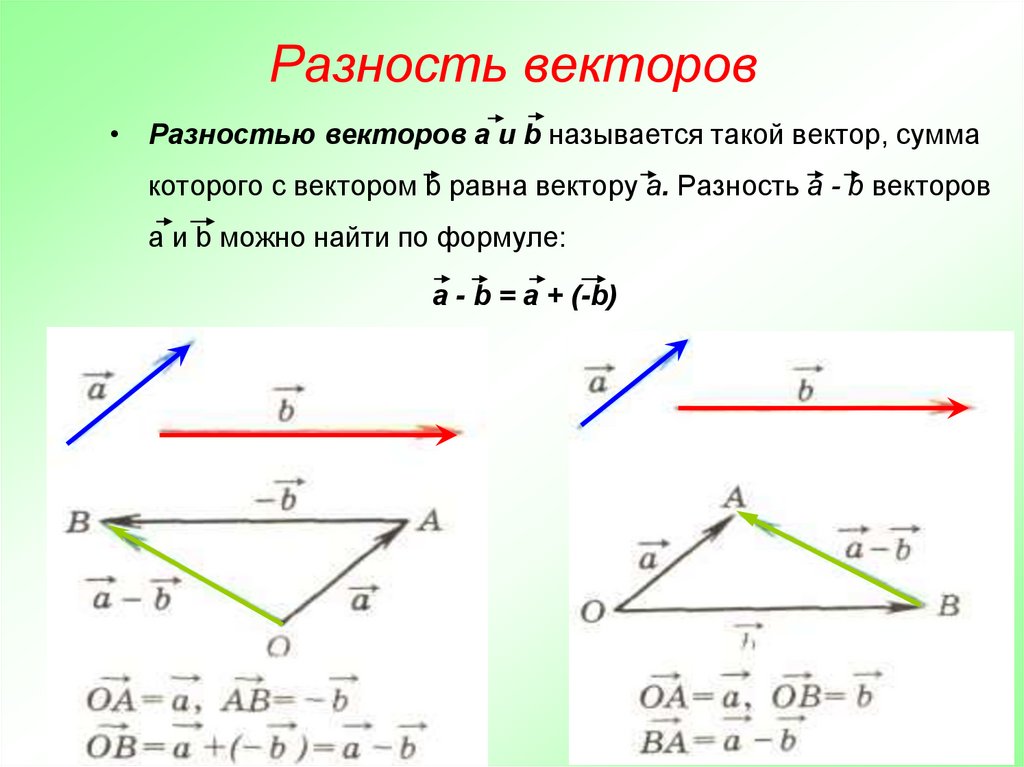 Эта характеристика верна в любом случае и является важной характеристикой векторов. Сложение векторов равно коммутативный . Векторы можно добавлять в любом порядке.
Эта характеристика верна в любом случае и является важной характеристикой векторов. Сложение векторов равно коммутативный . Векторы можно добавлять в любом порядке.
[латекс]\boldsymbol{\textbf{A}+\textbf{B}=\textbf{B}+\textbf{A}}.[/latex]
(Это верно для сложения обычных чисел как хорошо — вы получите тот же результат, если вы добавите, например, [латекс]\жирныйсимвол{2+3}[/латекс]или [латекс]\жирныйсимвол{3+2},[/латекс]).
Вычитание векторов — это прямое расширение сложения векторов. Чтобы определить вычитание (скажем, мы хотим вычесть [латекс]\textbf{B}[/латекс]из [латекс]\текстбф{А},[/латекс]написанного[латекс]\жирныйсимвол{\текстбф{А}-\текстбф {B}}[/latex], мы должны сначала определить, что мы подразумеваем под вычитанием.0296 отрицательный вектора[latex]\textbf{B}[/latex] определяется как [latex]\boldsymbol{-\textbf{B}};[/latex]то есть графически отрицательный для любого вектора имеет ту же величину, но в противоположном направлении , как показано на рисунке 13. Другими словами, [latex]\textbf{B}[/latex] имеет ту же длину, что и [latex]\boldsymbol{-\textbf{B}} ,[/latex], но указывает в противоположном направлении. По сути, мы просто переворачиваем вектор так, чтобы он указывал в противоположном направлении.
Другими словами, [latex]\textbf{B}[/latex] имеет ту же длину, что и [latex]\boldsymbol{-\textbf{B}} ,[/latex], но указывает в противоположном направлении. По сути, мы просто переворачиваем вектор так, чтобы он указывал в противоположном направлении.
Затем вычитание вектора[latex]\textbf{B}[/latex]из vector[latex]\textbf{A}[/latex] просто определяется как сложение [latex]\boldsymbol{ -\textbf{B}}[/latex]to[latex]\textbf{A}.[/latex]Обратите внимание, что вычитание векторов — это добавление отрицательного вектора. Порядок вычитания не влияет на результат.
[латекс]\boldsymbol{\textbf{A}-\textbf{B}=\textbf{A}+(-\textbf{B})}.[/latex]
Это аналогично вычитанию скаляров (где, например, [латекс]\boldsymbol{5-2=5+(-2)}[/латекс]).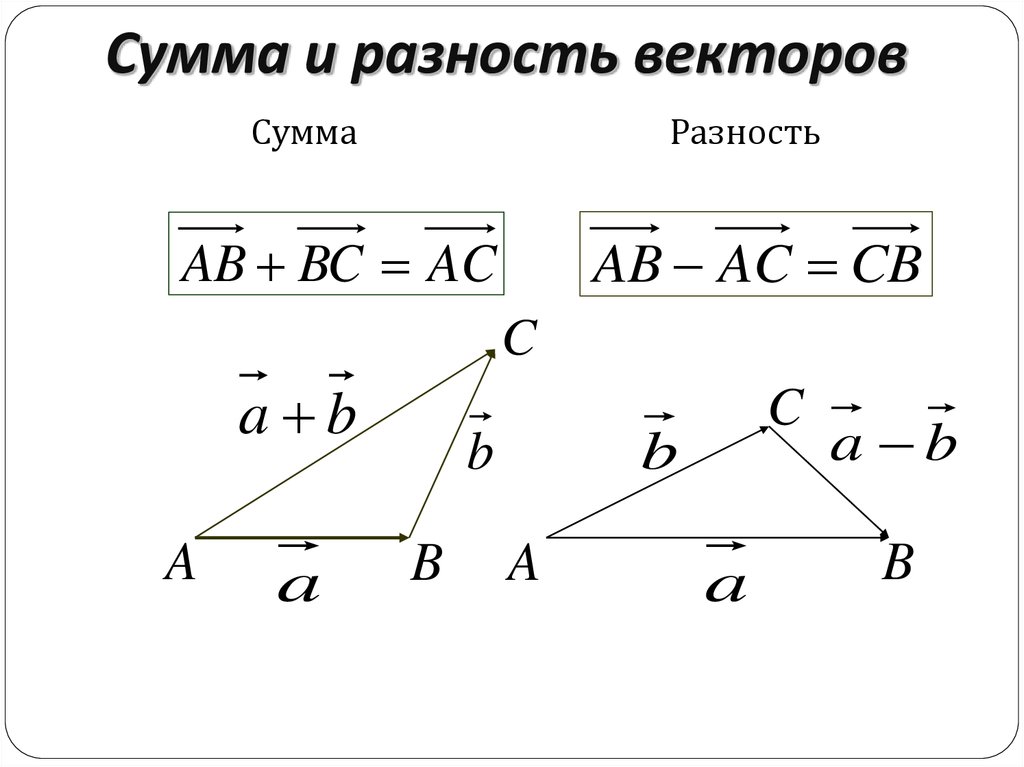 o}[/latex]к западу от севера). Если женщина совершает ошибку и путешествует в в противоположном направлении для второго этапа поездки, где она окажется? Сравните это место с расположением дока.
o}[/latex]к западу от севера). Если женщина совершает ошибку и путешествует в в противоположном направлении для второго этапа поездки, где она окажется? Сравните это место с расположением дока.
Стратегия
Мы можем представить первый этап поездки с помощью вектора[latex]\textbf{A},[/latex], а второй этап поездки с помощью вектора[latex] \textbf{B}.[/latex]Док расположен в месте[latex]\boldsymbol{\textbf{A}\:+\:\textbf{B}}.[/latex]Если женщина по ошибке путешествует в напротив 9о}[/latex]юго-восток. Мы представляем это как[latex]\boldsymbol{-\textbf{B}},[/latex], как показано ниже. Вектор[latex]\boldsymbol{-\textbf{B}}[/latex] имеет ту же величину, что и [latex]\textbf{B}[/latex], но направлен в противоположном направлении. Таким образом, она окажется в месте [латекс]\boldsymbol{\textbf{A}+(-\textbf{B})},[/latex]или[латекс]\boldsymbol{\textbf{A}-\textbf {B}}.[/latex]
Рисунок 15. Выполним сложение векторов для сравнения расположения дока,[latex]\boldsymbol{\textbf{A}+\textbf{B}},[/ латекс]с местом, куда по ошибке прибыла женщина,[латекс]\boldsymbol{\textbf{A}+(-\textbf{B})}. [/latex]
[/latex]
Решение
(1) Чтобы определить место, куда случайно попала женщина, нарисуйте векторы[latex]\textbf{A}[/latex]и[latex]\boldsymbol{-\textbf{B}} .[/latex]
(2) Поместите векторы от начала до конца.
(3) Нарисуйте результирующий вектор[latex]\textbf{R}.[/latex]
(4) Используйте линейку и транспортир для измерения величины и направления [latex]\textbf{R}.[/ латекс]
Рисунок 16.о}[/latex]юго-восток. 9о}[/latex]северо-восток.
Мы видим, что женщина окажется на значительном расстоянии от причала, если она отправится в противоположном направлении на второй этап поездки.
Обсуждение
Поскольку вычитание вектора аналогично сложению вектора с противоположным направлением, графический метод вычитания векторов работает так же, как и сложение.
Если бы мы решили пройти в три раза больше первого этапа пути, рассмотренного в предыдущем примере, то мы бы прошли[latex]\boldsymbol{3 \times 27,5\textbf{ м}},[/latex]или 82,5 м, в направлении[латекс]\boldsymbol{66. o}[/латекс]северо-восток. Это пример умножения вектора на положительное число 9.0200 скаляр . Обратите внимание, что величина меняется, но направление остается прежним.
o}[/латекс]северо-восток. Это пример умножения вектора на положительное число 9.0200 скаляр . Обратите внимание, что величина меняется, но направление остается прежним.
Если скаляр отрицательный, то умножение вектора на него изменяет величину вектора и дает новому вектору направление , противоположное . Например, если умножить на -2, величина удвоится, но изменится направление. Мы можем обобщить эти правила следующим образом: Когда вектор[латекс]\текстбф{А}[/латекс] умножается на скаляр[латекс]\жирныйсимвол{с},[/латекс]
- модуль вектора становится абсолютным значением[latex]\boldsymbol{cA},[/latex]
- , если [latex]\boldsymbol{c}[/latex] положительный, направление вектора не меняется,
- , если [латекс]\boldsymbol{c}[/латекс]отрицательно, направление меняется на противоположное.
В нашем случае [латекс]\boldsymbol{c=3}[/latex]и [латекс]\boldsymbol{\textbf{A}=27,5\textbf{ m}}.[/latex]Вектора умножаются на скаляры во многих ситуациях.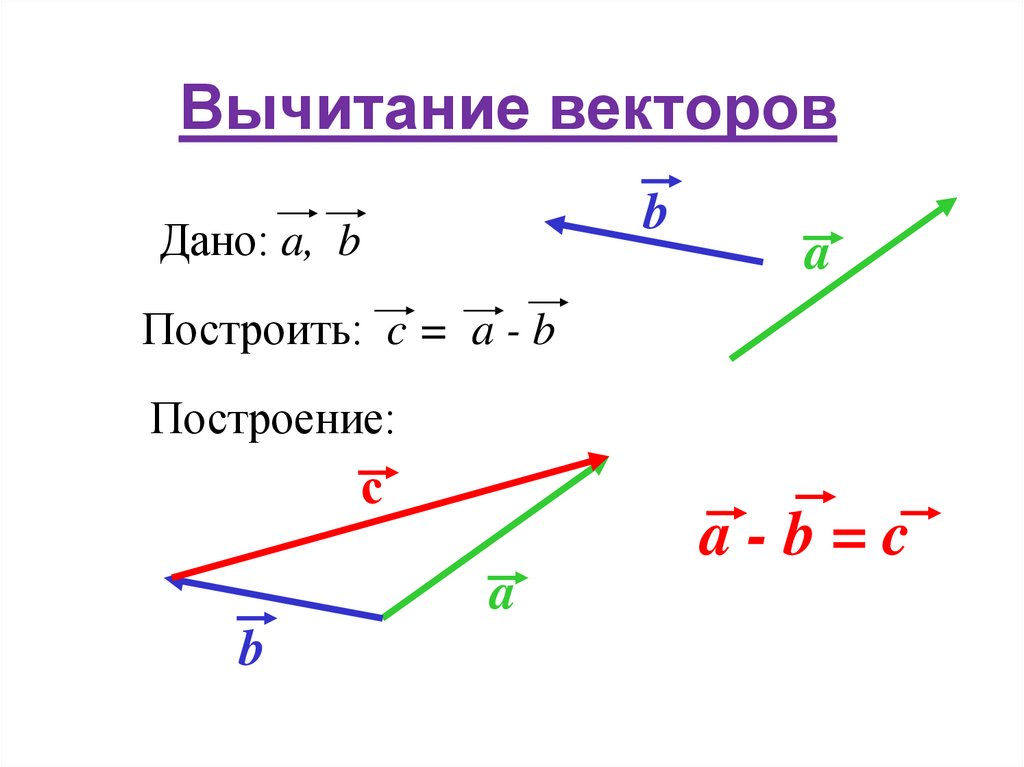 Обратите внимание, что деление является обратным умножению. Например, деление на 2 равносильно умножению на значение (1/2). Правила умножения векторов на скаляры такие же, как и при делении; просто рассматривайте делитель как скаляр между 0 и 1.
Обратите внимание, что деление является обратным умножению. Например, деление на 2 равносильно умножению на значение (1/2). Правила умножения векторов на скаляры такие же, как и при делении; просто рассматривайте делитель как скаляр между 0 и 1.
В приведенных выше примерах мы добавляли векторы для определения результирующего вектора. Однако во многих случаях нам нужно будет сделать обратное. Нам нужно будет взять один вектор и найти, какие другие векторы, сложенные вместе, дают его. В большинстве случаев это включает определение перпендикулярных компонентов одного вектора, например, x – и y -компонентов, или компонентов север-юг и восток-запад. 9o}[/latex]к северу от востока и хотите узнать, сколько кварталов нужно было пройти на восток и на север. Этот метод называется нахождением компонентов (или частей) смещения в восточном и северном направлениях, и он является обратным процессу, используемому для нахождения полного смещения. Это один из примеров нахождения компонентов вектора. В физике есть много приложений, где это может оказаться полезным. Мы скоро увидим это в главе 3.4 «Движение снаряда» и многое другое, когда мы рассмотрим 9.0200 сил в главе 4 «Динамика: законы движения Ньютона». Большинство из них включают поиск компонентов вдоль перпендикулярных осей (например, север и восток), так что задействованы прямоугольные треугольники. Аналитические методы, представленные в главе 3.3 Сложение и вычитание векторов: аналитические методы, идеально подходят для нахождения компонент вектора.
Это один из примеров нахождения компонентов вектора. В физике есть много приложений, где это может оказаться полезным. Мы скоро увидим это в главе 3.4 «Движение снаряда» и многое другое, когда мы рассмотрим 9.0200 сил в главе 4 «Динамика: законы движения Ньютона». Большинство из них включают поиск компонентов вдоль перпендикулярных осей (например, север и восток), так что задействованы прямоугольные треугольники. Аналитические методы, представленные в главе 3.3 Сложение и вычитание векторов: аналитические методы, идеально подходят для нахождения компонент вектора.
PHET EXPLORATIONS: MAZE GAME
Узнайте о положении, скорости и ускорении на «Арене боли». Используйте зеленую стрелку, чтобы переместить мяч. Добавьте больше стен на арену, чтобы усложнить игру. Постарайтесь достичь цели как можно быстрее.
Рисунок 18. Игра «Лабиринт»- Графический метод добавления векторов [latex]\textbf{A}[/latex]и[latex]\textbf{B}[/latex] включает рисование векторов на графике и добавление их с использованием прямого метод хвоста.
 Результирующий вектор[latex]\textbf{R}[/latex] определяется таким образом, что[latex]\boldsymbol{\textbf{A}+\textbf{B}=\textbf{R}}.[/latex]Величина и направление[latex]\textbf{R}[/latex] затем определяются с помощью линейки и транспортира соответственно.
Результирующий вектор[latex]\textbf{R}[/latex] определяется таким образом, что[latex]\boldsymbol{\textbf{A}+\textbf{B}=\textbf{R}}.[/latex]Величина и направление[latex]\textbf{R}[/latex] затем определяются с помощью линейки и транспортира соответственно. - графический метод вычитания вектора [latex]\textbf{B}[/latex]из [latex]\textbf{A}[/latex] включает добавление противоположного вектора[latex]\textbf{B},[/latex ] который определяется как [латекс]\boldsymbol{-\textbf{B}}.[/latex]В этом случае [латекс]\boldsymbol{\textbf{A}-\textbf{B}=\textbf{A} +(-\textbf{B})=\textbf{R}}.[/latex]Затем обычным методом сложения головы к хвосту получается результирующий вектор[latex]\textbf{R }.[/латекс]
- Сложение векторов коммутативно такой, что [латекс]\boldsymbol{\textbf{A}+\textbf{B}=\textbf{B}+\textbf{A}}.[/latex]
- Метод «голова к хвосту» сложения векторов включает рисование первого вектора на графике и последующее размещение хвоста каждого последующего вектора в начале предыдущего вектора.




 е.
вектор, длина которого равна единице).
е.
вектор, длина которого равна единице).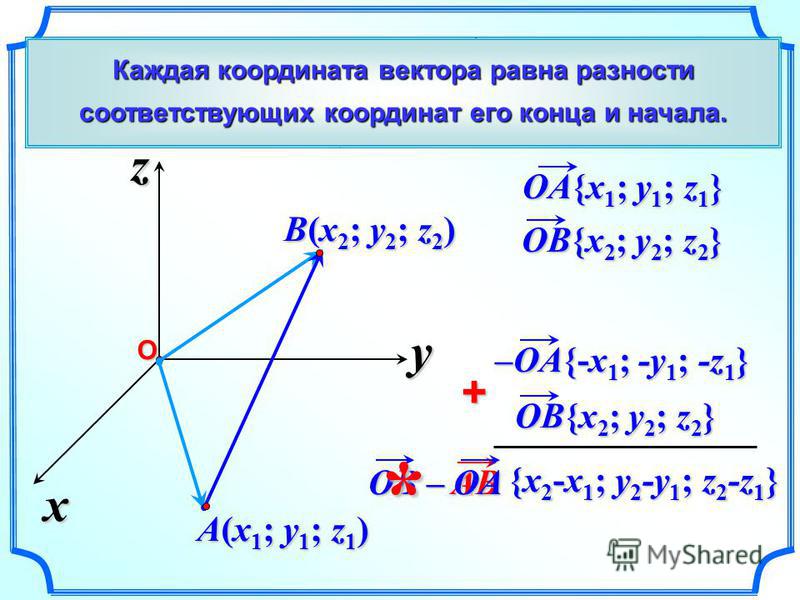 Наконец, если вектор перпендикулярен
оси l,
то x2= x1 и x2– x1=
0.
Наконец, если вектор перпендикулярен
оси l,
то x2= x1 и x2– x1=
0. Так как координата проекции начала
равна нулю, то обозначим .
Так как координата проекции начала
равна нулю, то обозначим .
 Но отсюда ,
а это и означает линейную зависимость
векторов и .
Но отсюда ,
а это и означает линейную зависимость
векторов и . Отложим три вектора от одной точки O.
Через точку Aпроведём
прямые, параллельные векторам и .
Тогда ,
причём векторы и коллинеарны
соответственно векторам и .
Поэтому найдутся числа x и y такие,
что ,
а значит .
Отложим три вектора от одной точки O.
Через точку Aпроведём
прямые, параллельные векторам и .
Тогда ,
причём векторы и коллинеарны
соответственно векторам и .
Поэтому найдутся числа x и y такие,
что ,
а значит .
 называются координатами
точки M. в
рассматриваемой системе координат. M(x,y,z).
Первая координата называется абсциссой,
вторая – ординатой, третья – аппликатой.
называются координатами
точки M. в
рассматриваемой системе координат. M(x,y,z).
Первая координата называется абсциссой,
вторая – ординатой, третья – аппликатой.
 Векторный калькулятор позволяет производить вычисления с векторами, используя координаты.
Векторный калькулятор позволяет производить вычисления с векторами, используя координаты.
 Результирующий вектор[latex]\textbf{R}[/latex] определяется таким образом, что[latex]\boldsymbol{\textbf{A}+\textbf{B}=\textbf{R}}.[/latex]Величина и направление[latex]\textbf{R}[/latex] затем определяются с помощью линейки и транспортира соответственно.
Результирующий вектор[latex]\textbf{R}[/latex] определяется таким образом, что[latex]\boldsymbol{\textbf{A}+\textbf{B}=\textbf{R}}.[/latex]Величина и направление[latex]\textbf{R}[/latex] затем определяются с помощью линейки и транспортира соответственно.