Виды треугольников – острый, равнобедренный, равносторонний (5 класс, математика)
4.4
Средняя оценка: 4.4
Всего получено оценок: 609.
Обновлено 11 Января, 2021
4.4
Средняя оценка: 4.4
Всего получено оценок: 609.
Обновлено 11 Января, 2021
При изучении математики ученики начинают знакомиться с разными видами геометрических фигур. Сегодня речь пойдет о различных видах треугольников.
Материал подготовлен совместно с учителем высшей категории Харитоненко Натальей Владимировной.
Опыт работы учителем математики — более 33 лет.
Определение
Геометрические фигуры, которые состоят из трех точек, которые не находятся на одной прямой,и отрезков, их соединяющих, называются треугольниками.
Отрезки, соединяющие точки, называются сторонами, а точки – вершинами. Вершины обозначаются большими латинскими буквами, например: A, B, C.
Стороны обозначаются названиями двух точек, из которых они состоят – AB, BC, AC. Пересекаясь, стороны образуют углы. Нижняя сторона считается основанием фигуры.
Пересекаясь, стороны образуют углы. Нижняя сторона считается основанием фигуры.
Виды треугольников
Треугольники классифицируют по углам и сторонам. Каждый из видов треугольника имеет свои свойства.
Существует три вида треугольников по углам:
- остроугольные;
- прямоугольные;
- тупоугольные.
Все углы остроугольного треугольника острые, то есть градусная мера каждого составляет не более 900.
Прямоугольный треугольник содержит прямой угол. Два других угла всегда будут острыми, так как иначе сумма углов треугольника превысит 180 градусов, а это невозможно. Сторона, которая, находится напротив прямого угла, называется гипотенузой, а две другие катетами. Гипотенуза всегда больше катета.
Тупоугольный треугольник содержит тупой угол. То есть угол, величиной больше 90 градусов. Два других угла в таком треугольника будут острыми.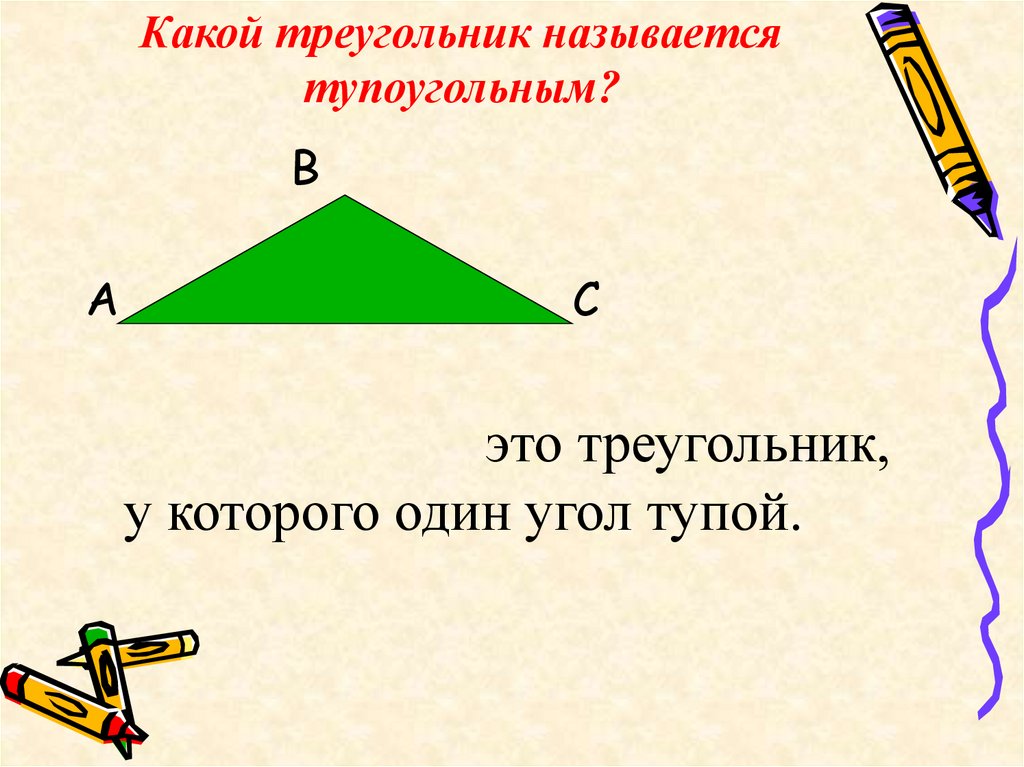
Пифагоровым треугольником называется прямоугольный треугольник, стороны которого равны 3, 4, 5.
Причем, большая сторона является гипотенузой.Такие треугольники часто используются для составления простых задач в геометрии. Поэтому, запомните: если две стороны треугольника равны 3 и 4, то третья обязательно будет 5, и треугольник непременно будет прямоугольным. Это упростит расчеты.
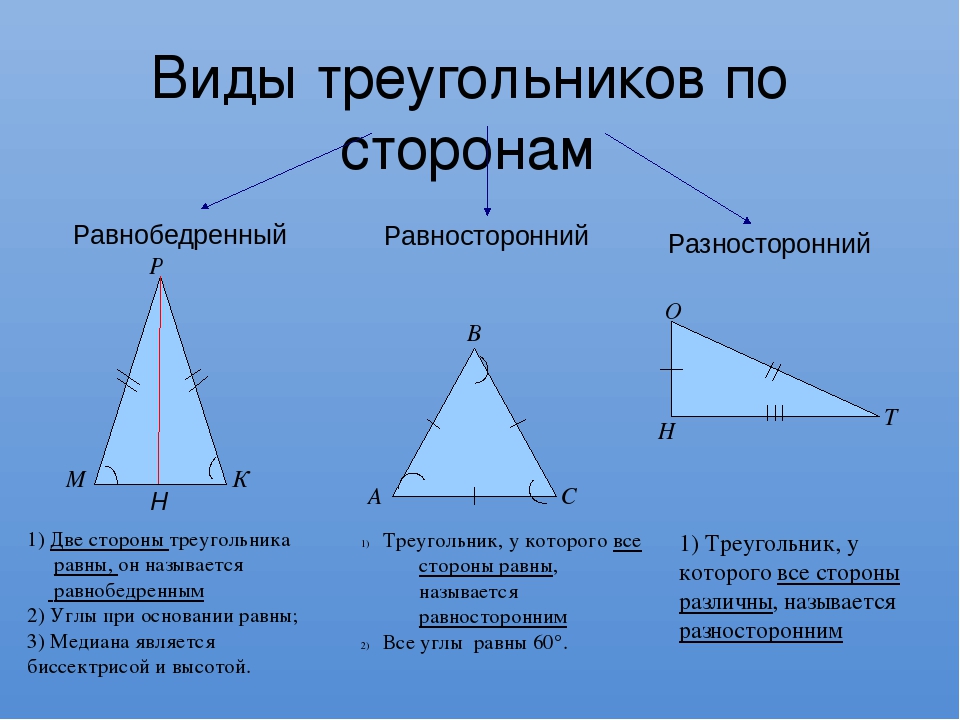
Виды треугольников по сторонам:
- равносторонние;
- равнобедренные;
- разносторонние.
Равносторонний треугольник – это треугольник, у которого все стороны равны. Все углы такого треугольника равны 600, то есть он всегда является остроугольным.
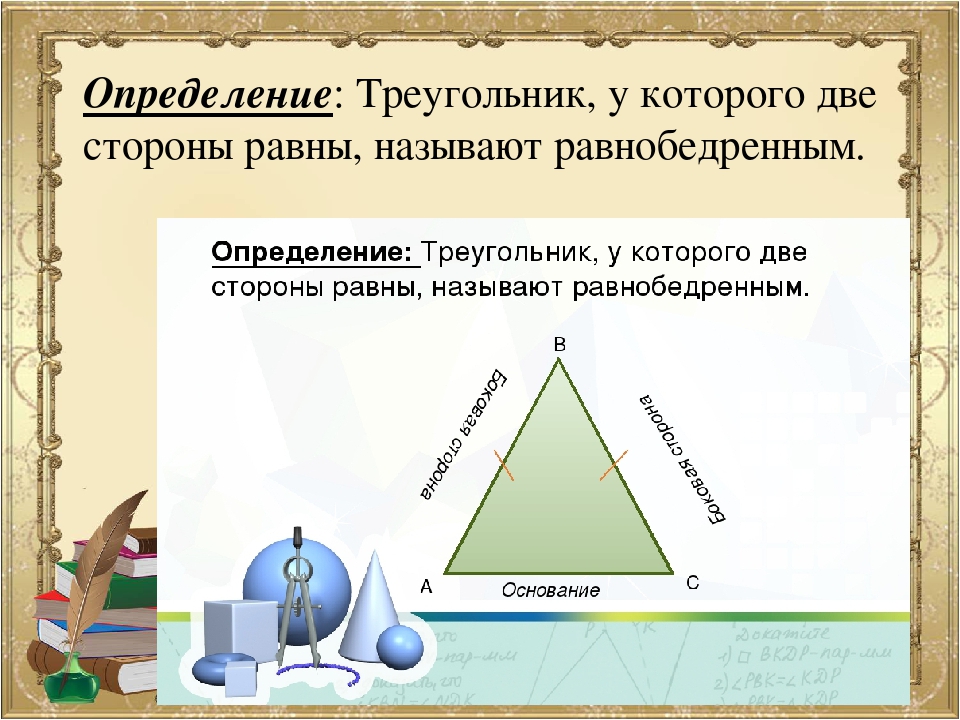
Равнобедренный треугольник – треугольник, у которого только две стороны равны. Эти стороны называются боковыми, а третья – основанием. Кроме того, углы при основании равнобедренного треугольника равны и всегда являются острыми.
Разносторонним или произвольным треугольником называется треугольник, у которого все длины сторон и все углы не равны между собой.
Если в задаче нет никаких уточнений по поводу фигуры, то принято считать, что речь идет о произвольном треугольнике.
Рис. 3. Виды треугольников по сторонам.Сумма всех углов треугольника, независимо от его вида, равна 180 градусам.
Напротив большего угла находится большая сторона. А также длина любой стороны всегда меньше суммы двух других его сторон. Эти свойства подтверждаются теоремой о неравенстве треугольника.
Существует понятие золотого треугольника. Это равнобедренный треугольник, у которого две боковые стороны пропорциональны основанию и равны определенному числу. В такой фигуре углы пропорциональны соотношению 2:2:1.
Задача:
Существует ли треугольник, стороны которого равны 6 см, 3 см, 4 см?
Решение:
Для решения данного задания нужно использовать неравенство a
Что мы узнали?
Из данного материала и из курса математики 5 класса, мы узнали, что треугольники классифицируются по сторонам и величине углов. Треугольники имеют определенные свойства, которые можно использовать при решении заданий.
Треугольники имеют определенные свойства, которые можно использовать при решении заданий.
Тест по теме
Доска почёта
Чтобы попасть сюда — пройдите тест.
Ненужное Существо
8/10
Михаил Хапёркин
10/10
Артём Санников
10/10
Алиса Муратшина
10/10
Светлана Филимонова
10/10
Оценка статьи
4.4
Средняя оценка: 4.4
Всего получено оценок: 609.
А какая ваша оценка?
Как называется треугольник на крыше
Главная » Разное » Как называется треугольник на крыше
названия частей, конструктивное строение кровли, из каких элементов состоит
Содержание:
Одним из этапов проектирования дома является определение конструкции крыши и вида кровельного покрытия. Большое значение при этом имеет дизайн строения, его назначение и конструктивные особенности. Однако наличие того или иного элемента кровли, материал для его изготовления и вид крыши зависит от множества других факторов. В частности, речь идет о климатических условиях, географическом положении и степени капитальности. К примеру, крыша бани или хозяйственной постройки имеет конструкцию, отличную от крыши дома. Для частного застройщика очень важно знать, из каких элементов состоит крыша, какие виды кровли подойдут именно в его случае.
Однако наличие того или иного элемента кровли, материал для его изготовления и вид крыши зависит от множества других факторов. В частности, речь идет о климатических условиях, географическом положении и степени капитальности. К примеру, крыша бани или хозяйственной постройки имеет конструкцию, отличную от крыши дома. Для частного застройщика очень важно знать, из каких элементов состоит крыша, какие виды кровли подойдут именно в его случае.
В целом крыша состоит из следующих частей:
- Стропильный каркас.
- Обрешетка.
- Защитная часть или кровля.
- Дополнительные горизонтально расположенные части: конек, ендова или разжелобок.
- Наклонные поверхности: скаты и ребра.
- Водосточные желоба по нижнему краю скатов для отвода талых и дождевых вод.
Конструктивные особенности крыши
Перед началом строительства крыши необходимо тщательно изучить строение крыши и непосредственно кровли. Ни одно цивилизованное строение невозможно представить без верхнего перекрытия, которое может быть двух видов:
Ни одно цивилизованное строение невозможно представить без верхнего перекрытия, которое может быть двух видов:
- Потолочное или чердачное перекрытие защищает строение от потерь тепла.
- Крыша защищает весь дом от различных природных явлений, таких как ветер, солнце и осадки.
Названия элементов и частей кровли
Все конструктивные элементы крыши предназначены для выполнения своей функции:
- Скат – главный элемент, представляющий собой наклонную плоскость, по которой осадки беспрепятственно отводятся с кровли. В какой-то степени скат гарантирует водонепроницаемость крыши.
- Ребра – выступающие углы в местах пересечения скатов.
- Ендова – внутренний угол, также образующийся при пересечении скатов.
- Спуск – нижняя часть ската.
- Капельник – низ спуска, предназначенный для защиты карниза и стены от воды.
- Карнизный свес – часть ската, расположенная горизонтально за плоскостью наружной стены.

- Фронтальный свес – часть ската, выступающая за фронтон.
- Желоб – элемент крыши, в котором собирается талая и дождевая вода. Располагается вдоль горизонтальной нижней кромки ската.
Собранная вода отводится по водосточной трубе, которая может располагаться у внешних стен здания (наружный водосток) или внутри стен (внутренний водосток). Второй вариант чаще всего используют при обустройстве плоской кровли.
Строения небольшой высоты и незначительной площади можно строить без водосточной системы, в этом случае вода со скатов стекает непосредственно на землю.
Используемое кровельное покрытие может укладываться вдоль ската или поперек него. Соединение листов может выполняться внахлест или в замок.
Большое значение имеет угол наклона скатов, который может выражаться в градусах или процентах. Уклон не позволяет осадкам собираться на крыше в большом количестве, особенно это относится к снежной массе.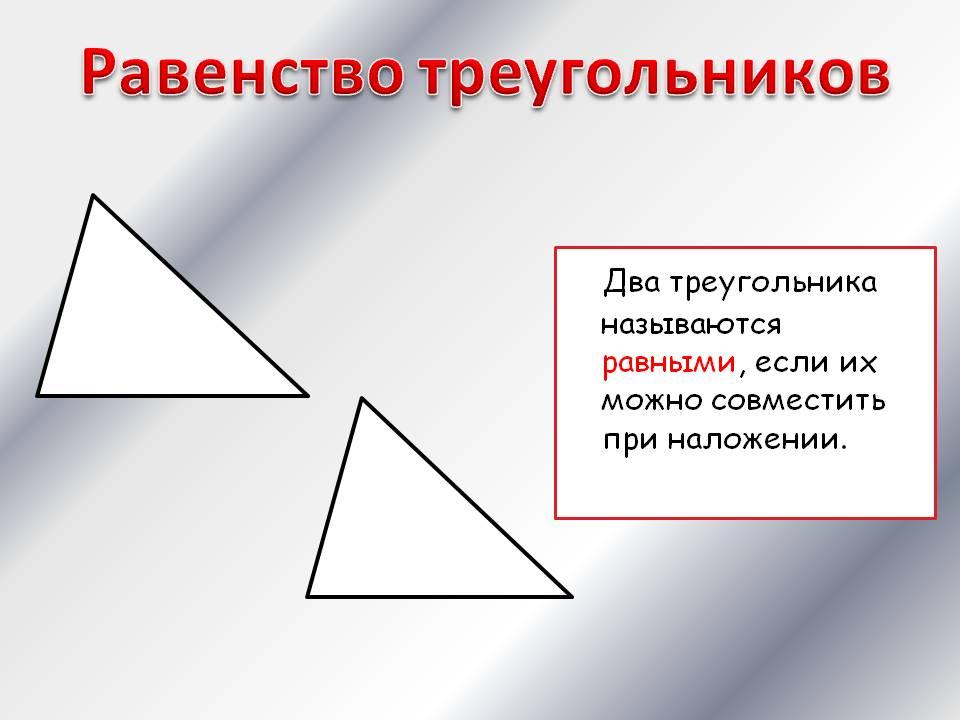
Геометрия строения крыши
Форма крыши может иметь различную геометрию, которая в большинстве случаев определяется видом строения:
- Крыша с одним скатом возводится над простыми строениями, например, баней, туалетом или беседкой, или постройками, примыкающими одной стороной к основному зданию. Такой вид кровли не требует большого количества материалов, но характеризуется долгим сроком эксплуатации.
- Двухскатная или щипцовая крыша состоит из двух скатов, имеющих определенный уклон. Треугольник, образуемый скатами, называют щипцом или фронтоном. Такая крыша пользуется огромной популярностью, возводится над многоэтажными домами и коттеджами.
- Крыша с четырьмя скатами может быть вальмовой или шатровой, используется при строительстве дачных домов.

- Крыша в виде купола является одним из самых старых видов, чаще всего такой вариант встречается над гостиницами или павильонами.
- Мансардная крыша является разновидностью двускатной конструкции.
- Сводчатые крыши используются в качестве перекрытий над промышленными или общественными зданиями прямоугольной формы.
- Коническая крыша лучше всего смотрится над зданиями круглой формы.
- Крыша в форме пирамиды возводится над квадратными или многоугольными строениями.
Кроме этого крыши могут быть чердачными и бесчердачными. В первом случае чердак может быть холодным или утепленными. Крыша без чердака служит перекрытием верхнего этажа здания, при этом допускается полная или частичная вентиляция, а также ее отсутствие.
Климатические условия местности во многом определяют угол наклона скатов конструктивные особенности крыши. В районах с преобладанием температуры воздуха выше ноля градусов крыша над домом может иметь небольшой уклон.
Стропильная система
Основанием крыши любого типа служит стропильная система, для изготовления которой в большинстве случаев используют доски или деревянные бруски. На эту конструкцию ложится вес кровли, поэтому для работы лучше выбирать высококачественную древесину, на которой нет большого количества сучков, трещин и гнили. Чаще всего стропильный каркас возводится из древесины хвойных пород. Предварительно пиломатериал тщательно просушивают. Иногда для работы используют бревна, но на высоте с таким материалом работать неудобно из-за его тяжести.
Опорой для стропилин служит мауэрлат, для его изготовления необходимо брать брус сечением 10*10 см или бревно, стесав перед укладкой его нижнюю часть. В домах из бруса или бревен в качестве этого элемента используется верхний венец коробки дома. Мауэрлат предназначен для распределения нагрузки на несущие стены дома.
В домах из бруса или бревен в качестве этого элемента используется верхний венец коробки дома. Мауэрлат предназначен для распределения нагрузки на несущие стены дома.
Рассчитывать сечение стропильных ног нужно очень внимательно с учетом нескольких критериев:
- Нагрузка от кровли и снежной массы.
- Расстояние между стропилинами.
- Параметры пролета.
- Угол наклона скатов.
Выделяют два вида стропильной системы: висячая и наслонная. В первом случае стропильные ноги опираются на наружные стены здания, второй вид подразумевает установку дополнительных опор на внутренних несущих стенах, перегородках или колоннах.
Обрешетка крыши
Назначение обрешетки – основание для кровельного материала, которое не позволяет ему прогибаться и деформироваться. Для некоторых покрытий делают сплошную обрешетку, но в большинстве случаев между элементами оставляют определенное расстояние в зависимости от кровельного материала.
Изготовление обрешетки необходимо выполнять по следующим правилам:
- Все элементы должны быть надежно зафиксированы на стропильном каркасе.
- Соединение элементов над стропилинами располагают в шахматном порядке.
- Сплошное основание лучше всего применять под рулонные кровельные материалы или плоские асбестоцементные плитки.
- На разреженную обрешетку укладывают асбестоцементные листы, черепицу и тонколистовую сталь.
- Шаг между элементами обрешетки, независимо от материала, должен иметь одинаковое значение по всей крыше.
Назначение и необходимость элементов конструкции
Независимо от степени сложности крыши, каждый элемент предназначен для выполнения своей функции. Строение кровли, форма и конструкция крыши определяется на одном из этапов проектирования дома или при составлении плана ремонтных работ.
Надежность и долговечность крыши зависит от правильной установки всех составляющих, включая основные части, кровельный материал, места примыкания к дополнительным элементам крыши. Покрытие для кровли станет хорошей защитой стропильной системы и всего строения только при условии приобретения кровли и дополнительной фурнитуры от одного производителя. В этом случае монтажные работы будут выполнены без лишних сложностей.
Покрытие для кровли станет хорошей защитой стропильной системы и всего строения только при условии приобретения кровли и дополнительной фурнитуры от одного производителя. В этом случае монтажные работы будут выполнены без лишних сложностей.
Составлять проект любого строения, особенно жилых домов, должен грамотный специалист. Этим могут заниматься только частные архитекторы или проектировщики, имеющие специальное разрешение. В готовом проекте содержится план дома, крыши с указанием всех узлов и деталей конструкции. Непосредственно строительством также должны заниматься профессиональные мастера, так как они знают названия частей крыши, их назначение и правильное расположение, выполнят работу на высшем уровне и в короткие сроки, а также предоставят гарантию.
youtube.com/embed/PkB3_wCcewY?feature=oembed» frameborder=»0″ gesture=»media» allowfullscreen=»»>треугольников — равносторонние, равнобедренные и чешуйчатые
Треугольник имеет три стороны и три угла | ||
Три угла всегда складываются в 180 ° |
Равносторонний, равнобедренный и чешуйчатый
Треугольникам даны три специальных имени, которые показывают, сколько сторон (или углов) равны.
Может быть 3 , 2 или нет равных сторон / углов:
Равносторонний треугольник Три равных стороны | |
Равнобедренный треугольник Две равные стороны | |
Скаленовый треугольник Нет равные стороны |
Как запомнить? По алфавиту идут 3, 2, нет:
- Равносторонний : «равный» — боковой (боковой означает сторона), поэтому все стороны имеют равные стороны
- Равнобедренный : означает «равноногие», а у нас две ноги , верно? Также i SOS celes имеет два одинаковых «S ides», соединенных стороной « O dd».

- Скален : означает «неровный» или «нечетный», поэтому нет равных сторон.
Какой угол?
Треугольники также могут иметь имена, которые сообщают вам, какой тип угла находится внутри :
Острый треугольникВсе углы меньше 90 ° | |
Прямой треугольникИмеет прямой угол (90 °) | |
Тупой треугольникИмеет угол более 90 ° |
Объединение имен
Иногда у треугольника будет два имени, например:
Правый равнобедренный треугольникИмеет прямой угол (90 °), а также два равных угла. Вы можете угадать, каковы равные углы? |
Поиграй с ним…
Попробуйте перетащить точки и составить разные треугольники:
Вы также можете поиграть с Интерактивным треугольником.
Уголки
Три внутренних угла всегда составляют 180 °
Периметр
Периметр — это расстояние по краю треугольника: просто сложите три стороны:
Площадь
Площадь составляет , половина базовой, умноженная на высоту .
- «b» — расстояние по основанию
- «h» — высота (измеренная под прямым углом к основанию)
Площадь = ½ × b × h
Формула работает для всех треугольников.
Примечание: более простой способ записать формулу — bh / 2
Пример: Какова площадь этого треугольника?
(Примечание: 12 — это высота , а не длина левой стороны)
Высота = h = 12
База = b = 20
Площадь = ½ × b × h = ½ × 20 × 12 = 120
Основание может быть с любой стороны. Убедитесь, что «высота» измеряется под прямым углом к »основанию». :
(Примечание: вы также можете рассчитать площадь по длинам всех трех сторон, используя формулу Герона. )
)
Почему область «половина bh»?
Представьте, что вы «удвоили» треугольник (перевернули его вокруг одного из верхних краев), чтобы получить квадратную форму (параллелограмм), которую можно изменить на простой прямоугольник:
ЗАТЕМ вся площадь составляет bh , что соответствует обоим треугольникам, поэтому только один будет ½ × bh .
.
Равнобедренный, равносторонний, тупой, острый и чешуйчатый
Треугольники можно классифицировать по различным свойствам, связанным с их углами и сторонами. На этой странице описаны наиболее распространенные классификации.
Классификация треугольников
Правые треугольники
Прямоугольный треугольник имеет один угол 90 ° и множество часто изучаемых тем:
Равносторонний треугольник
Равносторонний треугольник, показанный слева, имеет три равные стороны и три равных угла.
Каждый угол составляет 60 °
Равнобедренный треугольник
Равнобедренный треугольник, показанный слева, имеет две равные стороны и два равных угла.
Чешуйчатый треугольник
У чешуйчатого треугольника нет конгруэнтных сторон. Другими словами, каждая сторона должна иметь разную длину.
Острый треугольник
Острый треугольник имеет три острых угла (острый угол меньше 90 °)
Тупой треугольник
Тупой треугольник имеет тупой угол (тупой угол больше 90 °).На картинке слева заштриховано
.
Как определить, конгруэнтны ли треугольники
Два треугольника равны, если они имеют:
Но нам не обязательно знать все три стороны и все три угла … обычно достаточно трех из шести . |
Существует пять способов определить, совпадают ли два треугольника: SSS , SAS , ASA , AAS и HL .
1. SSS
(сбоку, сбоку, сбоку) SSS означает «сторона, сторона, сторона» и означает, что у нас есть два треугольника, все три стороны которых равны.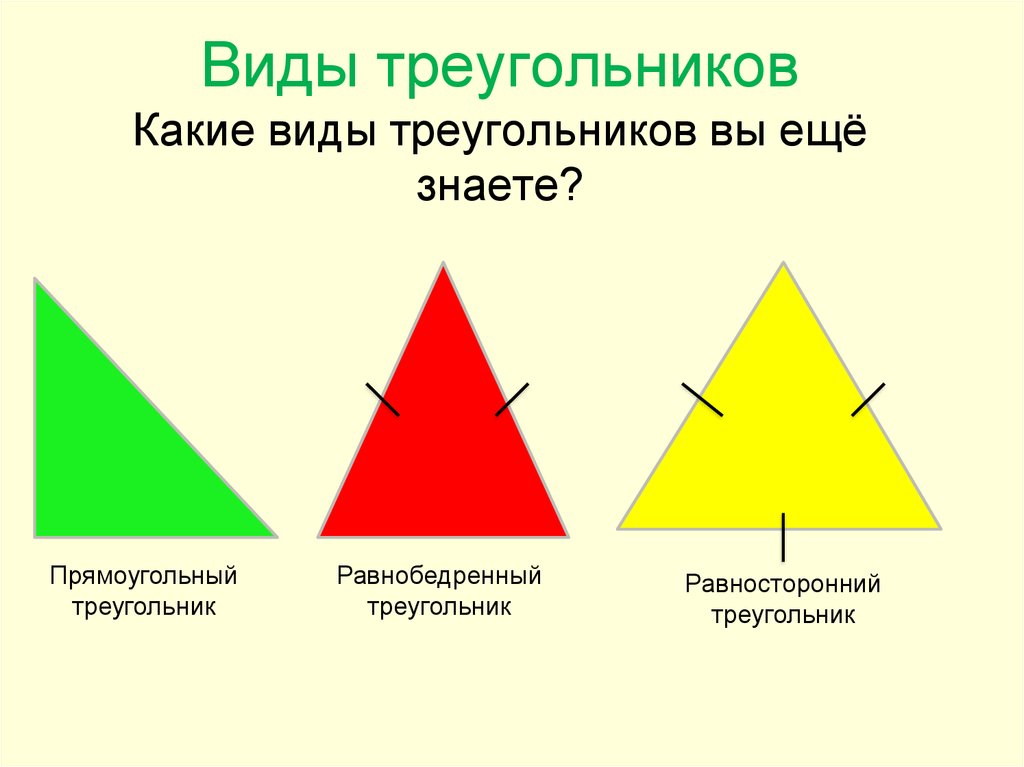
Например:
| соответствует: |
(Подробнее см. «Решение треугольников SSS»)
Если три стороны одного треугольника равны трем сторонам другого треугольника, треугольники конгруэнтны.
2. SAS
(сбоку, угол, сбоку)SAS означает «сторона, угол, сторона» и означает, что у нас есть два треугольника, у которых мы знаем, что две стороны и прилегающий угол равны.
Например:
| равно соответствует: |
(Дополнительные сведения см. В разделе «Решение треугольников SAS»)
Если две стороны и внутренний угол одного треугольника равны соответствующим сторонам и углу другого треугольника, треугольники конгруэнтны.
3. ASA
(угол, сторона, угол) ASA означает «угол, сторона, угол» и означает, что у нас есть два треугольника, из которых мы знаем, что два угла и включенная сторона равны.
Например:
| равно соответствует: |
(Дополнительные сведения см. В разделе «Решение треугольников ASA»)
Если два угла и включенная сторона одного треугольника равны соответствующим углам и стороне другого треугольника, треугольники конгруэнтны.
4. AAS
(угол, угол, сторона)AAS означает «угол, угол, сторона» и означает, что у нас есть два треугольника, где, как мы знаем, два угла и не включенная сторона равны.
Например:
| равно соответствует: |
(Дополнительные сведения см. В разделе «Решение треугольников AAS»)
Если два угла и сторона без включения одного треугольника равны соответствующим углам и стороне другого треугольника, треугольники совпадают.
5. HL
(гипотенуза, ножка)Это относится только к прямоугольным треугольникам!
HL означает « H ypotenuse, L eg» (самая длинная сторона прямоугольного треугольника называется «гипотенузой», две другие стороны называются «катетами»)
Это означает, что у нас есть два прямоугольных треугольника с
- одинаковая длина гипотенузы и
- : той же длины для одной из двух других ног .

Не имеет значения, на какой ноге треугольники можно вращать.
Например:
| равно соответствует: |
(см. Теорему Пифагора, чтобы узнать больше)
Если гипотенуза и один катет одного прямоугольного треугольника равны соответствующей гипотенузе и катету другого прямоугольного треугольника, эти два треугольника конгруэнтны.
Внимание! Не используйте «AAA»
AAA означает, что нам даны все три угла треугольника, но нет сторон.
Этой информации недостаточно, чтобы решить, конгруэнтны ли два треугольника!
Поскольку треугольники могут иметь одинаковые углы, но иметь разных размеров :
| соответствует , а не : |
Не зная хотя бы одной стороны, мы не можем быть уверены, конгруэнтны ли два треугольника.
.
конгруэнтных треугольников
Треугольники конгруэнтны, если у них
точно таких же трех сторон и точно тех же трех углов .
Что такое «Конгруэнтный» …?
Это означает, что одна форма может стать другой с помощью поворота, переворота и / или скольжения:
(подробнее см. Конгруэнт)
конгруэнтных треугольников
Когда два треугольника совпадают, у них будет ровно одинаковых трех сторон и ровно одинаковых трех углов .
Равные стороны и углы могут не находиться в одном и том же положении (если есть поворот или переворот), но они есть.
Те же стороны
Если стороны совпадают, то треугольники равны.
Например:
| соответствует: | |||
| , а также на: |
, потому что все они имеют одинаковых сторон .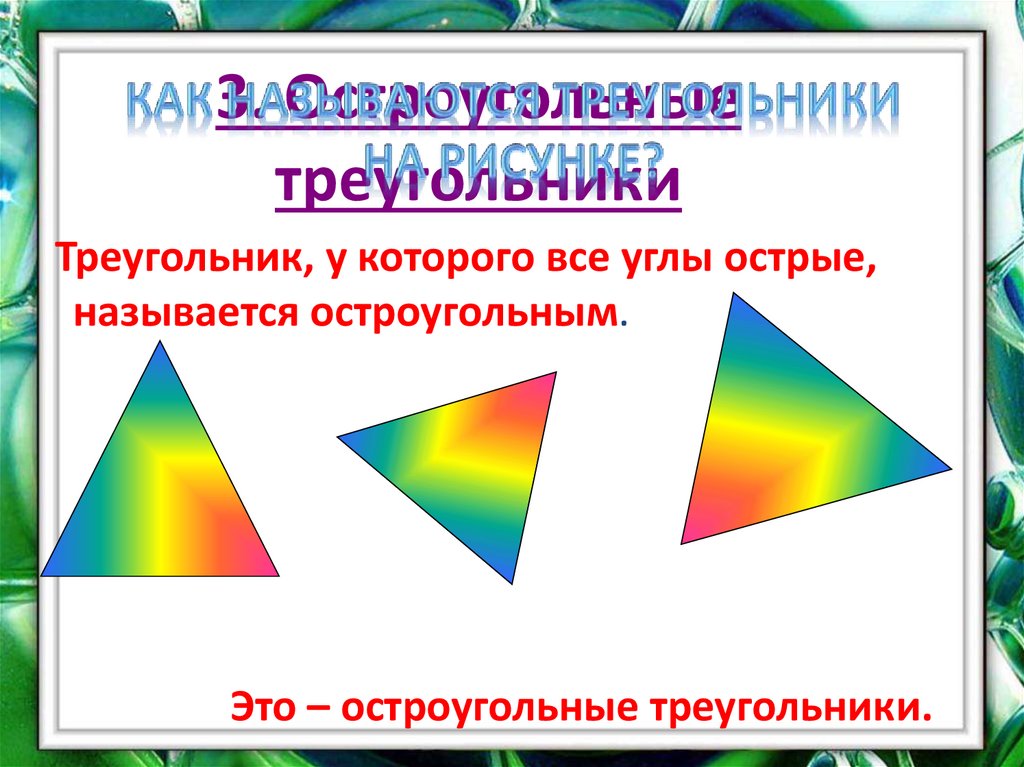
Но:
| НЕ соответствует: |
, потому что у двух треугольников разные стороны .
Одинаковые углы
Это тоже работает с углами? Не всегда!
Два треугольника с одинаковыми углами могут быть конгруэнтными:
| соответствует: |
только потому, что они того же размера
Но они могут НЕ совпадать из-за разных размеров :
| НЕ соответствует: |
, потому что, хотя все углы совпадают, один больше другого .
Таким образом, наличие одинаковых углов не гарантирует их совпадения.
Другие комбинации
Существуют и другие комбинации сторон и углов, которые могут работать . ..
..
… подробнее см. Как определить, совпадают ли треугольники
Артикул
Когда два треугольника совпадают, мы часто отмечаем соответствующие стороны и углы следующим образом:
| соответствует: |
Стороны, отмеченные одной линией, равны по длине.Аналогично для сторон, отмеченных двумя линиями. Также для сторон, отмеченных тремя линиями.
Углы, отмеченные одной дугой, равны по размеру. Аналогично для углов, отмеченных двумя дугами. Также для углов, отмеченных тремя дугами.
.
Что такое разносторонний треугольник? Определение, свойства, примеры
Разносторонний треугольник – Введение
Разносторонний треугольник – это треугольник, все стороны которого не равны, а все углы имеют разную величину. Мы знаем, что треугольник — это трехсторонний многоугольник, состоящий из трех ребер и трех вершин. Существует три типа треугольников в зависимости от длины его сторон:
Мы знаем, что треугольник — это трехсторонний многоугольник, состоящий из трех ребер и трех вершин. Существует три типа треугольников в зависимости от длины его сторон:
- Равносторонний треугольник: Все стороны равны по длине.
- Равнобедренный треугольник: две стороны равны по длине.
- Разносторонний треугольник: Все стороны имеют разную длину.
Что такое разносторонний треугольник?
Разносторонний треугольник — это треугольник, в котором все стороны имеют разную длину и все углы разной величины.
Например:
На приведенном выше рисунке все три символа на каждой стороне различны, что означает, что все три стороны не равны. Кроме того, все три угла имеют разную меру. Итак, треугольник разносторонний.
Определение разностороннего треугольника
Разносторонний треугольник можно определить как треугольник, все три стороны которого имеют разную длину и все три угла имеют разную величину. Углы разностороннего треугольника подчиняются свойству суммы углов и всегда дают в сумме 180.
Углы разностороннего треугольника подчиняются свойству суммы углов и всегда дают в сумме 180.
Типы разносторонних треугольников
Разносторонний треугольник можно разделить на три категории: -разноугольный треугольник, каждый угол которого меньше 60°.
- Тупоугольный разносторонний треугольник
В тупоугольном разностороннем треугольнике по крайней мере один из углов треугольника больше 60°.
- Прямоугольный разносторонний треугольник
В прямоугольном разностороннем треугольнике один угол равен 90°.
Свойства разностороннего треугольника
- У него три стороны разной длины.
- Имеет три угла разных размеров.
- У него нет равных или параллельных сторон. Следовательно, в разностороннем треугольнике нет линии симметрии.
- Не имеет точечной или вращательной симметрии.
Свойство суммы углов треугольника
Сумма всех трех внутренних углов разностороннего треугольника равна 180°.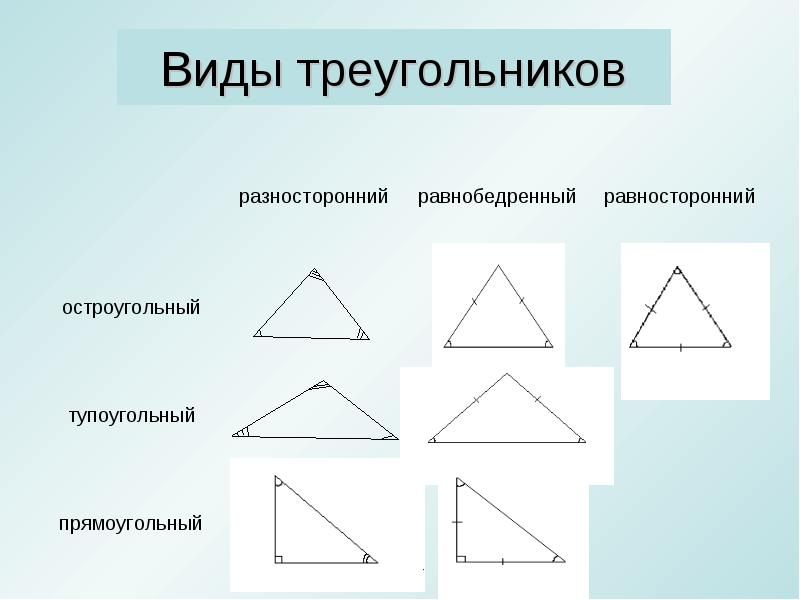 Это также известно как свойство суммы углов треугольника.
Это также известно как свойство суммы углов треугольника.
В $\Delta\text{ABC}, ∠\text{A} + ∠\text{B} + ∠\text{C} = 180°$
Разница сторон или углов не влияет на Основные свойства треугольника.
Например: В $\Delta\text{PQR}, ∠\text{P} = 60°, ∠\text{Q} = 70°$
По свойству суммы углов треугольника
$∠\ text{P} + ∠\text{Q} + ∠\text{R} = 180°$
$60° + 70° + ∠\text{R} = 180°$
$130° + ∠\text{R } = 180°$
$∠\text{R} = 50°$
Площадь разностороннего треугольника
Формула для расчета площади разностороннего треугольника аналогична формуле для расчета площади любого другого треугольника .
1. Если указаны основание и высота 92$
2. Когда известны стороны треугольника
Когда у нас нет основания и высоты для разностороннего треугольника, а стороны известны, тогда применяем формулу Герона.
Площадь треугольника $= \sqrt{s(s-a)(s-b)(s-c)}$ квадратных единиц
Где s — полупериметр треугольника, поэтому
$\text{s}=\ frac{a+b+c}{2}$
Здесь a, b и c обозначают стороны треугольника.
Пример: Стороны треугольника равны 3 см, 4 см и 5 см. 92$
Равносторонний треугольник против разностороннего треугольника против равнобедренного треугольника
Периметр разностороннего треугольника
Периметр любого треугольника = сумма всех сторон треугольника.
Если стороны треугольника равны единицам «a», единицам «b» и единицам «c», то
Периметр $= \text{a} + \text{b} + \text{c}$ единиц
Пример: Рассмотрим заданный треугольник.
Периметр треугольника $= 7 + 12 + 15 = 34 \text{см}$
Решенные примеры
1. Чему равен периметр треугольника со сторонами 10 см, 12 см и 13 см?
Решение : Периметр = сумма всех сторон треугольника $= 10 + 12 + 13 = 35 \text{см}$
2. Найдите площадь треугольника со сторонами 20 см, 21 см , и 29 см.
Решение : Пусть $a = 20 \text{см}, b = 21 \text{см}$ и $c = 29 \text{см}$
$\text{s}=\frac{ 20+21+29}{2}=\frac{70}{2}=35$ 92$
3.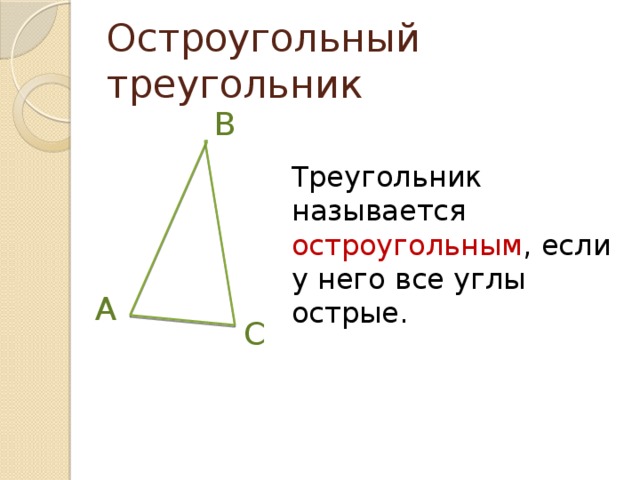 В PQR, $∠\text{P} = 30°, ∠\text{Q} = 60°$ , найдите значение $∠\text{R}$ . Кроме того, какой тип треугольника называется?
В PQR, $∠\text{P} = 30°, ∠\text{Q} = 60°$ , найдите значение $∠\text{R}$ . Кроме того, какой тип треугольника называется?
Решение : В PQR, по свойству суммы углов треугольника,
$∠\text{P} + ∠\text{Q} + ∠\text{R} = 180°$
$30° + 60° + ∠\text{R} = 180°$
$∠\text{R} = 180° – 30° – 60° = 90°$
Прямоугольный разносторонний треугольник.
Практические задачи
1
Какие из следующих сторон могут быть сторонами разностороннего треугольника?
3 см, 13 см и 13 см
6 см, 6 см и 6 см
10 см, 12 см и 13 см
Ничего из перечисленного
Правильный ответ: 10 см, 12 см, и 13 см
10 см, 12 см и 13 см — разные стороны треугольника.
2
Что из следующего неверно для разностороннего треугольника?
У него три неравные стороны.
Имеет три неравных угла.
Не имеет вращательной симметрии.
Имеет 3 линии симметрии.
Правильный ответ: имеет 3 оси симметрии.
Разносторонний треугольник не имеет оси симметрии.
3
Если периметр треугольника равен 24 см, а две стороны равны 5 см и 7 см, то чему будет равна третья сторона?
7 см
8 см
10 см
12 см
Правильный ответ: 7 см
Периметр треугольника $= 5+12+x = 24 \text{см}$
$x = 7 \text{cm}$
Часто задаваемые вопросы
Что такое теорема о неравномерном неравенстве?
Теорема о разнонаправленном неравенстве утверждает, что если одна сторона треугольника имеет большую длину, чем другая сторона, то угол, противолежащий большей стороне, имеет большую меру, и наоборот, если один угол больше другого угла, сторона, противоположная больший угол будет длиннее.
Может ли разносторонний треугольник быть прямоугольным?
Да, разносторонний треугольник может быть прямоугольным. Мы называем их прямоугольными разносторонними треугольниками.
Мы называем их прямоугольными разносторонними треугольниками.
Назовите примеры двух уникальных разносторонних треугольников.
Примеры двух уникальных треугольников, которые также являются разносторонними: $30$$-$$60$$-$$90$ и $40$$-$$50$$-$$90$.
Названия геометрических фигур — английская грамматика здесь
Английские названия геометрических фигур, определения и примеры;
Содержание
Список геометрических фигур
- Нонагон
- Эллипс
- Прямоугольный
- Прямоугольная призма
- Октагон
- Конус
- Треугольник
- Разносторонний треугольник
- Стрела
- Куб
- Цилиндр
- Звезда
- Семиугольник
- Шестигранник
- Полумесяц
- Пирамида
- Прямоугольный треугольник
- Параллелограмм
- Ромб
- Площадь
- Пентагон
- Трапеция
- Круг
- Овальный
- Декагон
- Сердце
- Крест
(для более имен фигур )
Геометрические фигуры могут быть названы как фигура или область, замкнутая границей, которая создается путем объединения определенного количества кривых, точек и линий.
Квадрат представляет собой четырехстороннюю область, которая создается путем соединения 4 отрезков. Отрезки в квадрате — это все равные прямые. Вместе они образуют 4 прямых угла.
Если мы говорим о круге, который является другой формой геометрии, не имеет прямых линий. Это скорее комбинация кривых, которые все связаны между собой. В окружности угол не найти.
Прямоугольник
Подобно квадрату, прямоугольник также создается путем соединения четырех отрезков. Однако разница есть только между квадратом и прямоугольником. Кроме того, прямоугольник имеет два отрезка, которые длиннее двух других отрезков. Так, в геометрии прямоугольник еще называют вытянутым квадратом.
Так, в геометрии прямоугольник еще называют вытянутым квадратом.
Треугольник
Треугольник состоит из трех связанных отрезков. В отличие от квадрата, в треугольнике углы могут быть разных размеров. Они не всегда являются правильными углами. Треугольники называются в зависимости от типа углов, которые находятся внутри самого треугольника. Например, если треугольник имеет один прямой угол, он будет известен как прямоугольный треугольник.
Однако, если все углы треугольника меньше 90 градусов, он будет называться остроугольным. Если какой-либо из углов в треугольнике больше 90 градусов, то он будет известен как тупоугольный треугольник. Наконец, есть равноугольный треугольник, у которого все углы треугольника равны 60 градусов. С другой стороны, треугольник также можно идентифицировать или пометить по типу его сторон. У разностороннего треугольника нет равных сторон. У равнобедренного треугольника две стороны равны. Равносторонний треугольник имеет три равные стороны.