Как обозначается ранг матрицы: Ранг матрицы

Глава 07. Ранг матрицы

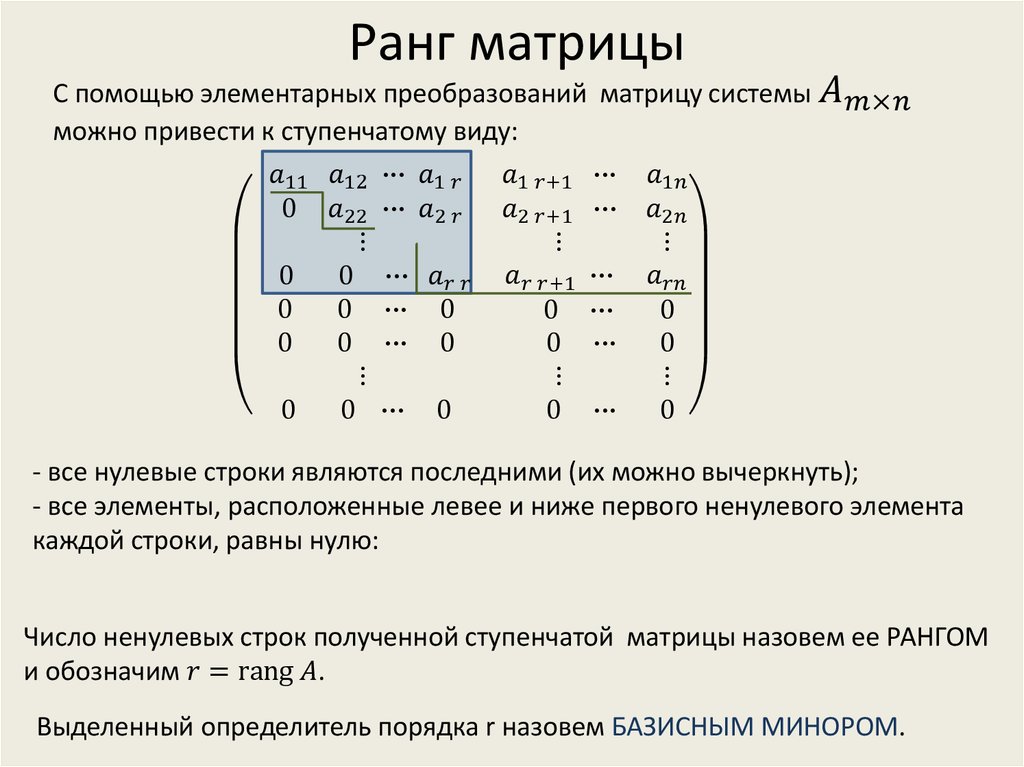
Рассмотрим прямоугольную матрицу (1.1.1), содержащую N строк и M столбцов. Выделим в ней произвольным образом квадратную матрицу K–го порядка. Определитель этой матрицы называется Минором K–го порядка матрицы А. Очевидно, что в общем случае таких миноров K–го порядка может быть несколько, а максимальный порядок миноров равен минимальному из чисел M и N, т. е. K £ min(N; M). Далее, из всех возможных миноров матрицы А Выделим те из них, которые Отличны от нуля. В свою очередь, среди этих миноров можно найти по крайней мере один минор наибольшего порядка.

Определение

Наибольший порядок отличных от нуля миноров называется Рангом матрицы А. Ранг матрицы обозначается rangA или r(A).

Из определения следует:

1.Ранг матрицы A Не превосходит меньшего из ее размеров, т. е. K £ min(N; M

).

2.Ранг матрицы равен нулю тогда, когда все элементы матрицы равны нулю, т. е. A=0.

3.Для квадратной матрицы N–го порядка R(A) = N тогда и только тогда, когда матрица A – невырожденная.

Пример

Вычислить ранг матрицы

.

Решение

Матрица A имеет размер 4´3, поэтому rangA £ 3. Однако, все определители матрицы A равны нулю. Следовательно, rangA £ 2. Нетрудно видеть, что максимальный порядок миноров этой матрицы, отличных от нуля, равен 2.

Определение

Отличный от нуля минор матрицы, порядок которого равен рангу матрицы, называется Базисным минором этой матрицы. Столбцы и строки этой матрицы, участвующие в образовании базисного минора, также называются Базисными.

Пример

Вычислить ранг матрицы

.

Решение

Матрица A имеет четвертый порядок, поэтому R(A) £ 4. Однако |A| = 0, так как матрица

A содержит нулевой столбец, поэтому R(A) £ 3. Все подматрицы третьего порядка тоже содержат нулевой столбец и поэтому имеют нулевые определители значит R(A) £ 2. Все подматрицы второго порядка либо имеют нулевой столбец (второй или четвертый), либо имеют пропорциональные столбцы (первый и третий), поэтому тоже имеют нулевые определители; таким образом R(A) £ 1. Поскольку матрица A содержит ненулевые элементы, т. е. невырожденные подматрицы первого порядка, то R(A) = 1.

В общем случае определение ранга матрицы перебором всех миноров достаточно трудоемко. Для облегчения этой задачи используются перечисленные ниже Элементарные преобразования, сохраняющие ранг матрицы.

1. Отбрасывание нулевой строки (столбца).

2. Умножение всех элементов строки (столбца) на число, не равное нулю.

3. Изменение порядка строк (столбцов), а также прибавление к каждому элементу одной строки (столбца) линейной комбинации соответствующих элементов другой строки (столбца).

4. Транспонирование матрицы.

Теорема

Ранг матрицы не изменится при элементарных преобразованиях.

< Предыдущая		Следующая >

Ранг матрицы — Студопедия

Поделись  

Мы видели, что линейные операторы можно представить матрицами. Одна и та же матрица может представлять в одних базисах один оператор, а в других базисах — другой. Можно доказать, что все такие операторы имеют один и тот же ранг. Поэтому корректно следующее определение.

Рангом матрицы называется ранг любого оператора, представляемого этой матрицей, т.е. размерность образа этого оператора.

Таким образом, если удастся найти какой–нибудь способ вычисления ранга матрицы, то ранг оператора можно будет определить по рангу его матрицы. Такой способ предлагается в следующем утверждении.

Теорема. Ранг матрицы равен максимальному числу ее линейно независимых столбцов.

Доказательство см. A = r ). По теореме ранг матрицы равен максимальному числу ее линейно независимых столбцов. Поэтому, чтобы определить ранг линейного оператора, удобно выбрать такую его матрицу, у которой число линейно независимых столбцов было очевидно. Эта цель достигается с помощью элементарных преобразований строк матрицы (и соответствующих преобразований базисов). Отметим, что преобразования строк матрицы соответствуют преобразованиям в Ym , а преобразования столбцов матрицы соответствуют преобразованиям в Xn .

С помощью элементарных преобразований строк преобразуем матрицу A так, чтобы в максимальном числе столбцов оказалось по одной единице (в разных строках у разных столбцов), а остальные элементы столбцов были бы нулями. Очевидно, что такие столбцы линейно независимы. Они называются базисными и их количество равно рангу преобразованной матрицы. Такая матрица называется редуцированной (или гауссовой) и обозначается Aред . Ее ранг равен рангу исходной матрицы A .

Утверждение. Элементарные преобразования строк матрицы не меняют линейных соотношений между ее столбцами.

Из этого утверждения следует, что элементарные преобразования не меняют ранга матрицы.

Матрицы A и B , получающиеся друг из друга элементарными преобразованиями строк, мы будем называть эквивалентными и обозначать A ~ B .

Таким образом, A ~ Aред и Rg A = Rg Aред .

Замечание. Кроме метода Гаусса, существуют и другие методы вычисления ранга матрицы (метод окаймляющих миноров и т.д.), однако только метод Гаусса позволяет использовать редуцированную матрицу для решения большинства задач линейной алгебры, например, при исследовании линейной зависимости векторов, нахождении разложения вектора по базису, при исследовании оператора по его матрице, решении систем линейных уравнений и нахождении собственных векторов операторов.



линейная алгебра — Важность ранга матрицы

Ранг матрицы, вероятно, является наиболее важным понятием, которое вы изучаете в Матричной алгебре. Есть два способа посмотреть на ранг матрицы. Один из теоретических настроек, а другой из прикладных. {n \times 1}$, то $Ax$ порождает $p$-мерное подпространство. Давайте посмотрим на это в 2D-режиме. Например, если 9{2 \times 1}$, затем $\left( \begin{array}{c} у_1 \\ y_2 \end{массив} \right) = y = Ax = \left( \begin{массив}{c} х_1+2х_2\ 2x_1 + 4x_2 \end{массив} \right)$.

Ранг матрицы $A$ равен $1$, и мы находим, что $y_2 = 2y_1$, что есть не что иное, как прямая, проходящая через начало координат на плоскости.

Произошло следующее: все точки $(x_1,x_2)$ на плоскости $x_1 — x_2$ были сопоставлены с линией $y_2 = 2y_1$. При внимательном рассмотрении видно, что все точки на плоскости $x_1 — x_2$ вдоль линии $x_1 + 2x_2 = c = \text{const}$ были сопоставлены с одной точкой $(c,2c)$ на $y_1 — плоскость y_2$. Таким образом, единственная точка $(c,2c)$ на плоскости $y_1 — y_2$ представляет собой прямую линию $x_1 + 2x_2 = c$ на плоскости $x_1 — x_2$.

По этой причине вы не можете решить линейную систему, если она имеет недостаточный ранг. Матрица $A$ с недостаточным рангом отображает $x$ в $y$, и это преобразование не является ни (точками в плоскости $y_1 — y_2$, не лежащими на прямой $y_2 = 2y_1$, например, $(2,3)$, не отображается на, что не дает решений), ни взаимно однозначно (каждой точке $(c,2c)$ на прямой $y_2 = 2y_1$ соответствует прямая $x_1 + 2x_2 =c$ в $x_1 — x_2 $ плоскости, что приводит к бесконечным решениям).

Здесь можно сделать следующее наблюдение: произведение наклонов прямой $x_1 + 2x_2 = c$ и $y_2 = 2y_1$ равно $-1$. В общем случае это верно и для более высоких измерений. 92$ своих записей. Итак, если мы знаем, что матрица имеет низкий ранг, то мы можем сжать и сохранить матрицу, а также выполнять с ее помощью эффективные операции с матрицами. Приведенные выше идеи могут быть распространены на любой линейный оператор, и они фактически составляют основу для различных методов сжатия. Вы также можете найти разложение по сингулярным значениям, которое дает нам хороший (хотя и дорогой) способ сделать аппроксимации матрицы низкого ранга, что позволяет сжимать.

С точки зрения решения линейной системы, когда квадратная матрица имеет недостаточный ранг, это означает, что у нас нет полной информации о системе, следовательно, мы не можем решить систему.

Ранг матрицы | Реальная статистика с использованием Excel

Определение 1 : Ранг матрицы A , обозначенный рангом ( A ), является максимальным количеством независимых строк в A .

Наблюдение : Здесь мы рассматриваем каждую строку в матрице A как вектор-строку. Таким образом, rank( A ) = размерность диапазона набора строк в A (см. Определение 2 линейных независимых векторов). Для m  ×  n матрица A , четко ранг( A ) ≤ m .

Получается, что ранг матрицы A также равен рангу столбца, т.е. максимальному количеству независимых столбцов в A

(по свойству 1). Таким образом, если A является матрицей размером m × n , то rank( A ) ≤ min( m , n ). Это также означает, что rank( A ) = размер промежутка строк в A = размер промежутка столбцов в A (см. Определение 3 линейных независимых векторов).

Свойство 1 : для любой матрицы A rank( A ) = максимальное количество независимых столбцов в A .

Доказательство: пусть A будет m  ×  n матрицей, и пусть p = ранг столбца A , то есть максимальное количество независимых векторов-столбцов в A . Теперь пусть C ₁ , …, C _p любая основа для размаха векторов-столбцов в A . Таким образом, любой столбец

A _j в A может быть однозначно выражен как линейная комбинация базовых элементов, и поэтому существуют b _ij такие, что A _i  = . Таким образом, A = CB , где C — это матрица размером m × p , столбцы которой равны C ₁ , …, C _p  и B = [ b _ij ], a p  ×  n  матрица.

Поскольку A = CB , каждая строка в A может быть выражена как линейная комбинация строк в B , а именно . Это означает, что диапазон строк в A является подмножеством диапазона строк в B , а rank( A ) ≤ rank( B ) ≤ p = ранг столбца A .

Применяя аналогичный аргумент к A ^T , мы заключаем, что rank( A ^T ) ≤ ранга столбца A ^T . Но явно ранг ( A ^T ) = ранг столбца A и ранг столбца A ^T = ранг ( A ). Таким образом, мы заключаем, что ранг столбца A ≤ rank( A ). Объединение обоих выводов вместе доказывает, что ранг ( A ) = ранг столбца А .

Наблюдение : поскольку каждое из преобразований, описанных в свойстве 9 одновременных линейных уравнений (т. е. преобразование в методе исключения Гаусса), не изменяет количество независимых строк в матрице, ранг матрицы A равен количество ненулевых строк, оставшихся после применения исключения Гаусса.

Свойство 2 : Квадратная матрица n  ×  n обратима тогда и только тогда, когда ее ранг равен п .

Доказательство: как было замечено непосредственно перед примером 9 в Simultaneous Linear Equations, мы можем использовать исключение Гаусса, чтобы инвертировать квадрат n  ×  n  матрицы A. Процедура дает обратную тогда и только тогда, когда ранг A это n .

Наблюдение : Это означает, что квадратная матрица A обратима тогда и только тогда, когда ее строки линейно независимы. Поскольку квадратная матрица обратима тогда и только тогда, когда обратима ее транспонированная форма, это также означает, что матрица обратима тогда и только тогда, когда ее столбцы линейно независимы.

Наблюдение : поскольку исключение Гаусса сохраняет ранг матрицы, мы можем переформулировать выводы, сделанные в разделе «Одновременные линейные уравнения» относительно решений одновременных линейных уравнений, в следующем свойстве.

Собственность 3 : для матрицы м × n A и M × 1 Вектор колонны C , если ранг ( A | C ) = Ранг ( A ) = N тогда уравнение AX = C имеет единственное решение. Если ранг( A|C ) = rank( A ) < n существует бесконечное число решений, и если rank( A|C ) > rank( A ), решений нет.

В случае, когда C = 0, AX = 0 имеет единственное решение, а именно тривиальное решение X = 0, когда rank( A ) = n и бесконечное число решений в противном случае .

Свойство 4 : Следующие эквивалентны для n × n матрица A :

• A обратим
• от А ≠ 0
• X = 0 является единственным решением AX = 0
• AX = C имеет единственное решение для всех n  × 1 векторов C
• ранг( А ) = n

Доказательство. Это комбинация свойств 2 и 3 и свойства 4 определителей и одновременных линейных уравнений.

Наблюдение : Обратите внимание, что если AX = C имеет единственное решение для некоторого n 1 × 1 вектор-столбца C , то по свойству 3 ранг( A ) = n 0 и, следовательно, по свойству 900 2, A является обратимым. И наоборот, если A обратимо, то для любого n × 1 вектор-столбец C , X = A ^-1 C = 3 90 C 9002.

Наблюдение : Поскольку матрица n × n A обратима тогда и только тогда, когда rank( A ) = n , из следствия 4 из линейных независимых векторов следует, что строки в A образуют базис для набора всех 1 × n векторов-строк. Точно так же столбцы в A образуют основу для набора всех векторов-столбцов n ×  1.

Свойство 5 : Для квадратной матрицы A , если существует матрица B такая, что AB = I или BA = I , то A обратима и A ^-1 = B .

Доказательство. Предположим сначала, что существует квадратная матрица B такая, что BA  = I . Теперь, если AX = 0, то X = IX = ( BA ) X = B ( AX ) = B 9009,0.0029 AX = 0 имеет только тривиальное решение X = 0, что по свойству 4 означает, что A обратимо, а A ^-1 существует. Thus, B  = BI = B ( AA ^-1 ) = ( BA ) A ^-1 = IA ^-1 = A ^-1 , и поэтому B = A ^-1

Теперь предположим, что AB = I . По приведенному выше результату мы заключаем, что B обратим и A = B ^-1 . Но тогда AB = I = BA , и по определению 5 матричных операций A обратимо и A ^-1 = B .