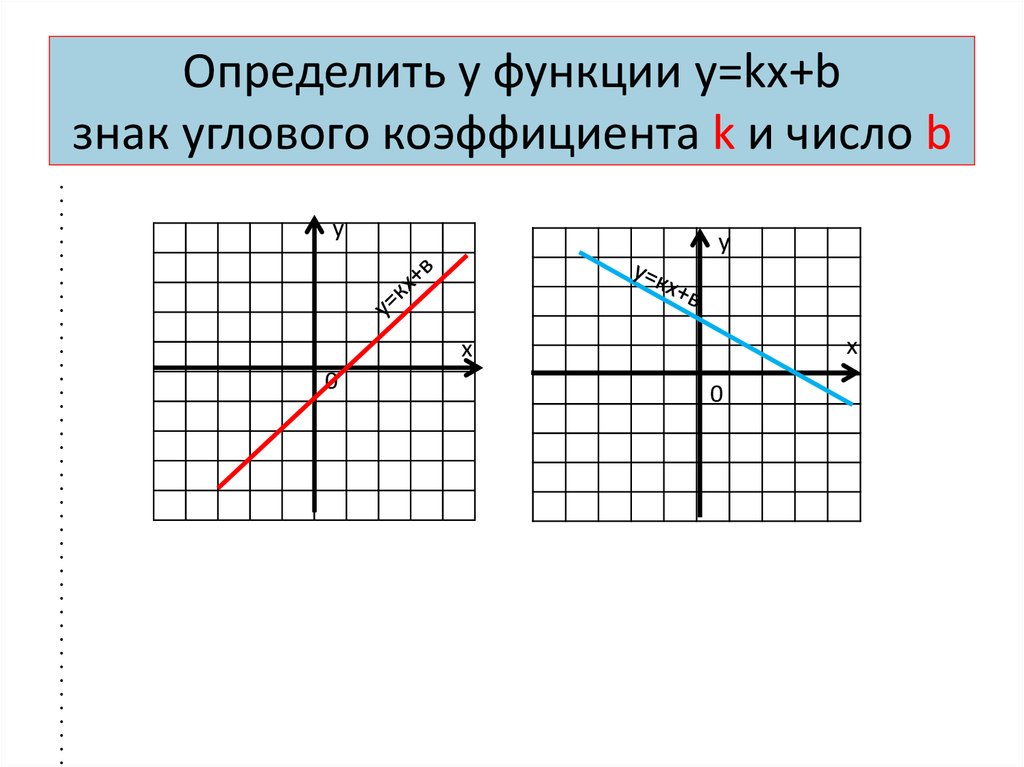
Как найти k и b по графику линейной функции?
В новой 9 задаче профильного ЕГЭ много заданий на линейные функции. Самое сложное, что нужно сделать, решая эти задачи – определить формулу линейной функции, т.е. найти \(k\) и \(b\) по графику. Примеры таких заданий (решения будут внизу статьи):
В статье я расскажу про два простых способа найти \(k\) и \(b\), если известен график линейной функции.
Способ 1
Первый способ основывается на трех фактах:
-
Линейная функция пересекает ось \(y\) в точке \(b\).
Примеры:Но не советую определять так \(b\), если прямая пересекает ось не в целом значении или если точка пересечения вообще не видна на графике. Для таких случаев пользуйтесь вторым способом.
Примеры:
-
Если функция возрастает, то знак коэффициента \(k\) плюс, если убывает – минус, а если постоянна, то \(k=0\).

Примеры:
-
Чтоб конкретнее определить \(k\) надо построить на прямой прямоугольный треугольник так, чтобы гипотенуза лежала на графике функции, а вершины треугольника совпадали с вершинами клеточек. Далее, чтоб определить \(k\) нужно вертикальную сторону треугольника поделить на горизонтальную и поставить знак согласно возрастанию/убыванию функции.
Примеры:
Пример (ЕГЭ)
Давайте пока что не будем искать формулу иррациональной функции, сосредоточимся только на линейной функции.
\(b=3\) – это сразу видно. Функция идет вниз, значит \(k<0\).
Достроим прямую до прямоугольного треугольника. Вершинами будут жирные точки, которые нам дали в задаче.
\(k=-\frac{AC}{BC}=-\frac{1}{3}\).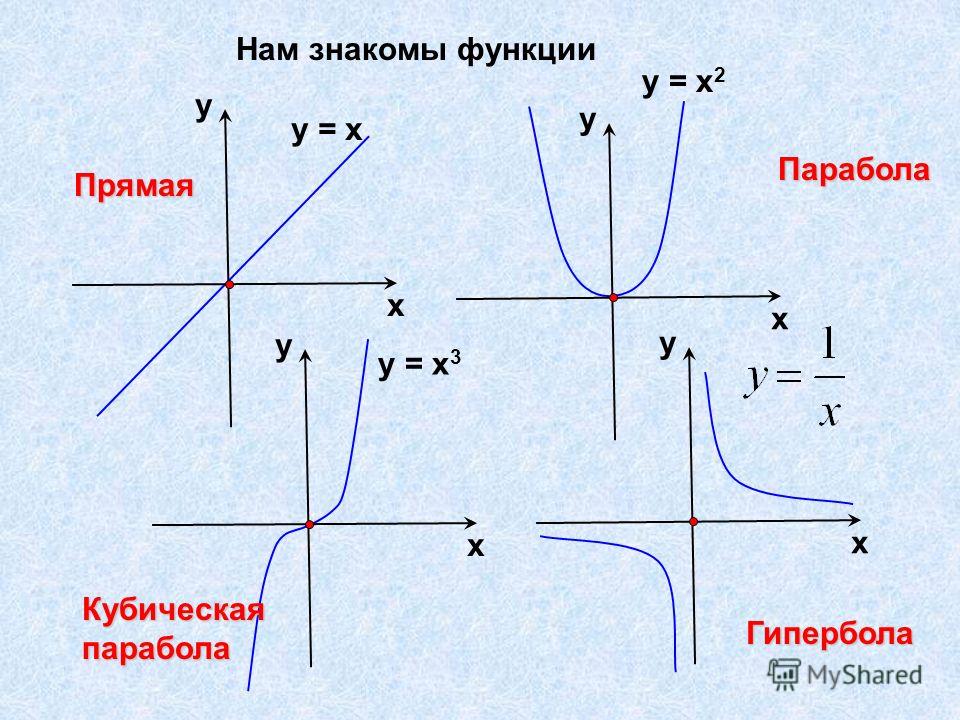 Получается \(g(x)=-\frac{1}{3}x+3\).
Получается \(g(x)=-\frac{1}{3}x+3\).
Способ 1 быстрее способа 2, но не во всех ситуациях помогает. Поэтому важно владеть и вторым способом тоже.
Способ 2
Вы обращали внимание, что в задачах ЕГЭ на прямых всегда жирно выделяют 2 точки? Так вот, чтобы найти формулу линейной функции, достаточно подставить координаты этих точек в формулу \(f(x)=kx+b\) и решить получившуюся систему уравнений.
Пример (ЕГЭ)
Обозначим жирные точки какими-нибудь буквами и найдем их координаты.
\(A(-2;2)\) и \(B(2;-5)\) подставим эти значения вместо \(x\) и \(f(x)\) в формулу \(f(x)=kx+b\):
Получим:
\(\begin{cases}2=-2k+b\\-5=2k+b\end{cases}\)
Теперь найдем \(k\) и \(b\), решив эту систему.
Для этого сложим уравнения друг с другом, чтобы исчезло \(k\):
\(2+(-5)=-2k+b+2k+b\)
\(-3=2b\)
\(b=-1,5\)
Теперь подставим найденное \(b\) во второе уравнение системы и найдем \(k\):
\(-5=2k-1,5\)
\(-5+1,5=2k\)
\(-3,5=2k\)
\(k=-1,75\)
Получается \(f(x)=-1,75x-1,5\).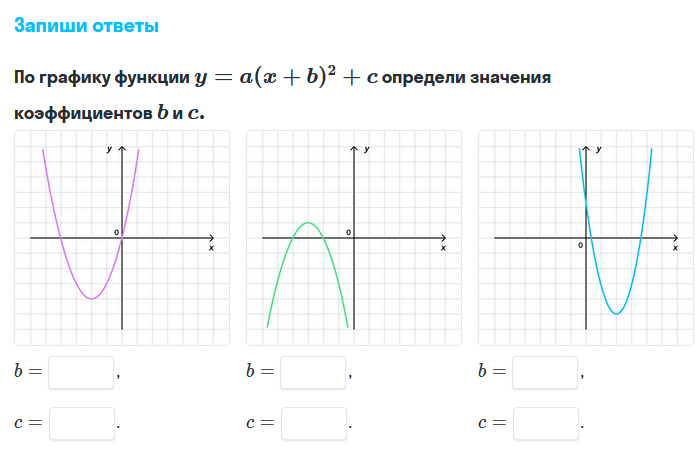 Остается последний шаг – вычислим при каком иксе функция, то есть \(f(x)\), равна \(16\):
Остается последний шаг – вычислим при каком иксе функция, то есть \(f(x)\), равна \(16\):
\(16=-1,75x-1,5\)
\(17,5=-1,75x\)
\(x=-10\).
Ответ: \(-10\).
Пример (ЕГЭ)
Чтоб решить задачу, нам понадобятся формулы каждой из двух функций. Давайте формулу нижней функции найдем с помощью способа 1, а формулу верхней с помощью способа 2. Начнем с нижней функции.
Функция \(f(x)\) возрастает, значит \(k>0\). \(k=+\frac{AC}{BC}=\frac{4}{4}=1,b=1\). \(f(x)=x+1\).
Теперь перейдем к функции \(g(x)\). Найдем координаты точек \(D\) и \(E\): \(D(-2;4)\), \(E(-4;1)\). Можно составить систему:
\(\begin{cases}4=-2k+b\\1=-4k+b\end{cases}\)
Вычтем второе уравнение из первого, чтоб убрать \(b\):
\(4-1=-2k+b-(-4k+b)\)
\(3=2k\)
\(k=1,5\)
Найдем \(b\):
\(4=-2\cdot 1,5+b\)
\(4=-3+b\)
\(b=7\)
\(g(x)=1,5x+7\).
\(x+1=1,5x+7\)
\(x-1,5x=7-1\)
\(-0,5x=6\)
\(x=6:(-0,5)\)
\(x=-12\).
Ответ: \(-12\).
Картинку в хорошем качестве, можно скачать нажав на кнопку «скачать статью».
Смотрите также:
Как определить a, b и c по графику параболы
Скачать статью
Алгебра. Урок 5. Графики функций
Смотрите бесплатные видео-уроки на канале Ёжику Понятно по теме “Графики функций”.
Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
- Декартова система координат
- Функция
Прямая
Парабола
Гипербола
Квадратный корень
- Возрастающая/убывающая функция
- Наибольшее/наименьшее значение функции
- Примеры решений заданий из ОГЭ
Система координат – это две взаимно перпендикулярные координатные прямые, пересекающиеся в точке, которая является началом отсчета для каждой из них.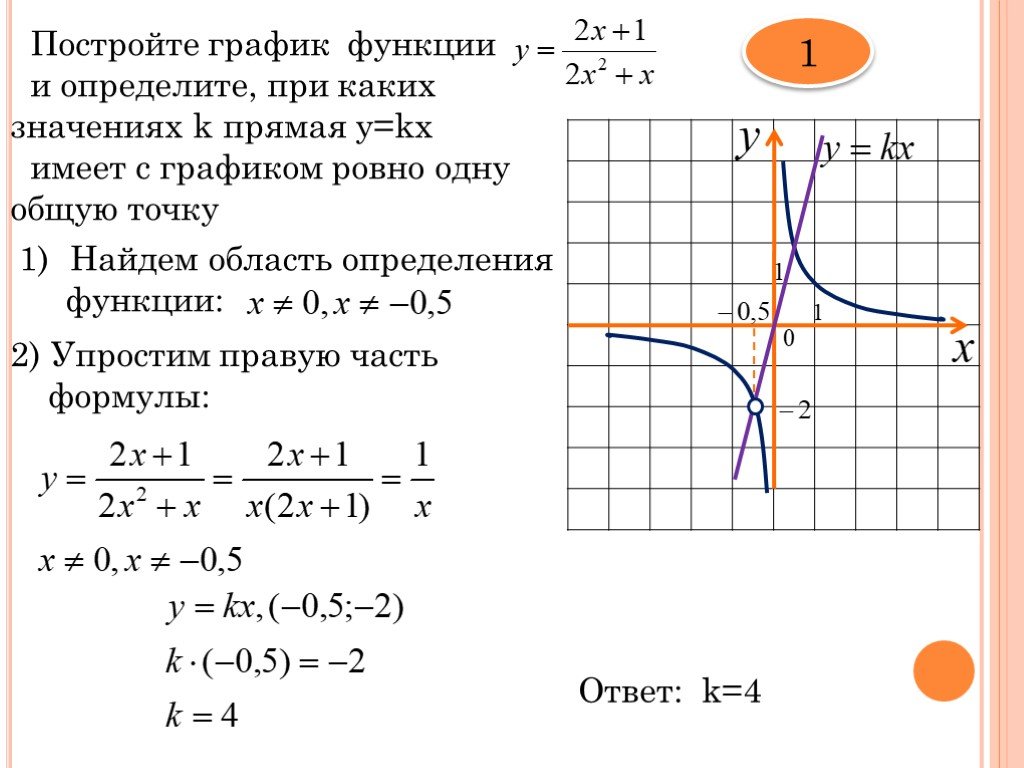
Координатные оси – прямые, образующие систему координат.
Ось абсцисс (ось x ) – горизонтальная ось.
Ось ординат (ось y ) – вертикальная ось.
Функция – это отображение элементов множества X на множество Y. При этом каждому элементу x множества X соответствует одно единственное значение y множества Y.
Линейная функция – функция вида y=ax+b где a и b – любые числа.
Графиком линейной функции является прямая линия.
Рассмотрим, как будет выглядеть график в зависимости от коэффициентов a и b:
Если a>0, прямая будет проходить через I и III координатные четверти.
b – точка пересечения прямой с осью y.
Если a<0, прямая будет проходить через II и IV координатные четверти.
b – точка пересечения прямой с осью y.
Если a=0, функция принимает вид y=b.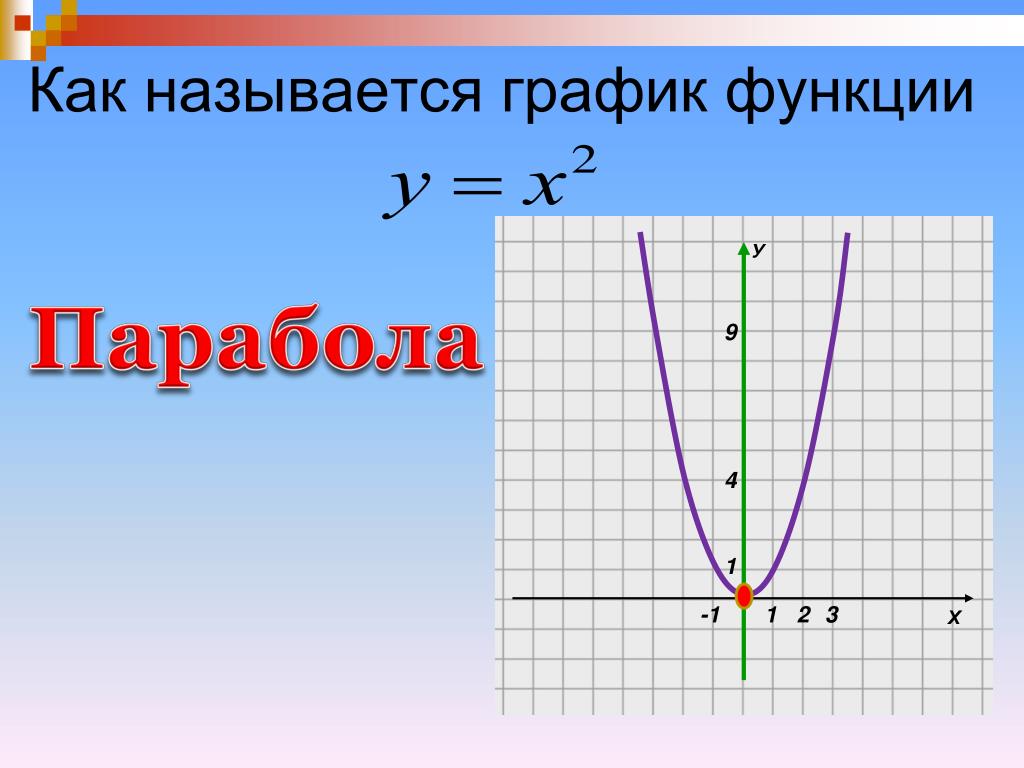
Отдельно выделим график уравнения x=a.
Важно: это уравнение не является функцией так как нарушается определение функции (функция ставит в соответствие каждому элементу x множества X одно единственно значение y множества Y). Данное уравнение ставит в соответствие одному элементу x бесконечное множества элементов y. Тем не менее, график данного уравнения построить можно. Просто не будем называть его гордым словом «Функция».
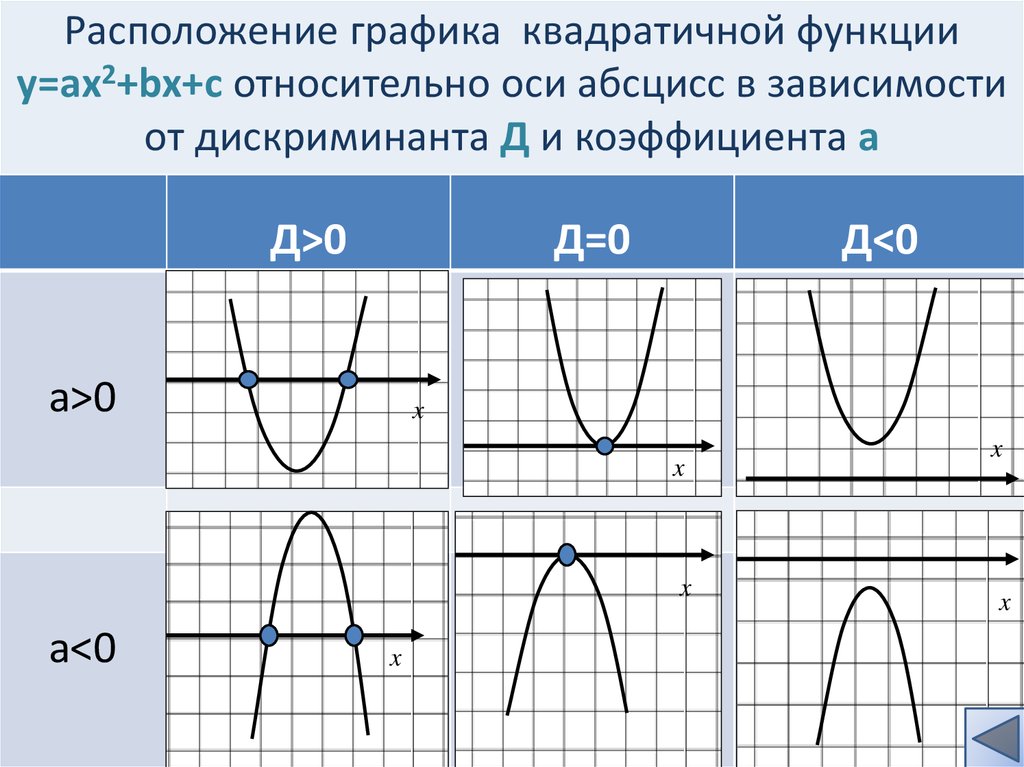
Графиком функции y=ax2+bx+c является парабола.
Для того, чтобы однозначно определить, как располагается график параболы на плоскости, нужно знать, на что влияют коэффициенты a,b,c:
- Коэффициент a указывает на то, куда направлены ветки параболы.
- Если a>0 , ветки параболы направлены вверх.
- Если a<0 , ветки параболы направлены вниз.
- Коэффициент c указывает, в какой точке парабола пересекает ось y.
- Коэффициент b помогает найти xв – координату вершины параболы.

xв=−b2a
- Дискриминант позволяет определить, сколько точек пересечения у параболы с осью .
- Если D>0 – две точки пересечения.
- Если D=0 – одна точка пересечения.
- Если D<0 – нет точек пересечения.
Графиком функции y=kx является гипербола.
Характерная особенность гиперболы в том, что у неё есть асимптоты.
Асимптоты гиперболы – прямые, к которым она стремится, уходя в бесконечность.
Ось x – горизонтальная асимптота гиперболы
Ось y – вертикальная асимптота гиперболы.
На графике асимптоты отмечены зелёной пунктирной линией.
Если коэффициент k>0, то ветви гиперолы проходят через I и III четверти.
Если k < 0, ветви гиперболы проходят через II и IV четверти.
Чем меньше абсолютная величина коэффиента k (коэффициент k без учета знака), тем ближе ветви гиперболы к осям x и y.
Функция y = x имеет следующий график:
Функция y = f(x)возрастает на интервале, если большему значению аргумента (большему значению x) соответствует большее значение функции (большее значение y).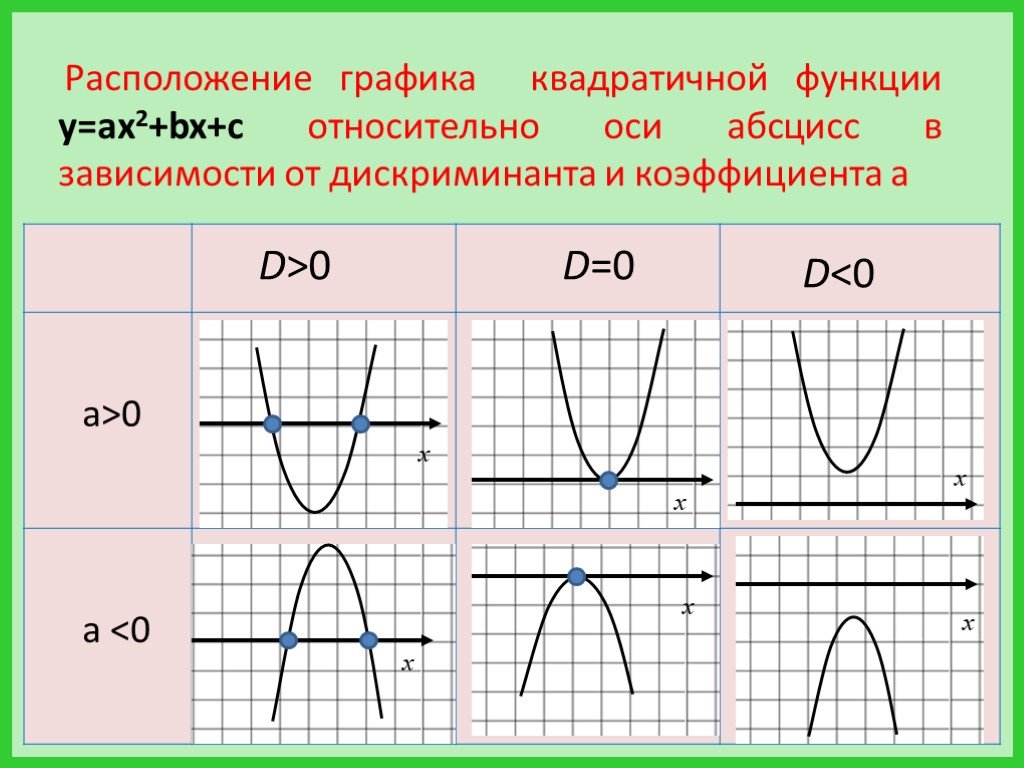
То есть чем больше (правее) икс, тем больше (выше) игрек. График поднимается вверх (смотрим слева направо)
Примеры возрастающих функций:
Функция y = f(x)убывает на интервале, если большему значению аргумента (большему значению x) соответствует меньшее значение функции (большее значение y).
То есть чем больше (правее) икс, тем меньше (ниже) игрек. График опускается вниз (смотрим слева направо).
Примеры убывающих функций:
Для того, чтобы найти наибольшее значение функции, находим самую высокую точку на графике и смотрим, какая у нее координата по оси ординат (по оси y). Это значение и будет являться наибольшим значением функции.
Для того, чтобы найти наименьшее значение функции, находим самую нижнюю точку на графике и смотрим, какая у нее координата по оси ординат (по оси y). Это значение и будет являться наименьшим значением функции.
Скачать домашнее задание к уроку 5.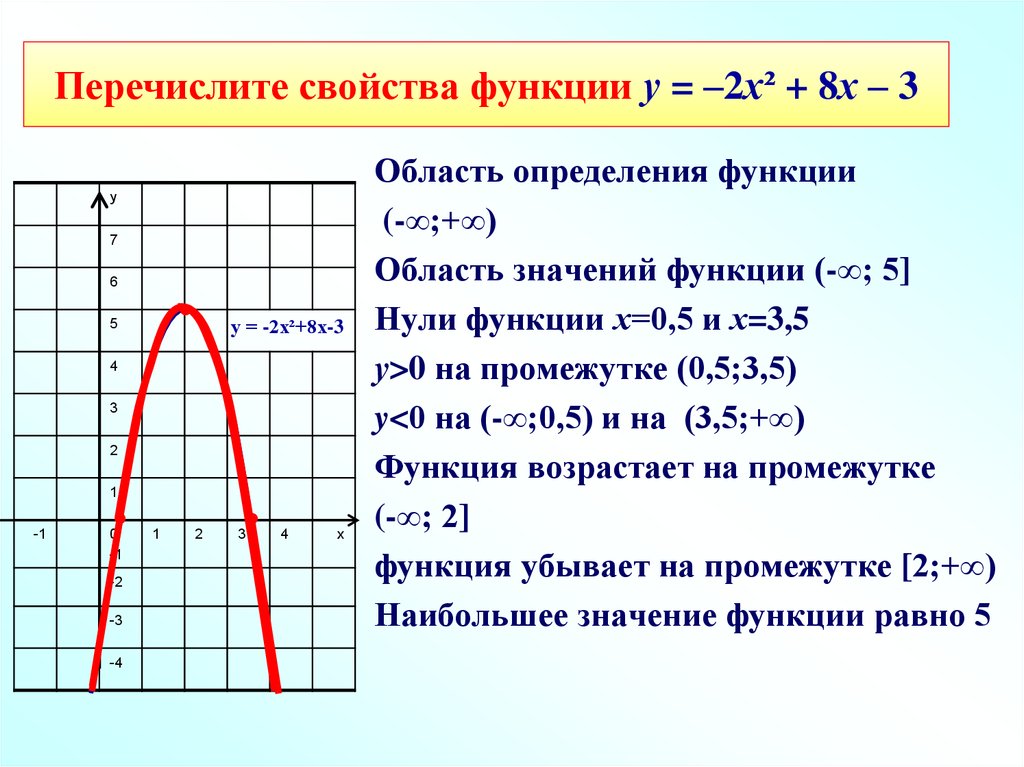
Отношения и определение того, является ли отношение функцией — Задача 3
Используйте тест вертикальной линии, чтобы определить, представляет ли график функцию. Если вертикальная линия перемещается по графику и в каждый момент времени касается графика только в одной точке, то график является функцией. Если вертикальная линия касается графика более чем в одной точке, то график не является функцией.
домен диапазон вход выход функция связь тест вертикальной линии
Одна из замечательных особенностей функций заключается в том, что мы знаем, что что-то является функцией, если каждый x имеет ровно один y, но иногда вам не дают баллы, вам не дают числа, все, что вам дают, это забавный график.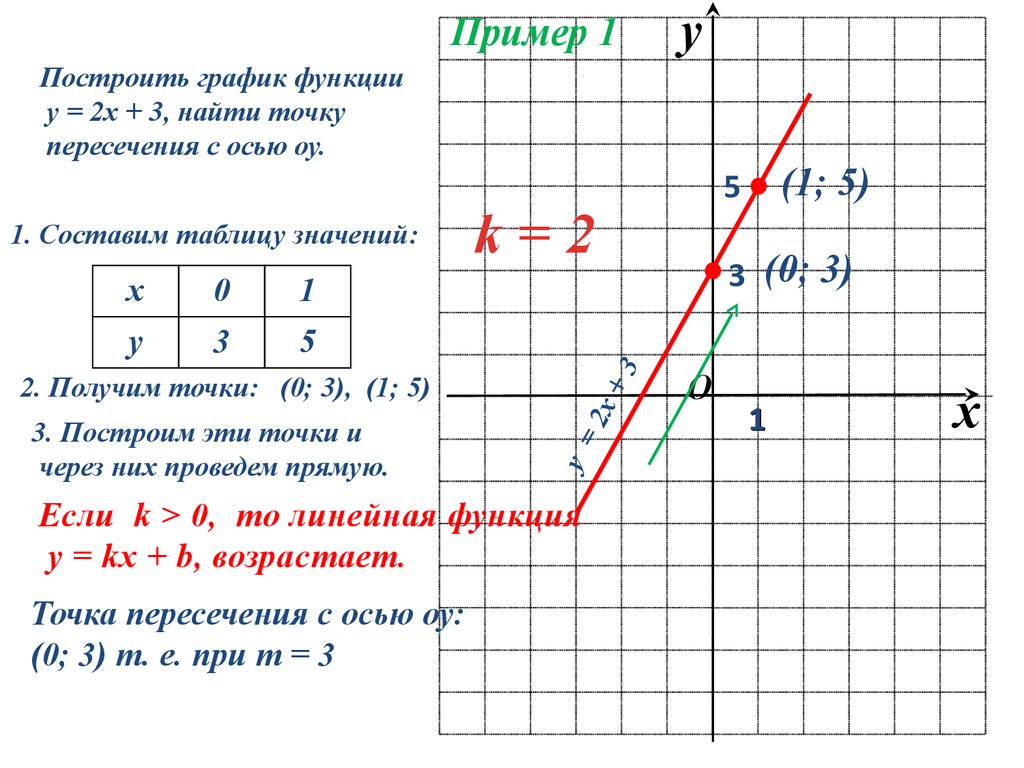 Итак, о чем я хочу поговорить здесь, так это о том, как вы можете сказать, что что-то является функцией, просто основываясь на графике, и вы увидите, что это на самом деле довольно просто. Он использует так называемый тест вертикальной линии.
Итак, о чем я хочу поговорить здесь, так это о том, как вы можете сказать, что что-то является функцией, просто основываясь на графике, и вы увидите, что это на самом деле довольно просто. Он использует так называемый тест вертикальной линии.
Итак, что я собираюсь сделать, так это просмотреть эти графики и нарисовать вертикальные линии, и если они совпадают, если моя вертикальная линия пересекается с графиком более одного раза в каждой строке, тогда это не функция, потому что это представляет место, где значение x имеет два значения y.
Давайте проверим. Думайте об этом как о своем карандаше, это большой карандаш. Что бы вы сделали с графиком на бумаге, так это возьмите свой карандаш, положите его туда, а затем проведите им по графику, посмотрите, не попали ли вы в какие-либо места на этом графике, где ваш карандаш пересекает волнистую линию более чем в одном месте. И вы увидите на этом графике множество мест, посмотрите.
Я просто попал в свой график, например, раз, два, три, четыре, например, 10 раз, что бы это ни было, не имеет значения, я попал в него более одного раза, так что это не функция.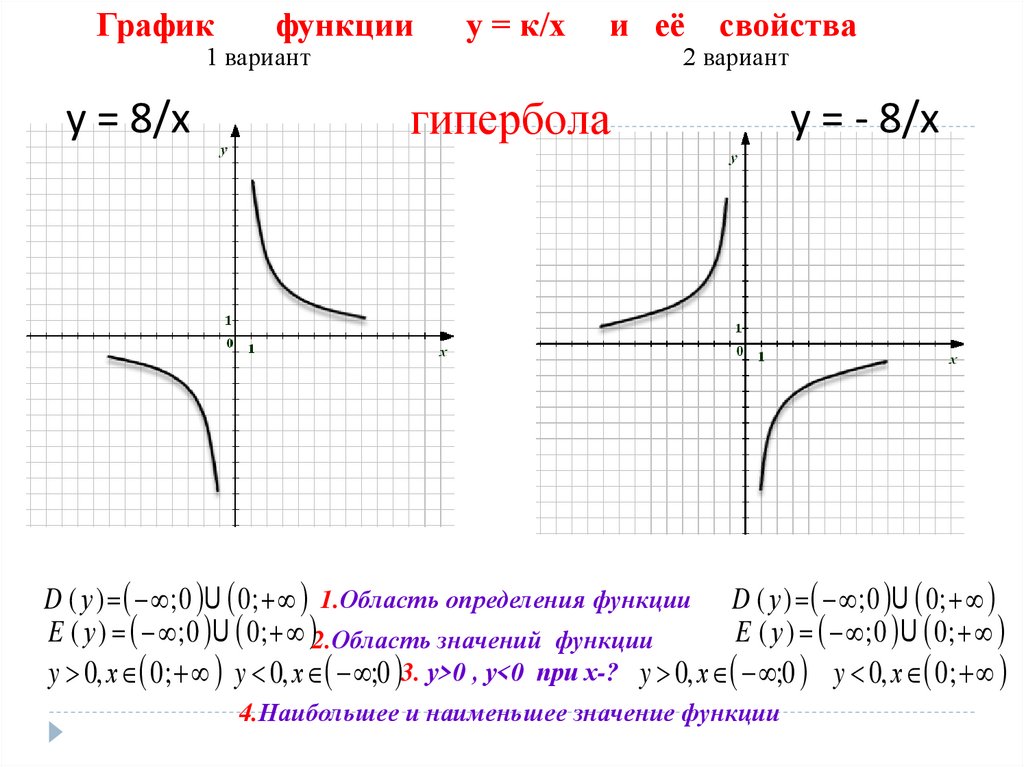 Это значение x прямо здесь, что бы оно ни было, имеет множество значений y, есть значение y, есть еще одно, нет никого, это не функция. Каждый x получает только одно значение y.
Это значение x прямо здесь, что бы оно ни было, имеет множество значений y, есть значение y, есть еще одно, нет никого, это не функция. Каждый x получает только одно значение y.
Давайте попробуем нарисовать следующий график с помощью карандаша и убедитесь, что он вертикальный, а не горизонтальный. Вертикаль о-о! Вы можете видеть, как карандаш попадает в те места, где вертикальная линия пересекает график более чем в одном месте. Это снова означает, что x имеет два значения y, а не функцию.
Вот пара, которые немного отличаются, когда вы используете тест вертикальной линии здесь. Проверьте это, куда бы я ни двигал пером, оно пересекает график правильно только один раз, я никогда не попадаю на эту линию графика более одного раза. Итак, в этом случае да, это функция, потому что это значение x имеет только одно значение y.
Здесь очень похоже, когда я использую перо и перемещаю его вертикально по графику, я нигде не нажимаю на фигуру дважды, я нажимаю только один раз, поэтому d, да, это тоже функция.
Если вы больше ничего не помните из этого видео, надеюсь, вы помните тест на вертикальную линию. Если график проходит тест вертикальной линии, то это функция. Под этим я подразумеваю, что если вы двигаете ручкой, и она нажимает только один раз, то да, это функция, если она нажимает более одного раза, нет, это не функция.
Лично мне нравятся эти задачи. Я думаю, что они не слишком сложны и в них нет чисел, так что это круто.
Используйте график, чтобы определить, где функция увеличивается, уменьшается или остается постоянной | Колледж Алгебра |
Скорость изменения и поведение графиков
В рамках изучения того, как изменяются функции, мы можем определить интервалы, в течение которых функция изменяется определенным образом. Мы говорим, что функция возрастает на интервале, если значения функции увеличиваются по мере увеличения входных значений в этом интервале. Точно так же функция убывает на интервале, если значения функции уменьшаются по мере увеличения входных значений на этом интервале.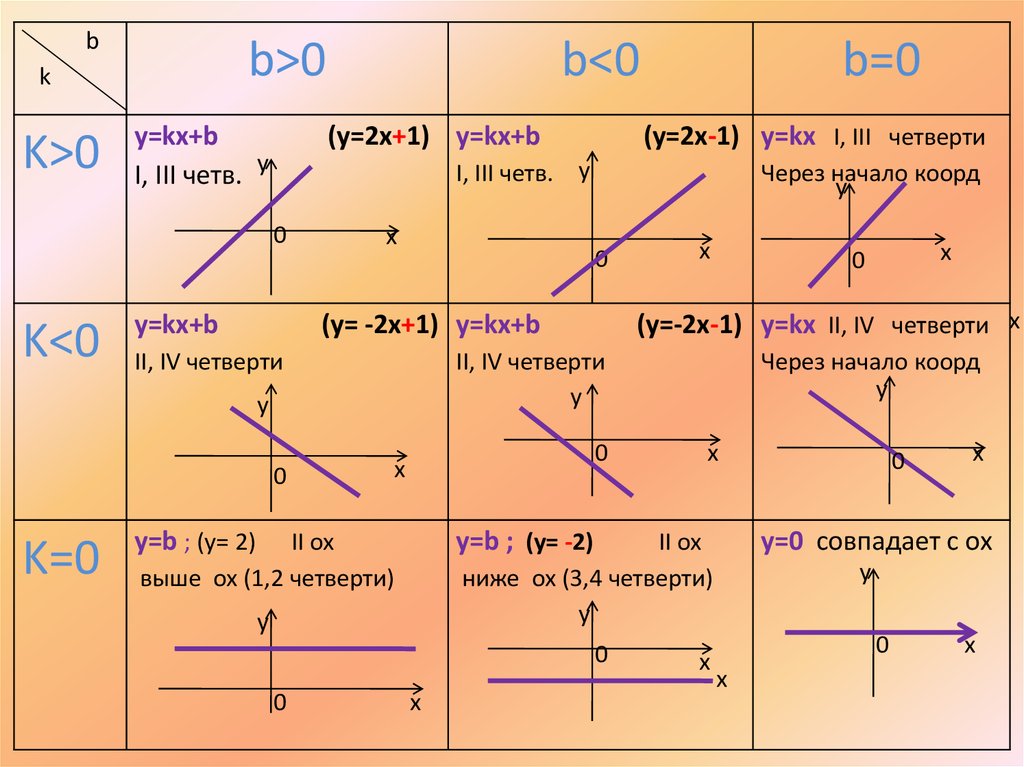
и уменьшается на
(−2,2)\left(-2\text {,}2\справа)(−2,2)
. В этом видео также объясняется, как найти, где функция увеличивается или уменьшается.
В то время как некоторые функции возрастают (или убывают) во всей своей области, многие другие нет. Значение входа, при котором функция изменяется с возрастающей на убывающую (по мере движения слева направо, то есть по мере увеличения входной переменной), называется локальный максимум
 Форма множественного числа — «локальные минимумы». Вместе локальные максимумы и минимумы называются локальными экстремумами или локальными экстремальными значениями функции. (Форма единственного числа — «экстремум».) Часто термин местный заменяется термином относительный 9.0058 . В этом тексте мы будем использовать термин локальный .
Форма множественного числа — «локальные минимумы». Вместе локальные максимумы и минимумы называются локальными экстремумами или локальными экстремальными значениями функции. (Форма единственного числа — «экстремум».) Часто термин местный заменяется термином относительный 9.0058 . В этом тексте мы будем использовать термин локальный .Ясно, что функция не возрастает и не убывает на интервале, где она постоянна. Функция также не возрастает и не убывает в экстремумах. Обратите внимание, что мы должны говорить о локальных экстремумах, потому что любой данный локальный экстремум, как определено здесь, не обязательно является самым высоким максимумом или самым низким минимумом во всей области определения функции.
Для функции на рисунке 4 локальный максимум равен 16, и он приходится на
х=-2х=-2х=-2
. Локальный минимум равен
Локальный минимум равен
−16-16−16
и приходится на
x=2x=2x=2
.
Рисунок 4
Чтобы найти локальные максимумы и минимумы на графике, нам нужно наблюдать за графиком, чтобы определить, где график достигает своей самой высокой и самой низкой точки, соответственно, в пределах открытого интервала. Подобно вершине американских горок, график функции в локальном максимуме выше, чем в соседних точках с обеих сторон. График также будет ниже в локальном минимуме, чем в соседних точках. Рисунок 5 иллюстрирует эти идеи для локального максимума.
Рис. 5. Определение локального максимума.
Эти наблюдения приводят нас к формальному определению локальных экстремумов.
A Общее примечание: локальные минимумы и локальные максимумы
Функция
fff
является возрастающей функцией на открытом интервале, если >f\left(a\right)f(b)>f(a)
для любых двух входных значений
aaa
и
bbb
в заданном интервале, где
б>аб>аб>а
.
Функция
fff
является убывающей функцией на открытом интервале, если
f(b)
для любых двух входных значений
aaa
и
bbb
в заданном интервале, где
b>ab>ab>a
.
Функция
fff
имеет локальный максимум на
x=bx=bx=b
, если существует интервал
(a,c)\left(a,c\right)(a,c)
с
a
такое, что для любого
xxx
в интервале
(a,c)\left(a,c\right)(a,c)
,
f(x) ≤f(b)f\влево(x\вправо)\le f\влево(b\вправо)f(x)≤f(b)
. Аналогично,
Аналогично,
fff
имеет локальный минимум в точке
x=bx=bx=b
, если существует интервал
(a,c)\left(a,c\right)(a,c)
с
a
такое, что для любого
xxx
в интервале
(a,c)\left(a,c\right)(a,c)
,
f(x)≥f(b)f\left(x\right)\ge f \left(b\right)f(x)≥f(b)
.
Пример 7. Поиск возрастающих и убывающих интервалов на графике
Учитывая функцию
p(t)p\left(t\right)p(t)
на графике ниже, определите интервалы, на которых функция кажется возрастающей.
Рисунок 6
Решение
Мы видим, что функция не является постоянной на любом интервале.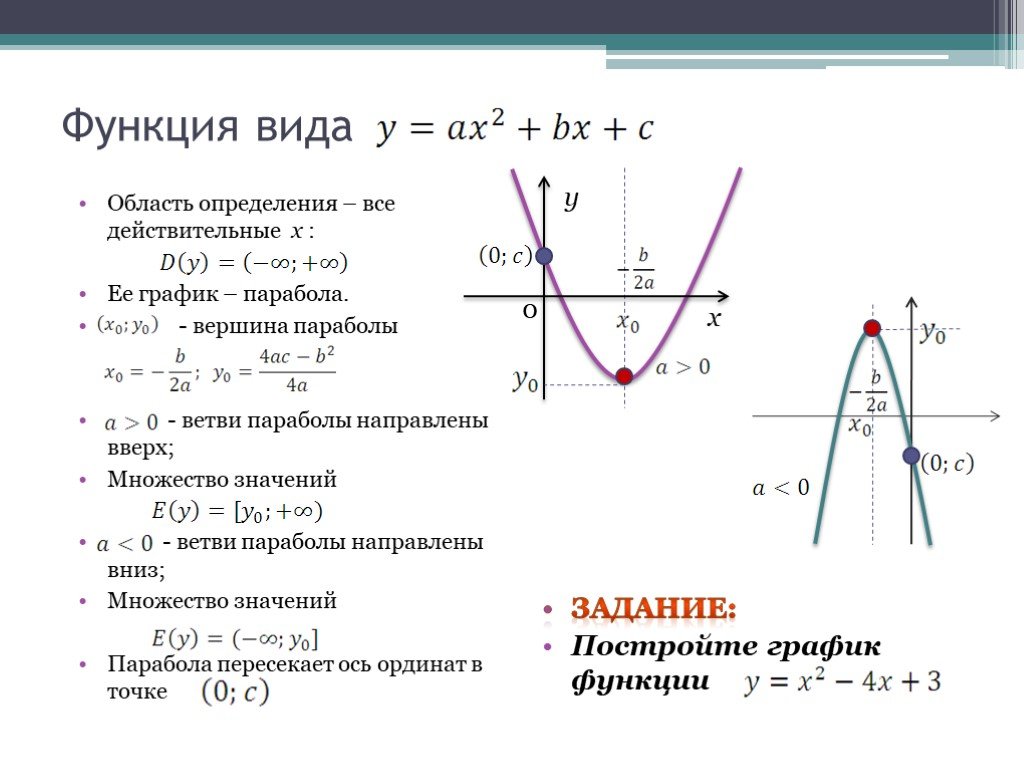 Функция увеличивается там, где она наклонена вверх, когда мы движемся вправо, и уменьшается там, где она наклонена вниз, когда мы двигаемся вправо. Функция увеличивается с
Функция увеличивается там, где она наклонена вверх, когда мы движемся вправо, и уменьшается там, где она наклонена вниз, когда мы двигаемся вправо. Функция увеличивается с
t=1t=1t=1
до
t=3t=3t=3
и с
t=4t=4t=4
.
В обозначении интервала мы бы сказали, что функция возрастает на интервале (1,3) и интервале
(4,∞)\влево(4,\infty \вправо)(4,∞)
.
Пример 8. Нахождение локальных экстремумов на графике
График функции
f(x)=2x+x3f\left(x\right)=\frac{2}{x}+\frac{x}{3 }f(x)=x2+3x
. Затем используйте график, чтобы оценить локальные экстремумы функции и определить интервалы, на которых функция возрастает.
Раствор
Используя технологию, мы обнаруживаем, что график функции выглядит так, как показано на рисунке 7.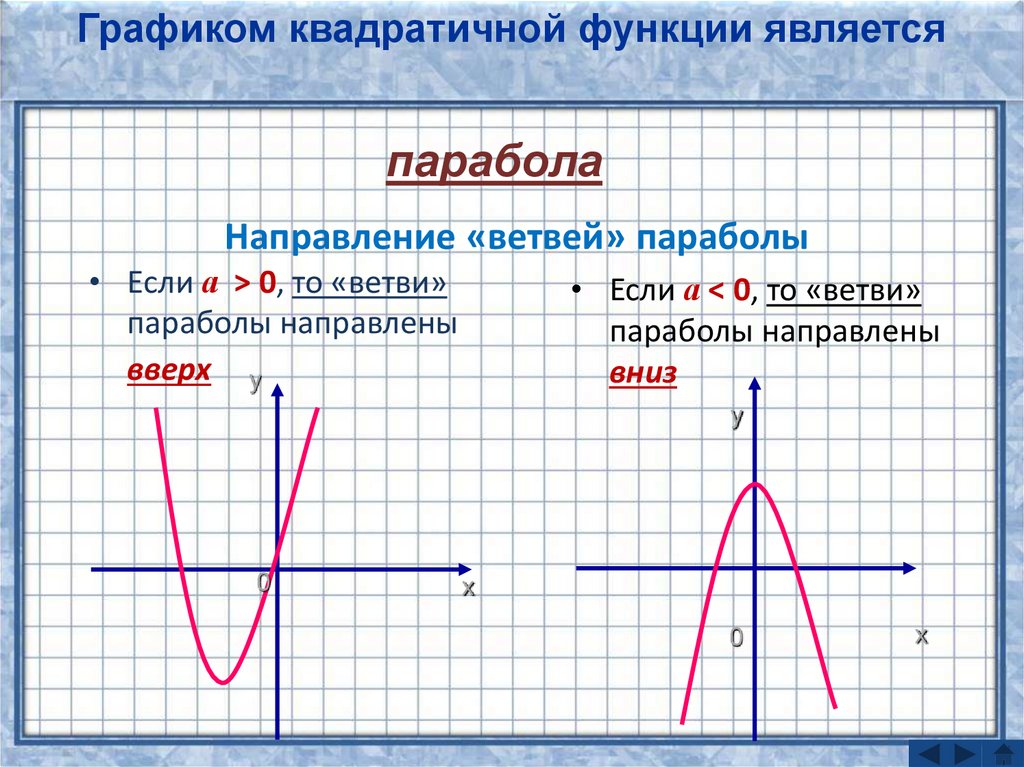 Похоже, что существует нижняя точка или локальный минимум между 9{2}-15x+20\\f(x)=x3−6×2−15x+20
Похоже, что существует нижняя точка или локальный минимум между 9{2}-15x+20\\f(x)=x3−6×2−15x+20
для оценки локальных экстремумов функции. Используйте их, чтобы определить интервалы, на которых функция увеличивается и уменьшается. Решение
Пример 9. Поиск локальных максимумов и минимумов на графике
Для функции
fff
, график которой показан на рисунке 9, найти все локальные максимумы и минимумы.
Рисунок 9
Решение
См. график
fff
. График достигает локального максимума на
x=1x=1x=1
, потому что это самая высокая точка в открытом интервале около
x=1x=1x=1
. Локальным максимумом является
yyy
-координата
x=1x=1x=1
, что равно
222
.
График достигает локального минимума в точке
x=−1 \text{ }x=-1\text{ } x=−1
, поскольку это самая нижняя точка открытого интервала около
х=-1х=-1х=-1
. Локальным минимумом является y -координата
x=-1x=-1x=-1
, что равно
-2-2-2
.
Теперь мы вернемся к функциям нашего инструментария и обсудим их графическое поведение в таблице ниже. 9{2}}f(x)=x21| Функция | Увеличение/уменьшение | Пример |
|---|---|---|
| Постоянная функция f(x)=cf\left(x\right)={c}f(x)=c | По возрастанию (−∞,0)\left(-\infty,0\right)(−∞,0) По убыванию (0,∞)\left(0,\infty\right)(0, ∞) | |
| Кубический корень f(x)=x3f\left(x\right)=\sqrt[3]{x}f(x)=3x
| Увеличение | |
| Квадратный корень f(x)=xf\left(x\right)=\sqrt{x}f(x)=x | Увеличение по (0,∞)\left(0,\infty\right)(0,∞) | |
| Абсолютное значение f(x)=∣x∣f\left(x\right)=|x|f(x)=∣x∣ | По возрастанию (0,∞)\left(0,\infty\right)(0,∞) По убыванию (−∞,0)\left(-\infty,0\right)(−∞, 0) |
Лицензии и атрибуции
Контент по лицензии CC, совместно используемый ранее
- Precalculus.