Метод подсчёта количества решений | by Iuliia Averianova | NOP::Nuances of Programming
Линейные алгебраические уравнения — одни из самых простых уравнений, которые мы можем решить. Если в уравнении только одна переменная, решение тривиально, в то время как для системы линейных уравнений существует множество способов найти уникальные решения.
В этой статье нас интересует частный случай линейного уравнения с несколькими переменными. Хорошо известно, что подобное уравнение имеет бесконечное число решений. Мы наложим определённые ограничения и в значительной степени сократим количество решений.
Общая форма интересующего нас уравнения:
где n и m — положительные целые числа.
Наша задача — найти число решений этого уравнения, предполагая, что xᵢ являются целыми числами. Это предположение значительно снижает число решений заданного уравнения.
Давайте начнём с частного случая общего уравнения:
Нетрудно найти все решения этого уравнения методом простого счёта.
Мы видим, что уравнение имеет шесть решений. Также нетрудно предположить, что, если мы заменим правую часть определённым положительным целым числом m, решения будут выглядеть так:
и мы сможем подсчитать число решений — m+1.
Это было просто, верно?
Теперь возьмём немного более сложный вариант с тремя переменными, скажем:
С несколько большими усилиями, чем в предыдущем примере, находим решения в виде наборов из трёх чисел (x₁, x₂, x₃):
Число решений в этом случае равно 10.
Легко представить, что метод прямого счёта может стать очень утомительным для уравнения с большим количеством переменных. Он также становится утомительным, если целое число в правой части уравнения становится больше — например, если в правой части у нас будет 8, а не 3, решений будет уже 45. Разумеется, не хотелось бы искать все эти решения методом прямого счёта.
Значит, нужен эффективный метод.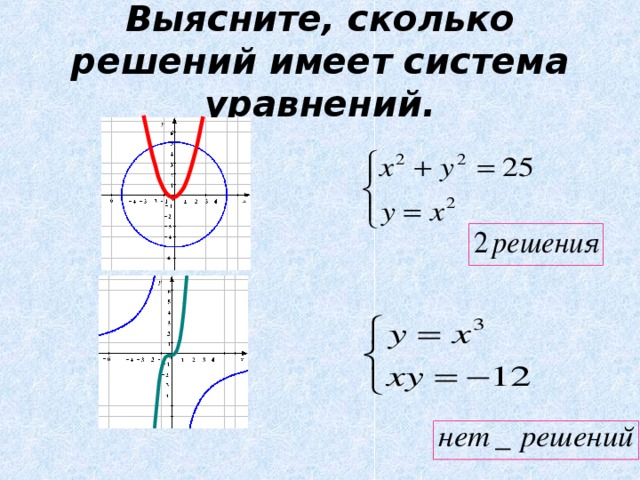
Существует ещё один способ, которым можно решить предыдущие два уравнения. Давайте снова начнём с этого уравнения:
Одним из решений было (5, 0). Давайте преобразуем его в:
Мы разложили решение на нули и единицы, соответствующие каждому числу. Ненулевую часть (в данном случае 5) мы разложили на соответствующее число единиц, а ноль преобразовали в ноль. Таким же образом мы можем разложить и другое решение:
Мы поменяли прежнее расположение нуля, чтобы получить новое решение. Итак, два числа в парах (обозначенные красным и голубым) разделены нулём (чёрный) в разложенном виде. Таким же образом запишем оставшиеся решения:
Записав решения таким образом, видим закономерность. Кажется, все решения — это просто перестановки нулей и единиц. Вопрос о том, сколько существует решений, становится эквивалентным вопросу
В данном случае у нас есть 6 местоположений в разложенной конфигурации для размещения нулей и единиц.
Мы можем выбрать простейшее решение в качестве начальной конфигурации:
Теперь всё, что нам нужно найти, это общее число способов, которыми можно заполнить шесть местоположений пятью единицами и одним нулём.
Подобные задачи подсчёта мы можем решить различными способами, но наиболее эффективным будет способ, разработанный в такой области математики как комбинаторика, которая даёт нам формулу для числа способов перестановки r объектов в n местоположений:
где n! (читается как “n факториал”) определяется как произведение всех целых чисел от 1 до n, т.е. n! =
1 × 2 × 3 × ⋅ ⋅ ⋅ × n. Мы также определяем 0! = 1.Эта формула обычно записывается в компактной форме как:
Теперь, возвращаясь к задаче, мы можем использовать эту формулу для нахождения числа способов перестановки пяти единиц в шести местоположениях:
Это то же самое число, что мы получили методом прямого счёта!
Выглядит многообещающе, поэтому давайте проверим, сможем ли мы найти таким способом число решений второго линейного уравнения:
Некоторые решения можно записать в разложенном виде:
В этот раз нам нужно заполнить тремя единицами и двумя нулями пять местоположений.
Используя формулу мы можем найти число способов расположения чисел:
И опять то же число, что мы получили методом прямого счёта. Мы можем также найти число решений для нерешённого случая, где в правой части уравнения 8 вместо 3. Одним из решений будет:
а нам нужно найти число способов разместить 8 единиц в 10 местоположениях, и это будет:
как и утверждалось выше.
Если мы уверены в том, что этот метод работает для всех случаев, нам нужна общая формула. Напомним, что общее уравнение имеет вид:
Простейшее решение этого уравнения:
Поскольку существует n переменных, количество нулей в этом решении равно n-1. Таким образом, разложение выглядит так:
В разложенной конфигурации видим m и n-1 нулей (как утверждалось выше).
Следовательно, общее число местоположений, которые нужно заполнить, равно (m+n-1). Единственное, что остаётся — найти число способов, которыми можно заполнить m+n-1 местоположений m единиц, что определяется по формуле:
Это наш конечный результат.
(1/2)
система-уравнений
задан 17 Авг ’20 18:17
Dan27
9●2
изменен 17 Авг ’20 18:17
старыеновыеценные
|
Ясно, что $%y\ge1$%. Из первого уравнения следует, что $%x$% не может быть отрицательным. Тогда второе уравнение даёт $%x-1=\sqrt{y-1}\cdot(1-\frac1x)$%. Подходит $%x=1$%, где $%y=6$%. Если $%x\ne1$%, то сокращаем на $%x-1$% и приходим к равенству $%\sqrt{y-1}=x$%, то есть $%y=x^2+1$%. ссылка отвечен 17 Авг ’20 19:18 falcao |
3+x=7$%. Решение у такого уравнения ровно одно так как правая часть возрастает. Итого имеем два решения системы.Ваш ответ
Если вы не нашли ответ, задайте вопрос.
Здравствуйте
Математика — это совместно редактируемый форум вопросов и ответов для начинающих и опытных математиков, с особенным акцентом на компьютерные науки.
Присоединяйтесь!
регистрация »
отмечен:
система-уравнений
×364
задан
17 Авг ’20 18:17
показан
1229 раз
обновлен
17 Авг ’20 19:18
Связанные вопросы
Отслеживать вопрос
по почте:
Зарегистрировавшись, вы сможете подписаться на любые обновления
по RSS:
Ответы
Ответы и Комментарии
Как найти количество решений в системе уравнений?
В зависимости от того, как линейные уравнения в системе касаются друг друга, у системы будет разное количество решений. Здесь вы познакомитесь с тем, как найти количество решений в системе уравнений.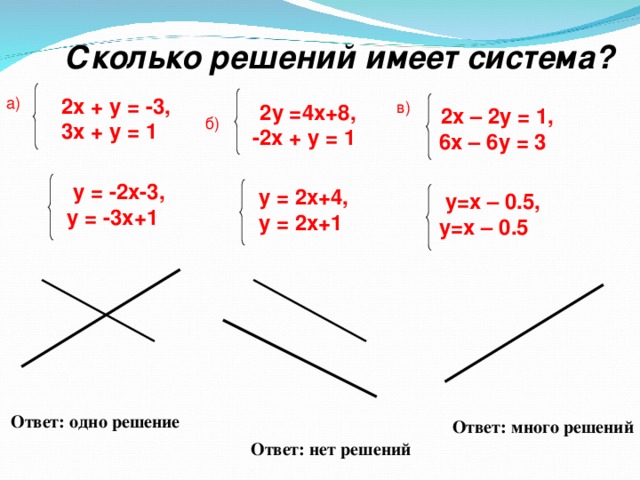
Система линейных уравнений обычно имеет единственное решение, но иногда она может не иметь решения (параллельные прямые) или иметь бесконечное число решений (одна и та же прямая).
Похожие темы
- Как решать системы уравнений
- Как решать системы уравнений Word задачи
Линейное уравнение с двумя переменными — это уравнение вида \(ax + by + c = 0\), где \(a , b, c ∈ R\), \(a\) и \(b ≠ 0\). Когда мы рассматриваем систему линейных уравнений, мы можем найти количество ответов, сравнивая коэффициенты переменных уравнений. 92 ≠ 0\).
- Если \(\frac{a_1}{a_2}≠ \frac{b_1}{b_2}\), то будет уникальных решений . Если мы построим график, линии будут пересекаться. Этот тип уравнения называется согласованной парой линейных уравнений.
- Если \(\frac{a_1}{a_2}= \frac{b_1}{b_2}=\frac{c_1}{c_2}\), то будет бесконечно много решений .
Линии совпадут. Этот тип уравнения называется зависимой парой линейных уравнений с двумя переменными. - Если \(\frac{a_1}{a_2}= \frac{b_1}{b_2}≠\frac{c_1}{c_2}\), то будет нет решение . Если мы построим график, линии будут параллельны. Уравнение такого типа называется несовместной парой линейных уравнений.
Линии совпадут. Этот тип уравнения называется зависимой парой линейных уравнений с двумя переменными.Количество решений в системе уравнений – Пример 1:
Сколько решений имеет следующая система?
\(y=-2x-4\), \(y=3x+3\)
Решение:
Сначала перепишем уравнение к общему виду:
\(-2x-y-4 =0\)
\(3x-y+3=0\)
Теперь сравните коэффициенты:
\(\frac{a_1}{a_2}\)\(=-\frac{2}{3}\)
\(\frac{b_1}{b_2}\)\ (=-\frac{1}{1}=1\)
\(\frac{a_1}{a_2}≠ \frac{b_1}{b_2}\), следовательно, эта система уравнений будет иметь только одно решение .
Упражнения на количество решений в системе уравнений
Найдите количество решений в каждой системе уравнений.
- \(\цвет{синий}{2x\:+\:3y\:-\:11\:=\:0,\:3x\:+\:2y\:-\:9\:=\ :0}\)
- \(\color{blue}{y=\frac{10}{3}x+\frac{9}{7},\:y=\frac{1}{8}x-\frac{3}{4 }}\)
- \(\color{blue}{y=\frac{8}{5}x+2,\:y=\frac{8}{5}x+\frac{5}{2}}\)
- \(\color{синий}{y=-x+\frac{4}{7},\:y=-x+\frac{4}{7}}\)
- \(\цвет{синий}{один\:решение}\)
- \(\цвет{синий}{один\:решение}\)
- \(\цвет{синий}{нет\:решение}\)
- \(\цвет{синий}{бесконечно\:много\:решения}\)
Команда математиков без усилий
Связанная с этой статьей
Как найти количество решений в системе уравнений Число решений в системе уравнений
Другие математические статьи
- О нас
- Свяжитесь с нами
- Оптовые заказы
- Политика возврата
Математика без усилий: мы помогаем учащимся полюбить математику — © 2023
Число решений системы уравнений алгебраически
Утверждение, что два математических выражения одной или нескольких переменных идентичны, называется уравнением .
Линейные уравнения — это уравнения, в которых степени всех рассматриваемых переменных равны. Степень линейного уравнения всегда равна единице. Решение одновременной пары линейных уравнений — это пара значений переменных «x» и «y», которые удовлетворяют всем уравнениям в указанном наборе уравнений.
Пара линейных уравнений с двумя переменными
Уравнение, которое можно записать в виде ax + by + c = 0 , где a, b и c — действительные числа, а a и b не равны нулю, равно называется линейным уравнением с двумя переменными x и y. (или это условие должно выполняться, если a и b оба не равны нулю на a 2 + b 2 ≠ 0).
например: Рассмотрим пару линейных уравнений с двумя переменными: 3x + 2y = 6,
Подставить x = 2 и y = 0 в левой части (LHS) следующим образом:
⇒ LHS = 3(2) + 2(0)
Следовательно, x = 2 и y = 0 являются решением уравнения 2x + 3y = 6.
Теперь, если x = 1 и y = 1 подставить в уравнение 2x + 3y = 6, тогда:
LHS = 3(1) + 2(1)
= 3 + 2
= 5 ≠ RHS
Следовательно, x = 1 и y = 1 не является решением уравнения.
Алгебраически это означает, что точка (2, 0) лежит на прямой, представляющей уравнение 3x + 2y = 6, а точка (1, 1) на ней не лежит.
Таким образом, каждое решение, удовлетворяющее уравнению, является точкой на линии, представляющей его.
Два подобных линейных уравнения с двумя переменными x и y. Подобные уравнения называются парой линейных уравнений с двумя переменными .
Алгебраически общая форма пары линейных уравнений с двумя переменными x и y имеет вид:
A 1 x + B 1 Y + C 1 = 0 и
A 2 X + B 2 Y + C 2 = 0
9002, где A , а , где A , а , где A , а , где A , а , а .
1 , B 1 , C 1 , A 2 , B 2 , C 2 — это реальные числа ( ∈ R ) и 1 2 + B 1 2 ≠ 0, а 2 2 + б 2 2 ≠ 0.Возможны различные случаи для пары линейных уравнений с двумя переменными
Для трех разных типов линий: пересекающихся, параллельных и совпадающих линий возможны три различных случая для определения пары линейных уравнений с двумя переменными.
- Линии могут пересекаться друг с другом в одной точке.
В результате пара уравнений имеет единственное решение (непротиворечивая пара уравнений).
например: 2x – 4y = 0 и 6x + 8y – 40 = 0
Пересекающиеся линии: 2x – 4y = 0 и 6x + 8y – 40 = 0
- Линии могут быть параллельными друг другу.
В результате уравнения не имеют решения (несовместимая пара уравнений).
например: 2x + 4y – 8 = 0 и 4x + 8y – 24 = 0
Параллельные линии: 2x + 4y – 8 = 0 и 4x + 8y – 24 = 0
- .
В результате уравнения имеют бесконечно много решений (зависимая или непротиворечивая пара уравнений)
например: 4x + 6y – 18 = 0 и 8x + 12y – 36 = 0
Пересекающиеся прямые: 4x + 6y – 18 = 0 и 8x + 12y – 36 = 0
Теперь предположим пару уравнений: a 1 x + b 1 y + c 1 = 0 и + b 2 y + c 2 = 0 теперь их графическая и алгебраическая интерпретация, соответствующая отношениям сравнения, дается как:
| Comparing ratios | Graphical Representation | Algebraic Interpretation | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
Intersecting Lines | Exactly one Solution (unique) | ||||||||||||
Совпадение Прямые | Бесконечное множество решения | ||||||||||||
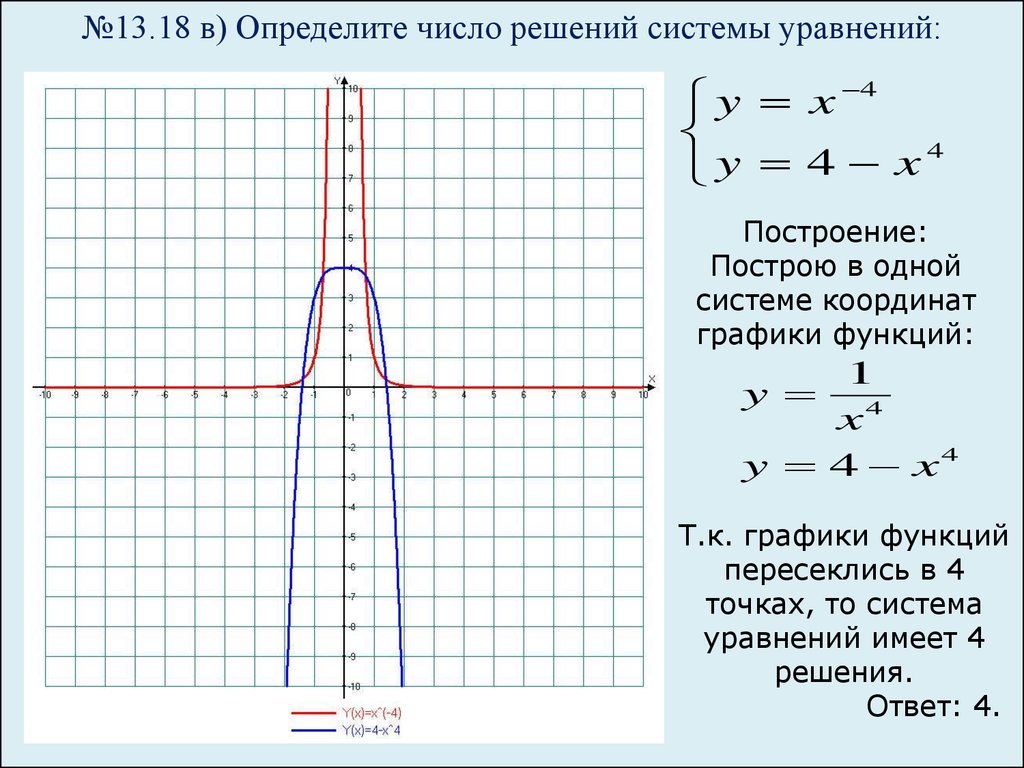. 8х – 4у + 10 = 0 и 4х – 2у + 9 = 0. Решение:
Задача 2. Определить количество решений следующих пар линейных уравнений: 6x + 2y = 4 и 7x – 3y = 13.
Задача 3: Определить графическое представление и количество решений следующих пар линейных уравнений: 6x – 5y = 11; – 12х +10у = –22.
Задача 4: Составьте пары линейных уравнений в следующих текстовых задачах и найдите их решения графически. В классе 20 учеников. Если мальчиков на 6 больше, чем девочек, найдите количество мальчиков и девочек в классе. Решение:
|
