Как определить модуль скорости тела: чему равен модуль скорости тела m=4,0 кг,если модуль его импульса р=60 кг*м/с?

Модуль силы, скорости, импульса. Что это?!

В статье разберемся, что такое модуль. Модуль силы, скорости, импульса, что это всё? Давайте разбираться!

Абсолютная величина, известная так же, как модуль, это всегда некое неотрицательное число, чье определение всегда зависит от типа числа. Символически модуль обозначается как: | x |.

Сила и модуль силы

В процессе изучения физики приходится сталкиваться с различными явлениями, рассчитывать скорость, силу и многие другие параметры. Не менее важно понять какими методами, и в каких единицах делаются расчеты по характеристикам этих явлений. Одна из физических величин это сила. Сила представляет собой величину, которая способна показать меру воздействия на тело посредством другого тела или со стороны полей. Взаимодействие образуется за счет тех полей, которые создаются самими телами в случае контакта. Всего различают четыре вида взаимодействия: слабое, сильное, гравитационное, электромагнитное. Сила обозначается буквой F от латинского слова fortis, что в переводе означает сильный.

Что такое модуль силы?

Сила является векторной величиной, это значит, что она обладает, так как направлением, так и модулем. Не так часто встречается случай, когда на тело воздействует одна единственная величина, чаще всего их несколько. В таком случае речь о равнодействующей силы, которая формируется за счет суммирования всех сил, влияющие на тело одновременно. Стоит отметить, что параметр равнодействующая сила является искусственным и создан только для удобства проведения расчетов.

Но что же это модуль силы? Модуль является абсолютной величиной. Это такая величина, которая отражается числом с плюсом во всех случаях. Другими словами характеристики какого-то процесса или явления выражены конкретными числами. Каждая сила характеризуется направлением и величиной, эта величина и есть модуль, вот что это модуль силы.

Модуль равнодействующих двух сил определяется по формулам:

• F=F1 + F2 (в случае сил с одинаковым направлением)
• F=F1 — F2 (силы с разным направлением)

Для модуля равнодействующих нескольких сил все намного сложнее. Для начала надо вводить систему координат, записать и высчитать проекции сил, потом использовать теорему Пифагоры.

Исаак Ньютон внес серьезный вклад в работу над различными видами сил. В связи с этим в качестве единицы измерения силы применяется Н (Ньютон).

Что это модуль скорости?

Каждое тело в процессе перемещения развивает энную скорость, которая характеризуется двумя параметрами: направление и модуль. Что же это модуль скорости

? Это число, обозначающее, насколько быстро перемещается тело. Сама скорость является вектором. У нее есть все свойства вектора перемещения, так как выражается посредством него и обладает всеми свойствами данного вектора.

Для определения модуля скорости необходимо учитывать закон движения со всеми своими правилами. Вычисление модуля скорости может осуществляться посредством графика движения. Если недостаточно понятно, что это модуль скорости тела можно использовать одно из понятий: скалярная величина и алгебраическая скорость. Скорость как вектор это величина с направлением и численным значением, при этих условиях модуль скорости тела это не что иное, как длина этого вектора.

Чаще всего речь о прямолинейном движении в рамках координат (x;t). В таком случае для определения данного параметра подойдет формула:

v = S/t = (x — x0)/t.

Это значит, что необходимо нужно отнять начальную координату от конечной координаты. Полученный результат нужно разделить на то время, за которое имело место изменение координаты.

Пример определения модуля скорости одного тела относительно другого на основе задачи: два тела перемещаются со скоростью 8 и 6 м/с. Направление их движения перпендикулярное друг другу. Поэтапное решение осуществляется таким образом:

1. Вычисляется скорость v₂₁ на базе закона сложения скоростей v₂ = v₂₁ + v₁, а значит v₂₁ = v₂ – v₁.
2. Определяется модуль скорости тела согласно теореме Пифагора.

Модуль импульса и модуль оси

Импульс представляет собой векторную величину, чье направление идентично направлению вектора скорости. Он может поменяться только в том случае, если произойдет изменение скорости под воздействием какой-то силы. Но что это модуль импульса и как он рассчитывается?

Модуль импульса определяется согласно произведению массы тела на скорость. Его можно легко вычислить, если есть данные по скорости и по массе.

Что это модуль оси? Разъяснение данного понятия, может быть сделана на основе определения понятия ось. Ось представляет собой прямую с заданным направлением. В каком-то роде можно сказать, что это нечто иное, как вектор с величиной модуля, которая тянется к бесконечности. Это и есть модуль оси. Для обозначения оси можно использовать любую букву: t, Z, Y, X и т.д. На ней определяется точка О, известная как начало отсчета. Все расстояния до других точек определяются относительно нее.

Для того чтобы сделать проекцию точки на ось, нужно провести перпендикулярную прямую через эту точку на саму ось. В таком случае проекция этой точки, сама точка.

---

Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:

---

Формула скорости в физике

Содержание:

• Определение и формула скорости
• Скорость в разных системах координат
• Частные случаи формул для вычисления скорости
• Единицы измерения скорости
• Примеры решения задач

Определение и формула скорости

Определение

Мгновенной скоростью (или чаще просто скоростью) материальной точки называется физическая величина равная первой производной от радиус–вектора $\bar{r}$ точки по времени (t). Обозначают скорость обычно буквой v. Это векторная величина. Математически определение вектора мгновенной скорости записывается как:

$$\bar{v}=\frac{d \bar{r}}{d t}=\dot{\bar{r}}(1)$$

Скорость имеет направление указывающее направление движения материальной точки и лежит на касательной к траектории ее движения. {2}=-1 \lt 0$$

Так как мы получили, что скорость в указанный момент времени отрицательна, следовательно, материальная точка движется против оси X.

Ответ. Против оси X.

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

Задание. Скорость материальной точки является функцией от времени вида:

$$v=10\left(1-\frac{t}{5}\right)$$

где скорость в м/с, время в c. Какова координата точки в момент времени равный 10 с, в какой момент времени точка будет на расстоянии 10 м от начала координат? Считайте, что при t=0 c точка началадвижение из начала координат по оси X.

Решение. Точка движется по оси X, cвязь координаты x и скорости движения определена формулой:

$$x=\int_{0}^{t} v d t=\int_{0}^{t} 10\left(1-\frac{t}{5}\right) d t=10 t-\frac{10 t^{2}}{2 \cdot 5}=10 t-t^{2}(2. {2}=-10(2.3)$$

При решении уравнения (2.3) нам подойдет корень равный:

$$t_{3}=5+6=11 (c)$$

Ответ. 1) $x=0 \mathrm{~m}$ 2) $t_{1}=8,8 \mathrm{c}, t_{2}=1,13 c, t_{3}=11 c$

Читать дальше: Формула средней скорости.

Эластичность и простое гармоническое движение

Твердое тело — это идеализация, потому что даже самый прочный материал слегка деформируется при приложении силы. Упругость — это область физики, изучающая отношения между деформациями твердого тела и силами, которые их вызывают.

Эластичные модули

В общем, модуль упругости представляет собой отношение напряжения к деформации. Модуль Юнга, объемный модуль и модуль сдвига описывают реакцию объекта на растягивающие, сжимающие и сдвигающие напряжения соответственно. Когда объект, такой как проволока или стержень, подвергается натяжению, длина объекта увеличивается. Модуль Юнга определяется как отношение напряжения растяжения к деформации растяжения. Напряжение растяжения — это мера деформации, вызывающей напряжение. Его определение представляет собой отношение растягивающей силы (F) и площади поперечного сечения, нормального к направлению силы (A) . Единицами напряжения являются ньютоны на квадратный метр (Н/м ² ). Деформация растяжения определяется как отношение изменения длины ( l _o − l ) до исходной длины ( l _o ). Штамм – это число без единиц измерения; следовательно, выражение для модуля Юнга равно

Если к объекту кубической формы приложена сила, толкающая каждую грань внутрь, возникает сжимающее напряжение. Давление определяется как сила на единицу площади P = F/A . Единицей давления в СИ является паскаль, который равен 1 ньютон/метр ² или Н/м ² . При равномерном давлении тело сожмется, и его относительное изменение объема (V) — деформация сжатия . Соответствующий модуль упругости называется объемным модулем и определяется как B = − P / (Δ V / V _o ). Отрицательный знак гарантирует, что B всегда будет положительным числом, поскольку увеличение давления вызывает уменьшение объема.

Приложение силы к верхней части объекта параллельно поверхности, на которой он стоит, вызывает деформацию. Например, толкните верхнюю часть книги, лежащей на столешнице, так, чтобы сила была параллельна поверхности. Форма поперечного сечения изменится с прямоугольника на параллелограмм из-за напряжение сдвига (см. рис. 1). Напряжение сдвига определяется как отношение тангенциальной силы к площади (A) нагруженной поверхности. Деформация сдвига представляет собой отношение горизонтального расстояния, на которое перемещается сдвигаемая поверхность (Δ x ) и высоты объекта (h) , что приводит к модулю сдвига :

Рисунок 1

Напряжение сдвига деформирует книгу.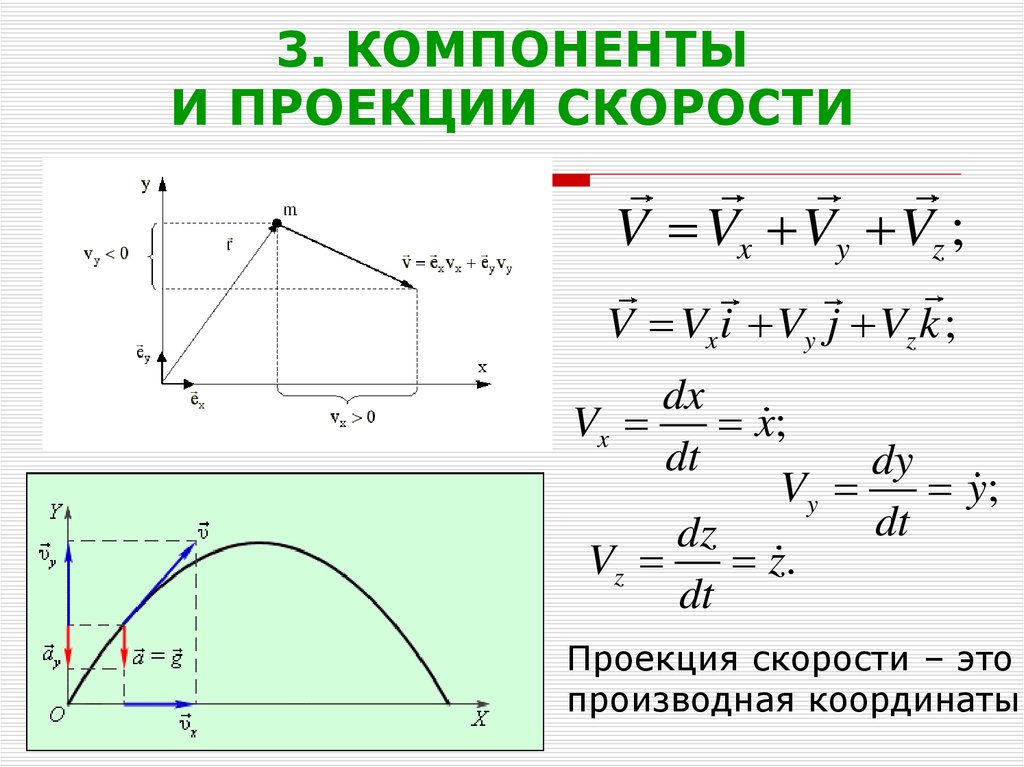

Закон Гука

Прямая зависимость между приложенной силой и изменением длины пружины, называемая законом Гука, равна F = − kx , где x — растяжение пружины, а k определяется как жесткость пружины . Единицами для k являются ньютоны на метр. Когда груз подвешен на конце пружины, при равновесии нисходящая сила тяжести, действующая на массу, должна быть уравновешена направленной вверх силой пружины. Эта сила называется восстанавливающая сила. Знак минус указывает, что направление восстанавливающей силы пружины противоположно направлению растяжения или смещения пружины.

Простое гармоническое движение

Масса, подпрыгивающая на конце пружины, совершает колебательное движение. Движение любой системы, ускорение которой пропорционально отрицательной величине смещения, называется простым гармоническим движением (SHM), т. е. F = ma = − kx . Некоторые определения относятся к SHM:

• Полная вибрация — это одно движение вниз и вверх.

• Время одного полного колебания составляет период, измеряется в секундах.

• Частота представляет собой число полных колебаний в секунду и определяется как величина, обратная периоду. Его единицами являются циклы в секунду или герц (Гц).

• Амплитуда есть абсолютное значение расстояния от максимального вертикального смещения до центральной точки движения, то есть наибольшего расстояния вверх или вниз перемещается масса от своего начального положения.

Уравнение, относящееся к периоду, массе и жесткости пружины: T = 2π√ m / k . Это отношение дает период в секундах.

Отношение СГМ к круговому движению

Аспекты SHM можно визуализировать, взглянув на его отношение к равномерному круговому движению. Представьте себе карандаш, приклеенный вертикально к горизонтальному поворотному столу. Посмотрите на вращающийся карандаш со стороны поворотного стола. Поскольку поворотный стол вращается с равномерным круговым движением, карандаш движется вперед и назад с простым гармоническим движением. Рисунок (а) иллюстрирует P как точка на ободе поворотного стола — положение карандаша. Точка P ′ указывает видимое положение карандаша при просмотре только компонента размером x . Вектор ускорения и компоненты вектора показаны на рисунке 2(b).

Рисунок 2

Связь между круговым движением и СГМ.

Ниже приводится доказательство взаимосвязи между SHM и одной составляющей равномерного кругового движения. Этот компонент движения наблюдается при взгляде на круговое движение со стороны. Максимальное перемещение составляющей равномерного кругового движения равно радиусу окружности (А) . Подставим радиус окружности (A) в уравнения для угловой скорости и углового ускорения, чтобы получить = r ω ² = А ω ² . Горизонтальная составляющая этого ускорения равна a = — A ω ^o sin θ = -ω ² x , используя x = A , как показано на рисунке . Поскольку ускорение пропорционально смещению, точка, вращающаяся с равномерным круговым движением, подвергается SHM, когда рассматривается только одна составляющая движения.

Простой маятник

Простой маятник представляет собой идеализированную модель массы, качающейся на конце безмассовой струны. Для малых дуг качания менее 15 градусов движение маятника приближается к SHM. Период маятника равен T = 2π√ l / g , где l — длина маятника, а g — ускорение свободного падения. Обратите внимание, что период маятника равен

, а не , в зависимости от массы маятника.

Энергия ШМ

Потенциальная энергия пружины по закону Гука равна P . E .=(1/2) kx ² . Полная энергия представляет собой сумму кинетической и потенциальной энергий в любой момент времени и сохраняется.

Калькулятор скорости поперечной волны

Автор Rahul Dhari

Отзыв Стивена Вудинга

Последнее обновление: 21 декабря 2022 г.

Содержание:

• Что такое поперечная волна?
• Как пользоваться калькулятором скорости поперечной волны?
• Пример: Что такое скорость поперечной волны в среде?
• Часто задаваемые вопросы

Калькулятор скорости поперечной волны определяет скорость поперечной волны при ее движении через тело. Эта скорость рассчитывается на основе два основных параметра или свойства материала, а именно плотность и модуль сдвига . Примером поперечной волны является сейсмическая волна. Вот почему скорость поперечной волны является ключевым параметром при анализе грунтов в области геотехнической оценки земельных участков. Чем выше скорость, тем меньше трясется земля. Читайте дальше, чтобы понять, что такое скорость поперечной волны и как рассчитать скорость поперечной волны.

🙋 Если вы хотите узнать больше о модуле сдвига, посетите калькулятор коэффициента Пуассона Omni.

Что такое поперечная волна?

Сдвиговая волна представляет собой тип волны, возникающей в сыпучих средах, когда частиц колеблются перпендикулярно направлению распространения волны. Сдвиговый тип нагрузки вызывает поперечную волну. В случае осевой деформации вы можете воспользоваться нашим калькулятором напряжений.

Силы сдвига вызывают изменение формы объемной среды и не вызывают изменения объема тела. Эти силы возникают парами, каждая из которых действует вдоль поверхности среды. Поперечная волна также известна как S-волна . Мы определяем скорость поперечной волны как квадратный корень из отношения модуля сдвига (модуля жесткости) к плотности материала. Скорость поперечной волны V _с в среде с модулем сдвига G и плотностью ρ можно записать по формуле скорости поперечной волны:

V _с = √(G / ρ)

Скорость поперечной волны составляет примерно половину скорости продольной волны. Скорость продольных волн V _L зависит от модуля упругости E и плотности.

V _L = √(E / ρ)

🔎 Вы можете рассчитать точную скорость продольных волн с помощью нашего калькулятора скорости звука в твердых телах.

Как пользоваться калькулятором скорости поперечной волны?

Выполните следующие шаги, чтобы найти скорость поперечной волны:

• Шаг 1: Введите модуль сдвига объемной среды.
• Шаг 2: Введите плотность материала.
• Шаг 3: Калькулятор скорости поперечной волны вернет ответ.

Пример: Что такое скорость поперечной волны в среде?

Теперь давайте рассмотрим пример. Найти скорость поперечной волны при распространении волны в медном стержне.

Вы можете нажать на расширенный режим калькулятора, чтобы напрямую выбрать материал из списка. В качестве альтернативы вы можете ввести значения модуля сдвига и плотности меди, которые равны

45 ГПа и 8940 кг/м³ соответственно.

• Шаг 1: Введите модуль сдвига , G = 45 ГПа .

• Шаг 2: Введите плотность материала, ρ = 8940 кг/м³ .

• Шаг 3: Калькулятор теперь будет использовать формулу скорости поперечной волны:

  В = √(G / ρ) = √(45 000 000 000 / 8 940) = 2 243,6 м/с

Скорость поперечной волны в меди равна 2,244 км/с .

Часто задаваемые вопросы

Что такое поперечная волна?

волн, генерируемых парой поперечных сил, действующих вдоль противоположных сторон тела, известны как поперечная волна. Частицы в этой волне колеблются перпендикулярно направлению распространения волны.

Что такое скорость поперечной волны?

Скорость, с которой поперечные волны распространяются в сыпучем веществе, называется скоростью поперечной волны. Это зависит от модуля сдвига и плотности материала.

No related posts.