что это такое? Как отмечать точки и строить фигуры на координатной плоскости?
Математика – наука довольно сложная. Изучая ее, приходится не только решать примеры и задачи, но и работать с различными фигурами, и даже плоскостями. Одной из наиболее используемых в математике является система координат на плоскости. Правильной работе с ней детей учат не один год. Поэтому важно знать, что это такое и как правильно с ней работать.

Давайте же разберемся, что представляет собой данная система, какие действия можно выполнять с ее помощью, а также узнаем ее основные характеристики и особенности.
Определение понятия
Координатная плоскость — это плоскость, на которой задана определенная система координат. Такая плоскость задается двумя прямыми, пересекающимися под прямым углом. В точке пересечения этих прямых находится начало координат. Каждая точка на координатной плоскости задается парой чисел, которые называют координатами.
В школьном курсе математики школьникам приходится довольно тесно работать с системой координат – строить на ней фигуры и точки, определять, какой плоскости принадлежит та или иная координата, а также определять координаты точки и записывать или называть их. Поэтому поговорим подробнее обо всех особенностях координат. Но прежде коснемся истории создания, а затем уже поговорим о том, как работать на координатной плоскости.
Историческая справка
Идеи о создании системы координат были еще во времена Птоломея. Уже тогда астрономы и математики думали о том, как научиться задавать положение точки на плоскости. К сожалению, в то время еще не было известной нам системы координат, и ученым приходилось пользоваться другими системами.
Изначально они задавали точки с помощью указания широты и долготы. Долгое время это был один из наиболее используемых способов нанесения на карту той или иной информации. Но в 1637 году Рене Декарт создал собственную систему координат, названную впоследствии в честь великого математика «декартовой».

После опубликования труда «Геометрия» система координат Рене Декарта завоевала признание в научных кругах.
Уже в конце XVII в. понятие «координатная плоскость» стало широко использоваться в мире математики. Несмотря на то что с момента создания данной системы прошло уже несколько веков, она до сих пор широко используется в математике и даже в жизни.
Примеры координатной плоскости
Прежде чем говорить о теории, приведем несколько наглядных примеров координатной плоскости, чтобы вы смогли представить ее себе. В первую очередь координатная система используется в шахматах. На доске каждый квадрат имеет свои координаты – одну координату буквенную, вторую – цифровую. С ее помощью можно определить положение той или иной фигуры на доске.
Вторым наиболее ярким примером может служить любимая многими игра «Морской бой». Вспомните, как, играя, вы называете координату, например, В3, таким образом указывая, куда именно целитесь. При этом, расставляя корабли, вы задаете точки на координатной плоскости.
Данная система координат широко применяется не только в математике, логических играх, но и в военном деле, астрономии, физике и многих других науках.
Оси координат
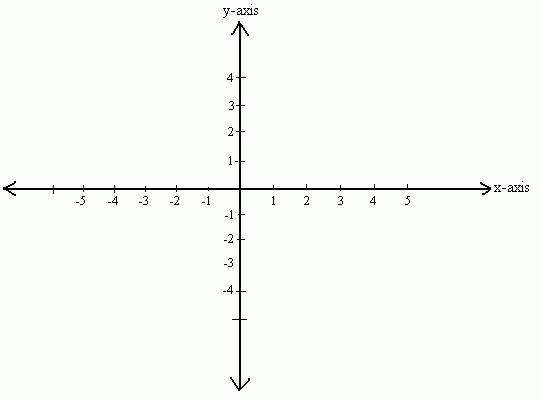
Как уже говорилось, в системе координат выделяют две оси. Поговорим немного о них, так как они имеют немалое значение.
Первая ось — абсцисс — горизонтальная. Она обозначается как (Ox). Вторая ось — ординат, которая проходит вертикально через точку отсчета и обозначается как (Oy). Именно эти две оси образуют систему координат, разбивая плоскость на четыре четверти. Начало отсчета находится в точке пересечения этих двух осей и принимает значение 0. Только в случае если плоскость образована двумя пересекающимися перпендикулярно осями, имеющими точку отсчета, это координатная плоскость.
Также отметим, что каждая из осей имеет свое направление. Обычно при построении системы координат принято указывать направление оси в виде стрелочки. Кроме того, при построении координатной плоскости каждая из осей подписывается.
Четверти
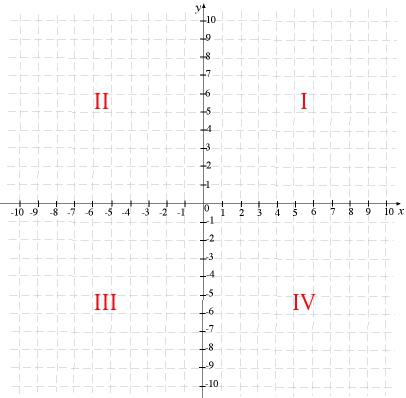
Теперь скажем пару слов о таком понятии, как четверти координатной плоскости. Плоскость разбивается двумя осями на четыре четверти. Каждая из них имеет свой номер, при этом нумерация плоскостей ведется против часовой стрелки.
Каждая из четвертей имеет свои особенности. Так, в первой четверти абсцисса и ордината положительная, во второй четверти абсцисса отрицательная, ордината — положительная, в третьей и абсцисса, и ордината отрицательные, в четвертой же положительной является абсцисса, а отрицательной — ордината.
Запомнив эти особенности, можно с легкостью определить, к какой четверти относится та или иная точка. Кроме того, эта информация может пригодиться вам и в том случае, если придется делать вычисления, используя декартову систему.
Работа с координатной плоскостью
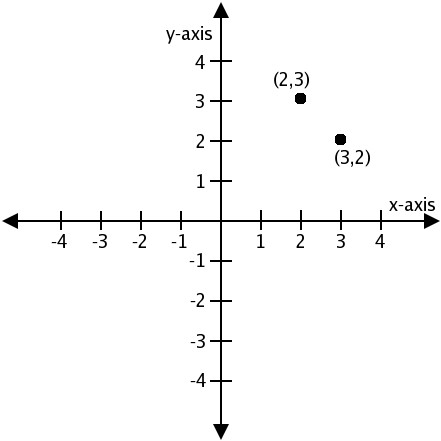 Когда мы разобрались с понятием плоскости и поговорили о ее четвертях, можно перейти к такой проблеме, как работа с данной системой, а также поговорить о том, как наносить на нее точки, координаты фигур. На координатной плоскости сделать это не так тяжело, как может показаться на первый взгляд.
Когда мы разобрались с понятием плоскости и поговорили о ее четвертях, можно перейти к такой проблеме, как работа с данной системой, а также поговорить о том, как наносить на нее точки, координаты фигур. На координатной плоскости сделать это не так тяжело, как может показаться на первый взгляд.В первую очередь строится сама система, на нее наносятся все важные обозначения. Затем уже идет работа непосредственно с точками или фигурами. При этом даже при построении фигур сначала на плоскость наносятся точки, а затем уже прорисовываются фигуры.
Далее мы поговорим подробнее о построении системы и непосредственно нанесении точек и фигур.
Правила построения плоскости
Если вы решили начать отмечать на бумаге фигуры и точки, вам понадобится координатная плоскость. Координаты точек наносятся именно на нее. Для того чтобы построить координатную плоскость, понадобится только линейка и ручка или карандаш. Сначала рисуется горизонтальная ось абсцисс, затем вертикальная — ординат. При этом важно помнить, что оси пересекаются под прямым углом.
Далее на каждой оси указывают направление и подписывают их с помощью общепринятых обозначений x и y. Также отмечается точка пересечения осей и подписывается цифрой 0.
Следующим обязательным пунктом является нанесение разметки. На каждой из осей в обоих направлениях отмечаются и подписываются единицы-отрезки. Это делается для того, чтобы затем можно было работать с плоскостью с максимальным удобством.
Отмечаем точку
Теперь поговорим о том, как нанести координаты точек на координатной плоскости. Это основа, которую следует знать, чтобы успешно размещать на плоскости разнообразные фигуры, и даже отмечать уравнения.
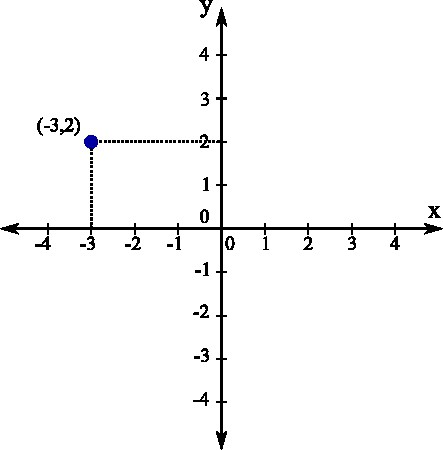
При построении точек следует помнить, как правильно записываются их координаты. Так, обычно задавая точку, в скобках пишут две цифры. Первая цифра обозначает координату точки по оси абсцисс, вторая — по оси ординат.
Строить точку следует таким образом. Сначала отметить на оси Ox заданную точку, затем отметить точку на оси Oy. Далее провести воображаемые линии от данных обозначений и найти место их пересечения — это и будет заданная точка.
Вам останется только отметить ее и подписать. Как видите, все довольно просто и не требует особых навыков.
Размещаем фигуру
Теперь перейдем к такому вопросу, как построение фигур на координатной плоскости. Для того чтобы построить на координатной плоскости любую фигуру, следует знать, как размещать на ней точки. Если вы умеете это делать, то разместить фигуру на плоскости не так уж и сложно.
В первую очередь вам понадобятся координаты точек фигуры. Именно по ним мы и будем наносить на нашу систему координат выбранные вами геометрические фигуры. Рассмотрим нанесение прямоугольника, треугольника и окружности.
Начнем с прямоугольника. Наносить его довольно просто. Сначала на плоскость наносятся четыре точки, обозначающие углы прямоугольника. Затем все точки последовательно соединяются между собой.
Нанесение треугольника ничем не отличается. Единственное – углов у него три, а значит, на плоскость наносятся три точки, обозначающие его вершины.
Касательно окружности тут следует знать координаты двух точек. Первая точка – центр окружности, вторая – точка, обозначающая ее радиус. Эти две точки наносятся на плоскость. Затем берется циркуль, измеряется расстояние между двумя точками. Острие циркуля ставится в точку, обозначающую центр, и описывается круг.
Как видите, тут также нет ничего сложного, главное, чтобы под рукой всегда были линейка и циркуль.
Теперь вы знаете, как наносить координаты фигур. На координатной плоскости это делать не так уж и сложно, как может показаться на первый взгляд.
Выводы
Итак, мы рассмотрели с вами одно из наиболее интересных и базовых для математики понятий, с которым приходится сталкиваться каждому школьнику.
Мы с вами выяснили, что координатная плоскость – это плоскость, образованная пересечением двух осей. С ее помощью можно задавать координаты точек, наносить на нее фигуры. Плоскость разделена на четверти, каждая из которых имеет свои особенности.

Основной навык, который следует выработать при работе с координатной плоскостью, – умение правильно наносить на нее заданные точки. Для этого следует знать правильное расположение осей, особенности четвертей, а также правила, по которым задаются координаты точек.
Надеемся, что изложенная нами информация была доступна и понятна, а также была полезна для вас и помогла лучше разобраться в данной теме.
Координаты точки. Координатная плоскость — урок. Математика, 6 класс.
Во многих ситуациях реальной жизни мы используем два числа (или другие символы), чтобы точно описать нужный нам объект.
Место в зрительном зале задаётся номером ряда и номером кресла в ряду.
На шахматной доске позиция шахматной фигуры задаётся названием столбца и номером ряда.

Любая карта (или глобус) разделена на квадраты, и, подобно шахматной доске, каждый квадрат задаётся двумя номерами.


На экране компьютера каждая точка задаётся двумя номерами.

Система координат

Французский философ и математик Рене Декарт (\(1596\)–\(1650\)) уже в XVII веке предложил метод двух координат для нахождения точки на плоскости. Поэтому система координат названа его именем.
Декартовую систему координат образуют:
1. две перпендикулярные прямые, на которых указано направление возрастания чисел. Горизонтальная прямая называется осью Ox, или осью абсцисс. Вертикальная прямая называется осью Oy, или осью ординат.
2. Точка пересечения прямых — начало координатной системы, она часто обозначается через букву O.
3. Отрезки на каждой оси длиной в одну единицу измерения.


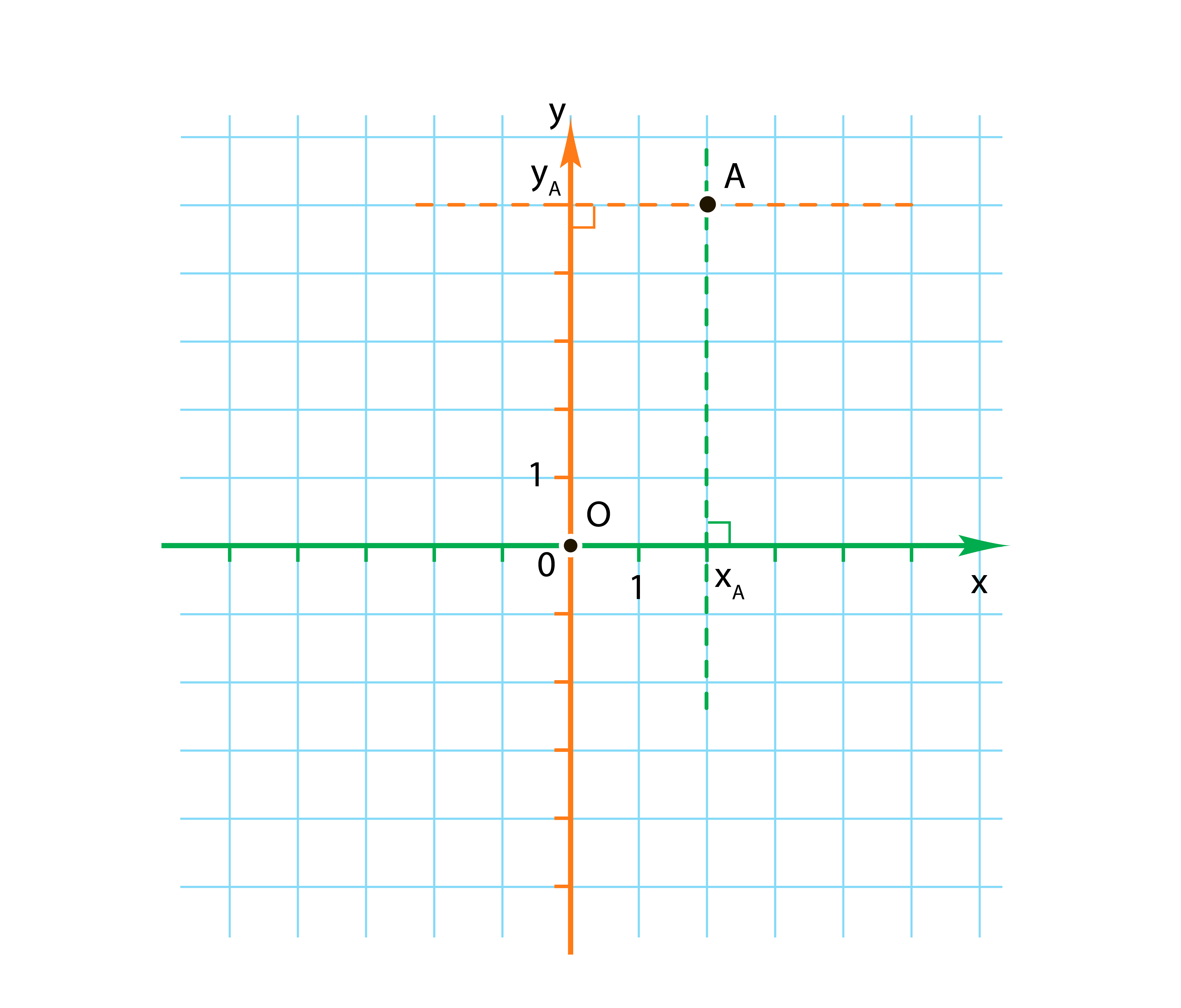
Для любой точки находят две координаты \(x\) и \(y\) (абсциссу и ординату) и записывают как AxA;yA.
На рисунке показаны координаты A2;4, то есть абсцисса точки \(A\) равна \(2\), а ордината точки \(A\) равна \(4\).
Если на плоскости выбрана система координат, то такую плоскость называют координатной плоскостью.
Так как оси координат делят плоскость на \(4\) части, каждая из них имеет номер и называется квадрантом.
В I квадранте находится положительная часть оси абсцисс и оси ординат.
Во II квадранте находится положительная часть оси ординат и отрицательная часть оси абсцисс.
В III квадранте находится отрицательная часть оси абсцисс и оси ординат.
В IV квадранте находится положительная часть оси абсцисс и отрицательная часть оси ординат.

Координаты на плоскости
Основные сведения о координатной плоскости
Каждый объект (например, дом, место в зрительном зале, точка на карте) имеет свой упорядоченный адрес (координаты), который имеет числовое или буквенное обозначение.
Математики разработали модель, которая позволяет определять положение объекта и называется координатной плоскостью.
Чтобы построить координатную плоскость нужно провести $2$ перпендикулярные прямые, на конце которых указываются с помощью стрелок направления «вправо» и «вверх». На прямые наносятся деления, а точка пересечения прямых является нулевой отметкой для обеих шкал.
Определение 1
Горизонтальная прямая называется осью абсцисс и обозначается х, а вертикальная прямая называется осью ординат и обозначается у.
Две перпендикулярные оси х и у с делениями составляют прямоугольную, или декартовую, систему координат, которую предложил французский философ и математик Рене Декарт.
Координатная плоскость
Координаты точки
Точка на координатной плоскости определяется двумя координатами.
Готовые работы на аналогичную тему
Чтобы определить координаты точки $A$ на координатной плоскости нужно через нее провести прямые, которые будут параллельны координатным осям (на рисунке выделены пунктирной линией). Пересечение прямой с осью абсцисс дает координату $x$ точки $A$, а пересечение с осью ординат дает координату у точки $A$. При записи координат точки сначала записывается координата $x$, а затем координата $y$.
Точка $A$ на рисунке имеет координаты $(3; 2)$, а точка $B (–1; 4)$.
Для нанесения точки на координатную плоскость действуют в обратном порядке.
Построение точки по заданным координатам
Пример 1
На координатной плоскости построить точки $A(2;5)$ и $B(3; –1).$
Решение.
Построение точки $A$:
- отложим число $2$ на оси $x$ и проведем перпендикулярную прямую;
- на оси у отложим число $5$ и проведем перпендикулярную оси $y$ прямую. На пересечении перпендикулярных прямых получим точку $A$ с координатами $(2; 5)$.
Построение точки $B$:
- отложим на оси $x$ число $3$ и проведем перпендикулярную оси х прямую;
- на оси $y$ отложим число $(–1)$ и проведем перпендикулярную оси $y$ прямую. На пересечении перпендикулярных прямых получим точку $B$ с координатами $(3; –1)$.
Пример 2
Построить на координатной плоскости точки с заданными координатами $C (3; 0)$ и $D(0; 2)$.
Решение.
Построение точки $C$:
- отложим число $3$ на оси $x$;
- координата $y$ равна нулю, значит точка $C$ будет лежать на оси $x$.
Построение точки $D$:
- отложим число $2$ на оси $y$;
- координата $x$ равна нулю, значит, точка $D$ будет лежать на оси $y$.
Замечание 1
Следовательно, при координате $x=0$ точка будет лежать на оси $y$, а при координате $y=0$ точка будет лежать на оси $x$.
Пример 3
Определить координаты точек A, B, C, D.$
Решение.
Определим координаты точки $A$. Для этого проведем через эту точку $2$ прямые, которые будут параллельными к координатным осям. Пересечение прямой с осью абсцисс дает координату $x$, пересечение прямой с осью ординат дает координату $y$. Таким образом, получаем, что точка $A (1; 3).$
Определим координаты точки $B$. Для этого проведем через эту точку $2$ прямые, которые будут параллельными к координатным осям. Пересечение прямой с осью абсцисс дает координату $x$, пересечение прямой с осью ординат дает координату $y$. Получаем, что точка $B (–2; 4).$
Определим координаты точки $C$. Т.к. она расположена на оси $y$, то координата $x$ этой точки равна нулю. Координата у равна $–2$. Таким образом, точка $C (0; –2)$.
Определим координаты точки $D$. Т.к. она находится на оси $x$, то координата $y$ равна нулю. Координата $x$ этой точки равна $–5$. Таким образом, точка $D (5; 0).$
Пример 4
Построить точки $E(–3; –2), F(5; 0), G(3; 4), H(0; –4), O(0; 0).$
Решение.
Построение точки $E$:
- отложим число $(–3)$ на оси $x$ и проведем перпендикулярную прямую;
- на оси $y$ отложим число $(–2)$ и проведем перпендикулярную прямую к оси $y$;
- на пересечении перпендикулярных прямых получаем точку $E (–3; –2).$
Построение точки $F$:
- координата $y=0$, значит, точка лежит на оси $x$;
- отложим на оси $x$ число $5$ и получим точку $F(5; 0).$
Построение точки $G$:
- отложим число $3$ на оси $x$ и проведем перпендикулярную прямую к оси $x$;
- на оси $y$ отложим число $4$ и проведем перпендикулярную прямую к оси $y$;
- на пересечении перпендикулярных прямых получаем точку $G(3; 4).$
Построение точки $H$:
- координата $x=0$, значит, точка лежит на оси $y$;
- отложим на оси $y$ число $(–4)$ и получим точку $H(0; –4).$
Построение точки $O$:
- обе координаты точки равны нулю, значит, точка лежит одновременно и на оси $y$, и на оси $x$, следовательно является точкой пересечения обеих осей (началом координат).
Онлайн урок: Координатная плоскость по предмету Математика 6 класс
Метод координат- это способ определения местоположения точки или тела с помощью чисел и других символов и некоторой системы координат.
Координаты и метод координат применяются и используются в различных сферах нашей жизни.
Например, координаты на картах и планах задаются числами. Для любой точки на поверхности Земли можно определить пару чисел (широту и долготу).
Координаты врача в больнице задаются номером этажа и номером кабинета.
Место в зрительном зале определяется парой чисел: номером ряда и номером кресла в ряду.

Место в поезде, указанное в билете, определяют два числа: номер вагона и номер полки.
Некоторый образ прямоугольной координатной системы прослеживается в знаменитых играх, таких как шахматы и «Морской бой».
На шахматной доске каждый квадрат имеет свои координаты: буквы латинского алфавита и цифры.

Похожая ситуация складывается в игре «Морской бой».
На игровом поле (поле состоит из квадрата 10х10, разлинованного в клетку) изображаются условные корабли в виде прямоугольников и квадратов.
Задача игроков определить место положения кораблей, тем самым вычеркнуть — «уничтожить» их с поля соперника.
Такое же поле (10х10) чертится пустым, чтобы отмечать на нем координаты сбитых кораблей соперника.
 Строки и столбцы задают нам подобие координатных осей, а каждый квадратик поля имеет свою координату: букву и число.
Строки и столбцы задают нам подобие координатных осей, а каждый квадратик поля имеет свою координату: букву и число.Применяется метод координат в создании различного рода таблиц.
Таблицы часто содержат большое количество упорядоченной информации.
Опять же, строки и столбцы задают нам подобие координатных осей, а координаты каждой ячейки таблицы задаются парой символов или чисел (в зависимости от специфики таблицы).
Например, таблица расписания уроков.
Конкретному времени и классу соответствует определенный урок.
Существуют специальные компьютерные программы, с помощью которых можно создавать таблицы, производить вычисления и анализировать данные.
Любой ячейке в такой таблице соответствует два символа, которые однозначно определяют ее, — это пара «число-буква».
Применение набора чисел для описания положения любой точки очень удобный инструмент.
Системы координат широко используются в современных науках и в технике.
В геодезии и картографии широта и долгота однозначно определяется положением на поверхности Земного шара.
Прямоугольная система координат применяется в военной типографии: земная поверхность на военных картах условно разбита на прямоугольники определенных размеров.
 Местоположение точки на такой карте отмечается, как в Декартовой системе координат.
Местоположение точки на такой карте отмечается, как в Декартовой системе координат.Кроме географических объектов военная карта несет информацию о составе войск, их дислокации и расположении, о количестве и расположении боевой техники, о составе войск, боевых действиях, происходящих и планируемых, и многое другое.
В космонавтике и астрономии с помощью особых координатных систем определяют положение звезд и иных небесных тел, вспомогательных точек на небесной сфере, а также положение и траектории летательных аппаратов.
В авиации наиболее часто используют одновременно три различные системы координат: земная, связанная и скоростная.
Земная жестко связана с Землей, применяется для определения летательного аппарата (как точки) относительно земных объектов.
Для расчета взлета, посадки и полетов на близкие расстояния используется прямоугольная система координат, в иных случаях используется более сложный расчет и система координат.
Связанная система координат служит для определения положения объектов внутри летательного аппарата.
Скоростная используется для определения положения летательного аппарата относительно воздушного потока и расчета аэродинамических параметров судна.
В морской навигации (мореплавании, судоходстве) географические координаты замеряют с помощью координатной сетки, которая состоит из взаимно параллельных линий.

Горизонтальные прямые — это линии параллелей.
Вертикальные прямые — это линии меридианов.
На левом крайнем и правом крайнем меридиане нанесена шкала географической широты точки.
На верхней и нижней параллели нанесены шкалы для измерения долготы точки.
Современные навигационные устройства, конечно, во многом превосходят бумажные из прошлого, так как они способны найти не только координаты точки, но и проложить безопасный маршрут до нее.
Даже и в этом случае нужна карта и система координат только электронная.
Программирование станков с программным управлением также тесно связана с применением системы координат.
Перемещение рабочих частей станка в пространстве при изготовлении детали задается с помощью прямоугольной системы координат.
Как вы смогли убедиться, координаты и метод координат широко используются во многих сферах нашей жизни.
Применение метода координат позволяет определить положение объекта как на плоскости, так и в пространстве.
Чтобы определить положение тела на плоскости, объект представляют точкой и находят координату этой точки на двух осях пространства.
Рассмотрим алгоритмы решения математических задач с помощью прямоугольной декартовой системы координат на плоскости.
Определение координат заданных точек на координатной плоскости.
Если на координатной плоскости задана некоторая точка А и требуется найти ее координаты, то это делается следующим образом.
Через точку А проводят две прямые: одна параллельная оси Оу, вторая — оси Ох.
Прямая, параллельная оси Оу, пересечет ось Ох в точке, которая является абсциссой точки А.
Прямая параллельная оси Ох, пересечет ось Оу в точке, которая является ординатой точки А.

Координата точки А записывается так:
А(хА;уА)
хА— абсцисса точки А (координата по оси Ох).
уА— ордината точки А (координата по оси Оу).
Построение точки на координатной плоскости по заданным координатам.
Чтобы построить точки на плоскости по заданным координатам, действуют в обратном порядке.
Отложить на оси Ох абсциссу точки А и провести перпендикулярную прямую оси Ох через отложенную координату хА.
На оси Оу отложить ординату точки А и провести перпендикулярную прямую оси Оу через отложенную координату уА.
На пересечении полученных перпендикулярных прямых получится точка А(хА; уА).
Разработка урока по математике на тему «Построение точек в координатной плоскости»
Муниципальное бюджетное общеобразовательное учреждение
«Средняя общеобразовательная школа № 2»
Урок математики по теме «Построение точек в координатной плоскости»
Раздел «Координаты на плоскости»
Класс 6.
Разработала: Бортукова Марина Александровна,
учитель математики,
первая квалификационная категория
г. Югорск
Цель: научить учащихся строить точки по заданным её координатам на координатной плоскости
Задачи:
1.образовательная — закрепить навыки свободно ориентироваться на координатной плоскости, научить строить точки по заданным её координатам;
2.воспитательная — продолжить формирование у школьников коммуникативной компетенции;
3. развивающая — учить четко и аккуратно выполнять геометрические построения;
развивать творческие способности школьников.
Планируемые результаты:
а) Личностные:
1. Интеллектуальная активность — интеллектуальные навыки, позволяющие учащемуся самостоятельно работать с источниками информации, анализировать и делать выводы на основе полученной информации.
2. Коммуникативные навыки — владение основными навыками работы в парах и группе.
3. Ответственность и адаптивность — личностные качества, позволяющие продуктивно действовать для реализации своих целей в соответствии с правами, потребностями и целями окружающих людей.
б) Метапредметные:
1. Познавательные действия — включают действия исследования и отбора необходимой информации, ее структурирования.
2. Коммуникативные действия — обеспечивают возможность сотрудничества — умение слышать, слушать и понимать товарища, планировать и согласованно выполнять совместную деятельность, уметь договариваться, правильно выражать свои мысли в речи, слушать и принимать во внимание мнение других, дискутировать, выступать публично.
3. Закрепление умений работать с информацией — находить, анализировать, управлять, оценивать и представлять информацию.
в) Предметные:
1. Освоение правил построения точек в координатной плоскости.
2. Развитие навыков работы в координатной плоскости, познавательных интересов, интеллектуальных способностей.
3. Овладение умениями работать с различными источниками информации, организовывать собственную информационную деятельность и планировать ее результаты.
Оборудование: ноутбуки, мультимедийный проектор, интерактивная доска, карточки с заданиями, оценочный лист.
Ход урока
Этапурока
Деятельность учителя
Деятельность ученика
Время
1.
Орг.
момент
Взаимное приветствие учителя и учеников, работа с классным журналом, проверка готовности к уроку кабинета и учеников.
Подписываем рабочие листы, записываем дату.
Создание атмосферы взаимопонимания и сотрудничества, благоприятный настрой учащихся на совместную работу
30 сек
2.
Актуализация знаний
1. Какой самый главный навык в математике? (счет)
Задание на доске.
Ребята задание выполняем устно, а ответ записываем себе в тетрадь.
Все готовы?
Берем в руки сигнальные линейки, если вы согласны с ответом, поднимаете зеленую линейку, если нет, то красную.
Молодцы вы замечательно справились с заданием, оцените себя:
За выполненное задание ставите 3 балла – все правильно, 2 – допустил ошибку, 1 – допустил 2 ошибки
Давайте повторим, что мы изучили на прошлом уроке? (Нахождение координаты заданной точки)
Для этого поставьте в соответствие координаты точек и точки расположенные на координатной плоскости, для этого вспомните алгоритм нахождения точек на координатной плоскости.
Алгоритм определения координат точки в координатной плоскости.
Провести (мысленно) перпендикулярные прямые из точки на оси координат.
Указать числа, соответствующие точкам пересечения прямых с осями координат.
Записать точку и в скобках её координаты: первая по оси абсцисс, вторая по оси ординат.
Задание на интерактивной доске.
Выполняют задание (устно считают, записывают ответы в тетради)
Один ученик проговаривает ответы, все остальные сигнализируют линейками.
Оценивают свой ответ
Отвечают на вопросы
Проговаривают алгоритм и соотносят координаты с точками
4 мин
5мин
3
Формулирование темы и цели урока
Итак, молодцы, вы прекрасно справились с заданием. Как вы думаете, что вы еще не умеете делать в координатной плоскости?
-Не умеем отмечать точки на координатной плоскости по заданным координатам
Это и будет темой нашего урока
На слайде появляется тема урока: «Построение точек в координатной плоскости»
Какова цель нашего сегодняшнего урока?
—Научиться строить точки на координатной плоскости.
Чтобы осуществить эту цель, какие задачи нам необходимо решить
1.Разработать алгоритм построения точек в координатной плоскости.
2.Учиться применять данный алгоритм для построения точек в координатной плоскости.
Отвечают на вопросы. Записывают тему урока.
Формулируют цель и задачи урока
1 мин
4.
Усвоение новых знаний
Валеологичекая пауза
Вы уже умеете определять координаты точек.
Что надо помнить, когда определяем координаты по точке на плоскости?
-Что первая координата всегда берётся на оси абсцисс, а вторая на оси ординат.
А теперь поработайте в парах и попробуйте разработать алгоритм построения точки
Алгоритм построения точек в координатной плоскости.
Найти на оси абсцисс число соответствующее первой координате (провести мысленно через неё перпендикулярную прямую).
Найти на оси ординат число соответствующее второй координате (провести мысленно через неё пунктирную прямую).
Отметить точку пересечения перпендикулярных прямых.
А теперь применим данный алгоритм для построения точек
Для этого выполним задание на доске, постройте точки соответствующие следующим координатам.
(1;8), (-1;3), (-1;5,5),
(-1,-1), (0;0), (1;-3),
(1,5;-2)
Молодцы!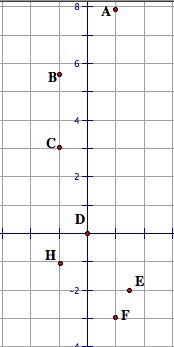
Фронтальная беседа
Дети отвечают на вопросы
Учащиеся разрабатывают алгоритм построения точки на координатной плоскости.
Учащиеся работают с интерактивной доской.
2 мин
1 мин
2-3 мин
5
А теперь давайте закрепим полученные навыки, для этого выполним задание в электронном практикуме «Координатная плоскость»
Файл: пять (за партами на рабочих листах)
Молодцы вы прекрасно справились с работой, оцените себя:
За выполненное задание ставите: 3 балла – все правильно, 2 – допустил ошибки и справил их, 1 – допустил ошибки
Желающие выходят к доске отмечают точки, все остальные работают на рабочем листе
7 мин
6
Первичное закрепление изученного материала
Откройте ноутбуки и в парах выполните задание в электронном практикуме «Координатная плоскость»:
Для этого справа откройте вкладку «Режим 2»
Нажмите на кнопку «открыть файл»
В открывшемся меню выберите «Ракета»
Нажимаем на кнопку координата и строим появляющиеся координаты на плоскости.
Молодцы вы справились с этим заданием, оцените себя.
За выполненное задание ставите: 3 балла – все правильно, 2 – допустил ошибки и исправил их, 1 – допустил ошибки
Выполняют работу в парах на ноутбуках
Оценивают свою работу
5 мин
7
Д.з
По выбору:
выполнить практическую работу по карточке (построить фигуру, последовательно соединяя точки на координатной плоскости)
придумать фигуру на координатной плоскости, записать координаты точек, которые надо отметить на координатной плоскости для получения вашей фигуры
Запись домашнего задания
30 сек
Контроль знаний
А теперь поработаем в группах на листах с одной из координатных четвертей
Вывешиваем работу на доске и оцениваем
За выполненное задание ставите: 3 балла – все правильно, 2 – допустил ошибки и исправил их, 1 – допустил ошибки
Выполняют работу по построению точек по заданным координатам
7 мин
8
Рефлексия
и итог урока
А сейчас давайте вспомним, какие задачи были нами поставлены на сегодняшнем уроке.
Удалось ли нам решить поставленные задачи?
Аргументируйте свой ответ.
Оцените свою работу на уроке сосчитайте количество баллов и выставьте оценку в оценочном листе:
11-12 баллов — оценка «5», 9-10 баллов – оценка «4», 7-8 баллов – оценка «3», 6 и менее баллов – оценка «2»
На столах лежат кружочки, нарисуйте на них с каким настроением вы уходите с урока, все ли вам понравилось, или у вас возникли какие то затруднения.
Спасибо за урок!
Вспоминают и воспроизводят задачи урока.
Приводят аргументы, подтверждающие правильность ответа
Оценивают свою деятельность на уроке и настроение после окончания урока.
Показывают смайлик учителю
4 мин
определение. Как отмечать точки и строить фигуры на координатной плоскости?
Математика – наука довольно сложная. Изучая ее, приходится не только решать примеры и задачи, но и работать с различными фигурами, и даже плоскостями. Одной из наиболее используемых в математике является система координат на плоскости. Правильной работе с ней детей учат не один год. Поэтому важно знать, что это такое и как правильно с ней работать.

Давайте же разберемся, что представляет собой данная система, какие действия можно выполнять с ее помощью, а также узнаем ее основные характеристики и особенности.
Определение понятия
Координатная плоскость — это плоскость, на которой задана определенная система координат. Такая плоскость задается двумя прямыми, пересекающимися под прямым углом. В точке пересечения этих прямых находится начало координат. Каждая точка на координатной плоскости задается парой чисел, которые называют координатами.
В школьном курсе математики школьникам приходится довольно тесно работать с системой координат – строить на ней фигуры и точки, определять, какой плоскости принадлежит та или иная координата, а также определять координаты точки и записывать или называть их. Поэтому поговорим подробнее обо всех особенностях координат. Но прежде коснемся истории создания, а затем уже поговорим о том, как работать на координатной плоскости.
Историческая справка
Идеи о создании системы координат были еще во времена Птоломея. Уже тогда астрономы и математики думали о том, как научиться задавать положение точки на плоскости. К сожалению, в то время еще не было известной нам системы координат, и ученым приходилось пользоваться другими системами.
Изначально они задавали точки с помощью указания широты и долготы. Долгое время это был один из наиболее используемых способов нанесения на карту той или иной информации. Но в 1637 году Рене Декарт создал собственную систему координат, названную впоследствии в честь великого математика «декартовой».

После опубликования труда «Геометрия» система координат Рене Декарта завоевала признание в научных кругах.
Уже в конце XVII в. понятие «координатная плоскость» стало широко использоваться в мире математики. Несмотря на то что с момента создания данной системы прошло уже несколько веков, она до сих пор широко используется в математике и даже в жизни.
Примеры координатной плоскости
Прежде чем говорить о теории, приведем несколько наглядных примеров координатной плоскости, чтобы вы смогли представить ее себе. В первую очередь координатная система используется в шахматах. На доске каждый квадрат имеет свои координаты – одну координату буквенную, вторую – цифровую. С ее помощью можно определить положение той или иной фигуры на доске.
Вторым наиболее ярким примером может служить любимая многими игра «Морской бой». Вспомните, как, играя, вы называете координату, например, В3, таким образом указывая, куда именно целитесь. При этом, расставляя корабли, вы задаете точки на координатной плоскости.
Данная система координат широко применяется не только в математике, логических играх, но и в военном деле, астрономии, физике и многих других науках.
Оси координат

Как уже говорилось, в системе координат выделяют две оси. Поговорим немного о них, так как они имеют немалое значение.
Первая ось — абсцисс — горизонтальная. Она обозначается как (Ox). Вторая ось — ординат, которая проходит вертикально через точку отсчета и обозначается как (Oy). Именно эти две оси образуют систему координат, разбивая плоскость на четыре четверти. Начало отсчета находится в точке пересечения этих двух осей и принимает значение 0. Только в случае если плоскость образована двумя пересекающимися перпендикулярно осями, имеющими точку отсчета, это координатная плоскость.
Также отметим, что каждая из осей имеет свое направление. Обычно при построении системы координат принято указывать направление оси в виде стрелочки. Кроме того, при построении координатной плоскости каждая из осей подписывается.
Четверти

Теперь скажем пару слов о таком понятии, как четверти координатной плоскости. Плоскость разбивается двумя осями на четыре четверти. Каждая из них имеет свой номер, при этом нумерация плоскостей ведется против часовой стрелки.
Каждая из четвертей имеет свои особенности. Так, в первой четверти абсцисса и ордината положительная, во второй четверти абсцисса отрицательная, ордината — положительная, в третьей и абсцисса, и ордината отрицательные, в четвертой же положительной является абсцисса, а отрицательной — ордината.
Запомнив эти особенности, можно с легкостью определить, к какой четверти относится та или иная точка. Кроме того, эта информация может пригодиться вам и в том случае, если придется делать вычисления, используя декартову систему.
Работа с координатной плоскостью
 Когда мы разобрались с понятием плоскости и поговорили о ее четвертях, можно перейти к такой проблеме, как работа с данной системой, а также поговорить о том, как наносить на нее точки, координаты фигур. На координатной плоскости сделать это не так тяжело, как может показаться на первый взгляд.
Когда мы разобрались с понятием плоскости и поговорили о ее четвертях, можно перейти к такой проблеме, как работа с данной системой, а также поговорить о том, как наносить на нее точки, координаты фигур. На координатной плоскости сделать это не так тяжело, как может показаться на первый взгляд.
В первую очередь строится сама система, на нее наносятся все важные обозначения. Затем уже идет работа непосредственно с точками или фигурами. При этом даже при построении фигур сначала на плоскость наносятся точки, а затем уже прорисовываются фигуры.
Далее мы поговорим подробнее о построении системы и непосредственно нанесении точек и фигур.
Правила построения плоскости
Если вы решили начать отмечать на бумаге фигуры и точки, вам понадобится координатная плоскость. Координаты точек наносятся именно на нее. Для того чтобы построить координатную плоскость, понадобится только линейка и ручка или карандаш. Сначала рисуется горизонтальная ось абсцисс, затем вертикальная — ординат. При этом важно помнить, что оси пересекаются под прямым углом.
Далее на каждой оси указывают направление и подписывают их с помощью общепринятых обозначений x и y. Также отмечается точка пересечения осей и подписывается цифрой 0.
Следующим обязательным пунктом является нанесение разметки. На каждой из осей в обоих направлениях отмечаются и подписываются единицы-отрезки. Это делается для того, чтобы затем можно было работать с плоскостью с максимальным удобством.
Отмечаем точку
Теперь поговорим о том, как нанести координаты точек на координатной плоскости. Это основа, которую следует знать, чтобы успешно размещать на плоскости разнообразные фигуры, и даже отмечать уравнения.

При построении точек следует помнить, как правильно записываются их координаты. Так, обычно задавая точку, в скобках пишут две цифры. Первая цифра обозначает координату точки по оси абсцисс, вторая — по оси ординат.
Строить точку следует таким образом. Сначала отметить на оси Ox заданную точку, затем отметить точку на оси Oy. Далее провести воображаемые линии от данных обозначений и найти место их пересечения — это и будет заданная точка.
Вам останется только отметить ее и подписать. Как видите, все довольно просто и не требует особых навыков.
Размещаем фигуру
Теперь перейдем к такому вопросу, как построение фигур на координатной плоскости. Для того чтобы построить на координатной плоскости любую фигуру, следует знать, как размещать на ней точки. Если вы умеете это делать, то разместить фигуру на плоскости не так уж и сложно.
В первую очередь вам понадобятся координаты точек фигуры. Именно по ним мы и будем наносить на нашу систему координат выбранные вами геометрические фигуры. Рассмотрим нанесение прямоугольника, треугольника и окружности.
Начнем с прямоугольника. Наносить его довольно просто. Сначала на плоскость наносятся четыре точки, обозначающие углы прямоугольника. Затем все точки последовательно соединяются между собой.
Нанесение треугольника ничем не отличается. Единственное – углов у него три, а значит, на плоскость наносятся три точки, обозначающие его вершины.
Касательно окружности тут следует знать координаты двух точек. Первая точка – центр окружности, вторая – точка, обозначающая ее радиус. Эти две точки наносятся на плоскость. Затем берется циркуль, измеряется расстояние между двумя точками. Острие циркуля ставится в точку, обозначающую центр, и описывается круг.
Как видите, тут также нет ничего сложного, главное, чтобы под рукой всегда были линейка и циркуль.
Теперь вы знаете, как наносить координаты фигур. На координатной плоскости это делать не так уж и сложно, как может показаться на первый взгляд.
Выводы
Итак, мы рассмотрели с вами одно из наиболее интересных и базовых для математики понятий, с которым приходится сталкиваться каждому школьнику.
Мы с вами выяснили, что координатная плоскость – это плоскость, образованная пересечением двух осей. С ее помощью можно задавать координаты точек, наносить на нее фигуры. Плоскость разделена на четверти, каждая из которых имеет свои особенности.

Основной навык, который следует выработать при работе с координатной плоскостью, – умение правильно наносить на нее заданные точки. Для этого следует знать правильное расположение осей, особенности четвертей, а также правила, по которым задаются координаты точек.
Надеемся, что изложенная нами информация была доступна и понятна, а также была полезна для вас и помогла лучше разобраться в данной теме.
Координатная плоскость — Math Open Reference
Координатная плоскость — открытый справочник по математикеДвумерная поверхность, на которой точки нанесены и расположены по их координатам x и y.
Попробуй это Перетащите точку A. При перетаскивании обратите внимание на два числа, определяющих ее положение на плоскости. Перетащите начало координат, чтобы изменить положение осей.Координатная плоскость — это двумерная поверхность, на которой мы можем рисовать точки, линии и кривые.Он имеет две шкалы, называемые осью x и осью y , расположенной под прямым углом друг к другу. Множественное число оси — это «оси» (произносится «AX-easy»). Точки на плоскости располагаются с помощью двух чисел — координат x и y. Это горизонтальные и вертикальные расстояния точки от определенного места, называемого исходной точкой.
X ось
Горизонтальный масштаб называется осью x . По мере продвижения вправо по шкале от нуля значения становятся положительными и увеличиваются.Когда вы идете влево от нуля, они становятся все более и более отрицательными.Y ось
Вертикальный масштаб называется осью y . Когда вы поднимаетесь от нуля, числа увеличиваются в положительном направлении. По мере того, как вы спускаетесь с нуля, они становятся все более отрицательными.Маркировка осей
Вдоль каждой оси вы увидите маленькие галочки с цифрами. Эти метки помогают судить о масштабе. Они показаны через каждые 5 единиц на рисунке выше, но могут иметь любое приращение и не обязательно должны быть одинаковыми по обеим осям.Происхождение
Точка пересечения двух осей (в нуле на обеих шкалах) называется началом координат. Начало координат — это точка, от которой измеряются все расстояния по осям x и y. На рисунке выше вы можете перетащить исходную точку, чтобы переместить ее в более подходящее место в любое время.Квадранты
 Две оси делят плоскость на четыре области, называемые квадрантами.
Первый квадрант, по соглашению, верхний правый, а затем они вращаются против часовой стрелки.На диаграмме выше они обозначены квадрантами 1,2 и т. Д. Их принято обозначать цифрами.
но мы говорим о них как о «первом, втором, третьем и четвертом квадрантах». Иногда они обозначаются римскими цифрами: I, II, III и IV.
Две оси делят плоскость на четыре области, называемые квадрантами.
Первый квадрант, по соглашению, верхний правый, а затем они вращаются против часовой стрелки.На диаграмме выше они обозначены квадрантами 1,2 и т. Д. Их принято обозначать цифрами.
но мы говорим о них как о «первом, втором, третьем и четвертом квадрантах». Иногда они обозначаются римскими цифрами: I, II, III и IV.
На диаграмме выше вы можете перетащить начало координат в любой угол и отображать только один квадрант за раз. если хотите.
Что попробовать
На рисунке вверху страницы сначала нажмите «сброс».- Перетащите исходную точку, включая перетаскивание полностью в угол, чтобы показать только один квадрант.
- Перетащите точку A в каждый квадрант. Первое число после A — это координата x , а второе — координата y . Обратите внимание, как знаки каждого изменения в каждом квадранте. Подробнее об этом см. Координаты точки
Другие темы о координатной геометрии
(C) Открытый справочник по математике, 2011 г.
Все права защищены.
Координаты точки — Math Open Reference
Координаты точки — Math Open Reference Пара чисел, определяющая положение точка на двумерном самолет ,Попробуй это Перетащите точку A. При перетаскивании обратите внимание на два числа, определяющих ее положение на плоскости.
Координаты точка представляют собой пару чисел, определяющих его точное местоположение на двумерном самолет. Напомним, что координатная плоскость имеет две оси, расположенные под прямым углом друг к другу, называемые осью x и y .Координаты данной точки показывают, как далеко по каждой оси расположена точка.
Заказанная пара
Координаты записываются в виде «упорядоченной пары», как показано ниже. Буква P — это просто название точки, и она используется, чтобы отличать ее от других. Два числа в скобках — координаты x и y точки.
Первое число (x) указывает, насколько далеко по оси x (горизонтальной) находится точка.
Вторая — это координата y и указывает, насколько далеко вверх или вниз по оси y двигаться.Это называется упорядоченной парой, потому что порядок двух чисел имеет значение — первое всегда координата x (по горизонтали).
Два числа в скобках — координаты x и y точки.
Первое число (x) указывает, насколько далеко по оси x (горизонтальной) находится точка.
Вторая — это координата y и указывает, насколько далеко вверх или вниз по оси y двигаться.Это называется упорядоченной парой, потому что порядок двух чисел имеет значение — первое всегда координата x (по горизонтали).Знак координаты важен. Положительное число означает переход вправо (x) или вверх (y). Отрицательные числа означают движение влево (x) или вниз (y). (На рисунке вверху страницы указаны значения осей, помеченные соответствующим знаком).
Абсцисса
Абсцисса — это другое название для координаты x (по горизонтали) точки.Произносится «ab-SISS-ah» (‘c;’ молчит). Не очень часто используется. Чаще всего используется термин «x-координата».
Ордината
Ордината — это другое название и (вертикальной) координаты точки. Произносится «ОРД-инет». Не очень часто используется. Чаще всего используется термин «y-координата».
Что попробовать
На рисунке вверху страницы сначала нажмите «сброс». Если вы предпочитаете это, вы можете перетащить начало координат в любой угол, чтобы отобразить только один квадрант.- Точка A находится в верхнем правом квадранте (первом квадранте). Обратите внимание, как координаты x и y положительны, потому что точка находится вверх и вправо от начала координат.
- Перетащите точку в верхний левый квадрант (второй квадрант). Обратите внимание, что координата x отрицательная, потому что она находится слева от начала координат, где значения x отрицательны.
- Перетащите точку в нижний правый квадрант (четвертый квадрант). Координата x снова положительна, потому что она находится справа от начала координат, но теперь координата y отрицательна из-за того, что она находится ниже начала координат.
Другие темы о координатной геометрии
(C) Открытый справочник по математике, 2011 г.
Все права защищены.
Введение в линии в координатной геометрии
Введение в линии в координатной геометрии — Открытый справочник по математикеПрямо линии в координатной геометрии — это та же идея, что и в обычной геометрии, за исключением того, что они нарисованы на координатная плоскость и мы можем сделать с ними больше.
Как определить строку
Рассмотрим линию на рис. 1. Как бы я определил эту конкретную линию? Какую информацию я мог бы дать вам по телефону, чтобы вы могли провести точно такую же линию на своем конце?

Рис 1.Как определить эту линию?
В координатной геометрии обычно используются три способа:
- Дайте координаты любых двух точек на линии
- Дайте координаты одной точки на линии, а наклон линии
- Приведите уравнение, определяющее линию.
Используя две точки
На рис. 2 линия определяется двумя точками A и B. Задав координаты двух точек, мы можем провести черту. Никакая другая линия не может пройти через обе эти точки, поэтому линия, которую они определяют, уникальна. Я мог бы позвонить вам по телефону и сказать «Проведите линию через (9,9) и (17,4)» , и вы сможете полностью восстановить ее на своей стороне.

Рис. 2. A, B определяют уникальную линию
Для интерактивной демонстрации линий, определяемых двумя точками, см.
Использование одной точки и наклона

Рис 3.Точка и наклон определяют линию
Другой распространенный метод — дать вам координаты одной точки и наклон линии. На данный момент вы можете думать о наклоне как о направлении линии. Итак, как только вы знаете, что линия проходит через определенную точку и в каком направлении она указывает, вы определили одну уникальную линию.
На рис. 3 мы видим линию, проходящую через точку A в точке (14,23). Мы также видим, что его наклон равен +2 (что означает, что он увеличивается на 2 для каждого по ширине).с этими двумя фактами мы можем установить уникальную линию.
Величину уклона обычно обозначают буквой м. Для получения дополнительной информации о наклоне и о том, как его определить, см. Наклон линии.
Уравнение прямой
После того, как вы определили линию с помощью метода точечного наклона, вы можете написать уравнения алгебры, которые описывают линию. Применяя алгебраические процессы к этим уравнениям, мы можем решать задачи, которые иначе были бы трудными. Эти и многие другие методы построения графиков описаны в томе по алгебре, но общая идея описана здесь, в Координатной геометрии.
Для описания линии обычно используются уравнения двух типов:
Обе формы на самом деле являются вариациями одной и той же идеи. В обоих случаях вам нужно знать координаты одной точки и наклон линии.
- В форме пересечения наклона заданная точка всегда находится на оси Y, и вы указываете координату Y этой точки (Его координата x всегда равна нулю).
- В форме точка-уклон вы можете использовать любую точку.
Место, где линия пересекает ось y, называется точкой пересечения и обычно обозначается буквой b. Подробнее об этом см. Перехват линии.

y = м (x-P x ) + P y
Рис. 4. Точечный уклон

y = mx + b
Рис 5. Наклон-пересечение
Если вы внимательно посмотрите на две формулы, вы увидите, что они очень похожи. Если вы возьмете вариант точечного наклона на рис. 4 и решите поместить P на ось y, его Координата x равна нулю, а ее координата y такая же, как и точка пересечения.Если вы замените эти вещи, вы получите формулу пересечения наклона справа на рис.Для чего используются уравнения?
- Вы можете использовать их, чтобы построить линию: Возьмите различные значения x, а затем используйте уравнение, чтобы найти соответствующие значения y. Постройте пары, чтобы построить линию.
- Если вы знаете только одну координату точки на прямой, вы можете найти другую.
Для получения дополнительной информации
Следующие страницы раскрывают каждую из концепций на этой странице:Другие разделы о координатной геометрии
(C) Открытый справочник по математике, 2011 г.
Все права защищены.
декартовых координат
Декартовы координаты могут использоваться, чтобы точно определить, где мы находимся на карте или графике.
декартовых координат
Используя декартовы координаты, мы отмечаем точку на графике цифрой , насколько далеко вдоль и насколько далеко она выше :
| Точка (12,5) находится на 12 единиц вперед и на 5 единиц вверх. |
Их также называют прямоугольных координат , потому что это похоже на то, как мы формируем прямоугольник.
Ось X и Y
| Направление влево-вправо ( по горизонтали ) обычно называется X . | |
| Направление вверх-вниз ( по вертикали ) обычно называется Y . |
| Сложите их вместе на графике … | |
… и мы готовы к работе | |
Где они пересекаются — это точка «0»,
| |
Ось : опорная линия, от которой расстояния измеряются.
Множественное число Axis — Axes , произносится как ax-eez
Пример:
Балл (6,4) это
6 единиц в поперечнике (в направлении x ) и
На 4 единицы вверх (в направлении и )
Итак, (6,4) означает:
Идите по 6, затем вверх по 4, затем «начертите точку».
И вы можете запомнить какая ось какая по:
x — это КРЕСТ, поэтому x — ПОПЕРЕЧНО страницы.
Сложить как 2 числовые строки
Это как если бы мы соединили две числовые линии, одна идет влево-вправо, а другая — вниз-вверх.
Направление
При увеличении x точка перемещается на вправо . | |
По мере увеличения y точка перемещается на вверх на . |
Запись координат
Координаты всегда записываются в определенном порядке:
- сначала горизонтальное расстояние,
- , затем вертикальное расстояние.
Это называется «заказанной парой » ( пара номеров в специальном заказе )
И обычно числа разделяются запятыми, а вокруг всего этого ставятся круглые скобки:
(3,2)
Пример: (3,2) означает 3 единицы вправо и 2 единицы вверх
Пример: (0,5) означает 0 единиц вправо и 5 единиц вверх.
Другими словами, всего на 5 единиц больше.
Начало
Точке (0,0) дается специальное имя «Начало», а иногда и буква «О».
Абсцисса и Ордината
Вы можете услышать слова «Абсцисса» и «Ордината» … это просто значения x и y:
- Абсцисса: значение по горизонтали («x») в паре координат: расстояние от до до точки
- Ордината: значение по вертикали («y») в паре координат: насколько вверх или вниз точка
«Декартово»…?
Они называются декартовыми , потому что идея была развита математиком и философом Рене Декартом , который также был известен как Картезиус .
Он также известен тем, что сказал «Я думаю, следовательно, я» .
А как насчет отрицательных значений X и Y?
Как и в случае с числовой линией, у нас могут быть и отрицательные значения.
Отрицательный: начало с нуля и направление в противоположном направлении :
- Отрицательный x идет влево
- Отрицательный y идет вниз
Итак, для отрицательного числа:
|
Четыре квадрантаКогда мы включаем отрицательные значения, оси x и y делят пространство на 4 части: Квадранты I, II, III и IV (пронумерованы против часовой стрелки) |
В квадранте I и x, и y положительны, но…
- в квадранте II x отрицательно (y все еще положительно),
- в квадранте III и x, и y отрицательны, а
- в квадранте IV x снова положительно, а y отрицательно.
Как это:
|
Пример: Точка «А» (3,2) находится на 3 единицы вперед и на 2 единицы вверх.
Оба x и y положительны, так что эта точка находится в «квадранте I»
Пример: точка «C» (-2, -1) проходит на 2 единицы в отрицательном направлении и на 1 единицу вниз (т. Е. В отрицательном направлении).
Оба x и y отрицательны, так что эта точка находится в «квадранте III»
Примечание: слово Quadrant происходит от quad , что означает четыре . Например, четырех младенцев, рожденных при одном рождении, называют четвероногими , четвероногие животные — четвероногими .а четырехугольник — четырехсторонний многоугольник.
Размеры: 1, 2, 3 и более …
Подумайте об этом:
| 1 | В числовую строку можно заходить только: , поэтому для любой позиции нужно всего одно число |
|---|---|
| 2 | Декартовы координаты могут идти: , поэтому для любой позиции нужно два числа |
| 3 | Как определить точку в реальном мире (например, кончик носа)? Нам нужно знать:
, то есть три числа , или 3 измерения! |
3 Размеры
Декартовы координаты могут использоваться для определения местоположения точек в 3 измерениях, как в этом примере:
| Здесь точка (2, 4, 5) показана в трехмерных декартовых координатах. |
На самом деле, эту идею можно продолжить в четырех и более измерениях — я просто не могу придумать, как проиллюстрировать это для вас!
,