Диаметр окружности круга • как найти ⬅️ формула
Основные понятия
Прежде чем погружаться в последовательность расчетов, важно понять разницу между понятиями.
Окружность — замкнутая плоская кривая, все точки которой равноудалены от центра, которая лежит в той же плоскости.
Круг — множество точек на плоскости, которые удалены от центра на расстоянии равном радиусу.
Если говорить проще, окружность — это замкнутая линия, как, например, обруч и велосипедное колесо. Круг — плоская фигура, ограниченная окружностью, как апельсин и тарелка.
Диаметр — отрезок, который соединяет две точки окружности и проходит через центр.
Радиус — отрезок, который соединяет центр окружности и любую точку на ней.
Как узнать диаметр. Формулы
В данной теме нам предстоит узнать четыре формулы:
- Общая формула. Исходя из основных определений нам известно, что значение диаметра равно двум радиусам: D = 2 * R, D — диаметр, где R — радиус.

- Если перед нами стоит задача найти диаметр по длине окружности:
D = L : π, где L — длина, π — это константа, которая выражает отношение длины окружности к диаметру, она всегда равна 3,14.
Чтобы получить правильный ответ, можно поделить столбиком или использовать онлайн калькулятор.
- Если известна площадь круга:
D = 2 * √(А : π), где А — площадь.
Для проверки можно всегда воспользоваться формулой для поиска площади круга: A = π * r2.
- Если есть чертеж окружности:
- Начертить внутри круга прямую горизонтальную линию. Ее месторасположение не играет значительную роль.
- Отметить точки пересечения прямой и окружности.
- Начертить при помощи циркуля две окружности, первую — с центром в точке A, вторую — с центром в точке B.

- Провести прямую через две точки, в которых произошло пересечение. Диаметр равен этому отрезку.
- Теперь осталось измерить диаметр круга при помощи линейки. Получилось!
Эти простые формулы могут пригодиться не только на школьных уроках, а также, если вы решите освоить профессию дизайнера интерьера, архитектора или модельера одежды. Также ты можешь прочитать — как найти длину окружности?
Как рассчитать диаметр зная длину окружности. Площадь круга
Возьмем циркуль. Установим ножку циркуля с иглой в точку «O », а ножку циркуля с карандашом будем вращать вокруг этой точки. Таким образом, мы получим замкнутую линию. Такую замкнутую линию называют — окружность .
Рассмотрим более подробно окружность. Разберёмся, что называют центром, радиусом и диаметром окружности.
- (·)O — называется центром окружности.
- Отрезок, который соединяет
центр и любую точку окружности, называется радиусом окружности .
 Радиус окружности обозначается буквой «R
». На рисунке выше —
это отрезок «OA
».
Радиус окружности обозначается буквой «R
». На рисунке выше —
это отрезок «OA
». - Отрезок, который соединяет
две точки окружности и проходит через её центр, называется диаметром окружности .
Диаметр окружности обозначается буквой «D ». На рисунке выше — это отрезок «BC ».
На рисунке также видно, что диаметр равен двум радиусам. Поэтому справедливо выражение «D = 2R ».
Число π и длина окружности
Прежде чем разобраться, как считается длина окружности, необходимо выяснить, что такое число π (читается как «Пи»), которое так часто упоминают на уроках.
В далекие времена математики Древней Греции внимательно изучали окружность и пришли к выводу, что длина окружности и её диаметр взаимосвязаны.
Запомните!
Отношение длины окружности к её диаметру является одинаковым
для всех окружностей и обозначается греческой буквой π («Пи»).
π
≈ 3,14…
Число «Пи» относится к числам, точное значение которых записать невозможно
ни с помощью обыкновенных дробей, ни с помощью десятичных дробей.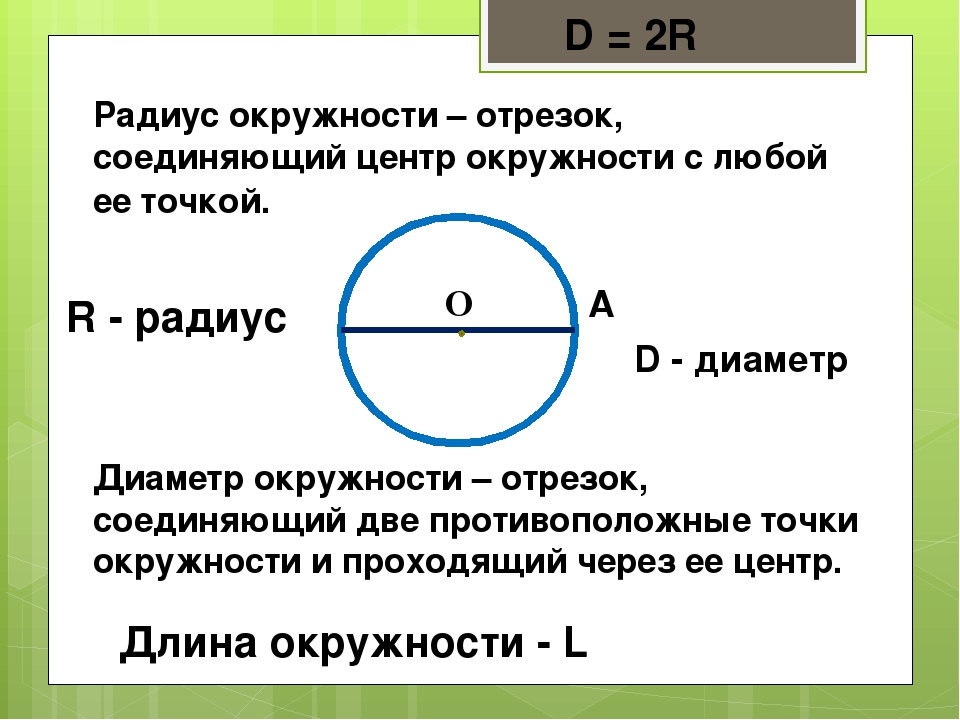 Нам
для наших вычислений достаточно использовать значение π
,
Нам
для наших вычислений достаточно использовать значение π
,
округленное до разряда сотых
π
≈ 3,14…
Теперь, зная, что такое число π , мы можем записать формулу длины окружности.
Запомните!
Длина окружности — это произведение числа π и диаметра окружности.
Длина окружности обозначается буквой «С
» (читается как «Це»).
C = π
D
C = 2π
R , так как D = 2R
Как найти длину окружности
Чтобы закрепить полученные знания, решим задачу на окружности.
Виленкин 6 класс. Номер 831
Условие задачи:
Найдите длину окружности, радиус которой равен 24 см. Число π округлите до сотых.
Воспользуемся формулой длины окружности:
C = 2π R ≈ 2 · 3,14 · 24 ≈ 150,72 см
Разберем обратную задачу, когда мы знаем длину окружности, а нас просят найти её диаметр.
Виленкин 6 класс. Номер 835
Условие задачи:
Определите диаметр окружности, если
её длина равна 56,52
дм. (π
≈ 3,14
).
(π
≈ 3,14
).
Выразим из формулы длины окружности диаметр.
C = π
D
D = С / π
D = 56,52 / 3,14 = 18
дм
Хорда и дуга окружности
На рисунке ниже отметим на окружности две точки «A » и «B ». Эти точки делят окружность на две части, каждую из которых называют дугой . Это синяя дуга «AB » и черная дуга «AB ». Точки «A » и «B » называют концами дуг .
И круг — геометрические фигуры, взаимосвязанные между собой. есть граничная ломаная линия (кривая) круга ,
Определение. Окружность — замкнутая кривая, каждая точка которой равноудалена от точки, называемой центром окружности.
Для построения окружности выбирается произвольная точка О, принятая за центр окружности, и с помощью циркуля проводится замкнутая линия.
Если точку О центра окружности соединить с произвольными точками на окружности, то все полученные отрезки будут между собой равны, и называются такие отрезки радиусами, сокращенно обозначаются латинской маленькой или большой буквой «эр» (r или R ). Радиусов в окружности можно провести столько же, сколько точек имеет длина окружности.
Радиусов в окружности можно провести столько же, сколько точек имеет длина окружности.
Отрезок, соединяющий две точки окружности и проходящий через ее центр, называется диаметром. Диаметр состоит из двух радиусов , лежащих на одной прямой. Диаметр обозначается латинской маленькой или большой буквой «дэ» (d или D ).
Правило.
d = 2r
D = 2R
Длина окружности вычисляется по формуле и зависит от радиуса (диаметра) окружности. В формуле присутствует число ¶, которое показывает во сколько раз длина окружности больше, чем ее диаметр. Число ¶ имеет бесконечное число знаков после запятой. Для вычислений принято ¶ = 3,14.
Длина окружности обозначается латинской большой буквой «цэ» (C ). Длина окружности пропорциональна ее диаметру. Формулы для расчета длины окружности по ее радиусу и диаметру:
C = ¶d
C = 2¶r
- Примеры
- Дано: d = 100 см.

- Длина окружности: C = 3,14 * 100 см = 314 см
- Дано: d = 25 мм.
- Длина окружности: С = 2 * 3,14 * 25 = 157 мм
Секущая окружности и дуга окружности
Всякая секущая (прямая линия) пересекает окружность в двух точках и делит ее на две дуги. Величина дуги окружности зависит от расстояния между центром и секущей и измеряется по замкнутой кривой от первой точки пересечения секущей с окружностью до второй.
Дуги окружности делятся секущей на большую и малую, если секущая не совпадает с диаметром, и на две равные дуги, если секущая проходит по диаметру окружности.
Если секущая проходит через центр окружности, то ее отрезок, расположенный между точками пересечения с окружностью, есть диаметр окружности, или самая большая хорда окружности.
Чем дальше секущая расположена от центра окружности, тем меньше градусная мера меньшей дуги окружности и больше — большей дуги окружности, а отрезок секущей, называемый хордой , уменьшается по мере удаления секущей от центра окружности.
Определение. Кругом называется часть плоскости, лежащая внутри окружности.
Центр, радиус, диаметр окружности являются одновременно центром, радиусом и диаметром соответствующего круга.
Так как круг — это часть плоскости, то одним из его параметров является площадь.
Правило. Площадь круга (S ) равна произведению квадрата радиуса (r 2 ) на число ¶.
- Примеры
- Дано: r = 100 см
- Площадь круга:
- S = 3,14 * 100 см * 100 см = 31 400 см 2 ≈ 3м 2
- Дано: d = 50 мм
- Площадь круга:
- S = ¼ * 3,14 * 50 мм * 50 мм = 1 963 мм 2 ≈ 20 см 2
Если в круге провести два радиуса к разным точкам окружности, то образуется две части круга, которые называется секторами . Если в круге провести хорду, то часть плоскости между дугой и хордой называется сегментом окружности .
§ 117. Длина окружности и площадь круга.1. Длина окружности. Окружностью называется замкнутая плоская кривая линия, все точки которой находятся на равном расстоянии от одной точки (О), называемой центром окружности (рис.
Окружность вычерчивается с помощью циркуля. Для этого острую ножку циркуля ставят в центр, а другую (с карандашом) вращают вокруг первой до тех пор, пока конец карандаша не вычертит полной окружности. Расстояние от центра до любой точки окружности называется её радиусом. Из определения следует, что все радиусы одной окружности равны между собой.
Отрезок прямой линии (АВ), соединяющий две любые точки окружности и проходящий через её центр, называется диаметром . Все диаметры одной окружности равны между собой; диаметр равен двум радиусам.
Как найти длину окружности? Практически в некоторых случаях длину окружности можно найти путём непосредственного измерения. Это можно сделать, например, при измерении окружности сравнительно небольших предметов (ведро, стакан и т. п.). Для этого можно воспользоваться рулеткой, тесьмой или шнуром.
В математике применяется приём косвенного определения длины окружности. Он состоит в вычислении по готовой формуле, которую мы сейчас выведем.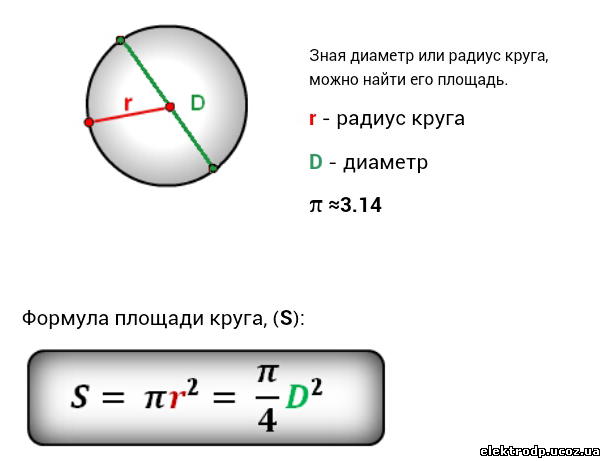
Если мы возьмём несколько больших и малых круглых предметов (монета, стакан, ведро, бочка и т. д.) и измерим у каждого из них длину окружности и длину диаметра, то получим для каждого предмета два числа (одно, измеряющее длину окружности, и другое — длину диаметра). Естественно, что для малых предметов эти числа будут небольшими, а для крупных — большими.
Однако если мы в каждом из этих случаев возьмём отношение полученных двух чисел (длины окружности и диаметра), то при тщательном выполнении измерения найдём почти одно и то же число. Обозначим длину окружности буквой С , длину диаметра буквой D , тогда отношение их будет иметь вид С: D . Фактические измерения всегда сопровождаются неизбежными неточностями. Но, выполнив указанный опыт и произведя необходимые вычисления, мы получим для отношения С: D примерно следующие числа: 3,13; 3,14; 3,15. Эти числа очень мало отличаются одно от другого.
В математике путём теоретических соображений установлено, что искомое отношение С: D никогда не меняется и оно равно бесконечной непериодической дроби, приближённое значение которой с точностью до десятитысячных долей равно 3,1416 . Это значит, что всякая окружность длиннее своего диаметра в одно и то же число раз. Это число принято обозначать греческой буквой π (пи). Тогда отношение длины окружности к диаметру запишется так: С: D = π . Мы будем ограничивать это число только сотыми долями, т. е. брать π = 3,14.
Это значит, что всякая окружность длиннее своего диаметра в одно и то же число раз. Это число принято обозначать греческой буквой π (пи). Тогда отношение длины окружности к диаметру запишется так: С: D = π . Мы будем ограничивать это число только сотыми долями, т. е. брать π = 3,14.
Напишем формулу для определения длины окружности.
Так как С: D = π , то
C = πD
т. е. длина окружности равна произведению числа π на диаметр.
Задача 1. Найти длину окружности (С ) круглой комнаты, если диаметр её D = 5,5 м.
Принимая во внимание изложенное выше, мы должны для решения этой задачи увеличить диаметр в 3,14 раза:
5,5 3,14 = 17,27 {м).
Задача 2. Найти радиус колеса, у которого длина окружности 125,6 см.
Эта задача обратна предыдущей. Найдём диаметр колеса:
125,6: 3,14 = 40 (см).
Найдём теперь радиус колеса:
40: 2 = 20 (см).
2. Площадь круга. Чтобы определить площадь круга, можно было бы начертить на бумаге круг данного радиуса, покрыть его прозрачной клетчатой бумагой и потом сосчитать клетки, находящиеся внутри окружности (рис. 28).
Но такой способ неудобен по многим причинам. Во-первых, вблизи контура круга получается ряд неполных клеток, о величине которых судить трудно. Во-вторых, нельзя покрыть листом бумаги большой предмет (круглую клумбу, бассейн, фонтан и др.). В-третьих, подсчитав клетки, мы всё-таки не получаем никакого правила, позволяющего нам решать другую подобную задачу. В силу этого поступим иначе. Сравним круг с какой-нибудь знакомой нам фигурой и сделаем это следующим образом: вырежем круг из бумаги, разрежем его сначала по диаметру пополам, затем каждую половину разрежем ещё пополам, каждую четверть — ещё пополам и т. д., пока не разрежем круг, например, на 32 части, имеющие форму зубцов (рис. 29).
Затем сложим их так, как показано на рисунке 30, т. е. сначала расположим 16 зубцов в виде пилы, а затем в образовавшиеся отверстия вложим 15 зубцов и, наконец, последний оставшийся зубец разрежем по радиусу пополам и приложим одну часть слева, другую — справа. Тогда получится фигура, напоминающая прямоугольник.
е. сначала расположим 16 зубцов в виде пилы, а затем в образовавшиеся отверстия вложим 15 зубцов и, наконец, последний оставшийся зубец разрежем по радиусу пополам и приложим одну часть слева, другую — справа. Тогда получится фигура, напоминающая прямоугольник.
Длина этой фигуры (основание) равна приблизительно длине полуокружности, а высота — приблизительно радиусу. Тогда площадь такой фигуры можно найти путём умножения чисел, выражающих длину полуокружности и длину радиуса. Если обозначим площадь круга буквой S , длину окружности буквой С , радиус буквой r , то можем записать формулу для определения площади круга:
которая читается так: площадь круга равна длине полуокружности, умноженной на радиус.
Задача. Найти площадь круга, радиус которого равен 4 см. Найдём сначала длину окружности, потом длину полуокружности, а затем умножим её на радиус.
1) Длина окружности С = π D = 3,14 8 = 25,12 (см).
2) Длина половины окружности C / 2 = 25,12: 2= 12,56 (см).
3) Площадь круга S = C / 2 r = 12,56 4 = 50,24 (кв. см).
§ 118. Поверхность и объём цилиндра.
Задача 1. Найти полную поверхность цилиндра, у которого диаметр основания 20,6 см и высота 30,5 см.
Форму цилиндра (рис. 31) имеют: ведро, стакан (не гранёный), кастрюля и множество других предметов.
Полная поверхность цилиндра (как и полная поверхность прямоугольного параллелепипеда) состоит из боковой поверхности и площадей двух оснований (рис. 32).
Чтобы наглядно представить себе, о чём идёт речь, необходимо аккуратно сделать модель цилиндра из бумаги. Если мы от этой модели отнимем два основания, т. е. два круга, а боковую поверхность разрежем вдоль и развернём, то будет совершенно ясно, как нужно вычислять полную поверхность цилиндра. Боковая поверхность развернётся в прямоугольник, основание которого равно длине окружности.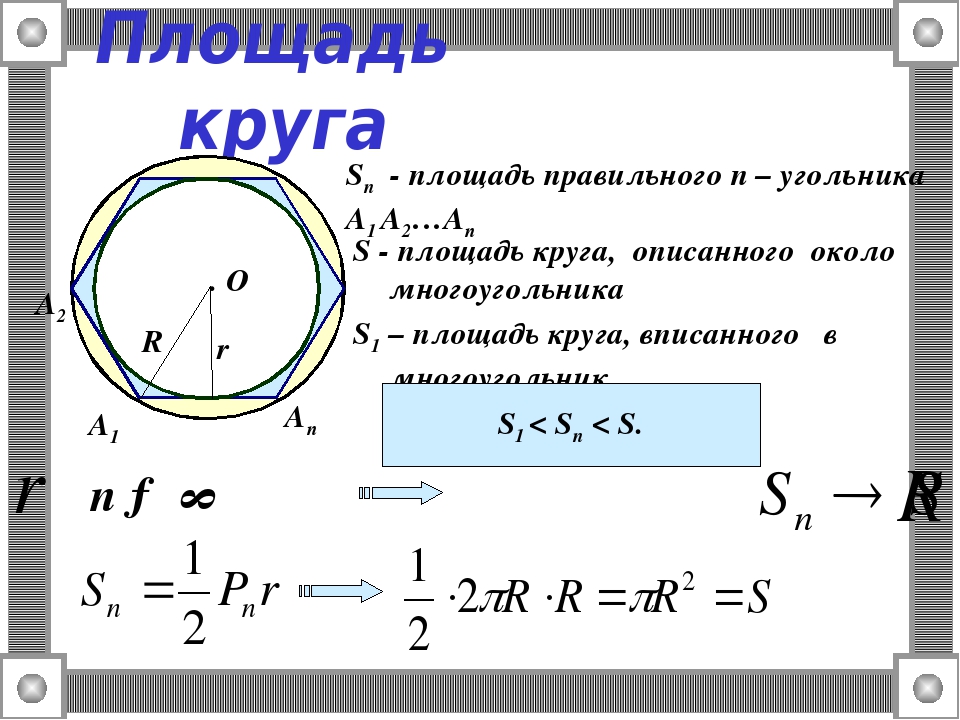 Поэтому решение задачи будет иметь вид:
Поэтому решение задачи будет иметь вид:
1) Длина окружности: 20,6 3,14 = 64,684 (см).
2) Площадь боковой поверхности: 64,684 30,5= 1972,862(кв.см).
3) Площадь одного основания: 32,342 10,3 = 333,1226 (кв.см).
4) Полная поверхность цилиндра:
1972,862 + 333,1226 + 333,1226 = 2639,1072 (кв. см) ≈ 2639 (кв. см).
Задача 2. Найти объём железной бочки, имеющей форму цилиндра с размерами: диаметр основания 60 см и высота 110 см.
Чтобы вычислить объём цилиндра, нужно припомнить, как мы вычисляли объём прямоугольного параллелепипеда (полезно прочитать § 61).
Единицей измерения объёма у нас будет кубический сантиметр. Сначала надо узнать, сколько кубических сантиметров можно расположить на площади основания, а затем найденное число умножить на высоту.
Чтобы узнать, сколько кубических сантиметров можно уложить на площади основания, надо вычислить площадь основания цилиндра. Так как основанием служит круг, то нужно найти площадь круга.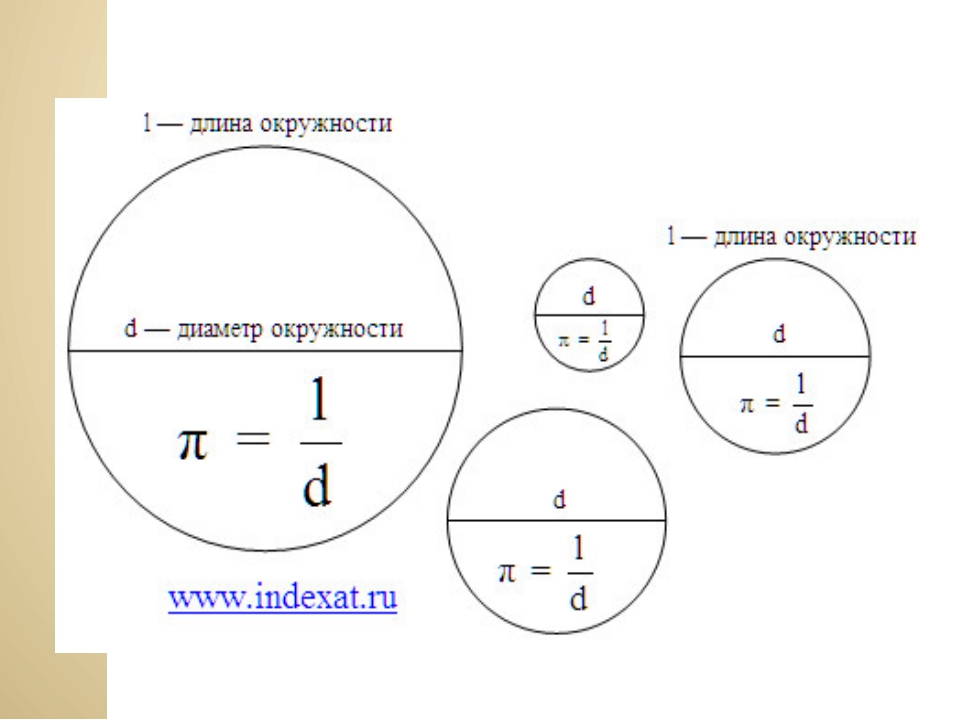 Затем для определения объёма умножить её на высоту. Решение задачи имеет вид:
Затем для определения объёма умножить её на высоту. Решение задачи имеет вид:
1) Длина окружности: 60 3,14 = 188,4 (см).
2) Площадь круга: 94,2 30 = 2826 (кв. см).
3) Объём цилиндра: 2826 110 = 310 860 (куб. см).
Ответ. Объём бочки 310,86 куб. дм.
Если обозначим объём цилиндра буквой V , площадь основания S , высоту цилиндра H , то можно написать формулу для определения объёма цилиндра:
V = S H
которая читается так: объём цилиндра равен площади основания, умноженной на высоту.
§ 119. Таблицы для вычисления длины окружности по диаметру.
При решении различных производственных задач часто приходится вычислять длину окружности. Представим себе рабочего, который изготовляет круглые детали по указанным ему диаметрам. Он должен всякий раз, зная диаметр, вычислить длину окружности. Чтобы сэкономить время и застраховать себя от ошибок, он обращается к готовым таблицам, в которых указаны диаметры и соответствующие им длины окружностей.
Приведём небольшую часть таких таблиц и расскажем, как ими пользоваться.
Пусть известно, что диаметр окружности равен 5 м. Ищем в таблице в вертикальном столбце под буквой D число 5. Это длина диаметра. Рядом с этим числом (вправо, в столбце под названием «Длина окружности») увидим число 15,708 (м). Совершенно так же найдём, что если D = 10 см, то длина окружности равна 31,416 см.
По этим же таблицам можно производить и обратные вычисления. Если известна длина окружности, то можно найти в таблице соответствующий ей диаметр. Пусть длина окружности равна приблизительно 34,56 см. Найдём в таблице число, наиболее близкое к данному. Таковым будет 34,558 (разница 0,002). Соответствующий такой длине окружности диаметр равен приблизительно 11 см.
Таблицы, о которых здесь сказано, имеются в различных справочниках. В частности, их можно найти в книжке «Четырёхзначные математические таблицы» В. М. Брадиса. и в задачнике по арифметике С. А. Пономарёва и Н.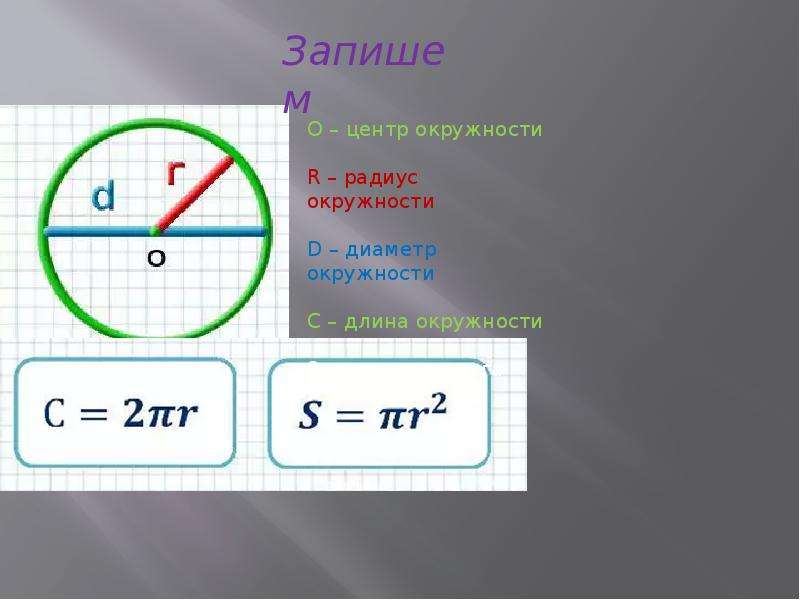 И. Сырнева.
И. Сырнева.
Окружность — замкнутая кривая, все точки которой находятся на одинаковом расстоянии от центра. Эта фигура является плоской. Поэтому решение задачи, вопрос которой состоит в том, как найти длину окружности, является достаточно простым. Все имеющиеся способы, мы рассмотрим в сегодняшней статье.
Описания фигуры
Кроме достаточно простого описательного определения существуют еще три математических характеристики окружности, которые уже сами по себе содержат ответ на вопрос, как найти длину окружности:
- Состоит из точек A и B и всех других, из которых AB можно увидеть под прямым углом. Диаметр данной фигуры равен длине рассматриваемого отрезка.
- Включает исключительно такие точки X, что отношение AX/BX неизменно и не равно единице. Если это условие не соблюдается, то это не окружность.
- Состоит из точек, для каждой из которых выполняется следующее равенство: сумма квадратов расстояний до двух других — это заданная величина, которая всегда больше половине длины отрезка между ними.

Терминология
Не у всех в школе был хороший учитель математики. Поэтому ответ на вопрос, как найти длину окружности, осложняется еще и тем, что не все знают основные геометрические понятия. Радиус — отрезок, который соединяет центр фигуры с точкой на кривой. Особым случаем в тригонометрии является единичная окружность. Хорда — отрезок, который соединяет две точки кривой. Например, под это определение подпадает уже рассмотренный AB. Диаметр — это хорда, проходящая через центр. Число π равно длине единичной полуокружности.
Основные формулы
Из определений непосредственно следуют геометрические формулы, которые позволяют рассчитать основные характеристики окружности:
- Длина равна произведению числа π и диаметра. Формулу обычно записывают следующим образом: C = π*D.
- Радиус равен половине диаметра. Его также можно рассчитать, вычислив частное от деления длины окружности на удвоенное число π. Формула выглядит так: R = C/(2* π) = D/2.
- Диаметр равен частному от деления длины окружности на π или удвоенному радиусу.
 Формула является достаточно простой и выглядит так: D = C/π = 2*R.
Формула является достаточно простой и выглядит так: D = C/π = 2*R. - Площадь круга равна произведению числа π и квадрата радиуса. Аналогично в этой формуле можно использовать диаметр. В этом случае площадь будет равна частному от деления произведения числа π и квадрата диаметра на четыре. Формулу можно записать следующим образом: S = π*R 2 = π*D 2 /4.
Как найти длину окружности по диаметру
Для простоты объяснения обозначим буквами необходимые для расчета характеристики фигуры. Пусть C — это искомая длина, D — ее диаметр, а число π приблизительно равно 3,14. Если у нас есть всего одна известная величина, то задачу можно считать решенной. Зачем это нужно в жизни? Предположим мы решили обнести круглый бассейн забором. Как вычислить необходимое количество столбиков? И тут на помощь приходит умение, как вычислить длину окружности. Формула выглядит следующим образом: C = π D. В нашем примере диаметр определяется на основе радиуса бассейна и необходимого расстояния до забора. Например, предположим, что наш домашний искусственный водоем составляет 20 метров в ширину, а столбики мы собираемся ставить на десятиметровом расстоянии от него. Диаметр получившейся окружности равен 20 + 10*2 = 40 м. Длина — 3,14*40 = 125,6 метров. Нам понадобятся 25 столбиков, если промежуток между ними будет около 5 м.
Например, предположим, что наш домашний искусственный водоем составляет 20 метров в ширину, а столбики мы собираемся ставить на десятиметровом расстоянии от него. Диаметр получившейся окружности равен 20 + 10*2 = 40 м. Длина — 3,14*40 = 125,6 метров. Нам понадобятся 25 столбиков, если промежуток между ними будет около 5 м.
Длина через радиус
Как всегда, начнем с присвоения характеристикам окружности букв. На самом деле они являются универсальными, поэтому математикам из разных стран вовсе не обязательно знать язык друг друга. Предположим, что C — это длина окружности, r — ее радиус, а π приблизительно равно 3,14. Формула выглядит в этом случае следующим образом: C = 2*π*r. Очевидно, что это абсолютно правильное равенство. Как мы уже разобрались диаметр окружности равен ее удвоенному радиусу, поэтому эта формула так и выглядит. В жизни этот способ тоже может часто пригодиться. Например, мы печем торт в специальной раздвижной форме. Чтобы он не испачкался, нам нужна декоративная обертка. Но как вырезать круг нужного размера. Здесь на помощь и приходит математика. Те, кто знают, как узнать длину окружности, сразу скажут, что нужно умножить число π на удвоенный радиус формы. Если ее радиус равен 25 см, то длина будет составлять 157 сантиметров.
Но как вырезать круг нужного размера. Здесь на помощь и приходит математика. Те, кто знают, как узнать длину окружности, сразу скажут, что нужно умножить число π на удвоенный радиус формы. Если ее радиус равен 25 см, то длина будет составлять 157 сантиметров.
Примеры задач
Мы уже рассмотрели несколько практических случаев полученных знаний о том, как узнать длину окружности. Но зачастую нас заботят не они, а реальные математические задачи, которые содержатся в учебнике. Ведь за них учитель выставляет баллы! Поэтому давайте рассмотрим задачу повышенной сложности. Предположим, что длина окружности составляет 26 см. Как найти радиус такой фигуры?
Решение примера
Для начала запишем, что нам дано: C = 26 см, π = 3,14. Также вспомним формулу: C = 2* π*R. Из нее можно извлечь радиус окружности. Таким образом, R= C/2/π. Теперь приступим к непосредственному расчету. Сначала делим длину на два. Получаем 13. Теперь нужно разделить на значение числа π: 13/3,14 = 4,14 см. Важно не забыть записать ответ правильно, то есть с единицами измерения, иначе теряется весь практический смысл подобных задач. К тому же за подобную невнимательность можно получить оценку на один балл ниже. И как бы досадно ни было, придется мириться с таким положением вещей.
Важно не забыть записать ответ правильно, то есть с единицами измерения, иначе теряется весь практический смысл подобных задач. К тому же за подобную невнимательность можно получить оценку на один балл ниже. И как бы досадно ни было, придется мириться с таким положением вещей.
Не так страшен зверь, как его малюют
Вот мы и разобрались с такой непростой на первый взгляд задачей. Как оказалось, нужно просто понимать значение терминов и запомнить несколько легких формул. Математика — это не так страшно, нужно только приложить немного усилий. Так что геометрия ждет вас!
В процессе выполнения строительных работ в быту или на производстве может появиться необходимость в измерении диаметра трубы, которая уже вмонтирована в систему водоснабжения или канализации. Также знать данный параметр необходимо на стадии проектирования прокладки инженерных коммуникаций.
Отсюда возникает необходимость разобраться с тем, как определить диаметр трубы. Выбор конкретного способа выполнения измерений зависит от размеров объекта и от того, доступно ли расположение трубопровода.
Определение диаметра в бытовых условиях
До того, как замерить диаметр трубы, нужно приготовить следующие инструменты и устройства:
- рулетка или стандартная линейка;
- штангенциркуль;
- фотоаппарат — его задействуют при необходимости.
Если трубопровод доступен для проведения замеров, а торцы труб можно без проблем измерить, тогда достаточно иметь в распоряжении обычную линейку или рулетку. При этом следует учитывать, что используют такой метод, когда к точности предъявляются минимальные требования.
В этом случае выполняют измерение диаметра труб в такой последовательности:
- Подготовленные инструменты прикладывают к месту, где находится самая широкая часть торца изделия.
- Потом отсчитывают количество делений, соответствующих размеру диаметра.
Данный способ позволяет узнавать параметры трубопровода с точностью, составляющую несколько миллиметров.
Для измерения внешнего диаметра труб с небольшим сечением можно задействовать такой инструмент как штангенциркуль:
- Раздвигают его ножки и прикладывают к торцу изделия.

- Затем их нужно сдвинуть так, чтобы они оказались плотно прижатыми к наружной стороне стенок трубы.
- Ориентируясь на шкалу значений приспособления, узнают требуемый параметр.
Этот метод определения диаметра трубы дает довольно точные результаты, до десятых миллиметра.
Когда трубопровод недоступен для обмера и является частью уже функционирующей конструкции водоснабжения или газовой магистрали, поступают следующим образом: штангенциркуль прикладывают к трубе, к ее боковой поверхности. Таким способом обмеряют изделие в тех случаях, если у измерительного приспособления длина ножек превышает половину диаметра трубной продукции.
Нередко в бытовых условиях возникает необходимость узнать, как измерять диаметр трубы, имеющей большое сечение. Существует простой вариант, как это сделать: достаточно знать длину окружности изделия и константу π, равную 3,14.
Сначала при помощи рулетки или куска шнура обмеряют трубу в обхвате. Потом подставляют известные величины в формулу d=l:π, где:
Потом подставляют известные величины в формулу d=l:π, где:
d – определяемый диаметр;
l – длина измеренной окружности.
К примеру, обхват трубы составляет 62,8 сантиметра, тогда d = 62,8:3,14 =20 сантиметров или 200 миллиметров.
Бывают ситуации, когда проложенный трубопровод полностью недоступен. Тогда можно применить метод копирования. Суть его заключается в том, что к трубе прикладывают измерительный инструмент или небольшой по размеру предмет, у которого известны параметры.
К примеру, это может быть коробок спичек, длина которого равна 5 сантиметрам. Потом этот участок трубопровода фотографируют. Последующие вычисления выполняют по фотографии. На снимке измеряют видимую толщину изделия в миллиметрах. Потом нужно перевести все полученные величины в реальные параметры трубы с учетом масштаба произведенной фотосъемки.
Измерение диаметров в производственных условиях
На больших строящихся объектах трубы до начала проведения монтажа в обязательном порядке подвергают входному контролю. Прежде всего, проверяют сертификаты и маркировку, нанесенную на трубную продукцию.
Прежде всего, проверяют сертификаты и маркировку, нанесенную на трубную продукцию.
Документация должна содержать определенную информацию, касающуюся труб:
- номинальные размеры;
- номер и дата ТУ;
- марка металла или вид пластика;
- номер товарной партии;
- итоги проведенных испытаний;
- хим. анализ выплавки;
- тип термической обработки;
- результаты рентгеновской дефектоскопии.
Кроме этого, на поверхности всех изделий на расстоянии примерно 50 сантиметров от одного из торцов всегда наносят маркировку, содержащую:
- наименование производителя;
- номер плавки;
- номер изделия и его номинальные параметры;
- дату изготовления;
- эквивалент углерода.
Длины труб в производственных условиях определяют мерной проволокой. Также не возникает сложностей с тем, как измерить диаметр трубы рулеткой.
Для изделий первого класса допустимой величиной отклонения в одну или другую сторону от заявленной длины являются 15 миллиметров. Для второго класса –100 миллиметров.
Для второго класса –100 миллиметров.
У труб наружный диаметр сверяют, пользуясь формулой d = l:π-2Δр-0,2 мм, где кроме вышеописанных значений:
Δр – толщина материала рулетки;
0,2 миллиметра– припуск на прилегание инструмента к поверхности.
Допускается отклонение величины внешнего диаметра от заявленной производителем:
- для продукции с сечением не более 200 миллиметров–1,5 миллиметра;
- для больших труб – 0,7%.
В последнем случае для проверки трубной продукции пользуются ультразвуковыми измерительными приборами. Для определения толщины стенок задействуют штангенциркули, у которых деление на шкале соответствует 0,01 миллиметра. Минусовой допуск не должен превышать 5% номинальной толщины. При этом кривизна не может быть более 1,5 миллиметра на 1 погонный метр.
Из вышеописанной информации ясно, что несложно разобраться с тем, как определить диаметр трубы по длине окружности или при помощи несложных измерительных инструментов.
Как вычислить диаметр трубы по окружности
Онлайн калькулятор диаметра круга. Как узнать диаметр круга, окружности.
При помощи нашего калькулятора вы легко сможете узнать диаметр круга или окружности.
Для того что бы вычислить диаметр круга необходимо знать его длину или площадь. Если нам известа одна из указаннх величин, для нас не составит труда вычислить диаметр круга.
Диаметр круга рассчитывается по следующим формулам:
- Если нам известна длина:
Формула для расчета диаметра круга через его длину:
D=P/π - Если нам известна площадь:
Формула для расчета диаметр круга через площадь:
D=2√S/π - Если нам известен диаметр:
Формула для расчета диаметр круга через радиус:
D=2R
Где D — диаметр круга, S – площадь круга, P – длина круга, R — радиус, π – число Пи которое всегда примерно равно 3,14.
Определение диаметра круга и калькулятор — Math Open Reference
r
Определение диаметра круга и калькулятор — Math Open Reference Расстояние по окружности до его центральной точки.
Попробуйте это Перетащите оранжевую точку. Синяя линия всегда будет диаметром круга.
Диаметр круга — это длина линии, проходящей через центр и касающейся двух точек на его крае. На рисунке выше перетащите оранжевые точки и убедитесь, что диаметр никогда не меняется.
Иногда слово «диаметр» используется для обозначения самой линии. В этом смысле вы можете увидеть «нарисуйте диаметр круга». В более современном понимании это длина линии, поэтому ее называют «диаметр круга составляет 3,4 сантиметра».
Диаметр также составляет аккорд. Хорда — это линия, соединяющая любые две точки на окружности. Диаметр — это хорда, проходящая через центральную точку круга. Это самый длинный аккорд любого круга.
Центр круга — это середина его диаметра. То есть делит его на две равные части, каждая из которых является радиус круга. Радиус составляет половину диаметра.
Если знаешь радиус
Учитывая радиус круга, диаметр можно рассчитать по формуле где:R — радиус окружности
Если знать окружность
Если вам известна длина окружности, диаметр можно найти по формуле, где:
C — длина окружности
π — Пи, примерно 3.
 142
142Если известен район
Если вам известна площадь круга, диаметр можно найти по формуле, где:
A — площадь круга
π — Пи, примерно 3,142
Калькулятор
Воспользуйтесь калькулятором выше, чтобы вычислить свойства круга.
Введите любое одно значение, и остальные три будут рассчитаны. Например: введите диаметр и нажмите «Рассчитать». Будут рассчитаны площадь, радиус и окружность.
Точно так же, если вы войдете в область, будет вычислен радиус, необходимый для получения этой области, а также диаметр и окружность.
Сопутствующие товары
Радиус Радиус — это расстояние от центра до любой точки на краю. Как видно из рисунка выше, диаметр равен двум линиям радиуса, расположенным вплотную друг к другу, поэтому диаметр всегда в два раза больше радиуса. Посмотреть радиус круга
Окружность Окружность — это расстояние по краю круга.Видеть Окружность круга для подробностей.
Что попробовать
- На рисунке выше нажмите «Сброс» и перетащите любую оранжевую точку.
 Обратите внимание, что диаметр в любой точке круга имеет одинаковую длину.
Обратите внимание, что диаметр в любой точке круга имеет одинаковую длину. - Щелкните «Показать радиус». Перетащите оранжевую точку в конце радиусной линии. Обратите внимание, что радиус всегда равен половине диаметра.
- Снимите флажок «фиксированный размер». Повторите вышесказанное и обратите внимание на то, что радиус всегда равен половине диаметра, независимо от размера круга.
Теорема Фалеса
Теорема Фалеса утверждает, что диаметр круга подает прямой угол в любую точку окружности. (см. рисунок справа).Независимо от того, где находится точка, треугольник образуется всегда прямоугольный треугольник. См. Теорему Фалеса для интерактивной анимации этой концепции.
Другие темы в круге
Общие
Уравнения окружности
Углы по окружности
Дуги
(C) Открытый справочник по математике, 2011 г.
Все права защищены.
Калькулятор кругов
Что такое площадь и периметр круга?
Набор точек на плоскости, одинаково удаленных от данной точки $ O $, представляет собой круг. Точка $ O $ называется центром окружности. Расстояние от центра круга до любой точки на окружности называется радиусом этого круга. Радиус круга должен быть положительным вещественным числом. Окружность с центром $ O $ и радиусом $ r $ обозначается $ c (O, r) $.
Точка $ O $ называется центром окружности. Расстояние от центра круга до любой точки на окружности называется радиусом этого круга. Радиус круга должен быть положительным вещественным числом. Окружность с центром $ O $ и радиусом $ r $ обозначается $ c (O, r) $.
Расстояние вокруг круга называется периметром или окружностью круга.Обычно обозначается как $ C $.
Если все вершины многоугольника принадлежат окружности, то многоугольник называется вписанным. Если все стороны многоугольника касаются окружности, то многоугольник называется описанным.
Метод определения длины окружности: Впишем в круг правильный многоугольник, например квадрат. Затем удвойте количество сторон этого многоугольника, чтобы получить восьмиугольник. Если продолжить процесс удвоения количества сторон правильные вписанные многоугольники, мы получаем бесконечную последовательность периметров правильных многоугольников, которая увеличивается.Эта возрастающая последовательность ограничена, поскольку периметры всех вписанных выпуклых многоугольников меньше периметра любого описанного многоугольника. Итак, эта возрастающая последовательность периметров имеет определенный предел. Этот предел — окружность. Следовательно, длина окружности — это предел периметра правильного многоугольника, вписанного в окружность, когда число его вершин бесконечно удваивается. Поскольку все круги похожи, отношение длины окружности к диаметру одинаковое для всех кругов.Это отношение длины окружности к диаметру обозначается греческой буквой $ \ pi \ приблизительно 3,14 $. Таким образом, формула длины окружности
Итак, эта возрастающая последовательность периметров имеет определенный предел. Этот предел — окружность. Следовательно, длина окружности — это предел периметра правильного многоугольника, вписанного в окружность, когда число его вершин бесконечно удваивается. Поскольку все круги похожи, отношение длины окружности к диаметру одинаковое для всех кругов.Это отношение длины окружности к диаметру обозначается греческой буквой $ \ pi \ приблизительно 3,14 $. Таким образом, формула длины окружности
$$ C = D \ times \ pi $$
или$$ C = 2 \ times r \ times \ pi $$
Архимед [Heath, T. L., it A History of Greek Mathematics, 2 vol., Oxford, 1921] дал приближение к $ \ pi $ с помощью $$ \ pi \ приблизительно \ frac {22} 7 = 3,142857142857 … $$
Метод определения площади круга: Площадь круга — это количество квадратных единиц внутри этого круга.2) $ и т. Д.
Работа с площадью и периметром круга со ступенями показывает полный пошаговый расчет для нахождения окружности и площади круга с радиусом длиной $ 8 \; in $ с использованием формул окружности и площади .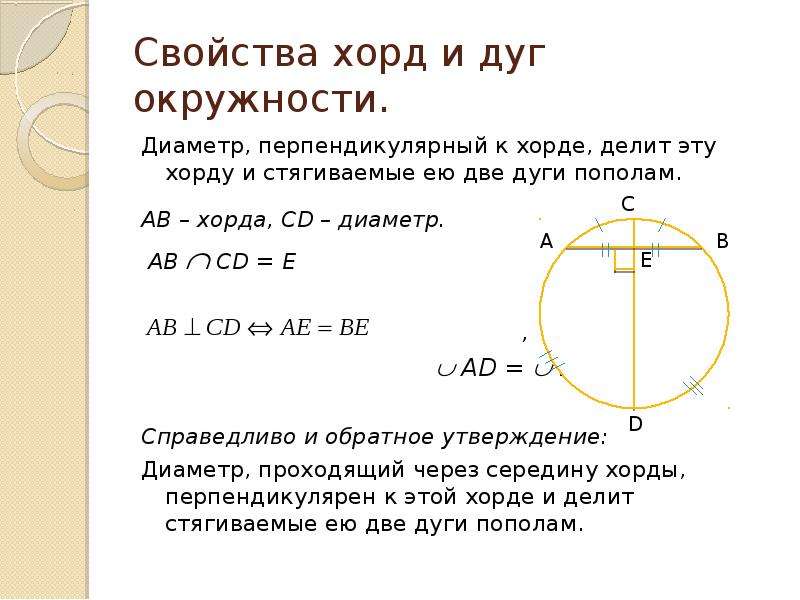 За любое другое значение длины радиуса круга, просто введите положительное действительное число и нажмите кнопку СОЗДАТЬ РАБОТУ. Учащиеся начальной школы могут использовать этот круговой калькулятор для создания работы, проверки результатов периметра и площади двухмерных фигур или эффективного выполнения домашних заданий.Они могут использовать эти методы для определения площади и длины частей круга.
За любое другое значение длины радиуса круга, просто введите положительное действительное число и нажмите кнопку СОЗДАТЬ РАБОТУ. Учащиеся начальной школы могут использовать этот круговой калькулятор для создания работы, проверки результатов периметра и площади двухмерных фигур или эффективного выполнения домашних заданий.Они могут использовать эти методы для определения площади и длины частей круга.
Калькулятор длины и диаметра в объем
Нажмите, чтобы перезагрузить страницу с уникальным веб-адресом для добавления в закладки или обмена текущими настройками
✕ очистить настройки
К сожалению, здесь не удалось отобразить графику, потому что ваш браузер не поддерживает холст HTML5.Приложения
Используйте этот калькулятор длины x диаметра для определения объема в следующих приложениях:
- Емкость вертикального цилиндрического контейнера для хранения от высоты и диаметра контейнера
- Горизонтальный цилиндрический резервуар вместимостью от длины и высоты резервуара
- Внутренний объем трубки для определения пропускной способности по длине и внутреннему диаметру трубки
- Количество воды, содержащейся в колодце или скважине, исходя из глубины воды и диаметра скважины
- Объем металлических стержней или кабелей по длине и диаметру, который затем может использоваться для расчета веса, если плотность материала известна
- Количество воды, которое может храниться в круглом резервуаре для хранения воды
Сопутствующие инструменты
Руководство пользователя
Этот инструмент рассчитает объем объекта цилиндрической формы по длине и диаметру. Никакого преобразования не требуется, поскольку единицы измерения длины, диаметра и объема можно выбрать независимо, поэтому этот калькулятор позволяет использовать любую комбинацию единиц измерения.
Никакого преобразования не требуется, поскольку единицы измерения длины, диаметра и объема можно выбрать независимо, поэтому этот калькулятор позволяет использовать любую комбинацию единиц измерения.
После ввода размеров длины и диаметра вычисленный объем будет показан в поле ответа. Также будет нарисовано изображение цилиндрической формы с отмеченными размерами, которое будет перерисовываться каждый раз при изменении любого из введенных входов или выбранных единиц.
Формулы
Формулы, используемые данным калькулятором для расчета объема объекта цилиндрической формы:
r = ø / 2
В = L · π · r²
В = L · π · (ø / 2) ²
Обозначения
- V = Объем
- L = длина
- ø = диаметр
- r = радиус
- π = Пи = 3.14159…
Объемные размеры — длина и диаметр
Введите размеры длины и диаметра для вычисляемого объекта и выберите соответствующие единицы для каждого введенного значения измерения.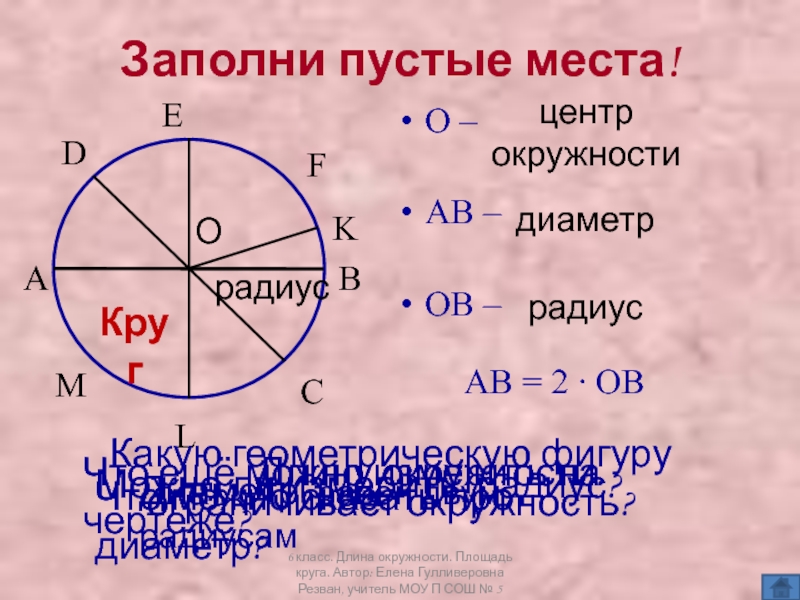
Для перевода длины и диаметра в разные единицы используются следующие коэффициенты пересчета в метрах (м):
- нанометр (нм) — 0,000000001 м
- микрометр (мкм) — 0,000001 м
- тысячная дюйма (тыс.) — 0.0000254 м
- миллиметр (мм) — 0,001 м
- сантиметр (см) — 0,01 м
- дюймов (дюйм) — 0,0254 м
- фут — 0,3048 м
- ярд — 0,9144 м
- метр (м) — 1 м
- километр (км) — 1000 м
- миль (миль) — 1609,344 м
- морская миля (морская миля) — 1852 м
Расчет объема
Это расчетный объем цилиндрического объекта, который этот инструмент вычисляет путем ввода значений длины и диаметра в формулу, описанную выше.Вы можете рассчитать объем в разных единицах, изменив выбор единиц под результатом.
Для перевода вычисленного объема в различные единицы используются следующие коэффициенты пересчета в кубических метрах (м³):
- кубический нанометр (куб нм) — 1 x 10 -27 м³
- кубических микрометров (куб мкм) — 1 x 10 -18 м³
- куб.
 т. (тыс.куб.) — 1.6387064 x 10 -14 м³
т. (тыс.куб.) — 1.6387064 x 10 -14 м³ - кубический миллиметр (куб мм) — 1 x 10 -9 м³
- кубический сантиметр (куб см) — 1 x 10 -6 м³
- миллилитр (мл) — 1 x 10 -6 м³
- чайная ложка (ч. Л., Сша) — 4.92892159375 x 10 -6 м³
- чайная ложка (ч.л., метрическая) — 5 x 10 -6 м³
- столовая ложка (Tbsp, usa) — 1.478676478125 x 10 -5 м³
- столовая ложка (столовая, метрическая) — 1,5 x 10 -5 м³
- кубических дюймов (у.е. дюйма) — 1,6387064 x 10 -5 м³
- жидких унций (жидких унций, дюймовых единиц) — 2,84130625 x 10 -5 м³
- жидких унций (жидких унций, сша) — 2,95735295625 x 10 -5 м³
- чашка (сша) — 2.365882365 x 10 -4 м³
- стакан (метрический) — 2,5 x 10 -4 м³
- пинта (пт, жидкость сша) — 4,73176473 x 10 -4 м³
- пинта (дюймовая, дюймовая) — 5,68 26125 x 10 -4 м³
- литр (л) — 1 x 10 -3 м³
- галлон (галлон, жидкость США) — 3,785411784 x 10 -3 м³
- галлон (галлон) — 4,54609 x 10 -3 м³
- кубических футов — 0,028316846592 м³
- баррель (баррель, нефть) — 0.
 158987294928 м³
158987294928 м³ - кубический ярд (cu yd) — 0,764554857984 м³
- куб.м — 1 м³
- килолитр (кл) — 1 м³
- мегалитр (ML) — 1000 м³
- кубический километр (куб км) — 1 x 10 +9 м³
- кубических миль (cu mi) — 4168181825,440579584 м³
- кубическая морская миля (cu nmi) — 6352182208 м³
Java: рассчитать диаметр круга и
Переполнение стека- Около
- Продукты
- Для команд
- Переполнение стека Общественные вопросы и ответы
- Переполнение стека для команд Где разработчики и технологи делятся частными знаниями с коллегами
- Вакансии Программирование и связанные с ним технические возможности карьерного роста
- Талант Нанимайте технических специалистов и создавайте свой бренд работодателя
Окружность, радиус, диаметр, число Пи, сектор, касательная
Окружность — геометрическое место точек плоскости, расстояние от которых до центра окружности равно.
Центр окръжности
Радиус: расстояние от центра окружности до его границы.
Диаметр: наибольшее расстояние от одной границы окружности до другой. Диаметр равен двум радиусам.
$d = 2\cdot r$
Периметр (длина окружности): длина границы окружности.
Длина окружности $= \pi \cdot$ диаметр $= 2 \cdot \pi \cdot$ радиус
Длина окружности $= \pi \cdot d = 2 \cdot \pi \cdot r$
$\pi$ — pi: число, равное 3,141592… или $\approx \frac{22}{7}$, то есть отношение $\frac{\text{длины окружности}}{\text{диаметр}}$ любого окружности.
Дуга: изогнутая линия, которая является частью окружности.
Дуги окружности измеряется в градусах или радианах.
Например: 90° или $\frac{\pi}{2}$ — четверть круга,
180° или $\pi$ — половина круга.
Сумма всех дуг окружности составляет 360° или $2\pi$
Хорда: отрезок прямой, соединяющей две точки на окружности.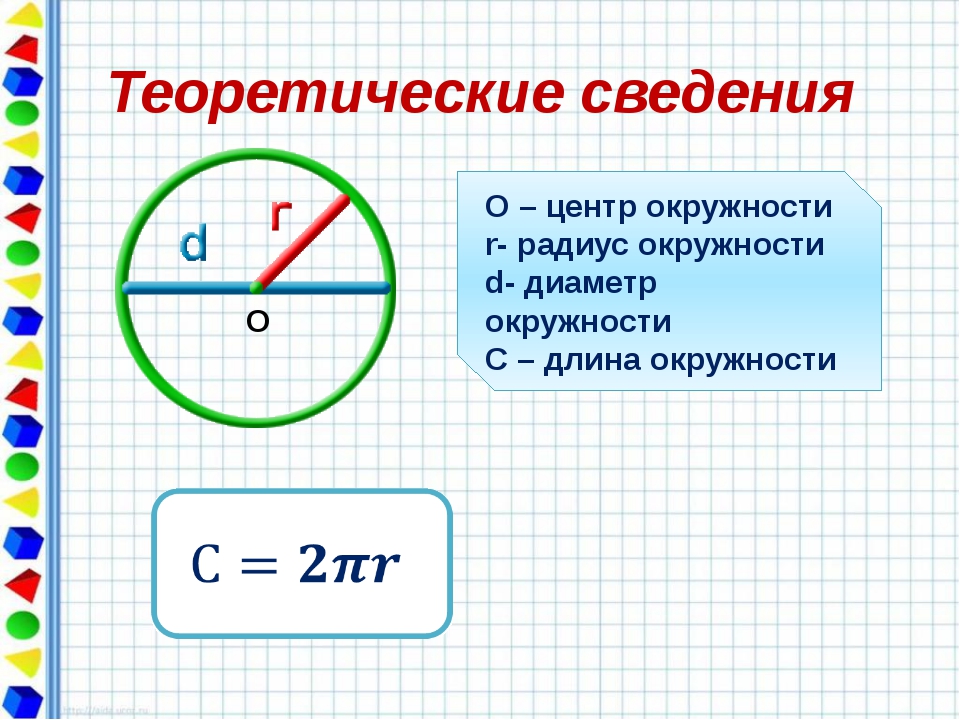 \circ$
\circ$
Хорды
Если две хорды пересекаются внутри окружности, как на рисунке выше, тогда:
$AX \cdot XB = CX \cdot XD$
формула, как найти длину круга и разницу между величинами
Очень часто при решении школьных заданий по математике или физике возникает вопрос — как найти длину окружности, зная диаметр? На самом деле никаких сложностей в решении этой проблемы нет, нужно только чётко представлять себе, какие формулы, понятия и определения требуются для этого.
Основные понятия и определения
- Радиус — это линия, соединяющая центр окружности и её произвольную точку. Он обозначается латинской буквой r.
- Хордой называется линия, соединяющая две произвольные точки лежащие на окружности.
- Диаметр — это линия, соединяющая два пункта окружности и проходящая через её центр. Он обозначается латинской буквой d.
- Окружность — это линия, состоящая из всех точек, находящихся на равном расстоянии от одной избранной точки, именуемой её центром.
 Её длину будем обозначать латинской буквой l.
Её длину будем обозначать латинской буквой l.
Площадь круга — это вся территория, заключённая внутри окружности. Она измеряется в квадратных единицах и обозначается латинской буквой s.
Пользуясь нашими определениями, приходим к выводу, что диаметр круга равен его самой большой хорде.
[warning]Внимание! Из определения, что такое радиус круга можно узнать, что такое диаметр круга. Это два радиуса отложенные в противоположных направлениях![/warning]
Диаметр окружности.
Нахождение длины окружности и её площади
Если нам дан радиус окружности, то диаметр окружности описывает формула d = 2*r. Таким образом, для ответа на вопрос, как найти диаметр круга, зная его радиус, достаточно последний умножить на два.
Формула длины окружности, выраженная через её радиус, имеет вид l = 2*П*r.
[warning]Внимание! Латинской буквой П (Пи) обозначается отношение длины окружности к её диаметру, и это есть непериодическая десятичная дробь. 2 = 4*s/П. Для определения самого диаметра потребуется извлечь корень квадратный из правой части. Получится d = 2*sqrt(s/П).
2 = 4*s/П. Для определения самого диаметра потребуется извлечь корень квадратный из правой части. Получится d = 2*sqrt(s/П).
Это интересно! Первый признак равенства треугольников: доказательство
Решение типовых заданий
- Узнаем, как найти диаметр, если дана длина окружности. Пусть она равняется 778,72 километра. Требуется найти d. d = 778,72/3,14 = 248 километров. Вспомним, что такое диаметр и сразу определим радиус, для этого определённое выше значение d разделим пополам. Получится r = 248/2 = 124 километра.
- Рассмотрим, как найти длину данной окружности, зная её радиус. Пусть r имеет значение 8 дм 7 см. Переведём это все в сантиметры, тогда r будет равняться 87 сантиметров. Воспользуемся формулой, как найти неизвестную длину круга . Тогда наше искомое будет равняться l = 2*3,14*87 = 546,36 см. Переведём наше полученное значение в целые числа метрических величин l = 546,36 см = 5 м 4 дм 6 см 3,6 мм.
 2/(4П) = 2209/12,56 = 175,87 кв. м.
2/(4П) = 2209/12,56 = 175,87 кв. м.
Это интересно! Что такое биссектриса треугольника: свойства, связанные с отношением сторон
Длина окружности
Окружность, диаметр, хорда геометрия 7 класс
Заключение
Исходя из приведённых выше рассуждений, можно прийти к выводу, что никаких сложностей в задачах, связанных с нахождением всевозможных характеристик окружности, нет. Достаточно хорошо выучить понятия и формулы, а также уметь производить арифметические действия, причём все выражения выводятся друг из друга.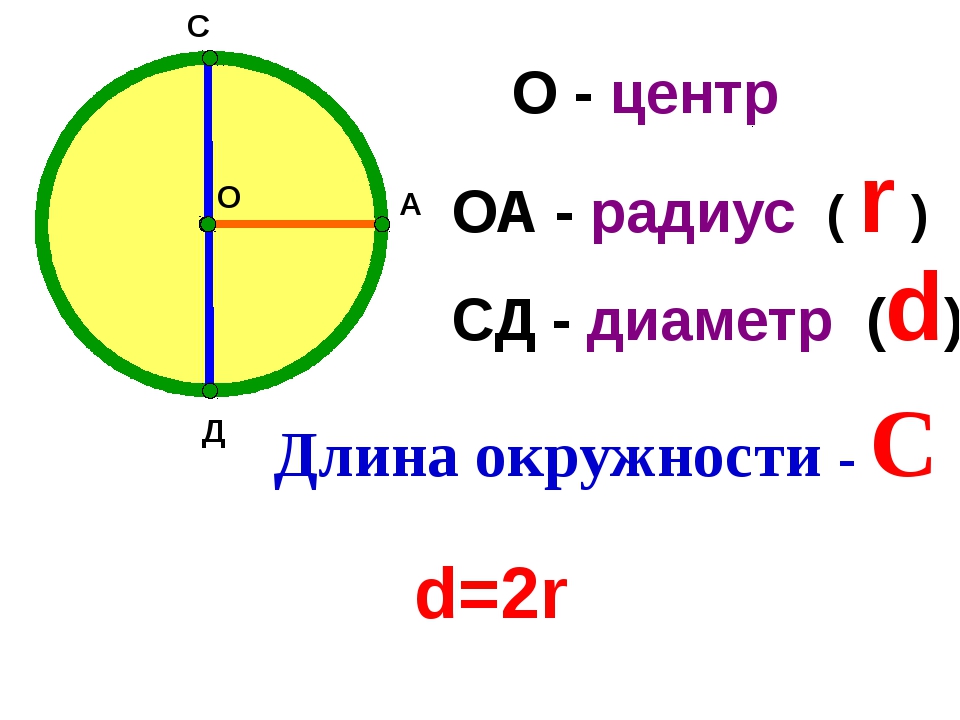
Это интересно! Чему равна и как найти площадь равностороннего треугольника
Окружность трубы 72 см диаметр получается. Как найти длину окружности: через диаметр и радиус
Калькулятор круга — это сервис, специально разработанный для расчета геометрических размеров фигур онлайн. Благодаря данному сервису Вы без проблем сможете определить любой параметр фигуры, в основе которой лежит круг. Например: Вы знаете объем шара, а необходимо получить его площадь. Нет ничего проще! Выберите соответствующий параметр, введите числовое значение и нажмите кнопку рассчитать. Сервис не только выдает результаты вычислений, но и предоставляет формулы, по которым они были сделаны. При помощи нашего сервиса вы без труда рассчитаете радиус, диаметр, длину окружности (периметр круга), площадь круга и шара, объем шара.
Вычислить радиус
Задача на вычисление значения радиуса – одна из самых распространенных. Причина тому достаточно проста, ведь зная этот параметр, вы без особого труда сможете определить значение любого другого параметра круга или шара. Наш сайт построен именно на такой схеме. Вне зависимости от того, какой вы выбрали исходный параметр, первым делом вычисляется значение радиуса и на его основе строятся все последующие вычисления. Для большей точности вычислений, сайт использует число Пи с округлением до 10-го знака после запятой.
Наш сайт построен именно на такой схеме. Вне зависимости от того, какой вы выбрали исходный параметр, первым делом вычисляется значение радиуса и на его основе строятся все последующие вычисления. Для большей точности вычислений, сайт использует число Пи с округлением до 10-го знака после запятой.
Рассчитать диаметр
Расчет диаметра – самый простой вид расчета из тех, что умеет выполнять наш калькулятор. Получить значение диаметра совсем нетрудно и вручную, для этого совсем не надо прибегать к помощи интернета. Диаметр равен значению радиуса умноженному на 2. Диаметр – важнейший параметр круга, который чрезвычайно часто используется в повседневной жизни. Уметь его правильно рассчитать и использовать должен абсолютно каждый. Воспользовавшись возможностями нашего сайта, вы вычислите диаметр с большой точностью за доли секунды.
Узнать длину окружности
Вы даже не представляете, как много вокруг нас круглых объектов и какую важную роль они играют в нашей жизни. Умение рассчитать длину окружности необходимо всем, от рядового водителя, до ведущего инженера-проектировщика. Формула для вычисления длинны окружности очень проста: D=2Pr. Расчет можно легко провести как на листке бумаги, так и при помощи данного интернет помощника. Преимущество последнего в том, что он проиллюстрирует все вычисления рисунками. И ко всему прочему, второй способ намного быстрее.
Умение рассчитать длину окружности необходимо всем, от рядового водителя, до ведущего инженера-проектировщика. Формула для вычисления длинны окружности очень проста: D=2Pr. Расчет можно легко провести как на листке бумаги, так и при помощи данного интернет помощника. Преимущество последнего в том, что он проиллюстрирует все вычисления рисунками. И ко всему прочему, второй способ намного быстрее.
Вычислить площадь круга
Площадь круга – как и все перечисленные перечисленные в этой статье параметры является основой современной цивилизации. Уметь рассчитать и знать площадь круга полезно всем без исключения слоям населения. Трудно представить область науки и техники, в которой не надо было бы знать, площадь круга. Формула для вычисления опять же нетрудная: S=PR 2 . Эта формула и наш онлайн-калькулятор помогут Вам без лишних усилий узнать площадь любого круга. Наш сайт гарантирует высокую точность вычислений и их молниеносное выполнение.
Рассчитать площадь шара
Формула для расчета площади шара ничуть не сложнее формул, описанных в предыдущих пунктах. S=4Pr 2 . Этот нехитрый набор букв и цифр уже многие годы дает людям возможность достаточно точно вычислять площадь шара. Где это может быть применено? Да везде! Например, вы знаете, что площадь земного шара равна 510 100 000 километров квадратных. Перечислять, где может быть применено знание этой формулы перечислять бесполезно. Слишком широка область применения формулы для вычисления площади шара.
S=4Pr 2 . Этот нехитрый набор букв и цифр уже многие годы дает людям возможность достаточно точно вычислять площадь шара. Где это может быть применено? Да везде! Например, вы знаете, что площадь земного шара равна 510 100 000 километров квадратных. Перечислять, где может быть применено знание этой формулы перечислять бесполезно. Слишком широка область применения формулы для вычисления площади шара.
Вычислить объем шара
Для вычисления объема шара используют формулу V=4/3(Pr 3). Она была использована при создании нашего онлайн сервиса. Сайт сайт дает возможность рассчитать объем шара за считанные секунды, если вы Вам известен любой из следующих параметров: радиус, диаметр, длинна окружности, площадь круга или площадь шара. Так же вы можете применять его для обратного вычисления, например, чтобы зная объем шара, получить значение его радиуса или диаметра. Спасибо, что кратко ознакомились с возможностями нашего калькулятора круга. Надеемся, Вам у нас понравилось, и вы уже добавили сайт в закладки.
И круг — геометрические фигуры, взаимосвязанные между собой. есть граничная ломаная линия (кривая) круга ,
Определение. Окружность — замкнутая кривая, каждая точка которой равноудалена от точки, называемой центром окружности.
Для построения окружности выбирается произвольная точка О, принятая за центр окружности, и с помощью циркуля проводится замкнутая линия.
Если точку О центра окружности соединить с произвольными точками на окружности, то все полученные отрезки будут между собой равны, и называются такие отрезки радиусами, сокращенно обозначаются латинской маленькой или большой буквой «эр» (r или R ). Радиусов в окружности можно провести столько же, сколько точек имеет длина окружности.
Отрезок, соединяющий две точки окружности и проходящий через ее центр, называется диаметром. Диаметр состоит из двух радиусов , лежащих на одной прямой. Диаметр обозначается латинской маленькой или большой буквой «дэ» (d или D ).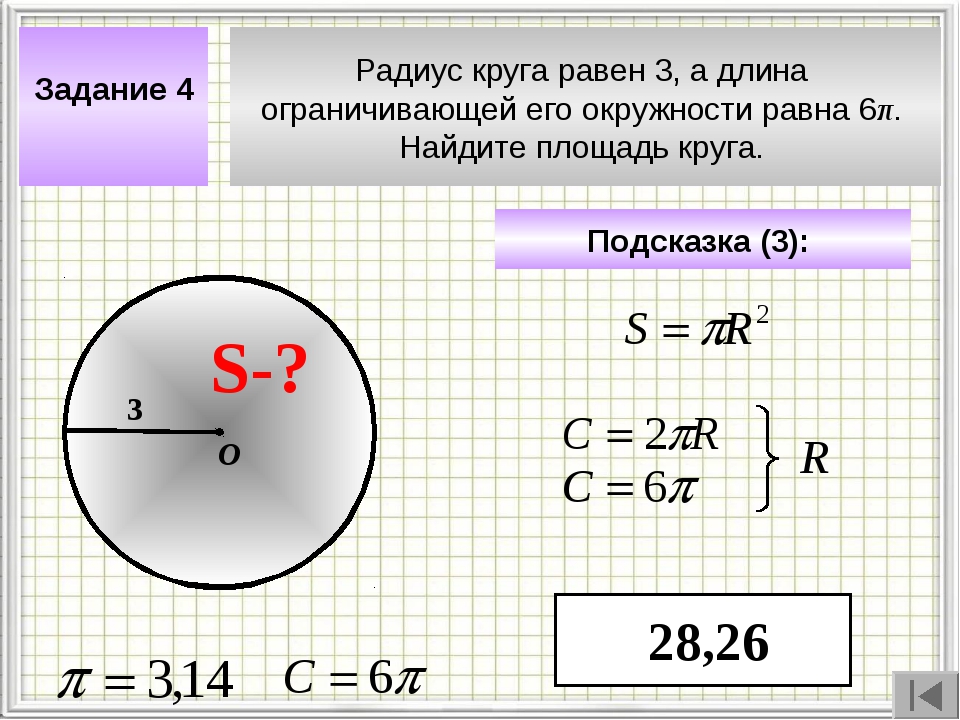
Правило. Диаметр окружности равен двум ее радиусам .
d = 2r
D = 2R
Длина окружности вычисляется по формуле и зависит от радиуса (диаметра) окружности. В формуле присутствует число ¶, которое показывает во сколько раз длина окружности больше, чем ее диаметр. Число ¶ имеет бесконечное число знаков после запятой. Для вычислений принято ¶ = 3,14.
Длина окружности обозначается латинской большой буквой «цэ» (C ). Длина окружности пропорциональна ее диаметру. Формулы для расчета длины окружности по ее радиусу и диаметру:
C = ¶d
C = 2¶r
- Примеры
- Дано: d = 100 см.
- Длина окружности: C = 3,14 * 100 см = 314 см
- Дано: d = 25 мм.
- Длина окружности: С = 2 * 3,14 * 25 = 157 мм
Секущая окружности и дуга окружности
Всякая секущая (прямая линия) пересекает окружность в двух точках и делит ее на две дуги. Величина дуги окружности зависит от расстояния между центром и секущей и измеряется по замкнутой кривой от первой точки пересечения секущей с окружностью до второй.
Дуги окружности делятся секущей на большую и малую, если секущая не совпадает с диаметром, и на две равные дуги, если секущая проходит по диаметру окружности.
Если секущая проходит через центр окружности, то ее отрезок, расположенный между точками пересечения с окружностью, есть диаметр окружности, или самая большая хорда окружности.
Чем дальше секущая расположена от центра окружности, тем меньше градусная мера меньшей дуги окружности и больше — большей дуги окружности, а отрезок секущей, называемый хордой , уменьшается по мере удаления секущей от центра окружности.
Определение. Кругом называется часть плоскости, лежащая внутри окружности.
Центр, радиус, диаметр окружности являются одновременно центром, радиусом и диаметром соответствующего круга.
Так как круг — это часть плоскости, то одним из его параметров является площадь.
Правило. Площадь круга (S ) равна произведению квадрата радиуса (r 2 ) на число ¶.
- Примеры
- Дано: r = 100 см
- Площадь круга:
- S = 3,14 * 100 см * 100 см = 31 400 см 2 ≈ 3м 2
- Дано: d = 50 мм
- Площадь круга:
- S = ¼ * 3,14 * 50 мм * 50 мм = 1 963 мм 2 ≈ 20 см 2
Если в круге провести два радиуса к разным точкам окружности, то образуется две части круга, которые называется секторами . Если в круге провести хорду, то часть плоскости между дугой и хордой называется сегментом окружности .
Если в задаче известны такие величины, как длина окружности, ее радиус или площадь круга, который ограничен данной окружностью, то вычисление диаметра будет несложным. Существует несколько способов, которыми можно высчитать диаметр окружности. Они довольно просты и вовсе не вызывают никаких трудностей, как многим кажется на первый взгляд.
Как найти диаметр окружности – 1 способ
Когда дано значение радиуса окружности, то можно считать задачу наполовину решенной, поскольку радиус представляет собой расстояние от точки, которая лежит в любом месте на окружности, до центра этой самой окружности. Все, что нужно сделать для нахождения диаметра в этом случае, это умножить данную величину радиуса на 2. Такой способ вычисления объясняется тем, что радиус является половиной диаметра. Поэтому, если известно, чему равен радиус, то и значение половины искомой величины диаметра уже фактически найдено.
Как найти диаметр окружности – 2 способ
Если в задаче дано только значение длины окружности, то для нахождения величины диаметра нужно просто поделить ее на число, известное как π, приблизительное значение которого равно 3,14. То есть, если значение длины равняется 31,4, то разделив его на 3,14, получаем значение диаметра, которое равняется 10.
Как найти диаметр окружности – 3 способ
Если в исходных данных приведено значение площади круга, то диаметр найти тоже просто. Все, что нужно сделать, это извлечь квадратный корень из данной величины и поделить полученный результат на число π. Это значит, что если значение площади равно 64, то при извлечении корня остается число 8. Если разделить полученную 8 на 3,14, то получим величину диаметра, которая равна примерно 2,5.
Как найти диаметр окружности – 4 способ
Внутри окружности нужно начертить при помощи линейки или угольника прямую горизонтальную линию от одной точки до другой. Пересечения этой прямой с линией окружностью пометьте буквами, например, А и В. Не имеет никакого значения, в какой из частей круга будет расположена эта прямая.
После этого нужно начертить еще две окружности. Но таким образом, чтобы точки А и В стали их центрами. Вновь образованные фигуры будут пересекаться в двух точках. Через них нужно провести еще одну прямую линию. После этого измеряем ее длину с помощью линейки. Значение измерения и будет равно длине диаметра, потому что последняя начерченная линия и есть сам диаметр.
Интересно, что еще очень далеко в прошлом для плетения корзин определенного размера прутики брали примерно в 3 раза длиннее. Ученые объяснили и доказали экспериментальным путем, что если длину любой окружности разделить на диаметр, то в результате получается почти одно и то же число.
– это плоская фигура, которая представляет собой множество точек равноудаленных от центра. Все они находятся на одинаковом расстоянии и образуют собой окружность.
Отрезок, который соединяет центр круга с точками его окружности, называется радиусом . В каждой окружности все радиусы равны между собой. Прямая, соединяющая две точки на окружности и проходящая через центр называется диаметром . Формула площади круга рассчитывается с помощью математической константы – числа π..
Это интересно : Число π. представляет собой соотношение длины окружности к длине ее диаметра и является постоянной величиной. Значение π = 3,1415926 получило применение после работ Л. Эйлера в 1737 г.
Площадь окружности можно вычислить через константу π. и радиус окружности. Формула площади круга через радиус выглядит так:
Рассмотрим пример расчета площади круга через радиус. Пусть дана окружность с радиусом R = 4 см. Найдем площадь фигуры.
Площадь нашей окружности будет равна 50,24 кв. см.
Существует формула площади круга через диаметр . Она также широко применяется для вычисления необходимых параметров. Данные формулы можно использовать для нахождения .
Рассмотрим пример расчета площади круга через диаметр, зная его радиус. Пусть дана окружность с радиусом R = 4 см. Для начала найдем диаметр, который, как известно, в два раза больше радиуса.
Теперь используем данные для примера расчета площади круга по приведенной выше формуле:
Как видим, в результате получаем тот же ответ, что и при первых расчетах.
Знания стандартных формул расчета площади круга помогут в дальнейшем легко определять площадь секторов и легко находить недостающие величины.
Мы уже знаем, что формула площади круга рассчитывается через произведение постоянной величины π на квадрат радиуса окружности. Радиус можно выразить через длину окружности и подставить выражение в формулу площади круга через длину окружности:
Теперь подставим это равенство в формулу расчета площади круга и получим формулу нахождения площади круга, через длину окружности
Рассмотрим пример расчета площади круга через длину окружности. Пусть дана окружность с длиной l
= 8 см. Подставим значение в выведенную формулу:
Итого площадь круга будет равна 5 кв. см.
Площадь круга описанного вокруг квадрата
Очень легко можно найти площадь круга описанного вокруг квадрата.
Для этого потребуется только сторона квадрата и знание простых формул. Диагональ квадрата будет равна диагонали описанной окружности. Зная сторону a
ее можно найти по теореме Пифагора: отсюда .
После того, как найдем диагональ – мы сможем рассчитать радиус: .
И после подставим все в основную формулу площади круга описанного вокруг квадрата:
В процессе выполнения строительных работ в быту или на производстве может появиться необходимость в измерении диаметра трубы, которая уже вмонтирована в систему водоснабжения или канализации. Также знать данный параметр необходимо на стадии проектирования прокладки инженерных коммуникаций.
Отсюда возникает необходимость разобраться с тем, как определить диаметр трубы. Выбор конкретного способа выполнения измерений зависит от размеров объекта и от того, доступно ли расположение трубопровода.
Определение диаметра в бытовых условиях
До того, как замерить диаметр трубы, нужно приготовить следующие инструменты и устройства:
- рулетка или стандартная линейка;
- штангенциркуль;
- фотоаппарат — его задействуют при необходимости.
Если трубопровод доступен для проведения замеров, а торцы труб можно без проблем измерить, тогда достаточно иметь в распоряжении обычную линейку или рулетку. При этом следует учитывать, что используют такой метод, когда к точности предъявляются минимальные требования.
В этом случае выполняют измерение диаметра труб в такой последовательности:
- Подготовленные инструменты прикладывают к месту, где находится самая широкая часть торца изделия.
- Потом отсчитывают количество делений, соответствующих размеру диаметра.
Данный способ позволяет узнавать параметры трубопровода с точностью, составляющую несколько миллиметров.
Для измерения внешнего диаметра труб с небольшим сечением можно задействовать такой инструмент как штангенциркуль:
- Раздвигают его ножки и прикладывают к торцу изделия.
- Затем их нужно сдвинуть так, чтобы они оказались плотно прижатыми к наружной стороне стенок трубы.
- Ориентируясь на шкалу значений приспособления, узнают требуемый параметр.
Этот метод определения диаметра трубы дает довольно точные результаты, до десятых миллиметра.
Когда трубопровод недоступен для обмера и является частью уже функционирующей конструкции водоснабжения или газовой магистрали, поступают следующим образом: штангенциркуль прикладывают к трубе, к ее боковой поверхности. Таким способом обмеряют изделие в тех случаях, если у измерительного приспособления длина ножек превышает половину диаметра трубной продукции.
Нередко в бытовых условиях возникает необходимость узнать, как измерять диаметр трубы, имеющей большое сечение. Существует простой вариант, как это сделать: достаточно знать длину окружности изделия и константу π, равную 3,14.
Сначала при помощи рулетки или куска шнура обмеряют трубу в обхвате. Потом подставляют известные величины в формулу d=l:π, где:
d – определяемый диаметр;
l – длина измеренной окружности.
К примеру, обхват трубы составляет 62,8 сантиметра, тогда d = 62,8:3,14 =20 сантиметров или 200 миллиметров.
Бывают ситуации, когда проложенный трубопровод полностью недоступен. Тогда можно применить метод копирования. Суть его заключается в том, что к трубе прикладывают измерительный инструмент или небольшой по размеру предмет, у которого известны параметры.
К примеру, это может быть коробок спичек, длина которого равна 5 сантиметрам. Потом этот участок трубопровода фотографируют. Последующие вычисления выполняют по фотографии. На снимке измеряют видимую толщину изделия в миллиметрах. Потом нужно перевести все полученные величины в реальные параметры трубы с учетом масштаба произведенной фотосъемки.
Измерение диаметров в производственных условиях
На больших строящихся объектах трубы до начала проведения монтажа в обязательном порядке подвергают входному контролю. Прежде всего, проверяют сертификаты и маркировку, нанесенную на трубную продукцию.
Документация должна содержать определенную информацию, касающуюся труб:
- номинальные размеры;
- номер и дата ТУ;
- марка металла или вид пластика;
- номер товарной партии;
- итоги проведенных испытаний;
- хим. анализ выплавки;
- тип термической обработки;
- результаты рентгеновской дефектоскопии.
Кроме этого, на поверхности всех изделий на расстоянии примерно 50 сантиметров от одного из торцов всегда наносят маркировку, содержащую:
- наименование производителя;
- номер плавки;
- номер изделия и его номинальные параметры;
- дату изготовления;
- эквивалент углерода.
Длины труб в производственных условиях определяют мерной проволокой. Также не возникает сложностей с тем, как измерить диаметр трубы рулеткой.
Для изделий первого класса допустимой величиной отклонения в одну или другую сторону от заявленной длины являются 15 миллиметров. Для второго класса –100 миллиметров.
У труб наружный диаметр сверяют, пользуясь формулой d = l:π-2Δр-0,2 мм, где кроме вышеописанных значений:
Δр – толщина материала рулетки;
0,2 миллиметра– припуск на прилегание инструмента к поверхности.
Допускается отклонение величины внешнего диаметра от заявленной производителем:
- для продукции с сечением не более 200 миллиметров–1,5 миллиметра;
- для больших труб – 0,7%.
В последнем случае для проверки трубной продукции пользуются ультразвуковыми измерительными приборами. Для определения толщины стенок задействуют штангенциркули, у которых деление на шкале соответствует 0,01 миллиметра. Минусовой допуск не должен превышать 5% номинальной толщины. При этом кривизна не может быть более 1,5 миллиметра на 1 погонный метр.
Из вышеописанной информации ясно, что несложно разобраться с тем, как определить диаметр трубы по длине окружности или при помощи несложных измерительных инструментов.
Главная » Сметы » Окружность трубы 72 см диаметр получается. Как найти длину окружности: через диаметр и радиус
Длина, площадь и диаметр окружностей.
Быстро посчитать длину окружности любого радиуса или диаметра можно помощью онлайн калькулятора длины окружности.Быстро посчитать площадь окружности любого радиуса или диаметра можно с помощью онлайн калькулятора расчета площади окружности.
длина окружности диаметром 1 дм
длина окружности диаметром 2 дм
длина окружности диаметром 3 дм
длина окружности диаметром 4 дм
длина окружности диаметром 5 дм
длина окружности диаметром 6 дм
длина окружности диаметром 7 дм
длина окружности диаметром 8 дм
длина окружности диаметром 9 дм
длина окружности диаметром 1 км
длина окружности диаметром 2 км
длина окружности диаметром 3 км
длина окружности диаметром 4 км
длина окружности диаметром 5 км
длина окружности диаметром 6 км
длина окружности диаметром 7 км
длина окружности диаметром 8 км
длина окружности диаметром 9 км
длина окружности диаметром 1 м
длина окружности диаметром 2 м
длина окружности диаметром 3 м
длина окружности диаметром 4 м
длина окружности диаметром 5 м
длина окружности диаметром 6 м
длина окружности диаметром 7 м
длина окружности диаметром 8 м
длина окружности диаметром 9 м
длина окружности диаметром 1 см
длина окружности диаметром 2 см
длина окружности диаметром 3 см
длина окружности диаметром 4 см
длина окружности диаметром 5 см
длина окружности диаметром 6 см
длина окружности диаметром 7 см
длина окружности диаметром 8 см
длина окружности диаметром 9 см
площадь окружности диаметром 1 дм
площадь окружности диаметром 2 дм
площадь окружности диаметром 3 дм
площадь окружности диаметром 4 дм
площадь окружности диаметром 5 дм
площадь окружности диаметром 6 дм
площадь окружности диаметром 7 дм
площадь окружности диаметром 8 дм
площадь окружности диаметром 9 дм
площадь окружности диаметром 1 м
площадь окружности диаметром 2 м
площадь окружности диаметром 3 м
площадь окружности диаметром 4 м
площадь окружности диаметром 5 м
площадь окружности диаметром 6 м
площадь окружности диаметром 7 м
площадь окружности диаметром 8 м
площадь окружности диаметром 9 м
площадь окружности диаметром 1 см
площадь окружности диаметром 2 см
площадь окружности диаметром 3 см
площадь окружности диаметром 4 см
площадь окружности диаметром 5 см
площадь окружности диаметром 6 см
площадь окружности диаметром 7 см
площадь окружности диаметром 8 см
площадь окружности диаметром 9 см
площадь окружности радиусом 1 дм
площадь окружности радиусом 2 дм
площадь окружности радиусом 3 дм
площадь окружности радиусом 4 дм
площадь окружности радиусом 5 дм
площадь окружности радиусом 6 дм
площадь окружности радиусом 7 дм
площадь окружности радиусом 8 дм
площадь окружности радиусом 9 дм
площадь окружности радиусом 1 м
площадь окружности радиусом 2 м
площадь окружности радиусом 3 м
площадь окружности радиусом 4 м
площадь окружности радиусом 5 м
площадь окружности радиусом 6 м
площадь окружности радиусом 7 м
площадь окружности радиусом 8 м
площадь окружности радиусом 9 м
площадь окружности радиусом 1 см
площадь окружности радиусом 2 см
площадь окружности радиусом 3 см
площадь окружности радиусом 4 см
площадь окружности радиусом 5 см
площадь окружности радиусом 6 см
площадь окружности радиусом 7 см
площадь окружности радиусом 8 см
площадь окружности радиусом 9 см
длина окружности радиусом 1 см
длина окружности радиусом 2 см
длина окружности радиусом 3 см
длина окружности радиусом 4 см
длина окружности радиусом 5 см
длина окружности радиусом 6 см
длина окружности радиусом 7 см
длина окружности радиусом 8 см
длина окружности радиусом 9 см
длина окружности радиусом 10 см
длина окружности радиусом 11 см
длина окружности радиусом 12 см
длина окружности радиусом 13 см
длина окружности радиусом 14 см
длина окружности радиусом 15 см
длина окружности радиусом 16 см
длина окружности радиусом 17 см
длина окружности радиусом 18 см
длина окружности радиусом 19 см
длина окружности радиусом 20 см
длина окружности радиусом 21 см
длина окружности радиусом 22 см
длина окружности радиусом 23 см
длина окружности радиусом 24 см
длина окружности радиусом 25 см
длина окружности радиусом 26 см
длина окружности радиусом 27 см
длина окружности радиусом 28 см
длина окружности радиусом 29 см
длина окружности радиусом 30 см
длина окружности радиусом 31 см
длина окружности радиусом 32 см
длина окружности радиусом 33 см
длина окружности радиусом 34 см
длина окружности радиусом 35 см
длина окружности радиусом 36 см
длина окружности радиусом 37 см
длина окружности радиусом 38 см
длина окружности радиусом 39 см
длина окружности радиусом 40 см
длина окружности радиусом 41 см
длина окружности радиусом 42 см
длина окружности радиусом 43 см
длина окружности радиусом 44 см
длина окружности радиусом 45 см
длина окружности радиусом 46 см
длина окружности радиусом 47 см
длина окружности радиусом 48 см
длина окружности радиусом 49 см
длина окружности радиусом 50 см
длина окружности радиусом 51 см
длина окружности радиусом 52 см
длина окружности радиусом 53 см
длина окружности радиусом 54 см
длина окружности радиусом 55 см
длина окружности радиусом 56 см
длина окружности радиусом 57 см
длина окружности радиусом 58 см
длина окружности радиусом 59 см
длина окружности радиусом 60 см
длина окружности радиусом 61 см
длина окружности радиусом 62 см
длина окружности радиусом 63 см
длина окружности радиусом 64 см
длина окружности радиусом 65 см
длина окружности радиусом 66 см
длина окружности радиусом 67 см
длина окружности радиусом 68 см
длина окружности радиусом 69 см
длина окружности радиусом 70 см
длина окружности радиусом 71 см
длина окружности радиусом 72 см
длина окружности радиусом 73 см
длина окружности радиусом 74 см
длина окружности радиусом 75 см
длина окружности радиусом 76 см
длина окружности радиусом 77 см
длина окружности радиусом 78 см
длина окружности радиусом 79 см
длина окружности радиусом 80 см
длина окружности радиусом 81 см
длина окружности радиусом 82 см
длина окружности радиусом 83 см
длина окружности радиусом 84 см
длина окружности радиусом 85 см
длина окружности радиусом 86 см
длина окружности радиусом 87 см
длина окружности радиусом 88 см
длина окружности радиусом 89 см
длина окружности радиусом 90 см
длина окружности радиусом 91 см
длина окружности радиусом 92 см
длина окружности радиусом 93 см
длина окружности радиусом 94 см
длина окружности радиусом 95 см
длина окружности радиусом 96 см
длина окружности радиусом 97 см
длина окружности радиусом 98 см
длина окружности радиусом 99 см
На этой странице представлена информация о длине, плащади и диаметре окружностей. Информация представлена в виде решения задачи перемножения диаметра или радиуса по простой математической формуле.
Как найти диаметр круга: определение, формула и пример — видео и стенограмма урока
Примеры
Отрезок AB — это диаметр. Точка C — это центр окружности, а также середина сегмента AB . Сегменты AC и CB имеют одинаковую длину и составляют половину диаметра каждый. AC и CB — каждый радиус окружности.Радиус круга — это сегмент, одна конечная точка которого находится на окружности, а другая конечная точка находится в центре окружности.
На окружности C нарисован только один диаметр. Однако каждая окружность имеет бесконечное количество возможных диаметров. Представьте, что вам нужно разрезать круглое печенье на две равные части. Независимо от того, как вы поворачиваете печенье, если вы сделаете один прямой надрез прямо через центральную точку печенья, вы разделите его по диаметру.
Формула
Формула для определения диаметра устанавливает соотношение между диаметром и радиусом. Диаметр состоит из двух сегментов, каждый из которых имеет радиус. Следовательно, формула: Диаметр = 2 * измерение радиуса. Вы можете сократить эту формулу как d = 2r .
На этом круге показаны сегменты DA и CB . DA — это радиус, поскольку у него одна конечная точка находится в центре окружности, а другая — на окружности. DA имеет длину 3,5 см. CB — это диаметр, поскольку он имеет обе конечные точки на окружности и проходит через центр окружности. Диаметр равен двукратному радиусу, поэтому диаметр этого круга равен 7 см, так как 2 * 3,5 равно 7.
Резюме урока
Диаметр круга — это сегмент, концы которого лежат на окружности, а его середина это центр круга. Расстояние от центра до точки на окружности называется радиусом.Каждый круг имеет бесконечное количество возможных диаметров. Формула для определения диаметра круга равна удвоенному радиусу (2 * радиус).
Примечания к диаметру
- Диаметр простирается от одной стороны окружности до другой со средней точкой в центре окружности.
- Чтобы вычислить диаметр, умножьте длину радиуса круга на 2.
Результаты обучения
В результате изучения этого урока вы впоследствии сможете:
- Записать формулу для определения диаметра круга, а также сократить ее
- Распознать значение диаметра, центра и радиуса круга
- Используйте то, что вы узнали, для вычисления диаметра окружности
Диаметр — определение, формулы, решенные примеры
Диаметр круга — это линия, проходящая через центр и пересекающаяся с окружностью на каждом конце.Это вдвое больше радиуса круга.
Что такое диаметр круга?
Диаметр окружности — это любой отрезок прямой, проходящий через центр окружности и концы которого лежат на окружности окружности. Диаметр также известен как самая длинная хорда круга.
Определение диаметра
Диаметр определяется как удвоенная длина радиуса круга. Радиус измеряется от центра круга до одной конечной точки круга, тогда как расстояние по диаметру измеряется от одного конца круга до точки на другом конце круга, проходящей через центр.Диаметр обозначается буквой D. На окружности круга есть бесконечные точки, это означает, что круг имеет бесконечное количество диаметров, и каждый диаметр круга имеет одинаковую длину.
Обратите внимание на следующий рисунок, на котором диаметр круга показан синей линией. Желтая линия от центра до одной конечной точки круга — это радиус, а внешняя граница, отмеченная черной пунктирной кривой, — это окружность круга.
Символ диаметра
Φ — это символ, который используется в технике для обозначения диаметра.Этот символ обычно используется в технических спецификациях и чертежах. Φ25 мм означает, что диаметр круга равен 25 мм.
Формула диаметра
Все мы знаем, что диаметр — это часть круга. Давайте разберемся с несколькими терминами, прежде чем изучать формулу диаметра круга.
- Радиус (r) — это длина отрезка прямой от центра круга до конечной точки на окружности.
- Окружность (C) относится к замкнутой границе круга.Он также известен как периметр круга. Мы можем вывести формулу диаметра из длины окружности и радиуса круга.
Диаметр окружности по окружности
Формулу диаметра легко вывести из длины окружности. Формула длины окружности: C = πd; здесь, C = окружность, d = диаметр круга, π = константа (3.141)
Формула диаметра с использованием окружности: Диаметр = Окружность ÷ π
Диаметр круга с использованием радиуса
Радиус — это длина отрезка прямой от центра окружности до конечной точки окружности, а диаметр в два раза превышает длину радиуса окружности.Используя это определение, формула для диаметра: D = Радиус × 2
Как определить диаметр?
Диаметр круга можно вычислить, если задан радиус или длину окружности.
Давайте попробуем использовать приведенные выше формулы на практической иллюстрации, чтобы найти диаметр. Обратите внимание на пример, приведенный ниже.
Пример: Джек нарисовал круг радиусом 3 единицы. Каков диаметр круга?
Раствор:
Дано: Радиус круга = 3 единицы
Диаметр круга = 2 × Радиус
.
= 2 × 3 = 6 шт.
Следовательно, диаметр круга равен 6 единицам.
Статьи по теме Диаметр
Ознакомьтесь с этими интересными статьями, чтобы узнать больше о диаметре и связанных с ним темах.
FAQ по диаметру
Что означает диаметр?
Диаметр — это прямая линия, которая проходит через центр круга и делит круг на две части. Это самая длинная хорда круга, которая пересекает окружность на каждом конце.
Что такое радиус и диаметр?
Радиус и диаметр круга — две важные части круга, которые взаимозависимы. Радиус круга — это отрезок прямой, который начинается от центра круга и заканчивается на окружности круга. Это половина диаметра круга, то есть Радиус = Диаметр / 2. Диаметр круга — это отрезок прямой, который проходит через центр круга и имеет две конечные точки на окружности.Это в два раза больше радиуса круга, то есть диаметр = 2 × радиус.
Что такое диаметр?
Если вы посмотрите на колесо цикла, шипы проходят от одного конца до другого через центр. Мы можем связать это с диаметром круга, поскольку диаметр — это отрезок прямой, который начинается с одного конца круга и заканчивается на другом конце круга, проходящем через центр.
Как найти диаметр по окружности?
Если длина окружности известна, то мы можем легко найти значение диаметра, подставив значения в формулу: Диаметр = C ÷ π; где C — длина окружности, а π — постоянная величина, равная 3.14.
Как найти площадь круга с диаметром?
Площадь круга рассчитывается по формуле: πr 2 . Если задан диаметр, мы можем найти радиус, разделив значение диаметра на 2. После получения радиуса мы можем подставить его значение в формулу: πr 2 , чтобы получить площадь круга или напрямую применить Формула площади с диаметром, A = π (d / 2) 2 = πd 2 /4
Как рассчитать диаметр?
Диаметр круга можно рассчитать по заданным параметрам.Если заданы такие параметры, как радиус, окружность или площадь, мы можем напрямую использовать следующие формулы.
- Диаметр = Окружность ÷ π (если дана окружность)
- Диаметр = 2 × Радиус (если указан радиус)
- Диаметр = 2√ [Площадь / π] (когда указана площадь)
Диаметр составляет половину радиуса?
Нет, диаметр не половина радиуса; это в два раза больше радиуса круга. Он представлен формулой: Диаметр = 2 × Радиус.
Вычисление размеров круга — DQYDJ — Не бросайте повседневную работу …
Ниже представлен калькулятор диаметра , который вычислит радиус, длину окружности и площадь круга, если вы знаете диаметр.
Знаете ли вы другое измерение? Вместо этого попробуйте один из связанных калькуляторов размеров круга:
Калькулятор диаметра
Что такое диаметр круга?
Диаметр круга — это расстояние от края до края круга, проходящего через его начало или центр.
Удобно, он вдвое больше радиуса круга. Если вы проведете два противоположных отрезка линии от начала круга до края, вы просто начнете диаметр.
Размеры окружности
Для описания окружности чаще всего используются три измерения:
- Диаметр — определено выше
- Радиус — расстояние от центра окружности до края, единица половина диаметра
- Окружность — длина внешней границы окружности
Исходя из диаметра, вы легко найдете два других.Следующие уравнения показывают, как вместо этого можно найти по ним диаметр.
Уравнение диаметра окружности от окружности:
d = c / \ pi
Если записать вместо радиуса, диаметр будет очень простым; он всего в два раза длиннее:
d = 2r
Размеры круга: O — начало координат, R — радиус, D — диаметр, C — длина окружности (Викимедиа)Площадь — это пространство, содержащееся в границах круга. Также легко найти у любого другого.2
Использование калькулятора диаметра
Вы можете ввести диаметр, а затем вычислить радиус и окружность в мил, дюймах, футах, ярдах, милях, миллиметрах, сантиметрах, метрах и километрах.
Вычислите площадь, используя следующие единицы: квадратных миль, квадратных дюймов, квадратных футов, квадратных ярдов, квадратных миль, акров, гектаров, квадратных миллиметров, квадратных сантиметров, квадратных метров и квадратных километров.
Чтобы запустить калькулятор, нажмите кнопку «Рассчитать размеры окружности» после ввода известного диаметра.
Вам понравился этот инструмент? Посетите другие наши калькуляторы и инструменты.
Диаметр, радиус и окружность окружностей [Видео и практика]
Диаметр, радиус и окружность окружностей
Привет, ребята! Добро пожаловать в это видео о радиусе, диаметре и окружности круга .
Круги существуют (круглые) с тех пор, как существует Земля. Люди могли видеть естественные круги, наблюдая за луной, солнцем и другими естественными круглыми формами.
Однако первое технологическое изобретение, использующее круглую форму, появилось только в 3500 г. до н.э., и это было изобретение гончарного круга. Затем, 300 лет спустя, они использовались для колес колесниц. Когда люди начали понимать ценность и использовать предметы круглой формы, они начали изучать круги.
Такие вещи, как радиус, диаметр и окружность, — это термины, которые помогают нам отслеживать различные измерения окружности.
Итак, давайте посмотрим, что представляет собой каждое из этих измерений.
Во-первых, давайте определим средней точки , чтобы вы поняли, о чем я говорю, когда я на нее ссылаюсь. Я нарисую круг. Середина — это точный центр круга. Итак, где-то здесь.
Теперь давайте посмотрим на эти другие термины.
Радиус — это длина от середины круга до внешнего края круга. Радиус обозначается строчной буквой «r».
Диаметр — это полная длина окружности, идущей от края через середину до другой стороны.Вот и вся эта длина прямо здесь. Диаметр круга обозначается буквой «d».
Итак, окружность — это расстояние по внешнему краю этой окружности. Окружность обозначается заглавной буквой «C».
Окружность сравнима с периметром формы, как у параллелограмма . Если бы вы разрезали линию круга, как если бы это была веревка, и разложили ее для измерения. Эта длина была бы эквивалентна окружности.Однако, поскольку круг имеет непрерывную кривую, мы используем слово , окружность , а не периметр , чтобы отличить его.
Теперь, когда мы рассмотрели, что такое радиус, диаметр и длина окружности, давайте посмотрим, как рассчитать каждый из них.
Если бы кто-то просто протянул вам лист бумаги с кружком…. Вообще-то, это было бы довольно странно.
Но, допустим, мы хотели найти радиус, диаметр и длину окружности этого круга, и все, что у нас есть, это линейка.
Проще всего начать с линейки и измерить от самого центра круга расстояние между внешним краем. Это будет диаметр .
Допустим, когда мы измерили, мы получили длину 9 см для диаметра. Что ж, мы знаем, что если наш радиус проходит от середины до внешнего края, то все, что нам нужно сделать, чтобы найти длину нашего радиуса, — это разделить длину диаметра на 2.
Итак, когда мы берем 9 и разделив его на 2, мы получим длину радиуса 4.5 см.
Формула для радиуса может быть записана как \ (r = \ frac {d} {2} \), а формула для диаметра может быть записана как \ (d = 2r \).
Теперь, чтобы найти окружности окружности, нам нужно будет использовать формулу.
Формула длины окружности: \ (C = \ pi \ times d \), или ее можно записать как \ (C = 2 \ times \ pi \ times r \). Либо работает!
Теперь вы можете спросить: «Откуда же взялось число Пи, и почему мы внезапно получаем длину окружности, если умножаем число Пи на наш диаметр? Кто это решил? » Если вы не задаете этот вопрос … Следует, и я все равно на него отвечу.
Pi — это символ, который мы используем в математике для обозначения числа 3,14. На самом деле это просто число Пи, округленное до ближайшей сотой. На самом деле у Пи нет конца и нет предсказуемой закономерности. Это просто продолжается.
Однако, когда вы видите символ \ (\ pi \), обычно (и в нашем случае) будет достаточно 3,14.
Пи — это не случайное число, придуманное математиками и заявленное «мы будем каждый раз умножать диаметр на число и называть его окружностью». Напротив, было обнаружено, что пи представляет собой постоянное отношение между окружностью и диаметром.
Вот почему и как мы получили формулу длины окружности.
Теперь возьмем круг диаметром 9 см и радиусом 4,5 см и вычислим длину окружности.
Я воспользуюсь формулой диаметра для этого.
Итак, длина окружности равна (я просто перепишу формулу, чтобы помочь нам следить за нашей работой), \ (C = \ пи \ умножить на d \), равна пи умноженному на диаметр. Итак, теперь все, что нам нужно сделать, это ввести наше число для диаметра. Это равно, и мы также сказали, что пи равно 3.14, \ (C = (3,14) (9 см) = 28,26 см \).
И вот наш ответ! Теперь, чтобы попрактиковаться, попробуйте нарисовать круг на листе бумаги и измерить свой диаметр линейкой. Затем найдите свой радиус и длину окружности.
Надеюсь, это видео было для вас полезным. Для получения дополнительной помощи не забудьте подписаться на наш канал, нажав ниже.
Увидимся в следующий раз!
Окружность круга — объяснение и примеры
Мы уже видели, как найти периметр многоугольника.Мы знаем, что круг — это не многоугольник. Следовательно, у него не должно быть периметра. Мы используем эквивалентную форму круга, называемую окружностью.
В этой статье, , мы обсудим, как найти окружность круга , формулу окружности круга, примеры и примеры задач об окружности круга.
Какова длина окружности?
Расстояние вокруг многоугольника, такого как квадрат или прямоугольник, называется периметром (P) .С другой стороны, расстояние по окружности называется окружностью (C) . Следовательно, длина окружности — это линейное расстояние края круга.
Зачем нужно вычислять длину окружности?
Определение окружности объекта важно в следующих случаях:
Если вы хотите купить бюстгальтер, брюки или свитер, вам необходимо знать расстояние вокруг вашей талии или груди. Хотя ваше тело не является идеальным кругом, вам придется измерить его окружность с помощью рулетки.Портные в основном используют эту технику для определения окружности платья.
Вам также необходимо знать длину окружности, делая поделки, ставя ограждение вокруг гидромассажной ванны или просто решая школьную математическую задачу.
Как найти длину окружности?
Как указывалось ранее, периметр или окружность круга — это расстояние вокруг круга или любой круглой формы. Окружность круга равна длине прямой линии, согнутой или изогнутой, чтобы образовать круг.Окружность круга измеряется в метрах, километрах, ярдах, дюймах и т. Д.
Существует два способа найти периметр или длину окружности . Первая формула предполагает использование радиуса, а вторая предполагает использование диаметра окружности. Важно отметить, что оба метода дают одинаковый результат.
Давайте посмотрим.
Длина окружности равна;
C = 2 * π * R = 2πR
где,
C = окружность или периметр,
R = радиус круга,
π = математическая константа, известная как Pi
Или
C = π * D = π D
где, D = 2R = диаметр круга
Для любого круга отношение его длины к диаметру равно константе, известной как пи.
Окружность / диаметр = Pi
C / D = Pi или C / 2R = pi
Приблизительное значение пи (π) = 22/7 = 3,1415926535897…. (не завершающееся значение)
Для упрощения вычисления окружности круга значение пи принимается равным 3,14 (π = 3,14).
Давайте рассмотрим несколько примеров ниже, чтобы усовершенствовать концепцию окружности.
Пример 1
Найдите длину окружности с радиусом 8 см.
Раствор
Окружность = 2 * π * R = 2πR
= 2 * 3.14 * 8
= 50,24 см.
Пример 2
Вычислите длину окружности круга диаметром 70 мм
Решение
Окружность = π * D = π D
= 3,14 * 70
= 219,8 мм
Пример 3
Рассчитайте периметр круглого цветника с радиусом 10 м.
Раствор
Окружность = 2 * π * R = 2πR
= 2 * 3.14 * 10
= 62,8 м.
Пример 4
Окружность круга составляет 440 ярдов. Найдите диаметр и радиус круга.
Раствор
Окружность = 2 * π * R = 2πR
440 = 2 * 3,14 * R
440 = 6,28R
Разделите обе стороны на 6,28, чтобы получить,
R = 70,06
Следовательно, радиус круга 70,06 ярда. Но, поскольку диаметр в два раза больше радиуса круга, диаметр равен 140.12 ярдов.
Пример 5
Диаметр колес велосипеда 100 см. Сколько оборотов сделает каждое колесо, чтобы преодолеть расстояние в 157 метров?
Решение
Рассчитайте окружность колеса велосипеда.
Окружность = π D
= 3,14 * 100
= 314 см
Чтобы получить количество оборотов колеса, разделите пройденное расстояние на окружность колеса.
Нам нужно преобразовать 157 метров в сантиметры перед делением, поэтому мы умножаем 157 на 100, чтобы получить 15700 см. Следовательно,
Число оборотов = 15700 см / 314 см
= 50 оборотов.
Пример 6
Отрезок проволоки в виде прямоугольника длиной 100 см и шириной 50 см отрезают и складывают, чтобы получился круг. Вычислите длину окружности и радиус образовавшейся окружности.
Решение
Окружность образованного круга = периметр прямоугольной проволоки.
Периметр прямоугольника = 2 (Д + Ш)
= 2 (100 + 50) см
= 2 * 150 см
= 300 см.
Следовательно, длина окружности будет 300 см.
Теперь вычислим его радиус.
Окружность = 2 π R
300 см = 2 * π * R
300 см = 2 * 3,14 * R
300 см = 6,28R
Разделите обе стороны на 6,28.
R = 47,77 см
Итак, радиус круга будет 47,77 см.
Пример 7
Радиус каждого колеса мотоцикла равен 0.85 м. Как далеко уедет мотоцикл, если каждое колесо сделает по 1000 оборотов? Предположим, мотоцикл движется по прямой.
Решение
Сначала найдите окружность колеса.
Окружность = 2 π R
= 2 * 3,14 * 0,85
= 5,338 м.
Чтобы найти пройденное расстояние, умножьте длину окружности колеса на количество сделанных оборотов.
Расстояние = 5,338 * 1000
= 5338 м
Следовательно, пройденное расстояние равно 5.338 километров.
Практические вопросы- Майку и его друзьям подают 12-дюймовую пиццу. Майк заинтересован в вычислении его окружности. Помоги ему!
- Периметр конкретного квадрата составляет 1/3 -го площади определенного круга. Если длина квадрата составляет L единиц, определите диаметр круга как L .
Ответы
- 12π дюймов или 37.67 дюймов
- 12L / π единиц
Как найти длину диаметра
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в виде ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; а также Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
Как рассчитать окружность и площадь круга
Ключевые термины
o Круг
o Эквидистант
o Радиус
o Диаметр
o Окружность
o Pi ( π )
Цели
o Определите некоторые основные части круга, такие как радиус и диаметр.
o Вычислить длину окружности
o Вычислить площадь круга
В этой статье мы рассмотрим геометрическую фигуру, которая не состоит из отрезков прямых, а вместо этого изогнута: круг.Мы применим то, что мы знаем об алгебре, к изучению окружностей и тем самым определим некоторые свойства этих фигур.
Введение в круги
Представьте себе точку P , имеющую определенное местоположение; Затем представьте все возможные точки, которые находятся на некотором фиксированном расстоянии r от точки P. Некоторые из этих точек проиллюстрированы ниже. Если бы мы нарисовали все (бесконечное количество) точек, которые находятся на расстоянии r от P, , мы получили бы круг, который показан ниже сплошной линией.
Таким образом, круг — это просто набор всех точек , равноудаленных (то есть все на одинаковом расстоянии) от центральной точки ( P в приведенном выше примере). Расстояние r от центра круга до самого круга называется радиусом ; Диаметр в два раза больше (2 r ) называется диаметром . Радиус и диаметр показаны ниже.
Окружность круга
Как и в случае с треугольниками и прямоугольниками, мы можем попытаться вывести формулы для площади и «периметра» круга.В отличие от треугольников, прямоугольников и других подобных фигур, расстояние по внешней стороне круга называется окружностью , а не периметром — однако концепция, по сути, та же. Однако вычислить длину окружности не так просто, как вычислить периметр прямоугольника или треугольника. Учитывая, что объект в реальной жизни имеет форму круга, один из подходов может заключаться в том, чтобы ровно один раз обернуть нить вокруг объекта, а затем выпрямить нить и измерить ее длину.Такой процесс проиллюстрирован ниже.
Очевидно, что по мере увеличения диаметра (или радиуса) круга круг становится больше, и, следовательно, длина окружности также увеличивается. Нас заставляют думать, что, следовательно, существует некоторая взаимосвязь между окружностью и диаметром. Оказывается, если мы измеряем длину окружности и диаметр любого круга, мы всегда обнаруживаем, что длина окружности чуть более чем в три раза больше диаметра.Два примера кружков ниже иллюстрируют эту точку, где D, — диаметр, а C — длина окружности каждого круга.
Опять же, в каждом случае длина окружности чуть больше трех диаметров круга. Если мы разделим длину окружности любого круга на его диаметр, мы получим постоянное число. Эта константа, которую мы обозначаем греческим символом π ( pi ), приблизительно равна 3.141593. Точное значение π неизвестно, и есть подозрение, что пи — иррациональное число (неповторяющееся десятичное число, которое, следовательно, не может быть выражено как дробь с целым числителем и целым знаменателем). Давайте запишем упомянутую выше взаимосвязь: частное окружности ( C ), деленное на диаметр ( D ), является постоянным числом π.
Мы можем получить выражение для окружности через диаметр, умножив обе части выражения, приведенного выше, на D, , таким образом выделив C.
Поскольку диаметр в два раза больше радиуса (другими словами, D = 2 r ), мы можем заменить 2 r на D в приведенном выше выражении.
Таким образом, мы можем вычислить длину окружности круга, если мы знаем радиус круга (или, следовательно, его диаметр).Для большинства вычислений, требующих десятичного ответа, часто достаточно оценки π как 3,14. Например, если круг имеет радиус 3 метра, то его окружность C будет следующей.
Ответ выше точный (хотя он написан в терминах символа π ). Если нам нужен приблизительный числовой ответ, мы можем оценить π как 3.14. Затем,
Символ ≈ просто означает «примерно равно».
Практическая задача : Окружность имеет радиус 15 дюймов. Какая у него окружность?
Решение : Начнем с рисования диаграммы ситуации. Этот подход может быть очень полезным, особенно в ситуациях, связанных с кругами, где радиус и диаметр легко спутать.
Поскольку нам дан радиус, мы должны либо вычислить длину окружности ( C ), используя выражение в терминах радиуса, либо мы должны преобразовать радиус в диаметр (удвоенный радиус) и использовать выражение в терминах диаметр. Для простоты воспользуемся первым подходом.
Это точный результат. Если нам нужен приблизительный десятичный результат, мы можем использовать π ≈ 3.14.
Площадь круга
Так же, как вычисление длины окружности сложнее, чем у треугольника или прямоугольника, так вычисляется и площадь. Давайте попробуем оценить площадь круга, нарисовав круг внутри квадрата, как показано ниже. Область круга заштрихована.
Нарисуем в окружности вертикальный и горизонтальный диаметры; обозначим эти диаметры как имеющие длину D. Обратите внимание на то, что по сравнению с квадратом, квадрат должен иметь также стороны длиной D .
Мы знаем, что квадрат (который представляет собой прямоугольник, длина и ширина которого равны) со сторонами длиной D имеет следующую площадь A квадрат (обратите внимание, что мы добавляем индекс, чтобы идентифицировать эту область как площадь квадрат — аналогичный индекс добавим в случае площади круга):
Поскольку круг диаметром D , очевидно, имеет меньшую площадь, чем квадрат со сторонами длиной D, , мы знаем, что площадь круга должна быть меньше D 2 .Осмотрев, мы можем предположить, что площадь A круга круга составляет примерно три четверти площади квадрата. Таким образом,
Как оказалось, это предположение близко к реальному результату. Посредством некоторой более сложной математики, которая выходит за рамки учебника, можно показать, что площадь круга в точности следующая:
Обратите внимание, что снова появляется число π .Давайте теперь сравним этот точный результат с нашим предположением сверху. Мы просто немного изменим выражение, имея в виду, что радиус ( r ) равен половине диаметра ( D ), другими словами, D = 2 r.
Так как D = 2 r, , затем
Подставим это значение вместо r в выражение для площади круга; мы должны сделать замену дважды.Затем мы можем несколько упростить выражение.
Поскольку π приблизительно равно 3,14, тогда
Таким образом, наше предположение было очень близко к фактической площади!
Практическая задача : Круг имеет диаметр 6 сантиметров.Какая у него площадь?
Решение : Обратите внимание, что указан диаметр , а не радиус. Таким образом, если мы хотим использовать выражение для площади в терминах радиуса, мы должны преобразовать диаметр в радиус (просто разделив диаметр пополам).
Теперь мы можем рассчитать площадь по следующей формуле.
Опять же, 9 квадратных сантиметров точный. Но,
Это приблизительный результат, но его будет достаточно во многих контекстах.
Практическая задача : Окружность окружности 8 π футов.Какая у него площадь?
Решение : Мы узнали, что длина окружности тесно связана с радиусом (и диаметром). Таким образом, используя это известное значение длины окружности, мы можем вычислить радиус и использовать его для определения площади. Сначала давайте решим выражение для окружности, чтобы получить радиус.
Мы хотим выделить р; , мы можем использовать тот же подход, что и при решении линейных уравнений.
Теперь, когда мы знаем радиус круга, мы можем вычислить его площадь.



 Радиус окружности обозначается буквой «R
». На рисунке выше —
это отрезок «OA
».
Радиус окружности обозначается буквой «R
». На рисунке выше —
это отрезок «OA
».

 Формула является достаточно простой и выглядит так: D = C/π = 2*R.
Формула является достаточно простой и выглядит так: D = C/π = 2*R.

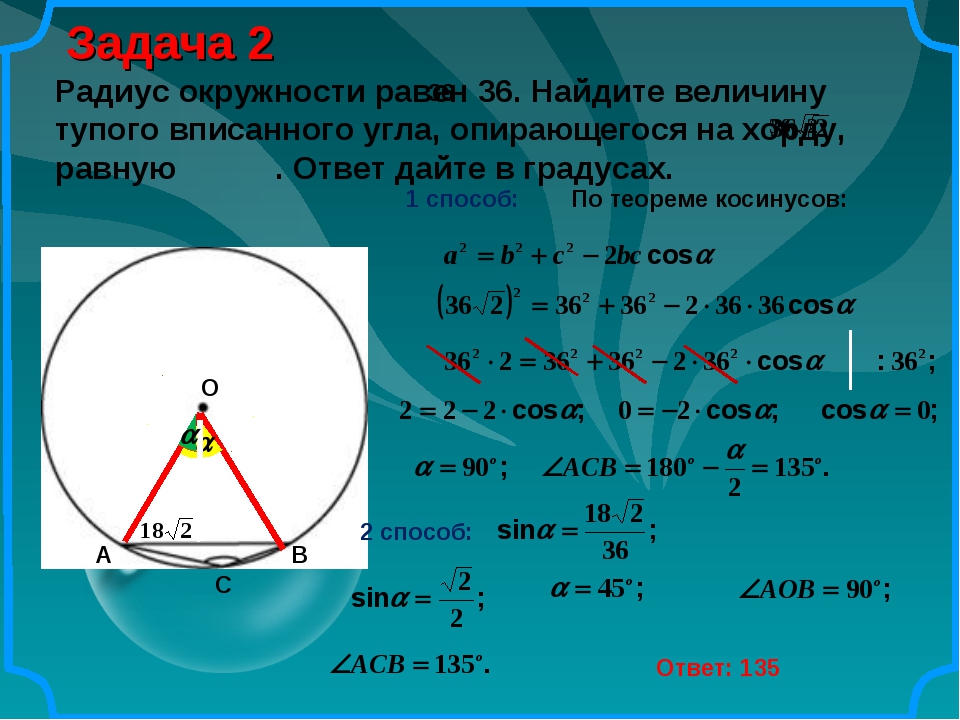 Обратите внимание, что диаметр в любой точке круга имеет одинаковую длину.
Обратите внимание, что диаметр в любой точке круга имеет одинаковую длину.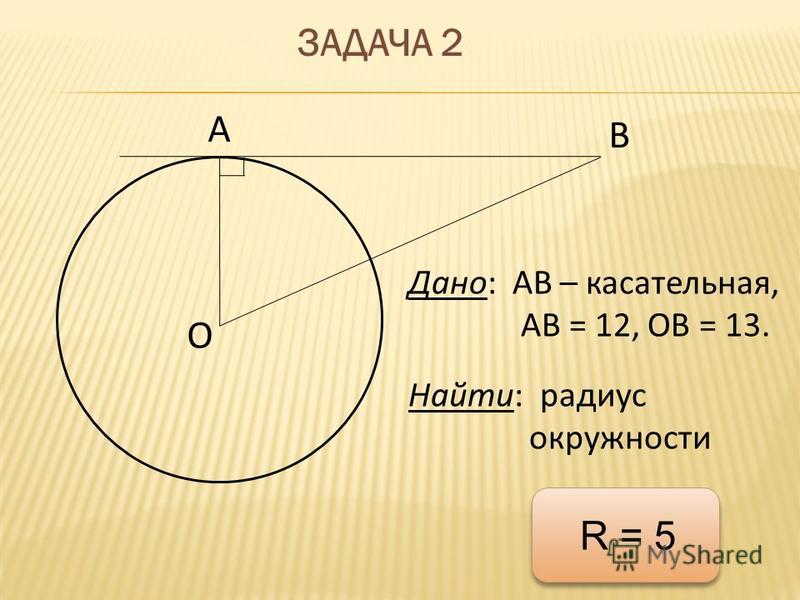 т. (тыс.куб.) — 1.6387064 x 10 -14 м³
т. (тыс.куб.) — 1.6387064 x 10 -14 м³ 158987294928 м³
158987294928 м³ Её длину будем обозначать латинской буквой l.
Её длину будем обозначать латинской буквой l. 2/(4П) = 2209/12,56 = 175,87 кв. м.
2/(4П) = 2209/12,56 = 175,87 кв. м.