Как построить график функции онлайн с модулем: Построение графиков с модулем онлайн · Как пользоваться Контрольная Работа РУ

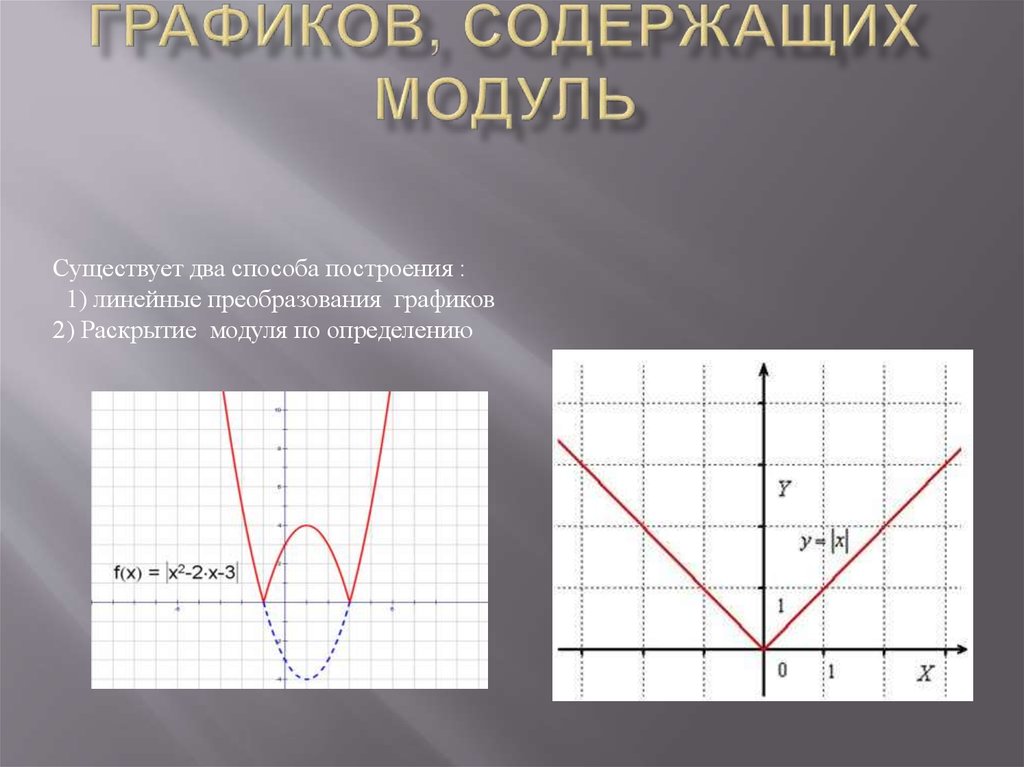
Построение графиков квадратичной функции, содержащей модуль

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

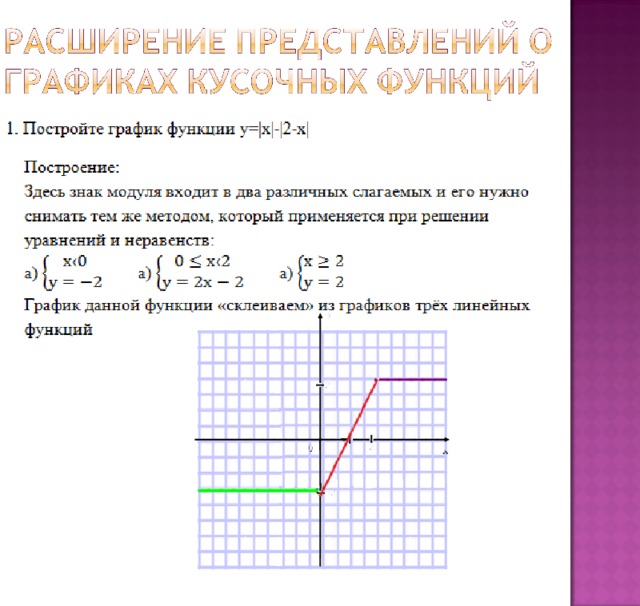
1. Построение графиков квадратичной функции, содержащей модуль

2. Актуализация опорных знаний

1.
2.
3.
4.
5.
6.
7.
8.
Определение квадратичной функции
Алгоритм построения квадратичной функции
Как, зная график функции y=f(x) построить графики следующих
функций:
y=f(-x)
y=-f(x)
y=f(x+m)
y=f(x)+n
y=f(x+m)+n
y=kf(x)
y=|f(x)|
y=f(|x|)

3.

Устно Дан график функции y = x2 – 4x + 3. Составьте формулу функции, график которой:1) симметричен данному относительно оси:
а) x;
б) y;
2) получается из данного параллельным переносом на
1а) y = –x2 + 4x – 3;
1б) y = x2 + 4x + 3
2
y = x2 – 6x + 6;
(1; 2)
3) получается из данного растяжением в 2 раза от оси
а) x;
б) y
4) получается из данного сжатием в 2 раза к оси
а) x;
б) y
3а) y = 0,25×2 – 2x + 3;
3б) y = 2×2 – 8x + 6;
4а) y = 4×2 – 8x + 3
4б) y = 0,5×2 – 2x + 1,5;
Найдите соответствия:
у х2 5
у 0,3х
2
у ( х 3)
2
у х 2 5
2

5. Построить график функции y=|-2×2 +8x -6|

1. Построим график функции y= -2×2 +8x -6
Ветви параболы направлены вниз
Вершина в точке:
b
8
2,
2a
4
y0 8 16 6 2
xo
Ось симметрии: х=2
Нули функции
Х1 =1, Х2 =3
х
0
1
2
3
4
у
-6
-0
2
0
-6
2. отразим части параболы,
расположенные в нижней части
полуплоскости, симметрично
относительно оси абсцисс.
Применение преобразований при построении графика функции
Y
2
Построим график функции y =| — 2 x +6 x -2 |
1.Сначала построим график функции
y = — 2 x 2+8 x -6
Преобразуем трехчлен:
2 x 8 x 6 2 x 4 x 3
2
2
2 x 2 2 x 2 4 4 3
2 x 2 1 2 x 2 2
2
2
6
2
1
0
-1
-2
y 2 x 2 2
2
-3
-4
-5
-6
2. отразим части параболы, расположенные в
нижней части полуплоскости, симметрично
относительно оси абсцисс.
1
x

7. Аналитическое построение

Построить график функции y=|x|x
По определению модуля: y = x2 ,x>0
— x2 ,x<0
x>0
y
0
x<0
x

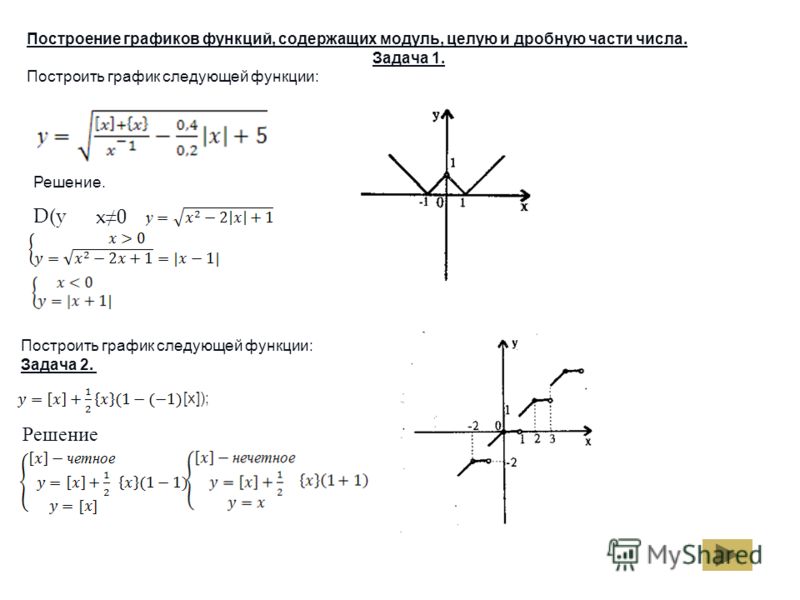
8. Построим график функции y=|x2-5x|+x-3 с помощью узловых точек

x2-5x=0, x(x-5)=0, x=0 илиx=5
|
||
x=0или x=5 разбивают числовую
прямую на три промежутка
0
5
I. x=-1;
(-1)2 -5(-1)>0
y=x2-5x+x-3 =x2-4x-3
Строим параболу и выделяем ту часть,
которая находится на промежутке ;0
II. x=1;
12 -5*1<0,
y=-x2+5x+x-3 =-x2 +6x-3
Строим параболу и выделяем ту часть,
которая находится на промежутке 0;5
III. x=6;
62 -5*6>0
y=x2-4x-3 Эту параболу уже строили, поэтому
выделим ту часть,
которая находится на промежутке 5;
Выделенные части являются графиком
функции
|||
x

9. Постройте графики функций:

Вариант 1
а) y=|x2 -4|
б) y=|2x-x2 |
Вариант 2
а)y=|x2 -1|
б) y=|x2 +2x-1|
Вариант 3
Вариант 4
а) y=|(x-3)2 -1| б) а) y=|-(x+2)2 +3|
y=x2 -|x-1|
б) y=|2+4|x|-x2|

10. Проверь себя !

Вариант 1
Вариант 2
а) y=|x2 -4|
а) y=|x2 -1|
б) y=|x2 +2x-1|
б) y=|2x-x2 |
Вариант3
Вариант 4
а) y=|(x-3)2 -1|
а) y=|-(x+2)2 +3|
б) y=x2 -|x-1|
б) y=|2+4|x|-x2|

11. Основные преобразования графиков:

параллельные переносы;
симметрии относительно осей координат;
растяжения (сжатия) от (к) осей (осям) координат;
преобразования, связанные с модулями.

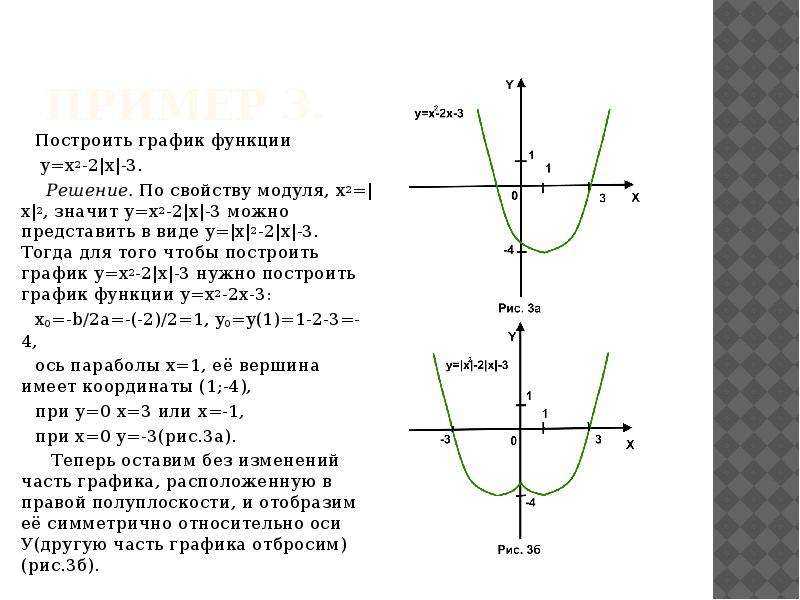
12. Алгоритм построения графика функции у = ах2 + bх +с.

1. Определить направление ветвей параболы.
2. Найти координаты вершины параболы
(т; п).
3. Провести ось симметрии.
4. Определить точки пересечения графика
функции с осью Ох, т.е. найти нули
функции.
5. Составить таблицу значений функции
с учетом оси симметрии параболы.

13. Перенос вдоль оси ординат

График функции y= f (x) + b при b >0
можно получить параллельным переносом вдоль
оси ординат графика функции y= f (x) на b
единиц вверх.
y= x2 +2
Y
2
1
y=x2
0 1
График функции y=f(x)-b при b>0 можно
получить параллельным переносом вдоль оси
ординат графика функции y=f(x) на b единиц
вниз
x
Y
1
0 1
-2
y=x2
x
y= x2 -2

14. Перенос вдоль оси ординат

График функции y= f(x)+b при b >0
можно получить так :
1. построить график функции y= f (x)
2.перенести ось абсцисс на b единиц
вверх
Y
2
На b
вверх
0
0
1
x
1
x
Y
График функции y=f(x)-b при b>0
можно получить так:
1. построить график функции y=f(x)
2 перенести ось абсцисс на единиц вниз
1
Вниз
На b
0
-2
0
x
1
x

15. Перенос вдоль оси абсцисс

График функции y= f (x + c) можно получить
параллельным переносом вдоль оси абсцисс графика
функции y= f (x) на |c| единиц влево при c >0 .
Y
y=x2
1
-2
0
1
x
y=(x+2)2
График функции y=f(x+c) можно получить
параллельным переносом вдоль оси абсцисс графика
функции y=f(x) на |c| единиц вправо при c<0
y=x2
Y
y=(x-2)2
1
0
1
2
x

16. Перенос вдоль оси абсцисс

График функции y= f (x + c) при c >0
можно получить так :
1. построить график функции y= f (x)
2.перенести ось ординат на |b| единиц
вправо
y
1
0
График функции y=f(x+c) при c<0
можно получить так:
1. Построить график функции y=f(x)
2. Перенести ось ординат на |c| единиц
влево
y
y
1
1
y
1
1 0
x
0
0 1
x

17.

Сжатие ( растяжение ) графика вдоль оси ординатГрафик функции y= b f (x)
при b>1 можно получить
растяжением графика функции
y= f (x) вдоль оси ординат
y=2×2
Y
1
y=x2
0 1
График функции y=bf(x) при
0<b<1 можно получить сжатием
графика функции y=f(x) вдоль
оси ординат
x
y=0,5×2
Y
1
0 1
y=x2
x

18. Симметрия относительно оси абсцисс

Чтобы построить график фунуции y= -f(x):
1. Строим график функции y=f(x)
2. Отражаем его симметрично относительно оси
абсцисс.
y=x2
0 1
x
y=-x2

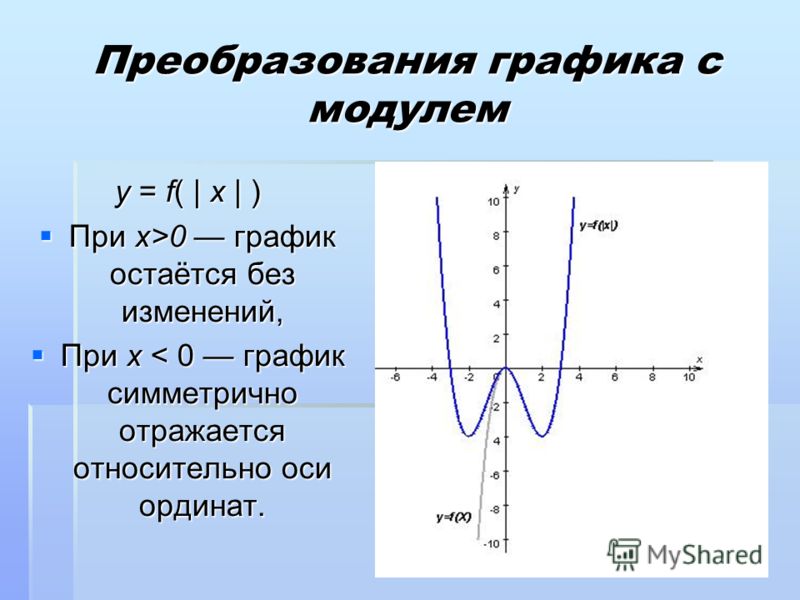
19. график функции y = f(|x|), y = |f(x)|

график функции y = f(|x|) получается из графика функции y = f(x)
следующим преобразованием:
1)
точки графика, имеющие неотрицательные абсциссы – неподвижны;
2) точки графика, имеющие отрицательные абсциссы заменяются на
точки, полученные из неподвижных отражением относительно оси y.
график функции y = |f(x)| получается из графика функции y = f(x)
следующим преобразованием:
1)
точки графика, имеющие неотрицательные ординаты – неподвижны;
2) точки графика, имеющие отрицательные ординаты, отражаются
относительно оси x.

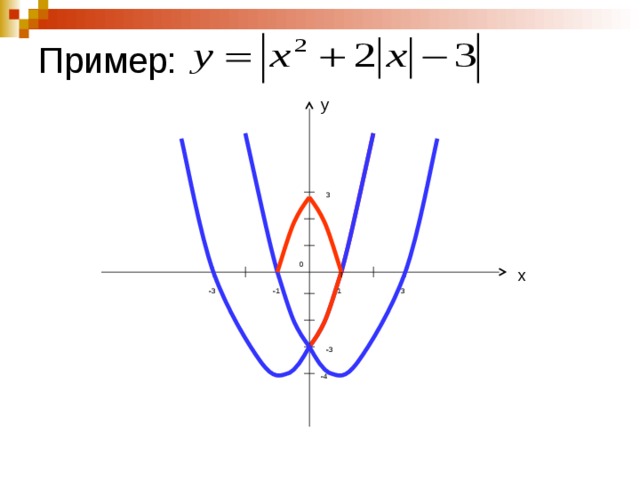
20. Функция, содержащая операцию « взятие модуля»

y
Чтобы построить график функции y= |f( x) |:
1. Строим график функции y= f(x),
2.Часть графика, расположенную в верхней
полуплоскости сохраняем.
3. Часть графика, расположенную в нижней
полуплоскости. отображаем симметрично
относительно оси абсцисс в верхнюю
полуплоскость.
0
x

English     Русский Правила

Основные правила преобразования графиков функций 9 класс онлайн-подготовка на Ростелеком Лицей

Введение

 

Наверняка многие из вас могут быстро и правильно построить графики некоторых функций, не прибегая к вычислениям значений точек. Всем известно, что график функции  – это прямая, а график функции  – это парабола. Но как построить, например, график функции , не вычисляя значения точек? Для этого существуют правила преобразования графиков функций.

 

 

Преобразование симметрии относительно оси

Ox

 

 

Предположим, что у нас есть функция  (график этой функции – это парабола) и необходимо построить график функции .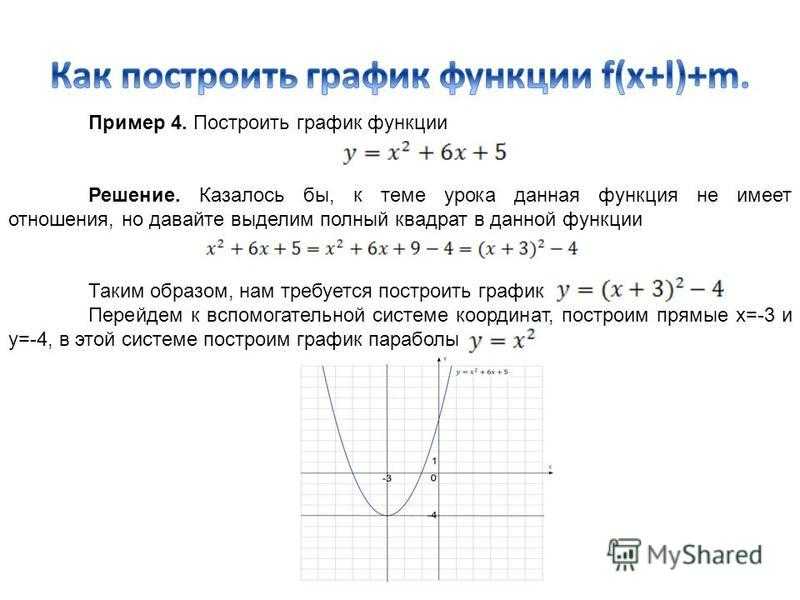 Вычислим значения некоторых точек для графиков этих функций.

 

Из таблиц видно, что одним и тем же значениям аргумента соответствуют противоположные значения функций. Графически это означает, что графики расположены симметрично относительно оси абсцисс. То есть заданная парабола () зеркально отобразится относительно оси  (см. Рис. 1).

Рис. 1. Графики функций  и

Таким образом, если у нас есть произвольный график , то для построения графика  необходимо график  симметрично отразить относительно оси  (см. Рис. 2). Такое преобразование называется преобразованием симметрии относительно оси .

Рис. 2. Преобразование симметрии относительно оси

Преобразование симметрии – зеркальное отражение относительно прямой.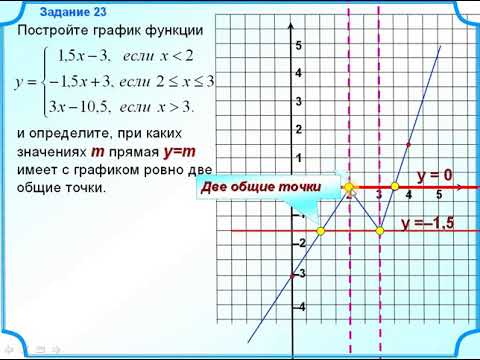 График  получается из графика функции  преобразованием симметрии относительно оси .

На рисунке 3 показаны примеры симметрии относительно оси .

Рис. 3. Симметрия относительно оси Ox

 

Параллельный перенос вдоль оси Oy

 

 

Предположим, что у нас есть функция  (график этой функции – это парабола) и необходимо построить график функции . Вычислим значения некоторых точек для графиков этих функций.

 

Из таблиц видно, что при одних и тех же значениях аргумента значения функции у графика  больше на 3 единицы. Графически это означает, что график функции  находится на 3 единицы выше, чем график функции  (см. Рис. 4).

Рис.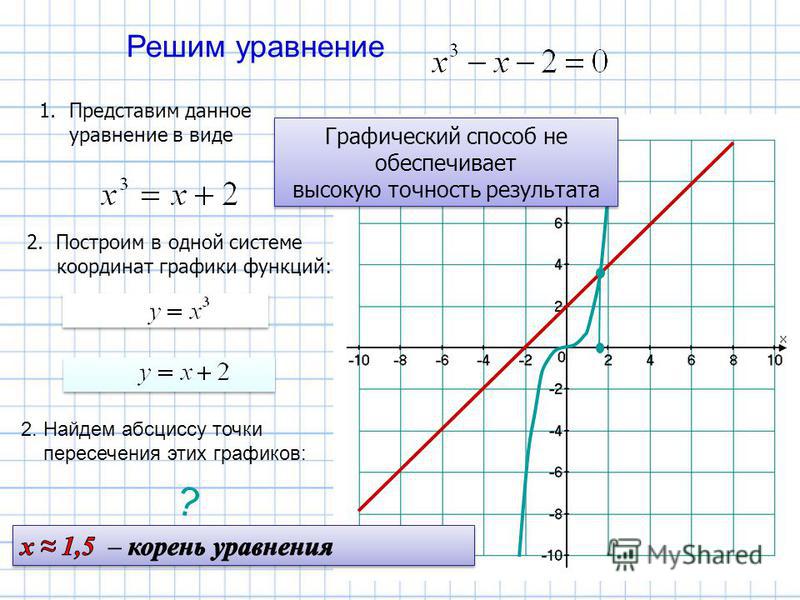 4. Графики функций  и

График  получается из графика функции параллельным переносом последнего вдоль оси ординат на  единиц вверх, если , и на  единиц вниз, если  (см. Рис. 5, 6).

Рис. 5. Параллельный перенос вдоль оси  (при )

Рис. 6. Параллельный перенос вдоль оси  (при )

 

Растяжение от оси Ox и сжатие к оси Ox

 

 

Предположим, что у нас есть функция  (график этой функции – это парабола) и необходимо построить график функции . Вычислим значения некоторых точек для графиков этих функций.

 

Из таблиц видно, что при одних и тех же значениях аргумента значения функции у графика  больше в 2 раза. Графически это означает, что график функции  сужается по сравнению с графиком функции  (см. Рис. 7).

Рис. 7. Графики функций  и

Если необходимо построить график функций , то из таблиц видно, что при одних и тех же значениях аргумента значения функции у графика  меньше в 2 раза, чем у . Графически это означает, что график функции  расширяется по сравнению с графиком функции  (см. Рис. 8).

Рис. 8. Графики функций  и

Чтобы построить график функции , где  и , нужно ординаты точек заданного графика умножить на . Такое преобразование называется растяжением от оси  с коэффициентом , если , и сжатием к оси, если  (см. Рис. 9, 10).

Рис. 9. Растяжение от оси

Рис. 10. Сжатие к оси

 

Параллельный перенос вдоль оси Ox

 

 

Предположим, что у нас есть функция , необходимо построить график функции . Вычислим значения некоторых точек для графиков этих функций.

 

Из таблиц видно, что одинаковым значениям функции соответствуют значения аргумента, отличающиеся на 2 единицы. Это означает, что график данной функции переместился на 2 единицы относительно оси ординат влево (см. Рис. 11), так как для получения одинаковых значений функций приходится брать значения аргумента на 2 меньше:

, при

 при

Следовательно, если необходимо было построить график функции , то сдвиг на 3 единицы относительно оси ординат был бы вправо (по сравнению с графиком функции ) (см. Рис. 11).

Рис. 11. Графики функций ,  и

График  получается из графика функции  параллельным переносом последнего на  единиц влево, если , и на  единиц вправо, если  (см. Рис. 12, 13).

Рис. 12. Параллельный перенос влево при

Рис. 13. Параллельный перенос вправо при

Обратите внимание на то, что по этому принципу из графика  не построить график , ведь мы добавили 1 не ко всем вхождениям  в это выражение. А вот график  построить можно, сдвинув исходный график на 1 влево (см. Рис. 14).

Рис. 14. Графики функции  и

 

Растяжение от оси Oy и сжатие к оси Oy

 

 

График функции , где  и , получается из графика функции  сжатием с коэффициентом  к оси  (если  указанное «сжатие» фактически является растяжением с коэффициентом ) (см. Рис. 15, 16).

 

Рис. 15. Сжатие к оси

Рис. 16. Растяжение от оси

Подобное преобразование мы уже рассматривали в случае построения графика функции .

 

Преобразование симметрии относительно оси Oy

 

 

Ранее мы рассматривали преобразование симметрии относительно оси Ox, то есть функция умножалась на (-1). Рассмотрим случай, когда на (-1) умножается только аргумент.

 

В этом случае график симметрично отображается относительно оси ординат, так как значения функций будут одинаковы при противоположных значениях аргумента:

для функции :

при

при

 

для функции :

при

при

График  получается из графика функции  преобразованием симметрии относительно оси  (см. Рис. 17).

Рис. 17. Преобразование симметрии относительно оси Oy

---

Построение графиков  и

Пусть дан график , построим график . Для начала раскроем модуль по определению:

 

Следовательно, те точки, в которых значения функции положительны или равны 0, остаются на месте, а все точки, в которых значения отрицательны, – отражаются относительно оси  (см. Рис. 18).

Рис.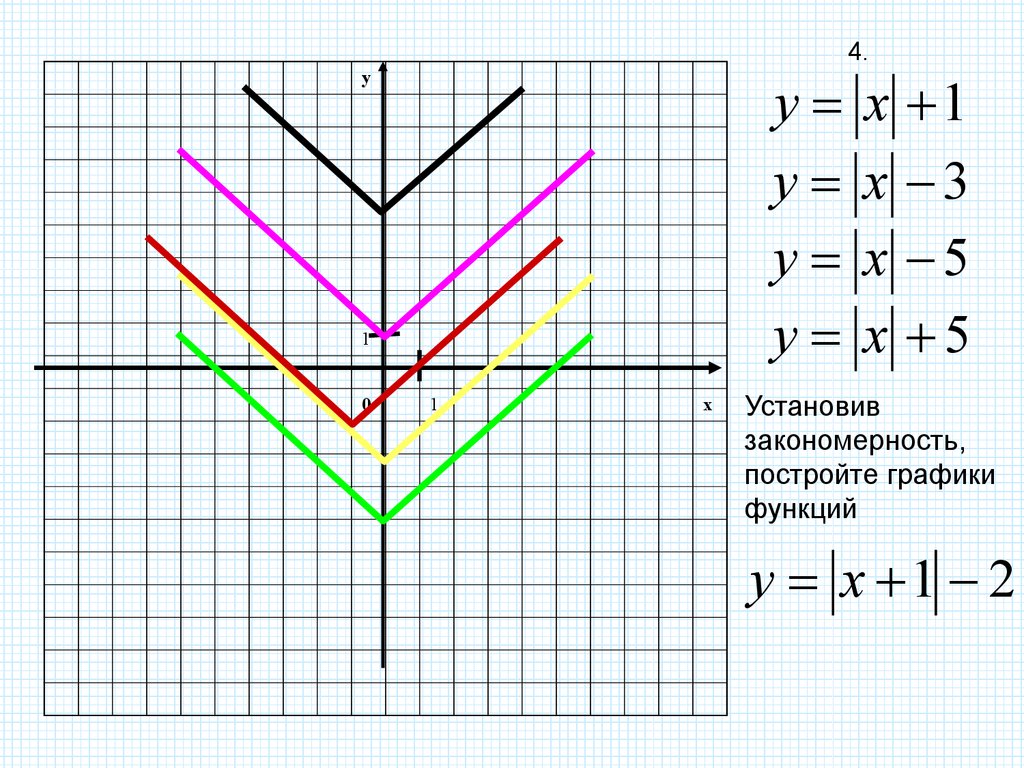 18. Графики функций  и  (красным цветом выделена общая часть этих графиков)

Для того чтобы построить график , нужно часть исходного графика, лежащую выше оси , оставить без изменения, а нижнюю отразить наверх относительно оси .

Пусть дан график , построим график . Для начала раскроем модуль по определению:

 

Следовательно, все точки с положительными или равными нулю абсциссами остаются без изменения, а все точки с отрицательными – заменяются точками с противоположными абсциссами (см. Рис. 19).

Рис.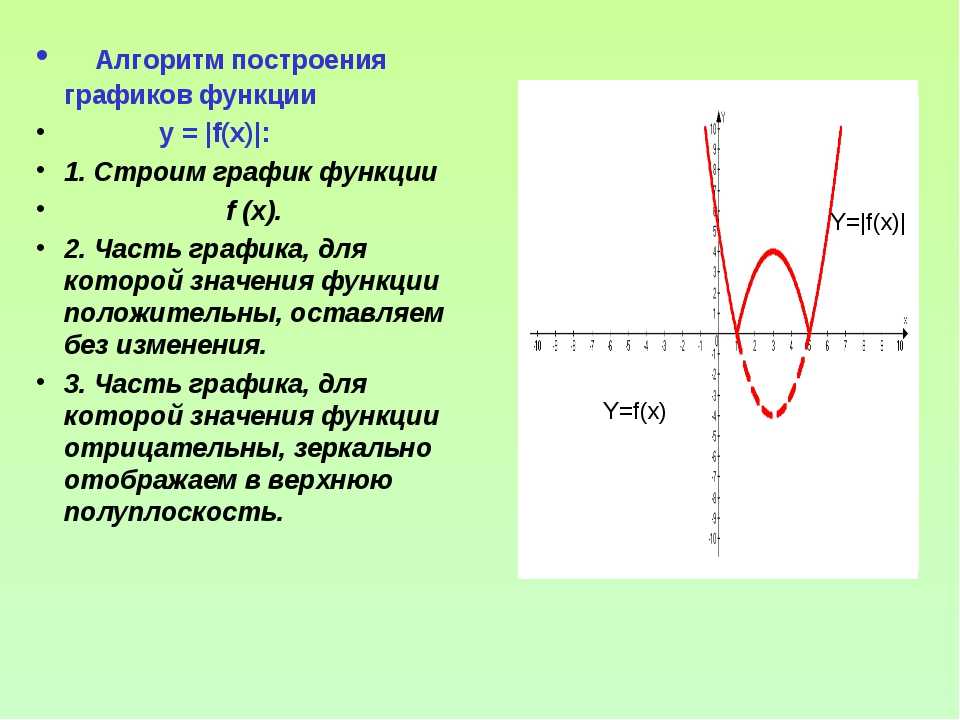 19. Графики функций  и  (красным цветом выделена общая часть этих графиков)

Для того чтобы построить график , нужно часть исходного графика, соответствующую значениям , оставить без изменений и отразить ее относительно оси  для значений .

 

Задача 1

 

 

Построить график функции .

 

Решение

Построим график заданной функции последовательно (см. Рис. 20):

1. Строим график .

2.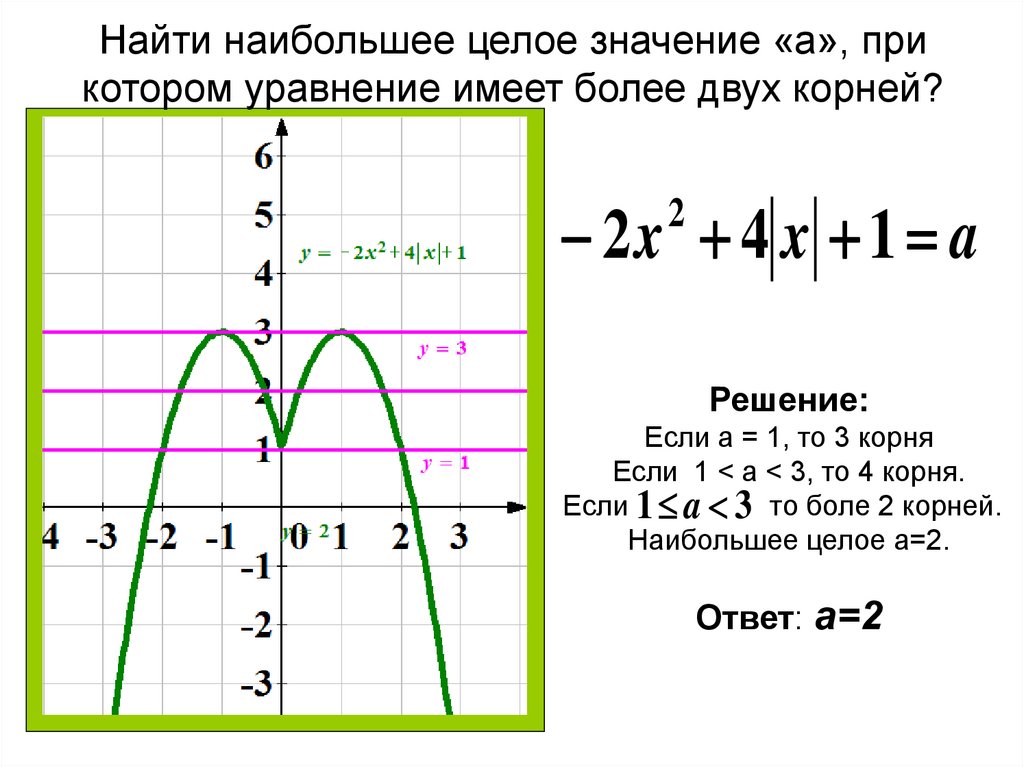 График  получается из графика  параллельным переносом последнего на 2 единицы вправо.

3. График  получается из графика функции  параллельным переносом последнего вдоль оси ординат на 3 единицы вверх.

Рис. 20. Иллюстрация к задаче

Мы могли бы сделать операции в обратном порядке, то есть сначала поднять график  на 3 единицы вверх, а потом получившийся график сдвинуть вправо на 2 единицы (см. Рис. 21).

Рис. 21. Иллюстрация к задаче

Обратите внимание, что не все графики функций можно строить в произвольном порядке.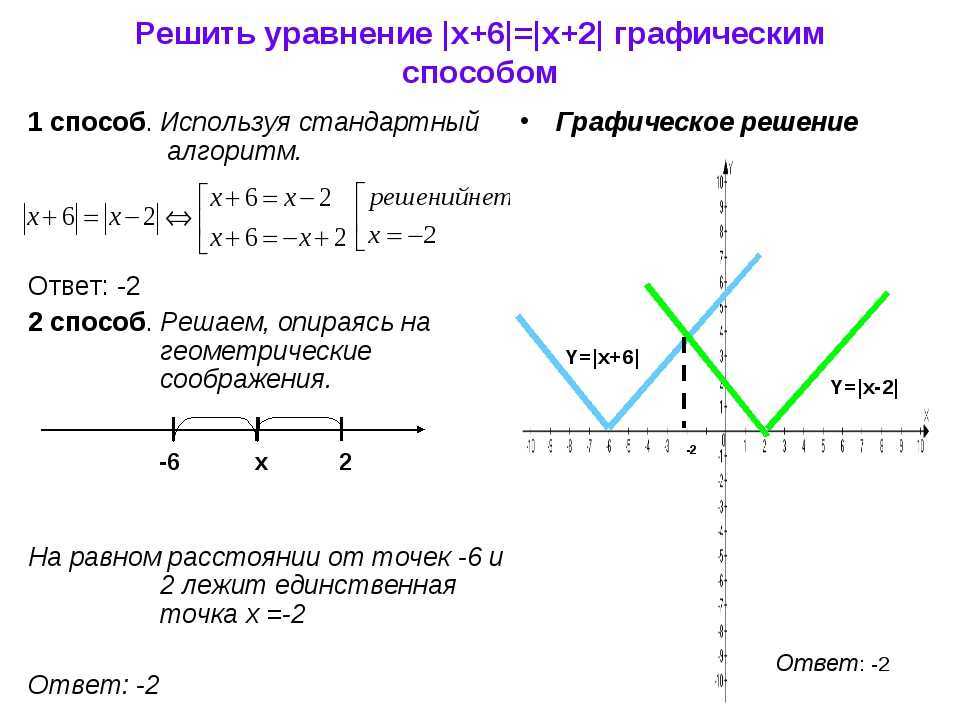 Например, для построения графика  сначала нужно построить график , затем график  (растяжение от оси ), а далее – график  (параллельный перенос вдоль оси ординат) (см. Рис. 22). Если же сделать в другой последовательности, то есть построить , то далее на 2 придется умножить всё выражение.

 – ПРАВИЛЬНО

 – НЕПРАВИЛЬНО

Рис. 22. Иллюстрация к задаче

---

Пример

Построить график .

Решение

1.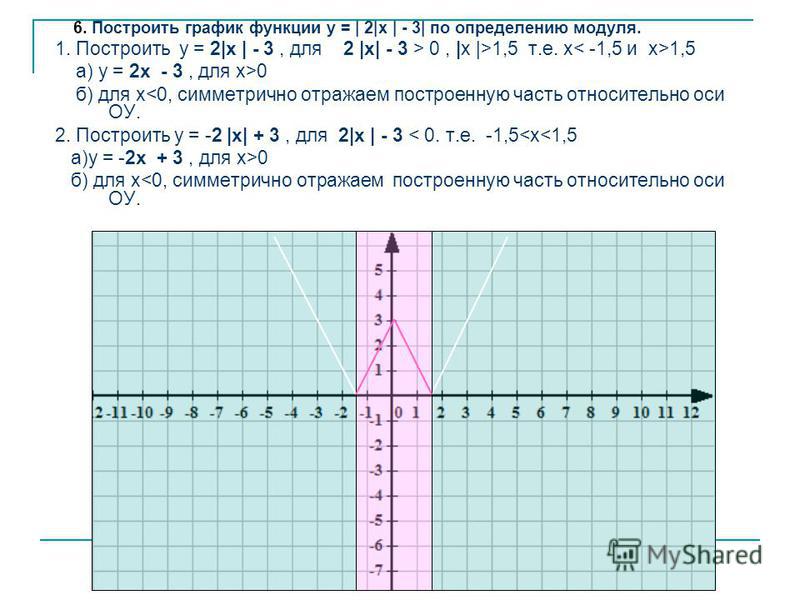 Строим график  (гипербола) (см. Рис. 23).

2. Строим график  (из аргумента вычитается 2, следовательно, сдвигаем график  на 2 единицы вправо) (см. Рис. 23).

3. Строим график  (домножение функции на (-1), следовательно, отражаем график  относительно оси ) (см. Рис. 24).

4. Строим график  (добавление 2 к функции, следовательно, сдвигаем график  на 2 единицы вверх) (см. Рис. 24).

5. Строим график  (модуль функции, следовательно, отражаем нижнюю часть графика  относительно оси , а верхнюю оставляем без изменений) (см. Рис. 25).

Рис.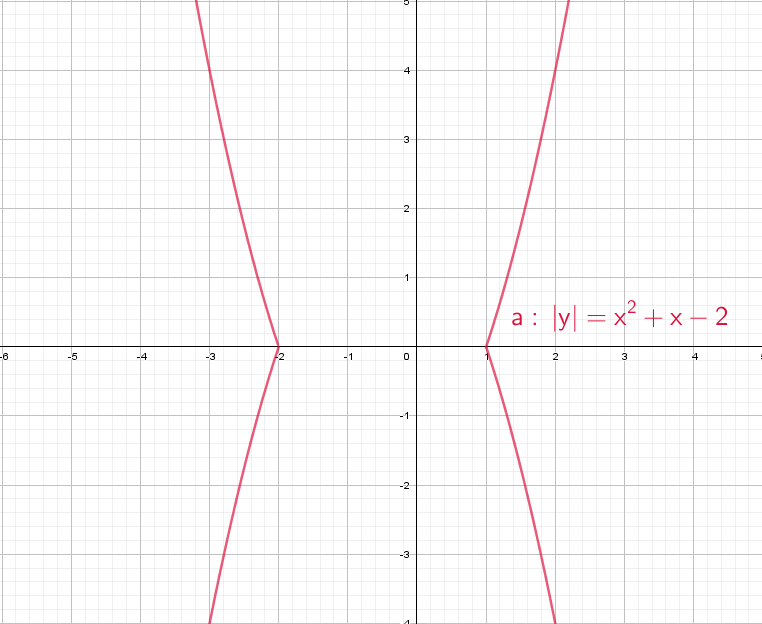 23. Иллюстрация к задаче

Рис. 24. Иллюстрация к задаче

Рис. 25. Иллюстрация к задаче (искомый график)

 

Список литературы

1. Мордкович А.Г. и др. Алгебра 9 кл.: Учеб. Для общеобразоват. Учреждений. – 4-е изд. – М.: Мнемозина, 2002. – 192 с.: ил.

2. Мордкович А.Г. и др. Алгебра 9 кл.: Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Т. Н. Мишустина и др. – 4-е изд.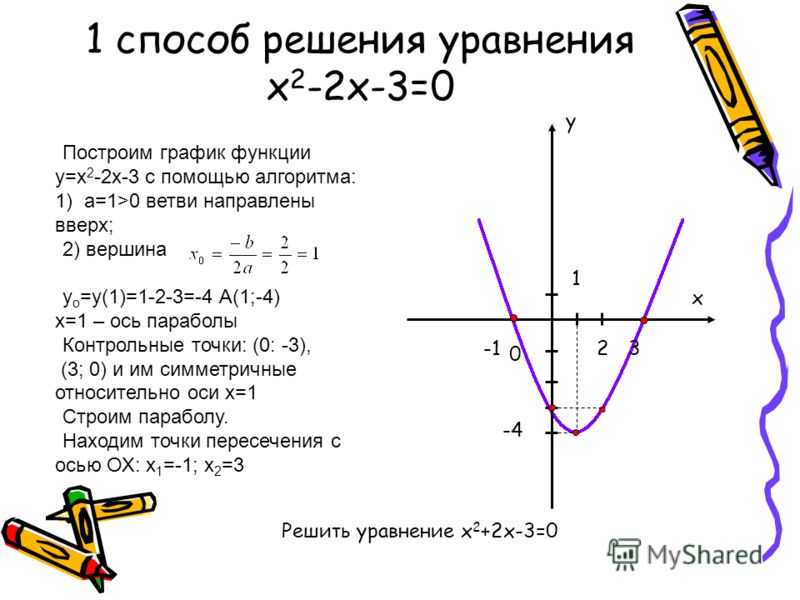 – М.: Мнемозина, 2002. – 143 с.: ил.

3. Макарычев Ю.Н. Алгебра. 9 класс : учеб.для учащихся общеобразоват. учреждений / Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, И.Е. Феоктистов. – 7-е изд., испр. и доп. – М.: Мнемозина, 2008.

5. Виленкин Н.Я., Сурвилло Г.С. и др. Алгебра 9 кл. С углубленным изучением математики. – М.: Просвещение, 2006.

 

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Интернет-сайт учебного центра «Резольвента» (Источник)

2. Интернет-сайт «Инфоурок» (Источник)

3. Интернет-сайт YouTube (Источник)

 

Домашнее задание

1. Упражнения 64, 66, 68 (б, г), 69 (в, ж), 70 (и) (стр. 65-69) Виленкин Н.Я., Сурвилло Г.С. и др. Алгебра 9 кл. (Источник).

2. Даны графики функций: а) ; б) ; в)

Какое уравнение будет иметь функция, график которой образуется из данных графиков функций: 1. при параллельном переносе вверх на 3 единицы; 2. при растяжении в 3 раза; 3. при параллельном переносе вправо на 3 единицы?

3. Постройте график функции .

 

Как построить график экспоненциальной функции — Объяснение!

Пошаговые примерыБольше примеров

Purplemath

Построение графика экспоненциальной функции похоже на построение графика, который вы делали ранее. Однако по природе экспоненциальных функций их точки, как правило, либо очень близки к одному фиксированному значению, либо слишком велики, чтобы их можно было удобно изобразить на графике.

На самом деле будет всего несколько точек, которые «разумно» использовать для рисования вашего изображения.

Содержание продолжается ниже

MathHelp.com

Чтобы выбрать разумные точки, вам потребуется хорошее понимание общего поведения экспоненты, чтобы вы могли заполнить пробелы.

Какое основное свойство экспонент?

Помните, что основное свойство экспонент состоит в том, что они изменяются в заданной пропорции в течение заданного интервала. Например, медицинский изотоп, который распадается наполовину по сравнению с предыдущим количеством каждые двадцать минут, и бактериальная культура, которая удваивается каждый день, демонстрируют экспоненциальное поведение, потому что за заданный промежуток времени (двадцать минут и один день соответственно) количество изменилась в постоянной пропорции (в полтора и два раза соответственно).

(Примечание: многие [«самые»?] экспоненты будут иметь беспорядочное время удвоения/уменьшения пополам, поэтому часто полезнее работать с точки зрения утроения, учетверения и т. д. времени, или данное упражнение может полностью игнорировать проблему , Если основание экспоненты не равно 2 [или ½], то не ожидайте, что время удвоения/уменьшения пополам будет подчеркнуто — или же не ожидайте, что время удвоения/уменьшения пополам будет хорошим аккуратным целым числом.)

Эта черта — наличие фиксированного времени деления пополам или удвоения — является основной для экспоненциальных функций. Но это может сделать график немного рискованным.

Такое поведение можно увидеть в любой базовой экспоненциальной функции, поэтому мы будем использовать y  = 2 ^x как представление всего класса функций:

В левой части x -ось, график отображается на оси x . Но ось x представляет y  = 0. Сможете ли вы когда-нибудь превратить 2 в 0, возведя его в степень? Конечно, нет. И положительная 2 не может превратиться в отрицательное число, если возвести его в степень.

Итак, линия, несмотря на свой внешний вид, никогда не опускается ниже оси

x в отрицательные значения y ; график y  = 2 ^x всегда фактически выше оси x , даже если только на исчезающе малую величину.

Так почему он выглядит так, как будто он прямо на оси? Помните, что делают отрицательные экспоненты: они говорят вам перевернуть основание на другую сторону дробной черты. Итак, если, скажем, x  = -4, приведенная выше экспоненциальная функция даст нам 2 ⁻⁴ , что равно 2 ⁴  = 16, а затем перевернуто снизу, чтобы получить 1/16, что довольно мало.

По характеру экспонент каждый раз, когда мы возвращаемся назад (то есть всякий раз, когда мы двигаемся дальше влево) на 1 по оси x , линия только наполовину меньше высоты над осью x , чем она. было для предыдущего значения x . То есть, в то время как

y  = 1/16 для x  = −4, линия будет только вдвое короче, при y  = 1/32, для x  = -5.

Таким образом, хотя линия на самом деле никогда не касается и не пересекает ось x , она чертовски близка! Вот почему, говоря практически, левая часть основной экспоненты имеет тенденцию быть направленной вдоль оси. Если вы увеличите график достаточно близко, вы в конечном итоге сможете увидеть, что график действительно выше оси x , но достаточно близко, чтобы не иметь никакого значения, по крайней мере, в том, что касается графика.

Если вы используете ТАБЛИЦУ или другую подобную функцию своего графического калькулятора для поиска точек на графике, вы должны знать, что ваш калькулятор вернет y — значение 0 для сильно отрицательных значений x . Ваш калькулятор может содержать только определенное количество знаков после запятой, и в конце концов он просто сдается и говорит: «Эй, ноль уже достаточно близко»:

Но вы не должны забывать, что это всего лишь признак ограничений технологии. Как я часто говорю своим ученикам: «Ученик умный, калькулятор глупый». Вы должны помнить, что независимо от того, что говорит калькулятор, график все равно находится выше оси x ; значения и по-прежнему положительны, хотя и очень, очень, очень малы.

Давайте снова посмотрим на график y  = 2 ^x :

Вы можете видеть, что в правой части оси x график взлетает до небес. Это опять-таки из-за удвоения экспоненты. Как только функции начинают заметно расти, они продолжают удваиваться, поэтому очень быстро становятся очень большими.

---

Обычно вы не будете наносить много точек в левой части графика, потому что y -значения настолько близки к нулю, что точки графика становятся неотличимыми от оси x . Вы будете рисовать ту сторону графика, которая движется поверх оси.

И, как правило, вы не будете строить много точек в правой части графика, потому что значения и становятся слишком большими. Вот почему я подробно рассказал об общей форме и поведении экспоненты: вам понадобятся эти знания, чтобы помочь вам в построении графика, поэтому убедитесь, что вы достаточно хорошо его понимаете.

Что нужно знать при построении экспоненты:

• Переменная функции будет в степени.
• Число, на котором стоит сила, называется базовым.
• Экспоненциальные функции имеют время удвоения (или деления пополам).
• Графики обычно выглядят довольно горизонтально для одной половины.
• Для второй половины графики обычно растут безумно быстро.
• С недоверием относитесь к тому, что говорит вам ваш калькулятор.
• Рисуйте аккуратно и аккуратно.

---

URL: https://www.purplemath.com/modules/graphexp.htm

Page 2Page 3Page 4

Изучение функций и их графиков учащимися с помощью Desmos – Technology Tools for Higher Education, The Practical Handbook Series

Ана Дафф

Desmos Graphing Calculator — это открытый онлайн-инструмент с широкими числовыми и визуальными универсальными возможностями.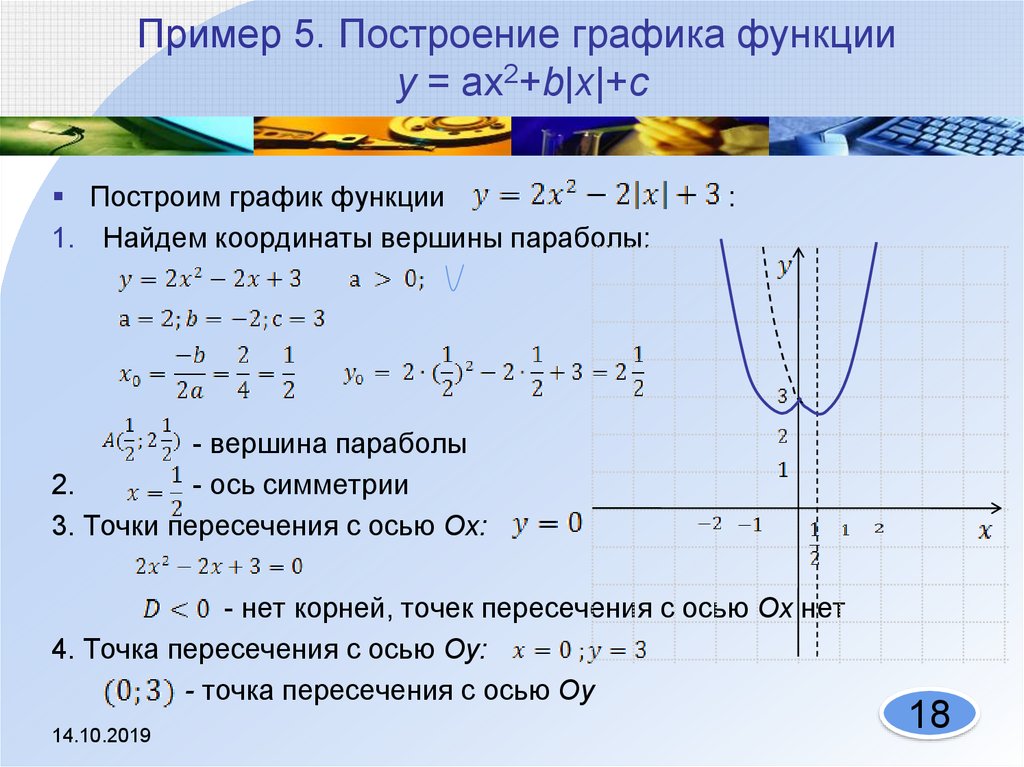 Он позволяет пользователю отображать и маркировать точки на декартовой плоскости, демонстрировать решения уравнений и неравенств, графически отображать функции и создавать регрессионные модели из наборов данных, среди прочих возможностей. Он имеет мощный встроенный инструмент калькулятора и инструмент ползунка, который позволяет пользователю создавать динамические визуальные эффекты, иллюстрирующие изменения или привлекающие внимание к определенным компонентам.

Преимущества обучения с помощью Desmos

• Открытый и бесплатный ресурс, не требующий регистрации или подписки
• Позволяет статическую и динамическую графическую демонстрацию и количественный анализ 2-мерных моделей
• Демонстрации и мероприятия могут быть предварительно созданы
• Требует от пользователей легко приобретаемых технологических навыков
• Позволяет легко обмениваться демонстрациями с другими пользователями

Ресурсы

• Ноутбук или мобильное устройство (Android или iOS)
• Интернет-браузер или приложение Desmos Graphing Calculator

Шаг 1. Создайте учетную запись на Desmos.com (необязательно)

Перейдите на сайт Desmos.com и перейдите по ссылке, чтобы начать построение графиков. У вас есть возможность создать учетную запись и войти в систему, что позволит вам сохранять, называть и искать свою работу. Последующие шаги реализации будут основываться на предположении, что вы вошли в свою учетную запись, чтобы воспользоваться этими функциями. Тем не менее, графическая функциональность Desmos не ограничивается владельцами учетных записей, и в этом случае можно сохранить доступ к своей работе, создав ссылку для общего доступа и сохранив ее на потом.

Шаг 2. Откройте графический калькулятор Desmos и создайте график

Нажмите «График без названия» и введите название графика (доступно только для зарегистрированных пользователей). Введите краткое описание действия: поместите курсор в строку 1, нажмите +  
(Добавить элемент), затем примечание « » и добавьте описание в строку 1.

Шаг 3. Укажите функцию, компоненты функции или данные, которые должны быть смоделированы функцией

Desmos позволяет пользователю явно указывать функцию(и) и моделировать данные с помощью функции, используя регрессию. Если задание используется как часть оценивания, попросите учащихся импортировать случайно сгенерированные данные (например, из документа Excel), чтобы получить вариативность в результирующих функциях.

Шаг 4. Создайте набор инструкций

Пусть результаты обучения определяют ваш набор инструкций. Обратите внимание, что задачи могут включать статическое и динамическое исследование модели, включая визуализацию изменений с помощью ползунка. Для лучшего прогресса задания можно организовать по папкам и руководствоваться примечаниями инструктора, встроенными в график Desmos. Оба могут быть добавлены, нажав на
+ (Добавить элемент), затем папку или заметку.

Шаг 4.

Предложите учащимся ознакомиться с учебными пособиями по графическим инструментам Desmos

В разделе «Справка» представлен большой банк интерактивных обучающих ресурсов для новых и опытных пользователей Desmos. Учащиеся могут научиться создавать ползунки и таблицы, определять ограничения домена и диапазона и выполнять регрессию, следуя простым интерактивным турам, предоставляемым Desmos. Библиотека видеоуроков обширна и легкодоступна для поиска, а руководство пользователя Desmos содержит основное руководство по инструментам Desmos.

Шаг 5. Предоставьте учащимся график(ы)

Нажмите на инструмент «Поделиться своим графиком» в левом верхнем углу. Созданная ссылка направит учащихся к диаграмме и позволит каждому учащемуся просматривать и изменять ее отдельно от других пользователей и не затрагивать созданную вами диаграмму. Обратите внимание, что вы также можете использовать этот инструмент для сохранения изображения графика (за некоторыми исключениями) и встраивания его в другие платформы.

Шаг 6. Включите калькулятор Desmos Graph Calculator в оценки

Включайте результаты исследования и извлеченные уроки учащимися в оценки с помощью инструмента «Поделиться своим графиком», с помощью которого учащиеся делятся ссылками или изображениями своей работы непосредственно или как часть отдельного документа для отправки. Обратите внимание, что ссылка будет включать диаграмму в том виде, в каком она была на момент создания ссылки.

• Избегайте путаницы, сводя к минимуму двусмысленность. Разработайте инструкции, соответствующие результатам обучения. Разбейте активность на компоненты и организуйте их по папкам. Направляйте учащихся к конкретным ресурсам по мере необходимости, выполняя задания по темам, которые могут нуждаться в пояснении. Воспользуйтесь обширной библиотекой видеороликов с практическими рекомендациями от Desmos и ее пользователей (доступных через любую поисковую систему с «Desmos + тема по выбору») в качестве ресурса для учащихся по конкретным задачам.
• Помните о времени и требуемых навыках.  Проверьте, сколько времени у вас уйдет на выполнение задания, а затем умножьте время на три. На протяжении всего теста размышляйте о своих знаниях учащихся, о диапазоне их навыков, связанных с технологиями и содержанием, и соответствующим образом корректируйте задание.
• Поощряйте решение проблем и устранение неполадок с помощью одноранговой поддержки — Покажите учащимся, как делиться работой с помощью инструмента «Поделитесь своим графиком», чтобы обращаться за помощью к другим во время занятия. Наблюдение за работой учащегося поможет определить, где учащийся допустил ошибку или наткнулся на камень преткновения.

Цифровые ресурсы

Руководство пользователя Desmos 

Примеры изучения функций через Desmos в действии:

• Демонстрация односторонних пределов
• Пример метода Ньютона
• Демонстрация функций и производных
• Данные моделирования с использованием примера функций
  

Экичи, Селил, и Плайли, Крис. «Моделирование динамики населения на основе запросов с помощью логистических дифференциальных и разностных уравнений». ПРИМУС 29.6 (2019): 553–570. Веб.

Годин, Шон. «В чем проблема? Ищем лжецов». Бюллетень — Математическая ассоциация Онтарио 56.4 (2018): 11–13. Веб.

Хойлс, Селия. «Преобразование математических практик учащихся и учителей с помощью цифровых технологий». Исследования в области математического образования. 20.3 1–20. Веб.

Набб, Кейт, и Муравска, Жаклин. «Мотивация исчисления с помощью одного вопроса». ПРИМУС 29.10 (2019): 1140–1153. Веб.

Шахриари, Рази и др. «Влияние использования технологий на понимание студентами исчисления и алгебры в колледже». Издательство диссертаций ProQuest, 2019 г.. Веб.

Ана Дафф — научный сотрудник факультета бизнеса и информационных технологий Технического университета Онтарио, где она преподает математику на первом курсе. Ее исследовательский опыт связан с математикой, в которой она имеет докторскую степень.