Как следует построить таблицу истинности логического выражения, алгоритм и примеры
Проблема определения истинности выражения встаёт перед многими науками. Любая доказательная дисциплина должна опираться на некоторые критерии истинности доказательств. Наука, изучающая эти критерии, называется алгеброй логики. Основной постулат алгебры логики заключается в том, что любое самое витиеватое утверждение может быть представлено в виде алгебраического выражения из более простых утверждений, истинность или ложность которых легко определить.
Для любого «алгебраического» действия над утверждением задаётся правило определения истинности или ложности измененного утверждения, исходя из истинности или ложности исходного утверждения. Эти правила записываются через таблицы истинности выражения. Прежде, чем составлять таблицы истинности, надо поближе познакомиться с алгеброй логики.
Содержание:
- Алгебраические преобразования логических выражений
- Отрицание
- Конъюнкция
- Дизъюнкция
- Импликация и эквивалентность
- Прочие логические функции
- Построение таблиц истинности
- Примеры
- Штрих Шеффера
- Стрелка Пирса
- Определение эквивалентности
Алгебраические преобразования логических выражений
Любое логическое выражение, как и его переменные (утверждения), принимают два значения: ложь или истина.
Ложь обозначается нулём, а истина — единицей. Разобравшись с областью определения и областью допустимых значений, мы можем рассмотреть действия алгебры логики.
Отрицание
Отрицание и инверсия — самое простое логическое преобразование. Ему соответствует частица «не.» Это преобразование просто меняет утверждение на противоположное. Соответственно, значение утверждения тоже меняется на противоположное. Если утверждение А истинно, то «не А» — ложно. Например, утверждение «прямой угол — это угол, равный девяносто градусов» — истина. Тогда его отрицание «прямой угол не равен девяноста градусам» — ложь.
Таблица истинности для отрицания будет такова:
| А | не А |
| Л | И |
| И | Л |
Конъюнкция
Конъюнкция аналогична умножению и соответствует союзу «и». Такое выражение будет верно, только если верны все утверждения, объединённые конъюнкцией.
То есть, утверждение «А и Б» будет истинным, только если А — истина и Б — истина. Во всех остальных случаях выражение «А и Б» ложно. Например, высказывание «Земля круглая и плоская» будет ложно, так как первая часть истина, а вторая — ложь.
Таблица истинности конъюнкции
| А | Б | А и Б |
| Л | Л | Л |
| Л | И | Л |
| И | Л | Л |
| И | И | И |
Дизъюнкция
Эта операция может быть обычной или строгой, их результаты будут различаться.
Обычная дизъюнкция или логическое сложение соответствует союзу «или». Она будет истинной если хотя бы одно из утверждений, входящих в неё — истина. Например, выражение «Земля круглая или стоит на трёх китах» будет истинным, так как первое утверждение — истинно, хоть второе и ложно.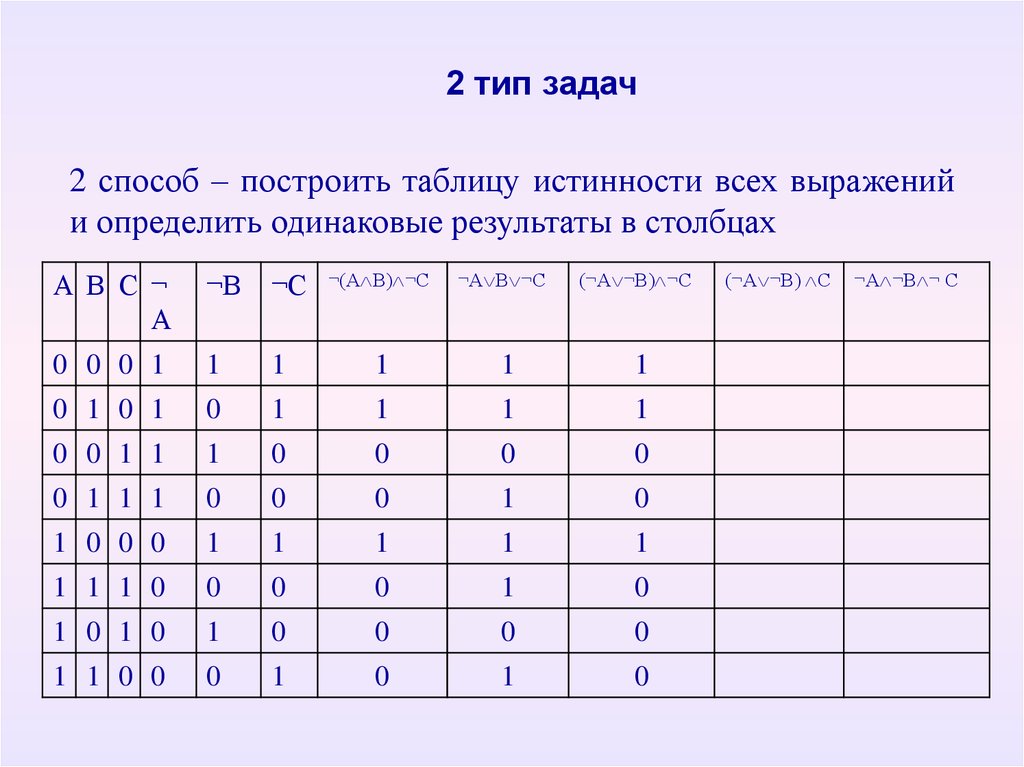
| А | Б | А или Б |
| Л | Л | Л |
| Л | И | И |
| И | Л | И |
| И | И | И |
Строгую дизъюнкцию или сложение по модулю также называют «исключающим или». Эта операция может принимать вид грамматической конструкции «одно из двух: либо …, либо …». Здесь значение логического выражения будет ложным, если все утверждения, входящие в него, имеют одинаковую истинность. То есть, оба утверждения либо вместе истинны, либо вместе ложны.
Таблица значений исключающего или
| А | Б | либо А, либо Б |
| Л | Л | Л |
| Л | И | И |
| И | Л | И |
| И | И | Л |
Импликация и эквивалентность
Импликация представляет собой следствие и грамматически может быть выражена как «из А следует Б».
Здесь утверждение А будет называться предпосылкой, а Б — следствием. Импликация может быть ложной, только в одном случае: если предпосылка истинна, а следствие ложно. То есть, ложь не может следовать из истины. Во всех остальных случаях импликация истинна. Варианты, когда оба утверждения имеют одинаковую истинность, вопросов не вызывают. Но почему верное следствие из неверной предпосылки — истина? Дело в том, что из ложной предпосылки может следовать что угодно. Это и отличает импликацию от эквивалентности.
В математике (и других доказательных дисциплинах) импликация используется для указания необходимого условия. Например, утверждение А — «точка О — экстремум непрерывной функции», утверждение Б — «производная непрерывной функции в точке О обращается в ноль». Если О, действительно, точка экстремума непрерывной функции, то производная в этой точке будет, и вправду, равна нулю. Если же О не является точкой экстремума, то производная в этой точке может быть нулевой, а может не быть.
То есть Б необходимо для А, но не достаточно.
Таблица истинности для импликации выглядит следующим образом:
| А | Б | из А следует Б |
| Л | Л | И |
| Л | И | И |
| Л | Л | |
| И | И | И |
Логическая операция эквивалентность, по сути, является взаимной импликацией. «А эквивалентно Б» означает, что «из А следует Б» и «из Б следует А» одновременно. Эквивалентность верна, когда оба утверждения либо одновременно верные, либо одновременно неверные.
| А | Б | А эквивалентно Б |
| Л | Л | И |
| Л | И | Л |
| И | Л | Л |
| И | И | И |
В математике эквивалентность используется для определения необходимого и достаточного условия.
Например, утверждение А — «Точка О является точкой экстремума непрерывной функции», утверждение Б — «В точке О производная функции обращается в ноль и меняет знак». Эти два утверждения эквивалентны. Б содержит необходимое и достаточное условие для А. Обратите внимание, что в данном примере утверждений Б на самом деле является конъюнкцией двух других: «производная в точке О обращается в ноль» и «производная в точке О меняет знак».
Прочие логические функции
Выше были рассмотрены основные логические операции, которые часто используются. Есть и другие функции, которые используются:
- Штрих Шеффера или несовместимость представляет собой отрицание конъюнкции А и Б
- Стрелка Пирса представляет сбой отрицание дизъюнкции.
Построение таблиц истинности
Чтобы построить таблицу истинности для какого-либо логического выражения, надо действовать в соответствии с алгоритмом:
- Разбить выражение на простые утверждения и обозначить каждое из них как переменную.
- Определить логические преобразования.
- Выявить порядок действий этих преобразований.
- Сосчитать строки в будущей таблице. Их количество равно два в степени N, где N — число переменных, плюс одна строка для шапки таблицы.
- Определить число столбцов. Оно равно сумме количества переменных и количества действий. Можно представлять результат каждого действия в виде новой переменной, если так будет понятней.
- Шапка заполняется последовательно, сначала все переменные, потом результаты действий в порядке их выполнения.
- Заполнение таблицы надо начать с первой переменной. Для неё количество строк делится пополам. Одна половина заполняется нулями, вторая — единицами.
- Для каждой следующей переменной нули и единицы чередуются вдвое чаще.
- Таким образом заполняются все столбцы с переменными и для последней переменной значение меняется в каждой строке.
- Потом последовательно заполняются результаты всех действий.
В итоге последний столбец отобразит значение всего выражения в зависимости от значения переменных.
Отдельно следует сказать о порядке логических действий. Как его определить? Здесь, как и в алгебре, есть правила, задающие последовательность действий. Они выполняются в следующем порядке:
- выражения в скобках;
- отрицание или инверсия;
- конъюнкция;
- строгая и обычная дизъюнкция;
- импликация;
- эквивалентность.
Примеры
Для закрепления материала можно попробовать составить таблицу истинности для ранее упомянутых логических выражений. Рассмотрим три примера:
- Штрих Шеффера.
- Стрелка Пирса.
- Определение эквивалентности.
Штрих Шеффера
Штрих Шеффера — это логическое выражение, которое можно записать в виде «не (А и Б)». Здесь две переменные, и два действия. Конъюнкция в скобках, значит, она выполняется первой.
В таблице будет шапка и четыре строки со значениями переменных, а также четыре столбца. Заполним таблицу:
| А | Б | А и Б | не (А и Б) |
| Л | Л | Л | И |
| Л | И | Л | И |
| И | Л | Л | И |
| И | И | И | Л |
Отрицание конъюнкции выглядит как дизъюнкция отрицаний. Это можно проверить, если составить таблицу истинности для выражения «не А или не Б». Проделайте это самостоятельно и обратите внимание, что здесь будет уже три операции.
Стрелка Пирса
Рассматривая Стрелку Пирса, которая представляет собой отрицание дизъюнкции «не (А или Б)», сравним её с конъюнкцией отрицаний «не А и не Б». Заполним две таблицы:
| А | Б | А или Б | не (А или Б) |
| Л | Л | Л | И |
| Л | И | И | Л |
| И | Л | И | И |
| И | И | И | Л |
| А | Б | не А | не Б | не А и не Б |
| Л | Л | И | И | И |
| Л | И | И | Л | Л |
| И | Л | Л | И | И |
| И | И | Л | Л | Л |
Значения выражений совпали.
Изучив два эти примера, можно прийти к выводу, как раскрывать скобки после отрицания: отрицание применяется ко всем переменным в скобках, конъюнкция меняется на дизъюнкцию, а дизъюнкция — на конъюнкцию.
Определение эквивалентности
Про утверждения А и Б можно сказать, что они эквивалентны, тогда и только тогда, когда из А следует Б и из Б следует А. Запишем это как логическое выражение и построим для него таблицу истинности. «(А эквивалентно Б) эквивалентно (из А следует Б) и (из Б следует А)».
Здесь две переменных и пять действий. Строим таблицу:
| А | Б | В = (из А следует Б) | Г = (из Б следует А) | Д = А эквивалентно Б | Е = В и Г | Д эквивалентно Е |
| Л | Л | И | И | И | И | И |
| Л | И | И | Л | Л | Л | И |
| И | Л | Л | И | Л | Л | И |
| И | И | И | И | И | И | И |
В последнем столбце все значения истинные.
Это значит, что приведенное определение эквивалентности верно при любых значениях А и Б. Значит, оно всегда истинно. Именно так с помощью таблицы истинности можно проверить корректность любых определений и логических построений.
Page not found — Сайт skobelevserg!
- Главная
- Информатика
- Практикумы
- Подготовка к ОГЭ
- Рабочие программы
- Используемая литература
- Об авторах
Unfortunately the page you’re looking doesn’t exist (anymore) or there was an error in the link you followed or typed. This way to the home page.
- Главная
- Информатика
- 5 класс (ФГОС)
- Информация вокруг нас
- Компьютер — универсальная машина для работы с информацией
- Ввод информации в память компьютера
- Управление компьютером
- Хранение информации
- Передача информации
- Кодирование информации
- Текстовая информация
- Представление информации в виде таблиц
- Наглядные формы представления информации
- Компьютерная графика
- Обработка информации
- 6 класс (ФГОС)
- Объекты окружающего мира
- Компьютерные объекты
- Отношения объектов и их множеств
- Разновидности объектов и их классификация
- Системы объектов
- Персональный компьютер как система
- Как мы познаем окружающий мир
- Понятие как форма мышления
- Информационное моделирование
- Знаковые информационные модели
- Табличные информационные объекты
- Графики и диаграммы
- Схемы
- Что такое алгоритм
- Исполнители вокруг нас
- Формы записи алгоритмов
- Типы алгоритмов
- Управление исполнителем Чертежник
- Компьютерный практикум
- 7 класс (ФГОС)
- Информация и информационные процессы
- Компьютер универсальное устройство для работы с информацией
- Обработка графической информации
- Обработка текстовой информации
- Технология мультимедиа
- 8 класс (ФГОС)
- Математические основы информатики
- Основы алгоритмизации
- Начала программирования
- 9 класс (ФГОС)
- Моделирование и формализация
- Алгоритмизация и программирование
- Обработка числовой информации в электронных таблицах
- Коммуникационные технологии
- 10 класс (ФГОС)
- Информация и информационные процессы
- Компьютер и его программное обеспечение
- Представление информации в компьютере
- Элементы теории множеств и алгебры логики
- Современные технологии создания и обработки информационных объектов
- 11 класс (ФГОС)
- Обработка информации в электронных таблицах
- Алгоритмы и элементы программирования
- Информационное моделирование
- Сетевые информационные технологии
- Основы социальной информатики
- Безопасность в сети Интернет
- Практикумы
- Google формы
- Основы работы в Microsoft PowerPoint
- Создание анимации в презентациях
- Основы работы в Microsoft Word
- Основы работы в Microsoft Excel
- Создание простейшей базы данных
- Практикум по MS Excel
- Подготовка к ОГЭ
- Рабочие программы
- Используемая литература
- Об авторах
- Блоги
- Сайты
таблиц истинности, тавтологии и логические эквивалентности
таблицы истинности, тавтологии и логические эквивалентности Математики обычно используют двузначное число .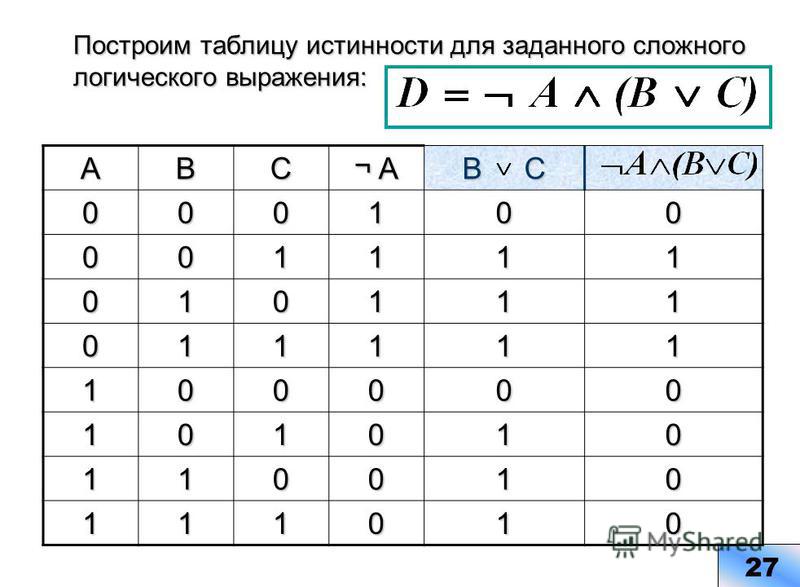
логика : Каждое утверждение либо Истина , либо Ложь . Это называется Закон исключенного третьего .
Утверждение в сентенциальной логике строится из простых утверждений с использованием логические связки , , , и . Правда или ложь утверждения, построенного с помощью этих связок, зависит от истинности или ложность его составляющих.
Например, составной оператор строится с использованием логических связок , и . Правда или ложность зависит от истины или ложность P, Q и R.
Таблица истинности показывает, как правда или ложь составного утверждения зависит от истинности или ложности простого утверждения, из которых он построен. Итак, мы начнем с рассмотрения таблицы истинности для пяти логических связок.
Вот таблица отрицания:
Эту таблицу легко понять. Если P равно true , его отрицание ложь . Если P равно false , то true .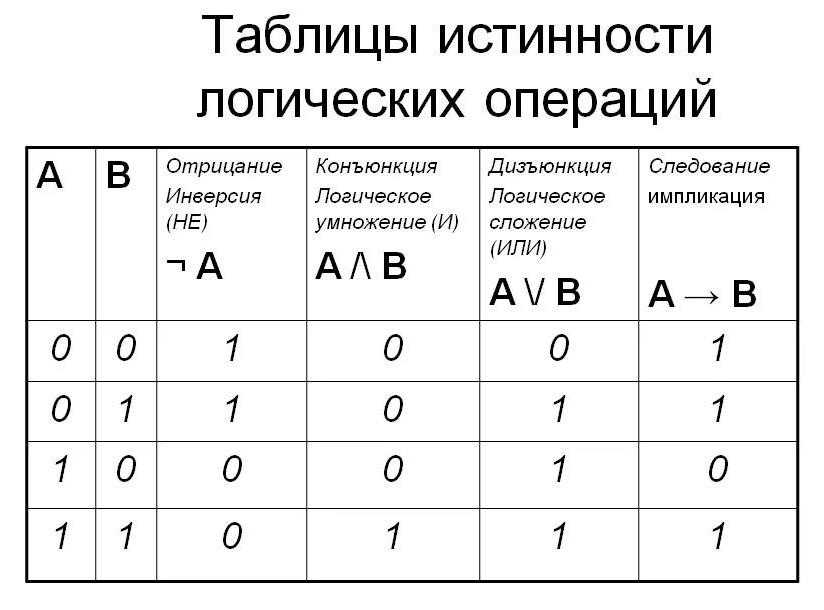
должно быть true , когда оба P и Q true и false иначе:
истинно , если либо P равно истинно , либо Q равно true (или оба — помните, что мы используем «или» во включающем смысле). всего ложь , если оба P и Q ложь .
Вот таблица логических следствий:
Чтобы понять, почему эта таблица именно такая, рассмотрим следующее. пример:
«Если ты получишь пятерку, я дам тебе доллар».
Утверждение будет верным , если я сдержу свое обещание и ложь если нет.
Предположим, что верно , что вы получаете пятерку, а это 9.0003 правда что я даю вам доллар. Поскольку я сдержал свое обещание, правда . Это соответствует первой строке таблицы.
Предположим, что верно , что вы получаете пятерку, но ложно что я даю вам доллар.
Поскольку я не сдержал своего обещания,
подразумевается false . Это соответствует второму
строку в таблице.
Что, если это ложь, что вы получили пятерку? Независимо от того, дам ли я вам долларов, я не нарушил своего обещания. Таким образом, вывод не может быть ложно, поэтому (поскольку это двузначная логика) оно должно быть истинным. Этот объясняет последние две строки таблицы.
означает, что P и Q равны эквивалент . Таким образом, двойная импликация верна , если P и Q оба истинны или если P и Q оба ложны ; в противном случае двойная импликация ложна.
Вы должны помнить — или уметь составлять — таблицы истинности для логических связок. Вы будете использовать эти таблицы для построения таблицы для более сложных предложений. Легче продемонстрировать что делать, чем описать это словами, так вы увидите порядок выработано на примерах.
Примечание.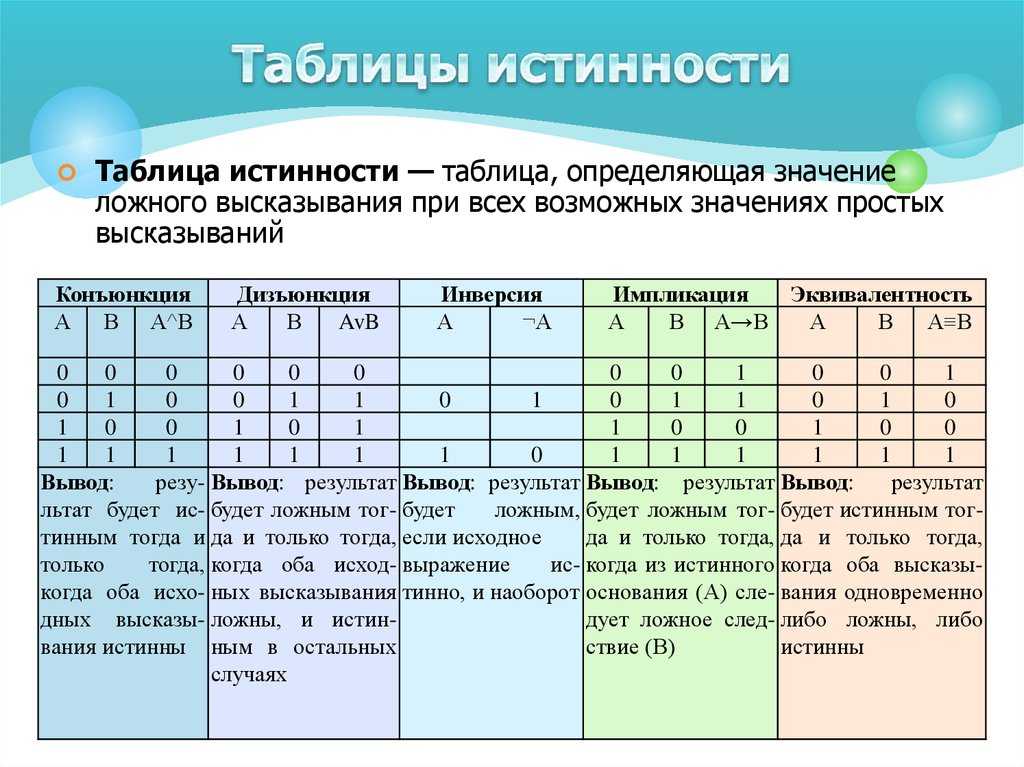
(а) Когда вы строите правду
таблице, вы должны рассмотреть все возможные назначения True (T) и
False (F) для операторов компонента. Например, предположим,
составные операторы — это P, Q и R. Каждый из этих операторов может быть
либо правда, либо ложь, так что есть возможности.
Когда вы перечисляете возможности, вы должны присвоить значения истинности к операторам компонентов систематическим образом, чтобы избежать дублирования или упущение. Самый простой подход — использовать лексикографический порядок . Таким образом, для составного оператора с три компонента P, Q и R, я бы перечислил возможности этого способ:
(б) Существуют различные способы составления таблиц истинности. Вы можете, для например, запишите значения истинности «под» логическим связки составного высказывания, постепенно дорастающие до столбец для «основной» связки.
Я буду записывать вещи длинным путем, создавая столбцы для каждого
«кусочек» составного высказывания и постепенно наращивая
к составному утверждению.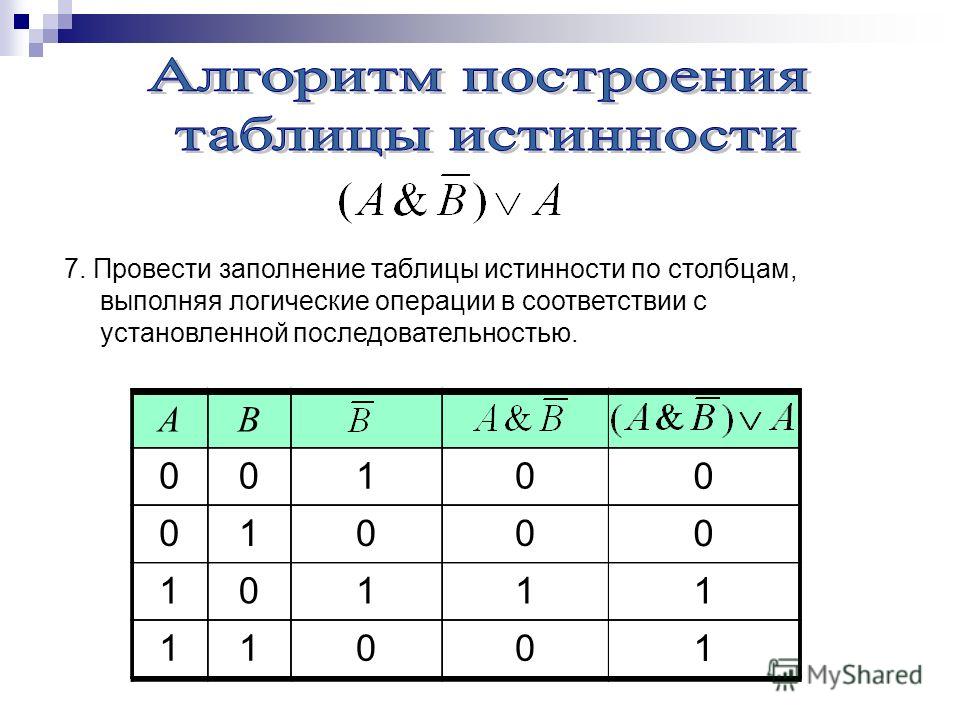
Любой стиль хорош, пока вы показываете
достаточно работы, чтобы оправдать ваши результаты.
Пример. Построить таблицу истинности для формула .
Во-первых, я перечисляю все альтернативы для P и Q.
Затем в третьем столбце я перечисляю значения на основе значений P. Я использую таблицу истинности для отрицание: когда P истинно, ложно, а когда P ложно, правда.
В четвертом столбце я перечисляю значения для . Проверьте сами, что это только ложь («F»), если P истинно («T»), а Q ложно («Ф»).
В пятом столбце приведены значения моего составного выражения. Это «и» из (третий столбец) и (четвертый столбец). «И» верно только в том случае, если обе части «и» верны; в противном случае оно ложно. Поэтому я смотрю на третья и четвертая колонки; если оба верны («T»), я ставлю T в пятой колонке, иначе ставлю F.
Тавтология есть формула, которая «всегда
истинно» — то есть истинно для всякого присвоения истины
значения его простых компонентов.
Вы можете рассматривать тавтологию как правило логики .
Противоположностью тавтологии является число . противоречие , формула, которая «всегда ложна». В Другими словами, противоречие ложно для любого присвоения истины значения его простых компонентов.
Пример. Покажите, что это тавтология.
Я строю таблицу истинности и показываю, что формула всегда верна.
Последний столбец содержит только Т. Следовательно, формула представляет собой тавтология.
Пример. Построить таблицу истинности для .
Вы можете видеть, что построение таблиц истинности для утверждений с большим количеством
связок или большого количества простых утверждений довольно утомительно и
подвержен ошибкам. Хотя могут быть некоторые приложения этого (например, для
цифровые схемы), в какой-то момент лучше всего было бы написать
программа для построения таблиц истинности (и это наверняка было сделано).
Суть здесь в том, чтобы понять, как значение истинности сложного утверждение зависит от истинностных значений его простых утверждений и его логические связи. В большинстве работ математики обычно не операторы использования, которые очень сложны с логической точки зрения. вид.
Пример. (a) Предположим, что P ложно и истинно. Скажите, является ли Q истинным, ложным или его истинной стоимость не может быть определена.
б) Предположим, что это неверно. Рассказывать является ли Q истинным, ложным или его истинностное значение не может быть определено.
а) Поскольку истинно, то либо Р истинно, либо истинно. Поскольку P ложно, оно должно быть истинным. Следовательно, Q должно быть ложным.
(b) Утверждение «если-то» ложно, когда часть «если»
истина, а часть «тогда» ложна. Поскольку ложно, верно. Утверждение «и» истинно только
когда обе части верны. В частности, должно быть истинным, поэтому Q ложно.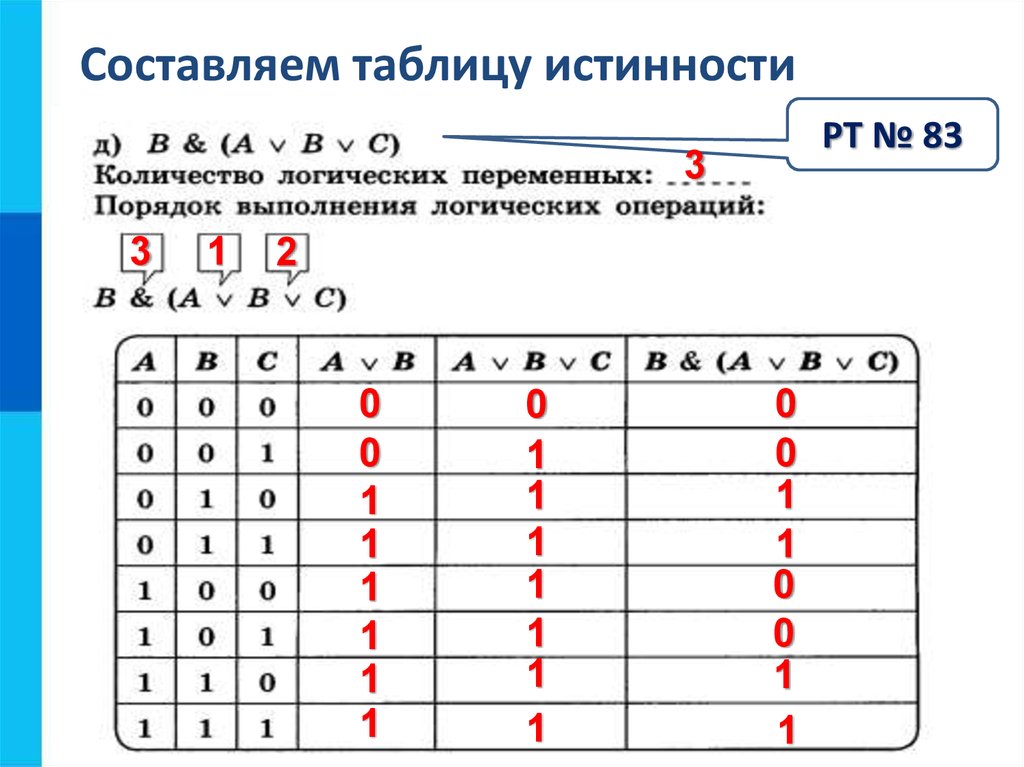
Пример. Предположим
» » правда.
» » неверно.
«У Кельвина Баттербола фиолетовые носки» — это правда.
Определить истинность утверждения
Для простоты пусть
П = «».
Q = «».
R = «У Кэлвина Баттербола фиолетовые носки».
Я хочу определить истинное значение . Поскольку мне были даны конкретные значения истинности для P, Q, и R, я составил таблицу истинности с одной строкой, используя данные значения для P, Q и R:
Следовательно, утверждение верно .
Пример. Определить истинное значение заявление
Утверждение » » неверно. Вы не можете сказать
действительно ли утверждение «Икабод Ксеркс ест шоколад
кексы» истинны или ложны — но это не имеет значения. Если
«если» часть утверждения «если-то» ложна,
то утверждение «если-то» истинно.
(Проверьте правду
таблица для тех, кто не уверен в этом!) Так что
данное утверждение должно быть истинным.
Два утверждения X и Y равны логически. эквивалент , если это тавтология. Другой способ сказать это: Для каждого присвоения значений истинности простых операторы , составляющие X и Y, операторы X и Y имеют одинаковые значения истинности.
С практической точки зрения вы можете заменить оператор в доказательство любым логически эквивалентным утверждением.
Чтобы проверить, являются ли X и Y логически эквивалентными, вы можете настроить таблица истинности, чтобы проверить, является ли тавтологией — что есть ли «все Т в столбце». Однако проще настроить таблицу, содержащую X и Y, а затем проверьте, совпадают ли столбцы для X и для Y.
Пример. Покажите, что и логически эквивалентны.
Поскольку столбцы для и идентичны, два оператора логически
эквивалент.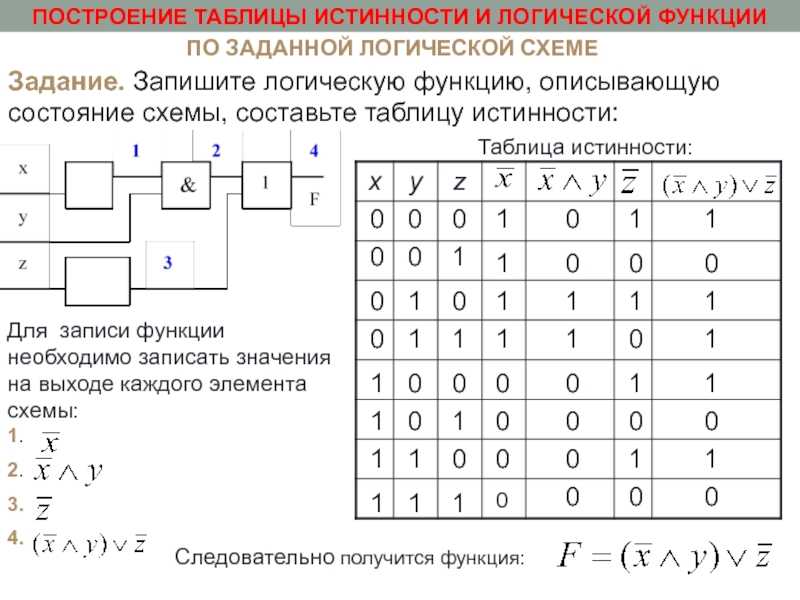
Эта тавтология называется Условное
Разъединение . Вы можете использовать эту эквивалентность для замены
условно дизъюнкцией.
Существует бесконечное количество тавтологий и логических эквивалентностей; Я перечислил несколько ниже; более обширный список приведен в конце эта секция.
Когда тавтология имеет форму бикондиционала, два утверждения которые составляют бикондиционал, логически эквивалентны. Следовательно, вы можно заменить одну сторону другой без изменения логического значение.
Вам часто придется отрицать математическое утверждение. К посмотрим, как это сделать, мы начнем с того, что покажем, как отрицать символические заявления.
Пример. Запишите отрицание следующие операторы, упрощая так, чтобы только простые операторы отрицается.
(а)
(б)
(a) Я отрицаю данное утверждение, затем упрощаю, используя логические
эквивалентности.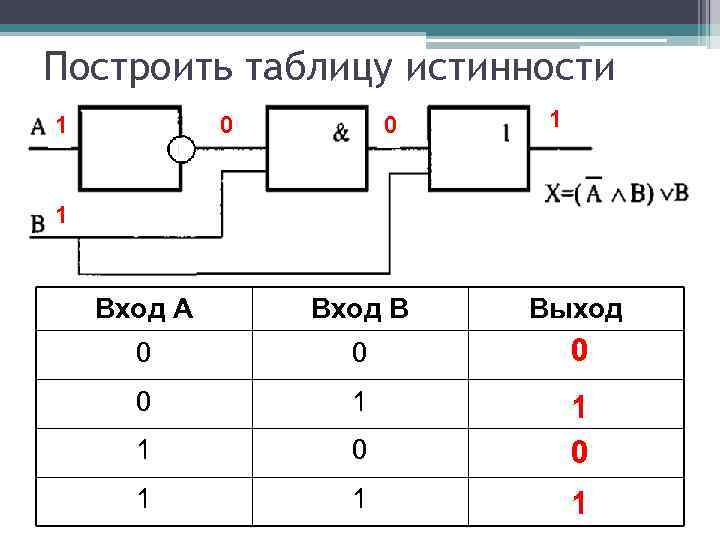
Я дал имена логических эквивалентностей на
правильно, чтобы вы могли видеть, какие из них я использовал.
(б)
Я показал это и есть логически эквивалентны в предыдущем примере.
В следующих примерах мы будем отрицать утверждения, написанные словами. Это более типично для того, что вам нужно делать в математике. идея состоит в том, чтобы преобразовать слово-выражение в символическое высказывание, затем используйте логические эквивалентности, как в предыдущем примере.
Пример. Используйте закон Де Моргана, чтобы написать отрицание следующего утверждения, упрощая так, что отрицаются только простые операторы:
«Кэлвина нет дома или Бонзо в кино».
Пусть С будет утверждением «Кальвин дома», а В будет заявление «Бонзо в движении». Данное утверждение является . Я должен отрицать утверждение, затем упростите:
Результат: «Кальвин дома, а Бонзо нет на
кино».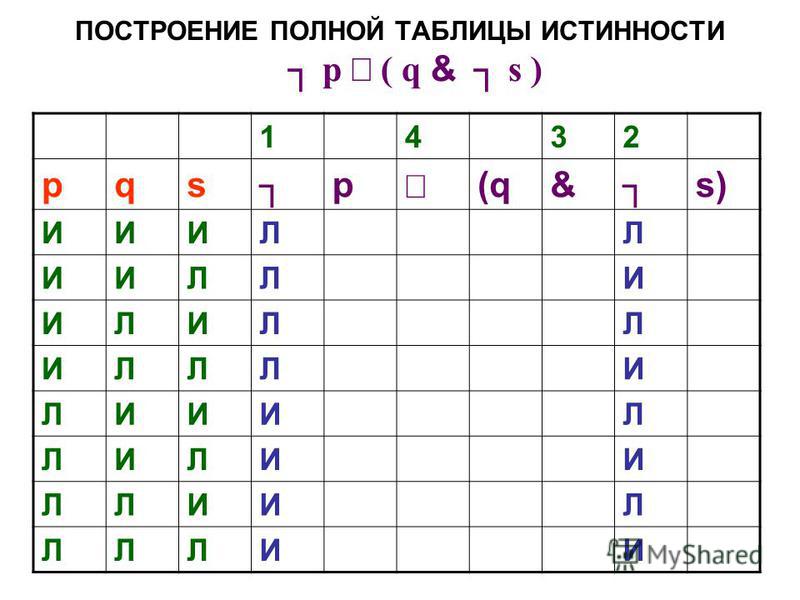
Пример. Используйте закон Де Моргана, чтобы написать отрицание следующего утверждения, упрощая так, что отрицаются только простые операторы:
«Если Фиби покупает пиццу, то Кэлвин покупает попкорн».
Пусть P будет утверждением «Фиби покупает пиццу», а C будет заявление «Кэлвин покупает попкорн». Данное утверждение является . Чтобы упростить отрицание, я буду использовать тавтологию условной дизъюнкции , которая гласит:
То есть я могу заменить на (или наоборот).
Вот вам и отрицание и упрощение:
Результат: «Фиби покупает пиццу, а Кэлвин не покупает». попкорн».
Далее мы применим нашу работу с таблицами истинности и отрицающими утверждениями к задачи на построение обратной, обратной и противопоставляется утверждению «если-то».
Пример. Замените следующий оператор на его противоположность:
«Если x и y рациональны, то рационально».
По контрапозитивной эквивалентности это утверждение совпадает с «Если не рационально, то это не так что и х, и у рациональны».
Этот ответ правильный в его нынешнем виде, но мы можем выразить его в немного лучший способ, который удаляет некоторые явные отрицания. Большинству людей позитивное утверждение легче понять, чем отрицательное утверждение.
По определению, действительное число равно 9.0003 иррациональный если это не рационально. Поэтому я мог бы заменить часть «если» противопоставляется слову «иррационально».
Часть противопоставления «тогда» есть отрицание утверждение «и». Вы могли бы переформулировать это так: «Это не случае, когда и x рационально, и y рационально». (Слово «оба» гарантируют, что отрицание применяется ко всему утверждение «и», а не только «х рационально».)
По закону Де Моргана это эквивалентно следующему: «x не является рациональным или
y нерационально».
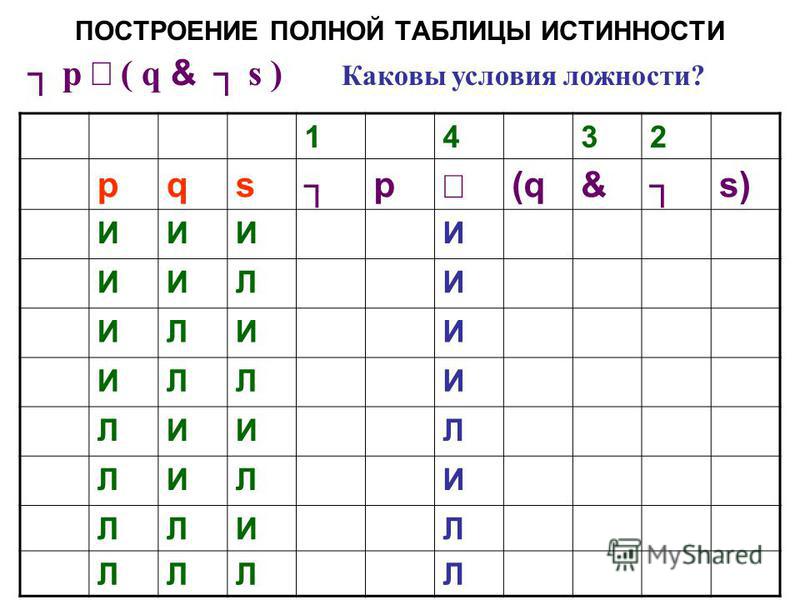В качестве альтернативы я мог бы сказать: «x есть
иррационально или у иррационально».
Собрав все вместе, я мог бы выразить противоположное как: «Если иррационально, то либо х иррационально или у иррационально».
(Как обычно, я добавил слово «либо», чтобы было понятно, что часть «тогда» — это целое утверждение «или».)
Пример. Покажите, что обратное и обратные условные логически эквивалентны.
Пусть условно. Обратное есть. Обратное.
Я мог бы показать, что обратное и обратное эквивалентны построение таблицы истинности для . Вместо этого я буду использовать некоторые известные тавтологии.
Начните с:
Помните, что я могу заменить утверждение логическим эквивалент. Например, на последнем шаге я заменил на Q, потому что два утверждения эквивалентны Двойное отрицание.
Пример. Предположим, что x — действительное число. Учитывать заявление
«Если , то ».
Постройте обратное, обратное и контрапозитивное. Определите истинность или ложность четырех утверждений — исходное утверждение, обратное, обратное и контрапозитивное — используя свои знания по алгебре.
Обратное: «Если , то».
Обратное: «Если , то».
Противоположное: «Если , то».
Исходное утверждение неверно: , но . Поскольку исходное утверждение эквивалентно контрапозитив, то контрапозитив также должен быть ложным.
Обратное верно. Обратное логически эквивалентно обратное, значит верно и обратное.
\новая страница
\centerline{\bigssbold Список тавтологий}
Контактная информация
Домашняя страница Брюса Икенаги
Copyright 2019 Брюс Икенага
Как составить таблицу истинности
Как составить таблицу истинности
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Домашняя страница > Логика > Символическая логика > Таблицы истинности | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| Философия 103: Введение в логику Как составить таблицу истинности Аннотация: Объясняются и иллюстрируются общие принципы построения таблиц истинности.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
lander.edu 
