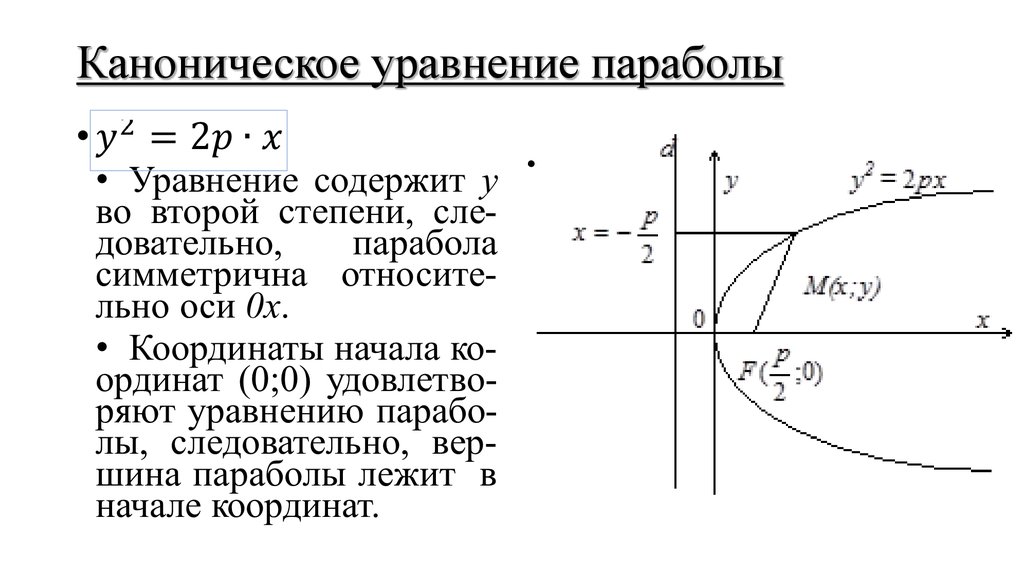
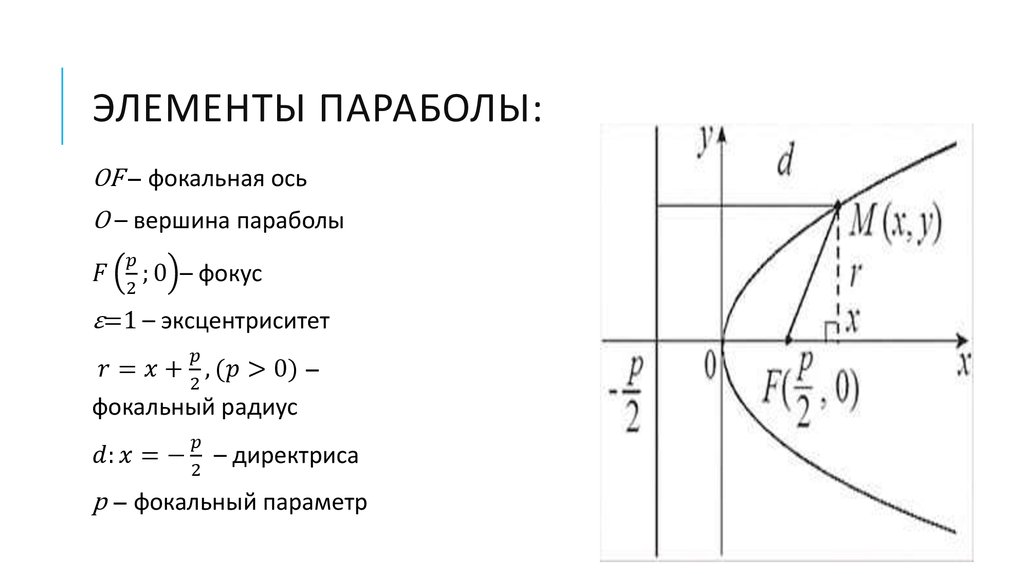
Приведите к каноническому виду уравнение второго порядка.
Пример 1:
Привести уравнение к каноническому виду, определить тип кривой и её эксцентриситет, изобразить ее на одном чертеже в старых и новых координатах:
4х2+25у2+8х -50у -71= 0
Решение от преподавателя:
Приводим квадратичную форму
B = 4x2 + 25y2
к главным осям, то есть к каноническому виду. Матрица этой квадратичной формы:
Находим собственные числа и собственные векторы этой матрицы:
(4 — λ)x1 + 0y1 = 0
0x1 + (25 — λ)y1 = 0
Характеристическое уравнение:
| = λ 2 — 29λ + 100 = 0 |
λ2 -29 λ + 100 = 0
D=(-29)2 — 4*1*100=441
Исходное уравнение определяет эллипс (λ1 > 0; λ2 > 0)
Вид квадратичной формы:
4x2 + 25y2
Выделяем полные квадраты:
для x1:
4(x12+2*1x1 + 1) -4*1 = 4(x1+1)2-4
для y1:
25(y12-2*1y1 + 1) -25*1 = 25(y1-1)2-25
В итоге получаем:
4(x1+1)2+25(y1-1)2 = 100
Разделим все выражение на 100
Полуоси эллипса:
a = 5;b = 2
Данное уравнение определяет эллипс с центром в точке:
C(-1; 1)
Найдем координаты фокусов F1(-c;0) и F2(c;0), где c — половина расстояния между фокусами
Итак, фокусы эллипса:
С учетом центра, координаты фокусов равны:
Тогда эксцентриситет будет равен:
Вследствие неравенства c эксцентриситет эллипса меньше 1.
Пример 2:
Привести к каноническому виду линии второго порядка:
Решение от преподавателя:
Пример 3:
Приведите к каноническому виду уравнение второго порядка и постройте линию, заданную этим уравнением.
Решение от преподавателя:
Пример 4:
Привести кривую 2-го порядка к каноническому виду и построить её:
Решение от преподавателя:
Преобразуем данное уравнение:
Получили уравнение параболы с вершиной в точке , ветви которой направлены вверх.
Строим данную параболу.
Пример 5:
Привести к каноническому виду линии второго порядка:
Решение от преподавателя:
Работа вам нужна срочно. Не волнуйтесь, уложимся!
Заполните, пожалуйста, данные для автора:
- 22423 авторов готовы помочь тебе.
- 2402 онлайн
Привести уравнение к каноническому виду : Чулан (М)
Сообщения без ответов | Активные темы | Избранное
Правила форума
В этом разделе нельзя создавать новые темы.

| RNT |
| ||
02/10/10 |
| ||
| |||
| Хорхе |
| |||
14/02/07 |
| |||
| ||||
| RNT |
| ||
02/10/10 |
| ||
| |||
| Хорхе |
| |||
14/02/07 |
| |||
| ||||
| RNT |
| ||
02/10/10 |
| ||
| |||
| ИСН |
| |||
18/05/06 |
| |||
|
| ||||
| Хорхе |
| |||
14/02/07 |
| |||
| ||||
| RNT |
| ||
02/10/10 |
| ||
| |||
| ИСН |
| |||
18/05/06 |
| |||
| ||||
| RNT |
| ||
02/10/10 |
| ||
| |||
| Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию |
| Страница 1 из 1 | [ Сообщений: 10 ] |
Модераторы: Модераторы Математики, Супермодераторы
Кто сейчас на конференции |
Сейчас этот форум просматривают: нет зарегистрированных пользователей |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
| Найти: |
Ваш ответ
1 Ответ
Если под канонической формой вы подразумеваете y-k=(1/4a)(x-h), где (h,k) — вершина, а a — расстояние между вершину и фокус и направляющую линию, то мы можем переписать уравнение как:
(x²-6x+9)-9-4y+13=0, (x-3)²+4-4y=0, 4(y -1)=(x-3)², y-1=¼(x-3)², поэтому вершина равна (3,1) и a=1.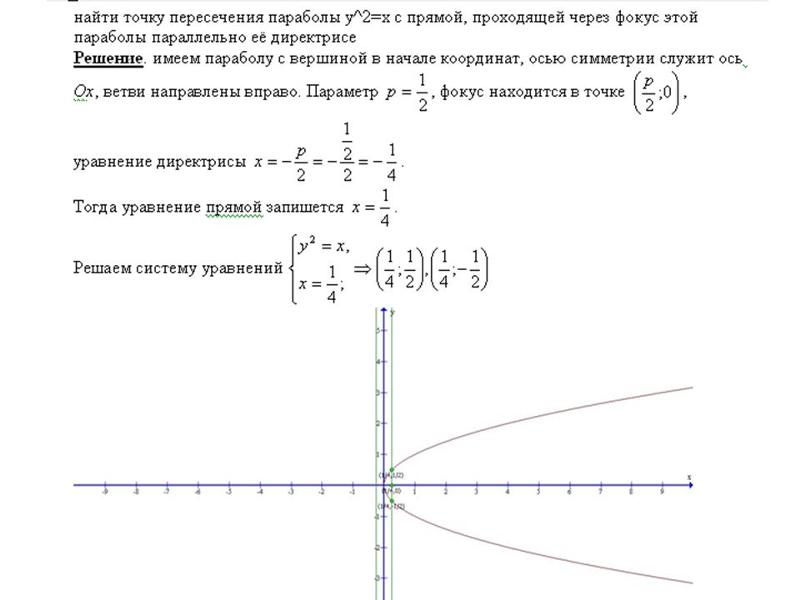
Фокус имеет ту же координату x, что и вершина: (h,k+a)=(3,2) и направляющая линия y=k-a=1-1=0 по оси x, y=0.
ответил 92+4y=0 И ОПРЕДЕЛИТЬ ЦЕНТР И РАДИУСспросил 2 февраля 2013 г. по алгебре 2 Ответы к анонимный | 548 просмотров
- стандартная форма уравнения
- центр и радиус окружности
1 ответ
Напишите уравнение параболы в вершинной форме, которая проходит через (0, −24) и имеет вершину (−6, −12) .
спросил 7 ноября 2017 г. по алгебре 2 Ответы к Эль | 2,8 тыс. просмотров
- не могли бы вы решить проблему и дать мне пошаговое руководство, как мне решить проблему
1 ответ
как преобразовать логическую функцию в каноническую форму?
спросил 11 июня 2014 г. в других математических темах к анонимный | 594 просмотра
1 ответ
найти стандартную форму уравнения параболы с вершиной в начале координат, вертикальной осью и проходящей через точку(13,13)
спросил
24 июля 2017 г. по алгебре 1 ответы
к
Пол Винсент
| 1.3k просмотров
по алгебре 1 ответы
к
Пол Винсент
| 1.3k просмотров
2 ответа
напишите уравнение 6x — 4y = 12 в форме пересечения наклона . Затем определите наклон и y-пересечение
спросил 20 декабря 2011 г. по алгебре 1 ответы к анонимный | 3,6 тыс. просмотров
- форма пересечения наклона
- как найти точку пересечения по оси y
- как найти точку пересечения по оси x
1 ответ
Напишите уравнение каждой параболы в виде вершины.
спросил 15 февраля 2013 г. по алгебре 2 Ответы к анонимный | 526 просмотров
- уравнение пораболы через вершину и точку
1 ответ
График параболы проходит через точки (3/2, 4/3) и (0, −6) и имеет горизонтальная касательная в точке (3/2, 4/3). Найдите уравнение параболы и нарисуйте ее график. 92-8y=20 в форме параболы?
спросил 29 мая 2013 г. по алгебре 2 Ответы к анонимный | 384 просмотра
- парабола
- alg 2
1 ответ
Как записать это уравнение в стандартной форме: 21x=7y+13
спросил
7 января 2014 г. по алгебре 1 ответы
к
[email protected]
| 311 просмотров
по алгебре 1 ответы
к
[email protected]
| 311 просмотров
- задачи по алгебре
- задачи по алгебре!!!
1 ответ
Напишите уравнение с наклоном-цел. форма для прямой, параллельной 4y=x, проходящей через точку (4,0)
спросил 29 ноября 2012 г. по алгебре 1 ответы к анонимный | 443 представления
- форма пересечения наклона
- пошаговые инструкции
- алгебра
- параллельные прямые
1.5 Двухмерные координатные преобразования
1.5 Двухмерные координаты
|
Далее: 1. 6 Правильная поза 6 Правильная поза |
Подразделы
1.5 Преобразование двумерных координат
Более мощные упрощения за счет изменения координат возможны в 2D.
Предположим, что в терминах координат и имеем частичное
дифференциальное уравнение:
Затем, если мы перейдем к новым координатам, вызовем их и , мы получим новое уравнение в частных производных вида:
Идея состоит в том, чтобы снова выбрать новые координаты и так далее. чтобы новое дифференциальное уравнение в частных производных было максимально простым.
Например, для гиперболического уравнения вам могут понравиться координаты
и такие, что и равны нулю. Чтобы узнать, за что
координаты, и в этом случае выражения для новых
коэффициенты , , и в новых координатах
необходимы. Их можно найти, записав общие
формулы преобразования из раздела 1. 4.2 для специального
случае двух измерений. Вы получаете, {D.4}:
4.2 для специального
случае двух измерений. Вы получаете, {D.4}:
| (1.12) |
1.5.1 Характерные координаты
Характеристические координаты – это координаты, для которых
и производные исключаются. Который
оставляет только производную, что значительно упрощает
уравнение в частных производных. сводится к двумерному
каноническая форма:
| (1.13) |
Прежде всего нужно выяснить, как этого можно достичь. С точки зрения
коэффициенты преобразованного уравнения, как обсуждалось выше,
и должен исчезнуть. Условие требует, согласно
приведенные формулы:
Это можно рассматривать как уравнение в частных производных для . Нелинейное уравнение первого порядка, чтобы быть уверенным.
 Аналогично для
исчезать,
Аналогично для
исчезать, Обратите внимание, что и должны удовлетворять тому же уравнению, но это должны быть разные решения. В противном случае они недействительны независимые координаты.
Чтобы решить уравнение для (похоже), разделите на :
и обратите внимание, что из вашего исчисления или термо,
Таким образом, строки константы должны удовлетворять обычному дифференциальное уравнение
Мы можем добиться этого, приняв константу интегрирования в решение этого обыкновенного дифференциального уравнения! Интеграция константы, как говорится, константы для решений.
Взяв другой знак за квадратный корень, можно получить второй независимая координата.
Итог, чтобы получить характеристические координаты, решить плюс и минус знак обыкновенных дифференциальных уравнений выше, и приравнять константы интегрирования к и .
Пара замечаний:
- Поскольку константы интегрирования не уникальны, характеристика
координаты нет.
 Но линии постоянные и есть
уникальны, и называются характеристическими линиями или характеристики .
Но линии постоянные и есть
уникальны, и называются характеристическими линиями или характеристики . - Эллиптические уравнения не имеют характеристик, т.к. квадратный корень в обыкновенном дифференциальном уравнении будет воображаемый. Координаты и должны быть реальными; вы делаете не хотят иметь дело с дифференциальными уравнениями в частных производных в комплексе координаты.
- Параболические уравнения имеют только одно семейство характеристических линии. Это потому, что квадратный корень равен нулю, поэтому, взяв другой корень не имеет значения.
Пример
Вопрос: Используйте характеристические координаты, чтобы уменьшить волновое уравнение в многомерной канонической форме
к эквивалентной ему двумерной канонической форме. Тогда решите это.Решение:
Сначала найдите характеристики, решив обыкновенный дифференциал приведенное выше уравнение:
Обратите внимание, что окончанием является скорость распространения волны, а не коэффициент в общем уравнении второго порядка.Решение простое:
где и – константы интегрирования (а также характерные координаты). Итак, линии представляют собой один набор характеристических линий, а линии другой набор.Теперь найдите коэффициент . Коэффициент был равен нулю, и производные второго порядка от и в формула для тоже равна нулю, значит, тоже равна нулю. Итак, волновое уравнение в характеристических координатах имеет вид
(1.14)
Обратите внимание, что это можно разделить, поэтому нет необходимости вычислять вон что это такое.Волновое уравнение теперь может быть легко решено. Интеграция с уважением давать
где постоянная интегрирования может быть любой произвольной функцией . Интегрирование по дает окончательное решение:
Вот первообразная , поэтому она произвольна, как и .Дополнительная постоянная интегрирования является произвольной функция .
Тем не менее, вы наверняка захотите получить решение с точки зрения физического координаты и , а не математическая характеристика координаты. Поэтому замените и используйте полученный уравнения для характеристик. Это дает окончательное решение:
(1.15) Это общее решение волнового уравнения. Чтобы решить конкретную проблему, вам все равно нужно будет выяснить, что и используют любые начальные и граничные условия есть. Один частный случай, в котором -диапазон вдвойне бесконечный, будет решен подробно позже.
Пример
Вопрос: Найдите и нарисуйте характеристики уравнения
Решение:
Выясните коэффициенты в характеристическом уравнении по глядя на уравнение в частных производных:
Обратите внимание, что существуют только характеристики для отрицательных значений .За положительное уравнение эллиптическое. И для нуля будет только одно направление для характеристик, горизонтальное.
Используйте разделение переменных для решения. Другими словами, возьмите факторы в одну сторону и -факторы в другую сторону:
Возведение обеих сторон в квадрат, чтобы избавиться от квадратного корня, дает
Это параболы.
Пример
Вопрос: Сократите уравнение
к двумерному каноническому виду.Решение:
Двумерная каноническая форма означает характерную форму. Найди обыкновенное дифференциальное уравнение для характеристик:
Решите его, используя разделение переменных:
Постоянные интегрирования — это новые координаты:
Решите уравнение в частных производных в этих координатах используя формулы, приведенные в начале этого раздела:
так
Уравнение в частных производных принимает вид
Избавьтесь и полностью используйте уравнения для характеристики:
Полученное уравнение в частных производных имеет вид
Она не выглядит легко разрешимой.
Пример
Вопрос: Найдите характеристические координаты уравнения
Решение:
Найдите обыкновенное дифференциальное уравнение для характеристики:
Найди решение:
Характеристическими координатами являются постоянные интегрирования:
Не нравится, что частичный дифференциал будет очень простой.
1.5.2 Параболические уравнения в двух измерениях
В параболическом случае имеется только одно уравнение для
характеристики, поскольку дискриминант равен нулю:
Таким образом, вы можете найти только одну характеристику координат, назовите ее .
Вам нужно будет взять другую координату что-то еще, скажем
. Вы хотите взять что-то простое, но это должно быть
не зависит от другой координаты.
Вы хотите взять что-то простое, но это должно быть
не зависит от другой координаты.
Тогда уравнения в частных производных упрощаются до
двумерная каноническая форма
| (1.16) |
Вы можете быть удивлены этим. При выборе мы всего лишь сделали нулевой коэффициент. Мы явно не делали ноль. Но автоматически равен нулю. Причина в том, что физ. свойства уравнений в частных производных не меняются только от потому что вы используете другие координаты. Параболическое уравнение должно оставаться параболическим; существуют принципиальные различия между физическим поведение параболических, эллиптических и гиперболических уравнений. И приведенное выше уравнение не было бы параболическим, если бы оно было ненулевым.
Пример
Вопрос: Сократите уравнение
к двумерному каноническому виду.Решение:
Напишите уравнение для характеристики
Квадратный корень равен нулю, поэтому уравнение параболическое.Решите уравнение и назовите постоянную интегрирования:
Итак, возьмите новые координаты как
Тогда окончательное дифференциальное уравнение в частных производных принимает вид
1.5.3 Эллиптические уравнения в двух измерениях
Характеристические линии являются решениями обыкновенного дифференциала
уравнение
Эллиптические уравнения не имеют вещественных характеристик, так как квадрат корень мнимый. Однако эллиптические уравнения все еще могут быть упрощенно, предполагая, что приведенное выше обыкновенное дифференциальное уравнение может решать аналитически.
Возьмите любой знак квадратного корня. Решите уравнение и вызовите
постоянная интегрирования, скажем, . Затем напишите эту интеграцию
постоянная в форме
Решите уравнение и вызовите
постоянная интегрирования, скажем, . Затем напишите эту интеграцию
постоянная в форме
| (1.17) |
где и являются реальными и . Другими словами, брать и .
Используя и в качестве новых координат, получается, что
уравнение в частных производных принимает двумерный канонический вид:
| (1.18) |
Вы можете заметить, что это очень похоже на то, что вы можете получить от вращая систему координат, как в предыдущем разделе. Однако, описанная выше процедура работает, даже если коэффициенты , , и исходного дифференциального уравнения в частных производных не являются константами.
Однако у этой процедуры есть существенные ограничения, т. {Г.5}
Пример
Вопрос: Сократите уравнение
к двумерному каноническому виду.

 Может быть это парабола, каноническое уравнение параболы . Но как преобразовать к каноническому виду я не знаю. Можно выделить квадрат двучлена, но, возможно, это делать не нужно.
Может быть это парабола, каноническое уравнение параболы . Но как преобразовать к каноническому виду я не знаю. Можно выделить квадрат двучлена, но, возможно, это делать не нужно. То есть задачи-то он решал, но всегда сомневался: а правильно ли, то ли он сделал, не то, да и вообще. Как-то вышел он с экзамена, открывает зачетку, а там в графе «оценка» написано «не знаю, что ставить».
То есть задачи-то он решал, но всегда сомневался: а правильно ли, то ли он сделал, не то, да и вообще. Как-то вышел он с экзамена, открывает зачетку, а там в графе «оценка» написано «не знаю, что ставить». Только от игрека что-то не то в скобках отнимается.
Только от игрека что-то не то в скобках отнимается.
 То, что я получил не похоже на
То, что я получил не похоже на 12.2010, 23:19
12.2010, 23:19  12.2010, 23:41
12.2010, 23:41  12.2010, 23:50
12.2010, 23:50  12.2010, 11:54
12.2010, 11:54  Но линии постоянные и есть
уникальны, и называются характеристическими линиями или характеристики .
Но линии постоянные и есть
уникальны, и называются характеристическими линиями или характеристики .
 Дополнительная постоянная интегрирования является произвольной
функция .
Дополнительная постоянная интегрирования является произвольной
функция . За
положительное уравнение эллиптическое. И для нуля будет
только одно направление для характеристик, горизонтальное.
За
положительное уравнение эллиптическое. И для нуля будет
только одно направление для характеристик, горизонтальное.