Сумма двух векторов. Законы сложения векторов. Сумма нескольких векторов. Правило параллелограмма. Вычитание векторов 9
Тема 24.
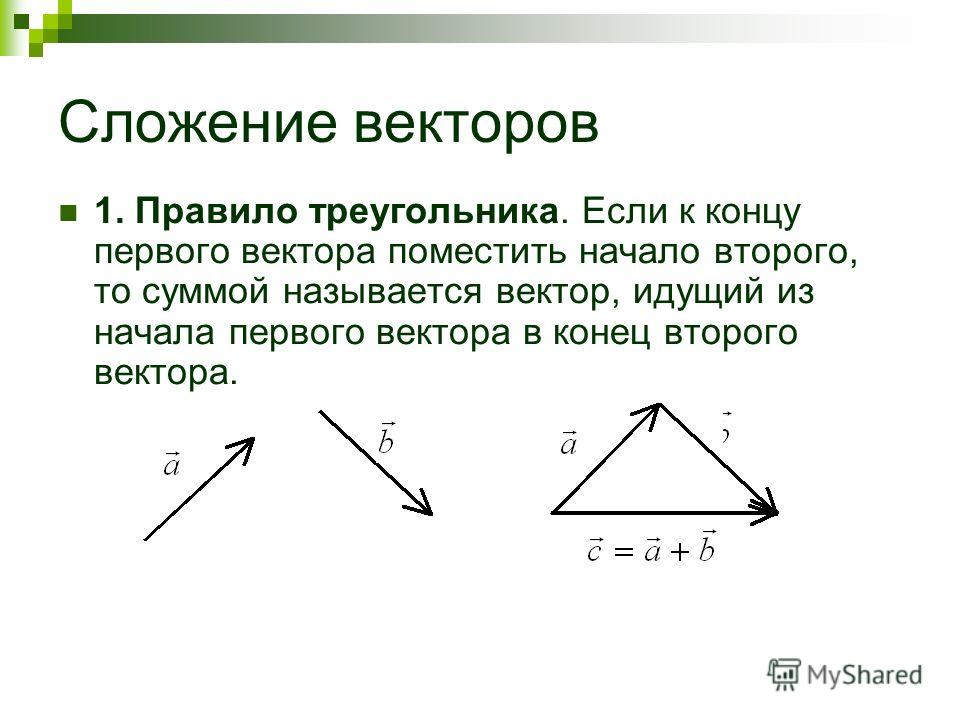
Сумма векторов. Разность векторов.
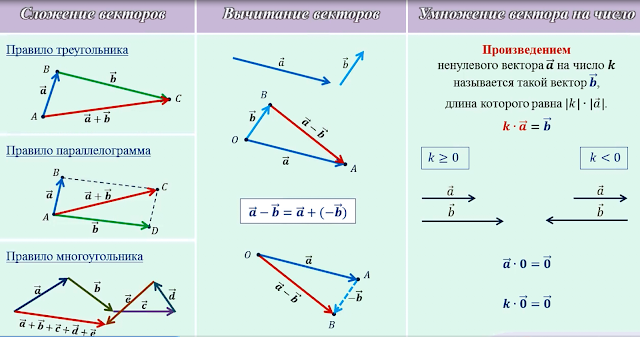
Рассмотрим пример. Пусть материальная точка переместилась из точки A в точку B, а затем из точки B в точку C. В результате этих перемещений, которые можно представить векторами AB⃗ и BC⃗, материальная точка переместилась из точки A в точку C. Поэтому результирующее перемещение можно представить вектором AC⃗. Поскольку перемещение из точки A в точку C складывается из перемещения из A в B и перемещения из B в C, то вектор AC⃗ естественно назвать суммой векторов AB⃗ и BC⃗:AC⃗=AB⃗+BC⃗.
Рассмотренный пример приводит нас к понятию суммы двух векторов.
Пусть a⃗ и b⃗ – два вектора. Отметим произвольную точку A и отложим от этой точки вектор AB⃗ равный a⃗. Затем от точки
Затем от точки
Сумма векторовa⃗ и b⃗ обозначается так: a⃗+b⃗.
Складывая по правилу треугольника произвольный вектор a⃗ с нулевым вектором, получаем, что для любого вектора a⃗ справедливо равенство
a⃗+0⃗=a⃗
Правило треугольника можно сформулировать также следующим образом: если A, B и C – произвольные точки, то AB⃗+BC⃗=AC⃗.
Это равенство справедливо для произвольных точек A, B и C, в частности, в том случае, когда две из них или даже все три совпадают.
Теорема
Для любых векторов a⃗,b⃗ и c⃗ справедливы равенства:
1. a⃗+b⃗=b⃗+a⃗ (переместительный закон).
2. a⃗+b⃗+c⃗=a⃗+b⃗+c⃗ (сочетательный закон).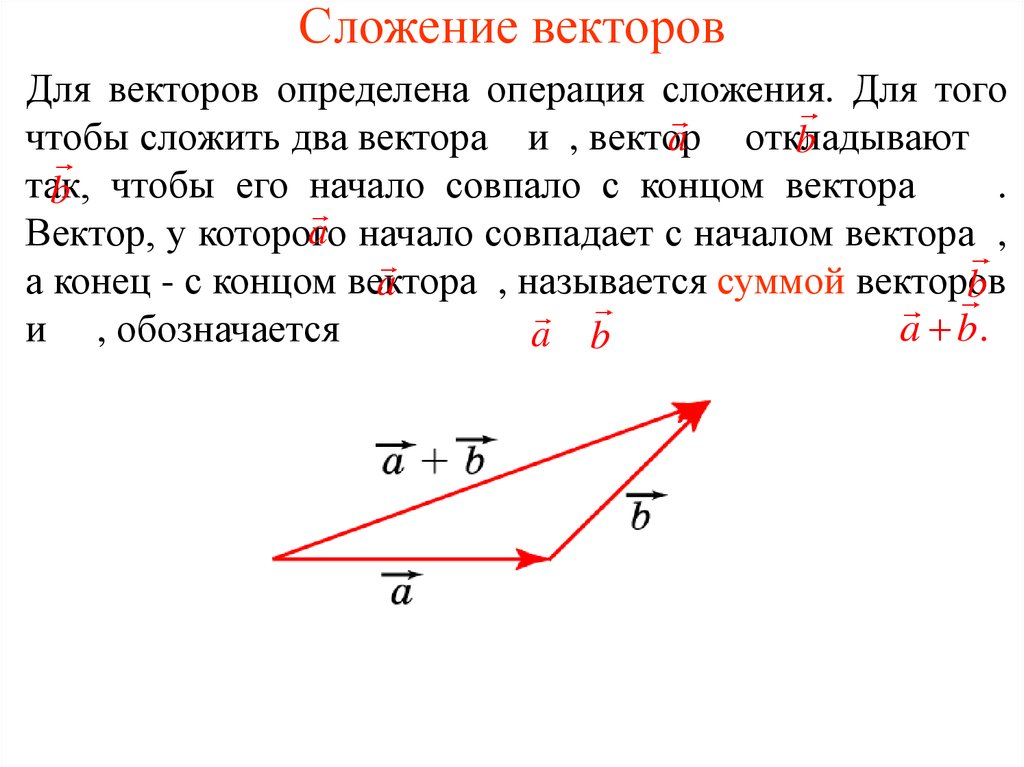
Докажем первое равенство. Рассмотрим случай, когда векторы a⃗ и b⃗ не коллинеарны. От произвольной точки A отложим векторы ABAD и на этих векторах построим параллелограмм ABCD. По правилу треугольника AC⃗=AB⃗+BC⃗=a⃗+b⃗. Аналогично AC⃗=AD⃗+DC⃗=b⃗+a⃗. Отсюда следует, что a⃗+b⃗=b⃗+a⃗.
При доказательстве первого свойства мы обосновали так называемое правило параллелограмма сложения неколлинеарных векторов: чтобы сложить неколлинеарные векторы a⃗ и b⃗, нужно отложить от какой-нибудь точки A векторы AB⃗=a⃗ и AD⃗=b⃗ и построить параллелограмм ABCD. Тогда вектор AC⃗ равен a⃗+b⃗. Правило параллелограмма часто используется в физике, например при сложении двух сил.
Сложение нескольких векторов производится следующим образом: первый вектор складывается со вторым, затем их сумма складывается с третьим вектором и т.д. Из законов сложения векторов следует, что сумма нескольких векторов не зависит от того, в каком порядке они складываются.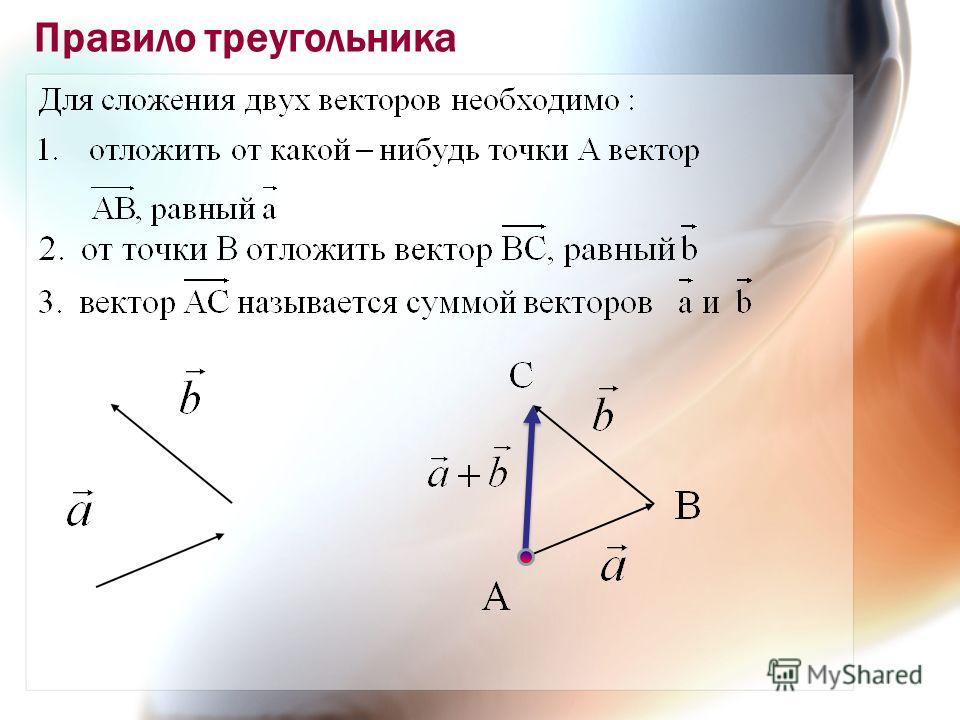
Аналогично можно построить сумму четырех, пяти и вообще любого числа векторов. Это правило построения суммы нескольких векторов называется правилом многоугольника.
Разностью векторов a⃗ и b⃗ называется такой вектор, сумма которого с вектором b⃗ равна вектору a⃗.
Разность векторов a⃗ и b⃗ обозначается так:a⃗-b⃗.
Рассмотрим задачу о построении двух векторов.
Даны векторы a⃗ и b⃗. Построить вектор a⃗-b⃗.
Отметим на плоскости произвольную точку O и отложим от этой точки векторы OA⃗=a⃗ и OB⃗=b⃗.
По правилу треугольника OB⃗+BA⃗=OA⃗ или b⃗+BA⃗=a⃗. Таким образом, сумма векторов BA⃗ и b⃗ равна a⃗. По определению разности векторов это означает, что BA⃗=a⃗-b⃗, то есть вектор BA⃗ искомый.
По определению разности векторов это означает, что BA⃗=a⃗-b⃗, то есть вектор BA⃗ искомый.
Пусть a⃗ – произвольный ненулевой вектор. Вектор a1⃗ называется противоположным вектору a⃗, если векторы a⃗ и a1⃗ имеют равные длины и противоположно направлены.
Вектор, противоположный вектору a⃗, обозначается так: -a⃗. Очевидно, что a⃗+-a⃗=0⃗.
Теорема
Для любых векторов a⃗ и b⃗ справедливо равенство a⃗-b⃗=a⃗+-b⃗.
Сегодня мы научились складывать и вычитать векторы. Узнали правило треугольника, правило параллелограмма и правило многоугольника.
Операция сложения двух векторов — правило треугольника.
Сложение
векторов и происходит
так: от произвольной точки A откладывается вектор ,
равный
,
далее от точки B откладываеься вектор ,
равный
,
и вектор представляет
собой сумму
векторов и .
Такой способ сложения двух векторов
назвается правилом
треугольника.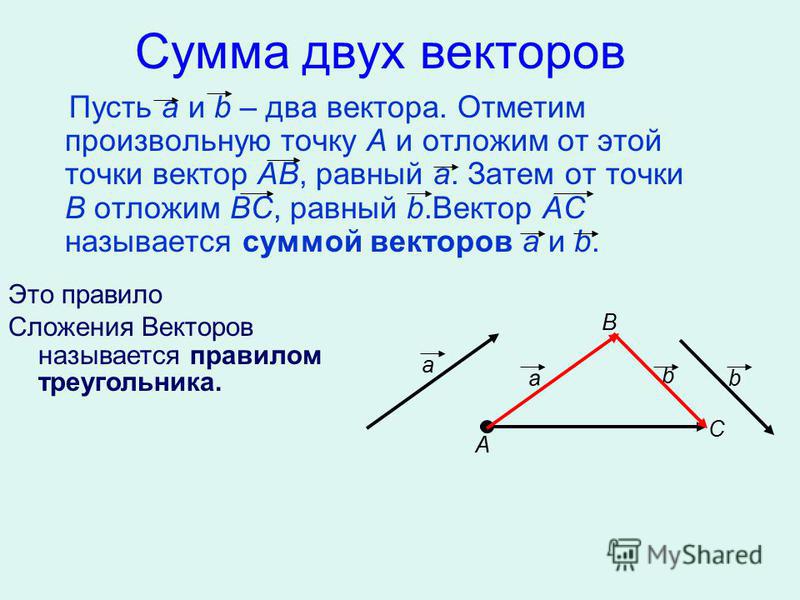
Проиллюстрируем сложение не коллинеарных векторов на плоскости по правилу треугольника.
А на чертеже ниже показано сложение сонаправленных и противоположно направленных векторов.
Сложение нескольких векторов — правило многоугольника.
Основываясь на рассмотренной операции сложения двух векторов, мы можем сложить три вектора и более. В этом случае складываются первые два вектора, к полученному результату прибавляется третий вектор, к получившемуся прибавляется четвертый и так далее.
Сложение нескольких векторов выполняется следующим построением. От произвольной точки А плоскости или пространства откладывается вектор, равный первому слагаемому, от его конца откладывается вектор, равный второму слагаемому, от его конца откладывается третье слагаемое, и так далее. Пусть точка B — это конец последнего отложенного вектора. Суммой всех этих векторов будет вектор .
Сложение
нескольких векторов на плоскости таким
способом называется правилом
многоугольника.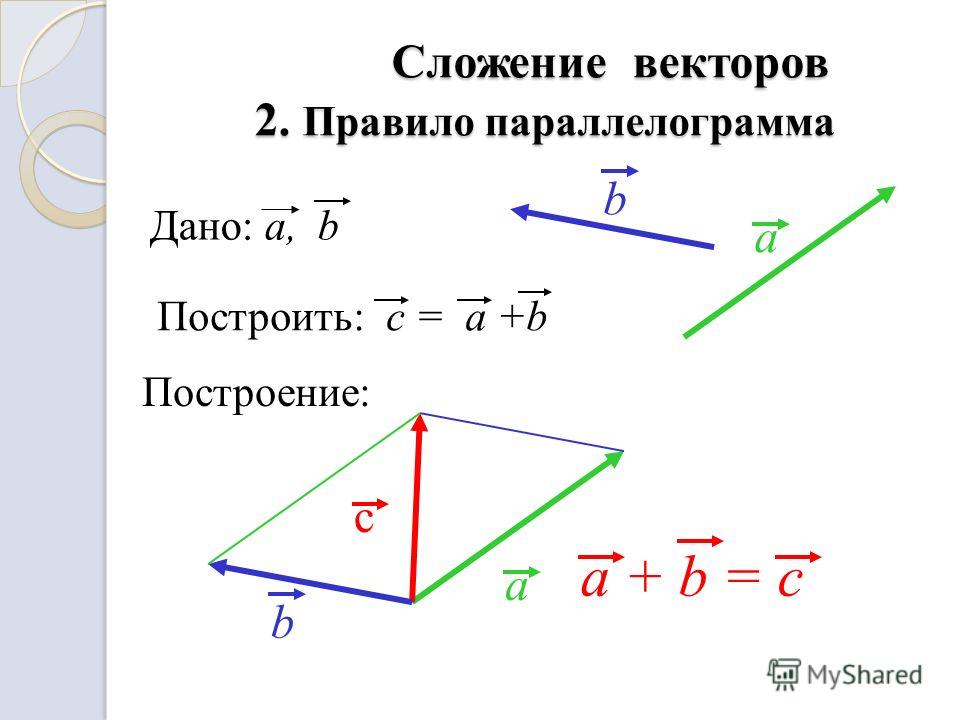 Приведем иллюстрацию правила
многоугольника.
Приведем иллюстрацию правила
многоугольника.
Абсолютно аналогично производится сложение нескольких векторов в пространстве.
Операция умножения вектора на число.
Умножение вектора на число k соответствует растяжению вектора в k раз при k > 1 или сжатию в раз при 0 < k < 1, при k = 1 вектор остается прежним (для отрицательных k еще изменяется направление на противоположное). Если произвольный вектор умножить на ноль, то получим нулевой вектор. Произведение нулевого вектора и произвольного числа есть нулевой вектор.
К примеру, при умножении вектора на число 2 нам следует вдвое увеличить его длину и сохранить направление, а при умножении вектора на минус одну треть следует уменьшить его длину втрое и изменить направление на противоположное. Приведем для наглядности иллюстрацию этого случая.
Определение.
Скалярным произведением двух векторов называется действительное число, равное
произведению длин умножаемых векторов
на косинус угла между ними.
Скалярное произведение векторов и будем обозначать как . Тогда формула для вычисления скалярного произведения имеет вид , где и — длины векторов и соответственно, а — угол между векторами и .
Из определения скалярного произведения видно, что если хотя бы один из умножаемых векторов нулевой, то .
Вектор можно скалярно умножить на себя. Скалярное произведение вектора на себя равно квадрату его длины, так как по определению .
Определение.
Скалярное произведение вектора на себя называется скалярным квадратом.
Формулу для вычисления скалярного произведения можно записать в виде , где — числовая проекция вектора на направление вектора , а — числовая проекция вектора на направление вектора .
Таким образом, можно дать еще одно определение скалярного произведения двух векторов.
Определение.
Скалярным произведением двух векторов и
называется
произведение длины вектора
на
числовую проекцию вектора
на
направление вектора
или
произведение длины вектора
на
числовую проекцию вектора
на
направление вектора
.
Это определение эквивалентно первому.
Длиной или модулем вектора называется длина отрезка, изображающего данный вектор. Длиной нулевого вектора называется число нуль.
Длина вектора на плоскости вычисляется по следующей формуле:
Длина вектора в трехмерном пространстве вычисляется по следующей формуле:
Формула длины вектора в n-мерном пространстве:
9. Угол между векторами. Условия параллельности и перпендикулярности.
Угол между векторами — угол между направлениями этих векторов (наименьший угол).
По определению, угол между двумя
векторами находится в промежутке [0°; 180°].
Угол между векторами обозначается
так: .
Если
векторы перпендикулярны, то угол между
ними равен 90º. Если векторы
сонаправлены, в частности один из них
или оба нулевые, то угол между ними равен 0о. Если противоположно
направленные векторы, то угол между
ними равен 180º. Угол между двумя
ненулевыми векторами находится с помощью
вычисления скалярного произведения.
По определению скалярное произведение
равно произведению длин векторов на
косинус угла между ними (скалярное
произведение для двух векторов с
координатами (x1; y1) и (x2;
y2) вычисляется по формуле: x1x2 + y1y2).
Угол между двумя
ненулевыми векторами находится с помощью
вычисления скалярного произведения.
По определению скалярное произведение
равно произведению длин векторов на
косинус угла между ними (скалярное
произведение для двух векторов с
координатами (x1; y1) и (x2;
y2) вычисляется по формуле: x1x2 + y1y2).
Условия параллельности и перпендикулярности векторов Так как скалярное произведение двух перпендикулярных векторов и равно 0, то условием перпендикулярности отличных от нуля векторов будет равенство . При умножении вектора на скаляр получаем вектор одного направления с при λ > 0и противоположного направления при λ < 0. Но всегда векторы будут параллельны. Поэтому условием параллельности векторов будет пропорциональность их соответствующих координат: .
10. Общее уравнение прямой.
Общие уравнения прямой
Через
каждую прямую в пространстве проходит
бесчисленное множество плоскостей. Любые две из них, пересекаясь, определяют
ее в пространстве. Прямую в пространстве
невозможно задать одним уравнением.
Следовательно, уравнения любых двух
таких плоскостей, рассматриваемые
совместно представляют собой уравнения
этой прямой. Для этого требуется система
двух или более уравнений.
Любые две из них, пересекаясь, определяют
ее в пространстве. Прямую в пространстве
невозможно задать одним уравнением.
Следовательно, уравнения любых двух
таких плоскостей, рассматриваемые
совместно представляют собой уравнения
этой прямой. Для этого требуется система
двух или более уравнений.
Пусть две плоскости и заданы общими уравнениями вида и , т.к. коэффициенты и не пропорциональны, то плоскости не параллельные. Тогда прямая в пространстве есть пересечение этих плоскостей:
Эти уравнения называются общими уравнениями прямой.
Однако при решении многих задач удобнее пользоваться другими уравнениями прямой, содержащими в явной форме некоторые ее геометрические характеристики.
Уравнения прямой, проходящей через точку параллельно вектору (канонические уравнения прямой)
| Пусть
прямая проходит через точку
параллельно
вектору
. , |
называемые каноническими уравнениями прямой в пространстве.
Уравнения прямой, проходящей через две данные точки
Пусть прямая проходит через две точки: , направляющим вектором такой прямой является вектор , и уравнения принимают вид:
уравнения прямой, проходящей через две данные точки.
Векторное уравнение прямой. Параметрические уравнения прямой
Положение
прямой в пространстве вполне определяется
заданием какой-либо её фиксированной
точки
и
направляющего вектора
,
параллельного этой прямой.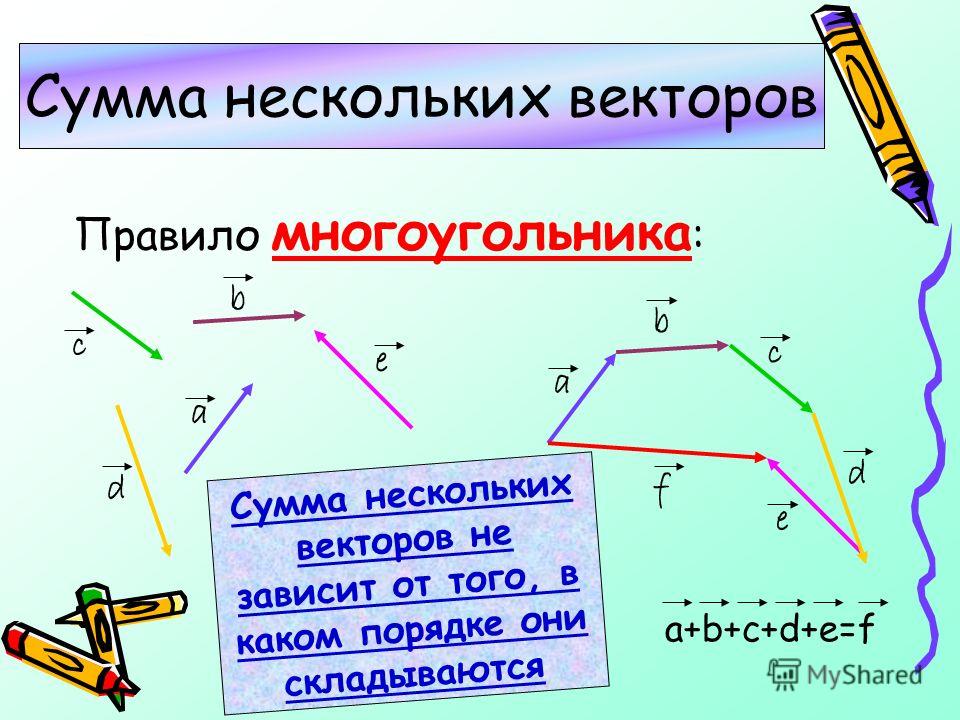
| Пусть прямая проходит через точку , лежащую на прямой параллельно вектору . Рассмотрим произвольную точку на прямой. Очевидно, что . Так как векторы и коллинеарны, то найдется такое число , что , причем число может принимать любое числовое значение в зависимости от положения точки на прямой. Множитель называется параметром. Обозначив радиус-векторы точек и соответственно через и , получаем . Это уравнение называется векторным уравнением прямой. Оно показывает, что каждому значению параметра соответствует радиус-вектор некоторой точки , лежащей на прямой. |
Так как векторы то
.
Полученные уравнения называются параметрическими уравнениями прямой. При изменении параметра изменяются координаты и и точка перемещается по прямой.
Замечание. Если принять каждую из равных дробей в канонических уравнениях прямой за некоторый параметр , , то можно получить параметрические уравнения .
Добавление векторов — Science Pickle
Добавление векторов немного сложнее, чем добавление скалярных величин (имеющих только величину), поскольку мы не можем добавлять направления и величины по отдельности. Чтобы добавить векторы точно , используйте их осевые компоненты. Если векторы имеют форму величины и направления, то вычислить их осевые составляющие. Чтобы быстро оценить сумму векторов, вы можете графически сложить их в любой форме: по величине и направлению или по осевым компонентам. Даже при математическом добавлении векторов полезно проверять свои результаты, добавляя их графически, поскольку при сложении векторов довольно часто встречаются ошибки со знаком.
Визуальное добавление векторов
Добавление векторов в веб-приложение
Если вы знакомы с добавлением векторов, нажмите одну из кнопок, чтобы запустить приложение. Ниже приведена вспомогательная информация о добавлении векторов, запуске приложений и дополнительных кнопках для запуска приложений.
Преимущества запуска веб-приложений
Хотя вы можете просматривать следующие иллюстрации и анимации, созданные с помощью веб-приложений, их самостоятельное выполнение имеет ряд преимуществ:
- Изображения будут больше.
- Вы можете сколько угодно рассматривать любое изображение, чтобы изучить и/или нарисовать то, что вам больше всего поможет.
- Есть дополнительные визуализации и действия для изучения.
- Проверьте свое понимание, предсказав результат новых настроек до внесения изменений в приложение.
- Вы можете сохранять скриншоты созданных вами визуализаций.

Предложение : Если вы перевели экран/компьютер в спящий режим с коротким интервалом времени, вы потеряете то, что просматриваете при запуске веб-приложения. Рассмотрите возможность изменения настроек, чтобы дать себе время работать с приложением по своему усмотрению.
Математическое сложение векторов
Чтобы математически сложить векторы, сложите их соответствующие компоненты , затем используйте теорему Пифагора для вычисления величины и тригонометрических функций для вычисления направления равнодействующей.
Например, предположим, что вы прошли 8 миль на восток (90°), а затем 4 мили на север (0°) (рис. 1). Вы не находитесь в 8 + 4 или 12 милях или 0 + 90 или 90º от исходной точки. В этом примере каждый вектор находится в направлении одной из осей, поэтому нам не нужно разбивать векторы на составляющие их значения. Мы можем использовать теорему Пифагора, чтобы вычислить, как далеко мы находимся от того места, где мы начали, и использовать арктангенс, чтобы вычислить направление, в котором мы находимся от нашей начальной точки.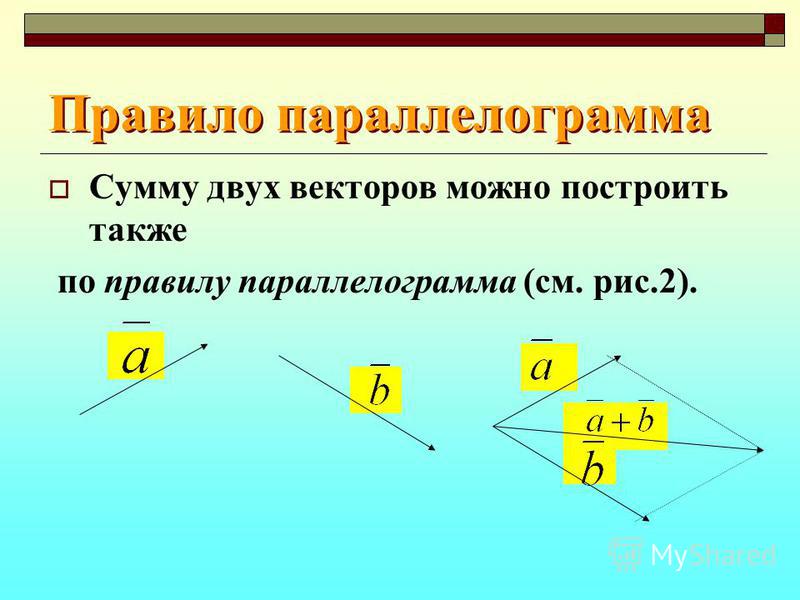 Дополнительные сведения см. в следующих разделах.
Дополнительные сведения см. в следующих разделах.
Рис. 1: Эти два вектора добавлены на основе принятого в навигации соглашения о направлении: 0° соответствует северу, а направление увеличивается по часовой стрелке. Оба вектора взяты из начала координат. Совет: Если векторы заданы в виде величины и направления, используйте полярную сетку для построения векторов от начала координат.
Рассчитайте величину равнодействующей
Используя теорему Пифагора:
Величина = √(8² + 4²) = 8,9
Рассчитайте направление равнодействующей
Направление = 90º – tan¯¹(4/8) = 63,4º (используйте рис. 3)
= tan¯¹(8/4) = 63,4º (используйте рис. 4)
Графическое дополнение «Хвост к кончику»
«Хвост к кончику» — это графическая форма сложения векторов, основанная на концепции, согласно которой векторы можно перемещать по графику. Два решения при графическом добавлении двух векторов, показанных на рисунке 1, показаны ниже. Красный вектор — это 8 миль к востоку (90º), а зеленый — 4 мили к северу (0 º).
Красный вектор — это 8 миль к востоку (90º), а зеленый — 4 мили к северу (0 º).
В этом решении сдвиньте конец второго вектора к кончику первого вектора. Направления и величины обоих векторов остаются прежними.
Если есть третий вектор, сдвиньте конец третьего вектора к вершине суммы первых двух векторов.
Рис. 2. Сдвиньте конец одного вектора к кончику второго вектора. Совет: прямоугольная сетка удобна для построения осевых компонентов.
Нарисуйте результирующий вектор от начала координат до вершины суммы двух векторов.
При использовании этой техники создайте масштаб для рисования векторов, чтобы пропорции величин были согласованными. Нарисуйте величины и направления векторов как можно точнее, чтобы результат был концептуально полезен и обеспечивал ценную проверку при математическом сложении векторов.
Рис. 3. Нарисуйте результирующий вектор (пурпурный) от начала координат до вершины суммы двух векторов.
Имеет ли значение, в каком порядке добавлять векторы? В приведенном выше примере имеет ли значение, идете ли вы сначала на восток или на север? Если на одном из ваших путей нет огненного болота, Горы Рока или колючей ивы, вы все равно окажетесь на том же расстоянии и в том же направлении, откуда начали. Подобно сложению чисел, сложение векторов в любом порядке дает тот же результат.
Рисунок 4: Сложение двух векторов в обратном порядке дает один и тот же результирующий вектор.
Анимации добавления векторов
Чтобы увидеть, как перемещаются векторы при добавлении двух или трех векторов, используйте веб-приложение Визуальное добавление векторов для создания случайных векторов, а затем переместите их в положение, где вектор хвосты совпадают с кончиками. Два примера использования приложения показаны на следующих анимациях.
Визуальное добавление векторов
Нажмите кнопку, чтобы запустить веб-приложение, Визуальное добавление векторов .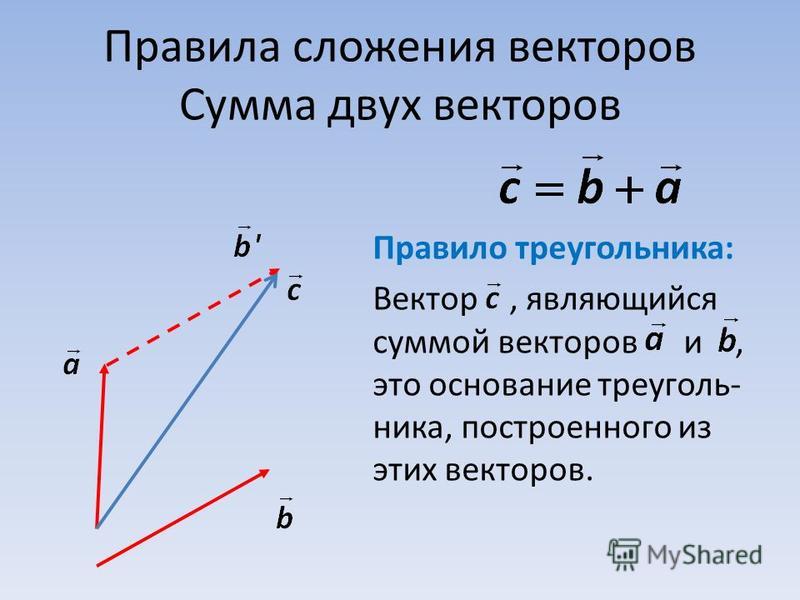
Благодарности
Большое спасибо Брендану Кроули, Алану Гулду, Максу Холлу и Матти Хорну за тестирование приложения во время бета-тестирования.
В анимации сложения двух векторов методом «хвост к кончику» обратите внимание, что при перемещении зеленого вектора к кончику красного вектора его длина и ориентация остаются прежними.
В анимации сложения трех векторов методом «хвост к кончику» обратите внимание, что при перемещении зеленого и синего векторов их длина и ориентация остаются прежними.
Представление и ясность
Существует несколько способов графического сложения векторов. Некоторые из них могут иметь для вас смысл; другие могут ввести в заблуждение. Понятны ли вам векторы и результирующий вектор из начала координат (рисунок 5)? Это обычный способ отображения векторов при их добавлении.
Чем полезно графическое добавление векторов?
Концептуальная работа с векторами так же важна, как и математическая.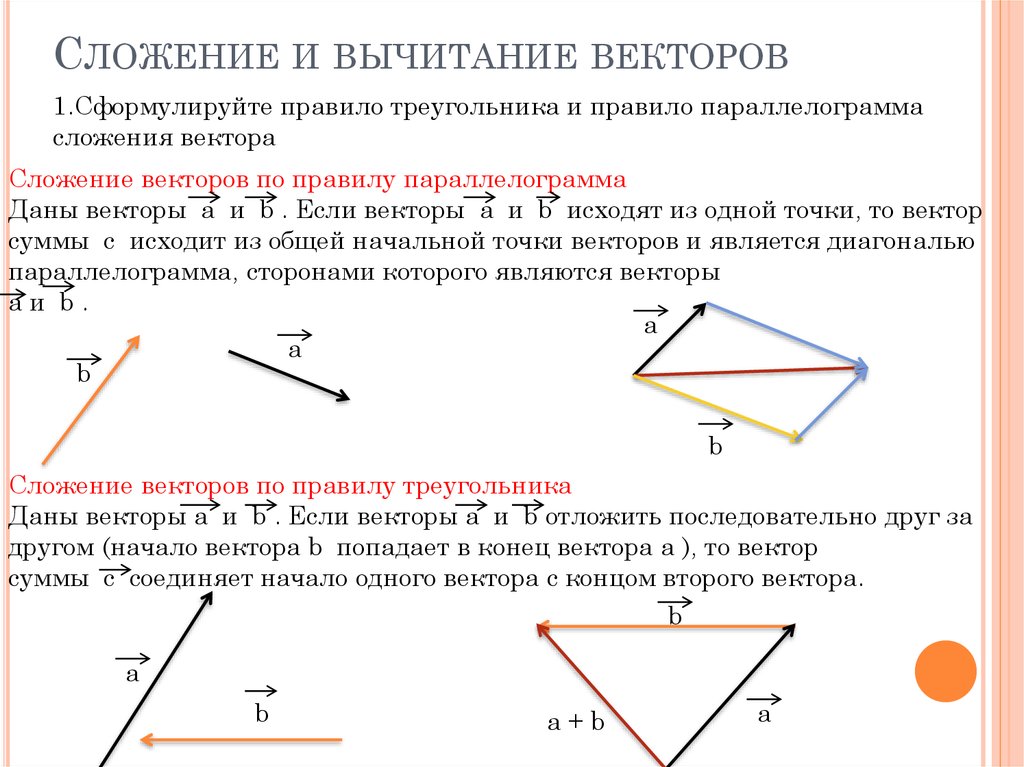 Если вы работаете с векторами математически, вычерчивание решения выявляет математические ошибки, особенно опечатки при работе с калькулятором или компьютерной программой и ошибки знаков.
Если вы работаете с векторами математически, вычерчивание решения выявляет математические ошибки, особенно опечатки при работе с калькулятором или компьютерной программой и ошибки знаков.
Векторы широко используются в науке, математике и технике, и ошибки могут быть более чем досадными; человеческие жизни зависят от точных расчетов построенных сооружений, навигации, передовых технологий, прогнозов погоды, поисково-спасательных операций и т. д.
Большинство оставшихся разделов Земных систем требуют твердого концептуального понимания и применения векторов. Научитесь графически работать с векторами.
Рис. 5: График добавляемых векторов и результирующего вектора из исходной точки.
Чем полезно математическое сложение векторов?
Работа с векторами, например, сложение векторов, необходима в технике и многих областях науки и математики. Эти дисциплины были бы резко ограничены без использования векторов. Например, для проектирования и строительства безопасных, устойчивых сооружений (зданий, мостов, дорог, плотин и т. д.), а также для анализа и прогнозирования движущихся объектов (самолеты, реактивные самолеты, ракеты и т. д.) требуются векторные вычисления. Высоко точный и точный 9Расчеты 0055 необходимы для значительной части человеческих технологий.
д.), а также для анализа и прогнозирования движущихся объектов (самолеты, реактивные самолеты, ракеты и т. д.) требуются векторные вычисления. Высоко точный и точный 9Расчеты 0055 необходимы для значительной части человеческих технологий.
Математическое сложение трех векторов
Концептуально сложение трех векторов ничем не отличается от сложения двух. Осталось только организовать.
В следующем примере добавляются три вектора, определяемые величиной и направлением.
| Вектор | Величина | Направление |
| 1 | 4,0 | 45,0º |
| 2 | 8.1 | 310,0º |
| 3 | 6,0 | 180,0º |
Преобразуйте модуль и направление вектора в осевые компоненты, а затем сложите их, чтобы найти результирующие компоненты.
| Вектор | Х | Д |
| 1 | 4,0 sin(45) = 2,8 | 4,0 cos(45) = 2,8 |
| 2 | 8,1 sin(310) = -6,2 | 8,1 cos(310) = 5,2 |
| 3 | 6 sin(180) = 0,0 | 6 cos(180) = -6,0 |
| Сумма | -3,4 | 2,0 |
Рис. 6: Необходимо добавить три вектора. Показаны компоненты каждого вектора. Значения находятся в тех же значениях, что и соответствующий им вектор. X представляет Восток, когда положительный, и Запад, когда отрицательный. Y представляет север, когда положительный, и юг, когда отрицательный.
6: Необходимо добавить три вектора. Показаны компоненты каждого вектора. Значения находятся в тех же значениях, что и соответствующий им вектор. X представляет Восток, когда положительный, и Запад, когда отрицательный. Y представляет север, когда положительный, и юг, когда отрицательный.
См. Прямоугольные треугольники и векторы для получения подробной информации о том, как компоненты вектора рассчитываются по величине и направлению.
Рассчитайте величину результирующей величины
, используя теорему Pythagorean:
величина = √ (2,0² + (-3,4) ²) = 3,9
Рассчитайте направление результирующего
= 270º + tan¯ (2.0/3.4 ) = 300,4º (Используйте рис. 8)
Разница между этим направлением и направлением, показанным на рис. 8, связана с ошибкой округления при использовании значений компонентов, ограниченных десятыми долями, по сравнению с использованием более точных значений в функции арктангенса.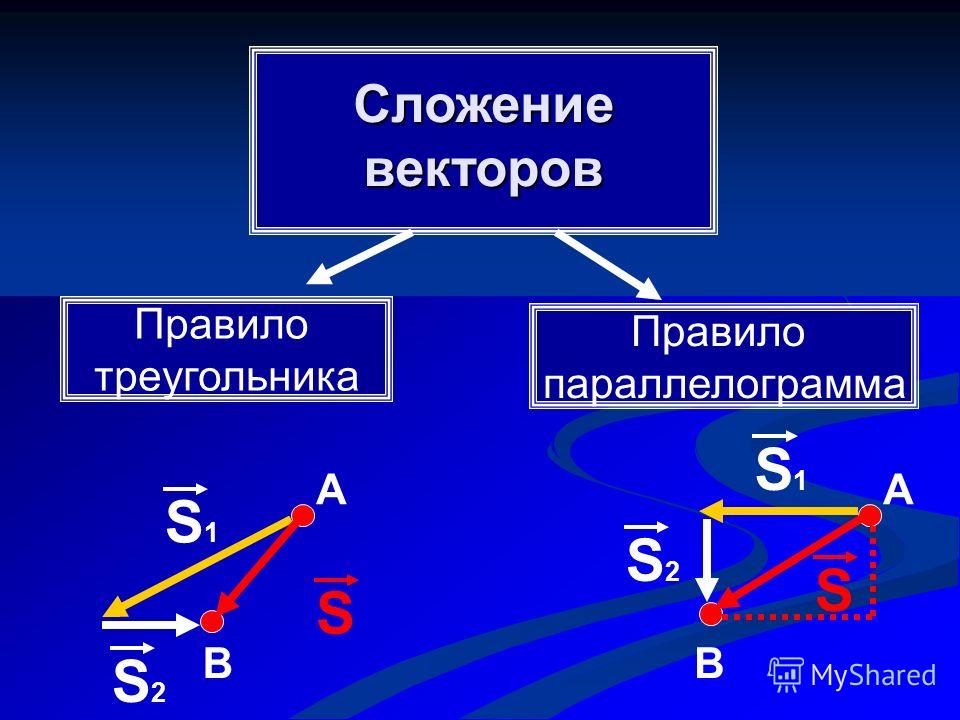
Графическое добавление трех векторов
Рис. 7. Сначала нарисуйте красный вектор (вектор 1) из начала координат, затем нарисуйте зеленый вектор (вектор 2) из вершины первого и, наконец, нарисуйте синий вектор (вектор 3) ) от кончика суммы первых двух.
Нарисуйте результат (пурпурный) от начала координат до вершины суммированных векторов.
Рисунок 8: Сложите векторы в другом порядке, результаты будут теми же. Есть шесть возможных способов сложить три вектора. Попробуйте нарисовать их самостоятельно.
Больше практики?
Нажмите кнопку «Добавление векторов в веб-приложение», чтобы получить неограниченное количество практических задач на добавление 2 или 3 векторов графически или математически. Для каждой проблемы предоставляется визуальная и числовая обратная связь.
Добавление веб-приложения Vectors
Нажмите кнопку, чтобы запустить веб-приложение.
Веб-приложение использует триггерное соглашение для направления, тогда как в приведенных выше примерах используется соглашение о навигации.
Снимок экрана веб-приложения «Добавление векторов». При использовании «Добавить графически» для создания результирующего вектора щелкните график или введите величину и направление в текстовые поля. При математическом сложении для обеспечения необходимой точности введите значения.
Как добавить векторы вместе
BY: Стивен Холцнер и
Обновлен: 03-26-2016
Из книги: Physics I Workbook For Dummies с онлайн-практикой
8. Манекены с онлайн-практикойИсследуйте книгу Купить на Amazon
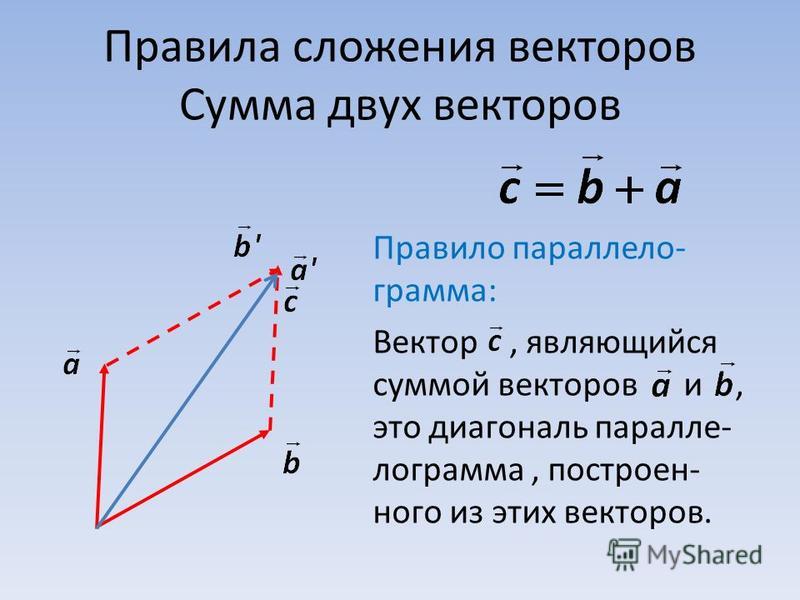
Вас часто просят добавить векторы при решении физических задач. Чтобы сложить два вектора, вы помещаете их голову к хвосту, а затем находите длину и величину результата. Порядок, в котором вы добавляете два вектора, не имеет значения.
Например, предположим, что вы направляетесь на большой конгресс по физике, и вам сказали, что вы должны пройти 20 миль на север, а затем 20 миль на восток, чтобы добраться туда. Под каким углом от вашего текущего местоположения находится конференц-центр и как далеко он находится?
Под каким углом от вашего текущего местоположения находится конференц-центр и как далеко он находится?
Вы можете написать эти два вектора следующим образом (где восток находится вдоль положительной оси x ):
(0, 20)
(20, 0)
В этом случае вам нужно сложить эти два вектора, и вы можете сделать это, просто добавив их x и y компоненты отдельно:
Посчитайте, и ваш результирующий вектор равен (20, 20). Вы только что завершили сложение векторов. Но вопрос задает вектор в терминах величины/угла, а не в координатах. Итак, какова величина вектора от вас к соглашению о физике? Вы можете увидеть ситуацию на следующем рисунке, где у вас есть x и y и вы хотите найти v .
Находка v не так сложно, потому что вы можете использовать теорему Пифагора:
Подставьте цифры, чтобы получить
Значит, до конгресса 48,3 мили. А угол тета? Вы знаете
А угол тета? Вы знаете
тета = тангенс –1 ( y / x ) = тангенс –1 (20/20) = 45 градусов
И все — теперь вы знаете, что конвенция находится на расстоянии 28,3 мили под углом 45 градусов.
Пример вопроса
Сложите два вектора на следующем рисунке. Один имеет звездную величину 5,0 и угол 45 градусов, а другой имеет звездную величину 7,0 и угол 35 градусов.
Правильный ответ: звездная величина 12,0, угол 39 градусов.
Разложите два вектора на их компоненты. Для первого вектора примените уравнение v x = v cos theta, чтобы найти координату x . Это 5,0, потому что 45 градусов = 3,5.
Примените уравнение v y = v sin theta, чтобы найти y координата первого вектора. Это 5,0 минус 45 градусов или 3,5.
 Таким образом, первый вектор равен (3.5, 3.5) в координатной форме.
Таким образом, первый вектор равен (3.5, 3.5) в координатной форме.Для второго вектора примените уравнение v x = v cos тета, чтобы найти координату x . Это 7,0, потому что 35 градусов = 5,7.
Примените уравнение v y = v sin theta, чтобы найти y координата второго вектора. Это 7,0 минус 35 градусов = 4,0. Таким образом, второй вектор равен (5.7, 4.0) в координатной форме.
Чтобы сложить два вектора, сложите их в виде координат: (3.5, 3.5) + (5.7, 4.0) = (9.2, 7.5).
Преобразование (9.2, 7.5) в форму величины/угла. Примените уравнение theta = tan –1 ( y / x ), чтобы найти угол, который равен tan –1 (7,5/9,2) = tan –1 (0,82) = 39градусов.
Применить уравнение
, чтобы найти величину, которая равна
.
Преобразование в две значащие цифры дает 12.
Практические вопросы
Добавьте вектор с величиной 13,0 и углом 27 градусов к вектору с величиной 11,0 и углом 45 градусов.
Добавьте вектор с величиной 16,0 и углом 56 градусов к вектору с величиной 10,0 и углом 25 градусов.
Добавьте два вектора: первый вектор имеет величину 22,0 и угол 19 градусов, а второй вектор имеет величину 19,0 и угол 48 градусов.
Добавьте вектор с величиной 10,0 и углом 257 градусов к вектору с величиной 11,0 и углом 105 градусов.
Ниже приведены ответы на практические вопросы:
Величина 23,7, угол 35 градусов
Для первого вектора используйте уравнение v x = v cos theta , чтобы найти координату x : 13,0 x cos 27 градусов = 11,6.
Используйте уравнение v y = v sin theta , чтобы найти координату y первого вектора: 13,0 x sin 27 градусов, или 5,90.
 Таким образом, первый вектор равен (11.6, 5.90) в координатной форме.
Таким образом, первый вектор равен (11.6, 5.90) в координатной форме.Для второго вектора используйте уравнение v x = v cos theta , чтобы найти координату x : 11,0 x cos 45 градусов = 7,78.
Используйте уравнение v y = v sin theta , чтобы найти координату y второго вектора: 11,0 x sin 45 градусов = 7,78. Итак, второй вектор равен (7.78, 7.78) в координатной форме.
Сложите два вектора в виде координат: (11.6, 5.90) + (7,78, 7,78) = (19,4, 13,7).
Преобразовать (19.4, 13.7) в форму величины/угла. Используйте уравнение тета = тангенс –1 ( y / x ), чтобы найти угол: тангенс –1 (13,7/19,4) = тангенс –1 (0,71) = 35 градусов.
Применить уравнение
, чтобы найти величину, которая равна
.
Величина 25,1, угол 44 градуса
Для первого вектора используйте уравнение v x = v cos theta , чтобы найти координату x : 16,0 x cos 56 градусов = 8,95.
Используйте уравнение v y = v sin theta , чтобы найти координату y первого вектора: 16,0 x sin 56 градусов, или 13,3. Таким образом, первый вектор равен (8.95, 13.3) в координатной форме.
Для второго вектора используйте уравнение v x = v cos theta , чтобы найти координату x : 10,0 x cos 25 градусов = 9,06.
Используйте уравнение v y = v sin theta , чтобы найти координату y второго вектора: 10,0 x sin 25 градусов = 4,23. Таким образом, второй вектор равен (9.
 06, 4.23) в координатной форме.
06, 4.23) в координатной форме.Добавьте два вектора в виде координат: (8.95, 13,3) + (9,06, 4,23) = (18,0, 17,5).
Преобразование вектора (18.0, 17.5) в форму величины/угла. Используйте уравнение тета = тангенс –1 ( y / x ), чтобы найти угол: тангенс –1 (17,5/18,0) = тангенс –1 (0,97) = 44 градуса.
Применить уравнение
, чтобы найти величину, которая равна
.
Величина 39,7, угол 32 градуса
Для первого вектора используйте уравнение v x = v cos theta , чтобы найти координату x : 22,0 x cos 19 градусов = 20,8.
Используйте уравнение v y = v sin theta , чтобы найти координату y первого вектора: 22,0 x sin 19 градусов, или 7,16. Таким образом, первый вектор равен (20.
 8, 7.16) в координатной форме.
8, 7.16) в координатной форме.Для второго вектора используйте уравнение v x = v cos theta , чтобы найти координату x : 19,0 x cos 48 градусов = 12,7.
Используйте уравнение v y = v sin theta , чтобы найти координату y второго вектора: 19,0 x sin 48 градусов = 14,1. Таким образом, второй вектор равен (12.7, 14.1) в координатной форме.
Сложите два вектора в виде координат: (20.8, 7.16) + (12.7, 14.1) = (33.5, 21.3).
Преобразование вектора (33.5, 21.3) в форму величины/угла. Используйте уравнение тета = тангенс –1 ( y / x ), чтобы найти угол: тангенс –1 (21,3/33,5) = тангенс –1 (0,64) = 32 градуса.
Применить уравнение
, чтобы найти величину, которая равна
.
Величина 5,2, угол 170 градусов
1.
 Для первого вектора используйте уравнение v x = v cos theta , чтобы найти координату x : 10,0 x cos 257 градусов = -2,25.
Для первого вектора используйте уравнение v x = v cos theta , чтобы найти координату x : 10,0 x cos 257 градусов = -2,25.Используйте уравнение v y = v sin theta , чтобы найти координату y первого вектора: 10,0 x sin 257 градусов, или -9,74. Итак, первый вектор равен (–2,25, –9,74) в координатной форме.
Для второго вектора используйте уравнение v x = v cos theta , чтобы найти координату x : 11,0 x cos 105 градусов = -2,85.
Используйте уравнение v y = v sin theta , чтобы найти координату y второго вектора: 11,0 x sin 105 градусов = 10,6. Таким образом, второй вектор равен (–2,85, 10,6) в координатной форме.
Сложите два вектора в виде координат: (–2,25, –90,74) + (–2,85, 10,6) = (–5,10, 0,86).


 Так как любой ненулевой вектор,
параллельный данной прямой, является
ее направляющим вектором, то для любой
точки
,
лежащей на данной прямой, вектор
коллинеарен
направляющему вектору
.
Поэтому их соответствующие координаты
должны быть пропорциональны,
следовательно, имеют место равенства:
Так как любой ненулевой вектор,
параллельный данной прямой, является
ее направляющим вектором, то для любой
точки
,
лежащей на данной прямой, вектор
коллинеарен
направляющему вектору
.
Поэтому их соответствующие координаты
должны быть пропорциональны,
следовательно, имеют место равенства:
 Таким образом, первый вектор равен (3.5, 3.5) в координатной форме.
Таким образом, первый вектор равен (3.5, 3.5) в координатной форме.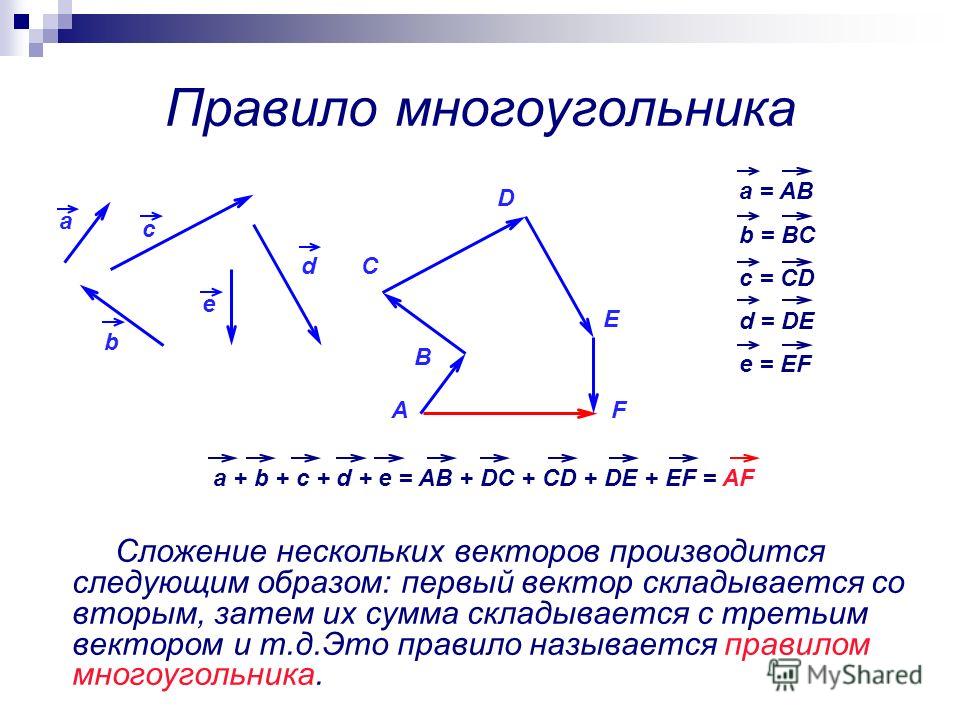
 Таким образом, первый вектор равен (11.6, 5.90) в координатной форме.
Таким образом, первый вектор равен (11.6, 5.90) в координатной форме.
 06, 4.23) в координатной форме.
06, 4.23) в координатной форме. 8, 7.16) в координатной форме.
8, 7.16) в координатной форме. Для первого вектора используйте уравнение v x = v cos theta , чтобы найти координату x : 10,0 x cos 257 градусов = -2,25.
Для первого вектора используйте уравнение v x = v cos theta , чтобы найти координату x : 10,0 x cos 257 градусов = -2,25.