Как проверить образуют ли векторы базис: Онлайн калькулятор. Проверить образуют ли вектора базис

Содержание

Линейные операции над векторами. Линейная зависимость и независимость системы векторов. Базис

1. Даны два вектора и. Определить проекции на координатные оси векторов:

1.1. .1.2. .1.3. .

1.4. .1.5. .1.6. .

2. Проверить коллинеарность векторов и. Установить, какой из них длиннее другого, во сколько раз? Сонаправлены ли они?

3. Найти длину вектора , его орт и направляющие косинусы.

4. Определить модули суммы и разности векторов и.

5. Радиус-вектор точки М составляет с осью угол, а с осью— угол, его длина. Найти координаты точки М,

если ее абсцисса отрицательна.

6. Векторы ,совпадают со сторонами. Определить координаты векторов, приложенных к вершинам треугольника и совпадающих с его медианами,и.

7. и. Определить длины диагоналей параллелограмма, построенного на векторах.

8. Даны модули векторов ,,. Определить.

Векторы иобразуют угол, причем,. Определитьи.

10. Даны векторы ,,. Разложить векторпо векторами.

11. По данным векторам ипостроить векторы:

11.1. ;

11.2. ;

11.3. .

12. Выяснить, являются ли указанные векторы линейно зависимыми или линейно независимыми:

12.1. ,.

12.2. ,.

12.3. ,,.

13. Установить, образуют ли базис векторы , которые линейно выражаются через векторы:

13.1. ,,;

, ,.

13.2. ,,;

, ,.

13.3. ,,;

, ,.

13.4. ,,;

, ,.

13.5. ,,;

, ,.

14. Показать, что векторы образуют базис и найти в этом базисе координаты вектора:

14.1. ,,.

14.2. ,,.

14.3. ,,.

14.

4. ,,.

14.5. ,,.

Дополнительные задания

Д-1. Дан вектор . Найти вектор, параллельный векторуи противоположно ему направленный, если.

Д-2. Дан вектор . Найти разложение векторапо этому же базису, если векторпараллелен вектору, противоположно ему направлен и.

Д-3. Построить векторы ,и. Разложить векторпо векторами.

Д-4. Найти вектор , коллинеарный вектору, образующий с ортомострый угол и имеющий длину.

Д-5. Доказать, что четырехугольник — ромб, если,, С ( 3, 5 , 2 ) ,.

Д-6. Даны векторы и. Найти орт биссектрисы угла междуи.

Д-7. Вектор составляет с координатными осямииуглы,, а с осьютупой угол. Найти его координаты, если.

Д-8. Известно, что равнобедренный. Найти координаты вершины С, если,, С. Сколько решений имеет задача?

Д-9. Даны вершины треугольника ,, С(-4, 0, 3 ). Найти длину медианы, проведенной из вершины.

Д-10. Определить, при каких значениях ивектораиколлинеарны.

Д-11. Найти базисы системы векторов ,,={1.2.1},, содержащие вектор.

Итоговый самоконтроль

С-1. Может ли вектор составлять с координатными осями углы 30, 120, 60^o?

С-2. Следует ли из равенства равенство?

С-3. Может ли угол между векторами быть равным 0, 30, 180, 175, 225^o?

С-4. Каково взаимное расположение точек , если:

С-4.1. Векторы иколлинеарны.С-4,2. .

С-4.3. .

С-5. Какому условию должны удовлетворять векторы, чтобы они могли образовать плоскую фигуру?

С-6. Как следует направить векторы и, чтобы длина векторабыла наибольшей? Наименьшей?

С-7. Какому условию удовлетворяют векторы и, если:

С-7.1.. >.С-7.2. <.

С-7.3.. .С-7.4.. .

С-8. Система векторов содержит:

С-8.1. Два равных вектора.

С-8.2. Два пропорциональных вектора.

Является ли она линейно зависимой?

С-9. Известно, что ,,линейно независимые векторы. Выяснить, линейно зависимы или линейно независимы векторы:

С-9.1. ,,.С-9.2. ,,.

С-9.3.. ,,,. С-9.4. ,,.

С-10. В треугольнике проведена медиана. Какой вид имеет разложение векторапо векторами?

С-11. В параллелограмме — середина стороны. Найти разложение векторапо векторами.

Задача 33 Даны векторы a 1 (1;3;5), a 2 (-2;-1;-1), a 3 (4;-2;4), b(-7;3;-1)

1 2 3

Ім’я файлу: математика.docx

Розширення: docx
Розмір: 292кб.
Дата: 27.01.2022
скачати
Пов’язані файли:
Концепції реалізації адміністративно-територіальної реформи пере
куликов версия для меня1.

docx
история.docx
bobkov.doc
619097.rtf

ВАРИАНТ №3

Задача 33

Даны векторы a₁(1;3;5), a₂(-2;-1;-1), a₃(4;-2;4), b(-7;3;-1). Показать, что векторы образуют базис трехмерного пространства и найти координаты вектора b в этом базисе.
Данная задача состоит из двух частей. Сначала необходимо проверить образуют ли векторы базис. Векторы образуют базис, если определитель, составленный из координат этих векторов, отличен от нуля, в противном случае вектора не являются базисными и вектор b нельзя разложить по данному базису.
Вычислим определитель матрицы:

1	3	5
-2	-1	-1
4	-2	4

∆ = 1*((-1)*4 — (-2)*(-1)) — (-2)*(3*4 — (-2)*5) + 4*(3*(-1) — (-1)*5) = 46
Определитель матрицы равен ∆ =46
Так как определитель отличен от нуля, то векторы образуют базис, следовательно, вектор X можно разложить по данному базису.

Т.е. существуют такие числа α₁, α₂, α₃, что имеет место равенство:
X = α₁ε₁ + α₂ε₂ + α₃ε₃
Запишем данное равенство в координатной форме:
(-7;3;-1) = α(1;3;5) + α(-2;-1;-1) + α(4;-2;4)
Используя свойства векторов, получим следующее равенство:
(-7;3;-1) = (1α₁;3α₁;5α₁😉 + (-2α₂;-1α₂;-1α₂😉 + (4α₃;-2α₃;4α₃😉
(-7;3;-1) = (1α₁ -2α₂ + 4α₃;3α₁ -1α₂ -2α₃;5α₁ -1α₂ + 4α₃)
По свойству равенства векторов имеем:
1α₁ -2α₂ + 4α₃ = -7
3α₁ -1α₂ -2α₃ = 3
5α₁ -1α₂ + 4α₃ = -1
Решаем полученную систему уравнений методом Крамера.
Ответ:

b =

-1

b = a₁ + 2a₂ -a₃

Задача 43

Обозначим через А — матрицу коэффициентов при неизвестных; X — матрицу-столбец неизвестных; B — матрицу-столбец свободных членов:

3	-2	-1
1	3	2
5	4	-3

Вектор B:
B^T=(-5,2,2)
С учетом этих обозначений данная система уравнений принимает следующую матричную форму: А*Х = B.
Если матрица А — невырожденная (ее определитель отличен от нуля, то она имеет обратную матрицу А

-1. Умножив обе части уравнения на А^-1, получим: А^-1*А*Х = А^-1*B, А^-1*А=Е.
Это равенство называется матричной записью решения системы линейных уравнений. Для нахождения решения системы уравнений необходимо вычислить обратную матрицу А^-1.
Система будет иметь решение, если определитель матрицы A отличен от нуля.
Найдем главный определитель.
∆=3•(3•(-3)-4•2)-1•(-2•(-3)-4•(-1))+5•(-2•2-3•(-1))=-66
Итак, определитель -66 ≠ 0, поэтому продолжаем решение. Для этого найдем обратную матрицу через алгебраические дополнения.
Пусть имеем невырожденную матрицу А:

a₁₁	a₁₂	a₁₃
a₂₁	a₂₂	a₂₃
a₃₁	a₃₂	a₃₃

Тогда:

A₁₁	A₂₁	A₃₁
A₁₂	A₂₂	A₃₂
A₁₃	A₂₃	A₃₃

где A_ij — алгебраическое дополнение элемента a_ij в определителе матрицы А, которое является произведением (—1)^i+j на минор (определитель) n-1 порядка, полученный вычеркиванием i-й строки и j-го столбца в определителе матрицы А.
Транспонированная матрица к матрице A имеет вид:

A^T=

3	1	5
-2	3	4
-1	2	-3

Вычисляем алгебраические дополнения.

A^T_1,1=(-1)¹⁺¹

3	4
2	-3

∆_1,1=(3•(-3)-2•4)=-17

A^T_1,2=(-1)¹⁺²

-2	4
-1	-3

∆_1,2=-(-2•(-3)-(-1•4))=-10

A^T_1,3=(-1)¹⁺³

-2	3
-1	2

∆_1,3=(-2•2-(-1•3))=-1

A^T_2,1=(-1)²⁺¹

1	5
2	-3

∆_2,1=-(1•(-3)-2•5)=13

A^T_2,2=(-1)²⁺²

3	5
-1	-3

∆_2,2=(3•(-3)-(-1•5))=-4

A^T_2,3=(-1)²⁺³

3	1
-1	2

∆_2,3=-(3•2-(-1•1))=-7

A^T_3,1=(-1)³⁺¹

1	5
3	4

∆_3,1=(1•4-3•5)=-11

A^T_3,2=(-1)³⁺²

3	5
-2	4

∆_3,2=-(3•4-(-2•5))=-22

A^T_3,3=(-1)³⁺³

3	1
-2	3

∆_3,3=(3•3-(-2•1))=11
Из полученных алгебраических дополнений составим присоединенную матрицу C:

-17	-10	-1
13	-4	-7
-11	-22	11

1 2 3скачати

5.

3: Основы — Математика LibreTexts

Последнее обновление
Сохранить как PDF

Идентификатор страницы: 291

Исайя Ланкхэм, Бруно Нахтергаэле и Энн Шиллинг
Калифорнийский университет, Дэвис

Базой конечномерного векторного пространства является остовный список, который также является линейно независимым. Мы увидим, что все базы конечномерных векторных пространств имеют одинаковую длину. Эта длина будет тогда называться измерением нашего векторного пространства.

Определение 5.3.1. Список векторов \((v_1,\ldots,v_m)\) является базисом для конечномерного векторного пространства \(V\), если \((v_1,\ldots,v_m)\) линейно независим и \(V = \Span(v_1,\ldots,v_m)\). 9m)\) является базисом \(\mathbb{F}_m[z]\).

Теорема 5.3.4. Если \(V=\Span(v_1,\ldots,v_m)\), , то либо \((v_1,\ldots,v_m)\) является основой \(V\) , либо некоторые \(v_i\) могут быть удалены, чтобы получить базис \(V\).

Доказательство. Предположим, что \(V=\Span(v_1,\ldots,v_m)\). Мы начинаем со списка \(\mathcal{S}=(v_1,\ldots,v_m)\) и итеративно проходим по всем векторам \(v_k\) для \(k=1,2,\ldots,m\) до определить, следует ли сохранить или удалить их из \(\mathcal{S}\):

Шаг 1. Если \(v_1=0\), то удалить \(v_1\) из \(\mathcal{S}\). В противном случае оставьте \(\mathcal{S}\) без изменений.

Шаг \(k\). Если \(v_k\in \Span(v_1,\ldots,v_{k-1})\), то удалите \(v_k\) из \(\mathcal{S}\). В противном случае оставьте \(\mathcal{S}\) без изменений.

Окончательный список \(\mathcal{S}\) по-прежнему охватывает \(V\), так как на каждом шаге вектор отбрасывался только в том случае, если он уже находился в диапазоне предыдущих векторов. {3}\), и это в точности тот базис, который получен применением процесса из доказательства теоремы 5.3. .4 (как вы должны быть в состоянии проверить).

Следствие 5.3.6. Каждое конечномерное векторное пространство имеет базис.

Доказательство. По определению конечномерное векторное пространство имеет остовный список. По теореме о редукции базиса 5.3.4 любой остовный список может быть сведен к базису.

Теорема 5.3.7. Каждый линейно независимый список векторов в конечномерном векторном пространстве \(V\) может быть расширен до базиса \(V\).

Доказательство. Предположим, что \(V\) конечномерна и что \((v_1,\ldots,v_m)\) линейно независима.

Так как \(V\) конечномерна, существует список \((w_1,\ldots,w_n)\) векторов, который охватывает \(V\). Мы хотим присоединить некоторые из \(w_k\) к \((v_1,\ldots,v_m)\), чтобы создать основу \(V\).

Шаг 1. Если \(w_1\in \Span(v_1,\ldots,v_m)\), то пусть \(\mathcal{S}=(v_1,\ldots,v_m)\). В противном случае \(\mathcal{S}=(v_1,\ldots,v_m,w_1)\).

Шаг \(k\). Если \(w_k\in\Span(\mathcal{S})\), то оставьте \(\mathcal{S}\) без изменений. В противном случае присоедините \(w_k\) к \(\mathcal{S}\).

После каждого шага список \(\mathcal{S}\) по-прежнему линейно независим, поскольку мы присоединили \(w_k\), только если \(w_k\) не было в промежутке предыдущих векторов. После \(n\) шагов, \(w_k\in \Span(\mathcal{S})\) для всех \(k=1,2,\ldots,n\). Поскольку \((w_1,\ldots,w_n)\) был связующим списком, \(\mathcal{S}\) охватывает \(V\), так что \(\mathcal{S}\) действительно является основой \ (В\). 94\). (На самом деле это даже базис.) Следуя алгоритму, изложенному в доказательстве теоремы о расширении базиса, мы видим, что \(e_1\not\in \Span(v_1,v_2)\). Следовательно, мы присоединяем \(e_1\), чтобы получить \(\mathcal{S}=(v_1,v_2,e_1)\). Обратите внимание, что теперь

\[ e_2=(0,1,0,0) = 1v_1+0v_2+(-1)e_1 \]

, так что \(e_2\in\Span(v_1,v_2,e_1)\), поэтому мы оставляем \(\mathcal{S}\) без изменений. 4\).

Исайя Ланкхэм, математический факультет Калифорнийского университета в Дэвисе
Бруно Нахтергаэле, математический факультет Калифорнийского университета в Дэвисе
Энн Шиллинг, математический факультет Калифорнийского университета в Дэвисе

Версии этого учебника в твердом и мягком переплете доступны онлайн на сайте WorldScientific.com.

Эта страница под названием 5.3: Bases распространяется по недекларированной лицензии, ее авторами, ремиксами и/или кураторами являются Исайя Ланкхэм, Бруно Нахтергаэле и Энн Шиллинг.

Наверх

Была ли эта статья полезной?

Тип изделия
Раздел или Страница
Автор
Исайя Ланкхэм, Бруно Нахтергаэле и Энн Шиллинг
Показать страницу TOC
нет
Теги
1. автортег:шиллинг
2. Основания

Линейные комбинации, SPAN и базисные векторы

Опубликовано 6 августа 2016 г.

Обновлен 20 февраля 2023 г.

Урок от Гранта Сандерсона

Фекторная адаптация по реке

1208.0034

«Математика требует небольшой дозы не гения, а свободы воображения, которая в большей дозе была бы безумием».
\qquad — Ангус К. Роджерс

В последней главе, наряду с идеями сложения векторов и скалярного умножения, я описал векторные координаты, где есть этот переход между парами чисел и двумерными векторами. .

Теперь я полагаю, что векторные координаты уже были знакомы многим из вас, но есть еще один интересный способ думать об этих координатах, который является центральным в линейной алгебре. Когда у вас есть пара чисел, предназначенных для описания вектора, например (3,−2)(3,-2)(3,−2), я хочу, чтобы вы думали о каждой координате как о скаляре, то есть думали о том, как каждая один растягивает или сжимает векторы. 9имеют специальное название: вместе они называются «основой» системы координат.

α=1 β=0,5\alpha=1\ \beta=0,5α=1 β=0,5

α=0,5 β=1,5\alpha=0,5\ \beta=1,5α=0,5 β=1,5

α=−1 β=−1,5\alpha=-1\ \beta=-1,5α=−1 β=−1,5

α=0,5 β=−1,5\alpha=0,5\ \beta=-1,5α=0,5 β =−1,5

У нас есть новая пара базисных векторов v→\overrightarrow{\mathbf{v}}v и w→\overrightarrow{\mathbf{w}}w. Найдите минутку, чтобы подумать обо всех различных векторах, которые вы можете получить, выбрав два скаляра, используя каждый из них для масштабирования одного из векторов, а затем добавляя их. Какие двумерные векторы вы можете получить, изменив свой выбор скаляров? 9.

Я подробнее остановлюсь на этом вопросе в одной из последующих глав, описывая взаимосвязь между различными системами координат, а сейчас я просто хочу, чтобы вы поняли, что любой способ численного описания векторов зависит от вашего выбора базисных векторов.

Линейные комбинации

Каждый раз, когда вы масштабируете два вектора и складываете их таким образом, это называется «линейной комбинацией» этих двух векторов. Откуда здесь слово «линейный»? Какое это имеет отношение к линиям? Что ж, когда вы умножаете скаляр на вектор, изменяется величина этого вектора. Умножение каждого действительного числа на вектор дает бесконечную линию, которая проходит через начало координат и точку, определяемую вектором.

Итак, линейная комбинация двух векторов — это метод объединения этих двух линий. Для большинства пар векторов, если вы позволите обоим скалярам свободно варьироваться и рассмотрите каждый возможный вектор, который вы можете получить, вы сможете достичь каждой возможной точки на плоскости. Каждый двухмерный вектор находится в пределах вашей досягаемости.

Однако, если два исходных вектора совпадут, линии, полученные в результате скалярного умножения, будут одной и той же линией, поэтому сложение их вместе не может дать вектор за пределами этой линии. Есть и третья возможность: оба ваших вектора могут быть вектором 0, и в этом случае вы просто застрянете в начале координат.

Span

Множество всех возможных векторов, которых можно достичь с помощью линейных комбинаций данной пары векторов, называется «span» этих двух векторов. Повторяя то, что мы только что видели в этом жаргоне, диапазон большинства пар 2D-векторов — это все векторы в 2D-пространстве, но когда они выстраиваются в линию, их диапазон — это все векторы, вершина которых находится на определенной линии.

Помните, я говорил, что линейная алгебра вращается вокруг сложения векторов и скалярного умножения? Промежуток двух векторов — это, по сути, способ узнать, какие все возможные векторы вы можете получить, используя эти два, используя только эти фундаментальные операции сложения векторов и скалярного умножения. 92R2

Векторы и точки

Самое время поговорить о том, как люди обычно думают о векторах как о точках. Становится очень скучно думать о целом наборе векторов, лежащих на прямой, и еще более скучно думать обо всех двумерных векторах одновременно, заполняющих плоскость.

Таким образом, когда имеешь дело с подобными наборами векторов, обычно каждый из них представляется точкой в пространстве, точкой на вершине этого вектора. Таким образом, если вы хотите подумать о каждом возможном векторе, вершина которого находится на определенной линии, просто подумайте о самой этой линии.

Аналогичным образом, чтобы представить себе все возможные двумерные векторы, представьте каждый из них как точку, в которой находится его конец. Затем, чтобы думать обо всех них сразу, вы можете просто думать о бесконечном плоском листе, который является двумерным пространством, оставляя стрелки за его пределами.

В общем, если вы думаете о векторе отдельно, думайте о нем как о стрелке, а если вы думаете о наборе, удобно думать о них как о точках.

Пролет в 3D

Идея пролета станет более интересной, если мы начнем думать о векторах в трехмерном пространстве. Например, если вы возьмете два вектора в трехмерном пространстве, которые не указывают в одном и том же направлении, что значит взять их промежуток?

Ну, их диапазон представляет собой набор всех возможных линейных комбинаций этих двух векторов, то есть всех возможных векторов, которые вы получаете, масштабируя каждый из двух, с которых вы начинаете, каким-то образом, а затем складывая их вместе.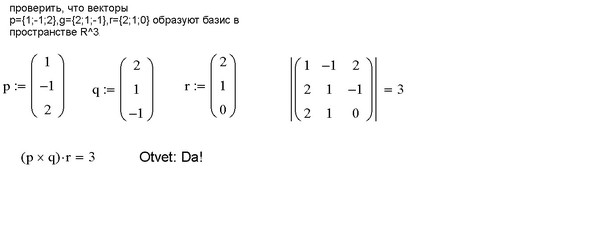 Вы можете представить себе поворот двух ручек для изменения двух скаляров, определяющих линейную комбинацию, добавление масштабированных векторов и отслеживание кончика результирующего вектора. Этот наконечник очерчивает что-то вроде плоского листа, прорезающего начало трехмерного пространства.

x→=av→+bw→\color{green}\overrightarrow{\mathbf{x}} \color{black}= \color{red}a\overrightarrow{\mathbf{v}} \color{black} + \color{purple}b\overrightarrow{\mathbf{w}}x

=av

+bw

Какие векторы в трехмерном пространстве не входят в этот отрезок?

Набор всех возможных векторов, вершины которых лежат на этом плоском листе, является размахом ваших двух векторов. Любой вектор, который не лежит на плоскости, не находится в промежутке.

Итак, что произойдет, если вы добавите третий вектор и учтете диапазон всех трех парней? Линейная комбинация трех векторов определяется почти так же, как и для двух: выберите три скаляра, используйте их для масштабирования каждого из ваших векторов, а затем сложите их все вместе. И снова размах этих векторов есть множество всех возможных линейных комбинаций.

x→=av→+bw→+cu→\color{green}\overrightarrow{\mathbf{x}} \color{black}= \color{red}a\overrightarrow{\mathbf{v}} \color {черный} + \color{purple}b\overrightarrow{\mathbf{w}} \color{black}+ \color{blue}c\overrightarrow{\mathbf{u}}x

=av

+bw

+cu

Могут произойти две вещи. Первая возможность — если ваш третий вектор окажется на промежутке первых двух. Тогда пролет не меняется, вы как бы застряли на том же плоском листе. Другими словами, добавление масштабированной версии третьего вектора к линейным комбинациям первых двух не дает вам доступа к каким-либо новым векторам. Это означает, что третий вектор также может быть выражен как линейная комбинация двух других:

u→=av→+bw→\color{blue}\overrightarrow{\mathbf{u}} \color{black}= \color{red}a\overrightarrow{\mathbf{v}} \color{black} + \color{purple}b\overrightarrow{\mathbf{w}}u

=av

+bw

Хотя есть и другая возможность, если вы просто случайным образом выберете третий вектор, это почти наверняка будет , а не . размах первого. Поскольку тогда он указывает в другом направлении, он открывает доступ ко всем возможным трехмерным векторам! Мне нравится думать об этом так: когда вы масштабируете новый третий вектор, он перемещается по промежутку первых двух, охватывая все пространство.

Это похоже на то, как если бы вы в полной мере использовали три свободно меняющихся скаляра, которые есть в вашем распоряжении, чтобы получить доступ ко всем трем измерениям пространства.

В случае, когда третий вектор находился на отрезке первых двух, или в случае, когда два вектора выстраиваются в линию, мы хотим, чтобы некоторая терминология описывала тот факт, что по крайней мере один из этих векторов является избыточным, а не добавляла что-нибудь к нашему промежутку. Всякий раз, когда это происходит, когда у вас есть несколько векторов, и вы можете удалить один из них, не уменьшая их диапазон, соответствующая терминология состоит в том, чтобы сказать, что они «линейно зависимы».

Другими словами, можно сказать, что один из векторов может быть выражен как линейная комбинация других. То есть он уже находится в пролете двух других. С другой стороны, если каждый вектор действительно добавляет еще одно измерение к промежутку, говорят, что они «линейно независимы».

Линейно зависимые: u→=av→+bw→ для некоторых a и bЛинейно независимые: u→≠av→+bw→ для всех a и b\begin{align*} \text{Линейно зависимые: }\quad \color {синий}\overrightarrow{\mathbf{u}} \color{black}&= \color{red}a\overrightarrow{\mathbf{v}} \color{black}+ \color{purple}b\overrightarrow{\ mathbf{w}} \quad\color{black}\text{ для некоторых }\color{red}a\color{black}\text{ и }\color{purple}b \\ \text{Линейно независимые: }\ quad \ color {синий} \ overrightarrow {\ mathbf {u}} \ color {black} & \ neq \ color {red} a \ overrightarrow {\ mathbf {v}} \ color {black} + \ color {purple} b \overrightarrow{\mathbf{w}} \quad\color{black}\text{для всех}\color{red}a\color{black}\text{и}\color{purple}b \end{align*} Линейно зависимый: u

Линейно-независимые: u

=av

+bw

для некоторых a и b=av

+bw

для всех a и b технического определения

90 пространство — это набор линейно независимых векторов, которые охватывают это пространство, учитывая то, как я описал базис ранее, и учитывая ваше понимание слов «промежуток» и «линейно независимый», почему это определение имеет смысл?

Ранее мы узнали, что любая пара векторов может образовать новый базис, если они не выстраиваются в линию.

Линейные операции над векторами. Линейная зависимость и независимость системы векторов. Базис

Задача 33 Даны векторы a 1 (1;3;5), a 2 (-2;-1;-1), a 3 (4;-2;4), b(-7;3;-1)

5.

Линейные комбинации, SPAN и базисные векторы

Линейные комбинации

Span

Векторы и точки

Пролет в 3D

Добавить комментарий Отменить ответ