Как решать модуль: Модуль — Умскул Учебник

Уравнения с модулем — презентация онлайн

Цель: повторить , обобщить и
систематизировать знания учащихся о
модуле и его свойствах, умения решать
различные уравнения , содержащие
модуль.

2. Определение модуля

а, если а 0,
а
а, если а 0.
ab a b
x
x
, y 0.
y
y
x x
2
2
x2 x
x y x
2
y
log a x 2 2 log a x

3. Геометрический смысл модуля

Геометрически x есть расстояние
от точки х числовой оси до начала
отсчёта – точки О.
x
x
0
x 0
x
x a
есть расстояние между
точками х и а числовой оси.
x
x
0
x a
x
0
a
x
a x 0
1.Простейшее уравнение,
содержащее модуль, где b>0:
f ( x) b,
f ( x) b
f ( x) b.
2.Уравнение более общего вида,
содержащее модуль:
g ( x) 0,
f ( x) g ( x) f ( x) g ( x),
f ( x) g ( x).

5. Простейшие уравнения вида ,b>0.

Простейшие уравнения вида f ( x) b ,b>0.
1.
По определению модуля
2 x 3 5,
2 x 8,
x 4,
2x 3 5
2 x 3 5 2 x 2 x 1.
Ответ : 1;4

6. Уравнения более общего вида

f ( x) g ( x)
Условие
g ( x) 0
2 x 0,
x 2,
x 2,
x 2,
3. x 4 3(2 x) x 4 3(2 x), x 4 6 3x, 4 x 2, x 0,5, x 0,5.
x 4 3(2 x) x 4 6 3x 2 x 10 x 5
Ответ : 0,5.

7. Уравнения вида

f ( x) g ( x) .
уравнение
f ( x) g ( x) 0, f ( x) g ( x),
f ( x) g ( x) f ( x) g ( x) ( f ( x) g ( x))( f ( x) g ( x)) 0
f ( x) g ( x) 0. f ( x) g ( x).
2
2
4
x ,
6 x 5 7 3 x ,
9 x 12,
3
12. 6 x 5 7 3 x
6 x 5 (7 3 x) 3 x 2
x 2 .
3
2 1
Ответ : ,1 .
3 3

8. Уравнения, приводимые к уравнениям, содержащим модуль.

Иррациональное уравнение
2 x 5 3x 10,
8. 4 x 20 x 25 3x 10 (2 x 5) 3x 10
3x 10 0
2
2
x 3,
2 x 5 3x 10, 5 x 15,
x 5,
2 x 5 3x 10, x 5,
x 5.
1
3x 10 0
3x 10
x
3
3
Ответ : 5.

9. Уравнения, приводимые к уравнениям, содержащим модуль.

f ( x) b f ( x) b
2
log a f ( x) b 2 log a f ( x) b
2

10. Уравнения, приводимые к уравнениям, содержащим модуль

Логарифмическое уравнение
x 27,
9. log 3 x 6 2 log 3 x 6 log 3 x 3 x 27
x 27.
Ответ : 27;27.
2

11. Иррациональные уравнения, содержащие модуль.

В силу того, что
однозначно
.
x 2,5 модуль x 4
раскрывается
2
2
5
9
x
x
4
4
x
2
0
x
2
5
,
2
5
9
x
x
4
5
2
x
2
5
9
x
x
4
2
x
5
2
x
5
0
;
x
0
,
2
2 2
2
9
x
x
4
4
x
2
0
x
,
9
x
3
6
x
4
x
2
0
x
0
,
5
x
1
6
x
0
,
1
x
0
.
x
3
,
x
2
,
5
;
x
2
,
5
;
5
x
2
,
5
;
x
2
,
5
;

12.

Замена модуля.x 2 1 t,
x2 1 t,
2
( x 2 1) 2 7 x 2 1 18 0 x 2 1 7 x 2 1 18 0 t 0,
t 0,
t 2 7t 18 0 t 9,
t 2
2
2
x 10,
x
1
9
,
x
10,
2
2
x 1 9 2
2
x 10
x 1 9 x 8
x 10.
Îòâåò : 10 ; 10.
Уравнения, содержащие несколько модулей
и те, которые не сводятся к виду │f(x) │= g(x) решаются
с помощью метода интервалов:
1.Найдём значения x, при которых значение выражений,
стоящих под знаком модуля, равны нулю.
2.Найденные значения x разбивают ОДЗ на промежутки.
3.Запишем на каждом из промежутков уравнение без
знаков модуля. Получим совокупность систем.

14. Уравнения, содержащие несколько модулей. ( Решаемые с помощью метода интервалов)

10. x 1 x 2 x 3
1.Найдём значения х, при которых значения
выражений, стоящих под знаком модуля, равны 0:
х -1 = 0 при х = 1.
х – 2=0 при х = 2.
2. Эти значения разбивают ОДЗ на промежутки:
( ;1), 1;2 , (2; ).
3.Запишем на каждом из промежутков данное
уравнение без знаков модуля.
Получим совокупность систем.

15. Уравнение, содержащее несколько модулей.

Метод интервалов
x 1,
x 1,
x 1,
(
x
1
)
(
x
2
)
x
3
,
x
1
x
2
x
3
,
3x 0,
1 x 2,
1 x 2,
1 x 2, x 0,
x 1 x 2 x 3
( x 1) ( x 2) x 3,
x 1 x 2 x 3,
x 2,
x 6.
x
2
,
x
2
,
x 2,
( x 1) ( x 2) x 3
x 1 x 2 x 3
x 6
Îòâåò : 0;6.

16. Домашнее задание: Решите уравнения

1. 2 x 3 5
2. 1
x 3
5
4
3. x 4 3( 2 x )
4. 8 5 x 2
5. 36 5 x x 3 6 x
6.( x 2 1) 7 x 2 1 18 0
7. x 2 x 3 5
8. 4 x 2 20 x 25 3 x 10
9.9 log 3 x 2 6
10. x 1 x 2 x 3
11. log 22 ( x ) 3 log 2 x 2 5 0
12. 6 x 5 7 3 x
13. 8 x 1 4 x `13
14. 25 9 x x 4 5 2 x

Как решать показательные уравнения с модулем. Методическая разработка «Уравнения с модулем

Главная » Карьера и Работа » Как решать показательные уравнения с модулем. Методическая разработка «Уравнения с модулем

Решение уравнений и неравенств с модулем часто вызывает затруднения. Однако, если хорошо понимать, что такое модуль числа , и как правильно раскрывать выражения, содержащие знак модуля , то наличие в уравнении выражения, стоящего под знаком модуля , перестает быть препятствием для его решения.

Немного теории. Каждое число имеет две характеристики: абсолютное значение числа, и его знак.

Например, число +5, или просто 5 имеет знак «+» и абсолютное значение 5.

Число -5 имеет знак «-» и абсолютное значение 5.

Абсолютные значения чисел 5 и -5 равны 5.

Абсолютное значение числа х называется модулем числа и обозначается |x|.

Как мы видим, модуль числа равен самому числу, если это число больше или равно нуля, и этому числу с противоположным знаком, если это число отрицательно.

Это же касается любых выражений, которые стоят под знаком модуля.

Правило раскрытия модуля выглядит так:

|f(x)|= f(x), если f(x) ≥ 0, и

|f(x)|= — f(x), если f(x)

Например |x-3|=x-3, если x-3≥0 и |x-3|=-(x-3)=3-x, если x-3

Чтобы решить уравнение, содержащее выражение, стоящее под знаком модуля, нужно сначала раскрыть модуль по правилу раскрытия модуля .

Тогда наше уравнение или неравенство преобразуется в два различных уравнения, существующих на двух различных числовых промежутках.

Одно уравнение существует на числовом промежутке, на котором выражение, стоящее под знаком модуля неотрицательно.

А второе уравнение существует на промежутке, на котором выражение, стоящее под знаком модуля отрицательно.

Рассмотрим простой пример.

Решим уравнение:

|x-3|=-x 2 +4x-3

1. Раскроем модуль.

|x-3|=x-3, если x-3≥0, т.е. если х≥3

|x-3|=-(x-3)=3-x, если x-3

2. Мы получили два числовых промежутка: х≥3 и х

Рассмотрим, в какие уравнения преобразуется исходное уравнение на каждом промежутке:

А) При х≥3 |x-3|=x-3, и наше уранение имеет вид:

Внимание! Это уравнение существует только на промежутке х≥3!

Раскроем скобки, приведем подобные члены:

и решим это уравнение.

Это уравнение имеет корни:

х 1 =0, х 2 =3

Внимание! поскольку уравнение x-3=-x 2 +4x-3 существует только на промежутке х≥3, нас интересуют только те корни, которые принадлежат этому промежутку. Этому условию удовлетворяет только х 2 =3.

Б) При x

Внимание! Это уравнение существует только на промежутке х

Раскроем скобки, приведем подобные члены. Получим уравнение:

х 1 =2, х 2 =3

Внимание! поскольку уравнение 3-х=-x 2 +4x-3 существует только на промежутке x

Итак: из первого промежутка мы берем только корень х=3, из второго — корень х=2.

МБОУ СОШ №17 г. Иванова

«Уравнения с модулем»
Методическая разработка

Составлена

учителем математики

Лебедевой Н.В.

20010 г.

Пояснительная записка

Глава 1. Введение

Раздел 2. Основные свойства Раздел 3. Геометрическая интерпретация понятия модуля числа Раздел 4.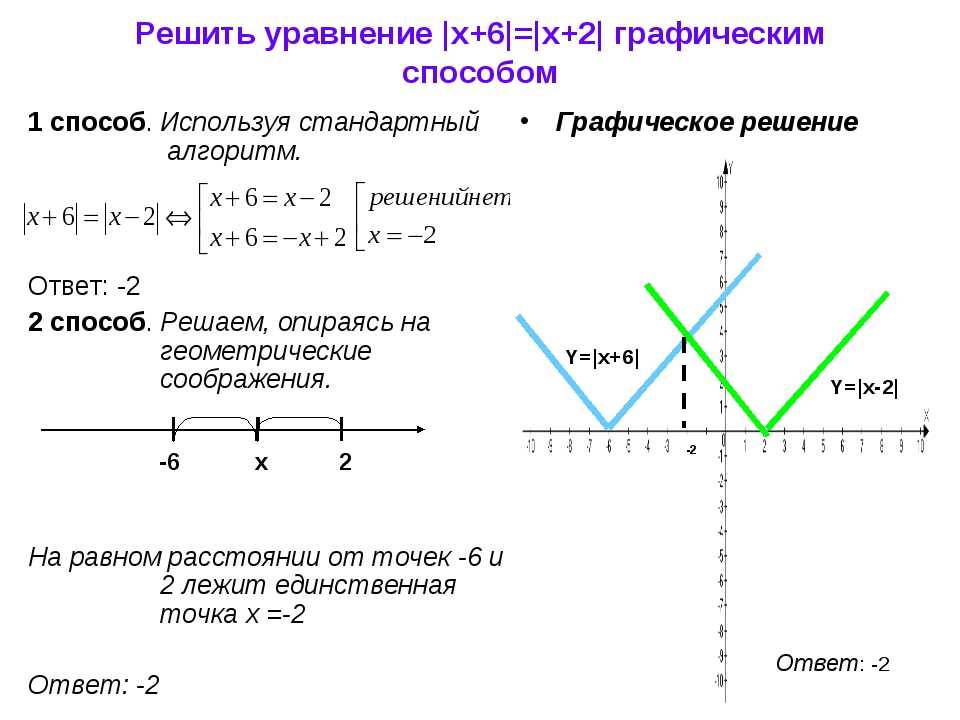 График функции у = |х| Раздел 5. Условные обозначения

Глава 2. Решение уравнений, содержащих модуль

Раздел 1.Уравнения вида |F(х)| = m (простейшие) Раздел 2. Уравнения вида F(|х|) = m Раздел 3. Уравнения вида |F(х)| = G(х) Раздел 4. Уравнения вида |F(х)| = ± F(х) (красивейшие) Раздел 5. Уравнения вида |F(х)| = |G(х)| Раздел 6. Примеры решения нестандартных уравнений Раздел 7. Уравнения вида |F(х)| + |G(х)| = 0 Раздел 8. Уравнения вида |а 1 х ± в 1 | ± |а 2 х ± в 2 | ± …|а n х ± в n | = m Раздел 9. Уравнения, содержащие несколько модулей

Глава 3. Примеры решения различных уравнений с модулем.

Раздел 1. Тригонометрические уравнения Раздел 2. Показательные уравнения Раздел 3. Логарифмические уравнения Раздел 4. Иррациональные уравнения Раздел 5. Задания повышенной сложности Ответы к упражнениям Список литературы

Понятие абсолютной величины (модуля) действительного числа является одной из существенных его характеристик.

Это понятие имеет широкое распространение в различных разделах физико-математических и технических наук. В практике преподавания курса математики в средней школе в соответствии с Программой МО РФ понятие «абсолютная величина числа» встречается неоднократно: в 6 – м классе вводиться определение модуля, его геометрический смысл; в 8 – м классе формируется понятие абсолютной погрешности, рассматривается решение простейших уравнений и неравенств, содержащих модуль, изучаются свойства арифметического квадратного корня; в 11 – м классе понятие встречается в разделе «Корень n -ой степени». Опыт преподавания показывает, что учащиеся часто сталкиваются с трудностями при решении заданий, требующих знания данного материала, а нередко пропускают, не приступая к выполнению. В текстах экзаменационных заданий за курс 9 – ого и 11 – ого классов также включены подобные задания. Кроме того, требования, которые предъявляют к выпускникам школ Вузы отличаются, а именно, более высокого уровня, чем требования школьной программы. Для жизни в современном обществе очень важным является формирование математического стиля мышления, проявляющегося в определённых умственных навыках. В процессе решения задач с модулями требуется умение применять такие приёмы, как обобщение и конкретизация, анализ, классификация и систематизация, аналогия. Решение подобных заданий позволяет проверить знание основных разделов школьного курса, уровень логического мышления, первоначальные навыки исследовательской деятельности. Данная работа посвящена одному из разделов – решению уравнений, содержащих модуль. Она состоит из трёх глав. В первой главе вводятся основные понятия и наиболее важные теоретические выкладки. Во второй главе предлагаются девять основных типов уравнений, содержащих модуль, рассматриваются методы их решения, разбираются примеры разного уровня сложности. В третьей главе предлагаются более сложные и нестандартные уравнения (тригонометрические, показательные, логарифмические и иррациональные). К каждому типу уравнений есть упражнения для самостоятельного решения (ответы и указания прилагаются). Основное назначение данной работы – это оказание методической помощи преподавателям при подготовке к урокам и при организации факультативных курсов. Материал также может быть использован в качестве учебного пособия для старшеклассников. Задания, предлагаемые в работе, интересны и не всегда просты в решении, что позволяет сделать учебную мотивацию учащихся более осознанной, проверить свои способности, повысить уровень подготовки выпускников школ к поступлению в Вузы. Дифференцированный подбор предлагаемых упражнений предполагает переход от репродуктивного уровня усвоения материала к творческому, а также возможность научить применять свои знания при решении нестандартных задач.

Определение

: Абсолютной величиной (модулем) действительного числа а называется неотрицательное число: а или –а.

Обозначение:

│ а │ Запись читается следующим образом: «модуль числа а» или «абсолютная величина числа а»

│ а, если а > 0

│а│ = │ 0, если а = 0 (1)

│ — а, если а
Примеры: 1) │2,5│ = 2,5 2) │-7│ = 7 3) │1 — √2│ = √2 – 1

Раскрыть модуль выражения:

а) │х — 8│, если х > 12 б) │2х + 3│, если х ≤ -2 │х – 8│= х – 8 │ 2х + 3│= — 2х – 3

Раздел 2.

Основные свойства. Рассмотрим основные свойства абсолютной величины. Свойство №1: Противоположные числа имеют равные модули, т.е. │а│=│- а│ Покажем верность равенства. Запишем определение числа – а : │— а│ = (2) Сравним совокупности (1) и (2). Очевидно, что определения абсолютных величин чисел а и – а совпадают. Следовательно, │а│=│- а│
При рассмотрении следующих свойств ограничимся их формулировкой, так как их доказательство приводится в Свойство №2: Абсолютная величина суммы конечного числа действительных чисел не превосходит суммы абсолютных величин слагаемых: │а 1 + а 2 +…+ а n │ ≤│а 1 │+│а 2 │+ … + │а n │ Свойство №3: Абсолютная величина разности двух действительных чисел не превосходит суммы их абсолютных величин: │а — в│ ≤│а│+│в│ Свойство №4: Абсолютная величина произведения конечного числа действительных чисел равна произведению абсолютных величин множителей: │а · в│=│а│·│в│ Свойство №5: Абсолютная величина частного действительных чисел равна частному их абсолютных величин:

Раздел 3.

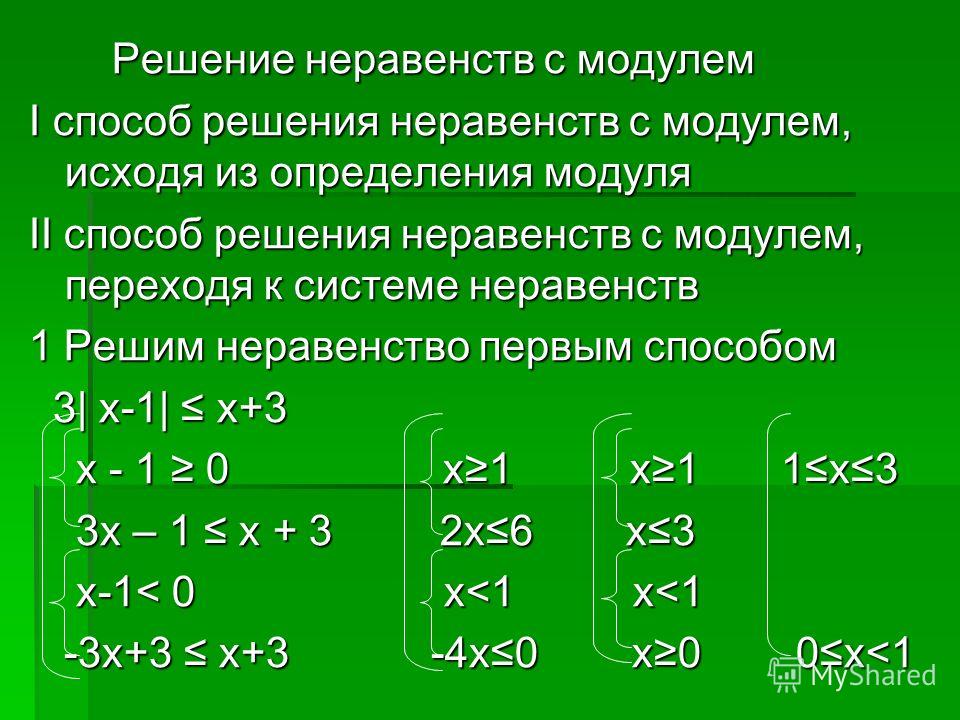Геометрическая интерпретация понятия модуля числа.

Каждому действительному числу можно поставить в соответствие точку на числовой прямой, которая будет геометрическим изображением данного действительного числа. Каждой точке на числовой прямой соответствует её расстояние от начала отсчёта, т.е. длина отрезка от начала отсчёта до данной точки. Это расстояние рассматривается всегда как величина неотрицательная. Поэтому длина соответствующего отрезка и будет геометрической интерпретацией абсолютной величины данного действительного числа

Представленная геометрическая иллюстрация наглядно подтверждает свойство №1, т.е. модули противоположных чисел равны. Отсюда легко понимается справедливость равенства: │х – а│= │а — х│. Также более очевидным становиться решение уравнения │х│= m, где m ≥ 0, а именно х 1,2 = ± m.

Примеры:

1) │х│= 4 х 1,2 = ± 4 2) │х — 3│= 1
х 1,2 = 2; 4

Раздел 4.

График функции у = │х│

Область определения данной функции все действительные числа.

Раздел 5. Условные обозначения.

В дальнейшем при рассмотрении примеров решения уравнений будут использованы следующие условные обозначения:

{ — знак системы [ — знак совокупности При решение системы уравнений (неравенств) находится пересечение решений входящих в систему уравнений (неравенств). При решении совокупности уравнений (неравенств) находится объединение решений входящих в совокупность уравнений (неравенств).

В этой главе мы рассмотрим алгебраические способы решения уравнений, содержащих один или более модуль.

Раздел 1. Уравнения вида │F (х)│= m

Уравнение данного вида называется простейшим. Оно имеет решение тогда и только тогда, когда m ≥ 0. По определению модуля, исходное уравнение равносильно совокупности двух уравнений: │F (х)│= m

Примеры:
№1.

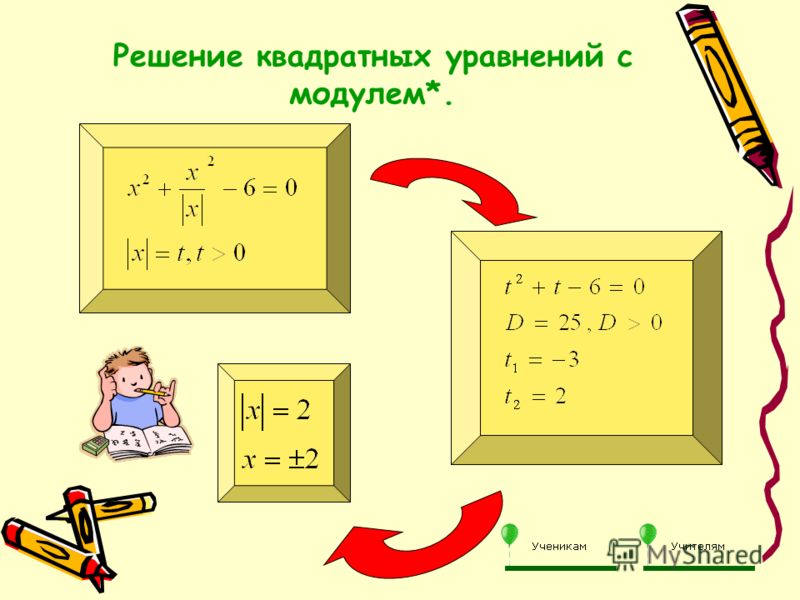
Решите уравнение: │7х — 2│= 9


Ответ: х 1 = — 1; х 2 = 1 4 / 7

№2

│х 2 + 3х + 1│= 1

х 2 + 3х + 2 = 0 х 2 +3х = 0 х 1 = -1; х 2 = -2 х · (х + 3) = 0 х 1 = 0; х 2 = -3 Ответ: сумма корней равна — 2 .

№3

│х 4 -5х 2 + 2│= 2 х 4 – 5х 2 = 0 х 4 – 5х 2 + 4 = 0 х 2 · (х 2 – 5) = 0 обозначим х 2 = m, m ≥ 0 х = 0; ±√5 m 2 – 5m + 4 = 0 m = 1; 4 – оба значения удовлетворяют условию m ≥ 0 х 2 = 1 х 2 = 4 х = ± 1 х = ± 2 Ответ: количество корней уравнения 7. Упражнения:

№1.

Решите уравнение и укажите сумму корней: │х — 5│= 3

№2

. Решите уравнение и укажите меньший корень: │х 2 + х│= 0

№3

. Решите уравнение и укажите больший корень: │х 2 – 5х + 4│= 4

№4

.Решите уравнение и укажите целый корень: │2х 2 – 7х + 6│= 1

№5

.Решите уравнение и укажите количество корней: │х 4 – 13х 2 + 50│= 14

Раздел 2. Уравнения вида F(│х│) = m

Аргумент функции в левой части находится под знаком модуля, а правая часть не зависит от переменной. Рассмотрим два способа решения уравнений данного вида.

1 способ:

По определению абсолютной величины исходное уравнение равносильно совокупности двух систем. В каждой из которых накладывается условие на подмодульное выражение. F (│х│) = m
Так как функция F(│х│) – чётная на всей области определения, то корни уравнений F(х) = m и F(- х) = m – это пары противоположных чисел. Поэтому достаточно решить одну из систем (при рассмотрении примеров указанным способом будет приводиться решение одной системы).

2 способ:

Применение метода введения новой переменной. При этом вводиться обозначение │х│= а, где а ≥ 0. Данный способ менее объёмный по оформлению.

Примеры: №1

. Решите уравнение: 3х 2 – 4│х│= — 1 Воспользуемся введением новой переменной. Обозначим │х│= а, где а ≥ 0. Получим уравнение 3а 2 — 4а + 1 = 0 Д = 16 – 12 = 4 а 1 = 1 а 2 = 1 / 3 Возвращаемся к исходной переменной: │х│=1 и │х│= 1 / 3 . Каждое уравнение имеет два корня. Ответ: х 1 = 1; х 2 = — 1; х 3 = 1 / 3 ; х 4 = — 1 / 3 .

№2.

Решите уравнение: 5х 2 + 3│х│- 1 = 1 / 2 │х│ + 3х 2
Найдём решение первой системы совокупности: 4х 2 + 5х – 2 =0 Д = 57 х 1 = -5+√57 / 8 х 2 = -5-√57 / 8 Заметим, что х 2 не удовлетворяет условию х ≥ 0. Решением второй системы будет число, противоположное значению х 1 . Ответ: х 1 = -5+√57 / 8 ; х 2 = 5-√57 / 8 .

№3 .

Решите уравнение: х 4 – │х│= 0 Обозначим │х│= а, где а ≥ 0. Получим уравнение а 4 – а = 0 а · (а 3 – 1) = 0 а 1 = 0 а 2 = 1 Возвращаемся к исходной переменной: │х│=0 и │х│= 1 х = 0; ± 1 Ответ: х 1 = 0; х 2 = 1; х 3 = — 1.
Упражнения:

№6.

Решите уравнение: 2│х│ — 4,5 = 5 – 3 / 8 │х│

№7

. Решите уравнение, в ответе укажите количество корней: 3х 2 — 7│х│ + 2 = 0

№8

. Решите уравнение, в ответе укажите целые решения: х 4 + │х│ — 2 = 0

Раздел 3. Уравнения вида │F(х)│ = G(х)

Правая часть уравнения данного вида зависит от переменной и, следовательно, имеет решение тогда и только тогда, когда правая часть функция G(х) ≥ 0. Исходное уравнение можно решить двумя способами:

1 способ:

Стандартный, основан на раскрытии модуля исходя из его определения и заключается в равносильном переходе к совокупности двух систем. │F (х)│ = G (х)

Данный способ рационально использовать в случае сложного выражения для функции G(x) и мене сложного – для функции F(х), так как предполагается решение неравенств с функцией F(х).

2 способ:

Состоит в переходе к равносильной системе, в которой накладывается условие на правую часть. │F (x )│= G (x )

Данный способ удобнее применять, если выражение для функции G(х) мене сложное, чем для функции F(х), так как предполагается решение неравенства G(х) ≥ 0. Кроме того, в случае нескольких модулей этот способ рекомендуется применять второй вариант.

Примеры: №1.

Решите уравнение: │х + 2│= 6 -2х
(1 способ) Ответ: х = 1 1 / 3

№2.

│х 2 – 2х — 1│= 2·(х + 1)
(2 способ) Ответ: Произведение корней – 3.

№3.

Решите уравнение,в ответе укажите сумму корней:
│х — 6│= х 2 — 5х + 9

Ответ: сумма корней равна 4.
Упражнения:

№9.

│х + 4│= — 3х

№10.

Решите уравнение, в ответе укажите число решений:│х 2 + х — 1│= 2х – 1

№11

. Решите уравнение, в ответе укажите произведение корней:│х + 3│= х 2 + х – 6

Раздел 4. Уравнения вида │F(x)│= F(x) и │F(x)│= — F(x)

Уравнения данного вида иногда называют «красивейшими». Так как правая часть уравнений зависит от переменной, решения существуют тогда и только тогда, когда правая часть неотрицательна. Поэтому исходные уравнения равносильны неравенствам:
│F(x)│= F(x) F(x) ≥ 0 и │F(x)│= — F(x) F(x)

Примеры: №1

. Решите уравнение, в ответе укажите меньший целый корень: │5х — 3│= 5х – 3 5х – 3 ≥ 0 5х ≥ 3 х ≥ 0,6 Ответ: х = 1

№2.

Решите уравнение, в ответе укажите длину промежутка: │х 2 — 9│= 9 – х 2 х 2 – 9 ≤ 0 (х – 3) (х + 3) ≤ 0 [- 3; 3] Ответ: длина промежутка равна 6.

№3

. Решите уравнение, в ответе укажите число целых решений: │2 + х – х 2 │= 2 + х – х 2 2 + х – х 2 ≥ 0 х 2 – х – 2 ≤ 0 [- 1; 2] Ответ: 4 целых решения.

№4

. Решите уравнение, в ответе укажите наибольший корень:
│4 – х —
│= 4 – х –
х 2 – 5х + 5 = 0 Д = 5 х 1,2 =
≈ 1,4

Ответ: х = 3.

Упражнения: №12. Решите уравнение, в ответе укажите целый корень: │х 2 + 6х + 8│= х 2 + 6х + 8№13. Решите уравнение, в ответе укажите число целых решений: │13х – х 2 — 36│+ х 2 – 13х + 36 = 0№14. Решите уравнение, в ответе укажите целое число, не являющееся корнем уравнения:

Раздел 5. Уравнения вида │F(x)│= │G(x)│

Так как обе части уравнения неотрицательные, то решение предполагает рассмотрение двух случаев: подмодульные выражения равны или противоположны по знаку. Следовательно, исходное уравнение равносильно совокупности двух уравнений: │F (x )│= │ G (x )│
Примеры:

№1.

Решите уравнение, в ответе укажите целый корень: │х + 3│=│2х — 1│
Ответ: целый корень х = 4.

№2.

Решите уравнение: │ х – х 2 — 1│=│2х – 3 – х 2 │
Ответ: х = 2.

№3

. Решите уравнение, в ответе укажите произведение корней:

Корниуравнения 4х 2 + 2х – 1 = 0 х 1,2 = — 1±√5 / 4 Ответ: произведение корней равно – 0,25. Упражнения: №15 . Решите уравнение, в ответе укажите целое решение:│х 2 – 3х + 2│= │х 2 + 6х — 1│ №16. Решите уравнение, в ответе укажите меньший корень:│5х — 3│=│7 — х│ №17 . Решите уравнение, в ответе укажите сумму корней:

Раздел 6. Примеры решения нестандартных уравнений

В данном разделе мы рассмотрим примеры нестандартных уравнений, при решении которых абсолютная величина выражения раскрывается по определению.

Примеры:

№1. Решите уравнение, в ответе укажите сумму корней: х · │х│- 5х – 6 = 0
Ответ: сумма корней равна 1 №2. . Решите уравнение, в ответе укажите меньший корень: х 2 — 4х ·
— 5 = 0
Ответ: меньший корень х = — 5. №3. Решите уравнение:

Ответ: х = -1. Упражнения: №18. Решите уравнение и укажите сумму корней: х · │3х + 5│= 3х 2 + 4х + 3
№19. Решите уравнение: х 2 – 3х =

№20. Решите уравнение:

Раздел 7. Уравнения вида │F(x)│+│G(x)│=0

Нетрудно заметить, что в левой части уравнения данного вида сумма неотрицательных величин. Следовательно, исходное уравнение имеет решение тогда и только тогда, когда оба слагаемых одновременно равны нулю. Уравнение равносильно системе уравнений: │F (x )│+│ G (x )│=0

Примеры: №1

. Решите уравнение:
Ответ: х = 2.

№2.

Решите уравнение: Ответ: х = 1.

Упражнения: №21.

Решите уравнение:

№22

. Решите уравнение, в ответе укажите сумму корней:

№23

. Решите уравнение, в ответе укажите количество решений:

Раздел 8. Уравнения вида │а 1 х + в 1 │±│а 2 х + в 2 │± … │а n х +в n │= m

Для решения уравнений данного вида применяется метод интервалов. Если его решать последовательным раскрытием модулей, то получим n совокупностей систем, что очень громоздко и неудобно. Рассмотрим алгоритм метода интервалов: 1). Найти значения переменной х , при которых каждый модуль равен нулю (нули подмодульных выражений):
2). Найденные значения отметить на числовой прямой, которая разбивается на интервалы (количество интервалов соответственно равно n +1 ) 3). Определить, с каким знаком раскрывается каждый модуль на каждом из полученных интервалов (при оформлении решения можно использовать числовую прямую, отметив на ней знаки) 4). Исходное уравнение равносильно совокупности n +1 систем, в каждой из которых указывается принадлежность переменной х одному из интервалов. Примеры:

№1

. Решите уравнение, в ответе укажите наибольший корень:
1). Найдём нули подмодульных выражений: х = 2; х = -3 2). Отметим найденные значения на числовой прямой и определим, с каким знаком раскрывается каждый модуль на полученных интервалах:
х – 2 х – 2 х – 2 — — + — 3 2 х 2х + 6 2х + 6 2х + 6 — + + 3)
— нет решений Уравнение имеет два корня. Ответ: наибольший корень х = 2.

№2.

Решите уравнение, в ответе укажите целый корень:
1). Найдём нули подмодульных выражений: х = 1,5; х = — 1 2). Отметим найденные значения на числовой прямой и определим, с каким знаком раскрывается каждый модуль на полученных интервалах: х + 1 х + 1 х + 1 — + +
-1 1,5 х 2х – 3 2х – 3 2х – 3 — — +
3).
Последняя система не имеет решений, следовательно, уравнение имеет два корня. В ходе решения уравнения следует обратить внимание на знак « — » перед вторым модулем. Ответ: целый корень х = 7.

№3.

Решите уравнение, в ответе укажите сумму корней: 1). Найдём нули подмодульных выражений: х = 5; х = 1; х = — 2 2). Отметим найденные значения на числовой прямой и определим, с каким знаком раскрывается каждый модуль на полученных интервалах: х – 5 х – 5 х – 5 х – 5 — — — +
-2 1 5 х х – 1 х – 1 х – 1 х – 1 — — + + х + 2 х + 2 х + 2 х + 2 — + + +
3).
Уравнение имеет два корня х = 0 и 2. Ответ: сумма корней равна 2.

№4

. Решите уравнение: 1). Найдём нули подмодульных выражений: х = 1; х = 2; х = 3. 2). Определим, с каким знаком раскрывается каждый модуль на полученных интервалах. 3).
Объединим решения первых трёх систем. Ответ: ; х = 5.
Упражнения:

№24.

Решите уравнение:

№25.

Решите уравнение, в ответе укажите сумму корней:

№26.

Решите уравнение, в ответе укажите меньший корень:

№27.

Решите уравнение, в ответе укажите больший корень:

Раздел 9. Уравнения, содержащие несколько модулей

Уравнения, содержащие несколько модулей, предполагают наличие абсолютных величин в подмодульных выражениях. Основной принцип решения уравнений данного вида – это последовательное раскрытие модулей, начиная с «внешнего». В ходе решения используются приёмы, рассмотренные в разделах №1, №3.

Примеры: №1. Решите уравнение:
Ответ: х = 1; — 11. №2. Решите уравнение:
Ответ: х = 0; 4; — 4. №3. Решите уравнение, в ответе укажите произведение корней:
Ответ: произведение корней равно – 8. №4. Решите уравнение:
Обозначим уравнения совокупности (1) и (2) и рассмотрим решение каждого из них отдельно для удобства оформления. Так как оба уравнения содержат более одного модуля, то удобнее осуществить равносильный переход к совокупностям систем.(1)

(2)


Ответ:
Упражнения: №36. Решите уравнение, в ответе укажите сумму корней: 5 │3х-5│ = 25 х №37. Решите уравнение, если корней более одного, в ответе укажите сумму корней: │х + 2│ х – 3х – 10 = 1 №38. Решите уравнение: 3 │2х -4│ = 9 │х│ №39. Решите уравнение, в ответе укажите количество корней на : 2 │ sin х│ = √2 №40 . Решите уравнение, в ответе укажите количество корней:

Раздел 3. Логарифмические уравнения.

Перед решением следующих уравнений необходимо повторить свойства логарифмов и логарифмической функции.

Примеры: №1.

Решите уравнение, в ответе укажите произведение корней: log 2 (х+1) 2 + log 2 │x+1│ = 6 О. Д.З. х+1≠0 х≠ — 1

1 случай: если х ≥ — 1, то log 2 (x+1) 2 + log 2 (x+1) = 6 log 2 (x+1) 3 = log 2 2 6 (x+1) 3 = 2 6 x+1 = 4 x = 3 – удовлетворяет условию х ≥ — 1 2 случай: если х log 2 (x+1) 2 + log 2 (-x-1) = 6 log 2 (x+1) 2 + log 2 (-(x+1)) = 6 log 2 (-(x+1) 3) = log 2 2 6- (x+1) 3 = 2 6- (x+1) = 4 x = — 5 – удовлетворяет условию х — 1
Ответ: произведение корней равно – 15.
№2. Решите уравнение, в ответе укажите сумму корней: lg
О.Д.З.

Ответ: сумма корней равна 0,5.
№3. Решите уравнение: log 5
О.Д.З.

Ответ: х = 9. №4. Решите уравнение: │2 + log 0,2 x│+ 3 = │1 + log 5 x│ О.Д.З. х > 0 Воспользуемся формулой перехода к другому основанию. │2 — log 5 x│+ 3 = │1 + log 5 x│
│2 — log 5 x│- │1 + log 5 x│= — 3 Найдём нули подмодульных выражений: х = 25; х = Эти числа делят область допустимых значений на три интервала, поэтому уравнение равносильно совокупности трёх систем.
Ответ: }

Модуль не назван в Python

ModuleNotFoundError: Модуль не назван в Python, когда:

• Неверное имя модуля
• Неверный путь к модулю
• Библиотека не установлена ​​
• Модуль не поддерживается
• Python 2 вместо Python 3

В этой статье мы обсудим причины и решения ошибки ModuleNotFoundError .

1. Неверное название модуля

Первая причина ModuleNotFoundError: модуль не назван, имя модуля неверно . Например, попробуем импортировать модуль os с двойным «s» и посмотрим, что получится:

 >>> import oss
Traceback (последний последний вызов):
  Файл "", строка 1, в 
ModuleNotFoundError: Нет модуля с именем «oss» 

Как видите, мы получили ModuleNotFoundError: Нет модуля с именем «oss».  Чтобы устранить ошибку, убедитесь, что вы используете правильное имя модуля.

Давайте импортируем модуль с правильным именем.

 >>> импорт ОС
>>> 

Как видите, ошибка устранена.

2. Неверный путь к модулю

Вторая причина – неверный путь к локальному модулю, который вы хотите импортировать. например, давайте посмотрим на структуру каталогов 

Структура проекта:

core.py
папка_1
---my_module.py

 

В этой папке у нас есть:

• core.py: это файл, который будет выполняться
• folder_1: папка содержит my_module.py

Теперь в core.py попробуем импортировать my_module.py

core.py

импортировать my_module #неверно

 

Вывод:

 ModuleNotFoundError: Нет модуля с именем 'my_module' 

Как видите, мы получили ошибку, потому что my_module.py не находится в пути, по которому мы выполнили core.py. Нам нужно определить путь модуля в следующем примере, чтобы устранить ошибку.

core. py

импортировать folder_1.my_module #правильно

 

Вывод:

 ...Программа завершена с кодом выхода 0
 

Теперь мы успешно импортировали m_module.

3. Библиотека не установлена ​​

Кроме того, вы можете получить ошибку ModuleNotFoundError: No module named , если пытаетесь импортировать библиотечный модуль, который не установлен в вашей виртуальной среде или на компьютере.

Поэтому, прежде чем импортировать библиотечный модуль, вам необходимо установить его с помощью любой системы управления пакетами.

Примечание: рекомендуется пунктов .

Например, попробуем импортировать библиотеку Beautifulsoup4, которая не установлена ​​в моем виртуальном окружении.

 >>> из bs4 импортировать BeautifulSoup
Traceback (последний последний вызов):
  Файл "", строка 1, в 
ModuleNotFoundError: Нет модуля с именем «bs4» 

Теперь давайте установим библиотеку и попробуем повторно импортировать ее:

 pip install beautifulsoup4
Собираем красивый суп4
  Использование кэшированных https://files. pythonhosted.org/packages/d1/41/e6495bd7d3781cee623ce23ea6ac73282a373088fcd0ddc809a047b18eae/beautifulsoup4-4.9.3-py3-none-any.whl
Требование уже выполнено: суповое сито > 1,2; python_version >= "3.0" в /home/py/Desktop/seo_pro/seo_env/lib/python3.6/site-packages (из beautifulsoup4) (1.9.5)
Установка собранных пакетов: beautifulsoup4
Успешно установил BeautifulSoup4-4.9.3 

Повторный импорт:

 >>> from bs4 import BeautifulSoup
>>> 

Как видите, после установки пакета программа работает.

4. Модуль не поддерживается

Когда библиотека выпускает новое обновление, добавляются новые модули, а другие удаляются для поддержки.

Если вы попытаетесь импортировать модуль, который не поддерживается библиотекой, вы получите ModuleNotFoundError: модуль не назван.

Чтобы убедиться, что модуль поддерживается, перейдите к документации пакета и проверьте, доступен ли модуль.

5. Python 2 вместо Python 3

Как вы знаете, некоторые библиотеки Python больше не поддерживают  Python 2. По этой причине вы получите ошибку ModuleNotFoundError , если запустите модуль, который не поддерживает Python 2 с Python 2.

Чтобы устранить ошибку:

Сначала давайте проверим нашу версию Python, используя эти две команды:

 python -V
# Питон 2.7.18
питон3 -V
# Питон 3.9.5
 

В моем случае Python 3 находится в команде python3 , поэтому я выполню программу, используя python3 . Если Python3 не найден на вашем устройстве, установите Python на Windows, Mac и Linux.

Заключение

В заключение, чтобы устранить ошибку ModuleNotFoundError: модуль не назван:

1. Убедитесь, что имя модуля неверно
2. Убедитесь, что путь к модулю неверен
3. Убедитесь, что библиотека установлена ​​
4. Убедитесь, что модуль поддерживается
5. Убедитесь, что вы используете Python 3

Наконец, я надеюсь, что ваша проблема решена.

Как исправить ModuleNotFoundError (без имени модуля) в Python

Также известная как ошибка (без имени модуля) в Python

Я действительно надеюсь, что причина, по которой вы получаете сообщение об ошибке ModuleNotFoundError no module named, заключается просто в том, что модуль, который вы пытаетесь включить, не установлен.

Однако, если вы работаете над более сложным проектом или ваш Python настроен неправильно, вы можете прочитать оставшуюся часть этой статьи, чтобы понять, как Python добавляет модули в вашу программу. А затем попытайтесь решить ее с помощью этого нового знания.

В таком случае, для тех, кто изучает визуальную скорость, вот видео, показывающее, как это исправить:

Как решить ModuleNotFoundError (учебник на YouTube)

Эта ошибка встречается и для других популярных модулей. Для каждого @utils, mysql, jwt, docker, matplotlib, selenium, pandas, pygame, tkinter, cv2, numpy, tensorflow, feras, request, pip, pil, api существует отдельный учебник.

Как работает импорт модулей Python?

Чтобы добавить новый модуль, используйте ключевое слово import, за которым следует имя пакета:

.

 имя модуля импорта 

Если модуль может быть найден в идеале, этого должно быть достаточно, чтобы начать его использовать.

Но если все пойдет не так, вы можете получить одну из следующих двух ошибок:

• ModuleNotFoundError : нет модуля с именем «имя модуля»
• ImportError : невозможно импортировать имя «имя модуля»

Но откуда Python знает, где искать модули?

Ну, многое происходит в одной строке. И нужно немного разобрать, чтобы понять.

Давайте разберем процесс, чтобы увидеть, что Python сделает, чтобы найти ваш модуль:

1. Будет найдено имя файла, связанное с импортированным пакетом.
2. Загрузить и инициализировать (если требуется) модуль.
3. Добавить необходимые имена в локальное пространство имен и текущую область действия программы.
4. Следующий интерпретатор Python попытается разрешить имя модуля
5. sys.modules — это карта словаря, которую Python будет использовать для поиска имен модулей, которые уже были загружены (другой модуль мог уже загрузить его и т. д.), и если это так, он станет доступны в области, из которой вы его импортируете.
6. Если предыдущий шаг не удался, Python будет использовать стандартную библиотеку Python . PSL содержит все встроенные модули, написанные на языке C, которые обеспечивают доступ к файловой системе, математической библиотеке и различным системным инструментам, решающим наиболее распространенные проблемы.
7. Если предыдущий шаг не удался, Python попытается разрешить модуль в sys.path, что, вероятно, было причиной того, что что-то пошло не так, когда вы получили ModuleNotFoundError no module named error .

Как исправить ModuleNotFoundError (модуль не назван) Ошибка

Ошибка ModuleNotFoundError: No module named возникает, когда Python либо не может найти модуль, который вы пытаетесь импортировать, либо имя импортируемого пакета написано с ошибкой, либо модуль не существует на вашем жестком диске.

По сути, все это означает, что вам нужно установить модуль/пакет , прежде чем его можно будет импортировать в вашу программу (с ключевым словом import. )

Но, конечно, это еще не все.

В этой статье эта ошибка будет рассмотрена более подробно.

А что, если все не так просто?

Если вы получаете ошибки импорта по более сложной причине, рассмотрите структуру зависимостей пакетов. Обычно это примерно следующее. (Обратите внимание, что пакеты могут включать в себя другие пакеты или «подпакеты».)

 └── проект
    ├── пакет
    │ ├── что-то.py
    └── другой пакет
        ├── цыпленок.py
        ├── rooster.py
        └── подпакет
            └── egg.py
 

Вот где различение между абсолютные и относительные пакеты могут иметь значение.

В приведенном выше примере вы можете использовать абсолютный импорт :

 импортный пакет. что-то 

Другой пример абсолютного импорта:

 импортировать otherpackage.chicken
импортировать otherpackage.rooster 

А вот и абсолютный путь к местонахождению яйца подпакета:

 импортировать otherpackage. subpackage.eggs 

Относительный импорт встречается гораздо чаще и, следовательно, более подвержен ошибки импорта . Ниже приведены 3 примера относительного импорта Python :

.

 # импорт из области видимости something.py 

from ..otherpackage импортный петух 
 from ..otherpackage импортный цыпленок
из ..otherpackage.chicken import lay_egg_function 

Вот еще один пример относительного импорта:

 # импорт из области Chicken.py 

из . импортировать курицу 
 из .rooster импортировать peck_seeds_function 

Как исправить ModuleNotFoundError и ImportError?

Теперь, когда мы немного лучше познакомились с тем, как Python импортирует пакеты, и рассмотрели абсолютный и относительный импорт, пришло время поближе взглянуть на ModuleNotFoundError (и ImportError) и посмотреть, как это можно исправить.

В подавляющем большинстве случаев эти ошибки возникают из-за того, что интерпретатору Python не удается разрешить имя модуля в sys. path (место, которое Python ищет после сбоя поиска модуля как в sys.modules, так и в стандартной библиотеке.

Использование ключевого слова from следует той же схеме. Если поиск не удался, Python выдаст ключевое слово ModuleNotFoundError for import. И ImportError для поиска по ключевому слову from.

Окончательное решение по исправлению ошибки ModuleNotFoundError No Module Named:

Один из способов избежать ошибок импорта — полностью отказаться от относительных путей.

1. Избегайте использования относительных путей
2. Попробуйте использовать абсолютный путь при импорте
3. Или используйте встроенную системную переменную PYTHONPATH:

   export PYTHONPATH=»${PYTHONPATH}:/your/project/»

Если вы используете приложение Python в Docker или Vagrant, этот последний пункт может стать ключом к устранению большинства ошибок вашего модуля.

Перейдите в свой bash и выполните следующую директиву в командной строке:

 # В Linux/Unix/MacOS/терминале 

экспортировать PYTHONPATH="${PYTHONPATH}:/путь/к/проекту/" 
установить PYTHONPATH=%PYTHONPATH%;C:\path\to\project\ 

(Очевидно, измените путь к своему проекту)

Это свяжет каталог вашего проекта с PYTHONPATH, и всякий раз, когда вы используете абсолютный импорт, ничто не должно мешать избежать ошибки ModuleNotFoundError.

Очень надеюсь, что в вашем случае все не так сложно 🙂

Ошибка ModuleNotFoundError нет модуля с именем может произойти по ряду причин, включая неправильные имена модулей, неправильные пути модулей и непреднамеренные циклические зависимости. В этом руководстве мы рассмотрим некоторые из наиболее распространенных причин этой ошибки и способы их устранения.

Что такое модули Python и зачем их импортировать?

Возможно, вы только начали работать с Python. Вы написали базовые программы на Python.

Чтобы продвигать свое приложение, в какой-то момент вам, скорее всего, потребуется начать включать Python 9.0206 модули , которые могут быть библиотеками ИИ, математики или физики.

Вероятно, вы не хотите тратить время на написание пакетов самостоятельно. Просто потому, что много модулей, которые делают именно то, что вам нужно, и делают это эффективно.

Эти модули находятся в свободном доступе. К счастью, программисты, которые были до нас, нашли время, чтобы создать их и распространять бесплатно.

Вот почему мы должны импортировать модули в Python.

Вот некоторая терминология и справочная информация:

1. Модуль Python — это просто файл с расширением .py. Когда дело доходит до создания собственных модулей Python, для папки требуется файл __init__.py, чтобы он считался пакетом.
2. Пакет Python может содержать другие пакеты (подпакеты)
3. Вы импортируете пакет, когда вам нужно добавить полезные функции, написанные кем-то другим, чтобы сэкономить время при написании вашего приложения.

Модуль не существует (еще не установлен)

Одной из распространенных причин ошибки ModuleNotFoundError: No module named является просто то, что модуль, который вы пытаетесь импортировать, не существует. Это может произойти, если вы неправильно написали имя модуля или пытаетесь импортировать модуль, которого нет в вашем пути Python.

Чтобы исправить это, убедитесь, что вы используете правильное имя модуля и что модуль находится в вашем пути Python (или, по крайней мере, в каталоге вашего проекта 9).