Этапы урока | Деятельность учителя, задания для учащихся | Деятельность ученика | Формируемые УУД |
1.Организационный момент (1мин.) | Приветствие учителя. Проверка готовности к уроку. Настрой на работу. | Слушают учителя, вступают в диалог | Умение слушать учителя, товарища |
2. (5мин.) | —Ребята, проверим выполнение домашнего задания. Как вы составили справочную таблицу? Какие записали примеры? Сформулируйте в виде правила отдельные свойства корня п-й степени. | Проверяют домашнее задание, задают вопросы, отвечают на вопросы, формулируют правила. | Познавательные: применение предметных знаний; выполнение учебных заданий. Регулятивные: выделение и осознание того, что уже пройдено; умение распознавать на слух вопросы и отвечать на них. Коммуникативные: умение с достаточной полнотой и точностью выражать свои мысли, слушать и вступать в диалог. |
3.Постановка целей и задач урока. Мотивация. (3мин) | -Мы с вами рассмотрели тему: «Корень п-й степени и его свойства». Как вы думаете, чем мы будем заниматься сегодня на уроке? -Правильно, повторим изученный материал, подготовимся к контрольной работе. | Отвечают на вопросы учителя, обосновывают свои ответы. Формулируют цель урока. | Познавательные: Постановка и формулирование проблемы; Самостоятельное формулирование познавательной цели. Регулятивные: Умение анализировать, Целеполагание. Прогнозирование. Коммуникативные: умение с достаточной полнотой и точностью выражать свои мысли, слушать и вступать в диалог, участвовать в коллективном обсуждении проблем. Личностные: Самооценка. |
4.Актуализация знаний с целью подготовки к контрольному уроку (7мин. | Фронтальный опрос. Поработаем устно. -Ответим на вопросы,( если вопрос вызывает затруднение, обращаемся за помощью к учебнику ( вопросы на экране): 1)что называют кубическим корнем из числа а? Пример. 2)что называют корнем 4-й степени из числа а? Пример. 3)что называют корнем п-й степени из числа а? 4)Сколько существует корней четной степени из чисел: 1, 0, 81? 5)Сколько существует корней нечетной степени из 1, 0, -27? 6)Что называют арифметическим корнем п-й степени из числа? Для каких чисел введено понятие арифметического корня степени п? Работа в паре ( с обсуждением решения): ) -Объясните, какие свойства корней степени п использованы при выполнении задания: а =5*4*3=60, б) = =1,5, в) * = = = * =2*3=6, г) = а2, е) = а. Верно ли выполнены вычисления и упрощения? (Да) | Отвечают на вопросы учителя, обосновывают свои ответы, работают с текстом учебника. | Познавательные: извлечение из текстов математической информации, Познавательные: Структурирование знаний, Выбор способов решения задач, анализ объектов и синтез. Регулятивные: умение оценивать правильность выполнения действия; планирование пути достижения цели; прогнозирование. Умение работать парами |
5.Обобщение и систематизация знаний (12мин.) | Работаем с учебником. В тетрадях и на доске выполняем1) №3.67(в-з). Ответы: в)25,г)27, ж)8, з)16. Какое свойство корней использовали? 2) выполним №3.71(а-в).Какое свойство использовали? 3) №3.73(а.б,в).Какое свойство использовали? 4)№3.57(а,б).Какое свойство использовали? 5)№3.61(а,б).Как избавиться от иррациональности в знаменателе? -Перечислите, какие задания мы выполнили при работе с корнями степени п? Вычислить значение корня, упростить выражение, вынести множитель из-под знака корня, внести множитель под знак корня, избавиться от иррациональности, применить формулы сокращенного умножения). | Формулируют свойства корней степени п, записывают решения, обосновывают выбор свойства, объясняют, как освободиться от корня в знаменателе дроби. | Познавательные: структурирование знаний, Выбор способов решения задач, анализ объектов и синтез. Регулятивные: умение оценивать правильность выполнения действия; планирование пути достижения цели; прогнозирование. |
6.Контроль усвоения, коррекция ошибок. (10мин.) | -Теперь проверим, как вы усвоили свойства корней степени п. Выполните самостоятельную работу. №1.Верно ли равенство: а8 = -5, б) 8=6, в) = -7 ? №2.Вычислите: а)5+ б) 4 + в) * №3.Вынесите множитель из -под знака корня: а) , б) №4.Внесите множитель под знак корня: а)2 , б)в при в≥0. Оценка «3». №4.Упростите: Оценка «4». №5.Упростите: 30 + + 5 Оценка «5». | Выполняют самостоятельную работу. | Регулятивные: умение выполнять работу по составленному плану, вносить коррективы после оценки работы. Познавательные: умение извлекать из математических текстов необходимую информацию. |
7.Домашнее задание. (2мин.) | -Дома выполните задания из учебника: №3.60(а-г), №3.63.Упростите выражения, используя свойства корней и вынесение множителя из-под знака корня. | Записывают домашнее задание, задают вопросы. | |
8.Рефлексия (3мин.) | —Подведем итог работы на уроке. Оцените свою деятельность: -у меня получилось… -было трудно… | Регулятивные: Оценка-осознание уровня и качества усвоения. Коммуникативные: умение полно и точно выражать свои мысли. Личностные: самооценка, |
Урок на тему: «Свойства корня степени n»
Технологическая карта урока по алгебре и началам анализа в 10 классе по теме «Свойства корня степени n»
Цель урока: повторить с учащимися определения и свойства корней степени п, совершенствовать практические навыки решения задач на применение свойств корней, применять полученные умения на практике.
предметные: уметь применять свойства корней степени n при выполнении преобразований выражений, находить значения корней степени п.
личностные: умение работать в парах, слушать собеседника и вести диалог, аргументировать свою точку зрения
метапредметные: уметь обрабатывать информацию; формировать коммуникативную компетенцию учащихся; выбирать способы решения задач в зависимости от конкретных условий; контролировать и оценивать процесс и результаты своей деятельности
Образовательные (формирование познавательных УУД): –сформировать у учащихся целостное представление о корне степени п, навыки рационального применения свойств корня п-й степени при решении задач.
Развивающие (формирование регулятивных УУД): – развивать логическое мышление, память, познавательный интерес, вырабатывать умение анализировать и сравнивать, развивать навыки самоконтроля.
Воспитательные (формирование коммуникативных и личностных УУД): – развитие любознательности и интереса к предмету, воспитание у учащихся навыков учебного труда, формирование ответственности за конечный результат, доброжелательного отношения друг к другу.
Необходимое оборудование: доска, экран, проектор, компьютер, карточки для индивидуальной работы.
Базовый учебник: С.М. Никольский, М.А. Потапов: «Алгебра и начала математического анализа». Учебник для общеобразовательных учреждений. — М.: Просвещение, 2019 г.
Этапы урока | Деятельность учителя, задания для учащихся | Деятельность ученика | Формируемые УУД |
1.Организационный момент (1мин.) | Приветствие учителя. Проверка готовности к уроку. Настрой на работу. | Слушают учителя, вступают в диалог | Умение слушать учителя, товарища |
2. (5мин.) | -Ребята, проверим выполнение домашнего задания. Как вы составили справочную таблицу? Какие записали примеры? Сформулируйте в виде правила отдельные свойства корня п-й степени. | Проверяют домашнее задание, задают вопросы, отвечают на вопросы, формулируют правила. | Познавательные: применение предметных знаний; выполнение учебных заданий. Регулятивные: выделение и осознание того, что уже пройдено; умение распознавать на слух вопросы и отвечать на них. Коммуникативные: умение с достаточной полнотой и точностью выражать свои мысли, слушать и вступать в диалог. |
3.Постановка целей и задач урока. Мотивация. (3мин) | -Мы с вами рассмотрели тему: «Корень п-й степени и его свойства». Как вы думаете, чем мы будем заниматься сегодня на уроке? -Правильно, повторим изученный материал, подготовимся к контрольной работе. Какова наша главная цель? Скажите, как вы понимаете слова М. Горького «Знать необходимо не за тем, чтобы только знать, а для того, чтобы научиться делать». Вот и вы постарайтесь хорошо подготовиться к контрольной работе. Запишем в тетрадях дату, тему урока. Пользуемся учебниками и справочными таблицами.. | Отвечают на вопросы учителя, обосновывают свои ответы. Формулируют цель урока. | Познавательные: Постановка и формулирование проблемы; Самостоятельное формулирование познавательной цели. Регулятивные: Умение анализировать, Целеполагание. Прогнозирование. Коммуникативные: умение с достаточной полнотой и точностью выражать свои мысли, слушать и вступать в диалог, участвовать в коллективном обсуждении проблем. Личностные: Самооценка. |
4.Актуализация знаний с целью подготовки к контрольному уроку (7мин.) | Фронтальный опрос. Поработаем устно. Ответим на вопросы, (если вопрос вызывает затруднение, обращаемся за помощью к учебнику (вопросы на экране): 1)что называют кубическим корнем из числа а? Пример. 2)что называют корнем 4-й степени из числа а? Пример. 3)что называют корнем п-й степени из числа а? 4)Сколько существует корней четной степени из чисел: 1, 0, 81? 5)Сколько существует корней нечетной степени из 1, 0, -27? 6)Что называют арифметическим корнем п-й степени из числа? Для каких чисел введено понятие арифметического корня степени п? Работа в паре ( с обсуждением решения): Объясните, какие свойства корней степени п использованы при выполнении задания: а) , б) , в) , г) , е). Верно ли выполнены вычисления и упрощения? (Да) | Отвечают на вопросы учителя, обосновывают свои ответы, работают с текстом учебника. | Познавательные: извлечение из текстов математической информации, Познавательные: Структурирование знаний, Выбор способов решения задач, анализ объектов и синтез. Регулятивные: умение оценивать правильность выполнения действия; планирование пути достижения цели; прогнозирование.
Умение работать парами |
5.Обобщение и систематизация знаний (12мин.) | Работаем с учебником. В тетрадях и на доске выполняем 1) №3.67(в-з). Ответы: в)25,г)27, ж)8, з)16. Какое свойство корней использовали? 2) №3. 3) №3.73(а.б,в).Какое свойство использовали? 4) №3.57(а,б).Какое свойство использовали? 5) №3.61(а,б).Как избавиться от иррациональности в знаменателе? Перечислите, какие задания мы выполнили при работе с корнями степени п? Вычислить значение корня, упростить выражение, вынести множитель из-под знака корня, внести множитель под знак корня, избавиться от иррациональности, применить формулы сокращенного умножения). | Формулируют свойства корней степени п, записывают решения, обосновывают выбор свойства, объясняют, как освободиться от корня в знаменателе дроби. | Познавательные: структурирование знаний, Выбор способов решения задач, анализ объектов и синтез. Регулятивные: умение оценивать правильность выполнения действия; планирование пути достижения цели; прогнозирование.
|
6.Контроль усвоения, коррекция ошибок. (10мин.) | -Теперь проверим, как вы усвоили свойства корней степени п. Выполните самостоятельную работу. №1.Верно ли равенство: а) , б) , в) ? №2.Вычислите: а) , б) в) №3.Вынесите множитель из-под знака корня: а) , б) №4.Внесите множитель под знак корня: а) , б) при b≥0. Оценка «3». №5.Упростите: Оценка «4». №6.Упростите: ценка «5». | Выполняют самостоятельную работу. | Регулятивные: умение выполнять работу по составленному плану, вносить коррективы после оценки работы. Познавательные: умение извлекать из математических текстов необходимую информацию. |
7. (2мин.) | -Дома выполните задания из учебника: №3.60(а-г), №3.63.Упростите выражения, используя свойства корней и вынесение множителя из-под знака корня. | Записывают домашнее задание, задают вопросы. |
|
8.Рефлексия (3мин.)
| Подведем итог работы на уроке. Оцените свою деятельность: — я был активный (пассивный), -было интересно(скучно), -у меня получилось… -было трудно… -что нового узнали на уроке? -достигли мы поставленной цели? Спасибо за урок. |
| Регулятивные: Оценка-осознание уровня и качества усвоения. Коммуникативные: умение полно и точно выражать свои мысли. Личностные: самооценка,
|
Решение квадратных уравнений с использованием квадратных корней
Ключевые понятия
- Решение квадратных уравнений с использованием квадратных корней
- Применение квадратного корня для квадратного уравнения
- Понимание положительного и отрицательного квадратного корня 2 + bx + c = 0 можно также представить как y = ax 2 + bx + c.
Решение квадратного уравнения с использованием квадратных корней
Как мы можем решить квадратное уравнение, используя квадратные корни?
Запишем заданное квадратное уравнение в квадратной форме, добавив константу, затем извлечем квадратный корень, чтобы найти значение переменной.
Использование квадратных корней при решении квадратных уравнений
Чтобы понять, что такое квадратные корни в квадратных уравнениях и как решать уравнение в форме x 2 = a,
Рассмотрим несколько примеров
Пример 1 :
Найдите решения уравнения x 2 = 121.

Решение:
Шаг 1. Данным уравнением является x² = 121 … (1)
Шаг 2. Увидев, что уравнение 1 квадратное, мы помним, что 12 квадратное. из 11.
x² = 121
x = ±√121
x = ±11
Решениями квадратного уравнения являются x = +11 и x = -11.
Пример 2:
Найдите решения уравнения x 2 = 100,
Решение:
Шаг 1: Данное уравнение имеет вид z² = 100 … (1)
Шаг 2: Глядя на уравнение, мы помним, что 100 — это квадрат 10.
x² = 100
x = 0 ±√
x = ±10
Решениями квадратного уравнения являются x = +10 и x = -10. (1)0019
Шаг 2: Глядя на уравнение, мы помним, что 144 является квадратом 12.
x 2 = 144
x = ±√144
x = ±12
Решения квадратного уравнения x = + 12 и х = -12.
Пример 4:
Найдите решения уравнения x² = 64.
Решение:
Шаг 1: Данным уравнением является x² = 64 … (1)
Шаг 2: Увидев уравнение, мы помним, что, видя уравнение 64 это квадрат 8.

x 2 = 64
x = ±√64
x = ±8
Решениями квадратного уравнения являются x = +8 и x = -8.
Пример 5:
Найдите решения уравнения x² = -36.
Решение:
Шаг 1: данное уравнение x²=-36.… (1)
Шаг 2: глядя на уравнение, мы помним, что 64 является квадратом 8.
x 2 = -36
9 x = ±√-36
Не существует действительного числа, которое можно умножить, чтобы получить отрицательное число, из которого можно получить квадратный корень.
Решить квадратное уравнение вида 𝒂𝒙
𝟐 +𝒃=𝒄Как решить уравнение вида ax 2 +b=c?
Сначала запишите уравнение в виде x 2 =a, где a — действительное число.
Извлеките квадратный корень из каждой части уравнения.
Тогда решите это.
Пример 1:
Найдите решение квадратного уравнения 4x 2 +5 = 69, используя квадратные корни.

Решение:
Шаг 1: Дано квадратное уравнение 4x 2 +5 = 69 … (1)
Шаг 2: Теперь запишем в виде x 2 = a,
получаем 4x 2 9019 4 4x 2 = 64
x 2 = 16
x = ±√16
x = ±4
Решения квадратного уравнения: x = +4 и x = -4
9003 Пример 2 :
Найдите решение квадратного уравнения x 2 – 1= 24, используя квадратные корни.
Решение:
Шаг 1: Дано квадратное уравнение х 2 – 1 = 24 … (1)
Шаг 2: Теперь запишем в виде х 2 = а,
получаем 5 х 20 900 24+1
x 2 = 25
x = ±√25
x = ±5
Найдите решение квадратного уравнения 3x 2 −4 = 26, используя квадратные корни.
Решение:
Шаг 1: Дано квадратное уравнение 3x 2 −4 = 26 … (1)
Шаг 2: Теперь запишем в виде x 2 = a,
2 = 9 1, мы получим 10 5 0 3 x 90 26+4
x 2 = 30
x = ±√10
x = ±10
Найдите решение квадратного уравнения 3x 2 +9 = 69, используя квадратные корни.

Решение:
Шаг 1: Дано квадратное уравнение 3x 2 +9 = 69..… (1)
Шаг 2: Теперь запишем в виде 3x 2 = 60,
4 2 получим 01019 = 603x 2 = 20
x = ±2√5
x = ±20
Лестница прислонена к стене, высота по стене 13 м, лестница отстоит от стены 14 м, какова длина лестницы?
Решение:
Пусть длина лестницы равна x м
Сейчас
√x = ±13²+14²
= ±√169+196
= ±√365
Поскольку длина лестницы не может быть отрицательной
Длина лестницы
Упражнение
- Найдите решения уравнения x 2 = 1.
- Найдите решения уравнения x² = 45,
- Найти решения уравнения x 2 = 16.
- Найти решения уравнения x² = 9.
- Найти решения уравнения x 2 = 81.
- Найти решение квадратного уравнения x 2 – 1 = 1, используя квадратные корни
- Найдите решение квадратного уравнения x² + 1 = 1, используя квадратные корни
- Найдите решение квадратного уравнения 5x 2 – 1 = 24, используя квадратные корни
- Найдите решение квадратного уравнения 5x 2 – 1 = 24, используя квадратные корни решение квадратного уравнения 6x 2 -13 23 с использованием квадратных корней.
 10. К дереву прислонена лестница, высота по стене 3 м, лестница отстоит от дерева на 4 м, какова длина лестницы?
10. К дереву прислонена лестница, высота по стене 3 м, лестница отстоит от дерева на 4 м, какова длина лестницы?
Концептуальная карта
Чему мы научились
- Решение квадратных уравнений с использованием квадратных корней
- Решение квадратного уравнения в форме x 2 = a
- Решение уравнения в форме ax 6 0 c5 2
Комплексные числа и квадратные уравнения: определение и упражнения
Перейти к содержимому
Комплексные числа и квадратные уравнения
Комплексные числа — это математическая структура, которая позволяет нам работать с числами, которые не являются реальными. Комплексное число записывается как a + bi, где a — действительная часть, а b — мнимая часть. Действительная часть — это та часть, которая похожа на обычное число, а мнимая часть — это число, умноженное на I, равное квадратному корню из -1. Комплексные числа можно использовать для решения квадратных уравнений.

Зарегистрируйтесь, чтобы получить бесплатный пробный тест и учебные материалы
+91
Подтвердите OTP-код (обязательно)
Я согласен с условиями и политикой конфиденциальности.
Комплексные числа могут быть представлены как a + bi, где a и b — действительные числа, а i — мнимая единица. Квадратный корень из отрицательного числа является мнимым. Квадратные уравнения — это уравнения вида ax2 + bx + c = 0, где a, b и c — действительные числа.
Комплексные числа можно использовать для решения квадратных уравнений. Например, квадратное уравнение x2 + 4x – 3 = 0 можно решить, используя комплексное число 3 + 2i. Сначала разложите уравнение x2 + 4x – 3 = 0 на (x + 3)2 = 0. Затем извлеките квадратный корень из каждой части уравнения.
x + 3 = 0
x = -3Комплексное число 3 + 2i можно использовать для решения уравнения x2 + 4x – 3 = 0. Сначала умножьте 3 + 2i само на себя.
3 + 2i = (3)(3) + (2)(2)i
Затем извлеките квадратный корень из каждой части уравнения.

3 + 2i = 9 + 4i
Комплексное число 3 + 2i является решением уравнения x2 + 4x – 3 = 0.
Комплексные числа представляют собой набор чисел, которые используются в математике и физике. Они создаются путем взятия действительного числа и добавления мнимого числа. Это мнимое число получается путем извлечения квадратного корня из -1. Это число записывается как I. Комплексные числа можно изобразить на координатной плоскости. Действительное число откладывается по оси абсцисс, а мнимое — по оси у.
Квадратные уравнения — это уравнения с квадратом переменной. Эта переменная обычно равна x. Квадратные уравнения можно решить, используя квадратную формулу. Эта формула записывается как:
Решениями уравнения являются значения x, которые делают уравнение верным.
Сопутствующее содержимое
Введение в трехмерную геометрию, систему координат и формулы Решения NCERT для класса 6 по математике Обработка данных Упражнение 9. 


 Проверка домашнего задания
Проверка домашнего задания Какова наша главная цель? Скажите, как вы понимаете слова М. Горького «Знать необходимо не за тем, чтобы только знать, а для того, чтобы научиться делать». Вот и вы постарайтесь хорошо подготовиться к контрольной работе. Запишем в тетрадях дату, тему урока. Пользуемся учебниками и справочными таблицами..
Какова наша главная цель? Скажите, как вы понимаете слова М. Горького «Знать необходимо не за тем, чтобы только знать, а для того, чтобы научиться делать». Вот и вы постарайтесь хорошо подготовиться к контрольной работе. Запишем в тетрадях дату, тему урока. Пользуемся учебниками и справочными таблицами..  )
)


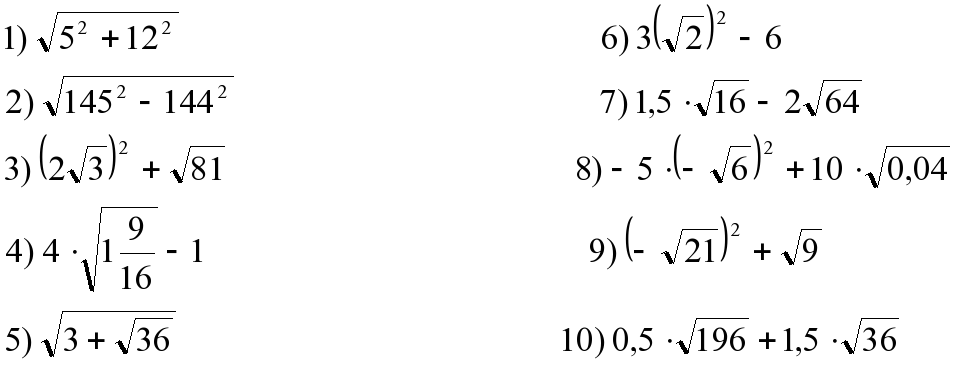 Проверка домашнего задания
Проверка домашнего задания


 71(а-в).Какое свойство использовали?
71(а-в).Какое свойство использовали?
 Домашнее задание.
Домашнее задание.




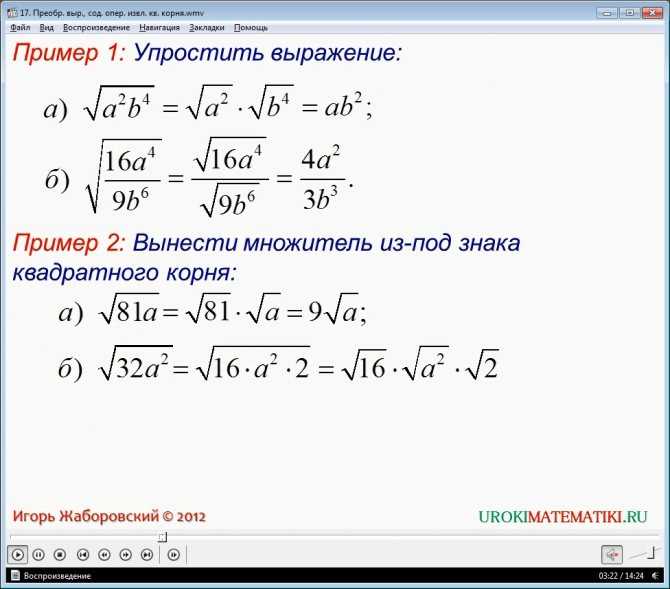 10. К дереву прислонена лестница, высота по стене 3 м, лестница отстоит от дерева на 4 м, какова длина лестницы?
10. К дереву прислонена лестница, высота по стене 3 м, лестница отстоит от дерева на 4 м, какова длина лестницы?

