Как решить по алгебре пример: Как решить примеры по алгебре 🚩 как решить такой пример 🚩 Математика

Как решить проблемы с математикой

140 456

РодителямИнтервью

Основные идеи

• Трудности в изучении математики знакомы многим детям.
• Их способности ни при чем: освоить эту науку мешают психологические причины.
• Красота и логика — только они помогут понять и полюбить этот предмет.

«Только и учим, что эту математику! — жалуется Ирина, мама 11-летней Алисы. — Дочь вроде бы формулы знает, а все равно спотыкается на каждом шагу. Иногда сложную задачу решит, а простую нет. Контрольные — это ужас для всей семьи. Ребенок весь на нервах, у нас с мужем головная боль. Никогда не знаешь, напишет она на четыре или двойку принесет. Занимаемся все выходные, и никакого прогресса!»

Я очень хорошо понимаю Алису. Помню, какую тоску навевали на меня в школе все эти уравнения, функции и тангенсы. Даже нелюбимые химия и физика были мне ближе: я могла хоть как-то соотнести их с собственным опытом. Но «а плюс b разделить на с» были бесконечно далеки от моей жизни.

Нас с Алисой нельзя назвать исключением. В каждом классе встречаются дети, для которых математика — сплошное мучение. А их родители мучаются вопросами, как к этому относиться и чем они могут помочь.

Нужна ли детям математика?

Проблемы эти есть повсюду. В 2012 году газета The New York Times начала дискуссию на тему, нужна ли детям алгебра, если каждый четвертый ученик в США не заканчивает школу из-за проблем с этим предметом.

А во Франции бывший министр образования и науки Клод Аллегрэ, сам ученый-геофизик, всерьез обсуждал вопрос об отмене преподавания математики в школе, поскольку многие дети не справляются даже с элементарными задачами.

Так нужна ли математика всем детям? Или кто-то может обойтись без нее?

«Моей дочке — нет, она гуманитарий, как и я, пойдет на филфак, — уверена 36-летняя Марина. — Нам главное, чтобы по литературе, русскому, истории были пятерки, а по математике — лишь бы не двойка».

«Это мучительный вопрос: насколько глубоко нужно знать математику тем, кому она вроде бы не нужна? — размышляет писатель и математик Леонид Костюков. — Но кто такие гуманитарии? На одну десятую — люди искусства, и на девять десятых — люди культуры.

Людям искусства (художнику, поэту, актеру) математика, наверное, для творчества не обязательна. Но людям культуры — историку, филологу, редактору, издателю, журналисту — никак не обойтись без системного мышления. А именно математика воспитывает, дисциплинирует ум».

Я впервые задумалась, не напрасно ли пренебрегала математикой, когда стала писать диссертацию. Тема была сугубо филологической — но каких же мучений мне стоило упорядочить весь огромный фактический материал и убедительно обосновать свою концепцию! Логическое мышление — вот с чем была проблема. Но раз я все же справилась с диссертацией, то, может, я не так безнадежна по части логики, как когда-то казалось мне и моим родителям?

Самый сложный предмет?

Если у ребенка возникают трудности с математикой, у нас всегда есть наготове ответ: значит, нет математических способностей. И на этом мы как бы закрываем тему: на нет и суда нет. Другими словами, мы легко соглашаемся: математика так трудна, что справиться с ней могут не все. И мы утешаемся тем, что по другим дисциплинам наш ребенок вполне (или прекрасно) успевает.

Леонид Костюков, опытный репетитор, уверен, что преподает один из самых легких предметов: «Курс математики устроен невероятно изящно, красиво, логично. Учить надо очень мало, гораздо больше нужно понимать. Если я не помню формулу, но помню, откуда она следует, — я могу ее быстро вывести. Ни в каких других школьных науках такой возможности нет».

По его мнению, если ребенок успевает по другим предметам, нет никаких причин, чтобы он не справился с математикой. «Если у него, например, хорошо идет английский, значит, с логикой у него все в порядке, потому что английский язык устроен очень логично. Более того, объективно он сложней, чем язык школьной математики. Значит, этот ребенок должен успевать и в математике». Так почему же на практике это не так?

Когда проблемы нарастают как снежный ком

«Математика дает наиболее чистое и непосредственное переживание истины», — полагал немецкий физик, лауреат Нобелевской премии Макс Лауэ в книге «Страницы жизни Ландау». И в каждом классе найдутся дети, которым знакомо это переживание, которые испытывают наслаждение, например, от красивого решения задачи.

Что отличает школьников, хорошо успевающих по математике?

«Как правило, это дети активные, любопытные, готовые рисковать, их не пугают проблемные ситуации, они любят делать открытия, — рассказывает детский психолог Елена Морозова. — А дети, которые боятся математики, зачастую не рассчитывают на себя, они слишком зависят от мнения родителей (учителей, одноклассников), не уверены в себе, легко верят в то, что они несообразительны.

Любая задача приводит такого ребенка в ступор: ему страшно само ожидание, что вот сейчас будет трудно и он окажется несостоятелен. Страх может стать причиной неудач и с другими предметами».

Он нарастает постепенно, как снежный ком. Например, напоминает детский психолог, в первых классах не все дети еще хорошо читают «и условие задачи могут просто не понять. Кроме того, у них еще не развито абстрактное мышление, им трудно представить себе картинку: вот поезд выходит из пункта А, а вот другой — из пункта Б, вот здесь они встречаются. И ребенок заведомо отказывается вникать в задачу: не буду даже и пытаться что-то с этим сделать».

То, что упущено в начальных классах, скажется потом, как ни в одном другом предмете. Именно потому, что в математике все логически связано

«Если по литературе я пропустил Грибоедова, это не помешает мне изучать Тургенева, — замечает Леонид Костюков. — Но если что-то упустил по алгебре, то у меня начнутся системные проблемы. Другие предметы представляют собой определенный набор тем. Математика же, по большому счету, — это развитие одной темы. А ведь иной раз оказывается, что не все старшие школьники твердо знают даже таблицу умножения».

Причина не в математике

«У нее плохие отношения с учителем», «над ним смеются одноклассники», «она переживает, что отец ушел из семьи» — причин для неуспеваемости по любому предмету может быть много. Но существуют ли причины, которые вызывают трудности именно с математикой?

Педагог-психолог Анн Сьети уверена: математические понятия способны пробудить самые глубокие переживания. «Условие», «требуется», «доказать», «необходимо, но недостаточно» — все эти слова могут бессознательно ассоциироваться с внутренними проблемами.

«Чего стоит только пресловутый «икс» — неизвестный, за которым таится неведомо что, — говорит она. — Или другой пример: одна из моих учениц не ставила скобки в уравнениях, забывая отделить одни числа от других. А потом выяснилось, что дома ей трудно оставаться одной в своей комнате — то есть воспринимать себя отдельно от других членов семьи.

Проблемы ребенка с математикой связаны не с его интеллектуальными способностями, а с чем-то внутри него, что мешает ему ясно мыслить и понимать учителя». Вот откуда столько тревожных эмоций, которые блокируют разум.

Не выучить, а понять

Признаем: очень часто школьные неудачи выводят родителей из себя. Мы злимся, возмущаемся и критикуем ребенка, который «не старается», «не хочет понять» и вообще «плохо соображает». А эксперты единодушны: главная задача родителей прямо противоположная — уменьшить его напряжение и переживания.

«Ребенка вообще не надо фиксировать на неудачах, — подчеркивает Елена Морозова. — Лучше сказать: да, это пока не получается, давай подумаем, как тебе помочь».

Однако это не значит «помочь выучить», как думают иногда родители

«Математику нужно понимать, почувствовать ее цельность, единство. Если просто зубрить, это будет лишь крайне утомительной и, главное, бессмысленной тренировкой для памяти», — предупреждает Леонид Костюков.

«Нужно не вдалбливать, а последовательно подводить ребенка к самостоятельному решению, — продолжает Елена Морозова. — И когда происходит этот инсайт, ребенок изумляется: «Надо же, я смог!» Получилось раз, другой, третий — и постепенно он начинает увлекаться, чувствовать свою состоятельность.

Конечно, лучше всего здесь поможет специалист — учитель, которого можно попросить о дополнительных занятиях, или опытный репетитор. Но и сами родители могут попробовать совершить эти открытия вместе с ребенком».

Не обязательно после этого ученик станет блистать на уроках и приносить пятерки. Хотя оценки и становятся лучше, если на них не зацикливаться, отмечает Анн Сьети: «В конце концов, у каждого свои цели. Для одного важно не оказаться худшим в классе. А другой мечтает стать ветеринаром. Главное, чтобы дети начали чувствовать себя лучше, избавившись от тревоги и страха, и стали получать удовольствие от занятий математикой».

«Нужно преподавать математику как особую теорию красоты»

Psychologies: Почему у многих детей математика вызывает скуку, страх, отвращение?

Александр Лобок, психолог: Это означает только одно: она принципиально неправильно для этого ребенка преподается в школе. Множество детей переживают унижение математикой. Долгие школьные годы они испытывают чувство своей непроходимой математической тупости, а учитель поддерживает это чувство либо в щадящей форме («Что поделаешь, у него гуманитарные мозги!»), либо в циничной и злобной («Ну ты тупой!»).

Многие учителя убеждены, что математические способности — «от бога» и что причина «невменяемости» миллионов детей, не понимающих математику, в их природной ограниченности. Тогда как задача школы — помочь каждому ребенку почувствовать математический азарт и желание заниматься. Если этот интерес и любовь возникнут, ребенок будет гораздо более успешен — в том числе и в традиционном математическом обучении.

Чаще всего проблемы возникают у детей гуманитарного склада. Как в них пробудить этот азарт?

Для детей-гуманитариев важно почувствовать смысл. А традиционная школьная программа довольно часто предлагает математику как набор абстрактной «цифири», даже не пытаясь объяснить ученикам, что математика — это прежде всего философия, позволяющая совершенно по-новому взглянуть на окружающий мир. Если же детям открыть дверцу в смыслы того, чем занимается математика, — у них появляется азарт и интерес.

Например, когда объясняешь и показываешь, что математика — это такое особое волшебство, которое позволяет обсчитать весь мир. И значит, найти что-то фундаментально общее во всем мире. Например, все можно взвесить, измерить — на этом основании сравнить мальчика Петю, его любимую кошку и папин автомобиль. И вообще, оказывается, сравнить можно все во Вселенной!

А еще дети не подозревают, что математика наполнена внутренней красотой, — им тоже об этом никто не рассказывает. А ведь любая последовательность орнаментов или игра архитектурных форм — это математика. И если детям преподавать математику как особую теорию красоты, это очень может их зацепить.

Значит ли это, что освоить школьный курс математики по силам каждому ребенку?

В том виде, в каком он сегодня существует, — разумеется, нет. Да это и не нужно. А вот постигнуть эстетические и философские основания математики — это по силам и нужно всем. Благодаря этому интерес к математике — причем к самой традиционной — возникает у каждого ребенка. В том числе у тех, кто всю жизнь этот предмет ненавидел и считал себя неспособным.

Но что же делать родителям, чьи дети учатся в традиционной школе и не справляются с математикой?

Это всегда глубоко индивидуальная проблема. Но общая рекомендация может быть такой: надо найти такого педагога, который по-настоящему увлечен и математикой, и детьми.

Об эксперте

Александр Лобок — психолог, автор книги «Другая математика».

Текст:Галина ЧерменскаяИсточник фотографий:Getty Images

Новое на сайте

Как пережить важное спортивное соревнование: мотивирующие советы топовых снукеристов

Подсказки психики: о чем говорит ваш гнев

«Написала книгу — и друзья отвернулись от меня. Неужели из зависти?»

«Люди постоянно обращаются ко мне на „ты“: как объяснить, что это нарушение моих границ?»

Что скрывают повторяющиеся сны

Как дать ребенку реализовать талант, не травмировав его: мнения психологов и жюри конкурса «Синяя птица»

Синдром годовщины: что это и почему так важно знать историю своих предков

Психология распродаж: как научиться экономить и перестать испытывать вину после шопинга

Как решать вирусные математические задачи

Помните задачу, которую недавно пытались решить всем интернетом: 8 ÷ 2(2 + 2)? У одних получался ответ 1, у других — 16.

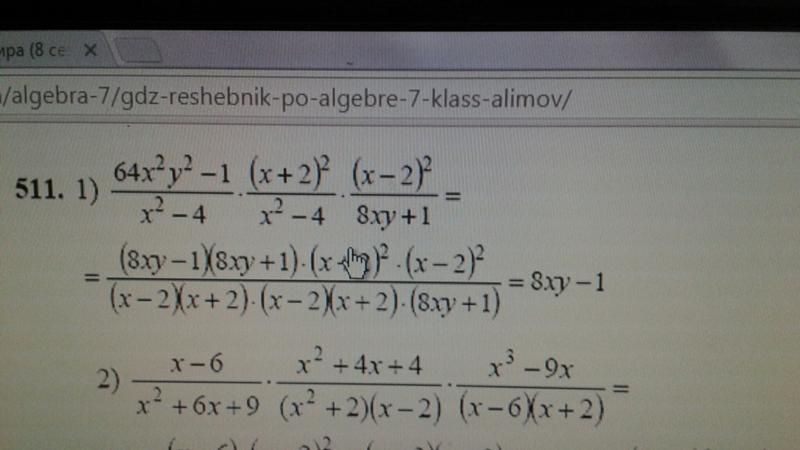Математик и журналистка Ивлин Лэмб в своей статье для Scientific American объясняет, в чем там настоящая сложность. Рассказываем с учебником в руках!

Сначала напомним суть проблемы. В задаче 8 ÷ 2(2 + 2) у одних получается ответ 16, у других — 1.

Ответ зависит от того, в какой последовательности производить вычисления. Правило последовательности действий можно найти в учебнике математики для третьего класса: «Действия в числовых выражениях выполняют в следующем порядке: 1) действия, записанные в скобках; 2) умножение и деление; 3) сложение и вычитание».

Значит, сначала необходимо вычислить 2 + 2 (получается 4), а затем 8 ÷ 2 ⋅ 4 (получается 16).

Однако в методическом пособии для преподавателей алгебры говорится: «В алгебре тот же порядок действий, что и в арифметике, но есть исключение: в алгебре знак умножения связывает компоненты действия сильнее, чем знак деления, поэтому знак умножения опускается. Например, a ÷ b ⋅ c = a ÷ (b ⋅ c)». Более того, автор методички упоминает, что математики Павел Александров и Андрей Колмогоров предлагали распространить этот алгебраический принцип и на арифметику, однако «это предложение не нашло поддержки».

Если вам в свое время вдолбили это в голову, вы, увидев, что знак умножения перед скобкой опущен, могли воспринять умножение как действие с более высоким приоритетом и действовать иначе: сначала вычислить 2 + 2 (получается 4), затем умножить результат на 2 (получается 8), затем вычислить 8 ÷ 8 и получить ответ 1.

Если так, то вы не одиноки — так же задачу решают и некоторые калькуляторы.

Но, считает математик и журналистка Ивлин Лэмб, проблема несколько шире, чем холивар, о котором скоро все забудут (предыдущий был всего полгода назад — тогда в задаче были другие числа, но те же знаки). Настоящая проблема в том, что люди берутся решать задачу, несмотря на возможное разночтение.

Если порядок вычислений предполагает разные варианты, значит, задача сформулирована неточно. Убедиться в этом должен прежде всего тот, кто задачу формулирует. Но и тот, кто пытается ее решить, должен иметь смелость сказать, что запись некорректна или в ней не хватает данных.

Однако

травмированные школой люди только рады получить лишнее подтверждение тому, что математика — это минное поле,

считает Лэмб. Вместо того чтобы решать очередную задачу из интернета, стоит разобраться, в чем подвох: корректные задачи вирусными не становятся.

О подвохе, кстати, предупреждают все в той же методичке: «Для устранения недоразумений […] предпочтительнее пользоваться в качестве знака деления чертой или ставить скобки». В таком случае выражение могло бы выглядеть иначе:

(8 ÷ 2)(2 + 2)

8 ÷ (2(2 + 2))

8
2(2 + 2)

8	⋅ (2 + 2)
2

• Моро М. И., Волкова С. И., Степанова С.В. Учебник: Математика 3-й класс. М.: Просвещение, 2014.

• Шустеф М.Ф. Методика преподавания алгебры. Курс лекций. Минск, 1967.

Читайте нас в Facebook, VK, Twitter, Instagram, Telegram (@tandp_ru) и Яндекс.Дзен.

Теории и практики

Теги

#математика для взрослых

#математик

#задачи

#алгебра

#математика

• 28 659

6 Решение алгебраических уравнений

Цель алгебраических уравнений — найти число или набор чисел, что делает уравнение верным. Иногда ответ может быть простым, в других случаях он может быть очень сложным, поэтому нам нужно иметь процесс, который позволяет нам найти и ответить, что является правильным.

Этот процесс направлен на то, чтобы получить букву слева от уравнение само собой. Для этого мы должны сбалансировать все, что мы делаем, чтобы одна часть уравнения с другой. Так, например, если вы добавите 4 к одной части уравнения вы должны также добавить четыре к другой.

Пример

Давайте посмотрим на несколько примеров:

Решите это уравнение: x + 7 = 12

Помните, что мы хотим изолировать x на одной стороне уравнение. Таким образом, в левой части мы получаем x, а в правой получить 12 минус 7. Ваш окончательный ответ будет x равно 5. Вот как выглядят шаги:

х + 7 7 = 12 — 7
х = 5

Чтобы проверить свою работу, достаточно подставить вернитесь к исходному уравнению для x.

5 + 7 = 12

Пример

Давайте попробуем вот это:

Решите следующее: 12x = 96

Давайте начнем с размышлений о том, на что мы пытаемся ответить. В В этом случае мы хотим знать, какое число, умноженное на 12, будет равно 96. Возможно, вы сможете понять это в своей голове, но давайте все равно по ступенькам.

12х = 96

Х = 8

Теперь давайте проверим нашу работу.

12 x 8 = 96 правильно, поэтому мы правильно выполнили эту задачу.

Пример

Давайте попробуем еще раз!

Найдите X: 6 (x + 3) = 10x

Сначала мы должны расширить нашу скобку, умножив все внутри скобки на минус 1.

6 х 3 = 10 х

Далее нам нужно решить, с какой стороны знака равенства мы находимся собирается изолировать x дальше. В этом случае легче получить все xs с правой стороны. Для этого нам нужно добавить 1 x к каждая сторона;

6 х 3 + х = 10 х + х

Обратите внимание, что крестики слева отменяют друг друга, и мы останется следующее:

6 (-3) = 11x
9 = 11 х

Далее мы должны разделить каждую сторону на 11.

=

Х=

или х = 0,8181

В некоторых случаях возможно отсутствие возможных решения уравнения или решения не делают, т.к. Там потому что важно всегда проверять свои решения.

Уравнения по алгебре — как решить?

$\begingroup$

У меня есть два уравнения, которые я хочу решить, но я могу решить первое, но не могу решить второе, вот пример: $$\begin{выравнивание*} 100 &= 120 \умножить на х\\ 0,83 &= 123/ х \end{align*}$$

Первое, что я знаю, как решить, в основном я делаю с обеих сторон уравнения с одной и той же операцией, обратной 120, которая является делением, чтобы разделить переменную.

Но когда я пытаюсь применить тот же метод к второму уравнению (умножая обе части уравнения на одно и то же число 120, в данном случае это не работает, как я ожидаю).

Я могу решить это, разделив 120 на 0,83, но это не тот же метод, что и выше.

Главное для меня здесь — это приобрести какой-то метод решения такого уравнения, и я научился разделять переменную, выполняя обратную операцию с обеих сторон, поэтому, если вы можете указать мне, что я я делаю неправильно здесь? Я предпочитаю оставаться с методом выше. Спасибо.

• алгебра-предварительное исчисление

$\endgroup$

4

$\begingroup$

Для второго уравнения умножьте обе части на $x$; это даст тебе $0,83x = 123,$$ Теперь вы находитесь в той же ситуации, что и первое уравнение, которое вы знаете, как решить.

В качестве альтернативы вы можете взять взаимное вознаграждение с обеих сторон и перейти от 0,83 доллара США = 123/x$$ к $$\frac{1}{0,83} = \frac{x}{123}.$$ С $$\frac{x}{123} = \frac{1}{123}\times x,$$ вы снова находитесь в той же ситуации, что и первое уравнение.

$\endgroup$

2

$\begingroup$

Во втором уравнении

0,83 = 123/x

0,83 = 123 X 1/x

0,83/123 = 1/x

Возьмем обратную величину предыдущего уравнения, и получим 1 903005.

Найдя значение x в приведенном выше уравнении, вы получите решение таким же образом, как и в уравнении 1 вашего вопроса.

$\endgroup$

$\begingroup$

При условии $x\neq0$ мы можем умножить обе части нашего уравнения на $x$, чтобы получить: $$\begin{выравнивание*} 0,83 &= 123/ х \ тогда и только тогда, когда 0,83x=123. \end{выравнивание*}$$ Затем мы делим обе части на $0,83$, так что LHS содержит только искомую переменную: $$\begin{align*} \dfrac{0,83x}{0,83}=\dfrac{123}{0,83}\Rightarrow x=\dfrac{123}{0,83}\приблизительно 148,19 \end{выравнивание*}$$

$\endgroup$

$\begingroup$

В основном,

для первого: $$ 100 = 120\х.