|
В предыдущей главе мы решали уравнения и неравенства аналитически, и сейчас вдохнём в эти
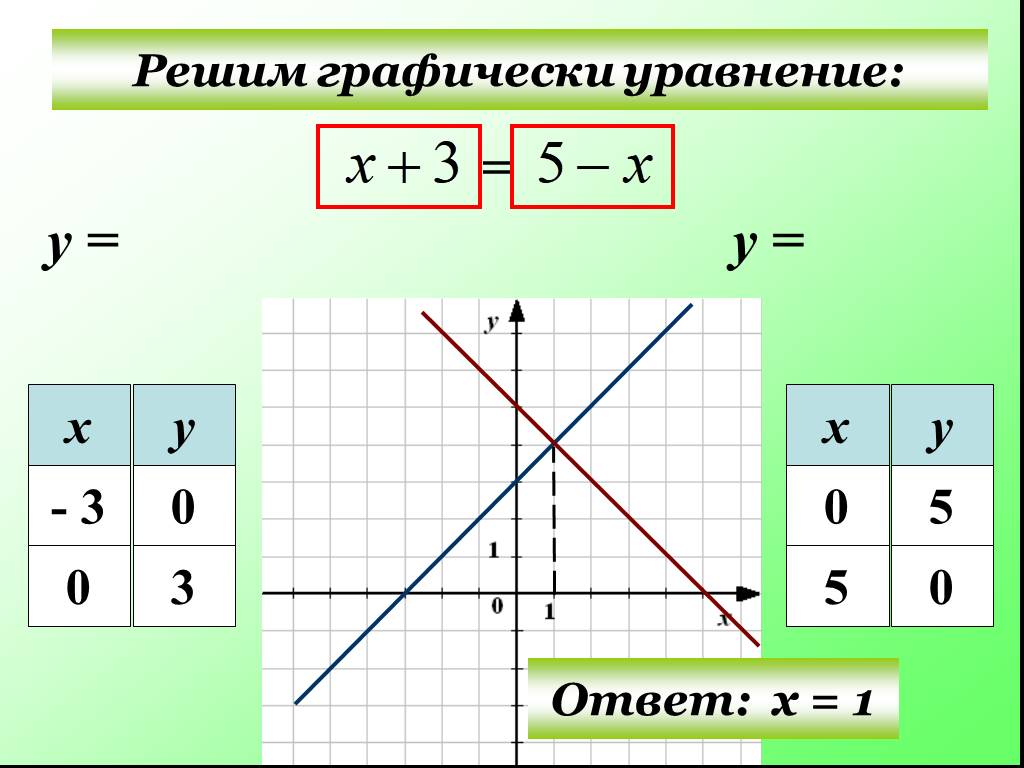
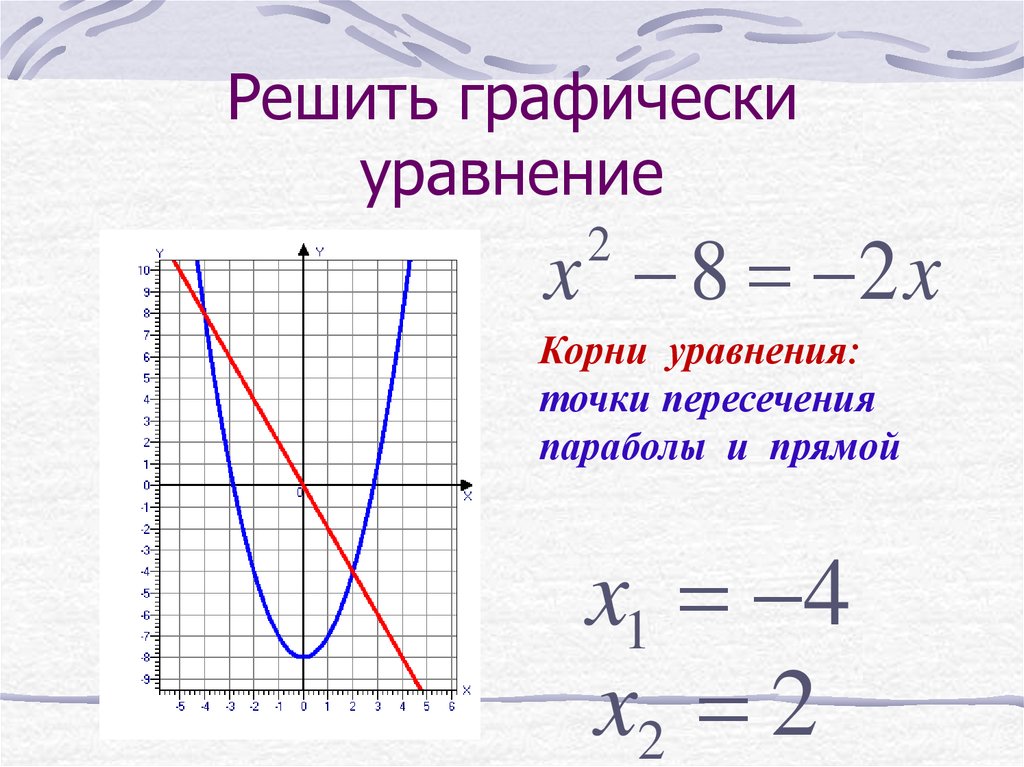
задачи геометрический смысл. И это вас вдохновит! – это будет просто, это будет круто и это будет красиво! А, главное, чрезвычайно полезно. Решением неравенства являются те промежутки, на которых график выше оси , Соответственно, решением неравенства является интервал . В случае нестрогих неравенств к решениям нужно добавить пограничные точки: и соответственно. А если вам не хочется возиться с нахождением опорных точек, «тыкая в них наугад» (ведь параболы бывают большие, размашистые), то есть общий случай: Чтобы решить уравнение , нужно построить графики и найти их точки пересечения. «Иксовые» координаты этих точек и будут решениями. Если графики не пересекаются, то действительных решений нет. Таким образом, вместо решения уравнения с вычерчиванием параболы,
представим его в виде и изобразим элементарные графики: Решением неравенства являются те промежутки, на которых график выше графика , и, наоборот: – там, где график ниже графика . Так, решением неравенства являются промежутки – поскольку на них парабола расположена выше прямой. И, наоборот, решением неравенства является промежуток , так как здесь парабола расположена ниже прямой. Аналогично для нестрогих неравенств. Кстати, всем ли понятно, как из общих правил получаются частные правила для и ? Элементарно. Это тот случай, когда , а эта функция задаёт ось . Когда удобно использовать графический метод? Прежде всего, в простых случаях. Так, при решении неравенства проще мысленно представить гиперболу, нежели использовать метод интервалов. Где гипербола Графический способ спасёт в экстремальных ситуациях, например, когда вы позабыли, как решать квадратное уравнение, а помощи ждать неоткуда. Используйте приём, описанный выше – вместо уравнения рассмотрИте с двумя простыми графиками, не построить которые – эт нужно постараться 🙂 Иногда графика эффективна в уравнениях «разнородными» функциями. Так, для решения уравнения не существует стандартных аналитических методов, но это не беда. Мысленно представляем график и график синуса (о котором позже), после чего сразу понятно, что уравнение имеет единственный корень . Кстати, в некоторых задачах нужно просто определить количество корней и / или их приблизительное расположение, и на этот вопрос зачастую легко ответит чертёж! Разумеется, графики должны быть простыми – это важнейшее условие применения графического метода. И после этого невероятно полезного параграфа возвращается к нашим функциям: 3.6. Показательная функция 3.4. СтепеннАя функция | Оглавление | |
Графическое решение уравнений
Задание. Решить уравнение ax² + bx + c = esin(hx+k) в диапазоне -2 ≤ x ≤ 2 при a=2, b=3
Для этого необходимо сначала построить таблицу и графики функций:
f1 = ax² + bx + c
f2 = esin(hx+k)
В ячейки D4:D12 таблицы с начальными условиями запишем последовательно текстовые подсказки для исходных данных: Xn, Xk, N, dX, a, b, c, h, k.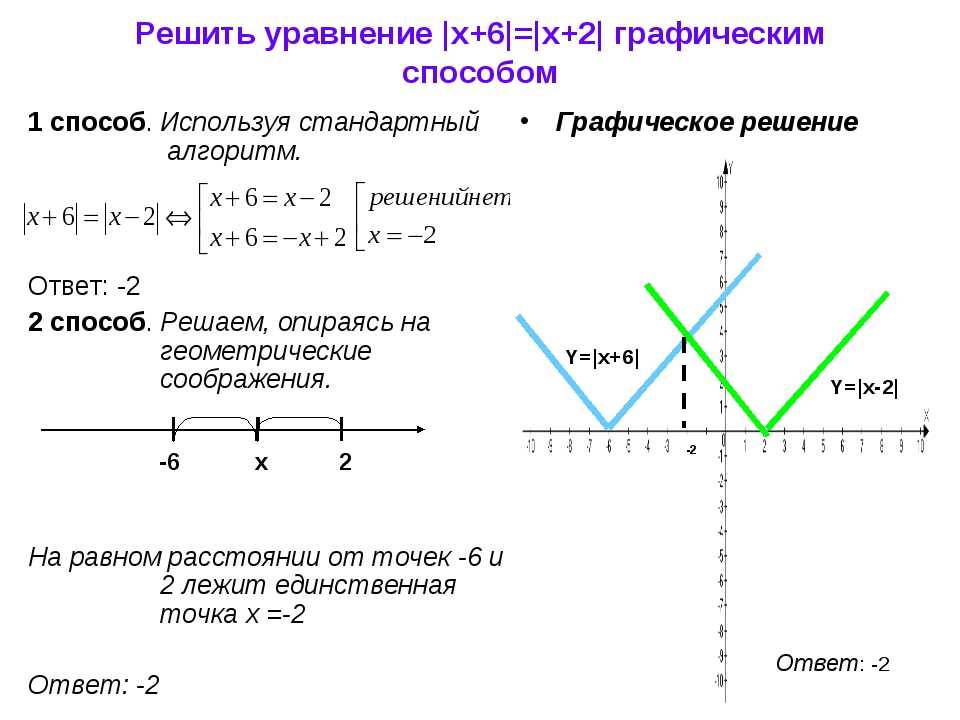
Зададим количество точек по оси X (количество строк таблицы) равным, например, N=15.
Заполним ячейки E4:E6 начальными значениями Xn, Xk, N, соответственно.
Из формулы для определения количества значений функций (строк таблицы) из предыдущего раздела:
Получим формулу для вычисления шага (приращения) по оси X:
Поэтому в ячейку E7 записываем формулу =(E5-E4)/(E6-1). Значение этой ячейки мы будем использовать для приращения аргумента функций X в основной таблице. В ячейки E8:E12 заносим значения коэффициентов a, b, c, h, k. Добавим еще две ячейки с ограничениями F4, F5:
Теперь заполняем шапку основной таблицы:
В данной задаче (как и в задаче табулирования функции) текущее значение X должно выражаться через относительный адрес (ссылка на предыдущую ячейку в столбце), а шаг изменения dX — через абсолютный адрес $E$7.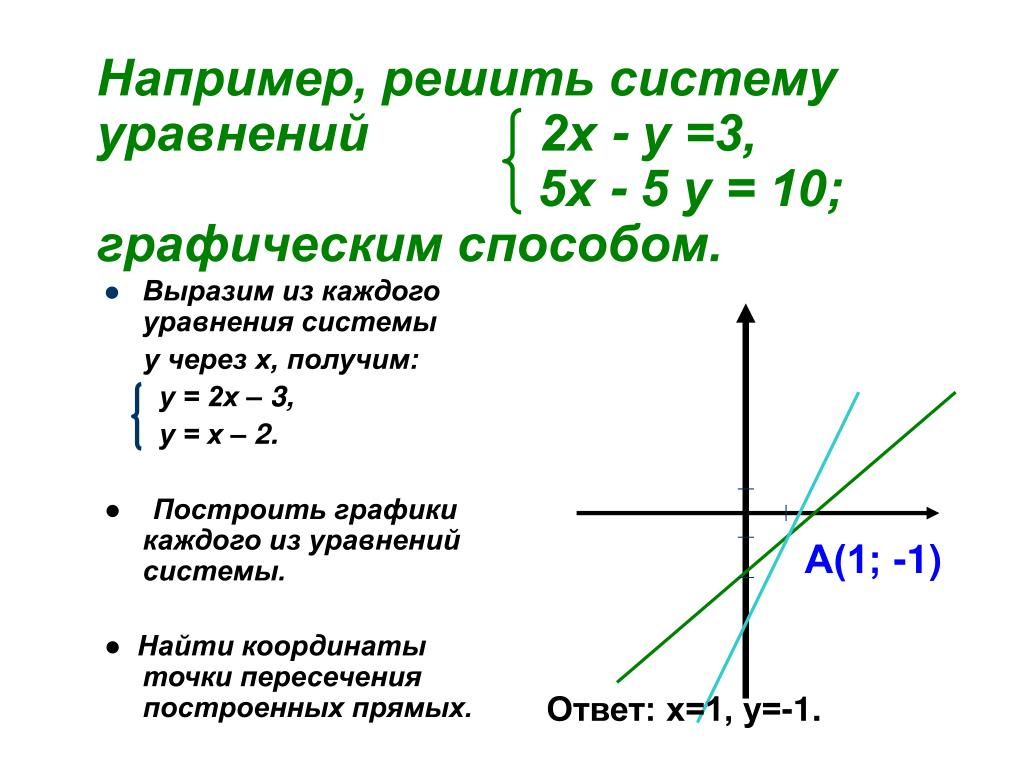
Записываем в ячейку A15 формулу =E4 (или =$E$4 — здесь это неважно, поскольку мы не собираемся копировать эту ячейку) — это начальное значение аргумента функций X равное Xn.
Заносим в ячейку A16 формулу =A15+$E$7 — эта формула вычисляет текущее значение аргумента X = X + dX.
Теперь выполняем автозаполнение (распространяем формулу из ячейки A16 на ячейки A17:A29). Для этого выделяем ячейку A16, перемещаем указатель мыши на маркер автозаполнения и “растягиваем” формулу до ячейки A29.
В результате этого будет заполнен первый столбец основной таблицы, содержащий значения аргумента функций X:
Записываем формулы для функций f1(x) и f2(x) в ячейки B15 и C15, используя в качестве аргумента x относительную ссылку на ячейку A15. 2+$E$9*A15+$E$10.
2+$E$9*A15+$E$10.
В ячейку C15 вводим формулу =EXP(SIN($E$11*A15+$E$12)).
В ячейку D15 заносим формулу разности функций =B15-C15 (адреса используем относительные, поскольку они должны меняться в каждой строке).
Теперь с помощью автозаполнения заполняем сразу три столбца (выделяем три смежные ячейки B15:D15, перемещаем указатель мыши на маркер автозаполнения (правый нижний угол самой правой ячейки
Затем нарисуем диаграмму. Выделяем всю таблицу с шапкой А14:D29, затем щелкаем по большой кнопке Точечная в группе Диаграмма на вкладке Вставка и выбираем Точечная с гладкими кривыми и маркерами:
В результате получится диаграмма следующего вида:
Корни уравнения находятся на пересечении графиков функций f1(x) и f2(x), то есть там, где третий (разностный) график f1(x) и f2(x) пересекает ось x (в четвертом столбце таблицы меняется знак).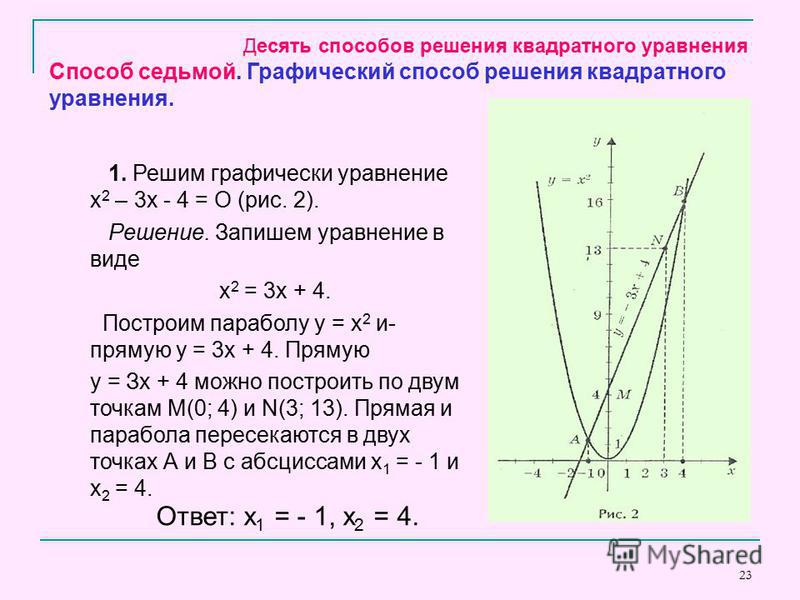 В этой задаче при заданных исходных данных получаем приближенное решение уравнения X1 ≈ -1,6 (значение x находится в промежутке между второй и третьей строчками таблицы) и X2 ≈ +0,4 (значение x находится в промежутке между девятой и десятой строчками таблицы).
В этой задаче при заданных исходных данных получаем приближенное решение уравнения X1 ≈ -1,6 (значение x находится в промежутке между второй и третьей строчками таблицы) и X2 ≈ +0,4 (значение x находится в промежутке между девятой и десятой строчками таблицы).
Это и есть графическое решение уравнения. По полученным графикам функций мы можем судить о количестве корней и их приближенному значению. Точное решение уравнения возможно с помощью инструмента Поиск решения.
« Назад
Вперед »
2.2 — Графическое решение уравнений
2.2 — Графическое решение уравненийПерехваты
- x-пересечение
- Точка пересечения с осью X — это точка, в которой график уравнения пересекает ось X. Пересечение по оси x можно найти, подставив y=0 в уравнение и найдя x. Х-пересечение также называется решением, корнем или нулем уравнения.
- Y-точка пересечения
- Точка пересечения с осью y — это точка пересечения графика уравнения с осью y.

Нет требования, чтобы уравнение имело точку пересечения x или y. Это также возможно, что может быть более одного перехвата.
Перехват, корень, ноль, решение?
Следующие операторы эквивалентны:
- Точка (a,0) является точкой пересечения x графика y=f(x)
- x=a является нулем или корнем функции f
- x=a является решением уравнения f(x)=0
- (x-a) является множителем f(x)
Поиск корней с помощью графического калькулятора
Чтобы найти корни функции с помощью графического калькулятора, может потребоваться поставить уравнение в стандартную форму f(x)=0. Для этого вам может понадобиться переместить все в одну сторону уравнения. Неважно, в какую сторону вы переместите термины, решения будет одинаковым в любом случае. Затем нарисуйте уравнение y=f(x) на калькуляторе.
Книга научит вас использовать функции масштабирования и трассировки вашего калькулятора, чтобы найти нули числа. функция. Есть гораздо более простой и точный способ.
функция. Есть гораздо более простой и точный способ.
- Используйте клавишу [Calc] (2 nd Trace) и выберите опцию zero (TI83) или root (TI82).
- Когда запрашивается левая или нижняя граница, используйте клавишу со стрелкой влево, чтобы установить курсор на слева от нуля и нажмите клавишу [Enter].
- Когда он запрашивает правую или верхнюю границу, используйте клавишу со стрелкой вправо, чтобы установить курсор на справа от нуля и нажмите клавишу [Enter].
- Когда будет запрошено предположение , используйте клавишу со стрелкой влево, чтобы вернуться к точке, ближайшей к х-пересечению, и нажмите клавишу [Enter].
- Возвращенная координата x представляет собой точку пересечения x, корень, ноль или решение, которое вы ищете.
Метод масштабирования и трассировки будет работать, но гораздо быстрее и точнее использовать
параметры в разделе [Расч. ].
].
Поиск пересечений с помощью графического калькулятора
Чтобы найти пересечение двух уравнений с помощью графического калькулятора, введите две функции введите в калькулятор как y 1 и y 2 и нарисуйте их оба. Поиграйте со смотровым окном, пока найди точку пересечения, а потом…
- Используйте клавишу [Calc] и выберите опцию пересечь .
- Будет запрошена первая кривая. Если активны только два графика, вы можете просто нажать [Enter] как по умолчанию это первая кривая. Если у вас более двух активных графиков, используйте кнопки вверх или вниз. клавиши со стрелками для выбора нужной функции, а затем нажмите клавишу ввода. Неважно, где на кривая нажимаешь ввод.
- Он запросит вторую кривую. Если активны только два графика, вы можете просто нажать [Войти]. Используйте клавиши со стрелками вверх или вниз, если вам нужно выбрать другую функцию.
- Затем он запрашивает предположение .
 Используйте клавиши со стрелками влево или вправо, чтобы перейти к позиции, близкой к
точки пересечения и нажмите [Enter].
Используйте клавиши со стрелками влево или вправо, чтобы перейти к позиции, близкой к
точки пересечения и нажмите [Enter]. - Возвращаются координаты x и y точки пересечения.
Можно найти решение уравнения в нестандартной форме, если y 1 сюжет левая часть уравнения, график y 2 является правой частью уравнения, и с использованием пересекаются с вариантом . Однако гораздо удобнее и экономнее по времени переписать уравнение в стандартной форме и вместо этого используйте опцию zero или root .
Как решать уравнения графически — Помощь с IGCSE GCSE Maths
ДОМ | Как решать уравнения графически В этом разделе я объясню вам, как решать уравнения графически. Это типичные вопросы экзаменов IGCSE GCSE по математике, поэтому будьте внимательны во время повторения математики. Я объясню вам шаг за шагом, как вы можете решать уравнения графически, чтобы вы лучше сдавали экзамены по математике. |



 И ещё этот метод хорош для лучшего понимания математики.
И ещё этот метод хорош для лучшего понимания математики. Ибо строить для решения –
затея как-то не очень 🙂 Уж лучше метод интервалов.
Ибо строить для решения –
затея как-то не очень 🙂 Уж лучше метод интервалов.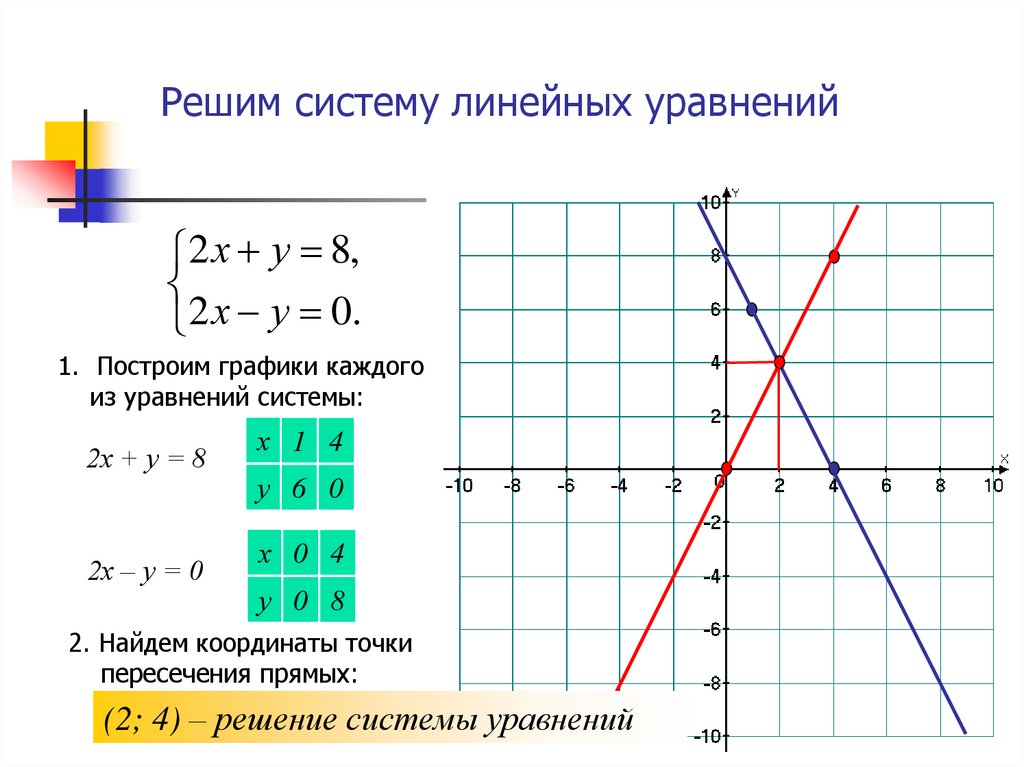
 Используйте клавиши со стрелками влево или вправо, чтобы перейти к позиции, близкой к
точки пересечения и нажмите [Enter].
Используйте клавиши со стрелками влево или вправо, чтобы перейти к позиции, близкой к
точки пересечения и нажмите [Enter].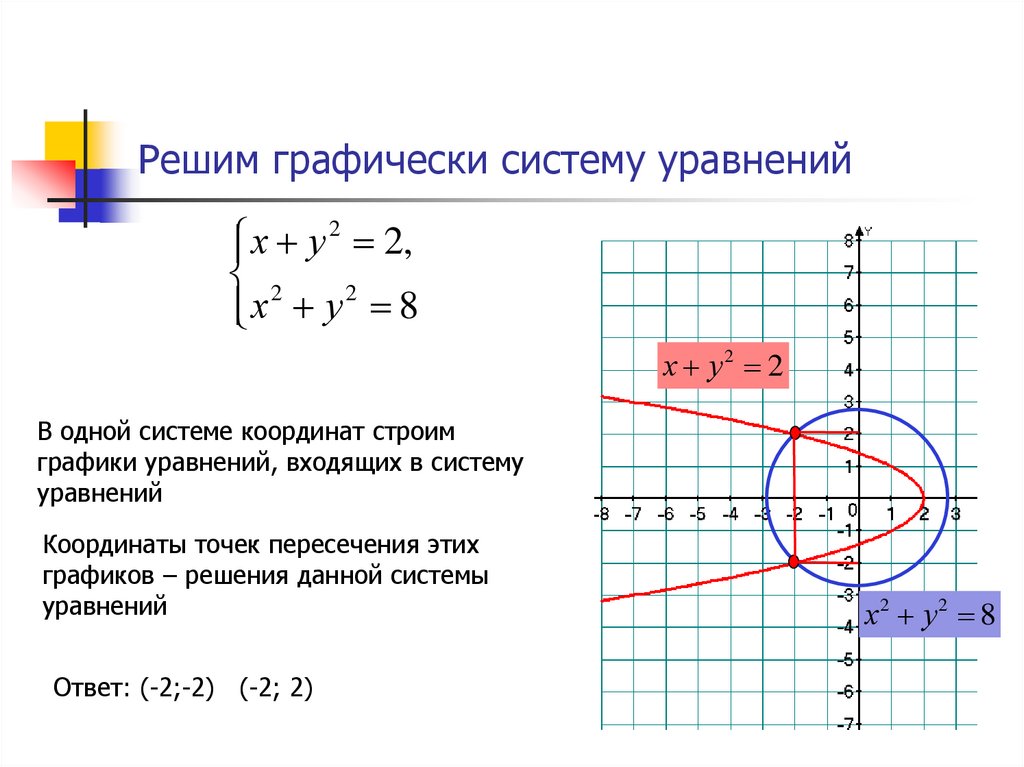 Графики «расстояние-время»
Графики «расстояние-время»