Минор и алгебраическое дополнение матрицы.
Минор и алгебраическое дополнение матрицы.Навигация по странице:
- Минор матрицы
- Алгебраическое дополнение матрицы
- Свойства алгебраического дополнения матрицы
Определение.
Минором Mij к элементу aij определителя n-го порядка называется определитель (n — 1)-го порядка, полученный из исходного определителя вычеркиванием i-той строки и j-того столбца.
Пример 1.
Найти миноры матрицы A
A = 571-410203
Решение:
| M11 = |
|
= |
|
| M11 = |
|
= 1·3 — 0·0 = 3 — 0 = 3 |
| M12 = |
|
= -4·3 — 0·2 = -12 -0 = -12 |
| M13 = |
|
= -4·0 — 1·2 = 0 — 2 = -2 |
| M21 = |
|
= 7·3 — 1·0 = 21 — 0 = 21 |
| M22 = |
|
= 5·3 — 1·2 = 15 — 2 = 13 |
| M23 = |
|
= 5·0 — 7·2 = 0 — 14 = -14 |
| M31 = |
|
= 7·0 — 1·1 = 0 — 1 = -1 |
| M32 = |
|
= 5·0 — 1·(-4) = 0 + 4 = 4 |
| M33 = |
|
= 5·1 — 7·(-4) = 5 + 28 = 33 |
Определение.
Алгебраическим дополнением Aij к элементу aij определителя n-го порядка называется число
Aij = (-1)i + j · Mij
Сумма произведений элементов строки (столбца) определителя на алгебраические дополнения к элементам этой строки (столбца) равна определителю матрицы:
n Σ aij·Aij = det(A) j = 1 Сумма произведений элементов строки (столбца) определителя на алгебраические дополнения к элементам другой строки (столбца) равна нулю:
n Σ akj·Aij = 0 (i ≠ k) j = 1 Сумма произведений элементов «произвольной» строки на алгебраические дополнения к элементам i-той строки определителя равна определителю, в котором вместо i-той строки записана «произвольная» строка.

Пример 2.
Найти алгебраические дополнения матрицы A
A11 = 571-410203
Решение:
A11 = (-1)1 + 1·M11 = (-1)2·1003 = 1·3 — 0·0 = 3 — 0 = 3
A12 = (-1)1 + 2·M12 = (-1)3·-4023 = -(-4·3 — 0·2) = -(-12 -0) = 12
A13 = (-1)1 + 3·M13 = (-1)4·-4120 = -4·0 — 1·2 = 0 — 2 = -2
A21 = (-1)2 + 1·M21 = (-1)3·7103 = -(7·3 — 1·0) = -(21 — 0) = -21
A22 = (-1)2 + 2·M22 = (-1)4·5123 = 5·3 — 1·2 = 15 — 2 = 13
A23 = (-1)2 + 3·M23 = (-1)5·5720 = -(5·0 — 7·2) = -(0 — 14) = 14
A31 = (-1)3 + 1·M31 = (-1)4·7110 = 7·0 — 1·1 = 0 — 1 = -1
A32 = (-1)3 + 2·M32 = (-1)5·51-40 = -(5·0 — 1·(-4)) = -(0 + 4) = -4
A33 = (-1)3 + 3·M33 = (-1)6·57-41 = 5·1 — 7·(-4) = 5 + 28 = 33
Онлайн калькуляторы с матрицами.
Упражнения с матрицами.
Минор k-го порядка
Минором порядка k заданной матрицы называется определитель любой квадратной матрицы k-го порядка, которая находится на пересечении произвольных k столбцов и k строчек прямоугольной матрицы.
k столбцов
k
строк
• •• *• *
• •• *
• •
•• *•
••
•*
•*
••
•*
••
•*
••
••
•*
•*
••
•*
••
•*
••
• | • | • | • |
• | • | * |
|
• | |||
• | • | * | • |
• | • | • |
|
• | |||
• | • | * | • |
• | • | • |
|
• | |||
• | • | * |
|
• | |||
• | • | • |
|
• |
* * * *
* * * *
* * * *
* * * *
| 1 | 5 | 2 |
|
| 3 | 1 | 2 |
|
|
| |||
| −2 | 0 | 5 |
|
|
|
Решение
Миноры первого порядка
|
| 1 |
| =1 |
| 5 |
| =5 |
| 2 |
| = 2 | ||||||
|
|
|
|
|
| |||||||||||||
|
| 3 |
| =3 |
| −2 |
| = −2 |
| 0 |
|
| = 0 | |||||
|
|
|
|
|
|
| ||||||||||||
| 1 | 5 | 2 |
|
| 3 | 1 | 2 |
|
|
| |||
| −2 | 0 | 5 |
|
|
|
Миноры второго |
| порядка |
|
|
|
|
|
|
| |||||||||||
| 1 | 5 |
| = −14 |
| 1 | 2 |
| = −4 |
| 5 | 2 |
|
| =8 | |||||
|
|
|
|
|
|
| ||||||||||||||
| 3 | 1 |
|
|
|
|
| 3 | 2 |
|
|
|
|
| 1 | 2 |
|
|
|
|
| 1 |
| 5 |
| =10 |
| 1 | 2 |
| =9 |
| 5 | 2 |
|
|
| = 25 | |||
|
|
|
|
|
|
| ||||||||||||||
| −2 | 0 |
|
|
| −2 | 5 |
|
|
| 0 | 5 |
|
|
|
| ||||
| 3 | 1 |
| = 2 |
| 3 | 2 |
| =19 |
| 1 | 2 |
|
|
| =5 | ||||
|
|
|
|
|
|
| ||||||||||||||
| −2 | 0 |
|
|
| −2 | 5 |
|
|
| 0 | 5 |
|
|
|
| ||||
Минор третьего порядка |
|
|
| ||||||||||
|
| 1 | 5 | 2 |
|
| 1 | 2 |
| 3 2 |
| 3 1 |
|
|
|
|
|
| |||||||||
|
|
|
|
|
|
| |||||||
|
| 3 | 1 | 2 |
| =1 | −5 | +2 | =1 5 −5 19 +2 2 = −86 | ||||
|
| −2 | 0 | 5 |
|
| 0 | 5 |
| −2 5 |
| −2 0 |
|
|
|
|
|
|
|
|
|
|
|
| |||
Рангом матрицы A называется максимальный порядок отличного от нуля минора этой матрицы.
Обозначение: r(A) или rang(A)
r(Am×n)≤min(m,n)
Пример. Определить ранг матрицы |
| 3 | 1 | −2 | 7 | 0 |
|
|
|
|
|
|
|
| |
|
| 1 | 2 | 0 | 5 | 2 |
|
|
|
|
Решение
m = 2 n =5 r ≤ min(m, n)
r ≤ min(2,5) r ≤ 2
13 12 = 6 −1 =5
r = 2
Базисным минором называется любой из отличных от нуля миноров матрицы А, порядок которого равен r(A).
Замечание. Базисных миноров может быть несколько.
Минор матрицы — способы, порядок и примеры вычисления » Kupuk.net
Одним из ключевых понятий в линейной алгебре является минор матрицы. Зная, что это такое и как его вычислить, определить ранг матриц любого порядка не составит труда. По сути, это определитель, находимый путём убирания из рассматриваемой матрицы вертикальных и горизонтальных полос, на пересечении которых находится элемент aij. Существует несколько видов алгебраических миноров, по значению которых можно судить об обратимости, а значит, и возможности нахождения линейной регрессии.
Общие сведения
При решении систем, состоящих из алгебраических и дифференциальных уравнений, для удобной их записи применяется таблица. Она содержит строки и столбцы, пересечение которых определяется элементами. Количество строк характеризуется числом уравнений, а столбцов — количеством неизвестных величин. После построения такой таблицы решение сводится к работе с ней. Совокупность элементов такой таблицы называют матрицей.
Над несколькими матрицами можно выполнять различные арифметические действия: преобразовывать, умножать, складывать. При этом допускается умножение строки на числа, отличные от нуля, сложение строк между собой и изменение их положения. Обозначают матрицу с помощью заглавной буквы латинского алфавита. Характеризуется она размерностью и может быть квадратной или прямолинейной.
При математической записи используют индексы. Первый из них обозначает строки, а второй — столбцы. На месте их пересечения находится элемент. То есть таблица вида m x n записывается как A = (aij)m, n, где: aij — элемент матрицы, располагающийся на пересечении и-той строки и йо-того столбца. Ранг же матрицы показывает наибольшее число линейно независимых столбцов или строк, при этом он не может превосходить размерность.
Важным параметром квадратной матрицы является определитель (детерминант). При его нахождении используется минор. Существует несколько его разновидностей:
- элемента;
- дополнительный;
- главный;
- базисный;
- окаймляющий.

В общем случае под определением минора матрицы понимают определитель, находимый с помощью удаления строки и столбца определённого элемента. При рассмотрении алгебраических дополнений совместно с ними используют понятие угловой минор.
Для энного порядка под ним понимают определитель, полученный из набора элементов, находящихся вместе пересечения начальных эн строк и эн столбцов. Тут следует отметить, что алгебраическое дополнение применяется к элементу aij определителя и берётся со знаком (-1)i+j.
Квадратная матрица
Минор принято разделять на элементный и матричный. Для лучшего понимания сначала следует разобрать минор квадратной матрицы. Рассматривать нужно её, так как минор — это определитель, а он бывает только у квадратной системы уравнений. Параметр элемента матрицы и определителя находят одинаково.
Вычисление минора обычно не вызывает трудностей. При этом стоит помнить простые правила определения детерминанта:
При этом стоит помнить простые правила определения детерминанта:
- для системы первого порядка определитель равен единственному элементу;
- в системах второго порядка детерминант находится из разницы произведений диагоналей в таблице;
- для вычисления определителя в матрицах высшего порядка используют рекурсивную формулу.
Пусть необходимо определить параметр элемента i, j. Для этого нужно посмотреть на записанную таблицу и выделить и-тую строчку и йо-тый столбец. На их пересечении будет стоять цифра, которая соответствует элементу aij. После вычёркивания элементов, расположенных от него по вертикали и горизонтали, оставшиеся в наборе и будут являться минором матрицы или определителя.
Например, пусть имеется определитель вида:
|2 5 7 8 9 |
|2 0 -2 21 13|
|2 -3 4 19 0|
|3 1 8 -2 1|
|4 6 5 -3 9 |
Нужно найти минор два три. На пересечении второй строчки и третьего столбца стоит цифра минус два. Убрав вторую соответствующую ей вертикаль и третью горизонталь, можно получить искомый минор M23:
Убрав вторую соответствующую ей вертикаль и третью горизонталь, можно получить искомый минор M23:
|2 5 7 8 9 |
|2 -3 1 8 0 |
|3 1 -2 1|
|4 6 -3 9|
Теперь, чтобы найти минор единицы, нужно вычислить определитель полученной матрицы четвёртого порядка. Для этого удобно использовать теорему Лапласа для разложения по любой строке. Выбирать лучше ту, где стоят нули. После преобразования полученный ответ и будет минором. Аналогично выполняют действия и для определителя.
Алгебраическое дополнение элемента находится по формуле: Aij = (-1) i+j * Мij. Это выражение справедливо для любой квадратной матрицы. Для рассматриваемого примера такое дополнение будет равно следующему произведению: A23 = (-1)2+3 * M23 = — M23. Минор и алгебраическое дополнение имеют численные значения. Но при вычислении последнего необходимо учитывать, что сумма произведения определителя на дополнение к элементам будет равняться определителю, а сложение произведений двух элементов столбца или строки даст в ответе ноль.
Главный и базисный определитель
Минором высшего уровня описывают систему, состоящую из столбцов и строк, число которых превышает два. То есть минор восьмого порядка представляет собой определитель, состоящий из восьми столбцов и такого же числа строк. Тут следует отметить, что исходная матрица должна иметь больший порядок.
В таблице высшего порядка можно выделить несколько миноров. Например, в матрице восьмого уровня выделить пять столбцов и пять строк. Брать горизонтальные и вертикальные линии можно произвольно. В местах пересечения будут находиться значения, обозначающие элементы минора пятого порядка.
Записывают их соответственно, начиная с первой строки. После того как все члены выписаны, должен получиться новый определитель пятого порядка. Таких миноров указанного порядка может быть несколько.
В таблице чисел имеется главная диагональ. Начинается она с правого верхнего угла, то есть с элемента a11, и заканчивается на последнем правом элементе.
В полученном миноре также можно выделить такую диагональ.
Если взять минор таким способом, что главная его диагональ будет состоять из элементов диагонали исходной таблицы, то такой минор называют главным. Иными словами, эта таблица, которая включает в себя элементы основной диагонали исходной матрицы. При этом необязательно, чтобы в главный минор матрицы были включены все главные элементы. Определитель же, находящийся из первых строк и столбцов, называется угловым минором матрицы.
Базисный определитель показывает, какой наибольший порядок может иметь полученный минор. Например, для системы данных, состоящей из семи строк и восьми столбцов, наибольший определитель может быть седьмого порядка. При этом базисным считается также последний определитель, который не равняется нулю. Если система уравнений имеет девятый порядок и при вычислениях выяснится, что система шестого уровня вырожденная, то предшествующий ему определитель также будет называться базисным. Значение базиса всегда будет наибольшим. Строки и столбцы, из которых состоит базис, называют также базисными. Их может быть несколько.
Значение базиса всегда будет наибольшим. Строки и столбцы, из которых состоит базис, называют также базисными. Их может быть несколько.
Когда из исходной таблицы выбран определитель не высшего порядка, то следующий за ним называется окаймляющим. Это значит, что необходимо добавить одну строку и столбец. Такого типа определителей может быть несколько, так как для того, чтобы их построить, можно добавить любую строку или столбец.
Решение задач
Для закрепления материала в школе и высших учебных заведениях учащимся предлагают выполнить расчёт несколько типовых заданий разной сложности. Умение их решать является доказательством понимания теории. Вот некоторые из них рекомендуемые для самостоятельного решения.
Найти в указанной матрице все определители второго уровня и алгебраические дополнения:
|5 7 3|
|8 5 6|
|6 8 10|
Для решения этой задачи нужно рассматривать первую и вторую строчки. Последовательно убирая строки и столбцы методом вычёркивания, можно получить шесть результатов:
Последовательно убирая строки и столбцы методом вычёркивания, можно получить шесть результатов:
В следующей задаче рассматривается квадратная матрица три на три, в которой необходимо найти дополнительную характеристику:
(1 2 0)
(-2 0 3)
(3 4 -2)
По условию в таблице имеется девять позиций, для которых можно найти дополнительный элемент. При решении нужно последовательно их все перебрать, вычёркивая соответственные столбцы и строки:

В следующем примере необходимо рассчитать первые три алгебраических дополнения. Пусть дана матрица A:
(1 2 -1)
(0 1 2)
(3 2 1)
Для нахождения первого параметра нужно вычеркнуть первый столбец и строку, при этом для определения знака использовать формулу: A = M (-1) j+i. В итоге получится определитель: A11 = |1 2| |2 1| = 1 — 4 = 3. Знак положительный, так как минус единица будет во второй степени. При этом можно отметить, что далее знак будет попросту чередоваться. Другие вычисления нужно делать аналогично: A12 = |0 2| |3 1| = (-6) * (-1) = 6; A13 = |0 1| |3 2| = -3.
Как видно из примеров, вычисления обычно не вызывают трудностей, но требуют внимательности и усидчивости. Особенно это касается нахождения обратной матрицы. Вычисляется она с помощью алгебраических дополнений, которые равны минорам, умноженным на минус единицу. Довольно часто знаки путают, и в итоге получается неправильный ответ. Поэтому в случае сложных систем есть резон использовать онлайн-калькуляторы.
Поэтому в случае сложных систем есть резон использовать онлайн-калькуляторы.
Использование интернет-калькулятора
В интернете есть определённая группа сайтов, позволяющая выполнять различные математические вычисления в автоматическом режиме. На их страницах содержится специальный скрипт, выполняющий нахождение минора матрицы онлайн любой сложности. При этом от потребителя не требуется никаких особых знаний, он даже и вовсе может ничего не понимать в алгебраических вычислениях.
Всё, что ему необходимо будет сделать для получения ответа, — это ввести исходные данные в предложенную форму и нажать кнопку «Вычислить». Система автоматически определит нужный алгоритм и, используя свойства матрицы, выведет на экран ответ. При этом, кроме результата, пользователю будет предоставлена возможность ознакомиться с подробным решением.
По отзывам потребителей, из множества таких сервисов можно выделить пять следующих сайтов:

Все указанные сайты доступны на русском языке, бесплатны, имеют простой и понятный интерфейс. На их страницах содержится справочная и теоретическая математическая информация. Кроме неё, для каждого раздела приводится типовой пример с объяснением. Использование онлайн-калькуляторов поможет сэкономить время и научит правильно выполнять действия по вычислению миноров.
Их использование будет полезным не только ученикам или студентам, желающим научиться самостоятельно решать задачи, но и инженерам, выполняющим сложные вычисления. Для специалистов они довольно востребованы, так как при самостоятельном решении небольшая ошибка по невнимательности приведёт к неправильному ответу, что исключено при расчёте в автоматическом режиме.
Для специалистов они довольно востребованы, так как при самостоятельном решении небольшая ошибка по невнимательности приведёт к неправильному ответу, что исключено при расчёте в автоматическом режиме.
Минор матрицы — способы, порядок и примеры вычисления
Одним из ключевых понятий в линейной алгебре является минор матрицы. Зная, что это такое и как его вычислить, определить ранг матриц любого порядка не составит труда. По сути, это определитель, находимый путём убирания из рассматриваемой матрицы вертикальных и горизонтальных полос, на пересечении которых находится элемент aij. Существует несколько видов алгебраических миноров, по значению которых можно судить об обратимости, а значит, и возможности нахождения линейной регрессии.
Содержание
- Общие сведения
- Квадратная матрица
- Главный и базисный определитель
- Решение задач
- Использование интернет-калькулятора
Общие сведения
При решении систем, состоящих из алгебраических и дифференциальных уравнений, для удобной их записи применяется таблица. Она содержит строки и столбцы, пересечение которых определяется элементами. Количество строк характеризуется числом уравнений, а столбцов — количеством неизвестных величин. После построения такой таблицы решение сводится к работе с ней. Совокупность элементов такой таблицы называют матрицей.
Она содержит строки и столбцы, пересечение которых определяется элементами. Количество строк характеризуется числом уравнений, а столбцов — количеством неизвестных величин. После построения такой таблицы решение сводится к работе с ней. Совокупность элементов такой таблицы называют матрицей.
Над несколькими матрицами можно выполнять различные арифметические действия: преобразовывать, умножать, складывать. При этом допускается умножение строки на числа, отличные от нуля, сложение строк между собой и изменение их положения. Обозначают матрицу с помощью заглавной буквы латинского алфавита. Характеризуется она размерностью и может быть квадратной или прямолинейной.
При математической записи используют индексы. Первый из них обозначает строки, а второй — столбцы. На месте их пересечения находится элемент. То есть таблица вида m x n записывается как A = (aij)m, n, где: aij — элемент матрицы, располагающийся на пересечении и-той строки и йо-того столбца. Ранг же матрицы показывает наибольшее число линейно независимых столбцов или строк, при этом он не может превосходить размерность.
Важным параметром квадратной матрицы является определитель (детерминант). При его нахождении используется минор. Существует несколько его разновидностей:
- элемента;
- дополнительный;
- главный;
- базисный;
- окаймляющий.
В общем случае под определением минора матрицы понимают определитель, находимый с помощью удаления строки и столбца определённого элемента. При рассмотрении алгебраических дополнений совместно с ними используют понятие угловой минор.
Для энного порядка под ним понимают определитель, полученный из набора элементов, находящихся вместе пересечения начальных эн строк и эн столбцов. Тут следует отметить, что алгебраическое дополнение применяется к элементу aij определителя и берётся со знаком (-1)i+j.
Квадратная матрица
Минор принято разделять на элементный и матричный. Для лучшего понимания сначала следует разобрать минор квадратной матрицы. Рассматривать нужно её, так как минор — это определитель, а он бывает только у квадратной системы уравнений. Параметр элемента матрицы и определителя находят одинаково.
Для лучшего понимания сначала следует разобрать минор квадратной матрицы. Рассматривать нужно её, так как минор — это определитель, а он бывает только у квадратной системы уравнений. Параметр элемента матрицы и определителя находят одинаково.
Вычисление минора обычно не вызывает трудностей. При этом стоит помнить простые правила определения детерминанта:
- для системы первого порядка определитель равен единственному элементу;
- в системах второго порядка детерминант находится из разницы произведений диагоналей в таблице;
- для вычисления определителя в матрицах высшего порядка используют рекурсивную формулу.
Пусть необходимо определить параметр элемента i, j. Для этого нужно посмотреть на записанную таблицу и выделить и-тую строчку и йо-тый столбец. На их пересечении будет стоять цифра, которая соответствует элементу aij. После вычёркивания элементов, расположенных от него по вертикали и горизонтали, оставшиеся в наборе и будут являться минором матрицы или определителя.
Например, пусть имеется определитель вида:
|2 5 7 8 9 |
|2 0 -2 21 13|
|2 -3 4 19 0|
|3 1 8 -2 1|
|4 6 5 -3 9 |
Нужно найти минор два три. На пересечении второй строчки и третьего столбца стоит цифра минус два. Убрав вторую соответствующую ей вертикаль и третью горизонталь, можно получить искомый минор M23:
|2 5 7 8 9 |
|2 -3 1 8 0 |
|3 1 -2 1|
|4 6 -3 9|
Теперь, чтобы найти минор единицы, нужно вычислить определитель полученной матрицы четвёртого порядка. Для этого удобно использовать теорему Лапласа для разложения по любой строке. Выбирать лучше ту, где стоят нули. После преобразования полученный ответ и будет минором. Аналогично выполняют действия и для определителя.
Алгебраическое дополнение элемента находится по формуле: Aij = (-1) i+j * Мij. Это выражение справедливо для любой квадратной матрицы. Для рассматриваемого примера такое дополнение будет равно следующему произведению: A23 = (-1)2+3 * M23 = — M23. Минор и алгебраическое дополнение имеют численные значения. Но при вычислении последнего необходимо учитывать, что сумма произведения определителя на дополнение к элементам будет равняться определителю, а сложение произведений двух элементов столбца или строки даст в ответе ноль.
Для рассматриваемого примера такое дополнение будет равно следующему произведению: A23 = (-1)2+3 * M23 = — M23. Минор и алгебраическое дополнение имеют численные значения. Но при вычислении последнего необходимо учитывать, что сумма произведения определителя на дополнение к элементам будет равняться определителю, а сложение произведений двух элементов столбца или строки даст в ответе ноль.
Главный и базисный определитель
Минором высшего уровня описывают систему, состоящую из столбцов и строк, число которых превышает два. То есть минор восьмого порядка представляет собой определитель, состоящий из восьми столбцов и такого же числа строк. Тут следует отметить, что исходная матрица должна иметь больший порядок.
В таблице высшего порядка можно выделить несколько миноров. Например, в матрице восьмого уровня выделить пять столбцов и пять строк. Брать горизонтальные и вертикальные линии можно произвольно. В местах пересечения будут находиться значения, обозначающие элементы минора пятого порядка.
Записывают их соответственно, начиная с первой строки. После того как все члены выписаны, должен получиться новый определитель пятого порядка. Таких миноров указанного порядка может быть несколько.
В таблице чисел имеется главная диагональ. Начинается она с правого верхнего угла, то есть с элемента a11, и заканчивается на последнем правом элементе. В полученном миноре также можно выделить такую диагональ.
Если взять минор таким способом, что главная его диагональ будет состоять из элементов диагонали исходной таблицы, то такой минор называют главным. Иными словами, эта таблица, которая включает в себя элементы основной диагонали исходной матрицы. При этом необязательно, чтобы в главный минор матрицы были включены все главные элементы. Определитель же, находящийся из первых строк и столбцов, называется угловым минором матрицы.
Базисный определитель показывает, какой наибольший порядок может иметь полученный минор. Например, для системы данных, состоящей из семи строк и восьми столбцов, наибольший определитель может быть седьмого порядка. При этом базисным считается также последний определитель, который не равняется нулю. Если система уравнений имеет девятый порядок и при вычислениях выяснится, что система шестого уровня вырожденная, то предшествующий ему определитель также будет называться базисным. Значение базиса всегда будет наибольшим. Строки и столбцы, из которых состоит базис, называют также базисными. Их может быть несколько.
При этом базисным считается также последний определитель, который не равняется нулю. Если система уравнений имеет девятый порядок и при вычислениях выяснится, что система шестого уровня вырожденная, то предшествующий ему определитель также будет называться базисным. Значение базиса всегда будет наибольшим. Строки и столбцы, из которых состоит базис, называют также базисными. Их может быть несколько.
Когда из исходной таблицы выбран определитель не высшего порядка, то следующий за ним называется окаймляющим. Это значит, что необходимо добавить одну строку и столбец. Такого типа определителей может быть несколько, так как для того, чтобы их построить, можно добавить любую строку или столбец.
Решение задач
Для закрепления материала в школе и высших учебных заведениях учащимся предлагают выполнить расчёт несколько типовых заданий разной сложности. Умение их решать является доказательством понимания теории. Вот некоторые из них рекомендуемые для самостоятельного решения.
Умение их решать является доказательством понимания теории. Вот некоторые из них рекомендуемые для самостоятельного решения.
Найти в указанной матрице все определители второго уровня и алгебраические дополнения:
|5 7 3|
|8 5 6|
|6 8 10|
Для решения этой задачи нужно рассматривать первую и вторую строчки. Последовательно убирая строки и столбцы методом вычёркивания, можно получить шесть результатов:
В следующей задаче рассматривается квадратная матрица три на три, в которой необходимо найти дополнительную характеристику:
(1 2 0)
(-2 0 3)
(3 4 -2)
По условию в таблице имеется девять позиций, для которых можно найти дополнительный элемент. При решении нужно последовательно их все перебрать, вычёркивая соответственные столбцы и строки:
При решении нужно последовательно их все перебрать, вычёркивая соответственные столбцы и строки:
В следующем примере необходимо рассчитать первые три алгебраических дополнения. Пусть дана матрица A:
(1 2 -1)
(0 1 2)
(3 2 1)
Для нахождения первого параметра нужно вычеркнуть первый столбец и строку, при этом для определения знака использовать формулу: A = M (-1) j+i. В итоге получится определитель: A11 = |1 2| |2 1| = 1 — 4 = 3. Знак положительный, так как минус единица будет во второй степени. При этом можно отметить, что далее знак будет попросту чередоваться. Другие вычисления нужно делать аналогично: A12 = |0 2| |3 1| = (-6) * (-1) = 6; A13 = |0 1| |3 2| = -3.
Как видно из примеров, вычисления обычно не вызывают трудностей, но требуют внимательности и усидчивости. Особенно это касается нахождения обратной матрицы. Вычисляется она с помощью алгебраических дополнений, которые равны минорам, умноженным на минус единицу. Довольно часто знаки путают, и в итоге получается неправильный ответ. Поэтому в случае сложных систем есть резон использовать онлайн-калькуляторы.
Использование интернет-калькулятора
В интернете есть определённая группа сайтов, позволяющая выполнять различные математические вычисления в автоматическом режиме. На их страницах содержится специальный скрипт, выполняющий нахождение минора матрицы онлайн любой сложности. При этом от потребителя не требуется никаких особых знаний, он даже и вовсе может ничего не понимать в алгебраических вычислениях.
Всё, что ему необходимо будет сделать для получения ответа, — это ввести исходные данные в предложенную форму и нажать кнопку «Вычислить». Система автоматически определит нужный алгоритм и, используя свойства матрицы, выведет на экран ответ. При этом, кроме результата, пользователю будет предоставлена возможность ознакомиться с подробным решением.
Система автоматически определит нужный алгоритм и, используя свойства матрицы, выведет на экран ответ. При этом, кроме результата, пользователю будет предоставлена возможность ознакомиться с подробным решением.
По отзывам потребителей, из множества таких сервисов можно выделить пять следующих сайтов:

Все указанные сайты доступны на русском языке, бесплатны, имеют простой и понятный интерфейс. На их страницах содержится справочная и теоретическая математическая информация. Кроме неё, для каждого раздела приводится типовой пример с объяснением. Использование онлайн-калькуляторов поможет сэкономить время и научит правильно выполнять действия по вычислению миноров.
Их использование будет полезным не только ученикам или студентам, желающим научиться самостоятельно решать задачи, но и инженерам, выполняющим сложные вычисления. Для специалистов они довольно востребованы, так как при самостоятельном решении небольшая ошибка по невнимательности приведёт к неправильному ответу, что исключено при расчёте в автоматическом режиме.
Предыдущая
МатематикаМагический квадрат — виды, правила и примеры решения
Следующая
МатематикаЗадачи на нахождение НОК и НОД для 6 класса
Сообщество Экспонента
- вопрос
- 22.
 09.2022
09.2022
Математика и статистика, Системы управления, Изображения и видео, Робототехника и беспилотники, Глубокое и машинное обучение(ИИ), Другое
Коллеги, добрый день. Необходимо использовать corrcoef, а массивы разной длины. Как сделать кол-во элементов одинаково?
Коллеги, добрый день. Необходимо использовать corrcoef, а массивы разной длины. Как сделать кол-во элементов одинаково?
8 Ответов
- вопрос
- 20.09.2022
Другое, Встраиваемые системы, Цифровая обработка сигналов, Системы управления
Здравствуйте!Возникла необходимость менять некоторое строчки в сишном файле автоматически, используя матлабовский скрипт. Прошерстил весь интернет, в т.ч. англоязычные форумы, не смог ничего найт…
Здравствуйте!Возникла необходимость менять некоторое строчки в сишном файле автоматически, используя матлабовский скрипт. Прошерстил весь интернет, в т. ч. англоязычные форумы, не смог ничего найт…
ч. англоязычные форумы, не смог ничего найт…
- MATLAB
20.09.2022
- Публикация
- 15.09.2022
Системы управления, Другое
Видел видос на канале экспоненты по созданию топливной системы. Вопрос заключается в наличии более полного описания готового примера или соответсвующее документации. Я новичок в симулинке и ещё многого не знаю. Адекватных и раскрытых пособий по созданию гидрав…
Моделирование гидравлических систем в simulink
- Публикация
- 10.09.2022
Системы управления, Электропривод и силовая электроника, Другое
Планирую написать книгу про модельно-ориентированное программирование с автоматическим генерированием кода применительно к разработке разнообразных микропроцессорных систем управления электроприводов. В этой книге в научно-практическо-методической форме я план…
Планирую написать книгу про модельно-ориентированное программирование с автоматическим генерированием кода применительно к разработке разнообразных микропроцессорных систем управления электроприводов.
- Публикация
- 24.08.2022
Цифровая обработка сигналов, Системы связи, Математика и статистика
&…
Здесь собрана литература по комбинированным методам множественного доступа, в которых используется разделение пользователей в нескольких ресурсных пространствах.
- вопрос
- 23.08.2022
Математика и статистика, Радиолокация, Цифровая обработка сигналов
Есть записанный сигнал с датчика (синус с шумом). Как определить соотношение сигнал/шум?
Есть записанный сигнал с датчика (синус с шумом). Как определить соотношение сигнал/шум?
4 Ответа
- ЦОС
- цифровая обработка сигналов
23.08.2022
- Публикация
- 23.08.2022
Цифровая обработка сигналов, Системы связи, Математика и статистика
&. ..
..
Здесь соборана литература по методам множественного доступа с поляризационным разделением и разделением по орбитальном угловому моменту.
- Публикация
- 16.08.2022
Цифровая обработка сигналов, Системы связи, Математика и статистика
Здесь собрана литература по методам множественного доступа с пространственным разделением.
- вопрос
- 22.07.2022
Изображения и видео, Цифровая обработка сигналов, Математика и статистика, Биология, Встраиваемые системы, Глубокое и машинное обучение(ИИ), Автоматизация испытаний, ПЛИС и СнК, Системы управления, Другое
Здравствуйте. Мне нужно обработать большое количество файлов с похожими названиями, каждый блок файлов относится к отдельному объекту, например: file_1_1.txt file_1_2.txt file_1_3.txt file_1_4.txt fil…
Здравствуйте. Мне нужно обработать большое количество файлов с похожими названиями, каждый блок файлов относится к отдельному объекту, например:
file_1_1.txt
file_1_2.txt
file_1_3.txt
file_1_4.txt
fil…
Мне нужно обработать большое количество файлов с похожими названиями, каждый блок файлов относится к отдельному объекту, например:
file_1_1.txt
file_1_2.txt
file_1_3.txt
file_1_4.txt
fil…
2 Ответа
- чтение
22.07.2022
- вопрос
- 17.07.2022
Математика и статистика, Цифровая обработка сигналов
Уважаемые коллеги, добрый вечер! В общем, возникла проблема следующего характера. Имеется сигнал, достаточно большой объем точек, длительность порядка 35-40 секунд. Он представлят собой последовательн…
Уважаемые коллеги, добрый вечер! В общем, возникла проблема следующего характера. Имеется сигнал, достаточно большой объем точек, длительность порядка 35-40 секунд. Он представлят собой последовательн…
- MATLAB
- Signal Processing
17.07.2022
методы, примеры нахождения и определения
В данной статье пойдет речь о таком понятии, как ранг матрицы и необходимых дополнительных понятиях. Мы приведем примеры и доказательства нахождения ранга матрицы, а также расскажем, что такое минор матрицы, и почему он так важен.
Мы приведем примеры и доказательства нахождения ранга матрицы, а также расскажем, что такое минор матрицы, и почему он так важен.
Минор матрицы
Чтобы понять, что такое ранг матрицы, необходимо разобраться с таким понятием, как минор матрицы.
Определение 1Минор k-ого порядка матрицы — определитель квадратной матрицы порядка k×k, которая составлена из элементов матрицы А, находящихся в заранее выбранных k-строках и k-столбцах, при этом сохраняется положение элементов матрицы А.
Проще говоря, если в матрице А вычеркнуть (p-k) строк и (n-k) столбцов, а из тех элементов, которые остались, составить матрицу, сохраняя расположение элементов матрицы А, то определитель полученной матрицы и есть минор порядка k матрицы А.
Из примера следует, что миноры первого порядка матрицы А и есть сами элементы матрицы.
Можно привести несколько примеров миноров 2-ого порядка. Выберем две строки и два столбца. Например, 1-ая и 2 –ая строка, 3-ий и 4-ый столбец.
При таком выборе элементов минором второго порядка будет -1302=(-1)×2-3×0=-2
Другим минором 2-го порядка матрицы А является 0011=0
Предоставим иллюстрации построения миноров второго порядка матрицы А:
Минор 3-го порядка получается, если вычеркнуть третий столбец матрицы А:
003112-1-40=0×1×0+0×2×(-1)+3×1×(-4)-3×1×(-1)-0×1×0-0×2×(-4)=-9
Иллюстрация, как получается минор 3-го порядка матрицы А:
Для данной матрицы миноров выше 3-го порядка не существует, потому что
k≤min(p, n)=min (3, 4)=3
Сколько существует миноров k-ого порядка для матрицы А порядка p×n?
Число миноров вычисляют по следующей формуле:
Cpk×Cnk, где Сpk=p!k!(p-k)! и Cnk=n!k!(n-k)! — число сочетаний из p по k, из n по k соответственно.
После того, как мы определились, что такое миноры матрицы А, можно переходить к определению ранга матрицы А.
Ранг матрицы: методы нахождения
Определение 2Ранг матрицы — наивысший порядок матрицы, отличный от нуля.
Rank (A), Rg (A), Rang (A).
Из определения ранга матрицы и минора матрицы становиться понятно, что ранг нулевой матрицы равен нулю, а ранг ненулевой матрицы отличен от нуля.
Нахождение ранга матрицы по определению
Определение 3Метод перебора миноров — метод, основанный на определении ранга матрицы.
Алгоритм действий способом перебора миноров:
Необходимо найти ранг матрицы А порядка p×n. При наличии хотя бы одного элемента, отличного от нуля, то ранг матрицы как минимум равен единице (т.к. есть минор 1-го порядка, который не равен нулю).
Далее следует перебор миноров 2-го порядка. Если все миноры 2-го порядка равны нулю, то ранг равен единице. При существовании хотя бы одного не равного нулю минора 2-го порядка, необходимо перейти к перебору миноров 3-го порядка, а ранг матрицы, в таком случае, будет равен минимум двум.
Аналогичным образом поступим с рангом 3-го порядка: если все миноры матрицы равняются нулю, то ранг будет равен двум. При наличии хотя бы одного ненулевого минора 3-го порядка, то ранг матрицы равен минимум трем. И так далее, по аналогии.
При наличии хотя бы одного ненулевого минора 3-го порядка, то ранг матрицы равен минимум трем. И так далее, по аналогии.
Найти ранг матрицы:
А=-11-1-202260-443111-7
Поскольку матрица ненулевая, то ее ранг минимум равен единице.
Минор 2-го порядка -1122=(-1)×2-1×2=4 отличен от нуля. Отсюда следует, что ранг матрицы А не меньше двух.
Перебираем миноры 3-го порядка: С33×С53=15!3!(5-3)!= 10 штук.
-11-12264311=(-1)×2×11+1×6×4+(-1)×2×3-(-1)×2×4-1×2×11-(-1)×6×3=0
-11-2220431=(-1)×2×1+1×0×4+(-2)×2×3-(-2)×2×4-1×2×1-(-1)×0×3=0
-1-1-22604111=(-1)×6×1+(-1)×0×4+(-2)×2×11-(-2)×6×4-(-1)×2×1-(-1)×0×11=0
-11-2220431=(-1)×2×1+1×0×4+(-2)×2×3-(-2)×2×4-1×2×1-(-1)×0×3=0
-1-1026-4411-7=(-1)×6×(-7)+(-1)×(-4)×4+0×2×11-0×6×4-(-1)×2×(-7)-(-1)×(-4)×11=0
1-1026-4311-7=1×6×(-7)+(-1)×(-4)×3+0×2×11-0×6×3-(-1)×2×(-7)-1×(-4)×11=0
1-2020-431-7=1×0×(-7)+(-2)×(-4)×3+0×2×1-0×0×3-(-2)×2×(-7)-1×(-4)×1=0
-1-2060-4111-7=(-1)×0×(-7)+(-2)×(-4)×11+0×6×1-0×0×11-(-2)×6×(-7)-(-1)×(-4)×1=0
Миноры 3-го порядка равны нулю, поэтому ранг матрицы равен двум.
Ответ: Rank (A) = 2.
Нахождение ранга матрицы методом окаймляющих миноров
Определение 3Метод окаймляющих миноров — метод, который позволяет получить результат при меньшей вычислительной работе.
Окаймляющий минор — минор Mok(k+1) -го порядка матрицы А, который окаймляет минор M порядка k матрицы А, если матрица, которая соответствует минору Mok , «содержит» матрицу, которая соответствует минору М.
Проще говоря, матрица, которая соответствует окаймляемому минору М, получается из матрицы, соответствующей окаймляющему минору Mok , вычеркиванием элементов одной строки и одного столбца.
Пример 3Найти ранг матрицы:
А=120-13-2037134-21100365
Для нахождения ранга берем минор 2-го порядка М=2-141
Записываем все окаймляющие миноры:
12-1-207341,20-10374-21,2-13071411,12-1341006,20-14-21036,2-13411065.
Чтобы обосновать метод окаймляющих миноров, приведем теорему, формулировка которой не требует доказательной базы.
Если все миноры, окаймляющие минор k-ого порядка матрицы А порядка p на n, равны нулю, то все миноры порядка (k+1) матрицы А равна нулю.
Алгоритм действий:
Чтобы найти ранг матрицы, необязательно перебирать все миноры, достаточно посмотреть на окаймляющие.
Если окаймляющие миноры равняются нулю, то ранг матрицы нулевой. Если существует хотя бы один минор, который не равен нулю, то рассматриваем окаймляющие миноры.
Если все они равны нулю, то Rank(A) равняется двум. При наличии хотя бы одного ненулевого окаймляющего минора, то приступаем к рассматриванию его окаймляющих миноров. И так далее, аналогичным образом.
Пример 4Найти ранг матрицы методом окаймляющих миноров
А=210-134210-12111-40024-14
Как решить?
Поскольку элемент а11 матрицы А не равен нулю, то возьмем минор 1-го порядка. Начнем искать окаймляющий минор, отличный от нуля:
2142=2×2-1×4=02041=2×1-0×4=2
Мы нашли окаймляющий минор 2-го порядка не равный нулю 2041.
Осуществим перебор окаймляющих миноров — (их(4-2)×(5-2)=6 штук).
210421211=0; 20-1410211=0; 20341-121-4=0;210421002=0; 20-1410024=0; 20341-102-14=0
Ответ: Rank(A) = 2.
Нахождение ранга матрицы методом Гаусса (с помощью элементарных преобразований)
Вспомним, что представляют собой элементарные преобразования.
Элементарные преобразования:
- путем перестановки строк (столбцов) матрицы;
- путем умножение всех элементов любой строки (столбца) матрицы на произвольное ненулевое число k;
путем прибавления к элементам какой-либо строки (столбца) элементов, которые соответствуют другой стоки (столбца) матрицы, которые умножены на произвольное число k.
Определение 5Нахождение ранга матрицы методом Гаусса — метод, который основывается на теории эквивалентности матриц: если матрица В получена из матрицы А при помощи конечного числа элементарных преобразований, то Rank(A) = Rank(B).
Справедливость данного утверждения следует из определения матрицы:
- в случае перестановки строк или столбцов матрицы ее определитель меняет знак. Если он равен нулю, то и при перестановке строк или столбцов остается равным нулю;
- в случае умножения всех элементов какой-либо строки (столбца) матрицы на произвольное число k, которое не равняется нулю, определитель полученной матрицы равен определителю исходной матрицы, которая умножена на k;
в случае прибавления к элементам некоторой строки или столбца матрицы соответствующих элементов другой строки или столбца, которые умножены на число k, не изменяет ее определителя.
Суть метода элементарных преобразований: привести матрицу ,чей ранг необходимо найти, к трапециевидной при помощи элементарных преобразований.
Для чего?
Ранг матриц такого вида достаточно просто найти. Он равен количеству строк, в которых есть хотя бы один ненулевой элемент. А поскольку ранг при проведении элементарных преобразований не изменяется, то это и будет ранг матрицы.
Проиллюстрируем этот процесс:
- для прямоугольных матриц А порядка p на n, число строк которых больше числа столбцов:
А~1b12b13⋯b1n-1b1n01b23⋯b2n-2b2n⋮⋮⋮⋮⋮⋮000⋯1bn-1n000⋯01000⋯00⋮⋮⋮⋮⋮⋮000⋯00, Rank(A)=n
или
А~1b12b13⋯b1kb1k+1⋯b1n01b23⋯b2kb2k+1⋯b2n⋮⋮⋮⋮⋮⋮⋮⋮000⋯1bkk+1⋯bkn000⋯00⋯0⋮⋮⋮⋮⋮⋮⋮⋮000⋯00⋯0, Rank(A)=k
- для прямоугольных матриц А порядка p на n, число строк которых меньше числа столбцов:
А~1b12b13⋯b1pb1p+1⋯b1n01b23⋯b2pb2p+1⋯b2n⋮⋮⋮⋮⋮⋮⋮⋮000⋯1bpp+1⋯bpn, Rank(A)=p
или
А~1b12b13⋯b1kb1k+1⋯b1n01b23⋯b2kb2k+1⋯b2n⋮⋮⋮⋮⋮⋮⋮⋮000⋯1bkk+1⋯bkn000⋯00⋯0⋮⋮⋮⋮⋮⋮⋮⋮000⋯00⋯0
- для квадратных матриц А порядка n на n:
А~1b12b13⋯b1n-1b1n01b23⋯b2n-1b2n⋮⋮⋮⋮⋮⋮000⋯1bn-1n000⋯01, Rank(A)=n
или
A~1b12b13⋯b1kb1k+1⋯b1n01b23⋯b2kb2k+1⋯b2n⋮⋮⋮⋮⋮⋮⋮⋮000⋯1bkk+1⋯bkn000⋯00⋯0⋮⋮⋮⋮⋮⋮⋮⋮000⋯00⋯0, Rank(A)=k, k<n
Пример 5Найти ранг матрицы А при помощи элементарных преобразований:
А=21-26300-11-12-75-24-1572-411
Как решить?
Поскольку элемент а11 отличен от нуля, то необходимо умножить элементы первой строки матрицы А на 1а11=12:
А=21-26300-11-12-75-24-1572-411~
Прибавляем к элементам 2-ой строки соответствующие элементы 1-ой строки, которые умножены на (-3). К элементам 3-ей строки прибавляем элементы 1-ой строки, которые умножены на (-1):
К элементам 3-ей строки прибавляем элементы 1-ой строки, которые умножены на (-1):
~А(1)=112-13300-11-12-75-24-1572-411~А(2)==112-133+1(-3)0+12(-3)0+(-1)(-3)-1+3(-3)1+1(-3)-1+12(-3)2+(-1)(-1)-7+3(-1)5+1(-5)-2+12(-5)4+(-1)(-5)-15+3(-5)7+1(-7)2+12(-7)-4+(-1)(-7)11+3(-7)=
=112-130-323-100-323-100-929-300-323-10
Элемент а22(2) отличен от нуля, поэтому мы умножаем элементы 2-ой строки матрицы А на А(2) на 1а22(2)=-23:
А(3)=112-1301-22030-323-100-929-300-323-10~А(4)=112-1301-22030-32+1323+(-2)32-10+203×320-92+1929+(-2)92-30+203×920-32+1323+(-2)32-10+203×32==112-1301-2203000000000000
- К элементам 3-ей строки полученной матрицы прибавляем соответствующие элементы 2-ой строки ,которые умножены на 32;
- к элементам 4-ой строки — элементы 2-ой строки, которые умножены на 92;
- к элементам 5-ой строки — элементы 2-ой строки, которые умножены на 32.
Все элементы строк равны нулю. Таким образом, при помощи элементарных преобразований ,мы привели матрицу к трапецеидальному виду, откуда видно, что Rank (A(4))=2 . Отсюда следует, что ранг исходной матрицы также равен двум.
Отсюда следует, что ранг исходной матрицы также равен двум.
Если проводить элементарные преобразования, то не допускаются приближенные значения!
Решение задач
от 1 дня / от 150 р.
Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Формула минорной гаммы | Hub Guitar
Hub Guitar
Ранее мы узнали о музыкальном алфавите и мажорной гамме. Качество звукоряда (мажор) определяется нотами в нем и их отношением к тоникеСлово, описывающее тональный центр музыкального произведения, с остальными тонами, разрешающимися на эту ноту. шкалы. Отсюда следует, что мы могли бы создать множество гамм, где «до» — самая низкая нота, потому что есть двенадцать нот, и мы можем завершить гамму любыми другими шестью. На самом деле существует 462 возможных гаммы «до», которые мы можем создать, используя 7 нот, в которых первой была «до».
На самом деле в музыке используются лишь немногие из этих комбинаций. Большая часть музыки основана на мажорной или минорной гамме, и эти две гаммы тесно связаны.
Чтобы узнать, как работают гаммы и аккорды, нам нужно понять, что такое «мажорная гамма» и что такое «минорная гамма».
Возможно, нам придется принять эти две вещи за чистую монету: наше определение «мажорной гаммы» — это серия из 7 нот, выбранных из набора 12, руководствуясь следующими шагами: целая, целая, половина, целая, целая. , целое, половина.
Building the Major Scale
The process
The result
C
D
E
F
G
A
B
C
Hear it
Hundreds of years of Музыка доказывает, что эта серия шагов надежна. Если нам нужен набор нот, который хорошо подходит для построения аккордов, наш выбор гамм ограничен. Наша шкала, вероятно, будет состоять из семи нот. Если бы было шесть, где-то был бы «пробел». Если бы было восемь, была бы дополнительная нота и дополнительные полутона. Полутоны в гамме являются основной причиной диссонанса. Относится к качеству двух или более нот, которые не имеют сильной гармонии. Это связано с тем, что ноты вибрируют на частотах, которые имеют некоторый конфликт, и этот конфликт слышен человеческому уху. Нам нужна гамма из семи нот с как можно меньшим количеством полушагов, чтобы увеличить гармонию и уменьшить диссонанс.
Нам нужна гамма из семи нот с как можно меньшим количеством полушагов, чтобы увеличить гармонию и уменьшить диссонанс.
Этот набор нот имеет важную особенность: «вишенки», обозначающие полутоны, расставлены как можно равномернее.
Мы можем создать большинство часто используемых гамм, просто перемещая эту последовательность полных шагов и полутонов, сохраняя при этом их отношения друг к другу.
Прежде чем мы начнем, давайте пронумеруем ноты до-мажорной гаммы по мере их появления.
Номера нот до мажор
1
2
3
4
5
6
7
Построение минорной гаммы
Теперь давайте возьмем наши скобки и вишенки, которые показывают соотношение шагов и полутонов, и перетащим их все влево. Мы будем перетаскивать, пока самая последняя скобка не окажется на C. (Раньше она была между A и B, а теперь между C и D.) Теперь наша последовательность выглядит так:
Процесс
Результат
C
D
E♭
F
G
A♭
B♭
C
Послушайте
Немногое изменилось: мы имеем дело с теми же двенадцатью нотами. Мы считаем «С» корнем. Кроме того, наши вишни и скобки имеют точно такое же отношение друг к другу, как и раньше; но все они были перетасованы влево. Если вы внимательно присмотритесь, вы все равно сможете найти расположение «целое, целое, половина, целое, целое, целое, половина», даже если оно начинается в другом месте последовательности и перетекает справа налево.
Мы считаем «С» корнем. Кроме того, наши вишни и скобки имеют точно такое же отношение друг к другу, как и раньше; но все они были перетасованы влево. Если вы внимательно присмотритесь, вы все равно сможете найти расположение «целое, целое, половина, целое, целое, целое, половина», даже если оно начинается в другом месте последовательности и перетекает справа налево.
Минорная гамма
Эта комбинация нот называется минорной гаммой . Минорная гамма создается по формуле, как и мажорная гамма. Формула минорной гаммы: целая, половина, целая, целая, половинная, целая, целая. Эта формула представляет собой ту же последовательность, что и формула мажорной гаммы, но начинается с другой ноты.
Ноты в минорной гамме
В до мажоре у нас были ноты до, ре, ми, фа, соль, ля и си. Теперь, когда мы построили гамму до минор, используя формулу минор, мы имеем до , D, E♭, F, G, A♭, B♭.
Номера гамм в минорной гамме
В нашей схеме нумерации раньше у нас были ноты 1, 2, 3, 4, 5, 6 и 7. Теперь, когда мы будем описывать эту гамму, мы будем сравнивать ее с той же мажорной шкала; мы скажем, что у него есть ноты 1, 2, ♭3, 4, 5, ♭6, ♭7. Это отражает новые ноты гаммы по сравнению с исходной мажорной гаммой, которая всегда является нашей точкой отсчета — в любой ситуации.
Теперь, когда мы будем описывать эту гамму, мы будем сравнивать ее с той же мажорной шкала; мы скажем, что у него есть ноты 1, 2, ♭3, 4, 5, ♭6, ♭7. Это отражает новые ноты гаммы по сравнению с исходной мажорной гаммой, которая всегда является нашей точкой отсчета — в любой ситуации.
Параллельный минор
Когда мы «переключаемся» с мажорной гаммы на минорную, используя один и тот же корень, отношение называется параллельным. Две музыкальные структуры (обычно мелодии) параллельны друг другу, когда они начинаются в одном и том же месте. указывают и следуют друг за другом в одном направлении. До мажор и до минор параллельны друг другу, как два поезда, идущие по разным путям. Многие композиторы пишут музыку, в которой ноты параллельного минора переходят в мажорную тональность или наоборот.
Относительный минор
Учитывая, что мы не меняли наши двенадцать нот и никогда не меняли расположение полных шагов и полутонов, можно предположить, что в гамме до мажор есть какая-то нота, которую можно считать основной. собственной минорной гаммы. Все, что мы сделали, это перетащили скобки так, чтобы минорная гамма начиналась с до. Однако, если вы снова посмотрите на до-мажорную гамму, вы увидите, что минорная формула присутствует, начиная с «ля» или шестой степени. гамма до мажор.
собственной минорной гаммы. Все, что мы сделали, это перетащили скобки так, чтобы минорная гамма начиналась с до. Однако, если вы снова посмотрите на до-мажорную гамму, вы увидите, что минорная формула присутствует, начиная с «ля» или шестой степени. гамма до мажор.
(От А): целый, половина, целый, целый, половина, целый, целый. Существует минорная гамма, состоящая из нот до-мажорной гаммы! Поскольку эти две гаммы так тесно связаны друг с другом, говорят, что это относительная минорная гамма — минорная гамма, которая может быть построена из нот мажорной гаммы. Например, гамма ля минор имеет A–B–C–D–E–F–G–, те же ноты, что и до мажор. Таким образом, ля является относительным минором до мажор. Относительный минор можно найти на шестой ступени любой мажорной гаммы. И наоборот, если вы посмотрите на гамму ля минор, вы увидите, что относительный мажор можно найти, начиная с третьей ступени.
Мы можем доказать , что минорная гамма имеет ♭3, ♭6 и ♭7, сравнив ля-минорную гамму с ля-мажорной гаммой.
A Major Scale
A
B
C♯
D
E
F♯
G♯
A
A Minor Scale
A
B
C
D
E
F
G
A
Key Task
- Для тональностей G и F выпишите ноты минорной гаммы.
Минор и Кофактор | Superprof
В этой статье мы обсудим, как вычислить миноры и кофакторы матриц. Итак, начнем с минора матрицы.
Минор матрицы
Чтобы найти минор матрицы, мы берем определитель каждой меньшей матрицы, полученный путем удаления соответствующих строк и столбцов каждого элемента в матрице. Поскольку в больших матрицах много строк и столбцов с несколькими элементами, мы можем сделать много миноров этих матриц. Мы помечаем эти миноры в соответствии со строкой и столбцом, которым они принадлежат.
Мы знаем, что в квадратной матрице одинаковое количество строк и столбцов. Он может иметь форму 2х2 или 3х3. Каждый элемент квадратной матрицы имеет свой минор.
Каждый элемент квадратной матрицы имеет свой минор.
Например, рассмотрим следующую простую квадратную матрицу:
Чтобы найти минор каждого элемента, мы удалим соответствующую строку и столбец каждого элемента и запишем миноры в матричном обозначении.
После записи матрицы в приведенной выше форме мы найдем определитель каждой матрицы для вычисления минора матрицы.
.
Лучшие репетиторы по математике
Поехали
Пример 1
Вычислите минор следующей матрицы:
Решение
Запишите матрицу в следующем виде. Приведенная ниже матрица получается путем исключения соответствующей строки и столбца каждого элемента.
Теперь мы вычислим определитель каждой меньшей квадратной матрицы. Мы знаем, что определитель квадратной матрицы обозначается и вычисляется следующим образом:
Мы знаем, что определитель квадратной матрицы обозначается и вычисляется следующим образом:
Результирующая матрица будет:
Пример 2
Рассчитайте несовершеннолетних по следующей матрице:
Решение
Устранение соответствующей строки и столбца каждого элемента, чтобы написать матрицу в следующей форме:
Теперь найдите определитель квадратной меньшей матрицы, чтобы найти миноры всех элементов матрицы:Кофактор
Кофактор матрицы связан с ее минором. Как только минор вычислен, мы складываем два числа a и b. Число, полученное в результате сложения этих двух чисел, становится значением степени -1. Обозначается как:
Здесь минор и представляет кофактор.
Еще один более простой способ понять кофактор матрицы 3×3 — рассмотреть следующее правило.
Найдя минор матрицы, меняем знаки по этому правилу, чтобы получить кофактор матрицы:
Помните, что это правило для матрицы 3×3.
Вычислим сомножители матриц в примерах 1 и 2.
Кофактор примера 1
В примере 1 была дана следующая матрица:
Мы нашли ее миноры, исключив соответствующие строки и столбцы каждого элемента. Результирующие миноры полученной матрицы были:
Теперь мы применим это правило, чтобы изменить знак каждого элемента в приведенной выше матрице.
Приведенная выше матрица является кофактором матрицы.
Кофактор примера 2
В примере 2 была дана следующая матрица:
Миноры элементов, полученные после удаления соответствующих строк и столбцов каждого элемента, были ниже: 9005 0 9 00005
9
Теперь применим это правило. Использование этого правила для изменения знаков элементов матрицы дает кофакторы.
Следовательно, приведенная выше матрица является кофактором матрицы.
Отношения миноров и кофакторов с другими понятиями матриц
Вам может быть интересно, какой смысл следовать этой громоздкой процедуре нахождения миноров и кофакторов матриц. Ну, эти два понятия относятся к другим понятиям матриц. Кофакторы и миноры используются для вычисления сопряженных и обратных матриц. Сопряженная матрица вычисляется путем транспонирования кофакторов матрицы. Они также упрощают процедуру нахождения определителей больших матриц, например, матрицы порядка 4×4.
Обратное правило
Мы используем следующее правило для вычисления обратной матрицы, используя ее определитель и кофакторы: матрица кофакторов
представляет транспонированную матрицу кофакторов. Транспонированная матрица кофактора известна как адъюгат матрицы.
Это правило гласит, что обратная матрица равна произведению обратной ее определителя на сопряженную матрицу A.
Как определить, является ли музыка мажорной или минорной
Распознавание между мажором и минором является важным базовым навыком для любого музыканта. Это один из первых шагов, который позволит вам по-настоящему погрузиться в музыку и понять, как она создается. Мне часто задают этот вопрос, так что давайте перейдем к делу.
Как определить, является ли песня или произведение мажорным или минорным? Есть два способа определить, является песня мажорной или минорной: на слух и на вид. Делая это на слух, прислушивайтесь к мажорным и минорным качествам музыки. При чтении нот ответ заключается в ключевой подписи и в том, как используются ноты и аккорды.
Это звучит достаточно просто, но требует некоторой практики, так что давайте рассмотрим детали. Сначала мы обсудим, как распознавать мажор и минор, читая нотную запись, а затем распознавать мажор и минор на слух.
В этой статье мы также рассмотрим, откуда берутся ключи. Я предлагаю вам прочитать его один раз, даже если вы знакомы с тональностями и гаммами. Понимание того, откуда они берутся, делает весь этот процесс намного проще!
Понимание того, откуда они берутся, делает весь этот процесс намного проще!
О чем этот урок
Как определить мажор или минор в нотах
Мы начнем с распознавания мажорной или минорной тональности в нотах. Но что такое ключ?
Мы используем термин «тональность» просто для обозначения мажорной или минорной гаммы, в которой мы играем. Как вы увидите в таблице ниже, у нас есть 12 мажорных и 12 минорных тональностей. Почему 12? Потому что каждая нота музыкального алфавита (все 12!) получает свою очередь, являясь первой нотой мажорной гаммы и первой нотой минорной гаммы. Каждый из них является ключом.
Например, вот гамма ля мажор (имеется в виду, что это мажорная гамма, начинающаяся с ноты ля).
Гамма ля мажорТеперь, если у нас есть музыка, в которой используется эта гамма, мы говорим, что эта музыка в тональности ля мажор:
Мендельсон: Симфония № 4 – тема 1-й части ля мажорИ здесь — это гамма ля минор (имеется в виду, что это минорная гамма начинается с ноты ля):
гамма ля минорЕсли мы посмотрим на музыку, в которой используется эта гамма, то музыка в тональности ля минор :
Мендельсон: Симфония № 4 – тема 4-й части ля минор Таким образом, с термином «тональность» мы просто говорим о том, какая гамма используется в любой момент. Если музыка меняет тональность, значит, изменилась гамма. Если две песни в одной тональности, это просто означает, что они используют одинаковую гамму.
Если музыка меняет тональность, значит, изменилась гамма. Если две песни в одной тональности, это просто означает, что они используют одинаковую гамму.
Подпись ключа: большая или второстепенная?
Так как же узнать тональность музыкального произведения? Для этого мы смотрим на нотную запись и видим, как организованы ноты. Если они есть, мы должны также обратить внимание на диезы и бемоли, потому что они дают важные подсказки.
К счастью, очень легко узнать, какие диезы или бемоли используются в пьесе, потому что они обычно пишутся в начале каждого нотоносца (сразу после ключа). Это известно как ключевая подпись .
Тональность написана на каждом нотоносце сразу после ключа.Вот таблица всех подписей ключей. Обратите внимание, что:
- Есть 2 набора ключей: один с диезами, а другой с бемолями;
- Каждая ключевая подпись рассчитана на 2 ключа: один основной и один дополнительный;
- Существует четкая схема того, как продвигаются подписи ключей.
 Мы начинаем с до-мажор, в котором нет диезов, переходим к тональности с 1-диезом, затем к тональности с 2-мя диезами и так далее, пока не дойдем до до-диез-мажор, в которой все ноты заточены (таким образом, 7 диезов).
Мы начинаем с до-мажор, в котором нет диезов, переходим к тональности с 1-диезом, затем к тональности с 2-мя диезами и так далее, пока не дойдем до до-диез-мажор, в которой все ноты заточены (таким образом, 7 диезов). - То же самое происходит и с бемолями: каждая новая тональность получает еще одну бемоль, пока мы не дойдем до до-бемоль мажор с 7 бемолями.
- Есть несколько других паттернов, которые вы могли бы заметить, но на этом уровне пока этого должно быть достаточно.
Этот второй пункт ОЧЕНЬ важен, прежде чем мы перейдем к следующим шагам. Каждая подпись ключа принадлежит одному основному ключу и одному дополнительному ключу.
Это означает, что тональность, которую мы находим в нотах, сужает наши варианты до двух возможных тональностей: одной мажорной и одной минорной. Наш следующий шаг будет заключаться в том, чтобы выяснить, какой из двух это.
Откуда берутся ключевые подписи?
Ключевые знаки существуют, потому что мажорные и минорные гаммы должны поддерживать образец полных шагов (также известных как «тона») и полутонов (также известных как «полутона») независимо от ноты, с которой они начинаются. Образец мажорной гаммы, например, таков: тон, тон, полутон, тон, тон, тон, полутон.
Образец мажорной гаммы, например, таков: тон, тон, полутон, тон, тон, тон, полутон.
Так уж получилось, что следуя этой схеме, начиная с ноты C, мы получаем все белые клавиши фортепиано:
Гамма до мажор использует только белые клавиши фортепианоНо если мы начнем с любой другой ноты, нам придется использовать один или несколько диезов или бемолей. Например, начиная с ноты ре, ноты фа-диез и до-диез (а не натуральная фа и натуральная до) необходимы для сохранения правильной картины тонов и полутонов. Другими словами, тональность ре мажор состоит из 2 диезов: фа-диез и до-диез.
Гамма ре мажорВот еще пример. Если бы мы начали с ноты си-бемоль и захотели получить мажорную гамму, мы бы обнаружили, что для сохранения правильной картины тонов и полутонов нам нужно сгладить 2 ноты: саму си (превратившуюся в си-бемоль) и ми ( становится ми-бемоль). Другими словами, тональность си-бемоль мажор состоит из двух бемолей: си-бемоль и ми-бемоль.
Гамма си-бемоль мажор То же самое касается минорных гамм. Диезы или бемоли нужны для того, чтобы сохранить правильную структуру тонов и полутонов. Именно в этом паттерне гамма обретает свое отчетливое звучание — свое особое качество. Если бы мы изменили шаблон, мы бы изменили сам масштаб.
Диезы или бемоли нужны для того, чтобы сохранить правильную структуру тонов и полутонов. Именно в этом паттерне гамма обретает свое отчетливое звучание — свое особое качество. Если бы мы изменили шаблон, мы бы изменили сам масштаб.
Так это майор или минор?
Итак, теперь, когда мы можем распознать тональность пьесы, нам осталось решить, представляет ли она мажорную или минорную гамму.
Для этого нам нужно найти подсказки в самой музыке. В общем, наиболее важными нотами и аккордами мажорной и минорной тональности являются:
- Тоника : это первая нота гаммы и построенный на ней аккорд;
- Доминанта : это пятая нота звукоряда и построенный на ней аккорд:
В этом подробном уроке о «тональности» мы узнаем, почему эти аккорды так важны, но в целом это потому, что вместе они устанавливают тонику как тонику. С практикой вы научитесь мгновенно видеть эти ноты и аккорды в любой тональности.
Видение тоники и доминанты в музыке поможет вам очень быстро отличить мажор от минора, но вот 5 советов для начала:
- тоника) или пятая нота звукоряда (известная как доминанта).
- Первый аккорд в музыке очень часто является первым аккордом звукоряда (тоникой). Если нет, то это пятый аккорд гаммы (доминанта).
- Последний аккорд также обычно является первым аккордом гаммы.
- Обратите особое внимание на бас. Первые и/или последние ноты произведения обычно являются тоникой.
- Если вы подозреваете, что тональность минорная, ищите в музыке повышенную септиму. «Поднятая септима» означает, что седьмая нота гаммы повышается на один полутон. Например, в ми миноре ищите ре-диез в музыке (это на 7 нот выше ми).
Примеры и упражнения
Теперь давайте проверим эти советы! Здесь у нас есть 4 коротких пьесы для фортепиано. Мы начнем с двух простых тактов из Менуэта Баха. Это мажор или минор?
Бах: Менуэт В тональности показан только один диез. Согласно нашей таблице тональностей это означает, что это может быть либо соль мажор, либо ми минор. При внимательном рассмотрении нот не должно быть сомнений, что это соль мажор:
Согласно нашей таблице тональностей это означает, что это может быть либо соль мажор, либо ми минор. При внимательном рассмотрении нот не должно быть сомнений, что это соль мажор:
- Первые две доли обрисовывают ноты соль мажор: G – B – D.
- Ноты в 3-й доле первого такта: ре — фа-диез — ля. Это аккорд ре мажор (и доминирующий аккорд соль).
- Второй такт состоит только из нот аккорда соль мажор.
В общем, каждая нота указывает на тональность соль мажор. Оранжевые цифры в обозначениях ниже соответствуют пунктам выше:
Показатели соль мажорДаже в таком небольшом количестве музыки советы, которые мы узнали о тонических и доминантных аккордах, действуют.
Далее идут 8 тактов из короткой фортепианной пьесы Гайдна. В чем ключ?
Гайдн: № 6 из 12 легких пьес для фортепианоВ тональности нет ни диезов, ни бемолей. Согласно нашей таблице тональностей, это означает либо до мажор, либо ля минор. Намеков на ля минор нет, но много на до мажор:
- Первый аккорд — до мажор с самой нотой до в басу.

- Последними нотами являются две «до» — одна в басу и одна в дисканте.
- Басовая нота, предшествующая этой последней ноте C, является ее собственной квинтой: G (обратите внимание, что ключ здесь заменен на басовую). Окончание с пятой, переходящей в первую, является сильным индикатором любой тональности.
- Первая фраза, заканчивающаяся в такте 4, также заканчивается аккордом до.
Вот еще один отрывок. Это из «Альбома для юношества » Шумана . Это мажор или минор?
Шуман: № 7 из «Альбом для юношества»Ключевая подпись показывает 1 бемоль. Согласно нашей таблице тональностей, это означает, что это произведение либо фа мажор, либо ре минор. Нет указаний на ре минор, но есть немало на фа мажор:
- Оптимистичная нота — это нота «до», которая переходит в «фа». Это еще раз отношение пять к одному! Это потому, что, когда F — первая нота, C — пятая. Как мы видели, уже одно это подтверждает фа мажор.
 Более того, после этого мелодия переходит от C к F еще два раза.
Более того, после этого мелодия переходит от C к F еще два раза. - В 3-м такте мы получаем ноты фа мажор, растянутые в арпеджио.
- Тоника фа мажор ведет к доминирующему аккорду фа (до мажор) в 4-м такте.
Далее первые 2 фразы из короткого произведения Чайковского. Это мажор или минор?
Чайковский: Похороны куклы из «Альбом для юношества», соч. 39’Ключевая подпись состоит из 3-х граней. Согласно нашей таблице тональностей, это означает, что эта музыка написана либо в ми-бемоль мажоре, либо в до миноре. Должно быть ясно, что все в музыке указывает на до минор:
- Первый аккорд — до минор (ноты до — ми-бемоль — соль), причем сама нота до является самой нижней нотой баса.
- Первая фраза снова заканчивается в такте 4 до минор, и ей предшествует аккорд G (его доминанта).
- Нота си-бемоль повышается на полтона и становится си-бемоль натуральной. Это именно то, что мы ожидали бы, если бы мы были в до миноре — повышенная 7-я нота.

- Если мы играем в до миноре, отрывок заканчивается на доминирующем аккорде (соль мажор). Как мы уже видели, это совершенно нормальный аккорд для окончания музыкальной фразы.
А как насчет фа-диез в басу в такте 7? Эта нота не в тональности до минор, значит ли это, что мы ошибаемся в нашем заключении?
Нет, мы не ошиблись. Несмотря на фа-диез, мы все еще в до миноре. Это вопрос гармонии. Не вдаваясь в подробности, скажем, что работа фа-диез состоит в том, чтобы усилить толчок к целевому аккорду соль мажор. Сам аккорд соль мажор по-прежнему принадлежит нашей домашней тональности до минор.
Как видите, подсказки о том, является ли произведение мажорным или минорным, всегда содержатся в нотах. Ищите тонику и ее доминанту, и вы узнаете ключ.
Как определить мажор или минор на слух
Опять же, это в основном вопрос практики. Это не значит, что на это уйдут годы! Это просто означает, что вам нужно какое-то время выполнять упражнения для слуха по 15–30 минут в день.
Вы, наверное, слышали, что мажор счастлив, а минор грустен, но это упрощение. Я понимаю, что это непопулярное мнение, но описание интервалов и гамм с настроениями и чувствами вводит в заблуждение. Это добавляет ненужный поверхностный слой к прослушиванию музыки. Вместо того, чтобы отвлекаться на выяснение того, является ли гамма «радостной» или «грустной», мы должны прислушаться к тому, является ли она на самом деле мажорной или минорной.
Звуки подобны цветам. Мы знаем красный цвет просто как «красный» (не описывая его как яркий, опасный или что-то еще), а синий цвет просто как синий (не прибегая к таким прилагательным, как спокойный, волнистый или что-то еще).
Таким же образом, есть определенное качество звука (что-то вроде цвета звука) для мажора и определенное качество звука для минора , и это то, что мы должны практиковать, чтобы распознавать на слух.
Распознавание мажорных и минорных трезвучий
Первый шаг — понять разницу между мажорными и минорными трезвучиями. Как вы, возможно, знаете из теории музыки, разница в третьем. Посмотрите на этот пример: трезвучие до мажор состоит из нот до – ми – соль, а трезвучие до минор состоит из нот до – ми-бемоль – соль. минорное трезвучие
Как вы, возможно, знаете из теории музыки, разница в третьем. Посмотрите на этот пример: трезвучие до мажор состоит из нот до – ми – соль, а трезвучие до минор состоит из нот до – ми-бемоль – соль. минорное трезвучие
Чтобы попрактиковаться в прослушивании и сравнении мажорных и минорных трезвучий на слух, вы можете сыграть их на клавиатуре, если она у вас есть, или использовать онлайн-приложение, такое как teoria.com
Распознавание мажорных и минорных гамм
Как только вы научитесь это делать достаточно хорошо, потренируйтесь слушать сами гаммы. Играйте и пойте мажорные и минорные гаммы на клавиатуре и просто привыкайте к их звучанию. (Пение важно, так как оно помогает усвоить звуки и очень помогает слуху).
Еще раз зайдите в онлайн-приложение, такое как teoria.com, и проверьте себя на весах. Цель состоит не в том, чтобы сделать все правильно и выйти из приложения как можно скорее. Цель состоит в том, чтобы погрузить ваш слух в звуки и стать более и более знакомыми с ними.
Это может занять несколько недель или месяцев, но умение различать мажорные и минорные гаммы останется у вас на всю жизнь.
У вас есть вопросы или комментарии? Дайте мне знать ниже или присоединяйтесь к нашему сообществу Facebook здесь. Мы будем рады видеть вас!
UW Преддипломное консультирование: несовершеннолетние
Несовершеннолетний является дополнительной областью специализации (25-35 кредитов). Вам не обязательно иметь несовершеннолетний, но вы можете пройти до трех в дополнение к основному. Посмотрите, есть ли интересующий вас несовершеннолетний в нашем списке несовершеннолетних.
Получение несовершеннолетнего
Несовершеннолетний предлагает вам возможность изучить отдел или междисциплинарную тему с меньшими затратами времени, чем основной. Если для основного требуется не менее 50 кредитов, для большинства несовершеннолетних требуется только от 25 до 35 кредитов.
Поскольку курсы по вашему дополнительному предмету также могут засчитываться в требования к общему образованию, при тщательном планировании вы сможете пройти один или два дополнительных предмета в рамках 180 кредитов, необходимых для получения степени.
Несовершеннолетние не являются обязательными. Вы можете пройти до трех несовершеннолетних на степень или вообще ни одного.
В чем я должен быть второстепенным?
Вы можете пройти дополнительный курс, связанный с основным. Например, если вы специализируетесь на химии, у вас уже будет фора на второстепенной математике, потому что степень по химии требует много математики.
В качестве альтернативы вы можете выбрать второстепенную специальность в области, которая в сочетании с вашей специализацией даст вам представление о той области, которую вы хотели бы продолжить в своей карьере, в аспирантуре или профессиональной школе. Например, вы можете специализироваться в области изучения окружающей среды и в области политологии, затем планировать поступить в юридическую школу, а затем специализироваться на экологическом праве. Или вы можете специализироваться на психологии и музыке, а затем продолжить обучение музыкальной терапии.
Или вы можете выбрать специальность по предмету, совершенно не связанному с вашей специальностью; это тоже вполне законно.
Например, если вы специализируетесь в области машиностроения, но увлекаетесь изобразительным искусством, вы можете выбрать второстепенную специальность «История искусств».
Подходит ли несовершеннолетний в моем протоколе?
Стоимость несовершеннолетнего трудно определить количественно. Несовершеннолетние не обязательно сделают вас более привлекательными для выпускников или профессиональных программ или работодателей. Вы можете обнаружить, что многие работодатели не особенно заинтересованы в вашей специальности, а тем более в вашей второстепенной. Несмотря на то, что вы можете завершить несовершеннолетний, связанный с карьерой, которую вы надеетесь продолжить после выпуска, несовершеннолетние в основном дают вам возможность более глубоко изучить некоторые из обширных ресурсов Университета.
Каковы требования для приема несовершеннолетних?
Любой студент бакалавриата со статусом не ниже второкурсника (завершено 45 кредитов), заявленный как основной, может объявить себя несовершеннолетним.
В UW-Seattle нет требований к поступающим в департаменты для несовершеннолетних, за исключением предпринимательства, которое ограничено возможностями и требует подачи заявления в Foster School of Business.
Исключение из правила, согласно которому у вас должно быть 45 кредитов и специальность, чтобы объявить второстепенной, – это морская биология; вы можете объявить несовершеннолетним в морской биологии в любое время.
Как мне объявить себя несовершеннолетним?
Чтобы объявить себя несовершеннолетним, обратитесь к старшему советнику отдела. Только консультант вашего основного отдела может подписать форму о признании несовершеннолетним; это делается для того, чтобы учащиеся соответствовали удовлетворительным требованиям успеваемости.
Крайних сроков для объявления несовершеннолетними нет, за исключением того, что вы не можете объявить несовершеннолетним после окончания срока подачи заявления на получение высшего образования.
Другими словами, вы не можете объявить себя несовершеннолетним после третьей недели квартала, в котором вы намереваетесь получить высшее образование.
Правила и положения
Несовершеннолетние не являются обязательными. Вы можете заработать до трех несовершеннолетних в рамках каждой полученной степени. Студентам постбакалавриата (студентам, уже получившим степень бакалавра) не может быть присвоена несовершеннолетняя степень.
Требования для объявления несовершеннолетним
- Любой студент бакалавриата со статусом не ниже второкурсника (завершено 45 кредитов), заявленный как основной, может объявить себя несовершеннолетним. Исключение из правила, согласно которому у вас должно быть 45 кредитов и специальность, чтобы объявить несовершеннолетней, – это морская биология; вы можете объявить несовершеннолетним в морской биологии в любое время.
- Только консультант вашего основного отдела может подписаться о признании несовершеннолетним; это делается для того, чтобы вы соответствовали требованиям удовлетворительной успеваемости в университете.
- Настоятельно рекомендуем вам встретиться с консультантом по второстепенным вопросам, чтобы обсудить предмет второстепенных вопросов и ваши планы по их завершению.
Кредиты, необходимые для получения несовершеннолетнего
- Для большинства несовершеннолетних требуется 25-35 кредитов. В некоторых случаях требования к биографическим данным увеличивают эту сумму.
- Большинству несовершеннолетних требуется как минимум 50% или 15 кредитов (в зависимости от того, что больше), которые должны быть заполнены по месту жительства в кампусе UW, предоставляющем несовершеннолетнему.
Классы
- Большинству несовершеннолетних требуется минимальный средний балл 2,00 для курсов, пройденных для завершения несовершеннолетнего.
- Некоторым несовершеннолетним может потребоваться минимальный балл по каждому предмету, пройденному для несовершеннолетнего. В таких случаях минимальная оценка за курс указывается как часть второстепенных требований, перечисленных в Общем каталоге.
- Если минимальная оценка за курс и минимальный средний балл не указаны, допускается любая проходная числовая оценка и минимальный средний балл.
- Пройденные курсы S/NS не могут быть засчитаны для несовершеннолетних.
Основные и второстепенные
- Вы не можете одновременно проходить основной и дополнительный курсы по одной и той же программе.
- После того, как вы закончите основной курс, вы, возможно, никогда не получите второстепенного в этой программе.
- Любой студент может объявить любого несовершеннолетним в UW-Seattle. Однако объявление несовершеннолетним не является задним ходом к поступлению в мажор. Если у факультета есть требования для поступления на специальность, вы должны подать заявку и выполнить эти требования, даже если вы уже заявили, что не являетесь второстепенным в этой области.
- У вас может быть основная специальность в одном колледже и дополнительная степень в другом. Вы выполните общеобразовательные требования колледжа по вашей специальности; вы не обязаны соответствовать общеобразовательным требованиям колледжа вашего несовершеннолетнего.
- У вас может быть основная степень по вечерней программе и дополнительная по дневной программе Вашингтонского университета в Сиэтле, или наоборот. Однако, поскольку для студентов программы вечернего образования существуют ограничения на посещение дневных занятий, учащиеся этой программы должны проконсультироваться со своим консультантом о возможных второстепенных вариантах.
- Вы можете совмещать основной курс в одном кампусе UW (Сиэтл, Ботелл, Такома) с дополнительным курсом в другом кампусе. Несовершеннолетние за пределами кампуса объявляются с помощью формы Change of Major/Minor, подаваемой в ваш родной кампус (а не в кампус, предлагающий несовершеннолетнего). Однако вы должны быть осторожны, чтобы соответствовать требованиям UW по месту жительства: по крайней мере, 45 из последних 60 кредитов должны быть получены в кампусе, дающем степень. Дополнительную информацию см. в разделе Межкампусная регистрация.
Допустимые перекрытия
- Несмотря на то, что вы не можете изучать одну и ту же программу в одно и то же время, некоторые специальности включают курсы более чем одного факультета.
В таких случаях вы можете перекрываться, но количество перекрытий может быть ограничено. Например, некоторые курсы по религии могут засчитываться в младшую сравнительную историю идей. Если вы являетесь младшим специалистом по сравнительной истории идей и специализировались на сравнительном религиоведении, вы можете без ограничений засчитывать эти курсы как в второстепенный, так и в основной курс. Тем не менее, второстепенное разнообразие ограничивает перекрытие с вашим основным до 10 кредитов. Обязательно ознакомьтесь с второстепенными требованиями, чтобы определить, насколько они совпадают с вашими основными.
- Курсы для несовершеннолетних также могут учитываться, если это уместно, при выполнении требований по иностранному языку, Q/SR, письму и областям знаний без ограничений.
Студенты бакалавриата
- Студенты, получившие степень бакалавра (студенты, уже получившие степень бакалавра), не могут получить степень несовершеннолетнего.
Консультирование
- На общие вопросы о несовершеннолетних может ответить консультант вашего основного отдела или консультант перед основным направлением, но вам настоятельно рекомендуется встретиться с консультантом по несовершеннолетним, чтобы обсудить предмет несовершеннолетнего и ваши планы относительно участия в нем.
Поступление в магистратуру
- В вашем заявлении на получение степени должны быть перечислены все несовершеннолетние, которые вы планируете закончить. Ваш главный консультант проведет аудит DARS для вашего несовершеннолетнего и включит его в ваше заявление на получение диплома.
- После того, как вы объявили о несовершеннолетнем уровне и включили его в свое заявление на получение степени, вы должны заполнить этот несовершеннолетний или отказаться от него официально, иначе вы не получите высшее образование. Это защитит вас от выпуска, когда вы фактически намерены продолжить, чтобы завершить несовершеннолетний.
- Если вы хотите добавить несовершеннолетнего после подачи заявления об окончании, обратитесь к своему консультанту, который обновит ваше заявление и уведомит отдел выпускных и академических документов. Вы не можете добавить несовершеннолетнего после крайнего срока подачи заявления на выпускной — третья пятница квартала, в котором вы планируете получить высшее образование — если в то же время вы не перенесете дату своего выпуска на более поздний квартал.
Подтверждение завершения несовершеннолетнего
- Информация о несовершеннолетних будет указана в вашей стенограмме.
- Несовершеннолетний должен быть присужден одновременно со степенью бакалавра.
Minors (that are also majors)
Aeronautics and Astronautics
American Indian Studies
Anthropology
Applied Mathematics
Aquatic and Fishery Sciences
Architecture
Art History
Atmospheric Sciences
Business Administration
Chemistry
Chinese
Cinema & Media Studies
Классические исследования
Сравнительная история идей
Сравнительное религиоведение
Вычислительные финансы и управление рисками
Управление строительством
Танцы
Датский
Науки о Земле и космосе
Английский язык
Гигиена окружающей среды
Науки об окружающей среде и управление наземными ресурсами
Экологические исследования
Европейские исследования
Финский
Гендер, женщины и сексуальность42 Исследования 90 География
Немецкий язык
Греческий язык
История
Информатика
Японский язык
Еврейский язык
Корейский язык
Латинский язык
Латиноамериканские и карибские исследования
Право, общество и правосудие
Лингвистика
Морская биология
Материаловедение и инженерия
Математика
Микробиология
Музыка
Ближневосточные языки и цивилизации
Норвежский язык
Океанография
Физика
Философия
Философия Estate
Скандинавские исследования
Славянские языки и литературы
Языки и литература Южной Азии (хинди и санскрит)
Spanish
Statistics
Swedish
Minors only
Acting
Aerospace Studies
Africa and the African Diaspora
American Sign Language
Applied Mathematics
Architectural Studies
Arctic Studies
Baltic Studies
Bioethics and Humanities
Business
Classics and Ancient History
Наука о климате
Сравнительные исламские исследования
Вычислительные финансы
Управление строительством
Наука о данных
Дизайн для повышения эффективности
Изучение инвалидности
Разнообразие
DXARTS
Экологическое восстановление
Образование, обучение и общество
Предпринимательство
Экологические культуры и ценности
Эстонский язык
Этика
Французский язык, литература и культура
Французский язык, социолингвистика2 Глобальная лингвистика4 и немецкий перевод
Здоровье
Греческие исследования
История науки
Права человека
Международные исследования
Трудовые исследования
Латышский
Лидерство
Литовский
Ближневосточные исследования
Военные науки
Военно-морские науки
Нейронные вычисления и инженерия
Науки о питании
Палеобиология
Португальский язык и португало-бразильские исследования
Государственная политика
Количественные науки
Россия, Восточная Европа и Центральная Азия Русский язык2
Русский язык2 Литература/славянские литературы
Славянские языки
Текстология и цифровые гуманитарные науки
Театроведение
Градостроительство и планирование
Городской экологический дизайн
Письмо
Несовершеннолетние, предлагаемые UW-Tacoma
Исследования американских индейцев
Исследования американских популярных культур
Прикладные вычисления
Азиатские исследования
Деловое администрирование
Аналитика бизнес-данных
Корпоративная ответственность
Экономика
Образование
Экология
Гендерные исследования
Глобальное взаимодействие
Здоровье и общество
Латиноамериканские исследования
Права человека (Такома)
Инновации и дизайн
Право и политика
Математика (Такома)
Музейное дело
Управление некоммерческими организациями
Некоммерческие исследования (Такома)
Политика
Публичная история
Религиоведение
Реставрация Экология
Социальные науки42 Методы исследования 9 и культуры
Управление спортивными предприятиями
Устойчивое развитие
Технические коммуникации (Такома)
Городские исследования
Несовершеннолетние, предлагаемые UW-Bothell
Актуарная наука
Биология (Ботелл)
Бизнес-администрирование (Ботелл)
Химия (Ботелл)
Информатика и разработка программного обеспечения
Творческое письмо
Исследования разнообразия
Экологическое восстановление (Ботелл)
Экономика (Ботелл)
Образование и общество 904 Исследования женщин и сексуальности (Ботелл)
Географические информационные системы
Глобальное здравоохранение (Ботелл)
Санитарное просвещение и продвижение
Исследования в области здравоохранения (Ботелл)
Права человека (Ботелл)
Информационные технологии
Математика (Ботелл)
Неврология (Ботелл)
Перформанс
Физика (Ботелл)
Политические исследования
Управление розничной торговлей
Наука, технологии и общество
Преподавание и обучение
Визуальное и медиаискусство
Несовершеннолетние, и основные специальности Сертификаты | Джорджтаунский колледж
Учащиеся в Джорджтаунском колледже могут выбрать специализацию, специализацию с второстепенным, двойную специализацию, двойную специализацию с второстепенным или специализацию в одной области с двумя второстепенными. Несовершеннолетний не требуется.
Несовершеннолетний не требуется.
Студенты Джорджтаунского колледжа могут получить сертификат по региональным исследованиям, которые предлагаются Школой дипломатической службы. Сертификаты являются функциональным эквивалентом несовершеннолетних, поэтому они считаются одним из (максимальных) трех академических компонентов, которые студент может выполнить для получения степени (т. Е. Основной плюс два других компонента). Не может быть двойного учета курсов между или среди программ.
| Программа | Майор 909:30 | Несовершеннолетний | Сертификат | Степень |
|---|---|---|---|---|
| Афроамериканские исследования | АБ | |||
| Африканистика | ||||
| Американская музыкальная культура | АБ | |||
| Американские исследования | АБ | |||
| Антропология | АБ | |||
| Арабистика | ||||
| Арабский | АБ | |||
Арт. | АБ | |||
| История искусства | АБ | |||
| Востоковедение | ||||
| Биохимия | БС | |||
| Биологическая физика | БС | |||
| Биология | БС | |||
| Бизнес-администрирование/бизнес-исследования 909:30 | ||||
| Биология глобального здравоохранения | БС | |||
| Католические исследования | ||||
| Химия | БС | |||
| Китайский | АБ | |||
| Классика | АБ | |||
| Когнитивные науки | ||||
| Информатика | АБ, БС | |||
| Творческое письмо | ||||
| Изучение инвалидности | ||||
| Экономика | АБ | |||
| Образование, расследование и правосудие | ||||
| Инженерное дело (двойная степень, предлагаемая Колумбийским университетом) | БА/БС | |||
| Английский | АБ | |||
| Европейские исследования | ||||
| Экологическая биология | БС | |||
| Экологические исследования | ||||
| Кино и СМИ | ||||
| Французский | АБ | |||
| немецкий | АБ | |||
| Мировая и сравнительная литература | АБ | |||
| Глобальное здравоохранение | ||||
| Глобальные исследования средневековья | АБ | |||
| Правительство | АБ | |||
| Греческий (современный) | ||||
| Иврит | ||||
| История | АБ | |||
| Междисциплинарные исследования | АБ | |||
| итальянский | АБ | |||
| Ислам и мусульманско-христианское взаимопонимание | ||||
| Японский | АБ | |||
| Еврейская цивилизация | ||||
| Журналистика 909:30 | ||||
| Исследования справедливости и мира | АБ | |||
| Корейский | ||||
| Латиноамериканские исследования | ||||
| Языкознание | АБ | |||
| Математика | АБ, БС | |||
| Гуманитарные медицинские науки | ||||
| Музыка | ||||
| Нейробиология | БС | |||
| Исполнительское искусство | ||||
| Персидский | ||||
| Философия | АБ | |||
| Философия и биоэтика | ||||
| Физика | АБ, БС | |||
| Политическая экономия 909:30 | АБ | |||
| Португальский | АБ | |||
| Психология | АБ | |||
| Здравоохранение | ||||
| Религия, этика и мировые отношения | ||||
| Русский | АБ | |||
| Российские и восточноевропейские исследования | ||||
| Русская литература и культура (в переводе) | ||||
| Наука, технологии и международные отношения | ||||
| Социология | АБ | |||
| Испанский | АБ | |||
| Испанский и португальский языки | АБ | |||
| Статистика | ||||
| Театральные и перформансные исследования | АБ | |||
| Теология и религиоведение | АБ | |||
| Турецкий | ||||
| Женские и гендерные исследования | АБ |
Сколько несовершеннолетних можно получить на экзамене по вождению?
Если ваш экзамен по вождению быстро приближается, вы, вероятно, будете обеспокоены ошибками. Но вот новость: ошибки случаются, и вы все равно можете пройти тест даже с несколькими ошибками.
Но вот новость: ошибки случаются, и вы все равно можете пройти тест даже с несколькими ошибками.
На самом деле мелкие ошибки вождения практически неизбежны при сдаче экзамена. Итак, какие они? И где проходит черта?
В этом руководстве:
- Что считается незначительной ошибкой на экзамене по вождению?
- Сколько несовершеннолетних разрешено в вашем тесте?
- Как избежать несовершеннолетних на экзамене по вождению
- Что является серьезной ошибкой на экзамене по вождению?
- Сколько специальностей вам разрешено?
- Влияют ли несовершеннолетние на страховой взнос?
Что считается незначительной ошибкой на экзамене по вождению?
Незначительная неисправность — это ошибка вождения, которая может произойти во время теста. Это само по себе не приведет к провалу теста, но вам обязательно нужно знать об этом, чтобы быть самым безопасным и компетентным водителем, которым вы можете быть. Некоторые примеры незначительных неисправностей включают в себя:
- Заглохание или неправильное использование сцепления и ручного тормоза
- Касание бордюра
- Слишком медленное вождение
- Нерешительность
- Неверная сигнализация
- Недостаток осведомленности об окружающем
- Несоблюдение правил техники безопасности в зависимости от погодных условий, таких как включение света и стеклоочистителей
Сколько несовершеннолетних допущено к тесту?
В вашем экзамене по вождению есть около 28 различных оценочных баллов, и в каждом из них есть флажок для того, получаете ли вы незначительную, серьезную или опасную ошибку – подробнее об этих двух последних ошибках позже.
Вы можете допустить до 15 незначительных ошибок на экзамене по вождению и все равно сдать его; 16 и выше считается провалом.
При этом, если вы получаете 3 или более несовершеннолетних в одной и той же оценочной категории — например, неправильно сигнализируя в нескольких случаях — это может привести к серьезной ошибке, которая является мгновенным отказом.
Как избежать несовершеннолетних при сдаче экзамена по вождению
По данным DVSA, только около 1% населения, успешно сдавшего экзамен по вождению, не будет иметь водительских прав. Крайне редко вообще не бывает несовершеннолетних. Итак, во что бы то ни стало стремитесь к вершине класса, но мы призываем вас не отчаиваться, если вы получите несовершеннолетних — вы в подавляющем большинстве, если вы это сделаете!
Однако, как и в любом тесте, есть несколько способов поставить себя в наилучшее положение, чтобы получить чистый результат:
- Практика делает совершенным: Если вы знаете, что параллельные парки не являются вашей сильной стороной, то не Не молитесь, чтобы вас не попросили исполнить его.

- Пересмотрите свою теорию: Есть причина, по которой вы должны пройти теоретический тест перед тем, как отправиться в путь, и именно применение всех этих знаний настроит вас на успех.
- Вернитесь к истокам: Зеркало, сигнал, маневр. Сохраняйте бдительность и дважды проверяйте все опасности, прежде чем тронуться с места. О, и стоит быть вопиющим с вашими проверками: ваш оценщик может не увидеть быстрый взгляд в сторону, когда вы смотрите в зеркало — сделайте очевидным то, что вы делаете.
- Откровенно поговорите со своим инструктором : попросите его регулярно давать отзывы о ваших успехах во время обучения, а также об обычных незначительных проблемах, возникающих в день экзамена.
- Личная подготовка: Выспитесь, наденьте удобную и прочную одежду. Приходите пораньше, чтобы не торопиться.
- Будьте спокойны: Не позволяйте нервам взять над вами верх.
 Потратьте несколько минут перед тем, как перевести дух, и помните, что люди совершают ошибки совершенно нормально.
Потратьте несколько минут перед тем, как перевести дух, и помните, что люди совершают ошибки совершенно нормально.
Что является серьезной ошибкой на экзамене по вождению?
Крупная неисправность классифицируется как серьезная или опасная. Серьезная неисправность может указывать на опасную неисправность — это то, что потенциально может вызвать опасность. Опасная неисправность – это вождение таким образом, что вы подвергаете опасности себя, других людей или имущество.
Если это произойдет, к сожалению, вы получите мгновенный отказ, хотя вам все равно придется продолжать тест и ждать отчета оценщика.
Примеры серьезных и опасных неисправностей включают:
- Отсутствие реакции на сигналы светофора
- Отсутствие наблюдения на перекрестках
- Отсутствие рулевого управления
- Невозможность безопасного трогания
- Не реагировать на дорожные знаки
- Превышение скорости
- Не проверять зеркала или слепые зоны при смене направления.

Точно так же, как мы упоминали ранее, большая ошибка может также состоять из трех второстепенных ошибок в одной и той же категории — сигнал повторного совершения одних и тех же ошибок.
Сколько специальностей вам разрешено?
Нет. Поскольку серьезная ошибка определяется как серьезная или опасная ошибка, к сожалению, получение одной из них приведет к мгновенному отказу.
Хотя неудача, несомненно, разочаровывает, не будьте слишком строги к себе. Согласно правительственному веб-сайту, данные за последние десять лет показывают, что более 50% людей не сдают экзамен по вождению с первого раза. Если вы все же потерпели неудачу, то попросите вашего инструктора дать конструктивный отзыв и попросите его объяснить причину, по которой ваша серьезная ошибка привела к неудаче с точки зрения безопасности. Так вы будете лучше подготовлены к следующему разу.
Влияют ли несовершеннолетние на страховой взнос?
Нет, не знают. Независимо от того, получаете ли вы 15 несовершеннолетних или 0, пропуск есть пропуск, и страховые компании не запрашивают отчет.



 В полученном миноре также можно выделить такую диагональ.
В полученном миноре также можно выделить такую диагональ. 09.2022
09.2022 Мы начинаем с до-мажор, в котором нет диезов, переходим к тональности с 1-диезом, затем к тональности с 2-мя диезами и так далее, пока не дойдем до до-диез-мажор, в которой все ноты заточены (таким образом, 7 диезов).
Мы начинаем с до-мажор, в котором нет диезов, переходим к тональности с 1-диезом, затем к тональности с 2-мя диезами и так далее, пока не дойдем до до-диез-мажор, в которой все ноты заточены (таким образом, 7 диезов).
 Более того, после этого мелодия переходит от C к F еще два раза.
Более того, после этого мелодия переходит от C к F еще два раза.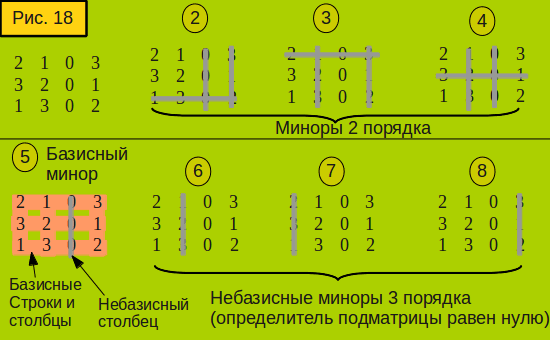
 Например, если вы специализируетесь в области машиностроения, но увлекаетесь изобразительным искусством, вы можете выбрать второстепенную специальность «История искусств».
Например, если вы специализируетесь в области машиностроения, но увлекаетесь изобразительным искусством, вы можете выбрать второстепенную специальность «История искусств». В UW-Seattle нет требований к поступающим в департаменты для несовершеннолетних, за исключением предпринимательства, которое ограничено возможностями и требует подачи заявления в Foster School of Business.
В UW-Seattle нет требований к поступающим в департаменты для несовершеннолетних, за исключением предпринимательства, которое ограничено возможностями и требует подачи заявления в Foster School of Business. Другими словами, вы не можете объявить себя несовершеннолетним после третьей недели квартала, в котором вы намереваетесь получить высшее образование.
Другими словами, вы не можете объявить себя несовершеннолетним после третьей недели квартала, в котором вы намереваетесь получить высшее образование.


 В таких случаях вы можете перекрываться, но количество перекрытий может быть ограничено. Например, некоторые курсы по религии могут засчитываться в младшую сравнительную историю идей. Если вы являетесь младшим специалистом по сравнительной истории идей и специализировались на сравнительном религиоведении, вы можете без ограничений засчитывать эти курсы как в второстепенный, так и в основной курс. Тем не менее, второстепенное разнообразие ограничивает перекрытие с вашим основным до 10 кредитов. Обязательно ознакомьтесь с второстепенными требованиями, чтобы определить, насколько они совпадают с вашими основными.
В таких случаях вы можете перекрываться, но количество перекрытий может быть ограничено. Например, некоторые курсы по религии могут засчитываться в младшую сравнительную историю идей. Если вы являетесь младшим специалистом по сравнительной истории идей и специализировались на сравнительном религиоведении, вы можете без ограничений засчитывать эти курсы как в второстепенный, так и в основной курс. Тем не менее, второстепенное разнообразие ограничивает перекрытие с вашим основным до 10 кредитов. Обязательно ознакомьтесь с второстепенными требованиями, чтобы определить, насколько они совпадают с вашими основными.
