параллельная, последовательная и комбинированная цепь
Решая задачи в области электроники и электрики, приходится сталкиваться с различными вычислениями. Чаще всего они связаны с упрощением электрических схем. Для этого используется метод эквивалента, когда часть цепи заменяется на один элемент с характеристиками, аналогичными ей. Но чтобы это сделать, необходимо знать, как посчитать сопротивление участка цепи и какие виды соединений бывают.
- Определение величины
- Сопротивление радиоэлемента
- Удельный параметр вещества
- Эквивалентная схема
- Расчёт импеданса
- Браузерный онлайн-калькулятор
- Практическое применение
- Простое соединение
- Комбинированный контур
Определение величины
Ток — это упорядоченное движение носителей заряда под действием электрического поля. Способность вещества проводить ток называют электропроводимостью. Чем больше носителей частиц имеет материал, тем большей проводимостью он обладает.
- Проводники. Характеризуются хорошей электропроводностью. К ним относят металлы и их сплавы, а также электролиты.
- Диэлектрики. Вещества, практически не проводящие электрический ток. В основном это газы, каучук, минеральные масла, пластмассы.
- Полупроводники. Материалы, обладающие двумя видами проводимости одновременно — дырочной и электронной. Это вещества, имеющие ковалентную связь: кремний, германий, селен.
Величина, обратная электропроводимости, называется электрическим сопротивлением. То есть это физическая величина, препятствующая прохождению тока. Кроме способности любого материала ограничивать количество проходящих через него зарядов, существует специальный радиоэлемент, ограничивающий силу тока — резистор.
Таким образом, существует два понятия сопротивления: радиоэлемент и физическая величина.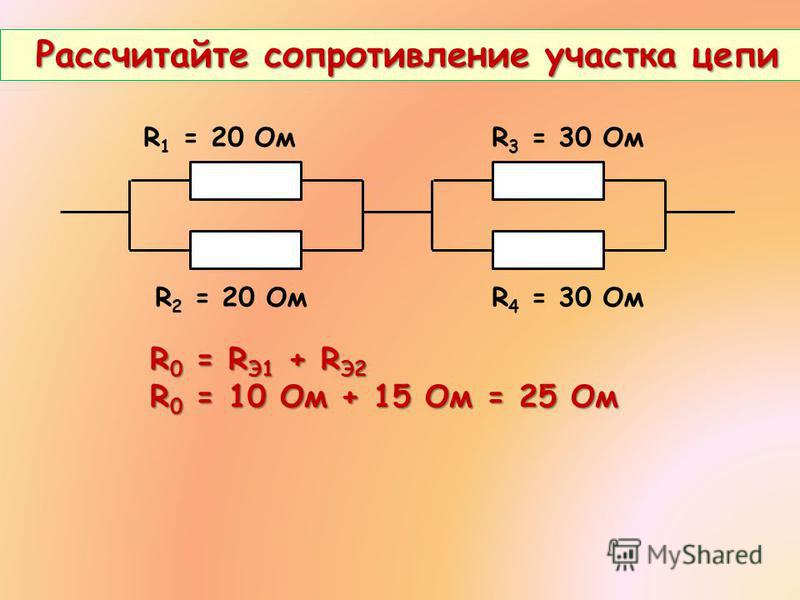
Сопротивление радиоэлемента
Термин «резистор» произошёл от латинского слова resisto — «сопротивляемость». Все резисторы делятся на постоянные и переменные. Последние позволяют изменять своё сопротивление. На схемах и в литературе такая радиодеталь подписывается латинской буквой R. Единицей измерения считается Ом. Графически резистор обозначается в виде прямоугольника с двумя выводами от середины краёв. Кроме номинального сопротивления, он характеризуется рассеиваемой мощностью и классом точности.
По своей сути это пассивный радиоэлемент, преобразующий часть электрической энергии в тепловую. Тем самым он ограничивает ток, линейно преобразовывая его силу в напряжение и наоборот. Главный параметр, описывающий сопротивление, находится согласно закону Ома для участка цепи по следующей формуле: R = U/I, где:
- R — электрическое сопротивление, Ом.
- U — разность потенциалов приложенная к элементу, В.
- I — сила тока, преходящая через резистор, А.

Но тут следует отметить, что этот закон справедлив только для резистивных цепей. То есть для тех, при расчёте которых ёмкостью и индуктивностью пренебрегают. Если же эту формулу применить к реактивным элементам, то для катушки индуктивности сопротивление будет равным нулю, а для конденсатора — бесконечным. Но это верно для постоянного тока и напряжения.
При переменных величинах напряжение на индуктивности не будет равно нулю, как и ток, проходящий через конденсатор. Такие случаи сопротивлением уже не описываются, поскольку оно предполагает постоянные значения тока и напряжения.
Удельный параметр вещества
Чтобы различать понятие и элемент, было введено название удельное электрическое сопротивление. Обозначается оно греческим символом ρ. В Международной системе единиц эта величина измеряется в Омах, умноженных на метр. Зависит она исключительно от свойства материала.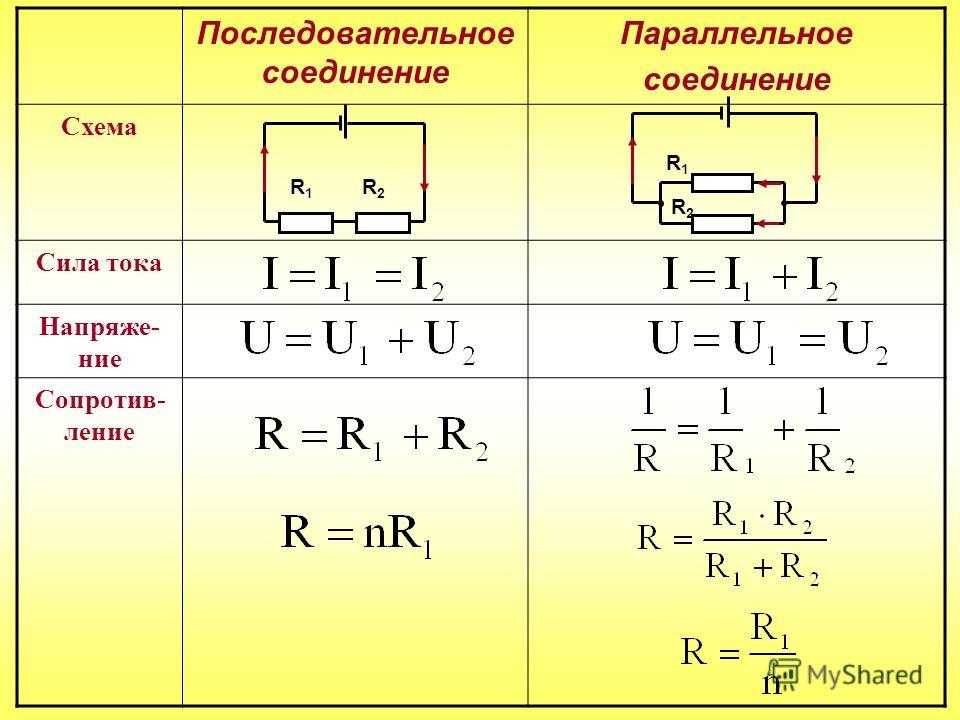
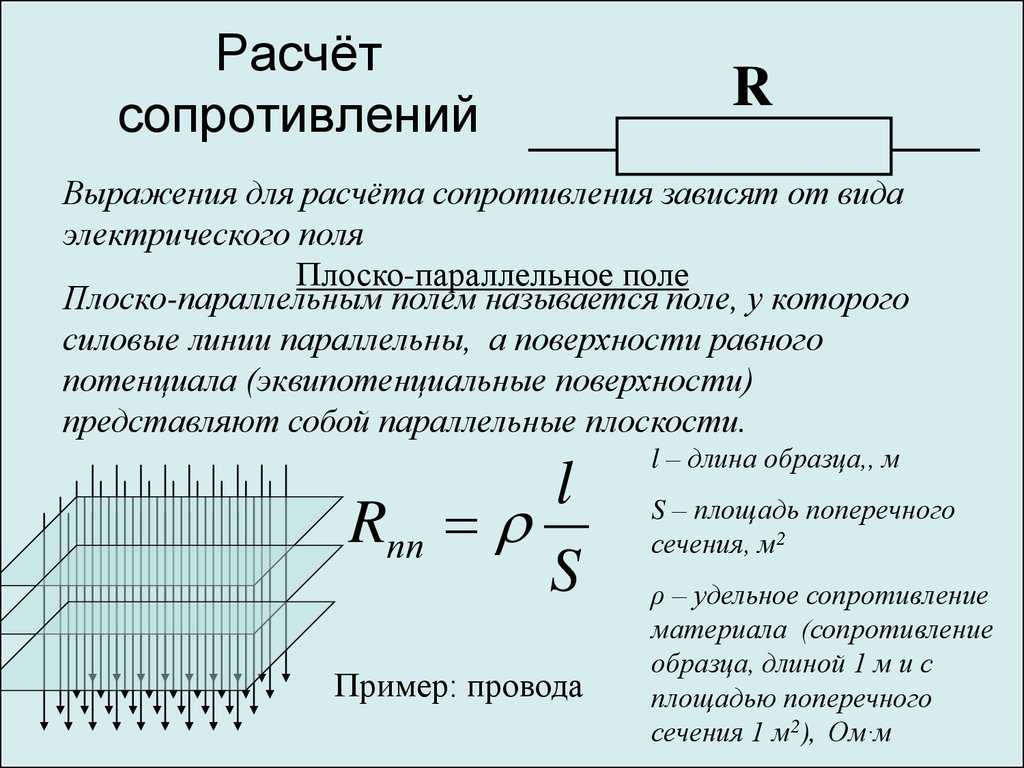
Для расчёта электрического сопротивления однородного вещества используется формула: R = ρ* l/S, где:
- l — длина проводника, м;
- S — площадь поперечного сечения, м2.
Поэтому в физическом смысле удельное сопротивление материала — это величина, обратная удельной проводимости, представляющая собой сопротивление однородного проводника единичной длины и площади поперечного сечения. А значит, она численно равна импедансу участка электрической цепи, выполненному из вещества длиною один метр и площадью поперечного сечения один метр квадратный.
Для каждого вещества удельное сопротивление известно и является справочной величиной. Например, для меди — 0,01724 Ом*мм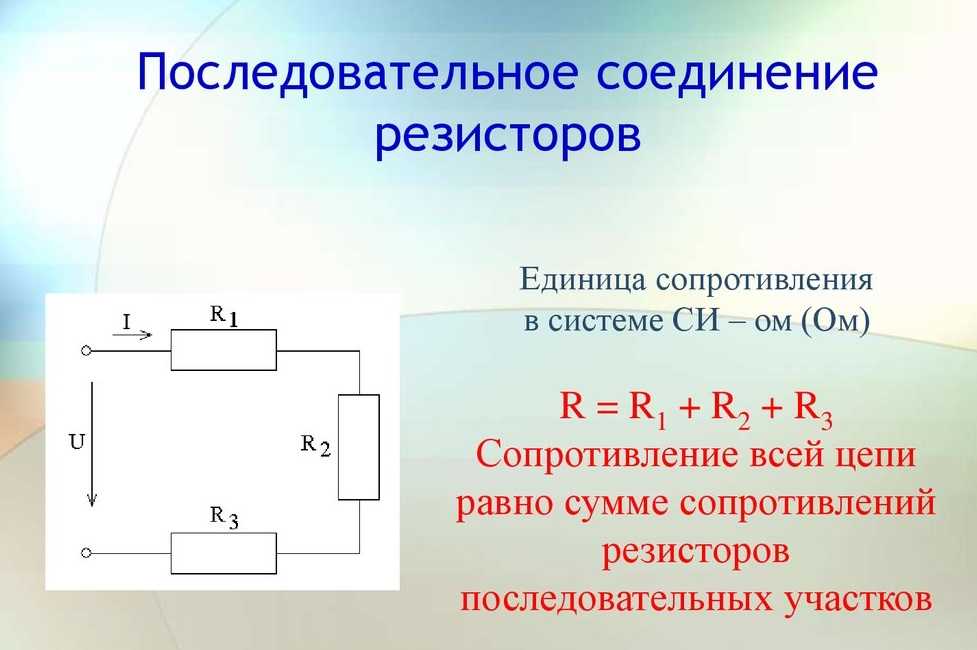
Эквивалентная схема
При расчётах сопротивления электрических цепей широко используется понятие «эквивалентная схема замещения». Её назначение — упростить сложную схему до вида, состоящую из минимума элементов. Иными словами, каждый сложный радиоэлемент можно представить в виде соответствующих ему эквивалентных простых радиодеталей: резистор, ёмкость, индуктивность, источники тока и напряжения. Это позволяет не только математически описать любую схему, но и рассчитать её параметры.
При этом обычно радиоэлементы идеализируются, то есть их паразитные параметры не учитываются. Так и для подсчёта сопротивления цепи каждый компонент представляется как идеальный резистор. После чего схема перерисовывается, и в результате на ней остаются только подключённые разными способами друг к другу резисторы.
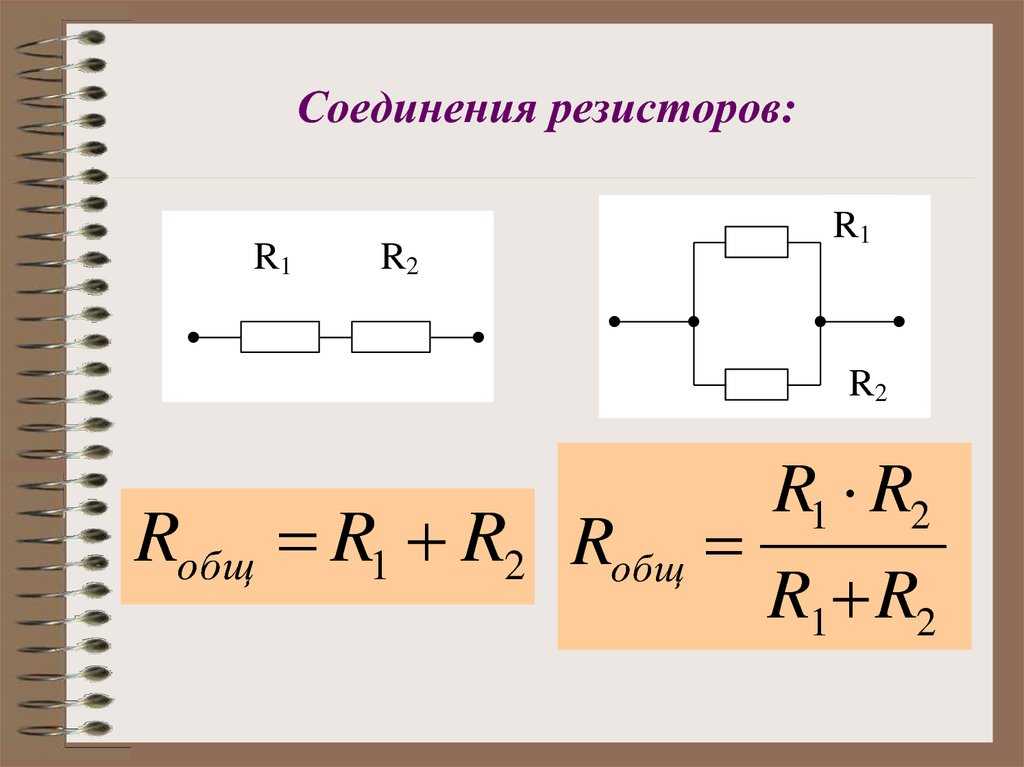
Существует два вида подключения:
- последовательное;
- параллельное.
Основными элементами электрической цепи являются узел, ветвь и контур.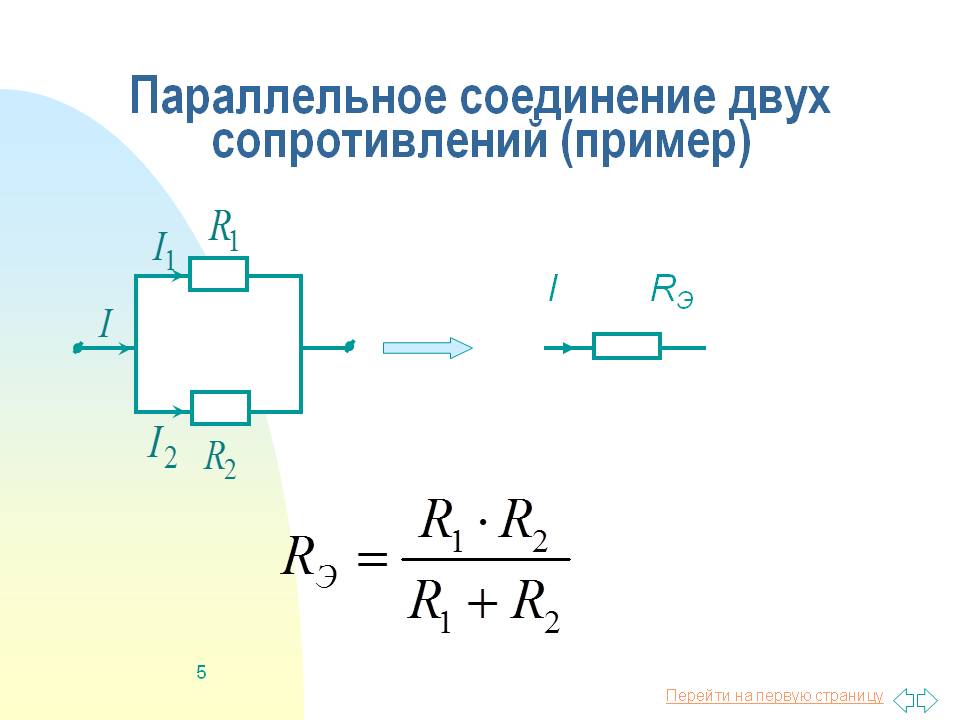 Узел — это место соединения двух и более ветвей. Ветвь — это последовательный участок цепи между двумя узлами, а контур — любая замкнутая цепь. Последовательное соединение состоит из элементов, при котором все компоненты цепи связаны так, что участок цепи, образованный из них, не имеет ни одного узла. А при параллельном соединении все компоненты электрической цепи контактируют между собой в двух узлах. При этом эти узлы напрямую не связаны.
Узел — это место соединения двух и более ветвей. Ветвь — это последовательный участок цепи между двумя узлами, а контур — любая замкнутая цепь. Последовательное соединение состоит из элементов, при котором все компоненты цепи связаны так, что участок цепи, образованный из них, не имеет ни одного узла. А при параллельном соединении все компоненты электрической цепи контактируют между собой в двух узлах. При этом эти узлы напрямую не связаны.
Расчёт импеданса
Методы вычисления общего сопротивления зависят от способа соединения резисторов. При расчётах общего импеданса за основу берутся законы Кирхгофа.
Так, первый его закон гласит: сумма токов в узле равна нулю. Или, если его перефразировать, значение тока, втекающего в узел, равно сумме токов, вытекающих из этого узла. Второй закон связан с электродвижущей силой, и его формулировка звучит так: сумма разности потенциалов в контуре равна сумме падений разности потенциалов на каждом резисторе в цепи.
При последовательном соединении все элементы располагаются друг за другом без ответвлений.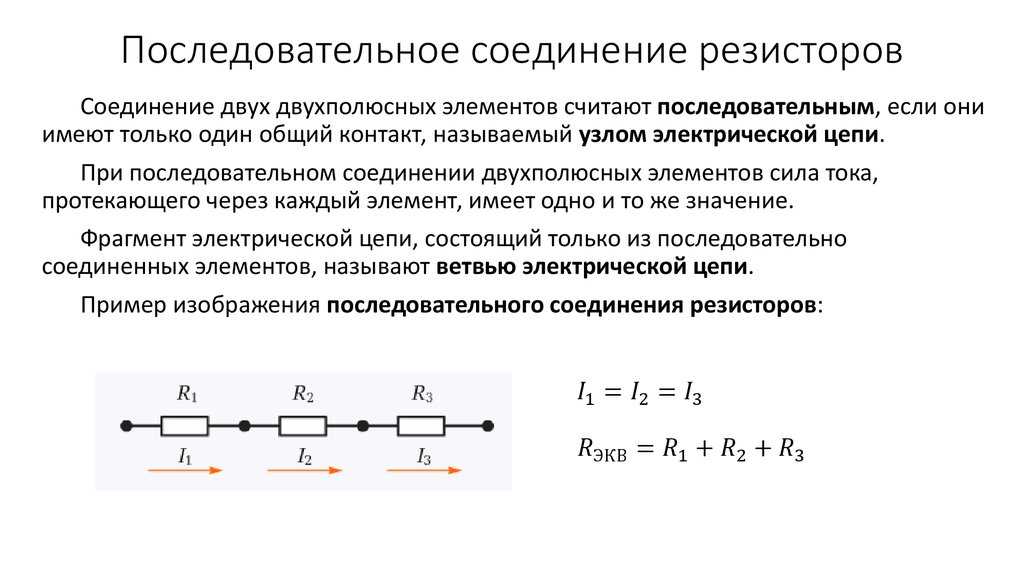 Так как согласно правилу Кирхгофа в любом месте ветви сила тока одинаковая I = I1 = In, то падение напряжения на первом элементе: U1 = I*R1, а на n: Un = I*Rn, где:
Так как согласно правилу Кирхгофа в любом месте ветви сила тока одинаковая I = I1 = In, то падение напряжения на первом элементе: U1 = I*R1, а на n: Un = I*Rn, где:
- In — сила тока, протекающая через резистор, А.
- Un — значение падения напряжения на резисторе, В.
- Rn — величина сопротивления элемента, Ом.
Общая разность потенциалов равна сумме всех напряжений, поэтому можно записать: U = U1+…+Un = I*(R1+…+Rn) = IRo.
В результате формула для расчёта сопротивления цепи в этом случае будет выглядеть следующим образом:
Ro = R1 +…+ Rn, где:
- Ro — общее сопротивление ветви.
- R1 — значение импеданса первого элемента.
- Rn — величина сопротивления n-го элемента.
Если цепь параллельная то это значит, что на этом участке несколько ветвей расходятся, а после опять соединяются. Получается, что сила тока в каждой ветви будет своя, а величина напряжения одинакова. Поэтому Uo = U1=…= Un, а Io = I1+…+In.
Uo/Ro = U1/R1+…+Un/Rn, или
1/Ro = 1/R1+…1/Rn.
В итоге эквивалентное сопротивление при параллельном соединении рассчитывается как произведение значений резисторов, делённое на сумму их произведений. Для двух резисторов формулу для нахождения общего сопротивления можно записать в виде: Ro = (R1*R2) / (R1+R2).
Браузерный онлайн-калькулятор
Если элементов в цепи немного, то, упрощая схему, довольно легко посчитать, используя формулы для параллельного и последовательного включения резисторов, общий импеданс цепи. Но если в схеме много элементов, да ещё она такая, что содержит и то, и другое соединение (комбинированная), проще воспользоваться браузерными онлайн-калькуляторами.
В их основе используются всё те же формулы для расчёта эквивалентного резистора, но все вычисления происходят автоматически. Существует огромное количество предложений таких калькуляторов.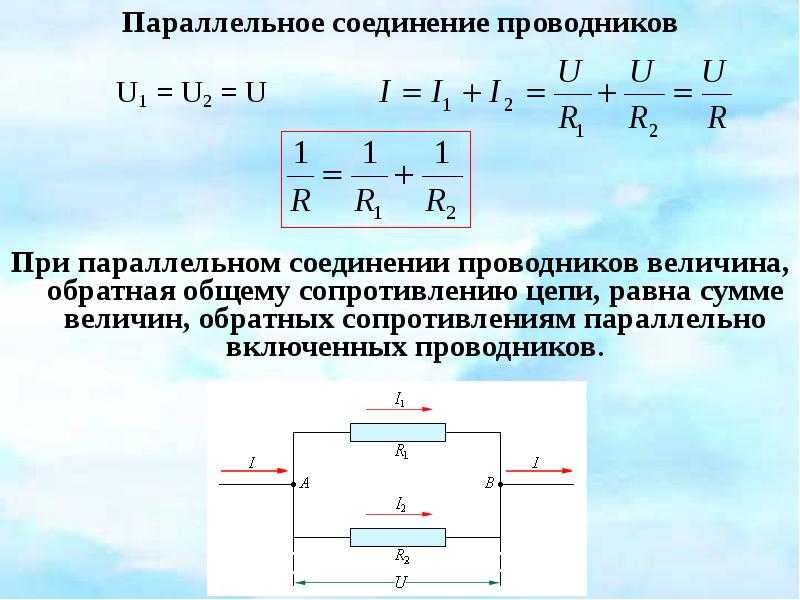 Но при этом все они работают одинаково. Онлайн-расчёт представляет собой программный код, в котором заложен алгоритм вычисления. Потребителю необходимо только в специальных ячейках указать, какой вид соединения используется, сколько элементов в контуре и сопротивления резисторов. Далее надо нажать кнопку «Рассчитать» и через считанные секунды получить ответ.
Но при этом все они работают одинаково. Онлайн-расчёт представляет собой программный код, в котором заложен алгоритм вычисления. Потребителю необходимо только в специальных ячейках указать, какой вид соединения используется, сколько элементов в контуре и сопротивления резисторов. Далее надо нажать кнопку «Рассчитать» и через считанные секунды получить ответ.
Необходимо отметить, что, если даже это в программе не указано, все значения вводятся только в Международной системе единиц, сила тока — ампер, напряжение — вольт, сопротивление — Ом. Тогда и ответ получится в Омах.
Бонусом является и то, что многие такие программы сразу рассчитывают и мощность элемента. Для этого используется формула: P = U2/Ro = I2*Ro, Вт.
Практическое применение
Чаще всего на практике расчёт общего сопротивления цепи выполняют для того, чтобы узнать потребляемую мощность той или иной схемы. При этом, зная общее сопротивление, можно найти и такие важные параметры цепи, как ток и напряжение. Поэтому и рисуют эквивалентную схему электрической цепи. Простые цепи состоят только из последовательных или параллельных участков, но чаще встречаются комбинированные соединения.
Поэтому и рисуют эквивалентную схему электрической цепи. Простые цепи состоят только из последовательных или параллельных участков, но чаще встречаются комбинированные соединения.
Перед тем как приступить к расчёту эквивалентного сопротивления, вся электрическая цепь разделяется на простые контуры. Как только импеданс каждого такого контура будет подсчитан, схема перерисовывается, но вместо контуров рисуется уже резистор. Затем всё повторяется, и это происходит до тех пор, пока не останется один элемент.
Простое соединение
Пусть будет дана схема, состоящая из трёх резисторов, включённых последовательно. При этом сопротивление R1и R2 одинаковое и равно 57 Ом, а сопротивление R3 составляет один килоОм. Для расчёта общего сопротивления цепи сначала понадобится привести значение R3 согласно Международной системе единиц.
R3 = 1 кОм = 1000 Ом.
Так как соединение последовательное, используется формула: Ro = R1+R2+R3. Подставив известные значения, рассчитывается эквивалентное значение: Ro = 57+57+1000 = 1114 Ом.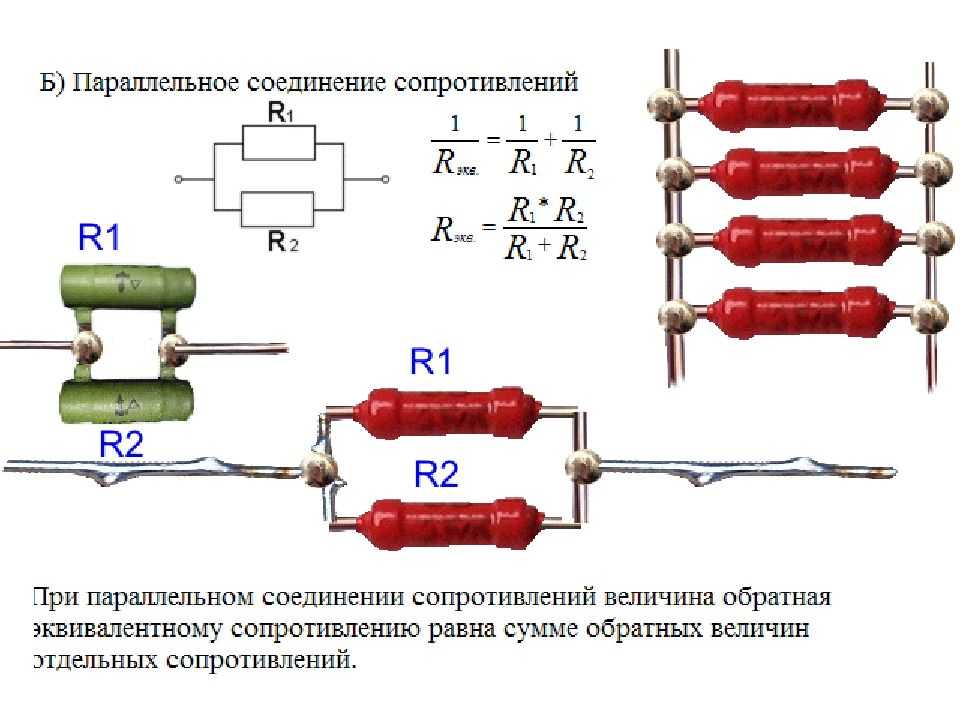
Если же те же самые резисторы будут расположены параллельно друг другу, то для расчёта общего сопротивления уже используется другое выражение:
1/Ro = 1/R1 + 1/R2 +1/R3.
Ro = R1*R2*R3 / (R1*R2+R2*R3+R1*R3).
Подставив исходные данные в эту формулу, получим:
Ro = 57*57*1000/ (57*57 +57*1000+ 57*1000) = 3249000/117249 = 27,7 Ом.
Комбинированный контур
Необходимо вычислить мощность и эквивалентное сопротивление смешанной цепи, состоящей из четырёх резисторов. Резистор R1 =R2 =5 Ом, R3= 10 Ом, R4 =3 Ом. На схему подаётся питание пять вольт.
Первоначально понадобится упростить схему. Сопротивления R3 и R4 включены относительно друг друга параллельно. Поэтому находится их объединённое сопротивление:
Rp = (R3*R4)/(R3+R4).
Rp = (10*3)/ (10+3) = 2,3 Ом.
Теперь схему можно перерисовать в виде трёх последовательно включённых резисторов и найти общее сопротивление путём сложения их величин:
Ro = R1+R2+Rp = 5+5+2,3 = 12,3 Ом.
Зная эквивалентное сопротивление, используя закон Ома, несложно вычислить силу тока в цепи и мощность эквивалентного резистора:
I = U/R = 5/2,3 = 2,2 A.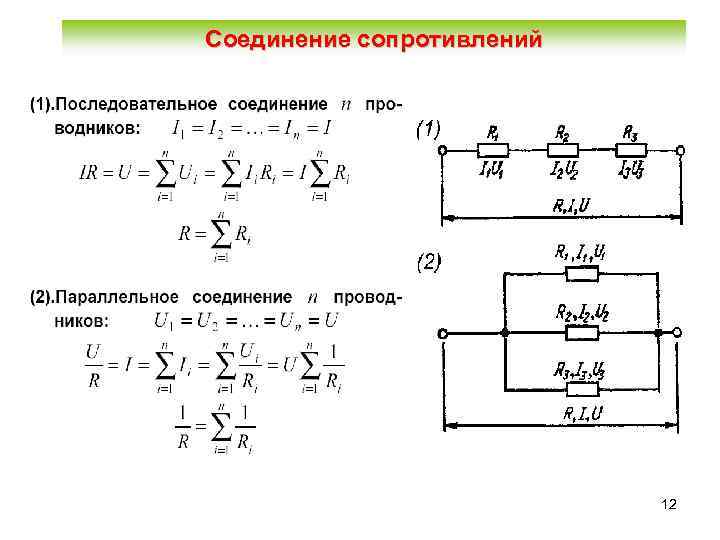
P = I*U = 2,2*5= 11 Вт.
Таким образом, путём постепенного упрощения схемы можно свести цепь из последовательно и параллельно соединённых резисторов к одному элементу. А затем рассчитать его сопротивление и требуемую мощность.
Расчет сопротивления цепи резисторов
Содержание
- 1 Пример 1
- 2 Пример 2
- 3 Пример 3
- 4 Пример 4
- 5 Пример 5
- 6 Пример 1
- 7 Пример 2
- 8 Пример 3
- 9 Пример 4
- 10 Пример 5
Разделы: Физика
Цели:
- Образовательная: систематизировать и закрепить знания учащихся о различных соединениях проводников, сформировать умения применять законы последовательного и параллельного соединений для расчёта электрических цепей, объединить знания, полученные на уроках физики и математики.
- Развивающая: развить мышление учащихся, активизировать познавательную деятельность через решение задач на расчет электрических цепей, развить умение рассчитывать параметры электрических цепей и совершенствовать полученные на уроке навыки.

- Воспитательная: формирование интереса к изучаемому предмету, продолжить формирование коммуникативных умений.
Тип урока: урок проверки и закрепления новых знаний по физике и математике.
Метод проведения урока: практический
Оборудование:
- Громов С.В. Учебник “Физики-9”;
- план урока;
- методика расчета участка электрической цепи постоянного тока;
- карточки-задания.
Сегодня на уроке мы должны применить полученные ранее знания о законах последовательного и параллельного соединений для расчёта участка электрической цепи, а также определить степень усвоения изученного материала с помощью карточек – заданий.
Прежде чем приступить к рассмотрению электрических цепей, вспомним то, что мы уже знаем и ответим на вопросы:
1) Какие виды соединений бывают и как они изображаются на электрических схемах?
2) Назовите законы последовательного соединения?
3) Назовите законы параллельного соединения?
4) Какая отличительная особенность параллельного соединения?
Рассмотрим расчёт участка электрической цепи на примере следующих задач:
1.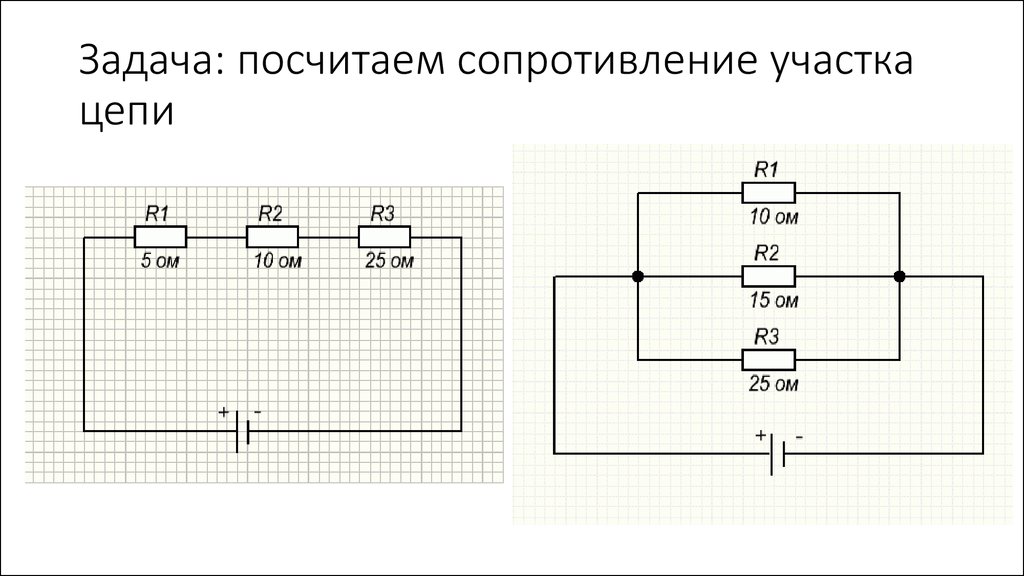 Рассчитайте общее электрическое сопротивление участка цепи?
Рассчитайте общее электрическое сопротивление участка цепи?
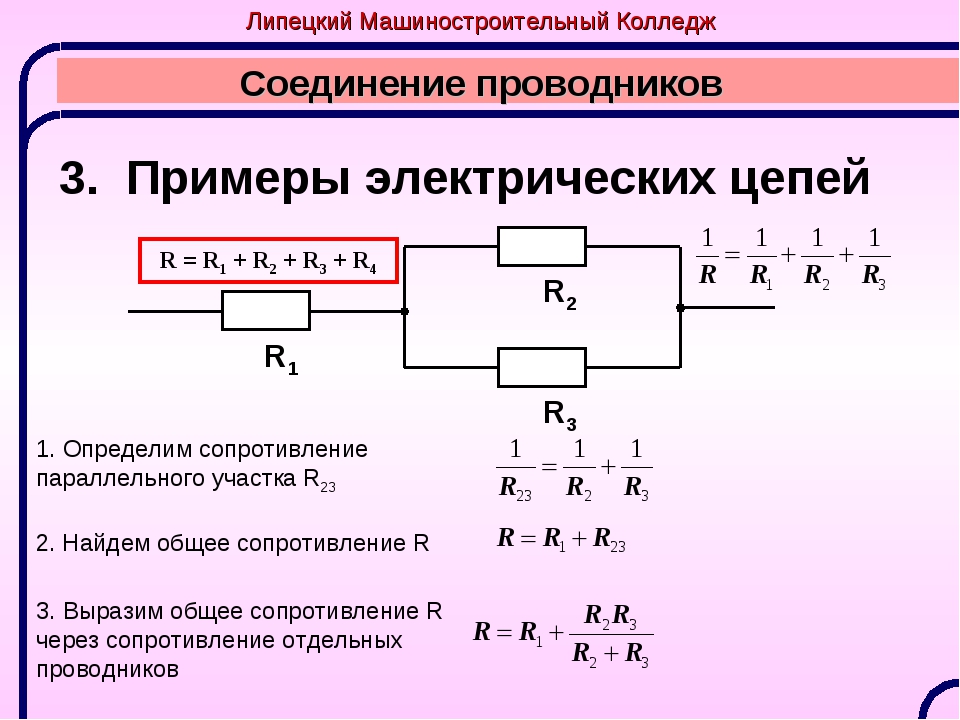
1) Наиболее удалённые от источника элементы – это резисторы R2 и R3.
2) Объединяем эти два резистора в первый участок и рассчитываем их общее сопротивление. Резисторы R2 и R3 подключены параллельно, т.к образуют в соединении два узла, следовательно:
Ом
3) Изображаем получившуюся в результате свёртывания резисторы R2 и R3 электрическую схему:
4) Полученные в результате объединения схему с двумя резисторами группируем во второй участок и рассчитываем их общее сопротивление. Так как резисторы R1 и Rоб.1 соединены последовательно, значит:
Ответ: общее сопротивление резисторов на участке электрической цепи 6 Ом.
2. Рассчитайте общее электрическое сопротивление участка цепи?
1) Резисторы R1 и R2 соединены между собой последовательно:
Изобразим полученный электрический участок цепи:
2) Резисторы R3 и R4 соединены между собой последовательно:
Изобразим полученный электрический участок цепи:
3) Полученные в результате объединения схему с двумя резисторами группируем в третий участок и рассчитываем их общее сопротивление. Так как резисторы Rоб.1 и Rоб.2 соединены параллельно, значит:
Так как резисторы Rоб.1 и Rоб.2 соединены параллельно, значит:
Ом
Ответ: общее сопротивление резисторов на участке электрической цепи 2,1 Ом.
3. Выполните задания самостоятельно по карточкам (дифференцированные), воспользовавшись памяткой расчета участка электрической цепи постоянного тока:
а) Рассчитайте общее электрическое сопротивление участка цепи?
б) Рассчитайте общее электрическое сопротивление участка цепи?
в) Рассчитайте общее электрическое сопротивление участка цепи?
Сегодня на уроке мы рассмотрели различные схемы участков электрических цепей, научились рассчитывать цепи, применяя законы последовательного и параллельного соединений, а также закрепили полученные знания с помощью карточек – заданий.
Расчет сопротивления цепи необходим при решении различных задач по электротехнике. Суть заключается в приведении сложной разветвленной электрической цепи к цепи с единственным эквивалентным сопротивлением, которую называют простой электрической цепью.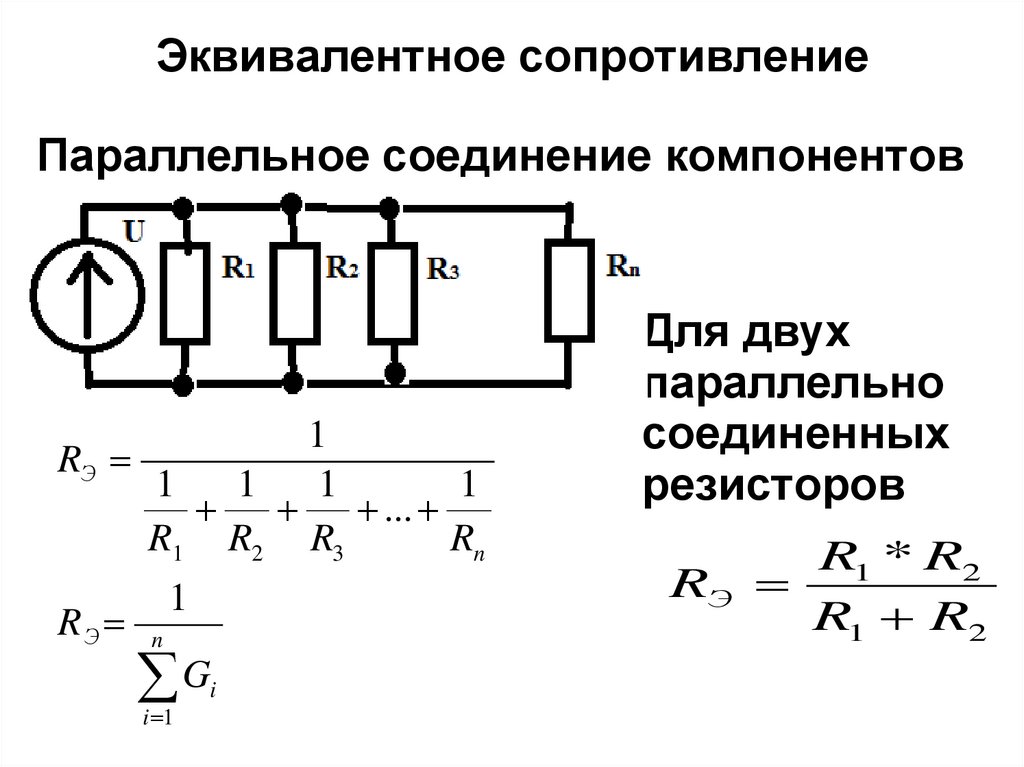
Пример 1
Цепь в данном примере состоит из двух последовательно соединенных сопротивлений, следовательно, их общее сопротивление будет равно сумме их сопротивлений. Подробнее о видах соединений тут.
Допустим, что R1=10 Ом R2=20 Ом, тогда
Пример 2
Два сопротивления соединены параллельно, значит при сворачивании схемы, общее сопротивление будет равно (значения R1,R2 такие же как и в примере 1)
Можно заметить, что при параллельном соединении общее сопротивление меньше, чем при последовательном в несколько раз.
Пример 3
В данном примере ситуация аналогична примеру 2, за тем лишь исключением, что сопротивлений три. Тогда общее сопротивление будет равно (R1,R2 прежние, R3=105 Ом)
Пример 4
Чтобы рассчитать общее сопротивление смешанного соединения проводников, необходимо для начала найти общее сопротивление резисторов R1 и R2 соединенных параллельно, а затем общее сопротивление, как сумму R12 и R3 соединенных последовательно.
Пример 5
Данная электрическая цепь сложнее, чем предыдущие, но как можно увидеть, она также состоит из последовательно или параллельно соединенных сопротивлений, которые можно постепенно сворачивать, приводя цепь к единственному эквивалентному сопротивлению R.
Путем сворачивания цепи с помощью преобразований последовательно и параллельно соединенных проводников, можно максимально упростить для дальнейшего расчета сколь угодно сложную схему. Исключением служат цепи содержащие сопротивления, соединенные по схеме звезда и треугольник.
Расчет сопротивления цепи необходим при решении различных задач по электротехнике. Суть заключается в приведении сложной разветвленной электрической цепи к цепи с единственным эквивалентным сопротивлением, которую называют простой электрической цепью.
Пример 1
Цепь в данном примере состоит из двух последовательно соединенных сопротивлений, следовательно, их общее сопротивление будет равно сумме их сопротивлений. Подробнее о видах соединений тут.
Подробнее о видах соединений тут.
Допустим, что R1=10 Ом R2=20 Ом, тогда
Пример 2
Два сопротивления соединены параллельно, значит при сворачивании схемы, общее сопротивление будет равно (значения R1,R2 такие же как и в примере 1)
Можно заметить, что при параллельном соединении общее сопротивление меньше, чем при последовательном в несколько раз.
Пример 3
В данном примере ситуация аналогична примеру 2, за тем лишь исключением, что сопротивлений три. Тогда общее сопротивление будет равно (R1,R2 прежние, R3=105 Ом)
Пример 4
Чтобы рассчитать общее сопротивление смешанного соединения проводников, необходимо для начала найти общее сопротивление резисторов R1 и R2 соединенных параллельно, а затем общее сопротивление, как сумму R12 и R3 соединенных последовательно.
Пример 5
Данная электрическая цепь сложнее, чем предыдущие, но как можно увидеть, она также состоит из последовательно или параллельно соединенных сопротивлений, которые можно постепенно сворачивать, приводя цепь к единственному эквивалентному сопротивлению R.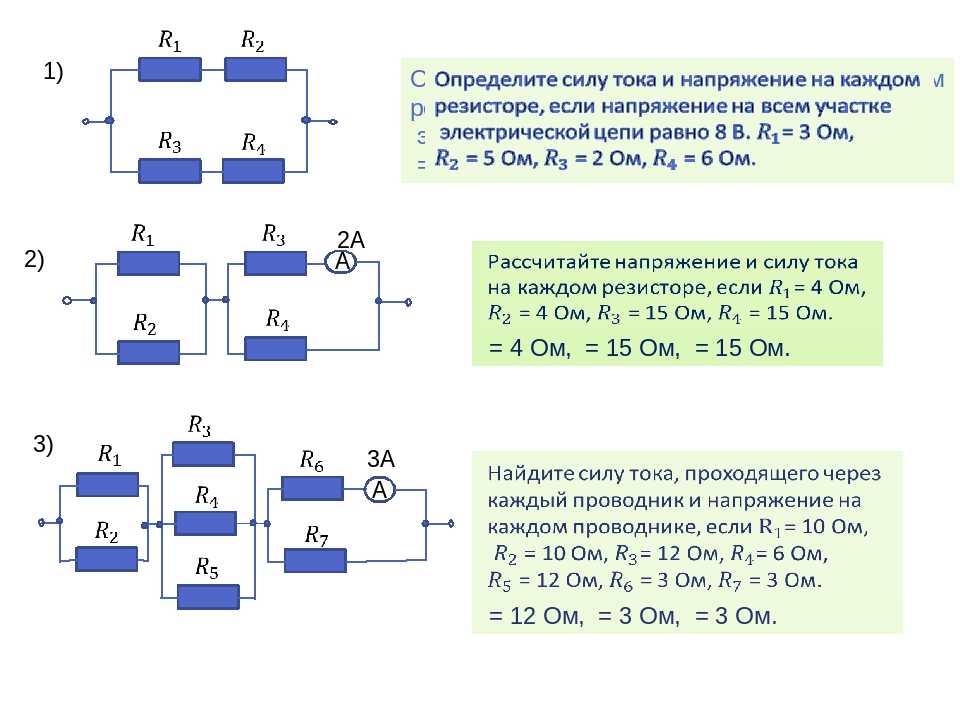
Путем сворачивания цепи с помощью преобразований последовательно и параллельно соединенных проводников, можно максимально упростить для дальнейшего расчета сколь угодно сложную схему. Исключением служат цепи содержащие сопротивления, соединенные по схеме звезда и треугольник.
Общее сопротивление цепи — правила, формулы и примеры вычисления
Величина, благодаря которой проводник способен не пропускать через себя ток или ограничивать его прохождение, называется электрическим сопротивлением цепи. Общее её значение для замкнутой схемы определяется с помощью формул. Их вид зависит от типа соединения элементов. Кроме того, если известны определённые характеристики, найти параметр можно, используя закон Ома для участка цепи.
Содержание
- Общие сведения
- Последовательное подключение
- Параллельное соединение
- Решение задач
Общие сведения
Прохождение электрического тока через проводник зависит от его проводимости.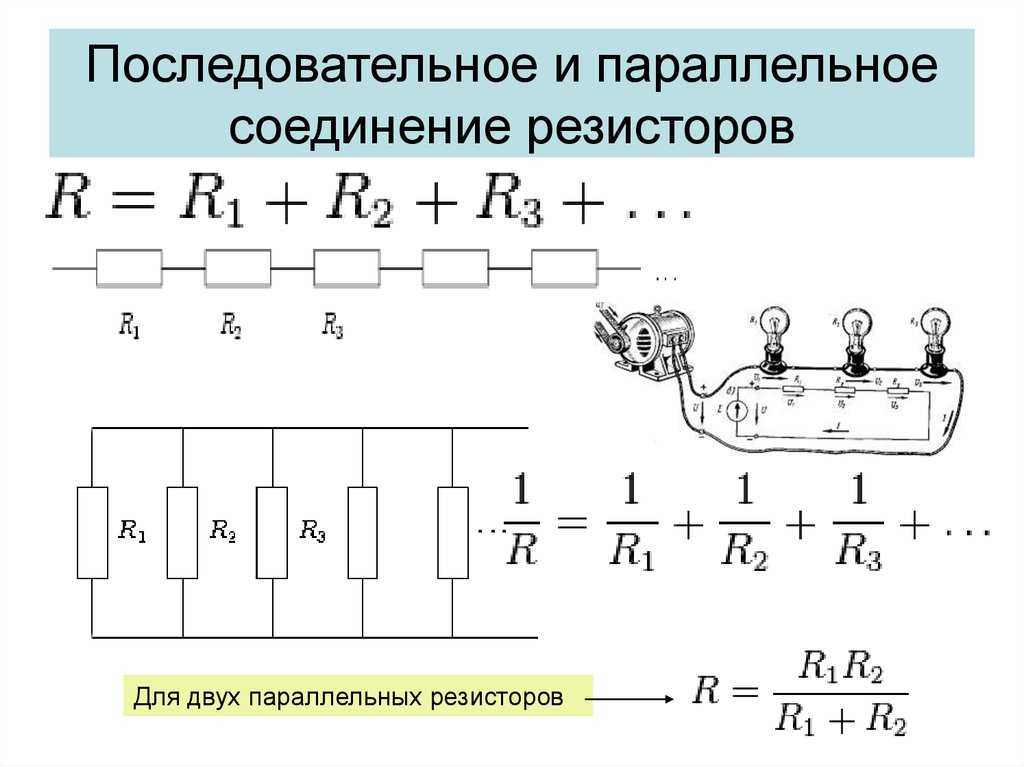 Это параметр пропорционален силе тока. Другими словами, он определяет способность вещества пропускать через себя электричество без потерь. Зависит проводимость от физических свойств материала, температуры, степени воздействия внешних сил. Обратной ей величиной является сопротивление, то есть характеристика проводника, показывающая его возможность сопротивляться прохождению тока.
Это параметр пропорционален силе тока. Другими словами, он определяет способность вещества пропускать через себя электричество без потерь. Зависит проводимость от физических свойств материала, температуры, степени воздействия внешних сил. Обратной ей величиной является сопротивление, то есть характеристика проводника, показывающая его возможность сопротивляться прохождению тока.
Связь между фундаментальными параметрами электротока экспериментально установил Симон Ом. Он выяснил, что сила тока в замкнутой цепи пропорциональна разности потенциалов (напряжению) и обратно пропорциональна сопротивлению: I = U / R. Так, если R равно нулю, то сила тока будет бесконечной.
Способность веществ препятствовать прохождению электротока используется при построении электрических цепей. Так, радиоэлемент, который называется резистором, установленный в определённом месте электроцепи, позволяет получить на нагрузке нужное значение напряжения или тока. Радиодеталь представляет собой двухполюсник, который имеет установленное значение сопротивления или может изменять его.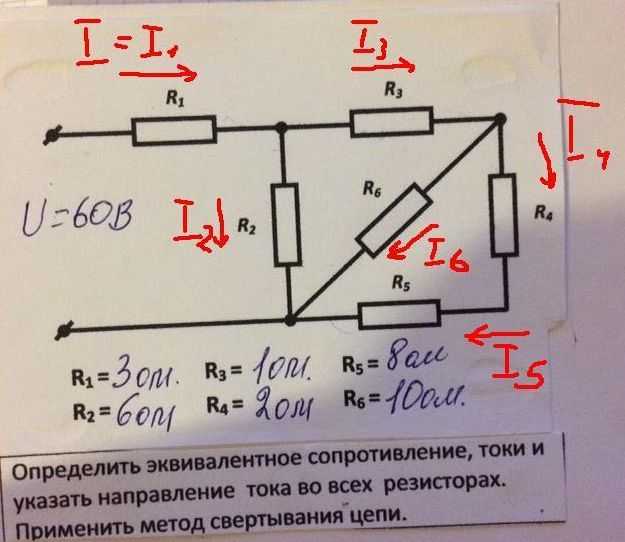
Реальная замкнутая электрическая цепь состоит из множества активных и пассивных радиоэлементов. Каждый из них обладает каким-то значением сопротивления. В этом случае говорят о внутреннем сопротивлении прибора.
Расчёт выходных характеристик цепи, а именно величин тока и напряжения, требует знания общего сопротивления всей замкнутой цепочки. Иными словами, все элементы, начиная от источника питания и заканчивая нагрузкой, заменяются эквивалентными резисторами. Для цепи сначала считают общее значение сопротивления, а затем вычисляют нужные характеристики. Относительно источника тока, нагрузки и других элементов каждый резистор может быть подключён:
- последовательно;
- параллельно.
Вид подключения влияет на общее сопротивление. Формула для его нахождения может быть довольно громоздкой из-за смешанного соединения, поэтому чаще расчёт ведётся в несколько этапов, на каждом из которых выполняется объединение одного или нескольких элементов.
Последовательное подключение
Для удобства при изображении разветвлённой электрической цепи все сопротивления чертят в виде прямоугольников, которые являются резисторами. У любого такого элемента можно выделить два вывода. Один является началом, а другой — концом. С учетом сказанного можно сформулировать определение для последовательного соединения проводников: подключение, при котором конец предыдущего элемента соединён с началом последующего, называют последовательным.
Любой проводник обладает электрическим сопротивлением. Целью преобразования является замена чередующейся последовательности одним резистором. При этом по своим электрическим свойствам он должен не отличаться от всей цепочки. Простыми словами это можно пояснить так: если взять два чёрных ящика, у которых есть по паре выводов, причём один будет содержать всю электроцепь, а другой быть её эквивалентом, то определить, в каком из них находится схема, а где эквивалент, будет невозможно.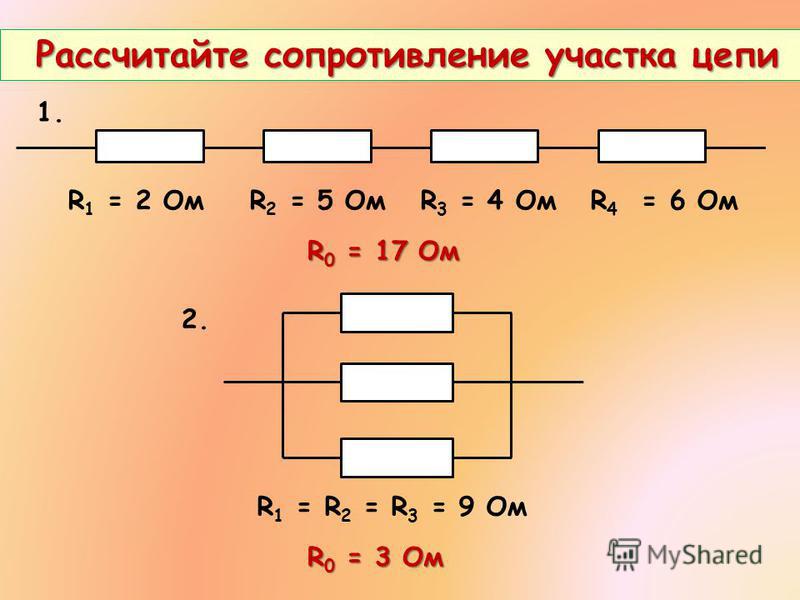
При последовательном соединении происходят следующие явления. Пусть имеется прямая цепочка, содержащая n резисторов: R1 + R2 + … +Rn. Сила тока — это величина, которая равняется заряду, протекающему за единицу времени. Можно представить, что в первом резисторе значение электротока будет больше, чем во втором. В результате возникнет «пробка», и скорость движения зарядов замедлится.
В точке соединения элементов произойдёт накопление электронов, что приведёт в ней к росту напряжения. Соответственно, сила тока на первом резисторе будет уменьшаться, а на втором, наоборот, увеличиваться. Это приведёт к выравниванию количества проходящих через резисторы зарядов, поэтому сила тока практически за мгновение во всей последовательной цепи станет одинаковой.
Напряжение — это работа, выполняемая по переносу заряда. По закону сохранения энергии общее её значение равняется их сумме на различных этапах. Общую разность потенциалов можно будет определить, сложив напряжения на каждом элементе. Такой вид подключения описывается следующими выражениями:
Такой вид подключения описывается следующими выражениями:
- I = I 1 = I 2 = … = In;
- U = U1 + U2 + … +Un.
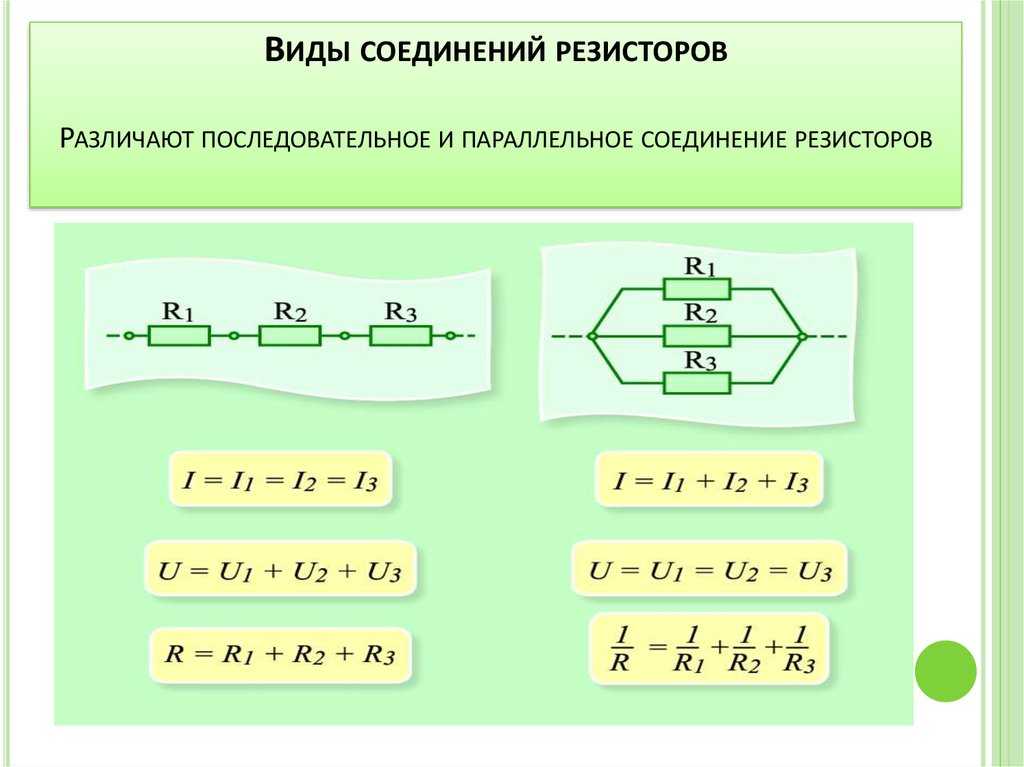
Эти равенства являются фундаментальными для нахождения параметров при повторении резисторов в цепи. Используя закон Ома, можно найти, чему будет равняться сопротивление цепи. Формула для его нахождения будет выглядеть так: Rпос = R 1 + R 2 +… + Rn.
Параллельное соединение
По распространённости такой вид соединения чаще встречается, чем последовательное подключение. При нём проводники соединены так, что начала всех резисторов сводятся в одну точку электрической цепи, а концы — в другую. Для того чтобы заменить разветвлённое подключение одним эквивалентным элементом, нужно знать, как правильно рассчитать ток и напряжение.
Пусть имеется цепь, состоящая из R1 + R2 + … +Rn параллельно включённых радиоэлементов.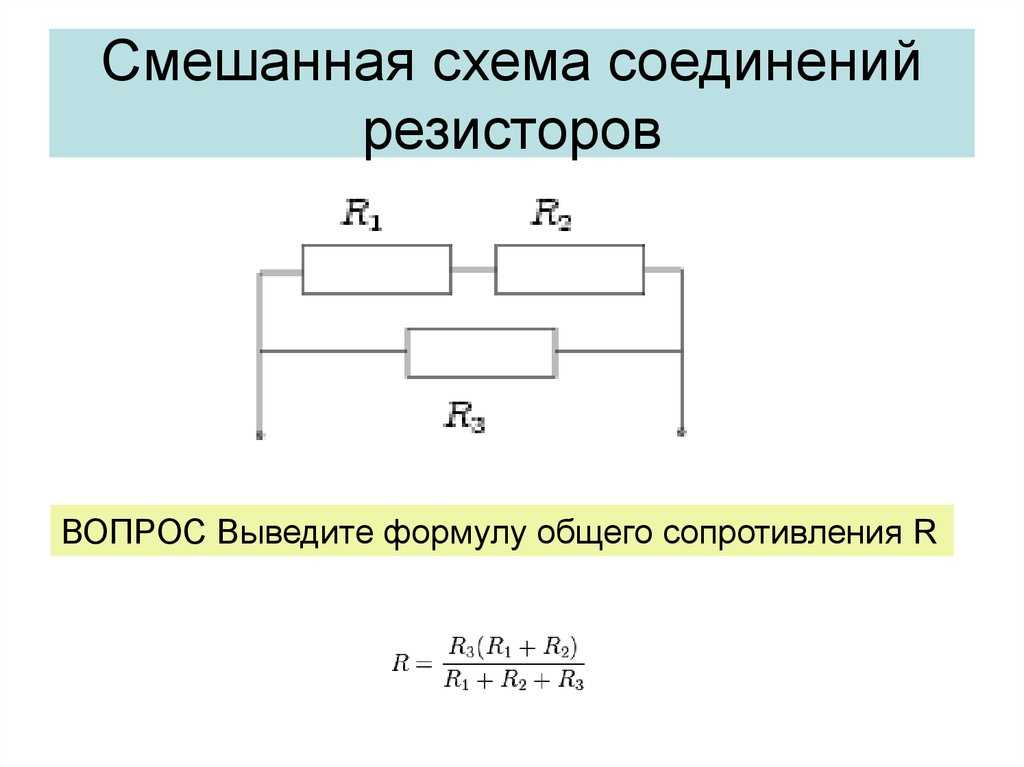 На неё подаётся напряжение U. На вход схемы поступает ток с силой I. Используя закон сохранения зарядов, можно выполнить следующие рассуждения: ток втекает в узел, к которому подсоединены начала всех резисторов, затем он растекается по их выводам.
На неё подаётся напряжение U. На вход схемы поступает ток с силой I. Используя закон сохранения зарядов, можно выполнить следующие рассуждения: ток втекает в узел, к которому подсоединены начала всех резисторов, затем он растекается по их выводам.
В результате через первую ветвь потечёт ток I1, вторую — I2, в энную — In. Поскольку заряд не может пропасть, то какое его количество втекло в узел, такое же должно разойтись по всем ветвям для одного и того же момента времени. Значит, сумма токов на всех выводах будет равняться поступающему на них значению.
Электростатическое поле является потенциальным, то есть работа по перемещению заряда из одной точки в другую не зависит от траектории, по которой перемещается носитель. Следовательно, при переносе одного кулона по любой ветви нужно будет совершить одинаковую работу. Из приведённых рассуждений следует, что при параллельном соединении формулы, с помощью которых можно рассчитать характеристики электрической цепи, будут следующими:
- I = I1 + I2 + … +In;
- U1 = U2 = … = Un.

Таким образом, вычисление эквивалентного сопротивления, которым можно будет заменить всю цепь в соответствии с законом Ома, выполняется по формуле: 1 / R пар = 1 / R 1 + 1 / R 2 + … + 1 / Rn. Для одинаковых проводников при вычислении сопротивления можно использовать приведённую формулу. Это позволяет в некоторых случаях упростить расчёт.
Согласно правилу сложения дробей c одинаковым знаменателем можно записать равенство: 1 / R1 + 1 / R2 + … + 1 / Rn = N / R1. Отсюда следует, что Rпар = R1 / N, где N равно числу резисторов. По аналогии можно посчитать общее сопротивление по упрощённой формуле для двух элементов: (1 / R1) + (1 / R2) = (R 2 + R 1) / R 1 * R 2. Это довольно удобные формулы для практического применения.
Решение задач
Для вычисления сопротивления любого смешанного соединения нужно запомнить всего две формулы — выражения для нахождения величины при последовательном и параллельном подключении. Поочерёдно комбинируя их применение, сложную схему можно заменить одним сопротивлением. Но не всегда приходится применять формулы. Есть задания, в которых неизвестную величину можно вычислить в уме.
Поочерёдно комбинируя их применение, сложную схему можно заменить одним сопротивлением. Но не всегда приходится применять формулы. Есть задания, в которых неизвестную величину можно вычислить в уме.
Например, пусть имеется параллельное подключение из четырёх резисторов. Сопротивления проводников равняются 10 Ом, 12 Ом, 15 Ом, 20 Ом. Нужно образовать из них резистор, не изменяющий характеристики электрической цепи. Чтобы выполнить расчёт в уме, следует каждый элемент представить в виде комбинации из 60-омных резисторов. Тогда к первому нужно будет добавить шесть, ко второму — пять, к третьему — четыре, к четвёртому — три. Общее количество резисторов получится 18. Значит, Rобщ = 60 / 18 = 10 / 3 = 3,3 Ом.
Из типовых задач, в которых необходимо найти сопротивление цепи, предлагающихся в школе на уроках физики, можно привести следующие:
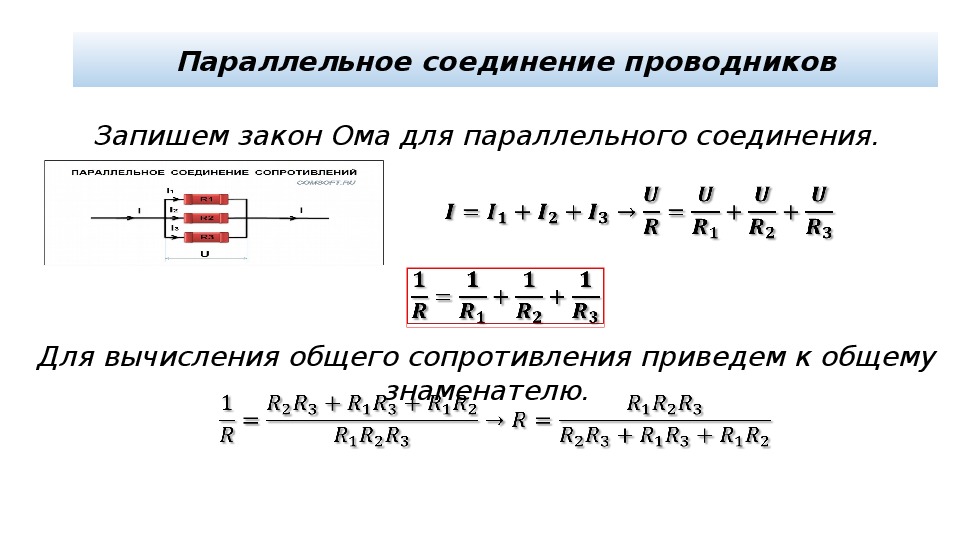 Сопротивление элементов составляет: R1 = R2 = 5 Ом, R3 = 15 Ом. В задаче три резистора подключены в линию, значит, их полное сопротивление равно: R = R 1 + R 2 + R 3 = 25 Ом. У вольтметра r внутреннее равно бесконечности. Следовательно, I = U / R = 100 / 25 = 4 A.
Сопротивление элементов составляет: R1 = R2 = 5 Ом, R3 = 15 Ом. В задаче три резистора подключены в линию, значит, их полное сопротивление равно: R = R 1 + R 2 + R 3 = 25 Ом. У вольтметра r внутреннее равно бесконечности. Следовательно, I = U / R = 100 / 25 = 4 A.Каково будет сопротивление каждого из резисторов, если при их последовательном соединении ток равен 3A, а при параллельном — 16A. Напряжение в сети составляет 120 В. При первом способе соединения Iпосл = U / (R1 + R2), при втором Iпар = U / Rпар = U * (R1 + R2) / R1 * R2. Из первой формулы следует, что R1 + R2 = U / Iпос. Тогда: I пар = U 2 / Iпос * R 1 * R 2 → R 1 * R 2 = U 2 / I пар * I пос. Используя теорему Виета, можно составить квадратное уравнение. После его решения искомые величины будут равны: R 1 = 30 Ом, R 2 = 10 Ом.
Следует отметить, что приборы для измерения тока, напряжения и даже ёмкости используют особенности вычисления сопротивления цепи. Так, вольтметр имеет бесконечно большой внутренний импеданс, что позволяет подключать его параллельно к измеряемым точкам без внесения изменения в протекающий сигнал.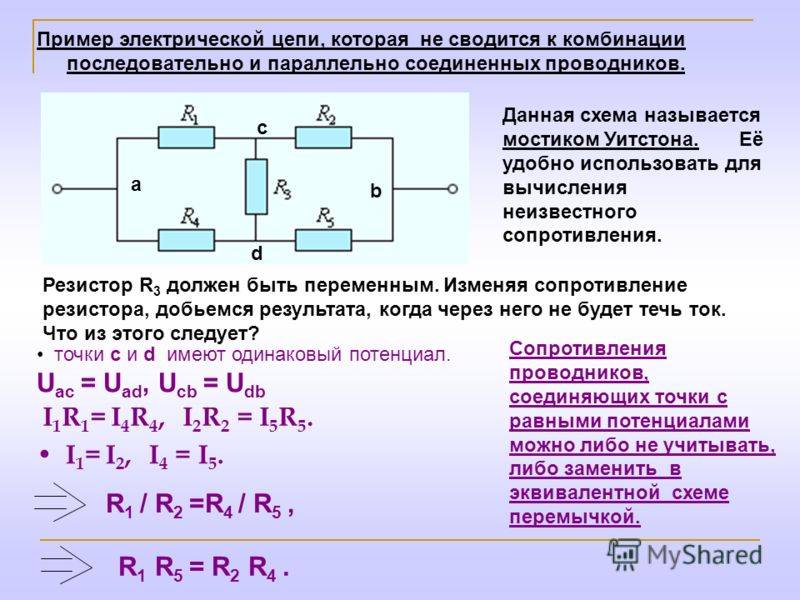
Амперметр же, наоборот, характеризуется пренебрежимо малой величиной внутреннего сопротивления, поэтому и подключают его в разрыв линии, на которой выполняют измерения.
Предыдущая
ФизикаУдельное электрическое сопротивление — формула, обозначение и физический смысл
Следующая
ФизикаДоклад на тему: «Траектория, путь и перемещение» — пример реферата
Сопротивление и удельное сопротивление
Сопротивление и удельное сопротивление
Независимо от того, подчиняется ли материал закону Ома, его сопротивление можно описать с помощью объемного удельного сопротивления. Удельное сопротивление и, следовательно, сопротивление зависят от температуры. В значительных диапазонах температур эту температурную зависимость можно предсказать по температурному коэффициенту сопротивления.
| Индекс Цепи постоянного тока | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Материалы, перечисленные в таблице, разделены на категории проводников, полупроводников и изоляторов на основе широких групп удельного сопротивления. Проводники имеют наименьшее удельное сопротивление, а изоляторы — наибольшее; полупроводники имеют промежуточное удельное сопротивление. Проводники имеют разную, но большую плотность свободного заряда, в то время как большинство зарядов в изоляторах связаны с атомами и не могут свободно перемещаться. Полупроводники занимают промежуточное положение, имея гораздо меньше свободных зарядов, чем проводники, но обладая свойствами, из-за которых количество свободных зарядов сильно зависит от типа и количества примесей в полупроводнике. Эти уникальные свойства полупроводников используются в современной электронике, что мы и рассмотрим в последующих главах. 9{-5} \dfrac{V}{m}.\end{align*}\] Значение Исходя из этих результатов, неудивительно, что медь используется для проводов для передачи тока, поскольку сопротивление довольно маленький.
PhETПросмотрите это интерактивное моделирование, чтобы узнать, как площадь поперечного сечения, длина и удельное сопротивление провода влияют на сопротивление проводника. Отрегулируйте переменные с помощью ползунков и посмотрите, станет ли сопротивление меньше или больше. Температурная зависимость удельного сопротивления Взглянув на таблицу \(\PageIndex{1}\), вы увидите столбец с пометкой «Температурный коэффициент». Удельное сопротивление некоторых материалов сильно зависит от температуры. В некоторых материалах, таких как медь, удельное сопротивление увеличивается с повышением температуры. На самом деле у большинства проводящих металлов удельное сопротивление увеличивается с повышением температуры. Повышение температуры вызывает усиление колебаний атомов в структуре решетки металлов, которые препятствуют движению электронов. В других материалах, таких как углерод, удельное сопротивление уменьшается с повышением температуры. Во многих материалах зависимость приблизительно линейна и может быть смоделирована линейным уравнением: 9оС\). Также обратите внимание, что температурный коэффициент \(\alpha\) отрицателен для полупроводников, перечисленных в таблице \(\PageIndex{1}\), а это означает, что их удельное сопротивление уменьшается с повышением температуры. Они становятся лучшими проводниками при более высокой температуре, потому что повышенное тепловое возбуждение увеличивает количество свободных зарядов, доступных для переноса тока. Это свойство уменьшаться \(\rho\) с температурой также связано с типом и количеством примесей, присутствующих в полупроводниках. СопротивлениеТеперь рассмотрим сопротивление провода или компонента. Сопротивление является мерой того, насколько сложно пропустить ток через провод или компонент. Сопротивление зависит от удельного сопротивления. Удельное сопротивление является характеристикой материала, используемого для изготовления провода или другого электрического компонента, тогда как сопротивление является характеристикой провода или компонента. Для расчета сопротивления рассмотрим отрезок токопроводящего провода площадью поперечного сечения A , длина L и удельное сопротивление \(\rho\). Величина электрического поля на отрезке проводника равна напряжению, деленному на длину, \(E = V/L), а величина плотности тока равна силе тока, деленной на сечение. площадь сечения, \(J = I/A\). Используя эту информацию и вспомнив, что электрическое поле пропорционально удельному сопротивлению и плотности тока, мы можем увидеть, что напряжение пропорционально току: \[\begin{align*} E &= \rho J \\[4pt] \dfrac{V}{L} &= \rho \dfrac{I}{A} \\[4pt] V &= \ left(\rho \dfrac{L}{A}\right) I. \end{align*}\] Определение: СопротивлениеОтношение напряжения к току определяется как сопротивление \(R \): \[R \equiv \dfrac{V}{I}. Сопротивление цилиндрического сегмента проводника равно удельному сопротивлению материала, умноженному на длину, деленную на площадь: \[R \equiv \dfrac{V}{I} = \rho \dfrac{L}{A}.\] Единицей сопротивления является ом, \(\Омега\). Для данного напряжения, чем выше сопротивление, тем меньше ток. Резисторы Обычным компонентом электронных схем является резистор. Резистор можно использовать для уменьшения протекающего тока или обеспечения падения напряжения. На рисунке \(\PageIndex{2}\) показаны символы, используемые для обозначения резистора на принципиальных схемах цепи. Два широко используемых стандарта для принципиальных схем предоставлены Американским национальным институтом стандартов (ANSI, произносится как «AN-see») и Международной электротехнической комиссией (IEC). Обе системы широко используются. В этом тексте мы используем стандарт ANSI для его визуального распознавания, но мы отмечаем, что для более крупных и сложных схем стандарт IEC может иметь более четкое представление, что облегчает его чтение. Зависимость сопротивления от формы и материалаРезистор можно смоделировать в виде цилиндра с площадью поперечного сечения A и длиной L , изготовленного из материала с удельным сопротивлением \(\rho\) (рисунок \( \PageIndex{3}\)). Сопротивление резистора равно \(R = \rho \dfrac{L}{A}\) . Рисунок \(\PageIndex{3}\): Модель резистора в виде однородного цилиндра длиной L и площадь поперечного сечения A . Его сопротивление потоку тока аналогично сопротивлению трубы потоку жидкости. Чем длиннее цилиндр, тем больше его сопротивление. Чем больше его площадь поперечного сечения А , тем меньше его сопротивление. Наиболее распространенным материалом для изготовления резисторов является углерод. Углеродная дорожка намотана на керамический сердечник, и к нему присоединены два медных вывода. Сопротивление объекта также зависит от температуры, так как \(R_0\) прямо пропорционально \(\rho\). Для цилиндра мы знаем \(R = \rho \dfrac{L}{A}\), поэтому, если L и A не сильно меняются с температурой, R имеет ту же температурную зависимость, что и \( \ро\). (Изучение коэффициентов линейного расширения показывает, что они примерно на два порядка меньше типичных температурных коэффициентов удельного сопротивления, поэтому влияние температуры на 9оС\). Многие термометры основаны на влиянии температуры на сопротивление (рис. \(\PageIndex{5}\)). Один из наиболее распространенных термометров основан на термисторе, полупроводниковом кристалле с сильной температурной зависимостью, сопротивление которого измеряется для получения его температуры. Устройство маленькое, поэтому быстро приходит в тепловое равновесие с той частью человека, к которой прикасается. Рисунок \(\PageIndex{5}\): Эти известные термометры основаны на автоматизированном измерении сопротивления термистора в зависимости от температуры. 9oC)\right) \\[5pt] &= 4.8 \, \Omega \end{align*} \]Значимость Обратите внимание, что сопротивление изменяется более чем в 10 раз по мере того, как нить нагревается до высокая температура и ток через нить накала зависит от сопротивления нити и приложенного напряжения. Если нить используется в лампе накаливания, начальный ток через нить при первом включении лампы будет выше, чем ток после того, как нить достигнет рабочей температуры. Упражнение \(\PageIndex{2}\)Тензорезистор — это электрическое устройство для измерения деформации, как показано ниже. Он состоит из гибкой изолирующей подложки, поддерживающей узор из проводящей фольги. Сопротивление фольги изменяется по мере растяжения подложки. Как изменится сопротивление тензорезистора? Влияет ли на тензодатчик изменение температуры?
Сопротивление коаксиального кабеля Длинные кабели иногда могут действовать как антенны, улавливая электронные шумы, то есть сигналы от другого оборудования и приборов. Стратегия Мы не можем использовать уравнение \(R = \rho \dfrac{L}{A}\) напрямую. Вместо этого мы смотрим на концентрические цилиндрические оболочки толщиной dr и интегрируем. Решение Сначала находим выражение для \(dR\), а затем интегрируем от \(r_i\) до \(r_0\), 9{r_0} \dfrac{1}{r} dr \\[5pt] &= \dfrac{\rho}{2\pi L} \ln \dfrac{r_0}{r_i}.\end{align*}\] Значение Сопротивление коаксиального кабеля зависит от его длины, внутреннего и внешнего радиусов и удельного сопротивления материала, разделяющего два проводника. Поскольку это сопротивление не бесконечно, между двумя проводниками возникает небольшой ток утечки. Этот ток утечки приводит к затуханию (или ослаблению) сигнала, передаваемого по кабелю. Упражнение \(\PageIndex{3}\)Сопротивление между двумя проводниками коаксиального кабеля зависит от удельного сопротивления материала, разделяющего два проводника, длины кабеля и внутреннего и внешнего радиусов двух проводников. проводник. Если вы проектируете коаксиальный кабель, как сопротивление между двумя проводниками зависит от этих переменных?
Phet: Цепь батареи и резистораПросмотрите это моделирование, чтобы увидеть, как приложенное напряжение и сопротивление материала, через который протекает ток, влияют на ток через материал. Вы можете визуализировать столкновения электронов и атомов материала, влияющие на температуру материала. Эта страница под названием 9.4: Сопротивление и сопротивление распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована OpenStax с помощью исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу. |




 Хотя приведенное выше определение включает в себя постоянный ток и напряжение, то же самое определение справедливо и для применения резисторов на переменном токе.
Хотя приведенное выше определение включает в себя постоянный ток и напряжение, то же самое определение справедливо и для применения резисторов на переменном токе.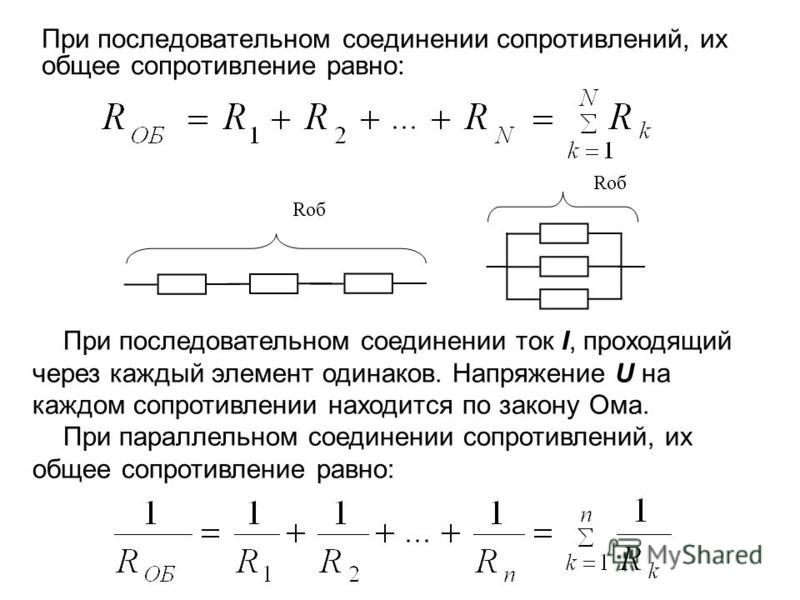 Экспериментально зависимость от этих свойств является прямой для широкого диапазона условий, и сопротивление провода может быть выражено как
Экспериментально зависимость от этих свойств является прямой для широкого диапазона условий, и сопротивление провода может быть выражено как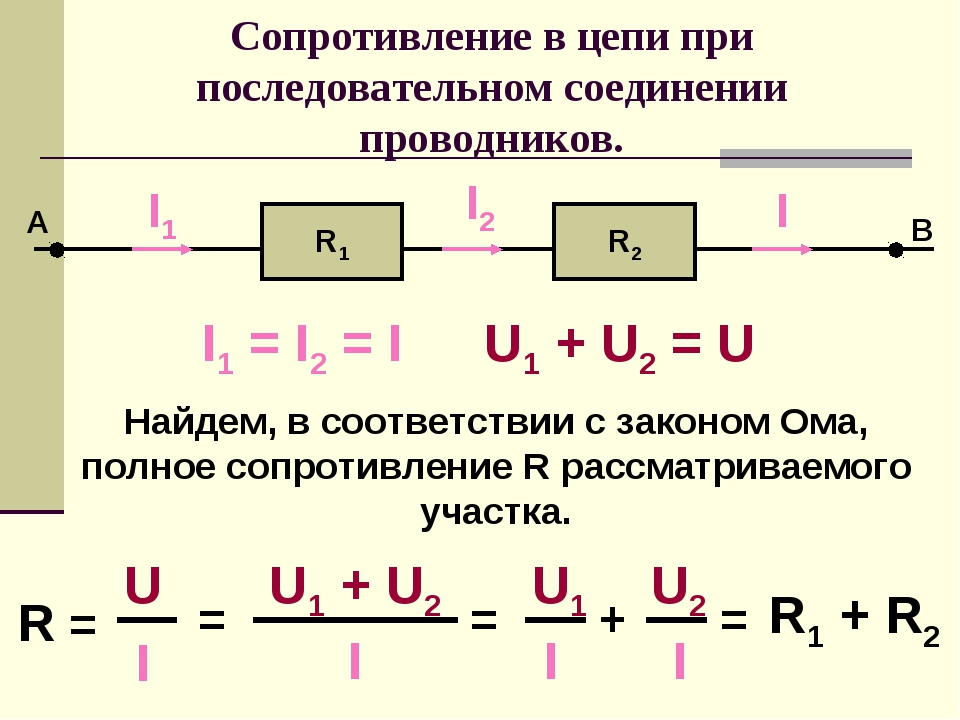
 Экспериментально зависимость от этих свойств является прямой для широкого диапазона условий, и сопротивление провода может быть выражено как 9омметры
Экспериментально зависимость от этих свойств является прямой для широкого диапазона условий, и сопротивление провода может быть выражено как 9омметры  0808
0808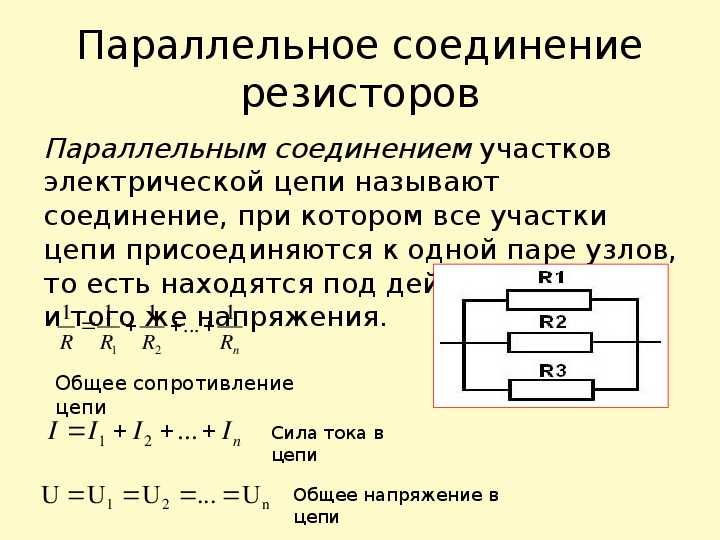 65
65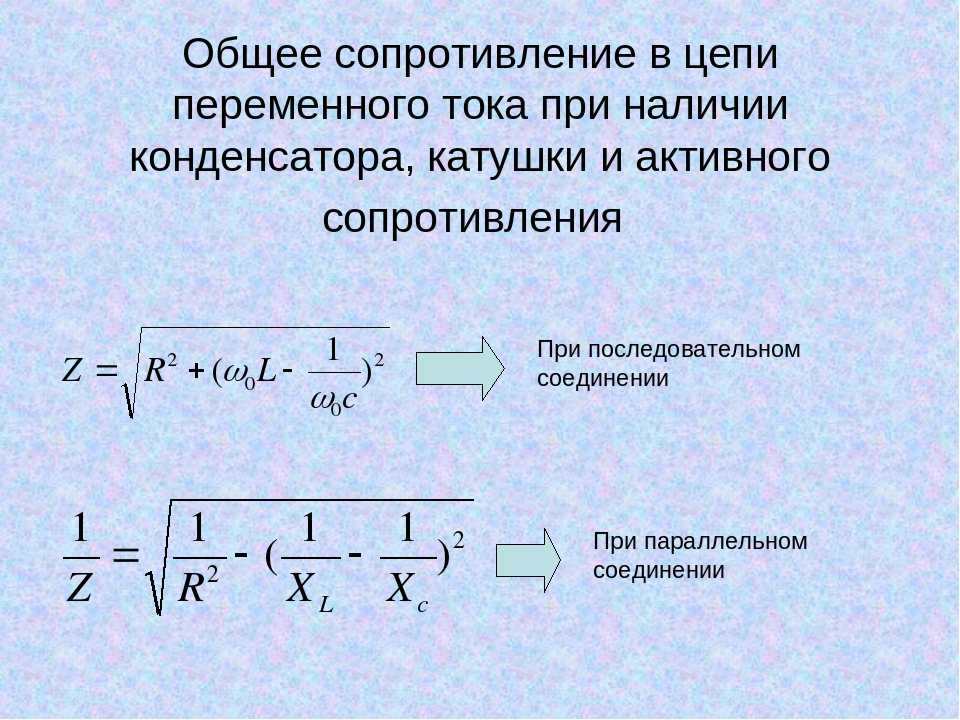 btinternet.com/~dtemicrosystems/beginner.htm
btinternet.com/~dtemicrosystems/beginner.htm  В «реальном» мире это почти никогда
делает, и с точки зрения новичка, вам не нужно беспокоиться об этом
далее, так как схем, с которыми вы, вероятно, столкнетесь в данный момент — и около 95% от
все те, с которыми вы столкнетесь в будущем — будут работать отлично, даже если они горячие
или холодно!
В «реальном» мире это почти никогда
делает, и с точки зрения новичка, вам не нужно беспокоиться об этом
далее, так как схем, с которыми вы, вероятно, столкнетесь в данный момент — и около 95% от
все те, с которыми вы столкнетесь в будущем — будут работать отлично, даже если они горячие
или холодно!  Это
должно быть очевидно, что формула работает и в обратную сторону, т.е. IxR=V, RxI=V, V/I=R
и V/R=I.
Это
должно быть очевидно, что формула работает и в обратную сторону, т.е. IxR=V, RxI=V, V/I=R
и V/R=I. выход. Учитывая это, теперь у нас есть две известные величины для использования в наших расчетах:
напряжение и ток. Используя треугольник закона Ома, требуемое сопротивление равно
рассчитывается по формуле «R=V/I», что дает нам 12/0,015=800 Ом (см. ниже
для «Вф»). Не забывайте, ток измеряется в амперах.
выход. Учитывая это, теперь у нас есть две известные величины для использования в наших расчетах:
напряжение и ток. Используя треугольник закона Ома, требуемое сопротивление равно
рассчитывается по формуле «R=V/I», что дает нам 12/0,015=800 Ом (см. ниже
для «Вф»). Не забывайте, ток измеряется в амперах.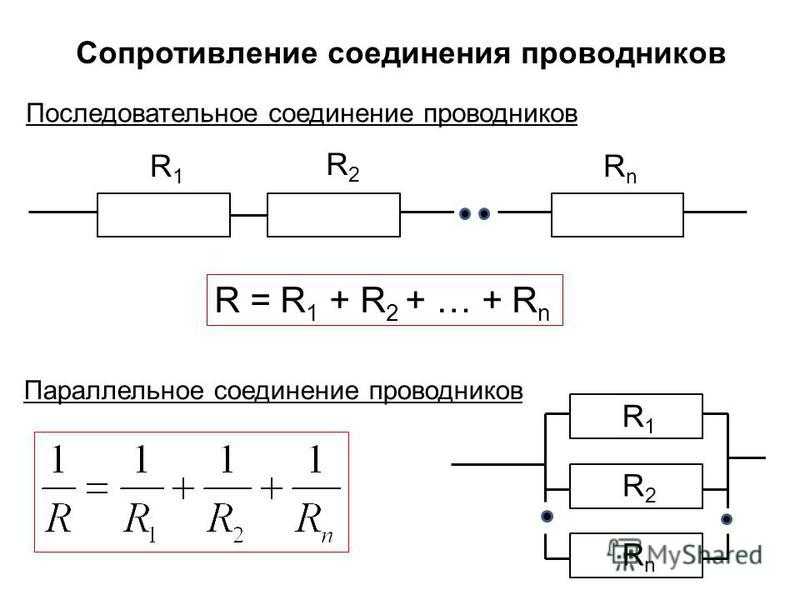
 Для наших целей допустим, что R1 равен 47K, R2 равен
150К, а R3 820К. Формула прямой линии для конечного значения: «Р» = 1/(
(1/R1) + (1/R2) + (1/R3) ).
Для наших целей допустим, что R1 равен 47K, R2 равен
150К, а R3 820К. Формула прямой линии для конечного значения: «Р» = 1/(
(1/R1) + (1/R2) + (1/R3) ).  ..), но это не так. На самом деле вы имеете полное право
ответ, ему просто не хватает последней функции «1/».
..), но это не так. На самом деле вы имеете полное право
ответ, ему просто не хватает последней функции «1/».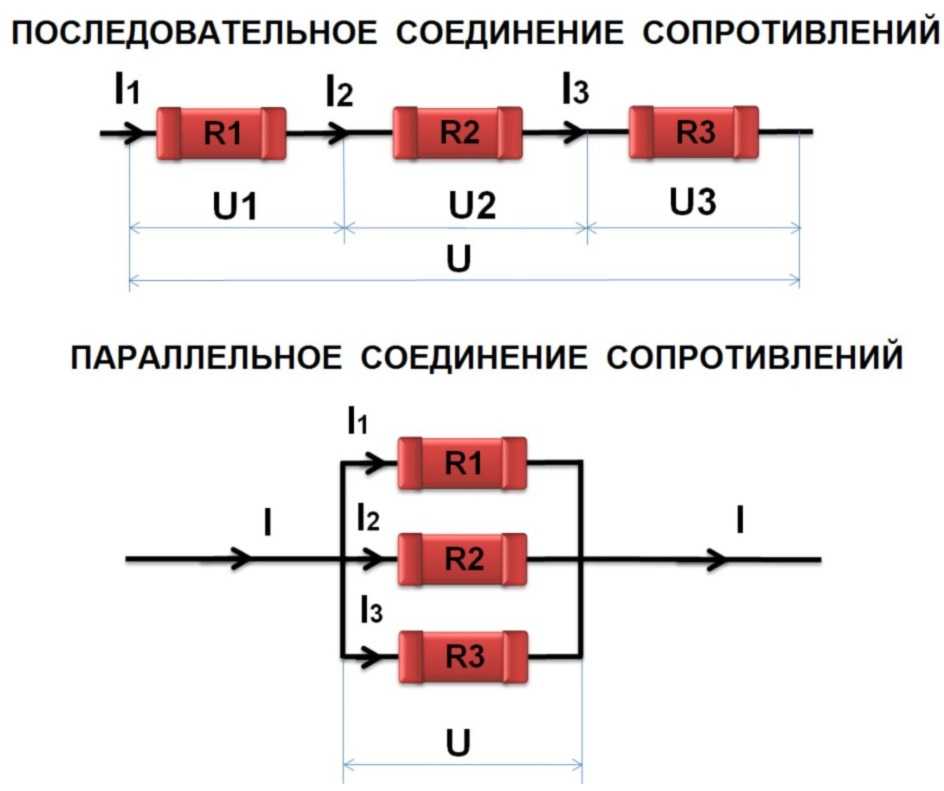
 Что касается безопасности,
если цепь будет постоянно потреблять определенное количество тока, независимо от
каков может быть этот ток, всегда используйте трансформатор с запасом по крайней мере на 50% больше.
ток, чем требует ваша схема. Никогда не используйте устройство с «достаточным» током,
потому что он станет слишком горячим, что вызовет характерные изменения напряжения и
ток указан. Эти изменения сложны, и мы не будем объяснять их здесь.
раздел для начинающих, но будьте осторожны при выборе трансформаторов.
Что касается безопасности,
если цепь будет постоянно потреблять определенное количество тока, независимо от
каков может быть этот ток, всегда используйте трансформатор с запасом по крайней мере на 50% больше.
ток, чем требует ваша схема. Никогда не используйте устройство с «достаточным» током,
потому что он станет слишком горячим, что вызовет характерные изменения напряжения и
ток указан. Эти изменения сложны, и мы не будем объяснять их здесь.
раздел для начинающих, но будьте осторожны при выборе трансформаторов.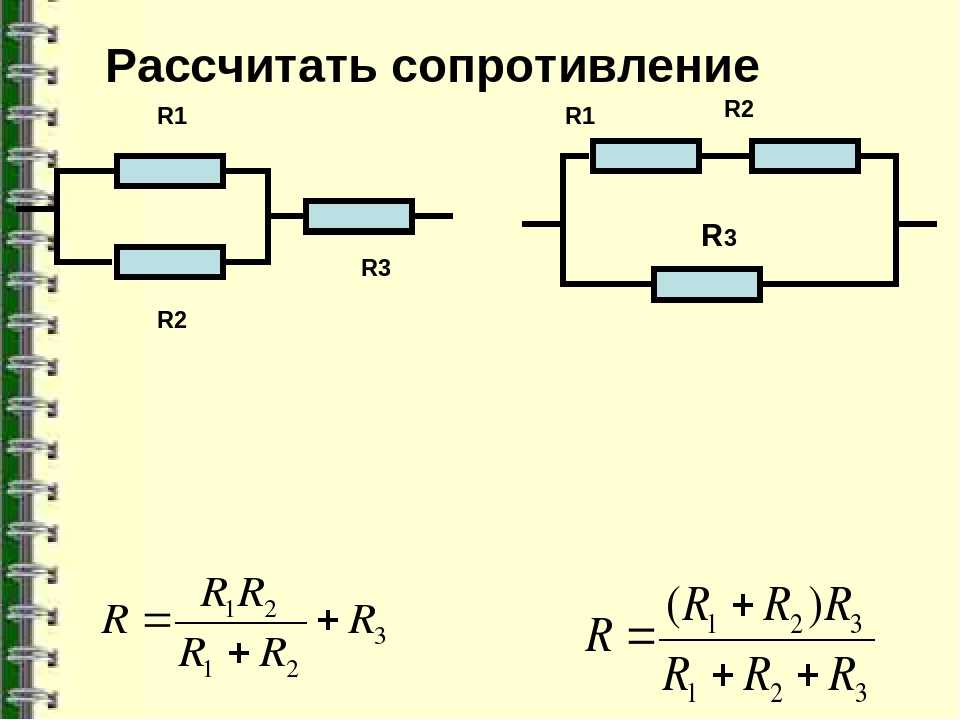 д., которые необходимы для поддержания тока. Все подобные устройства создают разность потенциалов и называются источниками напряжения. Когда источник напряжения подключен к проводнику, он прикладывает разность потенциалов В , которая создает электрическое поле. Электрическое поле, в свою очередь, воздействует на свободные заряды, вызывая ток. Величина тока зависит не только от величины напряжения, но и от характеристик материала, через который протекает ток. Материал может сопротивляться потоку зарядов, и мера того, насколько материал сопротивляется потоку зарядов, известна как удельное сопротивление . Это удельное сопротивление грубо аналогично трению между двумя материалами, которые сопротивляются движению.
д., которые необходимы для поддержания тока. Все подобные устройства создают разность потенциалов и называются источниками напряжения. Когда источник напряжения подключен к проводнику, он прикладывает разность потенциалов В , которая создает электрическое поле. Электрическое поле, в свою очередь, воздействует на свободные заряды, вызывая ток. Величина тока зависит не только от величины напряжения, но и от характеристик материала, через который протекает ток. Материал может сопротивляться потоку зарядов, и мера того, насколько материал сопротивляется потоку зарядов, известна как удельное сопротивление . Это удельное сопротивление грубо аналогично трению между двумя материалами, которые сопротивляются движению.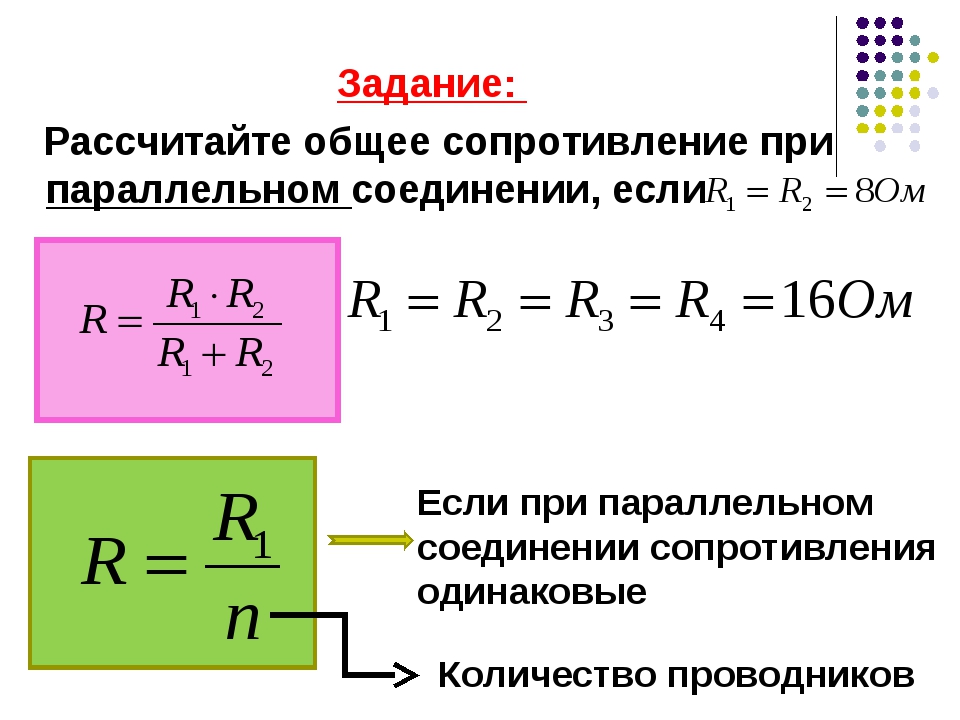 Эта зависимость может быть очень сложной. В некоторых материалах, в том числе и в металлах, при данной температуре плотность тока примерно пропорциональна напряженности электрического поля. В этих случаях плотность тока можно смоделировать как 9{-1}\).
Эта зависимость может быть очень сложной. В некоторых материалах, в том числе и в металлах, при данной температуре плотность тока примерно пропорциональна напряженности электрического поля. В этих случаях плотность тока можно смоделировать как 9{-1}\).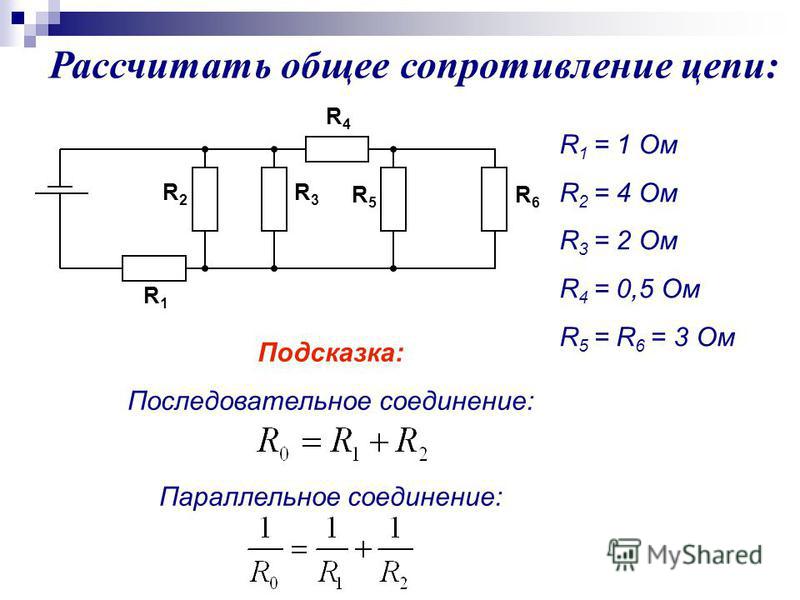 {-1}\)ConductorsSemiconductors [1]Insulators»>
{-1}\)ConductorsSemiconductors [1]Insulators»> 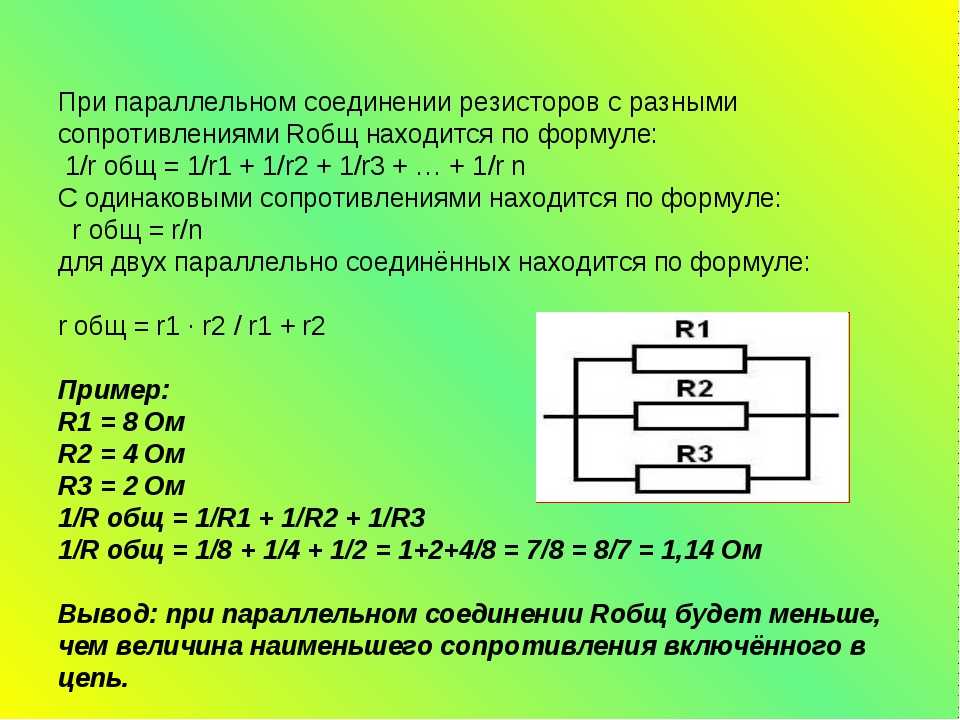 2}\). Третьей важной характеристикой является пластичность. Пластичность — это мера способности материала втягиваться в провода и мера гибкости материала, а медь обладает высокой пластичностью. Подводя итог, можно сказать, что для того, чтобы проводник был подходящим кандидатом для изготовления проволоки, необходимо, по крайней мере, три важные характеристики: низкое удельное сопротивление, высокая прочность на растяжение и высокая пластичность. Какие еще материалы используются для электропроводки и в чем их преимущества и недостатки?
2}\). Третьей важной характеристикой является пластичность. Пластичность — это мера способности материала втягиваться в провода и мера гибкости материала, а медь обладает высокой пластичностью. Подводя итог, можно сказать, что для того, чтобы проводник был подходящим кандидатом для изготовления проволоки, необходимо, по крайней мере, три важные характеристики: низкое удельное сопротивление, высокая прочность на растяжение и высокая пластичность. Какие еще материалы используются для электропроводки и в чем их преимущества и недостатки?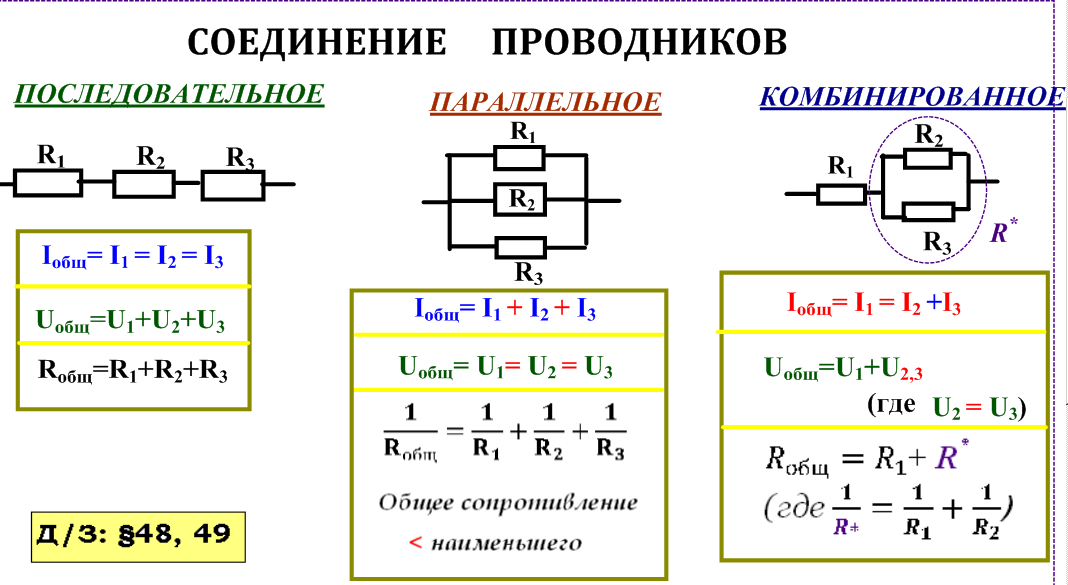 Золото не окисляется, что обеспечивает лучшее соединение между компонентами. У алюминиевых проводов есть свои недостатки. Алюминий имеет более высокое удельное сопротивление, чем медь, поэтому требуется больший диаметр, чтобы соответствовать сопротивлению на длину медных проводов, но алюминий дешевле меди, так что это не главный недостаток. Алюминиевая проволока не обладает такой высокой пластичностью и прочностью на растяжение, как медь, но пластичность и прочность на растяжение находится в пределах допустимых уровней. Есть несколько проблем, которые необходимо решить при использовании алюминия, и необходимо соблюдать осторожность при выполнении соединений. Алюминий имеет более высокую скорость теплового расширения, чем медь, что может привести к ослаблению соединений и возможной опасности возгорания. Окисление алюминия не проходит и может вызвать проблемы. При использовании алюминиевых проводов необходимо использовать специальные методы, а такие компоненты, как электрические розетки, должны быть рассчитаны на прием алюминиевых проводов.
Золото не окисляется, что обеспечивает лучшее соединение между компонентами. У алюминиевых проводов есть свои недостатки. Алюминий имеет более высокое удельное сопротивление, чем медь, поэтому требуется больший диаметр, чтобы соответствовать сопротивлению на длину медных проводов, но алюминий дешевле меди, так что это не главный недостаток. Алюминиевая проволока не обладает такой высокой пластичностью и прочностью на растяжение, как медь, но пластичность и прочность на растяжение находится в пределах допустимых уровней. Есть несколько проблем, которые необходимо решить при использовании алюминия, и необходимо соблюдать осторожность при выполнении соединений. Алюминий имеет более высокую скорость теплового расширения, чем медь, что может привести к ослаблению соединений и возможной опасности возгорания. Окисление алюминия не проходит и может вызвать проблемы. При использовании алюминиевых проводов необходимо использовать специальные методы, а такие компоненты, как электрические розетки, должны быть рассчитаны на прием алюминиевых проводов.

 Через проводник подключена батарея, создающая на нем разность потенциалов \(\Delta V\) (рис. \(\PageIndex{1}\)). Разность потенциалов создает электрическое поле, пропорциональное плотности тока, согласно \(\vec{E} = \rho \vec{J}\).
Через проводник подключена батарея, создающая на нем разность потенциалов \(\Delta V\) (рис. \(\PageIndex{1}\)). Разность потенциалов создает электрическое поле, пропорциональное плотности тока, согласно \(\vec{E} = \rho \vec{J}\). \]
\]
 Второй тип резистора — это металлопленочный резистор, который также имеет керамический сердечник. Дорожка изготовлена из оксида металла, обладающего полупроводниковыми свойствами, подобными углероду. Снова в концы резистора вставлены медные выводы. Затем резистор окрашивается и маркируется для идентификации. Резистор имеет четыре цветные полосы, как показано на рисунке \(\PageIndex{4}\). 9{-5} \, \Омега\), а сверхпроводники вообще не имеют сопротивления при низких температурах. Как мы видели, сопротивление связано с формой объекта и материалом, из которого он состоит.
Второй тип резистора — это металлопленочный резистор, который также имеет керамический сердечник. Дорожка изготовлена из оксида металла, обладающего полупроводниковыми свойствами, подобными углероду. Снова в концы резистора вставлены медные выводы. Затем резистор окрашивается и маркируется для идентификации. Резистор имеет четыре цветные полосы, как показано на рисунке \(\PageIndex{4}\). 9{-5} \, \Омега\), а сверхпроводники вообще не имеют сопротивления при низких температурах. Как мы видели, сопротивление связано с формой объекта и материалом, из которого он состоит.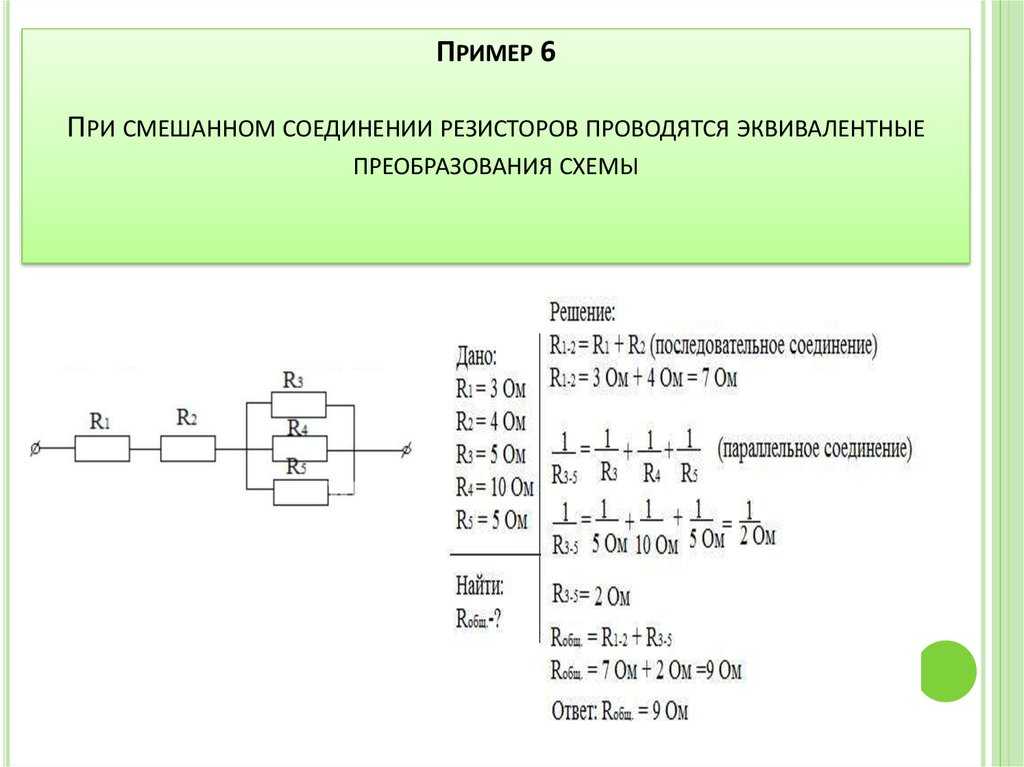

 Коаксиальные кабели используются во многих приложениях, требующих устранения этого шума. Например, их можно найти дома в соединениях кабельного телевидения или других аудиовизуальных соединениях. Коаксиальные кабели состоят из внутреннего проводника радиуса \(r_i\), окруженного вторым, внешним концентрическим проводником радиусом \(r_0\) (рисунок \(\PageIndex{6}\)). Пространство между ними обычно заполнено изолятором, например, полиэтиленом. Между двумя проводниками возникает небольшой радиальный ток утечки. Определить сопротивление коаксиального кабеля длиной 9 см.0554 л .
Коаксиальные кабели используются во многих приложениях, требующих устранения этого шума. Например, их можно найти дома в соединениях кабельного телевидения или других аудиовизуальных соединениях. Коаксиальные кабели состоят из внутреннего проводника радиуса \(r_i\), окруженного вторым, внешним концентрическим проводником радиусом \(r_0\) (рисунок \(\PageIndex{6}\)). Пространство между ними обычно заполнено изолятором, например, полиэтиленом. Между двумя проводниками возникает небольшой радиальный ток утечки. Определить сопротивление коаксиального кабеля длиной 9 см.0554 л .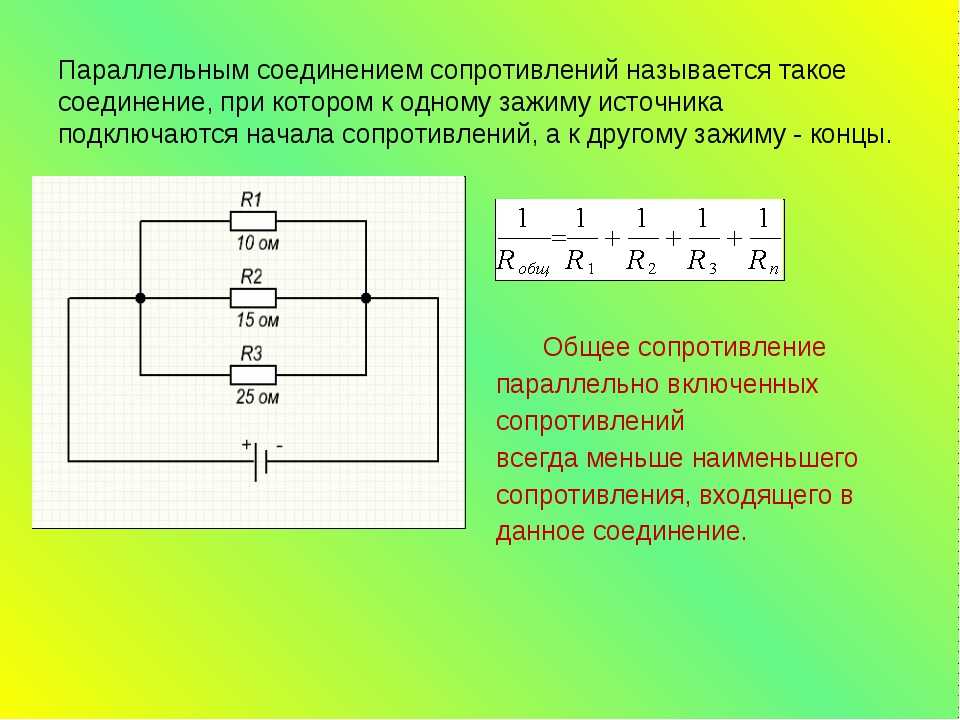
 Чем больше удельное сопротивление, тем выше сопротивление. Чем больше разница между внешним радиусом и внутренним радиусом, то есть чем больше отношение между ними, тем больше сопротивление. Если вы пытаетесь максимизировать сопротивление, выбор значений этих переменных будет зависеть от приложения. Например, если кабель должен быть гибким, выбор материалов может быть ограничен.
Чем больше удельное сопротивление, тем выше сопротивление. Чем больше разница между внешним радиусом и внутренним радиусом, то есть чем больше отношение между ними, тем больше сопротивление. Если вы пытаетесь максимизировать сопротивление, выбор значений этих переменных будет зависеть от приложения. Например, если кабель должен быть гибким, выбор материалов может быть ограничен.