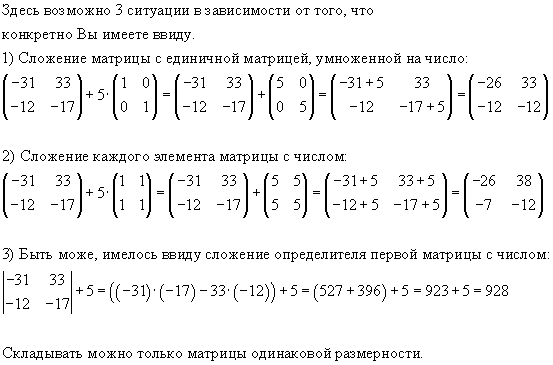Как складывать матрицы разных размеров: Как складывать матрицы разных размеров. Действия с матрицами

2 на 2 и 3 на 3, когда это возможно, можно ли разной размерности

Мы уже знаем, что матрица – это объект, который представляет собой совокупность взаимосвязанных строк (m) и столбцов (n). С ней можно проводить различные действия, от обычного вычитания до транспортирования. Разберёмся с самой простой матричной операцией – сложением.

Сложение матриц — теория

Сложение матриц – это алгоритм вычисления новой матрицы С при помощи попарного суммирования соответствующих элементов матриц А и В.

Формула:

\(с_{ij} = a_{ij} + b_{ij}\)

где i – номер строки, а j – номер столбца.

 

То есть, чтобы получить, например, элемент \(с_{11}\), нужно сложить \(а_{11}\) и \(b_{11}\). 

Когда это возможно, можно ли складывать матрицы разной размерности

Как сложение, так и вычитание матриц возможно только в том случае, когда они равны по размеру.

 

Также подметим, что нельзя складывать матрицы с обычными целыми числами и дробями. Порядок элементов в таблице менять нельзя.

Экономический смысл сложения матриц

Матрица имеет прикладное значение, так как часто используется в экономике для систематизации информации и облегчения вычислений. К примеру, с помощью неё можно предоставить отчёт о продажах:

 

Пусть \(х_{ij}\) – это количество определённого товара, проданного в определённом магазине за первый год. Матрица У – отчёт о продажах за второй год. Тогда, чтобы посчитать сумму продаж за оба года, нужно сложить отчёты Х и У.

Свойства операции сложения матриц

Свойств немного, и все они легки для запоминания:

1. Свойство коммутативности: A+ B = B + A.
2. Свойство ассоциативности: (A+ B) + C= A + (B + C).
3. Свойство дистрибутивности: (A+ B) * C= AC + BC.

При сложении А с нулевой матрицей 0, у которой все элементы равны нулю, исходная матрица не меняется:

А + О = А

При сложении А с противоположной матрицей (-А) сумма равна нулю:

А + (-А) = О

Примеры с решением на нахождение суммы матриц

Задача №1

Даны слагаемые:

 

Найти: С

Решение

\(с_{11} = а_{11} + б_{11} = 2 + 1 = 3\)

\(с_{12} = а_{12} + б_{12} = 3 + (-3) = 0\)

\(с_{21} = а_{21} + б_{21} = (-1) + 2 = 1\)

\(с_{22} = а_{22} + б_{22} = 4 + 5 = 9\)

Ответ:  

 

Задача №2

Даны слагаемые:

 

Найти: С

Решение: так как матрицы разного размера (А = 2 × 3; В = 3 × 2), данная операция невозможна.

Ответ: нет решения.

Не справляетесь с заданиями по учебе? Обращайтесь в ФениксХелп за помощью!

4.

1.3 Действия над матрицами

Ранее определили матрицу, как прямоугольную числовую таблицу, имеющую строк и столбцов, поэтому схематически матрицу можно изображать в виде прямоугольника (рис. 1).

Нулевой матрицей (нуль-матрицей) называют матрицу, все элементы которой равны нулю и обозначают 0.

Единичной матрицей называется квадратная матрица вида

.

Две матрицы и равны, если они одинакового размера и их соответствующие элементы равны.

Определим основные операции над матрицами.

Определение. Суммой двух матриц и одинакового размера называется матрица тех же размеров, элементы которой находятся по формуле . Обозначается .

Пример 6. .

Операция сложения матриц распространяется на случай любого числа слагаемых. Очевидно, что .

Еще раз подчеркнем, что складывать можно только матрицы одинакового размера; для матриц разных размеров операция сложения не определена.

Определение. Разностью матриц и одинакового размера называется такая матрица , что .

Определение. Произведением матрицы на число называется матрица , получающаяся из умножением всех ее элементов на , .

Определение. Пусть даны две матрицы и , причем число столбцов равно числу строк . Произведением на называется матрица , элементы которой находятся по формуле .

Обозначается .

Схематически операцию умножения матриц можно изобразить так:

а правило вычисления элемента в произведении:

Подчеркнем еще раз, что произведение имеет смысл тогда и только тогда, когда число столбцов первого сомножителя равно числу строк второго, при этом в произведении получается матрица, число строк которой равно числу строк первого сомножителя, а число столбцов равно числу столбцов второго.

Пример 7. Даны матрицы и . Найти матрицы и .

Решение.

Прежде всего заметим, что произведение существует, так как число столбцов равно числу строк .

Заметим, что в общем случае , т. е. произведение матриц антикоммутативно.

Найдем (умножение возможно).

Пример 8. Дана матрица . Найти .

Решение.

.

; .

.

Отметим следующий любопытный факт.

Как известно, произведение двух отличных от нуля чисел не равно нулю. Для матриц подобное обстоятельство может и не иметь места, то есть произведение ненулевых матриц может оказаться равным нуль-матрице.

Пример 9. Если и , то

.

Определение. Если – квадратная матрица, то обратной для нее матрицей называется матрица, обозначаемая и удовлетворяющая условиям , где – единичная матрица.

Из этого определения следует, что если матрица является обратной для , то и будет обратной для . Обратную матрицу имеет только квадратная матрица, определитель которой отличен от нуля. Такие матрицы называются невырожденными.

Приведем схему нахождения обратной матрицы.

1. Находим определитель данной квадратной матрицы .

2. Находим алгебраические дополнения ко всем элементам мат-рицы .

3. Записываем алгебраические дополнения элементов строк в столбцы.

4. Делим каждый элемент полученной матрицы на определитель матрицы .

Пример 10. Найти матрицу, обратную матрице .

Решение.

1. Найдем .

2. Ищем алгебраические дополнения каждого элемента матрицы :

; ; .

Получили алгебраические дополнения элементов первой строки. Аналогично для элементов второй и третьей строк получаем:

; ; .

; ; .

Объединяя 3 и 4 пункты, получаем обратную матрицу

.

Для проверки убедимся, что .

.

< Предыдущая		Следующая >

матриц — Сложение/умножение матриц разных размеров

спросил 7 лет, 6 месяцев назад

Изменено 1 год, 10 месяцев назад

Просмотрено 39 тысяч раз

$\begingroup$

У меня есть следующие две матрицы:

$$A=\begin{pmatrix}1 & -2\\3 & 1\end{pmatrix}\text{ и }B=\begin{pmatrix}1 & 3 & 2\\-1 & 0 & 2\end{pmatrix}$$

Итак, у меня есть две матрицы разного размера. Несколько источников говорят мне, что я не могу выполнять умножение или сложение с матрицами разных размеров. Так что я немного смущен. Могу ли я сделать это с этими? Как?

• матрицы

$\endgroup$

2

$\begingroup$

Предположим, у вас есть две матрицы $A$ и $B$ порядков $a_1\times a_2$ и $b_1\times b_2$ соответственно.

Матричное сложение/вычитание двух матриц будет определено тогда и только тогда, когда $a_1=b_1$ и $a_2=b_2$

Умножение матриц на них определено тогда и только тогда, когда $a_2=b_1$ для $AB$ должно быть определено и $b_2= a_1$ для определения $BA$. $AB$ будет иметь порядок $a_1\times b_2$, а $BA$ будет иметь порядок $b_1\times a_2$

$\endgroup$

2

$\begingroup$

Чтобы добавить две матрицы, они должны иметь одинаковые размеры, поэтому вы не можете добавлять свои матрицы.

Для умножения на матрицы $M$ и $N$ количество столбцов матрицы $M$ должно быть равно количеству строк матрицы $N$. В вашем случае вы можете умножить $A\cdot B$, потому что количество столбцов $A$ равно $2$, а количество строк $B$ равно $2$.

Вы не можете умножить $B\cdot A$, потому что количество столбцов $B$ равно $3$, а количество строк $A$ равно $2$.

$\endgroup$

$\begingroup$

Сложение и умножение матриц не определялись ни с того ни с сего. Матрица $m\times n$ описывает линейное преобразование из векторного пространства размерности $n$ в векторное пространство размерности $m$.

Сумма матриц соответствует преобразованию, которое представляет собой сумму

двух заданных преобразований. Добавление линейных преобразований требует, чтобы домен и диапазон были идентичными.

Произведение матриц соответствует преобразованию, которое является композицией двух заданных преобразований. Композиция линейных преобразований требует, чтобы диапазон первого был доменом второго.

Отсюда ограничения по размерам. Если они не соблюдены, результат не определен.

$\endgroup$

$\begingroup$

Итак, у меня две матрицы разного размера. Несколько источников говорят мне, что я не могу выполнять умножение или сложение с матрицами разных размеров.

Вы не можете добавлять матрицы разных размеров, как указано @meshal. Следовательно, A+B или B+A не могут быть выполнены. Однако вы можете умножить их. Вот как:

$$A=\begin{pmatrix}1 & -2\\3 & 1\end{pmatrix}\text{ и }B=\begin{pmatrix}1 & 3 & 2\\-1 & 0 & 2\end{pmatrix}$$

$$AB=\begin{pmatrix}1 & -2\\3 & 1\end{pmatrix}\text{ * }\begin{pmatrix}1 & 3 & 2\\-1 & 0 & 2\end{pmatrix}$$

$$AB=\begin{pmatrix}1\cdot \:1+\left(-2\right)\left(-1\right) &1\cdot \:3+\left(-2\right)\cdot \:0&1\cdot \:2+\left(-2\right)\cdot \:2\\ 3\cdot \:1+1\ cdot \left(-1\right)&3\cdot \:3+1\cdot \:0&3\cdot \:2+1\cdot \:2\end{pmatrix}$$

$$Наконец, AB=\ begin{pmatrix}3&3&-2\\ 2&9&8\end{pmatrix}$$

$\endgroup$

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

. Матрица

— R: Добавление двух матриц с разными размерами на основе столбцов

У меня есть 22 матрицы с одинаковым количеством строк (т.е. 691) и разным количеством столбцов (т.е. 22-25). Я должен добавить значения, соответствующие одной и той же строке, одному и тому же столбцу в каждой из матриц, в результате чего получается одна единственная матрица размером 691 * 25.

 fullanno1 имеет 691 строку и 25 столбцов:
>colnames(fullanno1)
[1] «кодирование-неMod3» «кодирование-синоним» «кодирование-синоним-почти-сращивание»
[4] «межгенный» «интрон» «миссенс»
[7] «миссенс-почти-сращивание» «почти-ген-3» «почти-ген-5»
[10] "сращивание-3" "сращивание-5" "стоп-выигрыш"
[13] "стоп-приобретен-близко-стык" "стоп-потерян" "утр-3"
[16] «УТР-5» «CTCF» «Э»
[19] "Нет" "PF" "R"
[22] «Т» «ТСС» «МЫ»
[25] "кодирование-неMod3-почти-сращивание"
fullanno2 имеет 691 строку и 22 столбца:
>colnames(fullanno2)
[1] «кодирующий-синоним» «кодирующий-синонимный-почти-сплайсинг» «межгенный»
[4] «интрон» «миссенс» «миссенс-почти-сплайс»
[7] «почти ген-3» «почти ген-5» «сращивание-3»
[10] "стык-5" "стоп-выиграл" "стоп-проигрыш"
[13] «УТР-3» «УТР-5» «CTCF»
[16] «Е» «Нет» «ПФ»
[19] «Р» «Т» «ТСС»
[22] «МЫ»
 

Каждая матрица представляет собой двойную матрицу с числовыми значениями. Как я могу сложить эти две матрицы, чтобы получить третью матрицу с размерами 691*25. Поскольку fullanno2 короче на три столбца, результирующая матрица для этих столбцов будет содержать значения только из первой матрицы.

Мой подход: Возьмите setdiff имен столбцов, чтобы получить столбцы, которых нет в меньшей матрице, привяжите их к меньшей матрице с нулями в качестве значений. Затем добавьте две матрицы.

 > имена столбцов <-setdiff (имена столбцов (fullanno1), имена столбцов (fullanno2))
[1] «кодирование-неMod3» «остановка-получено-почти-сращивание» «кодирование-неMod3-почти-сращивание»
> столбец <-0
>cbind(fullanno2,столбец)
>colnames(fullanno2)[23]<-column.name[1]
>cbind(fullanno2,столбец)
>colnames(fullanno2)[24]<-column.name[2]
>cbind(fullanno2,столбец)
>colnames(fullanno2)[25]<-column.name[3]
 

Но это становится утомительным для всех матриц. Какие-либо предложения?

• r
• матрица

Вы можете использовать совпадение вместе с именами столбцов . Например:

 > m1<-matrix(1,3,5)
> colnames(m1)<-LETTERS[1:5]
> m2<-матрица(1:9,3,3)
> имена столбцов (m2) <-c ("D", "A", "C")
> м1
     А Б В Г Д
[1,] 1 1 1 1 1
[2,] 1 1 1 1 1
[3,] 1 1 1 1 1
> м2
     Д А С
[1,] 1 4 7
[2,] 2 5 8
[3,] 3 6 9
> м3<-м1
> mcol<-match(имена столбцов(m2),имена столбцов(m1))
> м3[мкол]<-m3[мкол]+м2
> м3
     А Б В Г Д
[1,] 5 1 8 2 1
[2,] 6 1 93 1
[3,] 7 1 10 4 1
 

1

Итак, вы хотите просуммировать все матрицы, чтобы получить одну матрицу? Простой, но, возможно, медленный (я подозреваю, но, вероятно, это не имеет большого значения для ваших матриц) способ — использовать библиотеки plyr и reshape2 . Вы можете начать со списка ваших матриц:

 make.matrix <- function() {
 cols <- образец (месяц.имя, runif(1, 2, 12))
 матрица (rnorm (длина (столбцы) * 10), 10, длина (столбцы), dimnames = список (NULL, столбцы))
}
# Составьте 10 матриц, заполненных случайными числами, имея
# разное количество столбцов, названных в честь месяцев
my.
No related posts.