Как составить уравнение окружности: Mathway | Популярные задачи

2

«Кривые второго порядка». Уравнение окружности. Часть 1

Высшая математика / Практикум по аналитической геометрии

06.02.201525.11.2015

Задача №1. Определить центр и радиус окружности, заданной уравнением х²+у²-2х+4y-20=0.
Решение. Так как в заданном уравнении коэффициенты при х² и у² равны между собой и отсутствует член с произведением координат, го заданное уравнение действительно представляет собой уравнение окружности. Чтобы определить координаты центра и радиус окружности, необходимо уравнение привести к каноническому виду:
(х²-2х)+(y²+4у)=20, (x²-2х+1)+(у²+4х+4)=25, (x-1)²+(y+2)²=25.
Координаты центра и радиус окружности можно найти, не приводя данное уравнение к каноническому виду,

Рис.1

достаточно сравнить данное уравнение с уравнением окружности в общем виде:

Ответ: (1, —2), R = 5.
Задача №2. Составить уравнение окружности, проходя¬щей через точки А (—1;1) и В (1;-3), если центр ее лежит на прямой 2х-у+1=0.
Решение. Каноническое уравнение окружности:

(x-a)²+(y-b)² = r².

Так как окружность проходит через точки А и B, то координаты этих точек должны удовлетворять уравнению окружности. Имеем два уравнения:
(-1-а)² + (1-b)²=r², (1-а)² + (-3-b)² = r².
Если центр окружности лежит на прямой 2х-у+1=0, то координаты центра также должны удовлетворить уравнению прямой.
Имеем третье уравнение: 2а-b+1=0.

Рис.2

Решим систему уравнений:

Таким образом, координаты центра окружности найдены:

Чтобы определить г², получим: г² = 1+2а+5а²,

Уравнение окружности:

Ответ: 9х² + 9y² + 24x + 30у — 31 =0.

Задача №3.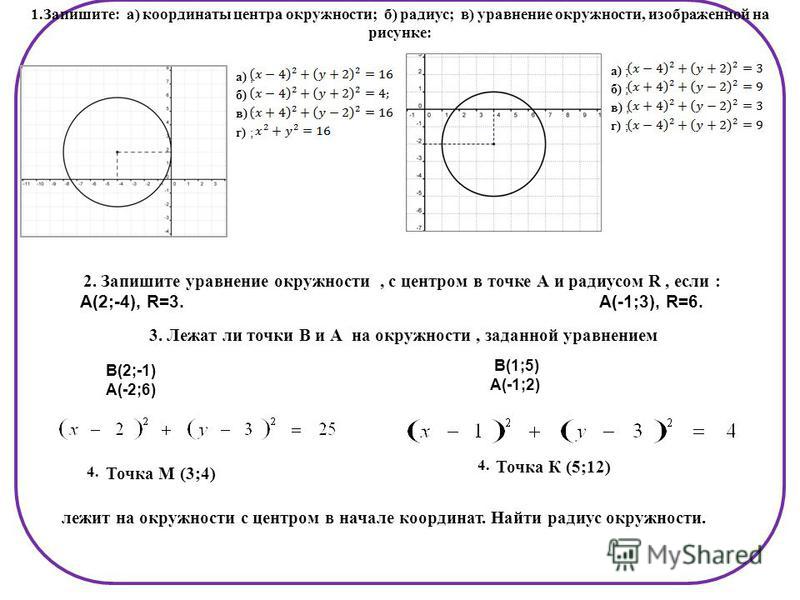 Составить уравнение окружности, если ее центр находится в точке С(5;4) и окружность отсекает от прямой х+2у-3=0 хорду, длина которой равна 8.
Решение. Искомое уравнение будет иметь вид:
(x-5)²+(у-4)²=r².
Определим расстояние центра С от данной прямой:

Так как радиус, перпендикулярный к хорде, делит ее пополам, то половина хорды будет равна 4 единицам.

Рис.3

По теореме Пифагора имеем:
г²=4²+CD²=16+20=36, r² = 36, r = 6.
Уравнение окружности: (х -5)²+(у — 4)² = 36.
Ответ: (х -5)²+(у — 4)² = 36.
Задача №4. Составить уравнение окружности, касающейся двух параллельных прямых 2х+у-5=0 и 2х+y+15=0, причем одной из них — в точке А(2; 1).
Решение. Определим диаметр окружности, для чего используем формулу расстояния точки от прямой

Уравнение прямой 2x+y+15=0, точка А(2; 1)

Воспользовавшись координатами точки A, можем составить такое уравнение:
(2 — а)²+(1 — b)² = 20.
Второе уравнение с неизвестными а и b получим, определив расстояние точки С от первой прямой

Поскольку точка С лежит по одну сторону от прямой

Рис. 4

вместе с началом координат, то расстояние АС
Решая полученную систему уравнений, найдем а=-2; b=-1.
Эту задачу рекомендуем решить самостоятельно другим способом.
Указания. Составить уравнение перпендикуляра А В к данным прямым и найти координаты точки В.
Ответ: (x+2)²+(у + 1)²=20.

Тегизаписать уравнение окружностинайти уравнение окружностинаписать уравнение окружностирешение уравнения окружностисоставить уравнение окружностиуравнение окружностиуравнение окружности онлайн

Уравнение окружности — Формула, Примеры

Уравнение окружности обеспечивает алгебраический способ описания окружности с учетом центра и длины радиуса окружности. Уравнение окружности отличается от формул, которые используются для вычисления площади или длины окружности. Это уравнение используется во многих задачах окружностей в координатной геометрии.

Чтобы изобразить окружность на декартовой плоскости, нам потребуется уравнение окружности. На листе бумаги можно нарисовать окружность, если известны ее центр и длина радиуса. Точно так же на декартовой плоскости мы можем нарисовать окружность, если знаем координаты центра и его радиус. Круг может быть представлен во многих формах:

• Общая форма
• Типовая форма
• Параметрическая форма
• Полярная форма

В этой статье давайте узнаем об уравнении окружности, его различных формах с графиками и решенными примерами.

1.	Что такое уравнение окружности?
2.	Различные формы уравнения окружности
3.	Уравнение окружности Формула
4.	Вывод уравнения окружности
5.	График уравнения окружности
6.	Как найти уравнение окружности?
7.	Преобразование общей формы в стандартную форму
8.	Преобразование стандартной формы в общую форму
9.	Часто задаваемые вопросы по уравнению окружности

Что такое уравнение окружности?

Уравнение окружности представляет положение окружности на декартовой плоскости. Зная координаты центра окружности и длину ее радиуса, мы можем написать уравнение окружности. Уравнение окружности представляет собой все точки, лежащие на окружности окружности. 92\).

Различные формы уравнения окружности

Уравнение окружности представляет положение окружности на декартовой плоскости. На листе бумаги можно нарисовать окружность, зная ее центр и длину радиуса. Используя уравнение окружности, как только мы найдем координаты центра окружности и ее радиус, мы сможем нарисовать окружность на декартовой плоскости. Существуют различные формы представления уравнения окружности,

• Общая форма
• Типовая форма
• Параметрическая форма
• Полярная форма

Давайте рассмотрим здесь две распространенные формы уравнения окружности — общий вид и стандартную форму уравнения окружности, а также полярную и параметрическую формы в деталях.

Общее уравнение окружности

Общая форма уравнения окружности: x ² + y ² + 2gx + 2fy + c = 0. Эта общая форма используется для определения координат центра окружности и радиуса, где g, f, c — константы. В отличие от стандартной формы, которую легче понять, общая форма уравнения окружности затрудняет поиск каких-либо значимых свойств любой данной окружности. Итак, мы будем использовать формулу заполнения квадрата, чтобы сделать быстрое преобразование из общей формы в стандартную форму. 92\)

Рассмотрим этот пример уравнения окружности (x — 4) ² + (y — 2) ² = 36 — это окружность с центром в точке (4,2) и радиусом 6.

Параметрическое уравнение окружности

Мы знаем, что уравнение окружности в общем виде имеет вид x ² + y ² + 2hx + 2ky + C = 0. Берем общую точку на границе окружности, сказать (х, у). Линия, соединяющая эту общую точку и центр окружности (-h, -k), образует угол \(\theta\). Параметрическое уравнение окружности можно записать в виде x ² + y ² + 2hx + 2ky + C = 0, где x = -h + rcosθ и y = -k + rsinθ.

Полярное уравнение окружности

Полярная форма уравнения окружности почти аналогична параметрической форме уравнения окружности. Обычно мы пишем полярную форму уравнения окружности для окружности с центром в начале координат. Возьмем точку P(rcosθ, rsinθ) на границе круга, где r — расстояние точки от начала координат. Мы знаем, что уравнение окружности с центром в начале координат и радиусом «p» равно x ² + у ² = р ² .

Подставьте значения x = rcosθ и y = rsinθ в уравнение окружности.

(rcosθ) ² + (rsinθ) ² = p ²
r ² cos ² θ + r ² sin ²

θ = p ²
r ² (cos ² θ + sin ² θ) = p ²
г ² (1) = р ²
г = р
где р — радиус окружности.

Пример: Найти уравнение окружности в полярной форме при условии, что уравнение окружности в стандартной форме: уравнение окружности в полярной форме, замените значения \(x\) и \(y\) на:

x = rcosθ
у = rsinθ

х = rcosθ
у = rsinθ
х ² + у ² = 9
(rcosθ) ² + (rsinθ) ² = 9
r ² cos ² θ + r ² sin ² θ = 9
r ² (cos ² θ + sin ² θ) = 9
г ² (1) = 9
г = 3

Уравнение окружности Формула

Формула уравнения окружности используется для расчета уравнения окружности. 2\).

• Для этого нам нужно всего лишь изменить константу 9, чтобы она соответствовала r ² как (x -3) ² + (y — 2) ² = 3 ² .
• Здесь мы должны отметить, что одной из распространенных ошибок является рассмотрение \(x_{1}\) как -3, а \(y_{1}\) как -2.
• В уравнении окружности, если знак перед \(x_{1}\) и \(y_{1}\) отрицателен, то \(x_{1}\) и \(y_{1}\) равны положительные значения и наоборот.
• Здесь \(x_{1}\) = 3, \(y_{1}\) = 2 и r = 3

Таким образом, окружность, представленная уравнением (x -3) ² + (y — 2) ² = 3 ² , имеет центр в точке (3, 2) и радиус 3. На приведенном ниже изображении показан график, полученный из этого уравнения окружности.

Как найти уравнение окружности?

Существует множество различных способов представления уравнения окружности в зависимости от положения окружности на декартовой плоскости.

Мы изучили формы представления уравнения окружности при заданных координатах центра окружности. Существуют определенные особые случаи, основанные на положении окружности в координатной плоскости. Давайте узнаем о методе нахождения уравнения окружности для общего и этих частных случаев. 92} = г\).

Шаг 3: Выразите ответ в требуемой форме уравнения окружности.

Уравнение окружности с центром в начале координат

В простейшем случае центр окружности находится в начале координат (0, 0), радиус которого равен r. (x, y) — произвольная точка на окружности.

Расстояние между этой точкой и центром равно радиусу окружности. Применим формулу расстояния между этими точками. 92\).

Если центр находится в начале координат, то \(x_1\)= 0 и \(y_1\)= 0.

Ответ: Уравнение окружности, если ее центр находится в начале координат, равно x ² + y ² = г ² .

Уравнение окружности с центром на оси x

Рассмотрим случай, когда центр окружности находится на оси x: (a, 0) — центр окружности с радиусом r. (x, y) — произвольная точка на окружности.

Расстояние между этой точкой и центром равно радиусу окружности. Применим формулу расстояния между этими точками. 92\)

Уравнение касания окружности с осью x

Рассмотрим случай, когда длина окружности касается оси x в некоторой точке: (a, r) ​​— центр окружности с радиусом r. Если окружность касается оси x, то координата y центра окружности равна радиусу r.

(x, y) — произвольная точка на окружности. Расстояние между этой точкой и центром равно радиусу окружности. Применим формулу расстояния между этими точками. 92\)

Уравнение касания окружности с осью y

Рассмотрим случай, когда длина окружности касается оси y в некоторой точке: (r, b) — центр окружности с радиусом r. Если окружность касается оси y, то координата x центра окружности равна радиусу r.

(x, y) — произвольная точка на окружности. Расстояние между этой точкой и центром равно радиусу окружности. Применим формулу расстояния между этими точками. 92\)

Уравнение окружности, касающейся обеих осей

Рассмотрим случай, когда окружность касается обеих осей в некоторой точке: (r, r) — центр окружности с радиусом r. Если окружность касается и оси x, и оси y, то обе координаты центра окружности становятся равными радиусу (r, r).

(x, y) — произвольная точка на окружности. Расстояние между этой точкой и центром равно радиусу окружности. Применим формулу расстояния между этими точками. 92 = 16\
г = 4 \)

Преобразование общей формы в стандартную форму

Это стандартное уравнение окружности с радиусом r и центром в (a,b): (x — a)

2 + (y — b) ² = r ² и рассмотрим общую форму как : x ² + y ² + 2gx + 2fy + c = 0. Вот шаги, которые нужно выполнить, чтобы преобразовать общую форму в стандартную:

Шаг 1: Объединить подобные члены и взять константу на другая сторона как х ² + 2gx + y ² + 2fy = — c -> (1)

Шаг 2: Использование тождества с совершенным квадратом (x + g) ² = x ² + 2gx + g ² найти значения выражения x ² + 2gx и y ² + 2fy как:

(x + g) ² = x ² + 2gx + g ² + 907 x 2 90 2gx = (x + g) ² — g ² -> (2)

(y + f) ² = y ² + 2fy + f ² ⇒ y ² + 2fy = (y + f) ² — f ² -> (3)

Подставляя (2) и (3) в (1), получаем уравнение в виде:

(x+g) ² — g ² + (y+f)

2 — f ² = — c

(x+g) ² + (y+f) ² = g ² + f ² — c

Сравнивая это уравнение со стандартной формой: (x — a) ² + (y — b) ² = r ² получаем,

Центр = (-g,-f) и радиус = \(\sqrt{g^2+f^2 — c}\) 9{2} — 9}\) = \(\sqrt{9 + 16 — 9}\) = \(\sqrt{16}\) = 4. Итак, радиус r = 4,

Преобразование стандартной формы в общую форму

Мы можем использовать алгебраическую формулу тождества (a — b) ² = a ² + b ² — 2ab, чтобы преобразовать стандартную форму уравнения окружности в общую форму. Давайте посмотрим, как сделать это преобразование. Для этого расширьте стандартную форму уравнения окружности, как показано ниже, используя алгебраические тождества для квадратов: 92 + 2gx + 2fy + с = 0\), где g, f, с — константы.

Статьи по теме Уравнение окружности

Ознакомьтесь со следующими страницами, посвященными уравнению окружности

• Уравнение окружности Калькулятор
• Длина окружности
• Все формулы круга
• Отношение длины окружности к диаметру

Важные примечания к уравнению окружности

Вот несколько моментов, которые следует помнить при изучении уравнения окружности 92 + axy + C = 0\), то это не уравнение окружности. В уравнении окружности нет члена \(xy\).

В полярной форме уравнение окружности всегда представляется в виде \(r\) и \(\theta\).

Радиус — это расстояние от центра до любой точки на границе круга. Следовательно, значение радиуса окружности всегда положительно.

 

Примеры уравнений окружности

1. Пример 1: Найдите уравнение окружности в стандартной форме для окружности с центром (2,-3) и радиусом 3.

   Решение:

   Уравнение окружности в стандартной форме запишется как: (x — x \(_1\)) ² + (у — у\(_1\)) ² = г ² . Здесь (x\(_1\), y\(_1\)) = (2, -3) — центр окружности и радиус r = 3.

   Представим эти значения в стандартной форме уравнения окружности :

   (х — 2) ² + (у — (-3)) ² = (3) ²
   (x — 2) ² + (y + 3) ² = 9 — искомая стандартная форма уравнения данной окружности.

2. Пример 2: Запишите уравнение окружности в стандартной форме для окружности с центром (-1, 2) и радиусом, равным 7.

   Решение:

   Уравнение окружности в стандартной форме записывается как: (х — х\(_1\)) ² + (у — у\(_1\)) ² = г ² . Здесь (x\(_1\), y\(_1\)) = (-1, 2) — центр окружности и радиус r = 7.

   Представим эти значения в стандартной форме уравнения окружности:

   (х — (-1)) ² + (у — 2) ² = 7 ²
   (x + 1) ² + (y — 2) ² = 49 — искомая стандартная форма уравнения данной окружности.

3. Пример 3: Найти уравнение окружности в полярной форме при условии, что уравнение окружности в стандартной форме: x ² + y ² = 16.

   Решение:

   Чтобы найти уравнение окружности в полярной форме, подставьте значения x и y на:

   x = rcosθ
   у = rsinθ

   x ² + y ² = 16

   (rcosθ) ² + (rsinθ) ² = 10 8

   ² θ + r ² sin ² θ = 16

   r ² (1) = 4

перейти к слайду перейти к слайду перейти к слайду

Отличное обучение в старшей школе с использованием простых подсказок

Увлекаясь зубрежкой, вы, скорее всего, забудете понятия. С Cuemath вы будете учиться визуально и будете удивлены результатами.

Записаться на бесплатный пробный урок

Практические вопросы по уравнению окружности

 

перейти к слайдуперейти к слайду

Часто задаваемые вопросы по уравнению окружности

Что такое уравнение окружности в геометрии? 92\).

Каково уравнение окружности, когда центр находится в начале координат?

В простейшем случае центр окружности находится в начале координат (0, 0), радиус которого равен r. (x, y) — произвольная точка на окружности. Уравнение окружности, когда центр находится в начале координат: x ² + y ² = r ² .

Что такое общее уравнение окружности?

Общая форма уравнения окружности: x ² + y 92 + 2hx + 2ky + C = 0\), где \(x = -h +rcos \theta\) и \(y = -k +rsin \theta\)

Что такое C в общем уравнении окружности?

Общая форма уравнения окружности: x ² + y ² + 2gx + 2fy + c = 0. 2 = 2\).

Что такое полярное уравнение окружности?

Полярное уравнение окружности с центром в начале координат: r = p, где p – радиус окружности.

Калькулятор уравнения окружности

  Исследование  Математика  Геометрия

Калькулятор уравнения окружности отображает стандартное уравнение формы окружности, параметрическое уравнение формы окружности и уравнение общей формы окружности по центру и радиусу окружности. Формулы находятся под калькулятором.

Уравнение окружности с учетом центра и радиуса

Центр

Радиус

Уравнение стандартной формы окружности

 

Уравнение общей формы окружности

  90 2  

Уравнение окружности

Уравнение окружности — это алгебраический способ определения всех точек, лежащих на окружности окружности. То есть, если точка удовлетворяет уравнению окружности, она лежит на окружности окружности. Существуют разные формы уравнения окружности:

• общая форма
• стандартная форма
• параметрическая форма
• полярная форма.

Общая форма Уравнение окружности

Общее уравнение окружности с центром в точке и радиусом:
,
где

При общей форме трудно рассуждать о свойствах окружности, а именно о центре и радиусе. Но его можно легко преобразовать в стандартную форму, в которой гораздо легче разобраться.

Стандартная форма Уравнение окружности

Стандартное уравнение окружности с центром и радиусом:

Вы можете преобразовать общую форму в стандартную, используя технику, известную как Завершение квадрата. Из этого уравнения окружности вы можете легко определить координаты центра и радиус окружности.

Параметрическое уравнение формы окружности

Параметрическое уравнение окружности с центром в точке и радиусом

Это уравнение называется параметрическим, потому что угол тета упоминается как «параметр».