Как сравнить логарифмы с разными основаниями: Как сравнивать логарифмы с разным основанием

Приемы и методы сравнения логарифмов

Сравнение значений логарифмов или значения логарифма с некоторым числом встречается в школьной практике решения задач не только как самостоятельная задача. Сравнивать логарифмы приходится, например, при решении уравнений и неравенств. Материалы статьи (задачи и их решения) располагаются по принципу “от простого к сложному” и могут быть использованы для подготовки и проведения урока (уроков) по данной теме, а также на факультативных занятиях. Количество рассматриваемых задач на уроке зависит от уровня класса, его профильного направления. В классах с углубленным изучением математики этот материал может быть использован для двухчасового урока-лекции.

1. (Устно.) Какие из функций являются возрастающими, а какие убывающими:

Замечание. Это упражнение является подготовительным.

2. (Устно.) Сравните с нулем:

Замечание. При решении упражнения № 2 можно использовать как свойства логарифмической функции с привлечением графика логарифмической функции, так и следующее полезное свойство:

если положительные числа a и b лежат на числовой прямой правее 1 или левее 1 (то есть a>1 и b>1 или 0<a<1 и 0<b<1), то log_ab > 0 ;
если положительные числа a и b лежат на числовой прямой по разные стороны от 1(то есть 0<a<1<b или 0<b<1<a), то log_ab < 0 [4].

Покажем использование этого свойства при решении № 2(а).

Так как

Так как функция y = log₇t возрастает на R₊, 10 > 7, то log₇10 > log₇7, то есть log₇10 > 1. Таким образом, положительные числа sin3 и log₇10 лежат по разные стороны от 1. Следовательно, log

sin3log₇10 < 0.

3. (Устно.) Найдите ошибку в рассуждениях:

. Функция y = lgt возрастает на R₊, тогда ,

Разделим обе части последнего неравенства на . Получим, что 2 > 3.

Решение.

Положительные числа и 10 (основание логарифма) лежат по разные стороны от 1. Значит, < 0. При делении обеих частей неравенства на число знак неравенства следует изменить на противоположный.

4. (Устно.) Сравните числа:

Замечание. При решении упражнений № 4(a–c) используем свойство монотонности логарифмической функции. При решении № 4(d) используем свойство:

если c > a >1, то при b>1 справедливо неравенство log_ab > log

cb.

Решение 4(d).

Так как 1 < 5 < 7 и 13 > 1, то log₅13 > log₇13.

5. Сравните числа log₂6 и 2.

Решение.

Первый способ (использование монотонности логарифмической функции).

2 = log₂4;

Функция y = log₂t возрастает на R₊, 6 > 4. Значит, log₂6 > log₂4  и log₂5 > 2.

Второй способ (составление разности).

Составим разность .

6. Сравните числа и -1.

Решение.

-1 = ;

Функция y =   убывает на R_+, 3 < 5. Значит, >  и > -1

.

7. Сравните числа и 3log₈26.

Решение.

Функция y = log₂t возрастает на R₊, 25 < 26. Значит, log₂25 < log₂26  и .

Решение.

Первый способ.

Умножим обе части неравенства на 3: 

Функция y = log ₅t возрастает на R₊ , 27 > 25. Значит,

Второй способ.

Составим разность
. Отсюда .

9. Сравните числа log₄26 и log₆17.

Решение.

Оценим логарифмы, учитывая, что функции y = log₄t и y = log₆t возрастающие на R₊:

Решение.

Учитывая, что функции   убывающие на R₊, имеем:

. Значит,

Замечание. Предложенный метод сравнения называют методом “вставки” или методом “разделения” (мы нашли число 4, разделяющее данные два числа).

11. Сравните числа log₂3 и  log₃5.

Решение.

Заметим, что оба логарифма больше 1, но меньше 2.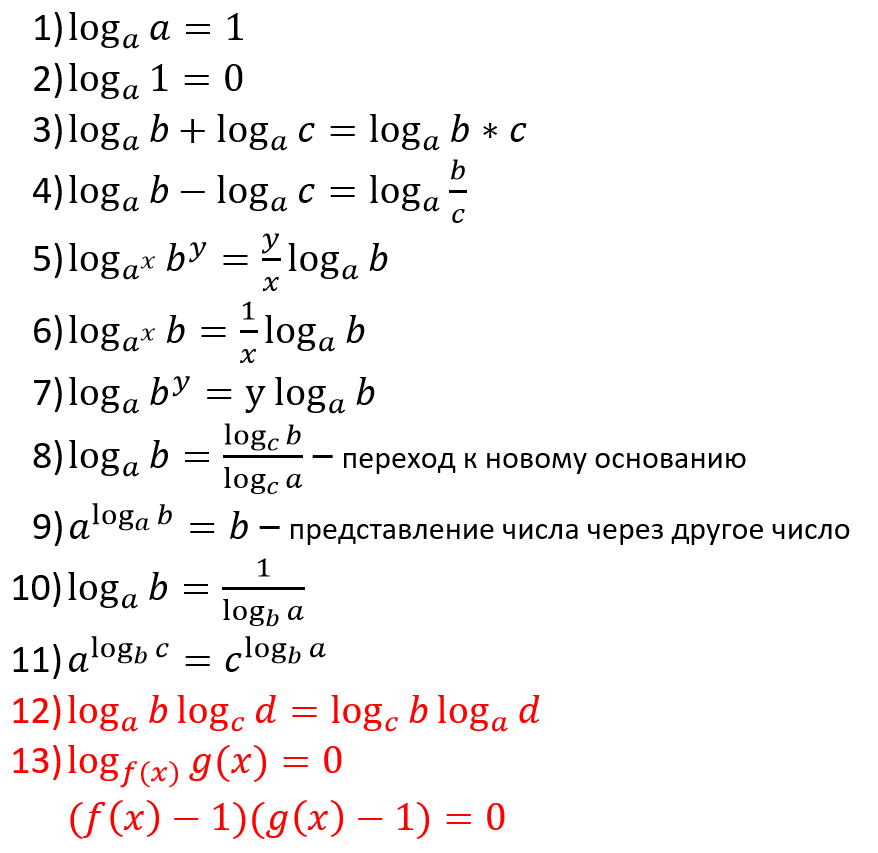

Первый способ. Попробуем применить метод “разделения”. Сравним логарифмы с числом .

Второй способ (умножение на натуральное число).

Замечание 1. Суть метода “умножения на натуральное число” в том, что мы ищем натуральное число k, при умножении на которое сравниваемых чисел

a и b получают такие числа ka и kb, что между ними находится хотя бы одно целое число.

Замечание 2. Реализация вышеописанного метода бывает весьма трудоемка, если сравниваемые числа очень близки друг к другу.
В этом случае можно попробовать сравнение методом “вычитания единицы”. Покажем его на следующем примере.

12. Сравните числа log₇8 и log₆7.

Решение.

Первый способ (вычитание единицы).

Вычтем из сравниваемых чисел по 1.

В первом неравенстве мы воспользовались тем, что

если c > a > 1, то при b > 1 справедливо неравенство log_ab > log_cb.

Во втором неравенстве – монотонностью функции y = log

ax.

Замечание. Вычитать из сравниваемых чисел можно любое натуральное число n. При этом часто бывает достаточно взять n = 1.

Второй способ (применение неравенства Коши).

13. Сравните числа log₂₄72 и log₁₂18.

Решение.

14. Сравните числа log₂₀80 и log₈₀640.

Решение.

Решение.

Пусть log₂5 = x . Заметим, что x > 0.

Получаем неравенство .

Найдем множество решений неравенства , удовлетворяющих условию x > 0.

Возведем обе части неравенства в квадрат (при x > 0 обе части неравенства положительны). Имеем 9x² < 9x + 28.

Множеством решений последнего неравенства является промежуток .

Учитывая, что x > 0, получаем: .

Ответ: неравенство верно.

Практикум по решению задач.

1. Сравните числа:

2. Расположите в порядке возрастания числа:

3. Решите неравенство 4⁴ – 2·2⁴⁺¹ – 3 < 0. Является ли число √2 решением данного неравенства? (Ответ: (–∞; log₂3); число √2 является решением данного неравенства.)

Заключение.

Методов сравнения логарифмов много. Цель уроков по данной теме – научить ориентироваться в многообразии методов, выбирать и применять наиболее рациональный способ решения в каждой конкретной ситуации.

В классах с углубленным изучением математики материал по данной теме может быть изложен в форме лекции. Такая форма учебной деятельности предполагает, что материал лекции должен быть тщательно отобран, проработан, выстроен в определенной логической последовательности. Записи, которые делает учитель на доске, должны быть продуманными, математически точными.

Закрепление лекционного материала, отработку навыков по решению задач целесообразно проводить на уроках-практикумах. Цель практикума – не только закрепить и проверить полученные знания, но и пополнить их. Поэтому задания должны содержать задачи разного уровня, от самых простых задач до задач повышенной сложности. Учитель на таких практикумах выступает в роли консультанта.

Литература.

1. Галицкий М.Л. и др.Углубленное изучение курса алгебры и математического анализа: Метод. рекомендации и дидактические материалы: Пособие для учителя.– М. : Просвещение, 1986.
2. Зив Б.Г., Гольдич В.А. Дидактические материалы по алгебре и началам анализа для 10 класса. – СПб.: “ЧеРо-на-Неве”, 2003.
3. Литвиненко В.Н., Мордкович А. Г. Практикум по элементарной математике. Алгебра. Тригонометрия.: Учебное издание. – М.: Просвещение, 1990.
4. Рязановский А.Р. Алгебра и начала анализа:500 способов и методов решения задач по математике для школьников и поступающих в вузы. – М.: Дрофа, 2001.
5. Садовничий Ю.В. Математика. Конкурсные задачи по алгебре с решениями. Часть 4. Логарифмические уравнения, неравенства, системы. Учебное пособие.-3-е изд., стер.-М.:Издательский отдел УНЦДО, 2003.
6. Шарыгин И.Ф., Голубев В.И.Факультативный курс по математике: Решение задач: Учеб. пособие для 11 кл. сред.шк.– М.: Просвещение, 1991.

Сравнение логарифмов

Ни для кого не секрет, что с помощью применения логарифмов мы упрощаем довольно много сложных алгебраических операций и не только. Логарифмы дают возможность заменять более сложные операции умножения на операции сложения, деление на вычитание. Согласитесь, ведь это намного проще. Если уже быть совсем точными, то логарифм заданного числа – это показатель степени, в которую нужно возвести другое, также заданное число, чтобы получить данное. На первый взгляд все запутано и непонятно, но это только на первый, на самом деле, все до нельзя просто. Для того, чтобы закреплять знания о логарифмах (да и не только о них), конечно же, рекомендовано после прочтения теории выполнять самостоятельные практические упражнения, это не только поможет усвоить материал, но и выявить все недочеты.

Но вернемся к логарифмам, а точнее к их сравнению. Разумеется, вам в голову может прийти вопрос: «что такое сравнение логарифмов? и как это делается?».

Зачем мы сравниваем логарифмы? Ответ достаточно прост. При решении неравенств и уравнений, довольно часто возникает вопрос, когда нужно определить принадлежность корня области допустимых значений или же сделать соотношение решений двух или более неравенств на числовой прямой, а решение, при этом, выражается иррациональным числом, которое, в свою очередь, записано с помощью логарифма. Вот тут-то нам и необходимо сравнение этих логарифмов.

Существуют несколько способов сравнения логарифмов. Какой из них использовать зависит, в первую очередь, от того, одинаковые основания у логарифмов или нет. Если первый вариант, то тут выход один – использовать монотонность логарифмических функций.

Если числа равные, но основания разные, то тут можно пойти несколькими путями:

1. Графический способ
2. Сравнение логарифмов через переход к одному основанию
3. Метод оценки
4. введение промежуточного числа
5. Алгебраические методы, которые, в свою очередь делятся еще на несколько.

Например: log[2,x]>log[4,x]

Если 0   1   2 , то

log   a x   1 > log   a x   2 — знак неравенства меняется

Если a > 1 и 0   1   2 , то

log   a x   1   a x   2 — знак неравенства не меняется

Если 1 1, то log   a x > log   b x

Если 0 1, то log   a x > log   b x

Если 1   a x   b x

Если 0   a x   b x

Исчисление

— Как сравнить логарифмы $\log_4 5$ и $\log_5 6$?

спросил 4 года, 6 месяцев назад

Изменено 12 дней назад

Просмотрено 1к раз

$\begingroup$

Мне нужно сравнить $\log_4 5$ и $\log_5 6$. 7 < 1$$ $$\log_{390625} 279936 < 1$$ вот почему у меня $\log_5 6 < \frac{8}{7} < \log_4 5$.

Но для доказательства мне нужна оценка обоих логарифмов (без этой оценки я не могу найти дробь для сравнения). Помогите найти более понятное решение (без графиков) $\endgroup$

2 925$$

Итак, $$\log_56={\log 6\over \log 5}<{\log 5\over \log 4}=\log _45$$

$\endgroup$

$\begingroup$

$$f(x) = \log_x(x+1)$$ — строго убывающая функция при $x>1$.

Вы можете убедиться в этом, найдя $f'(x)$ и заметив, что $f'(x)<0$ для всех $x>1$.

$\endgroup$

$\begingroup$

Лемма Если $v \geqslant u \geqslant x > 1$ и $y/x > v/u$, то $\log_x{y} > \log_u{v}$. 9{\beta-1}$, поэтому $\alpha > \beta$. $\square$

У нас есть $5/4 > 6/5$, поэтому лемма дает $\log_4{5} > \log_5{6}$. $\квадрат$

$\endgroup$

1

$\begingroup$

Я нашел еще одно решение $$\log_4 5 > \log_5 6$$ $$\log_4 (4+1) > \log_5 (5+1)$$ $$\log_4 4\cdot(1+0,25) > \log_5 5\cdot(1+0,2)$$ $$1+\log_4 (1+0,25) > 1+ \log_5 (1+0,2)$$ $$\log_4 (1+0,25) > \log_5 (1+0,2)$$ $$\log_4 (1+0,25) > \frac{\log_4 (1+0,2)}{\log_4 5}$$ $$\log_4 (1+0,25) > \log_4 (1+0,2) > \frac{\log_4 (1+0,2)}{\log_4 5}$$ КЭД

$\endgroup$

$\begingroup$

$$\frac54>\frac65\land 4<5\implies\frac{\log\dfrac54}{\log 4}>\frac{\log\dfrac65}{\log 5}\implies\frac{\log5 }{\log 4}>\frac{\log6}{\log 5}.$$

$\endgroup$

Предварительное исчисление по алгебре — Разница между логарифмами по разным основаниям

Задавать вопрос

спросил 11 лет, 7 месяцев назад

Изменено 11 лет, 7 месяцев назад

Просмотрено 2к раз

$\begingroup$

Каждый раз, когда я вижу логарифмическую функцию, и если так случается, что мне нужно взять производную или интеграл этой конкретной функции, я теряюсь и стараюсь избегать этой проблемы.

То, что я говорю, это $$\frac{\mathrm{d} }{\mathrm{d} x}\left ( \log _{10}x \right )$$ и $$\frac{\mathrm {d} }{\mathrm{d} x}\left ( \ln x \right )$$ одинаковы, т.е. $$\frac{1}{x}$$ Почему так? На самом деле они оба разные, верно? Один к по основанию 10 , а другой по основанию e , логарифм с основанием e называется наперианским или натуральным логарифмом, а что такое логарифм по основанию 10? неестественным или искусственным логарифмом? Они должны иметь разные производные, верно?

Это потому, что каждое свойство логарифмов верно для журналов обоих оснований? Есть ли для этого какая-то особая причина?

Это некоторые из основ, которые мне нужно прояснить, прежде чем я перейду к своим математическим исследованиям. Я буду очень рад, если кто-нибудь сможет дать мне представление об этих аспектах.

• алгебра-предварительное исчисление
• интуиция
• логарифмы
• обучение

$\endgroup$

3

$\begingroup$

В ваших рассуждениях две ошибки.

Во-первых, производные $\log_{10}x$ и $\ln x$ не совпадают. Поскольку $\log_{b}x=\ln x/\ln b$, мы имеем

$$\frac{\mathrm d}{\mathrm dx}\log_{b}x=\frac{\mathrm d} {\ mathrm dx} \ frac {\ ln x} {\ ln b} = \ frac1 {\ ln b} \ frac {\ mathrm d} {\ mathrm dx} \ ln x = \ frac1 {\ ln b} \ frac1x \;.$$

Во-вторых, неверно, что разные функции должны иметь разные производные. Функции, отличающиеся только аддитивной константой, имеют одну и ту же производную. Чтобы использовать пример, близкий к вашему,

$$\frac{\mathrm d}{\mathrm dx}\ln(cx)=c\frac1{cx}=\frac1x\;.$$

Это может показаться загадочным в этой форме, но становится яснее, если вместо этого написать

$$\frac{\mathrm d}{\mathrm dx}\ln(cx)=\frac{\mathrm d}{\mathrm dx}\left(\ ln x+\ln c\right)=\frac{\mathrm d}{\mathrm dx}\ln x=\frac1x\;,$$

, что показывает, что это связано с тем, что $\ln (cx)$ и $\ln x$ отличаются только на аддитивную константу.

$\endgroup$

2

$\begingroup$

Производные не идентичны.