ax2 bx c график функции
Вы искали ax2 bx c график функции? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и y x 2 bx c, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «ax2 bx c график функции».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как ax2 bx c график функции,y x 2 bx c,y x 2 c x,y x в квадрате парабола,y x2 bx c,ветвь параболы,ветвь параболы функция,ветвь параболы функция ее свойства и график,график квадратичная функция,график квадратичной,график квадратичной функции,график квадратичной функции y ax2 bx c,график квадратичной функции как строить,график квадратичной функции примеры,график парабола,график парабола функция,график параболы,график параболы как построить,график параболы как строить,график параболы формула,график параболы функции,график функции 2 y x bx c,график функции ax2 bx c,график функции y x 2 bx c,график функции y x2 bx c,график функции график параболы,график функции квадратного уравнения,график функции парабола,график функции парабола как строить,график функции парабола построить,график функции парабола примеры,график функции парабола формула,график функции параболы,графики квадратичной функции,графики квадратичных функций,графики параболы,графики параболы и их формулы,графики функций парабола,как называется график квадратичной функции,как найти вершину параболы графика функции y ax2 bx c,как найти нули функции по графику параболы,как построить график квадратичной функции,как построить график квадратного уравнения,как построить график параболы,как построить график параболы по уравнению,как построить график функции y ax2 bx c,как построить график функции квадратичной функции,как построить график функции квадратного уравнения,как построить график функции парабола,как построить квадратичную функцию,как построить параболу по квадратному уравнению,как построить функцию квадратичную,как решать квадратичная функция,как решать квадратичные функции,как решать функции квадратные,как решить квадратичную функцию,как составить таблицу значений функции параболы,как строить график квадратичной функции,как строить график параболы,как строить график параболы по уравнению,как строить график по уравнению параболы,как строить график функции парабола,как строить графики квадратичной функции,как строить квадратичную функцию,как строить квадратичную функцию график парабола,как строить параболу по квадратному уравнению,квадратичная парабола,квадратичная функция график,квадратичная функция как построить,квадратичная функция как решать,квадратичные функции и их графики,квадратичные функции как решать,квадратная функция и ее график,квадратные функции и ее график,нули функции параболы,парабола x в квадрате,парабола y x в квадрате,парабола график,парабола график как строить,парабола график функции,парабола график функции y ax2 bx c,парабола график функции примеры,парабола график функции формула,парабола графики функций,парабола квадратичная,парабола формула график функции,парабола функции,парабола функция,парабола функция ее свойства и график,параболы графики,параболы графики функций,параболы и их формулы,параболы построить график,построение графика параболы,построение параболы по квадратному уравнению,построение параболы по уравнению,построение параболы по уравнению квадратному,построить график квадратичной функции,построить график квадратичной функции примеры,построить график параболы,построить график функции квадратичной,построить параболу,постройте график квадратичной функции,приведите пример квадратичной функции график которой касается прямой y 4 в точке с абсциссой 2,пример квадратичной функции,решение квадратичной функции,с 3 график квадратичной функции,формула график парабола,формула графика параболы,формула квадратичной функции,формула параболы графика,функции парабола,функции параболы,функция ветвь параболы,функция квадратного уравнения,функция парабола,функция парабола ее свойства и график,функция параболы,функция параболы формула.
Решить задачу ax2 bx c график функции вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
Постройте график функции y x2 4x 3. Квадратичная и кубическая функции. Основные свойства квадратичной функции
Словари. Энциклопедии. История. Литература. Русский язык »
Русский язык »
Постройте график функции y x2 4x 3.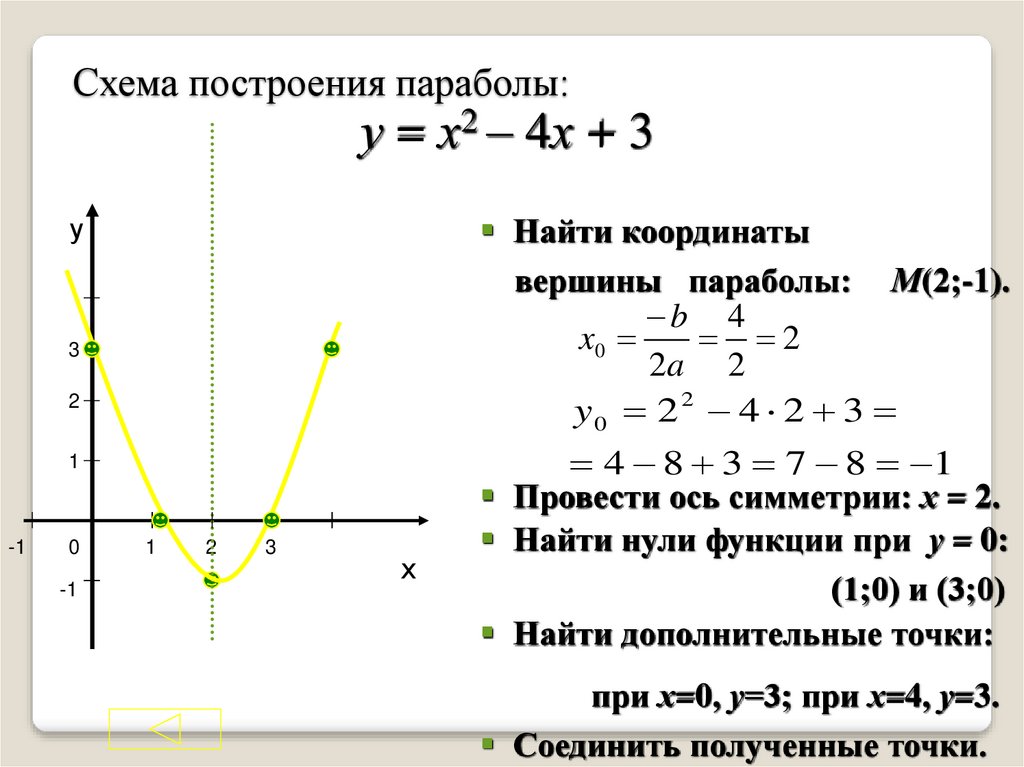
Квадратичная и кубическая функции. Основные свойства квадратичной функции
Разберем как строить график с модулем.
Найдем точки при переходе которых знак модулей меняется.
Каждое выражения, которое под модулем приравниваем к 0. У нас их два x-3 и x+3.
x=3 и x=-3
У нас числовая прямая разделится на три интервала (-∞;-3)U(-3;3)U(3;+∞). На каждом интервале нужно определить знак под модульных выражений.
1. Это сделать очень просто, рассмотрим первый интервал (-∞;-3). Возьмем с этого отрезка любое значение, например, -4 и подставим в каждое под модульное уравнение вместо значения х.
х=-4
x-3=-4-3=-7 и x+3=-4+3=-1
У обоих выражений знаки отрицательный, значит перед знаком модуля в уравнении ставим минус, а вместо знака модуля ставим скобки и получим искомое уравнение на интервале (-∞;-3).
y=— (x-3)-(— (x+3))=-х+3+х+3=6
На интервале (-∞;-3) получился график линейной функции (прямой) у=6
2.
Рассмотрим второй интервал (-3;3). Найдем как будет выглядеть уравнение графика на этом отрезке. Возьмем любое число от -3 до 3, например, 0. Подставим вместо значения х значение 0.
x-3=0-3=-3 и x+3=0+3=3
У первого выражения x-3 знак отрицательный получился, а у второго выражения x+3 положительный. Следовательно, перед выражением x-3 запишем знак минус, а перед вторым выражением знак плюс.
y=— (x-3)-(+ (x+3))=-х+3-х-3=-2x
На интервале (-3;3) получился график линейной функции (прямой) у=-2х
3.Рассмотрим третий интервал (3;+∞). Возьмем с этого отрезка любое значение, например 5, и подставим в каждое под модульное уравнение вместо значения х.
х=5
x-3=5-3=2 и x+3=5+3=8
У обоих выражений знаки получились положительными, значит перед знаком модуля в уравнении ставим плюс, а вместо знака модуля ставим скобки и получим искомое уравнение на интервале (3;+∞).
y=+ (x-3)-(+ (x+3))=х-3-х-3=-6
На интервале (3;+∞) получился график линейной функции (прямой) у=-6
4.
Теперь подведем итог.Постоим график y=|x-3|-|x+3|.
На интервале (-∞;-3) строим график линейной функции (прямой) у=6.
На интервале (-3;3) строим график линейной функции (прямой) у=-2х.
Чтобы построить график у=-2х подберем несколько точек.
x=-3 y=-2*(-3)=6 получилась точка (-3;6)
x=0 y=-2*0=0 получилась точка (0;0)
x=3 y=-2*(3)=-6 получилась точка (3;-6)
На интервале (3;+∞) строим график линейной функции (прямой) у=-6.
5. Теперь проанализируем результат и ответим на вопрос задания найдем значение k, при которых прямая y=kx имеет с графиком y=|x-3|-|x+3| данной функции ровно одну общую точку.
Прямая y=kx при любом значении k всегда будет проходить через точку (0;0). Поэтому мы можем изменить только наклон данной прямой y=kx, а за наклон у нас отвечает коэффициент k.
Если k будет любое положительное число, то будет одно пересечение прямой y=kx с графиком y=|x-3|-|x+3|. Этот вариант нам подходит.
Если k будет принимать значение (-2;0), то пересечений прямой y=kx с графиком y=|x-3|-|x+3| будет три.
Этот вариант нам не подходит.
Если k=-2, решений будет множество [-2;2], потому что прямая y=kx будет совпадать с графиком y=|x-3|-|x+3| на данном участке. Этот вариант нам не подходит.
Если k будет меньше -2, то прямая y=kx с графиком y=|x-3|-|x+3| будет иметь одно пересечение.Этот вариант нам подходит.
Если k=0, то пересечений прямой y=kx с графиком y=|x-3|-|x+3| также будет одно.Этот вариант нам подходит.
Ответ: при k принадлежащей интервалу (-∞;-2)U; график f(х) = х + 2 – это прямая, параллельная прямой f(х) = х, но сдвинутая на две единицы вверх и поэтому проходящая через точку с координатами (0,2) (потому что постоянная равна 2).
Построение графика сложной функции
Найдите нули функции. Нули функции – это значения переменной «х», при которых у = 0, то есть это точки пересечения графика с осью Х. Имейте в виду, что нули имеют не все функции, но это первый шаг процесса построения графика любой функции. Чтобы найти нули функции, приравняйте ее к нулю.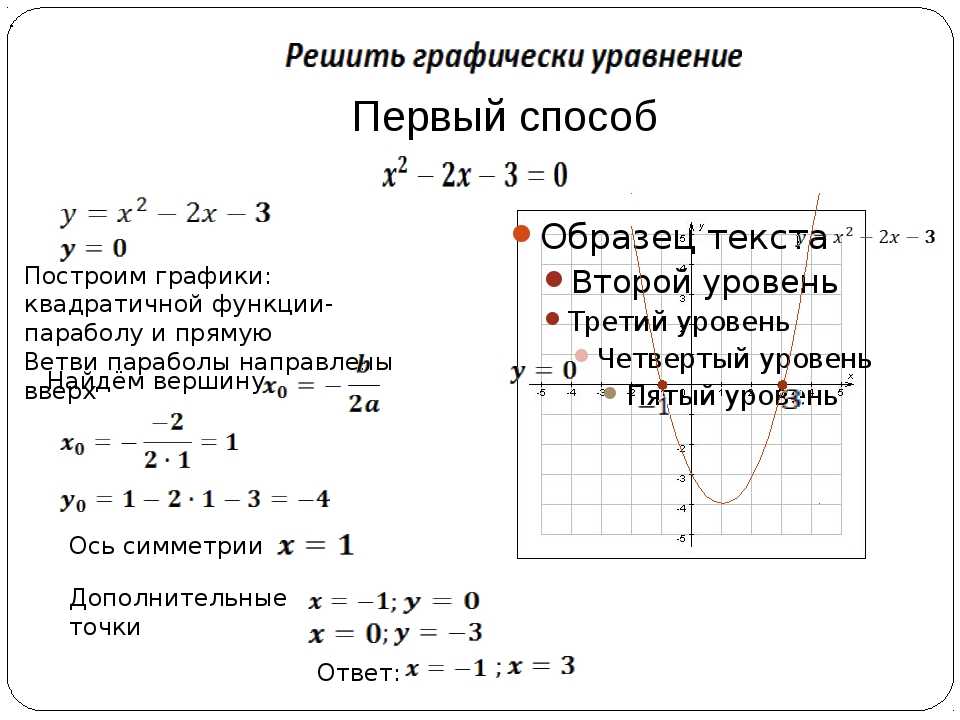
{2}}}}
), приравняйте знаменатель к нулю и найдите «х». В полученных значения переменной «х» функция не определена (в нашем примере проведите пунктирные линии через х = 2 и х = -2), потому что на 0 делить нельзя. Но асимптоты существуют не только в случаях, когда функция содержит дробное выражение. Поэтому рекомендуется пользоваться здравым смыслом:
«Натуральный логарифм» — 0,1. Натуральные логарифмы. 4. «Логарифмический дартс». 0,04. 7. 121.
«Степенная функция 9 класс» — У. Кубическая парабола. У = х3. 9 класс учитель Ладошкина И.А. У = х2. Гипербола. 0. У = хn, у = х-n где n – заданное натуральное число. Х. Показатель – четное натуральное число (2n).
«Квадратичная функция» — 1 Определение квадратичной функции 2 Свойства функции 3 Графики функции 4 Квадратичные неравенства 5 Вывод. Свойства: Неравенства: Подготовил ученик 8А класса Герлиц Андрей. План: График: -Промежутки монотонности при а > 0 при а
«Квадратичная функция и её график» — Решение.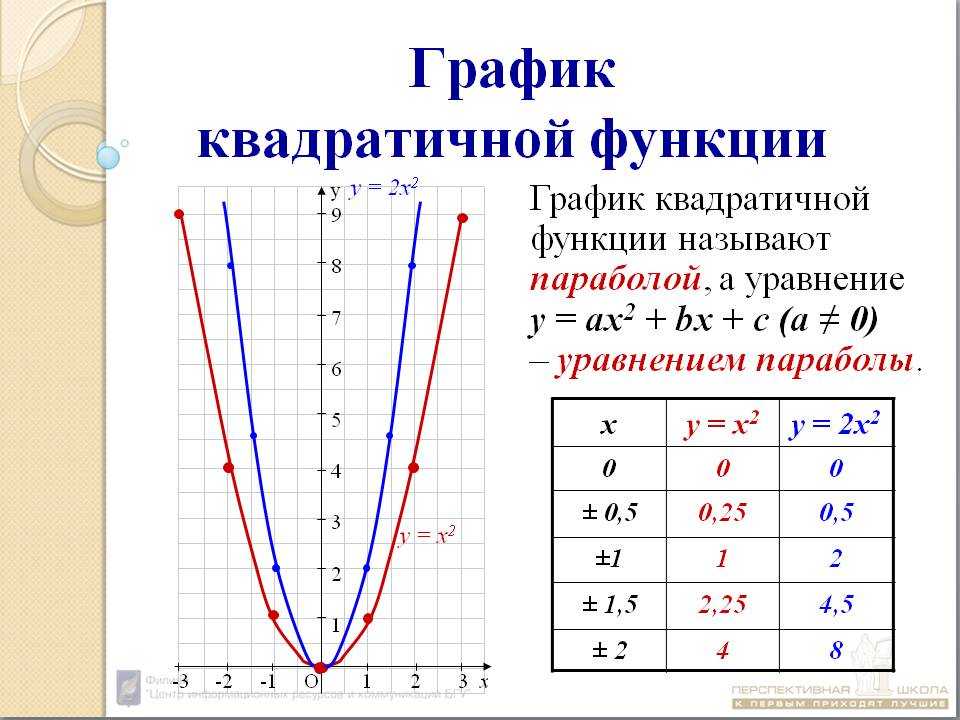
у=4x А(0,5:1) 1=1 А-принадлежит. При а=1 формула у=аx принимает вид.
«8 класс квадратичная функция» — 1) Построить вершину параболы. Построение графика квадратичной функции. x. -7. Построить график функции. Алгебра 8 класс Учитель 496 школы Бовина Т. В. -1. План построения. 2) Построить ось симметрии x=-1. y.
Как построить параболу? Существует несколько способов построения графика квадратичной функции. Каждый из них имеет свои плюсы и минусы. Рассмотрим два способа.
Начнём с построения графика квадратичной функции вида y=x²+bx+c и y= -x²+bx+c.
Пример.
Построить график функции y=x²+2x-3.
Решение:
y=x²+2x-3 — квадратичная функция. График — парабола ветвями вверх. Координаты вершины параболы
От вершины (-1;-4) строим график параболы y=x²(как от начала координат. Вместо (0;0) — вершина (-1;-4). От (-1;-4) идём вправо на 1 единицу и вверх на 1 единицу, затем влево на 1 и вверх на 1; далее: 2 — вправо, 4 — вверх, 2- влево, 4 — вверх; 3 — вправо, 9 — вверх, 3 — влево, 9 — вверх.
Если этих 7 точек недостаточно, далее — 4 вправо, 16 — вверх и т. д.).
График квадратичной функции y= -x²+bx+c — парабола, ветви которой направлены вниз. Для построения графика ищем координаты вершины и от неё строим параболу y= -x².
Пример.
Построить график функции y= -x²+2x+8.
Решение:
y= -x²+2x+8 — квадратичная функция. График — парабола ветвями вниз. Координаты вершины параболы
От вершины строим параболу y= -x² (1 — вправо, 1- вниз; 1 — влево, 1 — вниз; 2 — вправо, 4 — вниз; 2 — влево, 4 — вниз и т. д.):
Этот способ позволяет построить параболу быстро и не вызывает затруднений, если вы умеете строить графики функций y=x² и y= -x². Недостаток: если координаты вершины — дробные числа, строить график не очень удобно. Если требуется знать точные значения точек пересечения графика с осью Ох, придется дополнительно решить уравнение x²+bx+c=0 (или —x²+bx+c=0), даже если эти точки непосредственно можно определить по рисунку.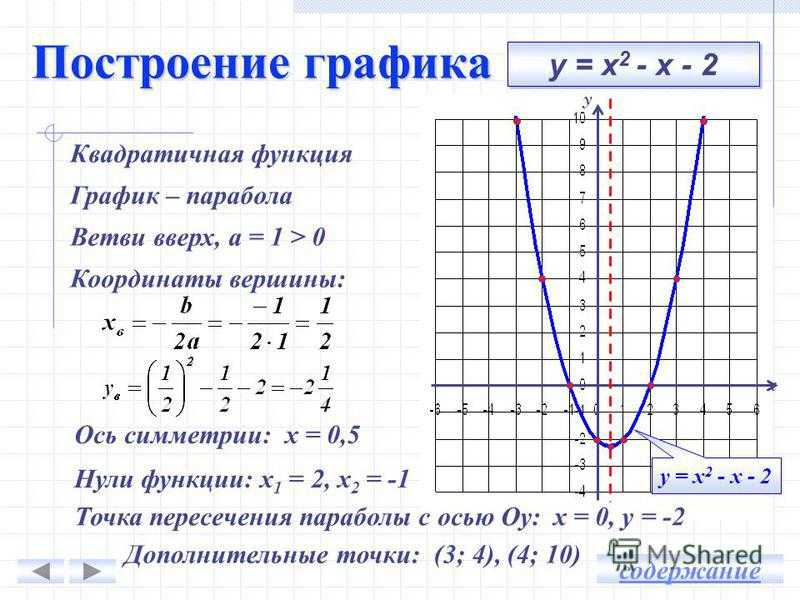
Другой способ построения параболы — по точкам, то есть можно найти несколько точек графика и через них провести параболу (с учетом того, что прямая x=хₒ является её осью симметрии). Обычно для этого берут вершину параболы, точки пересечения графика с осями координат и 1-2 дополнительные точки.
Построить график функции y=x²+5x+4.
Решение:
y=x²+5x+4 — квадратичная функция. График — парабола ветвями вверх. Координаты вершины параболы
то есть вершина параболы — точка (-2,5; -2,25).
Ищем . В точке пересечения с осью Ох y=0: x²+5x+4=0. Корни квадратного уравнения х1=-1, х2=-4, то есть получили две точки графике (-1; 0) и (-4; 0).
В точке пересечения графика с осью Оy х=0: y=0²+5∙0+4=4. Получили точку (0; 4).
Для уточнения графика можно найти дополнительную точку. Возьмем х=1, тогда y=1²+5∙1+4=10, то есть еще одна точка графика — (1; 10). Отмечаем эти точки на координатной плоскости. С учетом симметрии параболы относительно прямой, проходящей через её вершину, отметим еще две точки: (-5; 6) и (-6; 10) и проведем через них параболу:
Построить график функции y= -x²-3x.
Решение:
y= -x²-3x — квадратичная функция. График — парабола ветвями вниз. Координаты вершины параболы
Вершина (-1,5; 2,25) — первая точка параболы.
В точках пересечения графика с осью абсцисс y=0, то есть решаем уравнение -x²-3x=0. Его корни — х=0 и х=-3, то есть (0;0) и (-3; 0) — еще две точки графика. Точка (о; 0) является также точкой пересечения параболы с осью ординат.
При х=1 y=-1²-3∙1=-4, то есть (1; -4) — дополнительная точка для построения графика.
Построение параболы по точкам — более трудоёмкий, по сравнению с первым, способ. Если парабола не пересекает ось Oх, дополнительных точек потребуется больше.
Прежде чем продолжить построение графиков квадратичных функций вида y=ax²+bx+c, рассмотрим построение графиков функций с помощью геометрических преобразований. Графики функций вида y=x²+c также удобнее всего строить, используя одно из таких преобразований — параллельный перенос.
Рубрика: |
Функция y=x^2 называется квадратичной функцией.
Графиком квадратичной функции является парабола. Общий вид параболы представлен на рисунке ниже.
Квадратичная функция
Рис 1. Общий вид параболы
Как видно из графика, он симметричен относительно оси Оу. Ось Оу называется осью симметрии параболы. Это значит, что если провести на графике прямую параллельную оси Ох выше это оси. То она пересечет параболу в двух точках. Расстояние от этих точек до оси Оу будет одинаковым.
Ось симметрии разделяет график параболы как бы на две части. Эти части называются ветвями параболы. А точка параболы которая лежит на оси симметрии называется вершиной параболы. То есть ось симметрии проходит через вершину параболы. Координаты этой точки (0;0).
Основные свойства квадратичной функции
1. При х =0, у=0, и у>0 при х0
2. Минимальное значение квадратичная функция достигает в своей вершине. Ymin при x=0; Следует также заметить, что максимального значения у функции не существует.
3. Функция убывает на промежутке (-∞;0] и возрастает на промежутке }
строительных потоков | Parabola
В этой статье рассказывается все, что вам нужно знать о построении потока.
Если вы застряли на каком-то этапе, указанном ниже, свяжитесь с нами по адресу [email protected] — мы здесь, чтобы поддержать вас, и вместе мы можем создавать великие дела.
В этом разделе мы рассмотрим:
- Основные термины, которые необходимо знать при построении
- Работа с шагами
- Основные строительные блоки потока
- Навигация по холсту
- Добавление карточек
- Использование сочетаний клавиш
- Редактирование и обновление версий потока
Теперь приступим!
Ключевые строительные термины, которые необходимо знать
Поток: Это автоматизация, построенная в Parabola и похожая на блок-схему на вашем любимом листе миллиметровой бумаги.
Шаги: Потоки состоят из шагов и стрелок. Каждый шаг либо загружает данные в Parabola (импорт), либо выталкивает данные из Parabola (экспорт), либо преобразует данные в Parabola. Думайте об этом как о вашей хореографии данных или нотах.
На скриншоте ниже вы увидите два шага. Один из них представляет собой интеграцию импорта, извлекающую данные из Shopify, а другой — преобразование, которое определенным образом очищает данные.
Стрелки: Стрелки соединяют шаги и сообщают Parabola, как данные должны проходить через различные шаги.
Холст: Потоки строятся на холсте. Здесь вы добавляете и упорядочиваете шаги и стрелки.
Карточки: Карточки группируют шаги и делают процесс более организованным. Они также имеют редактор форматированного текста, чтобы дать подробные дескрипторы и предоставить дополнительный контекст для ваших групп шагов.
Работа с шагами
Параболические потоки состоят из ступеней. Каждый шаг выполняет определенную задачу, например поиск и замену или фильтрацию данных. Мы можем размещать шаги в любом месте нашего холста. Перетащите их и соедините друг с другом для передачи данных.
Основные строительные блоки потока
При построении потока начните с исходного шага для переноса данных в Parabola, а затем используйте шаги преобразования для внесения изменений в ваши данные, например удаления столбцов.
Потоки заканчиваются экспортом данных из Parabola, например обновлением таблицы Google или отправкой электронного письма. Parabola не хранит данные (кроме плоских файлов, таких как файлы CSV или Excel), поэтому потоки Parabola всегда извлекают данные непосредственно из вашего источника (например, Shopify, Shipstation, Facebook Ads) и экспортируют в пункт назначения для обновления безопасного хранения (например, Google). Таблицы, файлы CSV, Shopify).
Поиск шагов
Шаги можно найти с помощью панели инструментов конструктора в верхней части страницы. Вы можете выполнить поиск шагов, введя ключевые слова, или нажать «Интеграции» или «Преобразования», чтобы увидеть полный список шагов в этих разделах.
Чтобы понять, что делает шаг, наведите на него указатель мыши, и появится поясняющая подсказка:
Найдя нужный шаг, добавьте его на холст, нажав на шаг или перетащив его на холст.
. Вы можете разместить его где угодно.
Шаги, которые позволят вам извлекать данные в Parabola из вашего источника, можно найти в левой части раздела «Источники» на вкладке «Интеграции».
Шаги, позволяющие отправлять данные из Parabola, можно найти в правой части раздела «Назначения» на вкладке «Интеграции».
Шаги, позволяющие преобразовывать данные в Parabola, можно найти на вкладке «Преобразования». Вкладка «Преобразования» содержит различные разделы о том, как работают эти шаги.
Шаги настройки и редактирования
Если у вас есть шаг на холсте, вы можете настроить его, дважды щелкнув сам шаг или щелкнув значок шестеренки, который появляется ниже при наведении курсора на шаг.
Настройки шагов всегда находятся слева. После того, как вы сделали свой выбор, обязательно нажмите «Показать обновленные результаты», чтобы увидеть обновление ваших данных. Данные в Parabola всегда представлены в знакомом табличном формате.
При настройке шага вы также можете использовать панель «Поиск» в верхней части полученных данных.
Мы сосредоточим ваше внимание на столбцах и строках, которые содержат то, что вы ищете, но вы всегда можете расширить столбцы и строки, если вам нужно больше контекста.
Наконец, вы увидите 2-3 вкладки в нижней части окна шага.
Для шагов, на которых вы загружаете данные в Parabola, вкладки будут «Результаты» и «Документация».
Для шагов преобразования вкладки будут «Результаты», «Ввод» и «Документация».
Для шагов, где вы отправляете данные из Parabola, эти вкладки будут «Экспорт», «Ввод» и «Документация».
На вкладке «Результаты» показано, как выглядят ваши данные в настоящее время на основе того, что вы настроили на этом шаге.
Вкладка «Ввод» показывает входящие данные, поступающие на шаг. Может быть полезно сравнить данные, которые вы видите на вкладке «Ввод» и на вкладке «Результаты», чтобы убедиться, что ваш шаг настроен так, как вы хотите.
На вкладке «Документация» отображается полезная документация по шагу. Это поможет вам не отставать от шага, вместо того чтобы искать документацию в другом месте.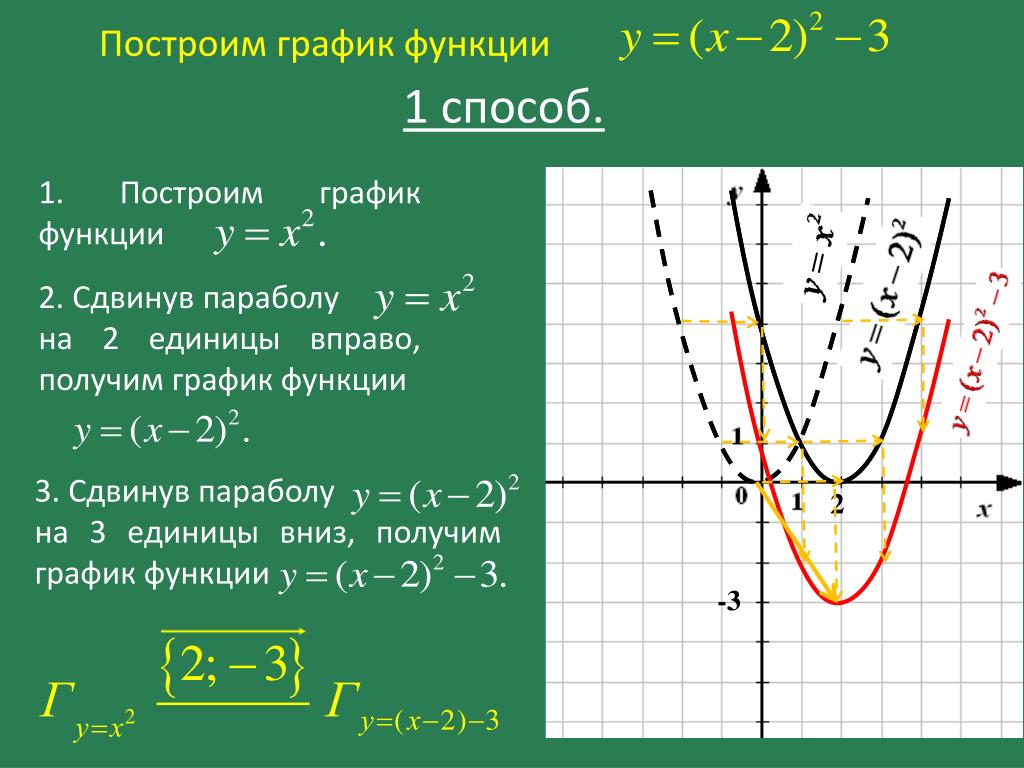
На вкладке «Экспорт» показано, как выглядят данные, которые вы будете экспортировать из Parabola.
Авторизация шага
Для наших шагов интеграции, когда вы подключаетесь к сторонней службе за пределами Parabola, первым шагом всегда будет авторизация шага. Нажав «Авторизовать», откроется небольшое окно, в котором вы сможете войти в эту внешнюю службу. Обратите внимание, что авторизация сторонних сервисов в настоящее время контролируется на уровне потока. Вам будет предложено повторно авторизоваться в той же службе при работе с другим потоком.
Если вам когда-нибудь понадобится добавить, отредактировать или удалить свою авторизацию, щелкните раскрывающийся список «Редактировать учетные записи» в верхнем левом углу вашего шага. Вы можете выбрать опцию «Добавить новую учетную запись» или нажать «Изменить», чтобы отредактировать или удалить существующую учетную запись. После того, как вы нажмете «Изменить», появится значок карандаша и корзины. Щелкнув значок карандаша, вы сможете отредактировать свою авторизацию, в том числе переименовать ее, а щелкнув значок корзины, вы удалите авторизацию.
Если вы удалите авторизацию таким образом, все остальные шаги в вашем потоке, связанные с той же авторизацией, также потеряют свою аутентификацию.
Соединение шагов стрелками
Стрелки — это способ, которым мы соединяем шаги и сообщаем Parabola, как передавать данные между шагами. Вы можете перетаскивать стрелки между шагами, чтобы соединить их. Вы также можете отключить ступеньки, потянув за стрелку принимающей ступеньки. После того, как шаги соединены, он останется подключенным, когда вы будете перемещать шаг(и) вокруг.
У нас также есть цели для перетаскивания, которые появляются всякий раз, когда вы вытягиваете новые шаги из боковой панели. Перетащив шаг в одну из целей перетаскивания, вы увидите, что шаг будет автоматически подключен, даже если он находится между двумя шагами.
Дублирование или удаление шагов
Чтобы дублировать шаг, наведите указатель мыши на шаг и щелкните средний значок «Дублировать», который появляется прямо под шагом.
Все настройки шага будут сохранены при дублировании шага, но будут дублироваться только шаги в рамках одного и того же потока. Чтобы иметь возможность копировать шаги между потоками, см. следующий раздел «Копирование и вставка шагов внутри и между потоками».
Чтобы удалить шаг, наведите курсор на шаг и щелкните значок «Корзина». Появится запрос подтверждения с просьбой подтвердить, что вы хотите удалить этот шаг. Вы также можете щелкнуть шаг и нажать клавишу «Удалить» на клавиатуре, чтобы также удалить шаг. После удаления шага его нельзя будет восстановить из корзины, поэтому будьте осторожны перед удалением шагов.
Копирование и вставка шагов внутри и между потоками
У нас также есть функция под названием «фрагменты», которая позволяет копировать и вставлять несколько шагов внутри потока и между потоками.
Чтобы создать фрагмент, сначала выберите шаги, которые вы хотите скопировать. Если вы скопируете шаги, соединенные вместе стрелками, их соединения будут сохранены при вставке.
Чтобы выбрать шаги, вы можете удерживать клавишу Shift и нажимать на каждый шаг, который хотите скопировать. Или вы можете, удерживая клавишу Shift, щелкнуть пустую часть холста, а затем перетащить поле, чтобы выбрать большую группу шагов. Если вы выбрали слишком много, удерживайте клавишу Shift и щелкните выбранный шаг, чтобы отменить его выбор.
Теперь скопируйте шаги с клавиатуры. Используйте клавишу Cmd/Ctrl + клавишу c для копирования. Вы также можете использовать меню браузера для копирования. Появится желтый баннер: «Скопировано в буфер обмена. Имейте в виду, что скопированные шаги могут содержать конфиденциальные данные».
Как только вы увидите это раскрывающееся сообщение, вы можете вставить его в текстовый документ, вы увидите что-то вроде этого:
parabola:cb:af4f35234fc747a5b0bbda8bf14fefcf
Это то, что мы называем фрагментом. Фрагменты не имеют срока действия, поэтому вы можете использовать их столько раз, сколько вам нужно. Вы даже можете поделиться ими с другими, даже если они в разных командах Parabola.
Чтобы вставить фрагмент, скопируйте всю эту строку, а затем используйте клавиатуру, чтобы вставить этот фрагмент в поток Parabola (клавиша Cmd/Ctrl + клавиша v для вставки).
Фрагменты будут содержать все, что они скопировали. Если вы скопируете шаг файла CSV или Excel, этот файл будет во фрагменте. Если вы скопируете интеграцию, такую как Google Таблицы или Shopify, она не будет содержать никаких сведений об авторизации, поэтому пользователям необходимо будет авторизоваться со своей собственной учетной записью. Будьте осторожны, делясь фрагментами, содержащими шаги API. Шаги API приведут к его настройкам, которые могут включать ключи API.
Перемещение шагов
Чтобы переместить один шаг в потоке, щелкните шаг вниз и переместите мышь. Вы увидите, что шаг перемещается туда, куда движется ваша мышь. Вы можете отпустить свой шаг, убрав палец с мыши.
Чтобы переместить несколько шагов в потоке, сначала выберите шаги, которые вы хотите переместить. Вы можете удерживать клавишу Shift и нажимать на каждый шаг, который хотите скопировать.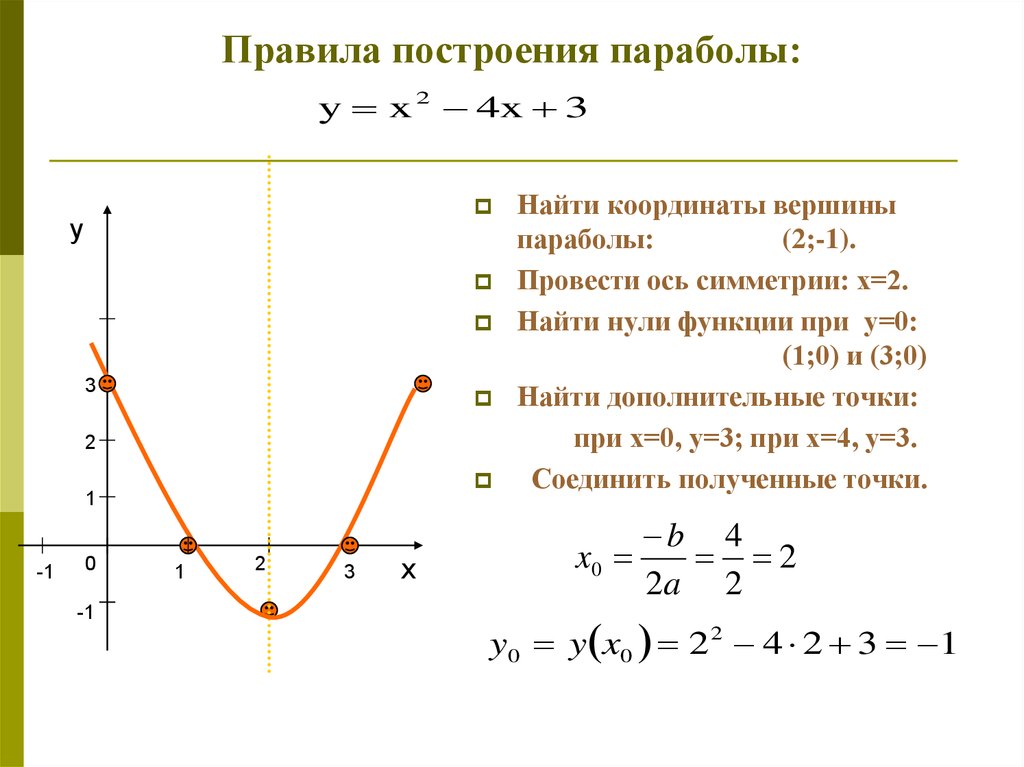
Или вы можете, удерживая клавишу Shift, щелкнуть пустую часть холста, а затем перетащить поле, чтобы выбрать большую группу шагов. Если вы выбрали слишком много, удерживайте клавишу Shift и щелкните выбранный шаг, чтобы отменить его выбор. Если вы скопируете шаги, соединенные вместе стрелками, их соединения будут сохранены при вставке.
После выбора шагов, которые вы хотите переместить, нажмите и удерживайте кнопку мыши и перемещайте ее. Точно так же, как вы перемещаете один шаг, вы увидите, что группа шагов перемещается вместе с вашей мышью. Просто отпустите шаги, убрав палец с мыши.
Навигация по холсту
Потоки строятся на холсте. Здесь вы добавляете и упорядочиваете шаги и стрелки. Мы создали холст, который намного больше экрана вашего компьютера, поэтому мы создали полезные функции для перемещения и навигации по вашему холсту.
Панорамирование
Для некоторых очень больших потоков вам нужно будет перемещаться по холсту и переходить ко всем шагам.
Вы можете щелкнуть и удерживать холст, а затем переместить мышь, чтобы переместить холст. Другой способ панорамирования — прокрутка. При использовании трекпада поместите два пальца на трекпад и перемещайте их. Холст движется, когда вы двигаете пальцами. При использовании мыши используйте колесо прокрутки. Вращение колеса прокрутки будет перемещать холст вверх и вниз. Удерживая клавишу Shift и вращая колесо, вы будете перемещаться по горизонтали влево и вправо.
Масштабирование
Вы можете увеличивать и уменьшать масштаб холста, чтобы настроить вид. Щелкните ползунок в правом нижнем углу и перетащите точку влево и вправо, чтобы уменьшить или увеличить уровень масштабирования. При использовании трекпада увеличивайте и уменьшайте масштаб, сводя и уменьшая масштаб. При использовании мыши с колесиком прокрутки удерживайте команду или клавишу Apple, а затем прокручивайте колесико для увеличения и уменьшения масштаба. Это масштабирование. Приятно отметить, что масштабирование использует середину холста в качестве точки отсчета, поэтому сочетание панорамирования и масштабирования — отличный способ эффективно перемещаться по холсту.
Добавление карточек
Карточки полезны для группировки шагов и организации вашего потока. В них есть редактор форматированного текста, помогающий документировать, что делает конкретная группа шагов. Чтобы добавить карточку на холст, перетащите «Новую карточку» с боковой панели в поток. Перетащите дополнительные шаги по мишеням карты, чтобы зафиксировать их на месте. Карточки можно связать с шагами, которые существуют в других карточках или на холсте. Они особенно полезны, когда у вас есть несколько соавторов в потоке, чтобы ваши товарищи по команде могли быстро понять, как вы построили поток, что он делает и на что им нужно обратить внимание.
Отменить/повторить
Вы можете отменить и повторить последние ~100 изменений потока во время сеанса. Когда вы отменяете и повторяете действия, шаги будут автоматически рассчитываться для восстановления их старых настроек и результатов. (Вы заметите, что отмена или повтор автоматически перемещает вас в соответствующее место на холсте.
) Обратите внимание, что история отмены/повторения вашего сеанса не сохраняется, когда вы покидаете страницу.
Использование сочетаний клавиш
Мы встроили сочетания клавиш, чтобы упростить и ускорить построение потока.
Ярлыки шагов
- d : Дублировать выбранные шаги
- удалить / пробел : Удалить выбранные шаги
- 90 027 пробел : Открыть настройки и результаты выбранного шага
- shift / команда : удерживайте, чтобы выбрать несколько шагов (щелкните их)
- shift + щелкните и перетащите: выберите несколько шагов в ограничивающей рамке
- щелкните правой кнопкой мыши : добавьте карту
- клавиши со стрелками : перемещение выбранного шага(ов) по сетке
- выход : выход из настроек и результатов выбранного шага
- f : поиск пути домой – перемещение холста к ближайшему шагу
- ⌘+Z (в macOS) и Ctrl+Z (в Windows): отменить последнее изменение 27 Shift+ Ctrl+Z (в Windows): повторить последнее изменение
- s или / : Откройте вкладку поиска панели инструментов Builder и начните вводить
- escape : Закройте панель инструментов Builder
- 9002 Вкладка 7: переход между разделами Integrations, Transforms и Cards
- клавиши со стрелками : переход к выделенному шагу или карточке
- ввод/возврат : добавление выделенного шага или карточки
0025
Информацию о редактировании и обновлении потока см.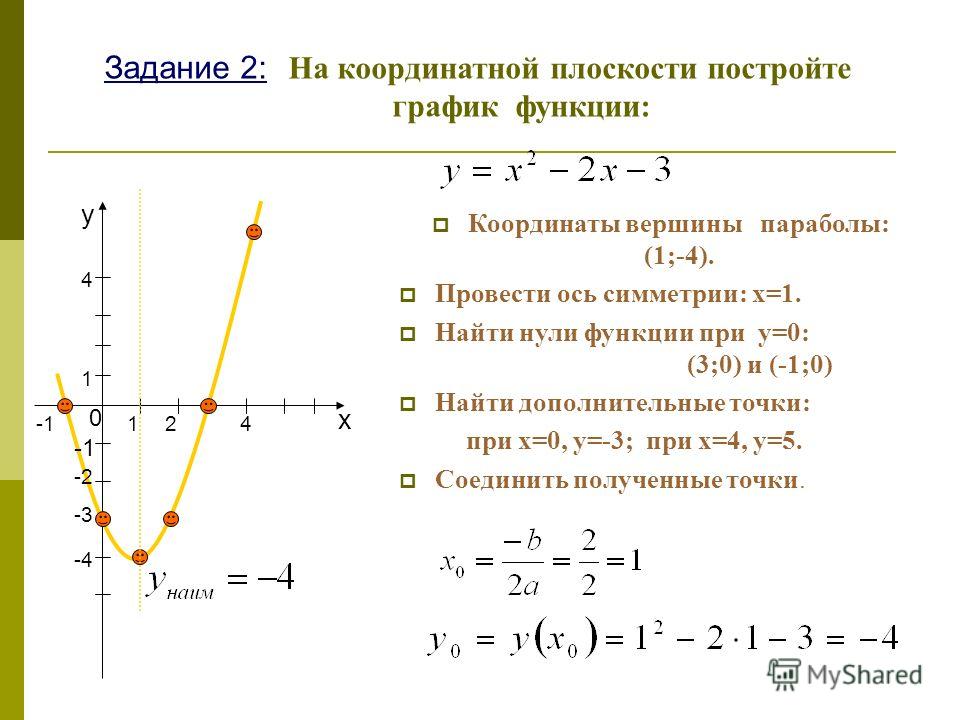
в следующей статье Обновление и запуск потока.
Как сделать параболическую тарелку для микрофона
Видеооператоры знают, что правило номер один для записи высококачественного звука — расположить микрофон как можно ближе к объекту съемки. В большинстве случаев это означает размещение звукоснимателя в нескольких дюймах от источника звука. Мы можем пойти на многое, чтобы расположить наши микрофоны как можно ближе к объектам съемки. Но иногда это не выход. Бывают случаи, когда вы просто не можете расположить микрофон близко к объекту съемки. Введите параболический микрофон.
Возможно, вам нужно запечатлеть крики койотов или песни пересмешников. Может быть, вы хотите записать темп квотербека (без захвата себя). Или, может быть, вам нужно потихоньку обезопасить свой звук, как шпион, для вашего шоу со скрытой камерой и криминалом. Иногда для производства требуется, чтобы вы приблизили этот микрофон, но это может поставить под угрозу вашу жизнь, повредить ваше оборудование или раскрыть ваше прикрытие.
Параболическая антенна для микрофона может быть самым звуковым решением.
Микрофон Para-what-ic?
Параболическая тарелка — это математическое чудо, которое собирает и фокусирует световые и звуковые волны в одной точке. Они используются в фарах, солнечных плитах и приемниках спутникового телевидения. Параболическая тарелка микрофона использует геометрию, чтобы превратить обычный микрофон в сверхнаправленный микрофон-монстр. Это позволяет записывать чистый звук на расстоянии нескольких сотен футов. Если вы не снимаете видео о спорте или дикой природе, вы можете использовать параболическую установку только в редких случаях.
Реклама
Если вы не готовы инвестировать в профессиональную параболу, вы можете сделать свою собственную параболическую антенну для микрофона. Для этого потребуется всего несколько простых инструментов и материалов, которые у вас уже могут быть. Ваша самодельная параболическая тарелка может работать не так хорошо, как профессионально изготовленная модель.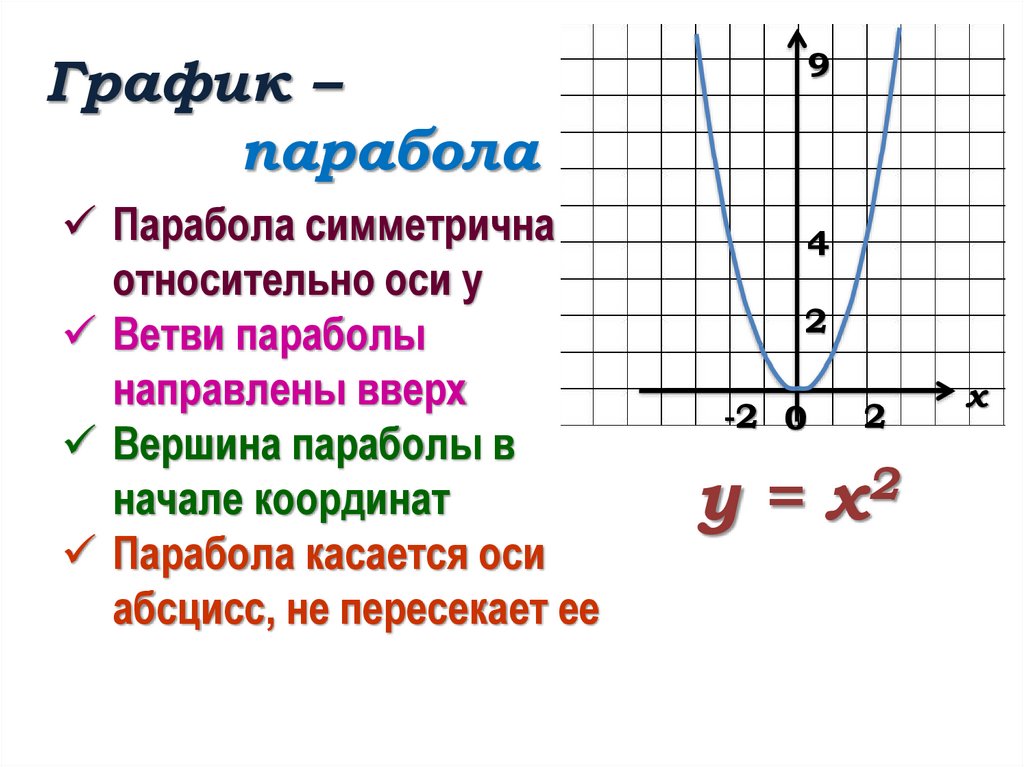
Это решение значительно улучшит вашу способность улавливать звуковые волны и может обеспечить всю необходимую вам мощность. Перед началом сборки важно знать, как работает параболическая антенна для микрофона.
Параболический микрофон Наука
Параболического микрофона не существует. Когда мы говорим о параболическом микрофоне, мы на самом деле имеем в виду запись звука с помощью обычного микрофона, усиленного параболической тарелкой. Парабола — это определенная геометрическая кривая, обладающая определенным математическим свойством. Когда прямая линия достигает какой-либо точки на внутренней поверхности параболической кривой, она отражается от склона в единую общую точку с центром перед кривой. Это положение является фокусом параболы.
С точки зрения звука это означает, что когда несколько звуковых волн от источника звука ударяются о наклонную внутреннюю стенку тарелки, они отражаются обратно в сфокусированное положение перед диском. Когда шквал звуковых волн попадает на параболическую тарелку, волны собираются вместе в фокусе.
Обычный микрофон в правильном положении может зафиксировать удивительное аналоговое усиление источника звука.
Выбор микрофона
Характеристики и функциональность параболической антенны для микрофона больше зависят от формы и конструкции, чем от качества самого микрофона. Однако наличие хорошего микрофона не помешает.
Передатчик с беспроводным микрофоном лежит на столе рядом с параболической тарелкой, сделанной своими руками. Для записи звука с параболической антенны подойдет любой обычный микрофон. Обычно с параболической тарелкой используются два типа микрофонов. Одним из вариантов является микрофон с направленной кардиоидной диаграммой направленности, такой как ручной микрофон. Другой вариант — использовать небольшой микрофон, например, петличный, со всенаправленной диаграммой направленности. В любом случае микрофон обычно крепится на кронштейне, который подвешивает его в фокусе тарелки. Элемент звукоснимателя обращен в чашу параболы. Мы решили использовать меньший по размеру и легкий беспроводной петличный микрофон.
Из-за всенаправленной схемы звукоснимателя мы добавили небольшую круглую заднюю пластину. Это поможет сфокусировать петлич на записи отраженного источника звука. Для записи звука мы подключили нашу беспроводную петличку к входу XLR нашей видеокамеры. Вы можете использовать любой портативный аудиомагнитофон, если хотите.
Положение микрофона
Ключом к записи наилучшего звука с вашей параболической тарелки является расположение микрофона прямо в фокусе отражения перед параболой. Сладкое пятно варьируется от блюда к блюду в зависимости от его глубины и диаметра. Мы хотели попробовать разные блюда. Мы установили наш петличный браслет на кронштейн C-образной стойки, чтобы мы могли легко перемещать его. Во время прослушивания в наушниках мы определили идеальное место для каждой тарелки.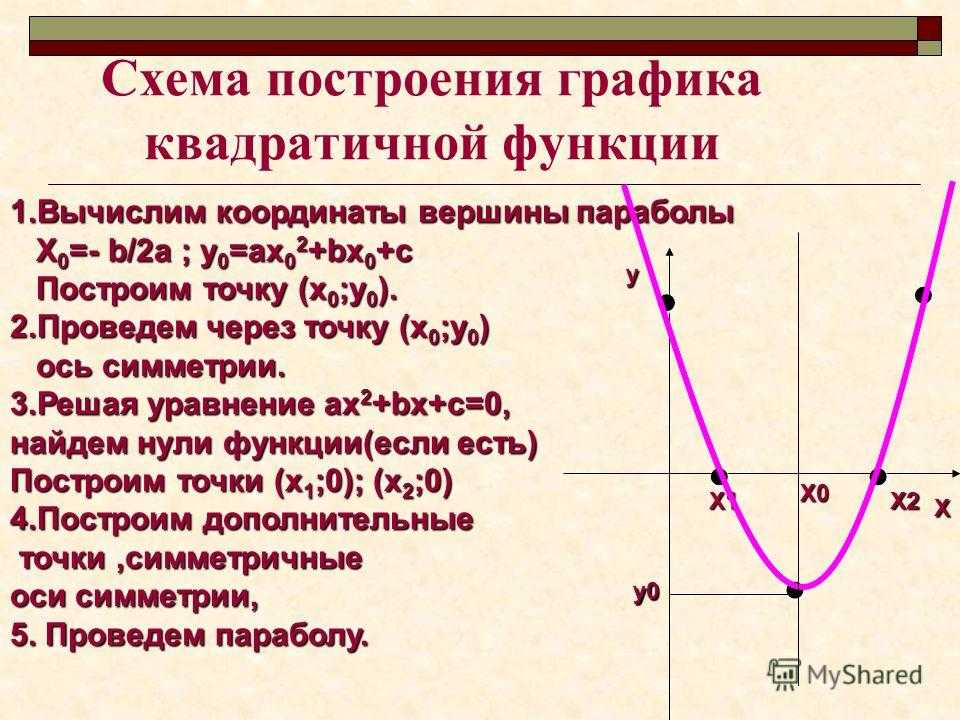
После того, как вы определили точку фокуса параболической антенны, выполните измерение и прикрепите опорный кронштейн, чтобы использовать его в качестве постоянного крепления для микрофона.
Выбор параболического микрофона
Самой важной частью параболического микрофона является антенна. Параболическая антенна для микрофона работает не как воронка или мегафон, а как отражатель звуковых волн. Размер, форма и материал чаши влияют на ее отражательную способность. Во многих конструкциях, сделанных своими руками, используются зонтики, сковороды, крышки для воков и другие инструменты для приготовления пищи. Вы можете использовать любой из них для создания параболической антенны для микрофона, которая улучшит характеристики вашего микрофона на большом расстоянии. Некоторые варианты лучше других. Как правило, вы хотите, чтобы блюдо имело баланс трех свойств: твердой поверхности, большого размера и правильной кривизны.
Параболическая тарелка использует геометрию, чтобы превратить обычный микрофон в сверхнаправленного монстра, способного записывать чистый звук на расстоянии нескольких сотен футов.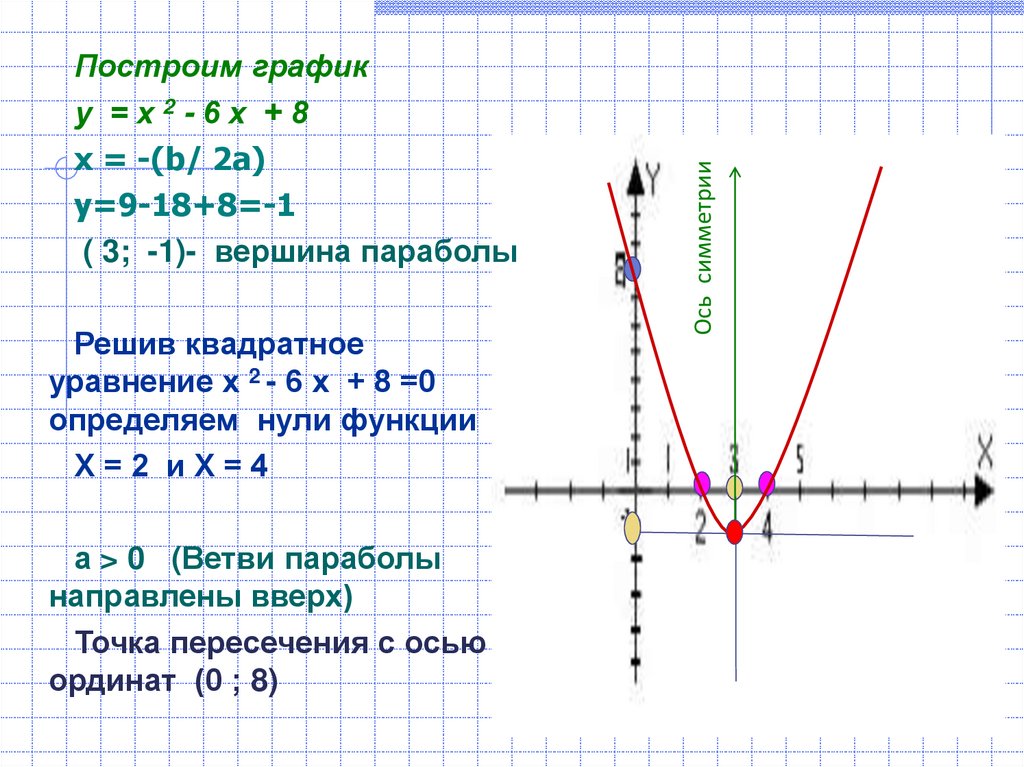
Кривая:
Поскольку истинная парабола представляет собой особую геометрическую кривую, немногие домашние блюда имеют полностью параболические характеристики. Хитрость заключается в том, чтобы найти тарелку, которая точно соответствует форме настоящей параболы. Если у вас есть доступ к старой спутниковой антенне, у вас есть отличный вариант. Хотя эти приемники имеют внеосевой фокус, они представляют собой функционирующую параболу. Тем не менее, тарелка любой формы будет в определенной степени улавливать звуковые волны. Для достижения наилучших результатов выберите ту, у которой плавно изогнутое дно, а не плоское.
Материал:
Идеальный материал для параболической антенны микрофона должен быть жестким и толстым, но легким. Пластиковая, акриловая и металлическая посуда обладает высокой отражающей способностью. Они не пропускают звуковые волны, что делает их более предпочтительным выбором. Посуда с отверстиями, например дуршлаг, не является хорошим отражателем, даже если она имеет правильную форму.
При тщательном осмотре тонкостенная металлическая посуда может вызвать небольшой металлический звон. Блюдо из толстого пластика или подобного материала может быть лучшим выбором.
Размер:
Звук, записанный с параболических микрофонных тарелок, обычно имеет низкочастотную характеристику. Это связано с наукой о звуковых волнах. Маленькие параболические тарелки просто не способны записывать весь спектр звука, необходимый для записи звука с полной точностью. Однако наука о звуковых волнах предполагает, что если все остальные аспекты тарелки идентичны. Большая парабола могла бы захватить низкие частоты. Так что больше на самом деле лучше. Тем не менее, тарелка, скорее всего, будет непрактично большой, прежде чем в этом случае можно будет записать хороший низкокачественный звук.
Лучший способ найти тарелку, которая одинаково хорошо отвечает всем трем критериям, — это купить настоящую параболическую тарелку у дилера. Профессиональные параболические тарелки легко доступны, но они могут быть дорогостоящими.
Если вам нужна высококачественная параболическая тарелка для создания серьезного звука, обратите внимание на JonyShot от JonyJib. (1250 долларов США; микрофон не входит в комплект). Он включает в себя 24-дюймовую тарелку с ручками, монтажную пластину для штатива и изолированное крепление для микрофона. В качестве более доступного варианта вы можете приобрести тарелку дальнего радиуса действия Sound Shark SS1. При этом используется стандартный петличный за 285 долларов.
Использование параболической тарелки
Крупным планом видеооператор в наушниках.Единственный способ убедиться, что вы записываете сильный и четкий сигнал, — это надеть наушники, чтобы вы могли контролировать источник звука и вносить коррективы во время записи. В зависимости от того, насколько далеко вы находитесь от объекта, даже небольшой поворот тарелки может сместить микрофон с цели, поэтому для записи требуется активный и внимательный оператор.
Тесты параболической микрофонной тарелки
Набор тестовых устройств: чаша для попкорна, зонт, сковорода, параболическая отражающая тарелка и крышка мусорного бака.
Для нашего проекта мы протестировали пять вариантов домотканых тарелок, чтобы определить, какой из них лучше всего построить:
- 6-дюймовая сковорода для омлета
- 10,5-дюймовый алюминиевый кожух для освещения магазина
- 12-дюймовая пластиковая чаша для попкорна
- 22-дюймовая пластиковая крышка мусорного бака
- 45-дюймовый зонт для гольфа
Наши тесты проводились путем воспроизведения двух разных саундтреков, циклического стрекотания сверчков, а затем музыкальной кровати на расстоянии примерно 30 футов. Мы прикрепили проверенный ручной кардиоидный микрофон и петличный микрофон к стойке C-стойки, направленной на наши тарелки, и слушали через наушники. Мы записали образцы, используя каждую чашку, а затем вернулись в монтажный отсек, чтобы проанализировать наши выводы. Хотя сложно оценить сравнительное качество во время записи, мы заметили явную разницу в частотной характеристике после загрузки клипов в наше приложение для редактирования и воспроизведения их на студийных мониторах.
На основе наших тестов мы определили, что наша 22-дюймовая крышка мусорного бака работает лучше всего. Его большой диаметр, равномерный изгиб и пластиковая конструкция помогли превзойти по производительности другие протестированные нами блюда. В этом тесте мы также узнали, где должен располагаться наш микрофон, поэтому обратите внимание на это во время тестов.
Сборка микрофона
Выбрав тарелку, пришло время собрать параболический микрофон своими руками. Вот что вам понадобится для тарелки, предназначенной для петличного микрофона. Мы выбрали этот вариант, так как он был легким и беспроводным. Если бы мы выбрали кардиоидный микрофон, нам бы понадобилось амортизирующее крепление, очень похожее на микрофон-пушку.
Набор финальных деталей для нашей параболической антенны для микрофона, сделанной своими руками.Материалы
- 22 дюйма пластик 32 гал. крышка мусорного бака
- 6-дюймовая полоса гибкого металлического ремня шириной 1/2 дюйма
- деревянный дюбель 24 x 1/4 дюйма
- крышка молочного кувшина
инструменты
- ножницы по металлу 90 007 Малая ножовка
- Лента клейкая
В дополнение к желаемому размеру и форме крышки, которую мы выбрали, мы обнаружили, что ее ручки идеально подходят для захвата; поэтому не было необходимости добавлять ручки.
Нам просто нужно было построить перекладину и крепление для микрофона.
Сборка
Во-первых, с помощью ножовки мы вырезаем кусок 1/4-дюймового дюбеля, примерно такого же диаметра, как крышка мусорного бака, чтобы он плотно входил в пазы на внутренней стороне ручки. Затем мы использовали клейкую ленту, чтобы закрепить его на месте. Поперечный стержень упал чуть южнее центра нашей крышки, охватывая нашу тарелку на 1 1/4 дюйма от средней линии.
Крупный план лабораторного микрофона, прикрепленного к металлической полосе, направленной внутрь мусорного бака параболическая тарелка. Затем с помощью ножниц по металлу мы отрезаем 6-дюймовый кусок гибкого плоского металлического ремня, который будет служить нашим центральным удлинением. держать петличный микрофон. Мы обернули один конец ремня вокруг центра дюбеля и закрепили его клейкой лентой. Затем мы придали ей небольшую кривую, наклонив ее вверх и наружу, чтобы она совпадала с центром нашей тарелки. Примерно в восьми дюймах от его нижней центральной точки, лежа на спине, мы прикрепили элемент звукоснимателя беспроводного петличного петлителя к нашему креплению.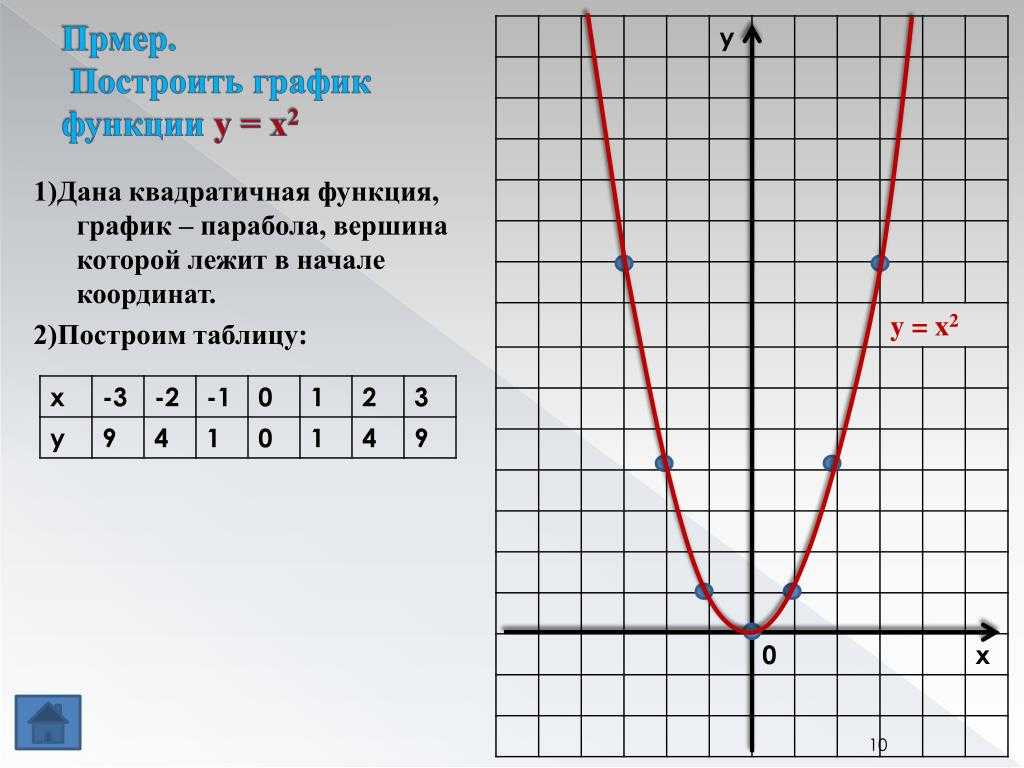
Закрепив шнур вдоль дюбеля и вокруг задней части тарелки скотчем, мы оставили достаточно провода, чтобы передатчик можно было закрепить на ремне оператора. Наконец, мы прикрепили 2-дюймовую крышку от молочного кувшина к задней части крепления микрофона. Это поможет направить всенаправленную схему захвата петличного микрофона обратно в тарелку.
Результаты
В то время как наше исследование заняло несколько часов, сама сборка заняла менее 30 минут. Общая стоимость проекта, за вычетом крышки от мусорного ведра, которая была у нас под рукой, но включая молоко, составила менее 25 долларов. Так что попробуйте. Если у вас нет крышки от мусорного ведра, которую можно было бы посвятить, используйте любую посуду, с которой вы можете справиться, или найдите профессионально сформированную параболу. Проявив немного творчества и немного простых научных данных, вы сможете использовать самодельный параболический параболический микрофон уже через час или около того.
Параболические микрофоны и футбол
Наиболее заметное место, где можно увидеть профессиональную параболическую микрофонную тарелку, находится в кулуарах футбольного матча NFL или NCAA.