Произведение синусов и косинусов: формулы, примеры
В данной статье рассмотрены формулы произведения синусов, косинусов, а также формулы произведения синуса на косинус. Допустим, есть необходимость вычислить произведение синусов или косинусов углов α и β. Формулы произведения позволяют перейти от произведения к сумме или разности синусов и косинусов углов α+β и α-β.
Приведем формулы произведения синуса на синус, косинуса на косинус и синуса на косинус.
Формулы произведения. Список
Приведем формулировки, а затем и сами формулы.
- Произведение синусов углов α и β равно полуразности косинуса угла α-β и косинуса угла α+β.
- Произведение косинусов углов α и β равно полусумме косинуса угла α-β и косинуса угла α+β.
- Произведение синуса угла α на косинус угла β равно полусумме синуса угла α-β и синуса угла α+β.
Для любых α и β справедливы формулы
- sin α·sin β=12cosα-β-cosα+β;
- cos α·cos β=12cosα-β+cosα+β;
- sin α·cos β=12sinα-β+sinα+β.

Вывод формул
Вывод описанных выше формул проводится с помощью формул сложения и на основе свойства равенства. Согласно этому свойству, если левую и правую части верного равенства сложить соответственно с левой и правой частями другого верного равенста, то в результате получится еще одно верное равенство. Покажем вывод формул произведения.
Сначала запишем формулы косинуса суммы и косинуса разности:
cosα+β=cos α·cos β-sin α·sin βcosα-β=cos α·cos β+sin α·sin β
Сложим эти равенства и получим:
cosα+β+cosα-β=cos α·cos β-sin α·sin β+cos α·cos β+sin α·sin βcosα+β+cosα-β=2·cos α·cos β
Отсюда
cos α·cos β=12cosα+β+cosα-β
Формула произведения косинусов доказана.
Перепишем формулу косинуса суммы следующим образом:
-cos(α+β)=-cos α·cosβ+sin α·sinβ
Добавим к равенству формулу cosα-β=cos α·cos β+sin α·sinβ.
Получим:
-cos(α+β)+cosα-β=-cos α·cosβ+sin α·sinβ+cos α·cos β+sin α·sinβ-cos(α+β)+cosα-β=2·sin α·sinβsin α·sinβ=12(cosα-β-cos(α+β))
Таким образом, выведена формула произведения синусов.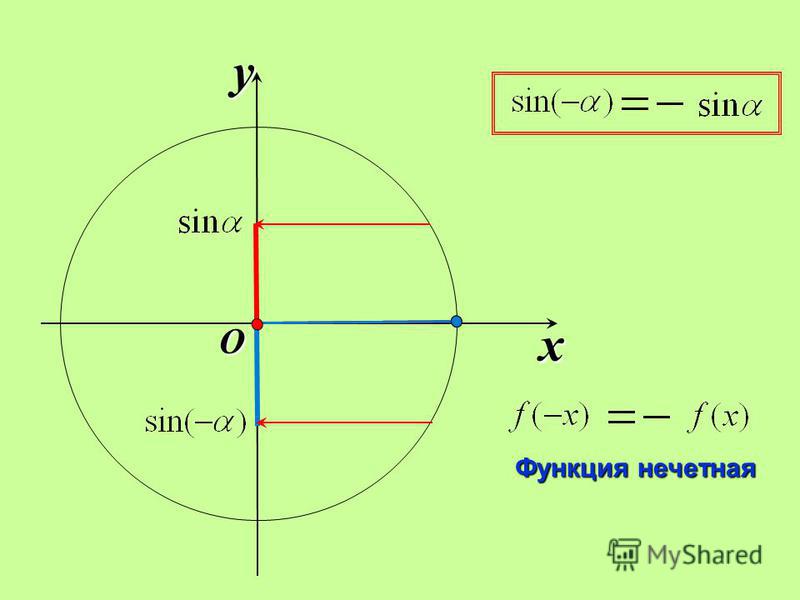
Теперь возьмем формулу синуса суммы, формулу синуса разности, и сложим их левые и правые части
sinα+β=sin α·cos β+cos α·sin βsinα-β=sin α·cos β-cos α·sin βsinα+β+sinα-β=sin α·cos β+cos α·sin β+sin α·cos β-cos α·sin βsinα+β+sinα-β=2sin α·cos βsin α·cos β=12(sinα+β+sinα-β)
Формула произведения синуса на косинус выведена.
Примеры использования
Приведем примеры использования формул произведения синусов, косинусов и синусов на косинус при решении задач.
Пусть α=60°, β=30°. Возьмем формулу произведения синусов и подставим в нее конкретные значения.
sin α·sin β=12(cosα-β-cosα+β)sin 60°·sin 30° =12(cos60°-30°-cos60°+30°)sin 60°·sin 30°=12(cos30°-cos90°)sin 60°·sin 30°=12(32-0)=34
Теперь вычислим значение выражения, обратившись к таблице основных значений тригонометрических функций.
sin60°·sin30°=32·12=34.
Таким образом, мы проверили формулу на практике и убедились, что формула справедлива.
Пример. Формулы произведения
Формулы произведенияНужно sin 75° умножить на cos 15° и вычислить точное значение произведения.
Мы не располагаем точными значениями синуса и косинуса данных углов, однако можем вычислить точное значение произведения sin 75°·cos 15° c помощью формулы произведения синуса на косинус.
sin 75°·cos 15°=12sin(75°-15°+sin(75°+15°))sin 75°·cos 15°=12sin60°+sin90°=1232+1=3+24
Также формулы произведения используются преобразования тригонометрических выражений.
Автор: Ирина Мальцевская
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
| 1 | Trovare la Derivata — d/dx | натуральный логарифм x | |
| 2 | Вычислим интеграл | интеграл натурального логарифма x по x | |
| 3 | Trovare la Derivata — d/dx | e^x | |
| 4 | Вычислим интеграл | интеграл e^(2x) по x | |
| 5 | Trovare la Derivata — d/dx | 1/x | |
| 6 | Trovare la Derivata — d/dx | x^2 | |
| 7 | Trovare la Derivata — d/dx | 1/(x^2) | |
| 8 | Trovare la Derivata — d/dx | sin(x)^2 | |
| 9 | Trovare la Derivata — d/dx | sec(x) | |
| 10 | Вычислим интеграл | интеграл e^x по x | |
| 11 | Вычислим интеграл | интеграл x^2 по x | |
| 12 | Вычислим интеграл | интеграл квадратного корня из x по x | |
| 13 | Trovare la Derivata — d/dx | cos(x)^2 | |
| 14 | Вычислим интеграл | интеграл 1/x по x | |
| 15 | Вычислим интеграл | интеграл sin(x)^2 по x | |
| 16 | Trovare la Derivata — d/dx | x^3 | |
| 17 | Trovare la Derivata — d/dx | sec(x)^2 | |
| 18 | Вычислим интеграл | интеграл cos(x)^2 по x | |
| 19 | Вычислим интеграл | интеграл sec(x)^2 по x | |
| 20 | Trovare la Derivata — d/dx | e^(x^2) | |
| 21 | Вычислим интеграл | интеграл в пределах от 0 до 1 кубический корень из 1+7x по x | |
| 22 | Trovare la Derivata — d/dx | sin(2x) | |
| 23 | Trovare la Derivata — d/dx | tan(x)^2 | |
| 24 | Вычислим интеграл | интеграл 1/(x^2) по x | |
| 25 | Trovare la Derivata — d/dx | 2^x | |
| 26 | График | натуральный логарифм a | |
| 27 | Trovare la Derivata — d/dx | cos(2x) | |
| 28 | Trovare la Derivata — d/dx | xe^x | |
| 29 | Вычислим интеграл | интеграл 2x по x | |
| 30 | Trovare la Derivata — d/dx | ( натуральный логарифм от x)^2 | |
| 31 | Trovare la Derivata — d/dx | натуральный логарифм (x)^2 | |
| 32 | Trovare la Derivata — d/dx | 3x^2 | |
| 33 | Вычислим интеграл | интеграл xe^(2x) по x | |
| 34 | Trovare la Derivata — d/dx | 2e^x | |
| 35 | Trovare la Derivata — d/dx | натуральный логарифм 2x | |
| 36 | Trovare la Derivata — d/dx | -sin(x) | |
| 37 | Trovare la Derivata — d/dx | 4x^2-x+5 | |
| 38 | Trovare la Derivata — d/dx | y=16 корень четвертой степени из 4x^4+4 | |
| 39 | Trovare la Derivata — d/dx | 2x^2 | |
| 40 | Вычислим интеграл | интеграл e^(3x) по x | |
| 41 | Вычислим интеграл | интеграл cos(2x) по x | |
| 42 | Trovare la Derivata — d/dx | 1/( квадратный корень из x) | |
| 43 | Вычислим интеграл | интеграл e^(x^2) по x | |
| 44 | Вычислить | e^infinity | |
| 45 | Trovare la Derivata — d/dx | x/2 | |
| 46 | Trovare la Derivata — d/dx | -cos(x) | |
| 47 | Trovare la Derivata — d/dx | sin(3x) | |
| 48 | Trovare la Derivata — d/dx | 1/(x^3) | |
| 49 | Вычислим интеграл | интеграл tan(x)^2 по x | |
| 50 | Вычислим интеграл | интеграл 1 по x | |
| 51 | Trovare la Derivata — d/dx | x^x | |
| 52 | Trovare la Derivata — d/dx | x натуральный логарифм от x | |
| 53 | Trovare la Derivata — d/dx | x^4 | |
| 54 | Оценить предел | предел (3x-5)/(x-3), если x стремится к 3 | |
| 55 | Вычислим интеграл | интеграл x^2 натуральный логарифм x по x | |
| 56 | Trovare la Derivata — d/dx | f(x) = square root of x | |
| 57 | Trovare la Derivata — d/dx | x^2sin(x) | |
| 58 | Вычислим интеграл | интеграл sin(2x) по x | |
| 59 | Trovare la Derivata — d/dx | 3e^x | |
| 60 | Вычислим интеграл | интеграл xe^x по x | |
| 61 | Trovare la Derivata — d/dx | y=x^2 | |
| 62 | Trovare la Derivata — d/dx | квадратный корень из x^2+1 | |
| 63 | Trovare la Derivata — d/dx | sin(x^2) | |
| 64 | Вычислим интеграл | интеграл e^(-2x) по x | |
| 65 | Вычислим интеграл | интеграл натурального логарифма квадратного корня из x по x | |
| 66 | Trovare la Derivata — d/dx | e^2 | |
| 67 | Trovare la Derivata — d/dx | x^2+1 | |
| 68 | Вычислим интеграл | интеграл sin(x) по x | |
| 69 | Trovare la Derivata — d/dx | arcsin(x) | |
| 70 | Оценить предел | предел (sin(x))/x, если x стремится к 0 | |
| 71 | Вычислим интеграл | интеграл e^(-x) по x | |
| 72 | Trovare la Derivata — d/dx | x^5 | |
| 73 | Trovare la Derivata — d/dx | 2/x | |
| 74 | Trovare la Derivata — d/dx | натуральный логарифм 3x | |
| 75 | Trovare la Derivata — d/dx | x^(1/2) | |
| 76 | Trovare la Derivata — d/d@VAR | f(x) = square root of x | |
| 77 | Trovare la Derivata — d/dx | cos(x^2) | |
| 78 | Trovare la Derivata — d/dx | 1/(x^5) | |
| 79 | Trovare la Derivata — d/dx | кубический корень из x^2 | |
| 80 | Вычислим интеграл | интеграл cos(x) по x | |
| 81 | Вычислим интеграл | интеграл e^(-x^2) по x | |
| 82 | Trovare la Derivata — d/d@VAR | f(x)=x^3 | |
| 83 | Вычислим интеграл | интеграл 4x^2+7 в пределах от 0 до 10 по x | |
| 84 | Вычислим интеграл | интеграл ( натуральный логарифм x)^2 по x | |
| 85 | Trovare la Derivata — d/dx | логарифм x | |
| 86 | Trovare la Derivata — d/dx | arctan(x) | |
| 87 | Trovare la Derivata — d/dx | натуральный логарифм 5x | |
| 88 | Trovare la Derivata — d/dx | 5e^x | |
| 89 | Trovare la Derivata — d/dx | cos(3x) | |
| 90 | Вычислим интеграл | интеграл x^3 по x | |
| 91 | Вычислим интеграл | интеграл x^2e^x по x | |
| 92 | Trovare la Derivata — d/dx | 16 корень четвертой степени из 4x^4+4 | |
| 93 | Trovare la Derivata — d/dx | x/(e^x) | |
| 94 | Оценить предел | предел arctan(e^x), если x стремится к 3 | |
| 95 | Вычислим интеграл | интеграл (e^x-e^(-x))/(e^x+e^(-x)) по x | |
| 96 | Trovare la Derivata — d/dx | 3^x | |
| 97 | Вычислим интеграл | интеграл xe^(x^2) по x | |
| 98 | Trovare la Derivata — d/dx | 2sin(x) | |
| 99 | Вычислить | sec(0)^2 | |
| 100 | Trovare la Derivata — d/dx | натуральный логарифм x^2 |
| 1 | Найти производную — d/dx | бревно натуральное х | |
| 2 | Оценить интеграл | интеграл натурального логарифма x относительно x | |
| 3 | Найти производную — d/dx | 92)||
| 21 | Оценить интеграл | интеграл от 0 до 1 кубического корня из 1+7x относительно x | |
| 22 | Найти производную — d/dx | грех(2x) | |
| 23 | Найти производную — d/dx | 9(3x) по отношению к x||
| 41 | Оценить интеграл | интеграл от cos(2x) относительно x | |
| 42 | Найти производную — d/dx | 1/(корень квадратный из х) | |
| 43 | Оценка интеграла 9бесконечность | ||
| 45 | Найти производную — d/dx | х/2 | |
| 46 | Найти производную — d/dx | -cos(x) | |
| 47 | Найти производную — d/dx | грех(3x) | 92+1|
| 68 | Оценить интеграл | интеграл от sin(x) по x | |
| 69 | Найти производную — d/dx | угловой синус(х) | |
| 70 | Оценить предел | ограничение, когда x приближается к 0 из (sin(x))/x 92 по отношению к х | |
| 85 | Найти производную — d/dx | лог х | |
| 86 | Найти производную — d/dx | арктан(х) | |
| 87 | Найти производную — d/dx | бревно натуральное 5х92 |
Тригонометрические функции.
 Доктора математики
Доктора математики(Архивный вопрос недели)
В прошлый раз мы рассмотрели некоторые детали, которые редко упоминаются при формулировании правил интерпретации алгебраических выражений. Я не уместился в обсуждении самого сложного случая: тригонометрических функций, которые при записи без круглых скобок, как это было традиционно, могут вызвать несколько вопросов. (Многое из того же верно и для логарифмов.)
Тригонометрические функции без скобок
Порядок произведений, мощностей и параметров тригонометрических функцийПытаюсь уточнить порядок операций применительно к тригонометрическим функциям. Я хочу знать, каков правильный порядок операций для такого выражения, как sin2x. Когда мы знаем, что умножение подразумевается? Когда в моем учебнике написано sin2x, я знаю, что это означает sin(2x). Но часто скобки отсутствуют. Правильно ли тогда предположить, что умножение всегда подразумевается в круглых скобках? Если это так, не означает ли это, что sinxcosy следует читать как sin(xcosy)? (Я тоже видел это в своем учебнике, но я знаю, что должен интерпретировать это как (sinx) (уютно).
) Я знаю, что всегда следует включать символы группировки, чтобы избежать двусмысленности; но когда их нет, как правильно интерпретировать эти выражения?
Если триггерные функции были написаны с использованием обычных обозначений для функций, т.е. \(\sin(2x)\), проблем не будет. Но тригонометрические функции возникли раньше современной записи функций (или даже понятия функции), и старая запись была «унаследована», так что, хотя сегодня многие авторы рекомендуют всегда использовать круглые скобки, старая форма по-прежнему распространена. Как указал Джим, если, как в \(\sin 2x\), умножение имеет приоритет над функцией (как если бы оно было в круглых скобках), то \(\sin x \cos y\), по-видимому, подразумевает, что умножение произошло до применения функции синуса, что сделало его \(\sin(x \cos y)\). И я никогда не видел «официального» объяснения этому.
Никаких правил, только люди
Я ответил:
Я обдумывал это несколько раз, и мой собственный вывод таков, что правил не существует .Здесь мы рассматриваем язык, который развился не по преднамеренному замыслу, а органично — с согласия его пользователей — точно так же, как развивается любой естественный язык. Лингвисты могут изучать язык, чтобы выяснить его правила, но по сути они реконструируют то, что существует без явных правил. Вы можете увидеть некоторые из этих разработок в порядке операций здесь: История порядка операций http://mathforum.org/library/drmath/view/52582.html
Все, что лингвист может сделать, чтобы понять язык, — это изучить, как его используют его носители. Языки (за исключением нескольких «искусственных языков») не изобретаются с готовым сводом правил, а органически развиваются по мере того, как люди говорят на них, постоянно меняясь. Большая часть изучаемой нами английской грамматики, которая предположительно состоит из определенного набора правил, на самом деле была навязана английскому языку учеными, которые считали, что любой допустимый язык должен соответствовать категориям, известным из латыни, в результате чего она часто не соответствует как мы говорим на самом деле.
Это, конечно, не главный вопрос, который мы обсуждаем, но он иллюстрирует тот факт, что нотация тригонометрии идиосинкразична и приемлема в основном потому, что «мы знаем ее, когда видим», не нуждаясь в правилах.
Правило здравого смысла
Я думаю, чтоосновное правило здравого смысла лежит в основе расхлябанности в использовании других форм, таких как второй и третий примеры, которые вы упомянули: грех 2x означает грех (2x) sin x cos y означает sin(x)cos(y) Они означают то, что они делают, просто потому, что мы знаем достаточно, чтобы НЕ ожидать, что sin 2x будет означать sin(2)*x sin x cos y будет означать sin(x*cos(y)) Возможно, есть также немного типографского рассмотрения : расстояние обычно предполагает, что 2x принадлежит как единое целое, как и sinx и cosy во втором примере.
В современных учебниках (особенно по математическому анализу) могут быть сложные выражения, составленные только для того, чтобы проверить свои навыки, без ссылки на то, будут ли они когда-либо действительно использованы; в таком контексте здравый смысл может оказаться бесполезным! Тогда применяется другая часть здравого смысла: когда есть возможность неправильного толкования, используйте круглые скобки. И наоборот, если выражение не имеет круглых скобок, предполагается, что автор хотел, чтобы оно читалось наиболее естественным образом (что бы это ни было).
Таким образом, можно проанализировать все употребления с лингвистической точки зрения и установить некоторые правила, например, «умножение предшествует тригонометрическим функциям, за исключением случаев, когда другая триггерная функция является множителем». Но что мы действительно делаем, читая эти выражения, так это руководствуемся здравым смыслом, основанным на математическом опыте. Это вообще помогает?
Другими словами, я не думал, что стоит пытаться придумать полный набор правил. 2-2)(8x)]
Я понимаю, что лучше всего использовать скобки и квадратные скобки, чтобы развеять любые сомнения, но было бы неправильно писать cos(a) (b), когда вы имеете в виду (b)cos(a)?
Когда круглые скобки не используются, например, с sin 2x, я знаю, что мы обычно принимаем это за sin(2x). Так что есть над чем подумать!
Бев
2-2)(8x)]
Я понимаю, что лучше всего использовать скобки и квадратные скобки, чтобы развеять любые сомнения, но было бы неправильно писать cos(a) (b), когда вы имеете в виду (b)cos(a)?
Когда круглые скобки не используются, например, с sin 2x, я знаю, что мы обычно принимаем это за sin(2x). Так что есть над чем подумать!
Бев
Это очень похоже на вопрос, на который я ответил, но с большим примером. Если бы мы когда-нибудь написали \(\cos(a)(b)\), то восприняли бы это как функцию произведения, как мы сделали бы с \(\cos ab\)? Если нет, то почему?
На самом деле есть быстрый ответ на этот конкретный вопрос: когда круглые скобки используются с функцией, они всегда заключают в себе весь аргумент. Тот факт, что круглые скобки необязательны для триггерных функций, не имеет значения; как только вы вообще используете круглые скобки, вы теряете право думать о них как о содержащих только один фактор аргумента.
Доктор Том вместо этого ответил на более важный вопрос:
Привет, Бев!
Хороший вопрос! Вы застали нас, математиков, со спущенными штанами. Я думаю, что в основном от лени мы даже пишем такие вещи
"грех х"
Почти любая другая функция, кроме тригонометрической (и, возможно, логарифмической), требует, чтобы параметры были заключены в круглые скобки.
Как только вы признаете законность такой формы, как «sin 2x», вы открываете банку с червями. Даже что-то вроде этого...
f (х) = грех х + соз х
Я думаю, что в основном от лени мы даже пишем такие вещи
"грех х"
Почти любая другая функция, кроме тригонометрической (и, возможно, логарифмической), требует, чтобы параметры были заключены в круглые скобки.
Как только вы признаете законность такой формы, как «sin 2x», вы открываете банку с червями. Даже что-то вроде этого...
f (х) = грех х + соз х
... тогда это могло означать, да?
f(x) = sin(x + cos(x)) Я думаю, все более или менее согласны с тем, что сложение обязательно выполняется после функции, так что \(\sin\alpha + \beta \ne \sin(\alpha + \бета)\). (С другой стороны, если известно, что \(\alpha\) и \(\beta\) являются углами, мы могли бы считать очевидным, что первая форма должна означать вторую, поскольку мы никогда не добавляем углы к отношениям.) Но такое правило обычно не указывается явно, и без таких правил возможно все.
Это прозвучит ужасно, но я так часто видел это небрежное использование, что просто «знаю», что имелось в виду.Мы, математики, просто делаем много «предполагаемой группировки». Например, ни один профессиональный математик никогда не напишет произведение таким образом: х2 Она всегда писала так: 2x Точно так же я бы никогда не написал... грех х 2 ... или даже (грех х)2 Я бы переместил 2 вперед, чтобы сделать это ... 2 грех х ... или это: 2 грех(х) Точно так же интерпретировать это... грех 2x ... поскольку «синус 2, умноженный на x» был бы очень необычным, поскольку во-первых, мы почти наверняка поместили бы «x» перед «sin 2»; и, во-вторых, если после «2» нет символа «градус», было бы невероятно маловероятно, что вы возьмете синус 2 радиана. 92\), потому что это просто не то, как мы пишем. Это способ устранить двусмысленность и добавить избыточность, чтобы мы могли распознавать ошибки. Аналогичное соглашение заключается в том, чтобы всегда писать радиальное в конце, чтобы убедиться, что винкулум не будет истолкован слишком далеко: \(2i\sqrt{3}\), а не \(2\sqrt{3}i\), что слишком похоже на \(2\sqrt{3i}\).


 )
Я знаю, что всегда следует включать символы группировки, чтобы избежать двусмысленности; но когда их нет, как правильно интерпретировать эти выражения?
)
Я знаю, что всегда следует включать символы группировки, чтобы избежать двусмысленности; но когда их нет, как правильно интерпретировать эти выражения? 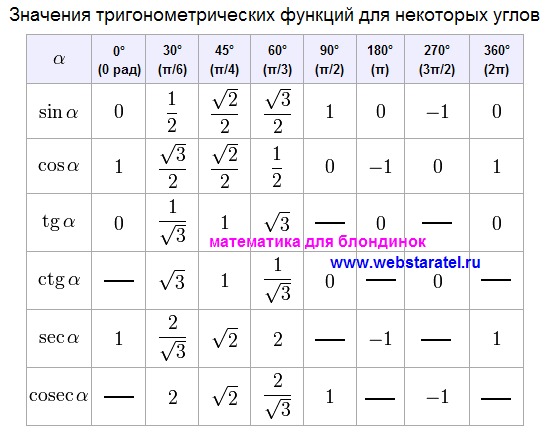 Здесь мы рассматриваем язык, который развился не по преднамеренному замыслу, а органично — с согласия его пользователей — точно так же, как развивается любой естественный язык. Лингвисты могут изучать язык, чтобы выяснить его правила, но по сути они реконструируют то, что существует без явных правил. Вы можете увидеть некоторые из этих разработок в порядке операций здесь:
История порядка операций
http://mathforum.org/library/drmath/view/52582.html
Здесь мы рассматриваем язык, который развился не по преднамеренному замыслу, а органично — с согласия его пользователей — точно так же, как развивается любой естественный язык. Лингвисты могут изучать язык, чтобы выяснить его правила, но по сути они реконструируют то, что существует без явных правил. Вы можете увидеть некоторые из этих разработок в порядке операций здесь:
История порядка операций
http://mathforum.org/library/drmath/view/52582.html 
 Я думаю, что в основном от лени мы даже пишем такие вещи
"грех х"
Почти любая другая функция, кроме тригонометрической (и, возможно, логарифмической), требует, чтобы параметры были заключены в круглые скобки.
Как только вы признаете законность такой формы, как «sin 2x», вы открываете банку с червями. Даже что-то вроде этого...
f (х) = грех х + соз х
Я думаю, что в основном от лени мы даже пишем такие вещи
"грех х"
Почти любая другая функция, кроме тригонометрической (и, возможно, логарифмической), требует, чтобы параметры были заключены в круглые скобки.
Как только вы признаете законность такой формы, как «sin 2x», вы открываете банку с червями. Даже что-то вроде этого...
f (х) = грех х + соз х
 Мы, математики, просто делаем много «предполагаемой группировки». Например, ни один профессиональный математик никогда не напишет произведение таким образом:
х2
Она всегда писала так:
2x
Точно так же я бы никогда не написал...
грех х 2
... или даже
(грех х)2
Я бы переместил 2 вперед, чтобы сделать это ...
2 грех х
... или это:
2 грех(х)
Точно так же интерпретировать это...
грех 2x
... поскольку «синус 2, умноженный на x» был бы очень необычным, поскольку во-первых, мы почти наверняка поместили бы «x» перед «sin 2»; и, во-вторых, если после «2» нет символа «градус», было бы невероятно маловероятно, что вы возьмете синус 2 радиана. 92\), потому что это просто не то, как мы пишем. Это способ устранить двусмысленность и добавить избыточность, чтобы мы могли распознавать ошибки. Аналогичное соглашение заключается в том, чтобы всегда писать радиальное в конце, чтобы убедиться, что винкулум не будет истолкован слишком далеко: \(2i\sqrt{3}\), а не \(2\sqrt{3}i\), что слишком похоже на \(2\sqrt{3i}\).
Мы, математики, просто делаем много «предполагаемой группировки». Например, ни один профессиональный математик никогда не напишет произведение таким образом:
х2
Она всегда писала так:
2x
Точно так же я бы никогда не написал...
грех х 2
... или даже
(грех х)2
Я бы переместил 2 вперед, чтобы сделать это ...
2 грех х
... или это:
2 грех(х)
Точно так же интерпретировать это...
грех 2x
... поскольку «синус 2, умноженный на x» был бы очень необычным, поскольку во-первых, мы почти наверняка поместили бы «x» перед «sin 2»; и, во-вторых, если после «2» нет символа «градус», было бы невероятно маловероятно, что вы возьмете синус 2 радиана. 92\), потому что это просто не то, как мы пишем. Это способ устранить двусмысленность и добавить избыточность, чтобы мы могли распознавать ошибки. Аналогичное соглашение заключается в том, чтобы всегда писать радиальное в конце, чтобы убедиться, что винкулум не будет истолкован слишком далеко: \(2i\sqrt{3}\), а не \(2\sqrt{3}i\), что слишком похоже на \(2\sqrt{3i}\).