Функции и их графики.
Дата проведения:
Тема урока: Четная и не четная функция
Цели урока:
Образовательные: ввести понятия четной и нечетной функции, обобщить и расширить знания учащихся о свойствах функции, продолжить работу над формированием умения определять и описывать свойства функции по графику.
Развивающие: совершенствовать навыки исследования свойств функции, развивать творческие и познавательные способности учащихся.
Воспитательные: помочь осознать учащимся свою причастность к математике как к части общечеловеческой культуры, воспитывать чувство взаимопомощи.
Методы: беседа, лекция
Литература: Погорелов
Оборудование: учебники, тетради, меловая доска, раздаточный материал
Ход урока
I. Организационный момент
Проверка домашнего задания(№ 98,99)
II.
1. Какими способами задается функция?
а) таблицей
в) графиком
3.Новая тема
Функцию у = f(x) называют чётной, если для любого значения х из множества Д(х) выполняется равенство f(-x) = f(x).
Функцию у = f(x) называют нечётной, если для любого значения х из множества Д(х) выполняется равенство f(-x) = — f(x).
Функция у = f(x) не является ни чётной, ни нечётной, если хотя бы в одной точке из множества Д(х) не выполняются эти равенства.
Если график функции симметричен относительно оси ординат Оу, то функция чётная.
Если график функции симметричен относительно начала координат, то функция нечётная.
Если график функции не симметричен, то функция не является ни чётной, ни нечётной
.
Периодическая функция ― функция, повторяющая свои значения через некоторый регулярный интервал, то есть не меняющая своего значения при добавлении к аргументу х некоторого фиксированного ненулевого числа (периода функции) на всей области определения.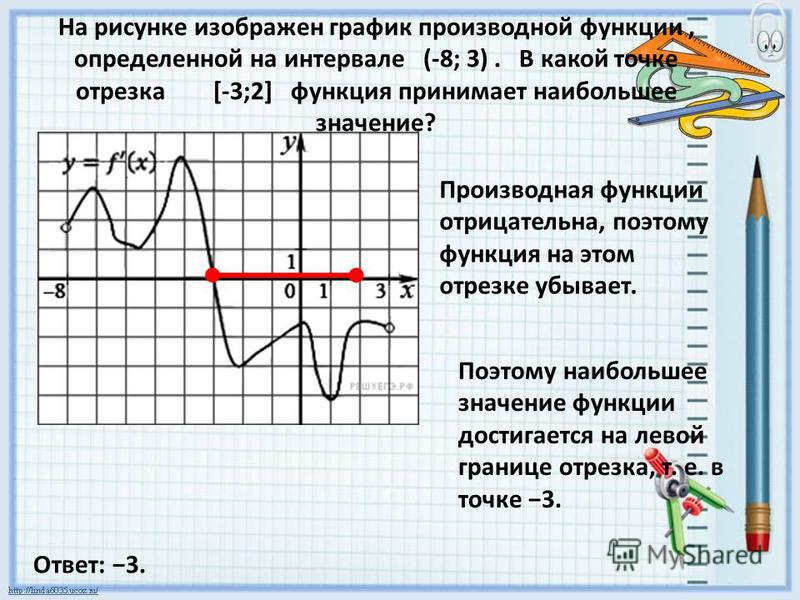
Функция называется периодической, если существует такое число T≠0 (период), что на всей области определения функции Д(х) выполняется равенство f(x) = f(x +T).
График периодической функции состоит из повторяющихся одинаковых кусков, каждый из которых получается параллельным переносом вправо или влево на Т единиц.
Непрерывность функции на отрезке Д(х) – означает, что график функции на данном промежутке не имеет точек разрыва. График непрерывной функции представляет собой сплошную неразрывную линию.
«Функции и их графики.»
Дата проведения:
Тема урока: Четная и не четная функция
Цели урока:
Образовательные: ввести понятия четной и нечетной функции, обобщить и расширить знания учащихся о свойствах функции, продолжить работу над формированием умения определять и описывать свойства функции по графику.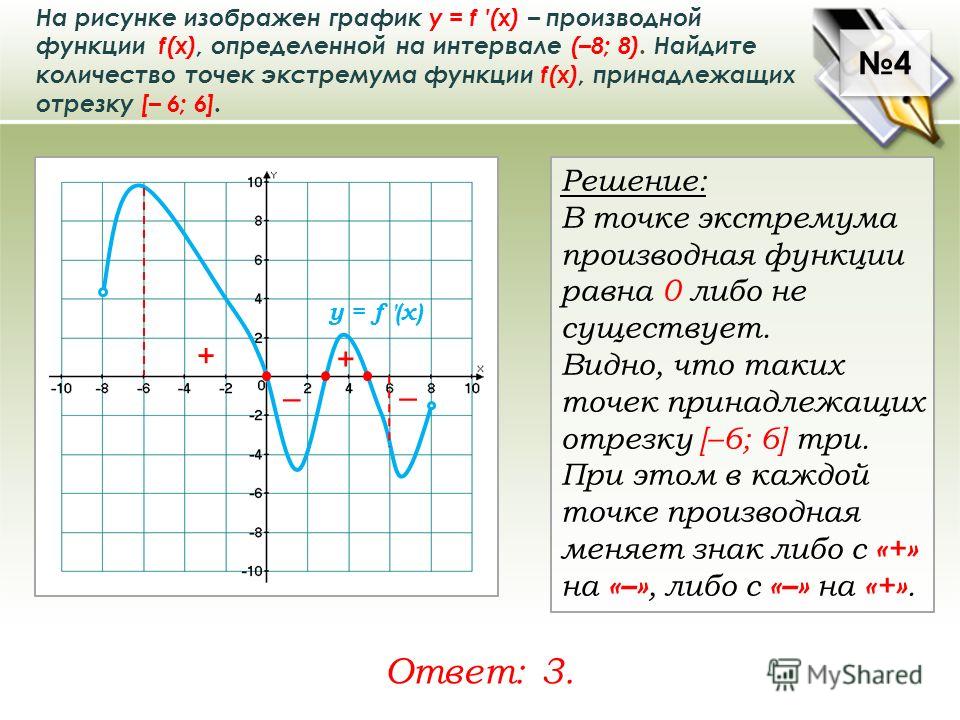
Развивающие: совершенствовать навыки исследования свойств функции, развивать творческие и познавательные способности учащихся.
Воспитательные: помочь осознать учащимся свою причастность к математике как к части общечеловеческой культуры, воспитывать чувство взаимопомощи.
Методы: беседа, лекция
Литература: Погорелов
Оборудование: учебники, тетради, меловая доска, раздаточный материал
Ход урока
I. Организационный момент
Проверка домашнего задания(№ 98,99)
II. Актуализация опорных знаний
1. Какими способами задается функция?
а) таблицей
в) графиком
3.Новая тема
Функцию у = f(x) называют чётной, если для любого значения х из множества Д(х) выполняется равенство f(-x) = f(x).
Функцию у = f(x) называют нечётной, если для любого значения х из множества Д(х) выполняется равенство f(-x) = — f(x).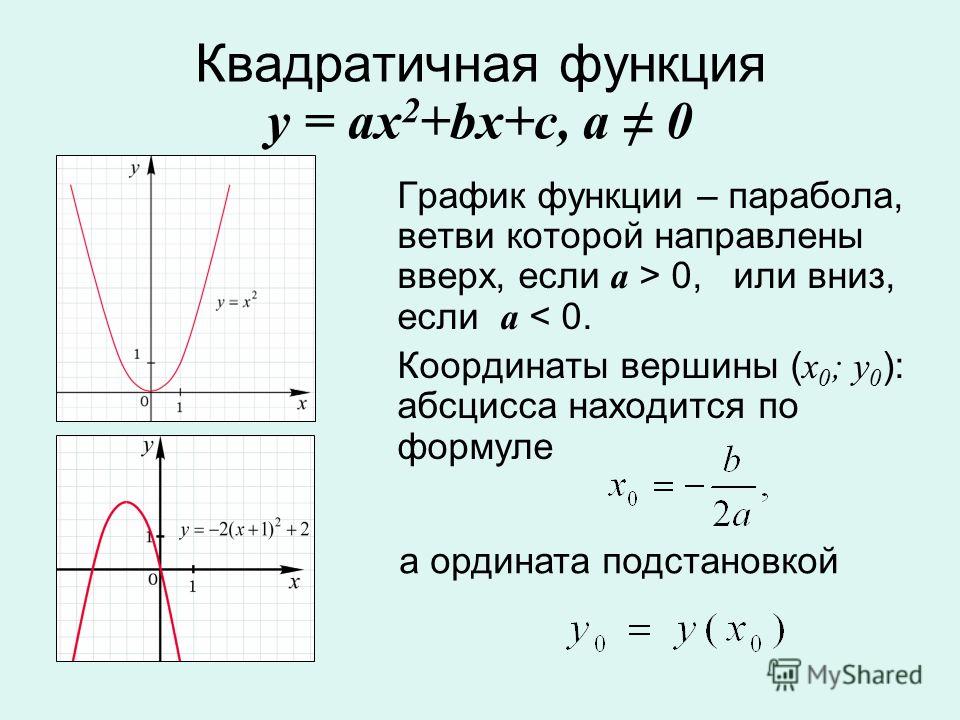
Функция у = f(x) не является ни чётной, ни нечётной, если хотя бы в одной точке из множества Д(х) не выполняются эти равенства.
Если график функции симметричен относительно оси ординат Оу, то функция чётная.
Если график функции симметричен относительно начала координат
Если график функции не симметричен, то функция не является ни чётной, ни нечётной.
Периодическая функция ― функция, повторяющая свои значения через некоторый регулярный интервал, то есть не меняющая своего значения при добавлении к аргументу х некоторого фиксированного ненулевого числа (периода функции) на всей области определения.
Функция называется периодической, если существует такое число T≠0 (период), что на всей области определения функции Д(х) выполняется равенство f(x) = f(x +T).
График периодической функции состоит из повторяющихся одинаковых кусков, каждый из которых получается параллельным переносом вправо или влево на Т единиц.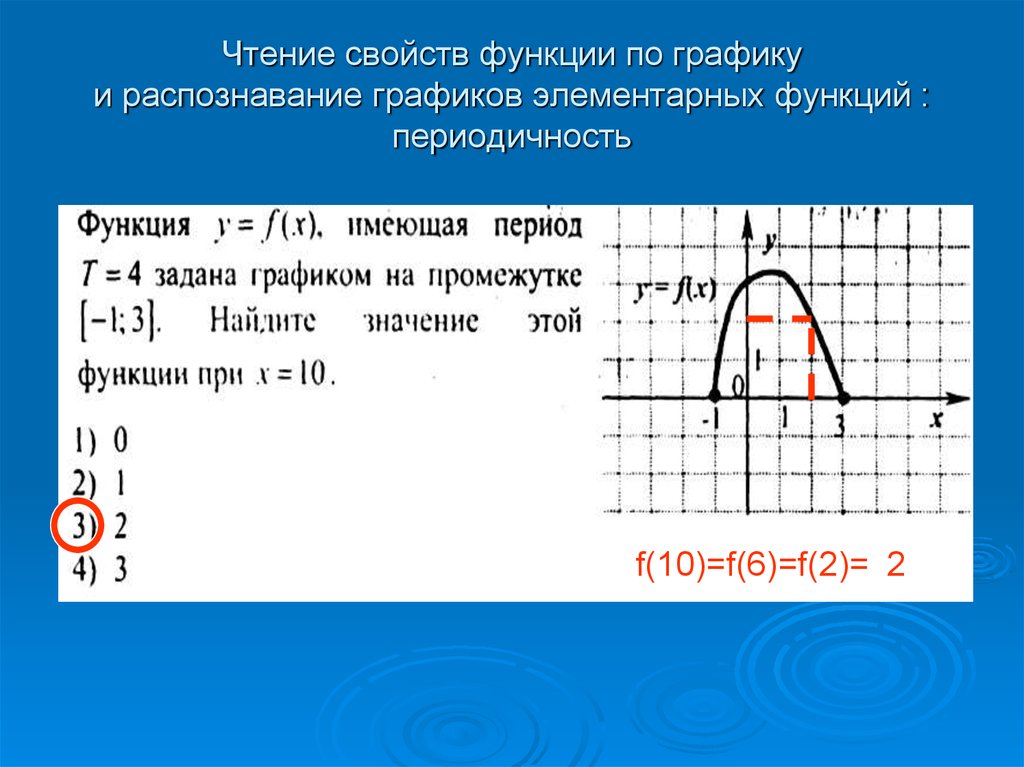
Непрерывность функции на отрезке Д(х) – означает, что график функции на данном промежутке не имеет точек разрыва. График непрерывной функции представляет собой сплошную неразрывную линию.
4.Закрепление
Полное руководство – mathsathome.com
Видеоурок по составным функциям
Как найти составные функции
Чтобы найти составную функцию:
- Определите внешнюю и внутреннюю функции.
- Напишите внешнюю функцию.
- Замените каждую 𝑥 внутренней функцией.
- При необходимости упростите.
Например, если и , рассчитайте .
1. Определите внешнюю и внутреннюю функции
Для составной функции . Это вход в .
При записи в виде , внешняя функция — это та, что написана слева, а внутренняя функция — справа.
— это внутренняя функция и внешняя функция.
2. Напишем внешнюю функцию
Напишем внешнюю функцию .
3. Замените каждый 𝑥 внутренней функцией
Каждый найденный 𝑥 должен быть заменен внутренней функцией .
и так, заменяем 𝑥 на 𝑥 2 .
.
В следующем примере мы сохраним и на этот раз вычислим .
1. Определите внешнюю и внутреннюю функции
Для составной функции , находится внутри . Это вход в .
Когда написано как , внешняя функция — это та, что написана слева, а внутренняя функция — справа.
— это внутренняя функция и внешняя функция.
2. Напишем внешнюю функцию
Напишем внешнюю функцию .
3. Замените каждый 𝑥 внутренней функцией
Каждый найденный 𝑥 должен быть заменен внутренней функцией .
и так, заменяем 𝑥 на 𝑥+3.
Мы должны возвести в квадрат все числа 𝑥+3, поэтому сначала заключаем их в скобки: (𝑥+3).
.
Порядок составных функций
Порядок составных функций имеет значение, поскольку другой порядок приводит к совершенно другой функции. Всегда заменяйте внутреннюю функцию справа внешней функцией слева. Например, если f( 𝑥) = 𝑥 +3 и G ( 𝑥 ) = 𝑥 2 , F (G ( 𝑥) = 𝑥 2 +3 и G (F ( 𝑥)) = 𝑥 2 +3 и G ( 𝑥)) = )=( 𝑥+3) 2 .
Всегда заменяйте внутреннюю функцию справа внешней функцией слева. Например, если f( 𝑥) = 𝑥 +3 и G ( 𝑥 ) = 𝑥 2 , F (G ( 𝑥) = 𝑥 2 +3 и G (F ( 𝑥)) = 𝑥 2 +3 и G ( 𝑥)) = )=( 𝑥+3) 2 .
Всегда заменяйте крайнюю правую функцию функцией слева от нее.
Например, означает, что подставляется в качестве ввода в .
означает, что подставляется как вход в .
Чтобы запомнить порядок составных функций, нарисуйте обратную стрелку от самой правой функции к самой левой.
Всегда заменяйте функцию справа на функцию слева.
Составные функции с числами
Составные функции могут быть вычислены, когда число является входом. Подставьте число в функции справа налево. Например, если f(𝑥)=2 𝑥 +1 и g( 𝑥)=𝑥 2 , то gf( 3) находится подстановкой 3 в 𝑑=) f() 2 𝑥 +1 , чтобы получить 7.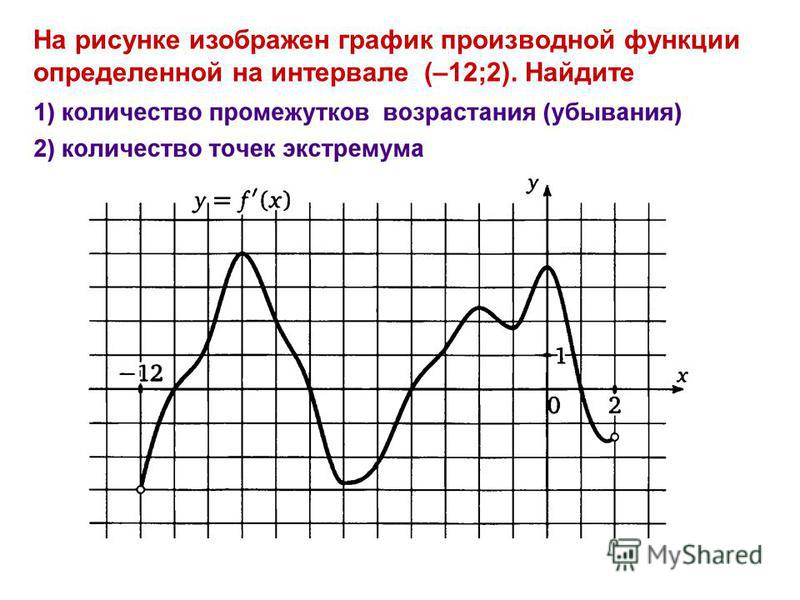 Затем подставьте 7 в 9.0023 g( 𝑥)=𝑥 2 чтобы получить 49. gf( 3) =49.
Затем подставьте 7 в 9.0023 g( 𝑥)=𝑥 2 чтобы получить 49. gf( 3) =49.
Когда входными данными составной функции являются числа, результирующий ответ также является числом.
Если ввод составной функции равен 𝑥, результирующим ответом будет другая функция.
При вводе чисел в составную функцию важно оценивать каждую функцию справа налево.
В приведенном ниже примере мы сначала подставляем 4 в g(𝑥), чтобы получить 2, а затем подставляем это значение 2 в f(𝑥), чтобы получить 11.
Что такое составные функции?
Составная функция — это функция, которая находится внутри другой функции. Одна функция заменяется на вход другой функции. Например, f[ g(𝑥) ] означает, что g( 𝑥 ) заменяется на каждые 𝑥 в функции f( 𝑥 ). Составная функция f[g( 𝑥 )] произносится как «f of g of 𝑥».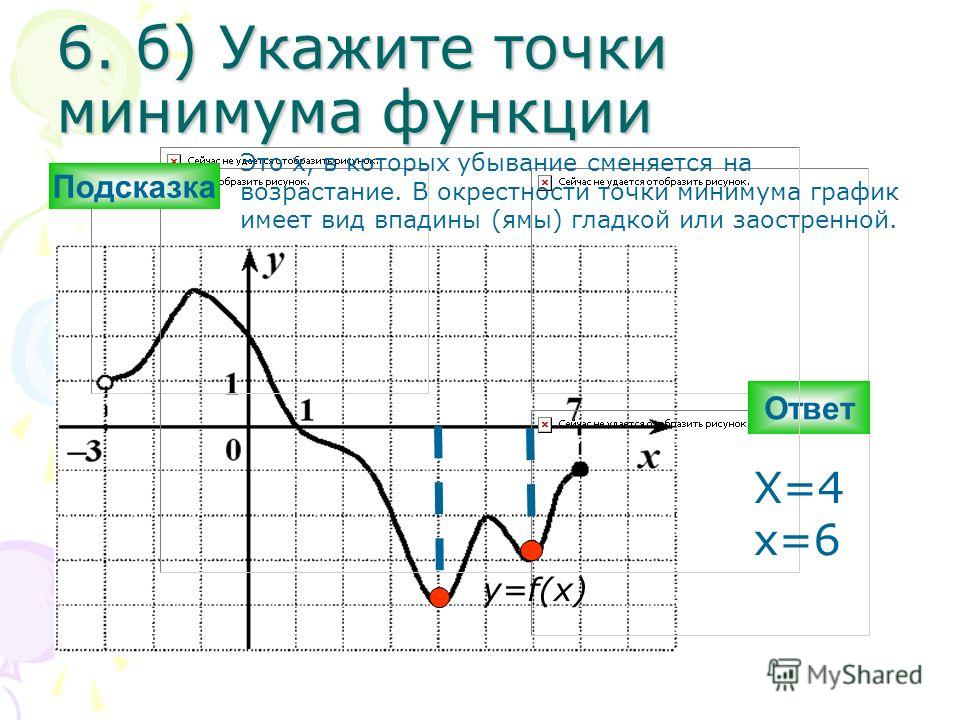
Например, в приведенной ниже составной функции заменяется на для формы .
Составная функция отличается от функций, из которых она состоит.
Обозначение составной функции
Составные функции могут быть записаны в различных обозначениях.
Функция, подставленная в качестве входных данных для другой функции, может быть записана как:
В математике символ круга ∘ используется для обозначения состава функций. Например, (f∘g)(𝑥) означает взять результат g и подставить его в f.
читается как «f из g», «f, составленный из g», «f круг g», «f вокруг g» или «f около g».
Диаграмма-стрелка составной функции
Диаграмма-стрелка может использоваться для объяснения составных функций. Входы первой функции перечислены слева. Стрелки соединяют эти входы с их выходами посередине. Эти выходные данные затем являются входными данными для следующей функции, выходные данные которой показаны справа.
Например, чтобы найти с помощью диаграммы со стрелкой ниже, введите 2, показанное красной стрелкой.
Первая стрелка показывает функцию . Когда мы возводим 2 в квадрат, мы получаем 4.
Вторая стрелка уходит от 4 и достигает результата 7. Это потому, что функция говорит нам добавить три к предыдущему результату. 4 + 3 = 7.
Следовательно =7.
Свойства составных функций
Составные функции обладают следующими свойствами:
- Обратная композиция функций равна композиции обратной обеих функций. (ф∘г) -1 = г -1 ∘f -1 .
- Композиция функций «один к одному» также является взаимно однозначной.
- Композиция онто-функций также является онто-функцией.
- Составные функции ассоциативны. То есть f∘(g∘h) = (f∘g)∘h.
- Композиция функций, вообще говоря, некоммутативна. Нельзя предполагать, что f[g(x)] = g[f(x)].
- Составная функция, содержащая хотя бы одну четную функцию, будет четной.

- Составная функция, состоящая из совершенно нечетных функций, также будет нечетной.
Составные функции с 3 функциями
Чтобы найти составную функцию, состоящую из трех функций, подставьте крайнюю правую функцию в среднюю функцию, а затем подставьте ее в крайнюю левую функцию. For example, if g(𝑥)= 𝑥 2 , f( 𝑥 )=3 𝑥+1 and h( 𝑥)= 1 / 𝑥 then h(g( f( 𝑥)))= 1 / (3𝑥+1) 2 .
Стрелки можно рисовать справа налево, чтобы помочь запомнить порядок составных функций. В примере h(g(f(𝑥))) функция f заменяется на функцию g, чтобы сформировать g(f(𝑥)).
г(f(𝑥)) = (3𝑥-1) 2 .
Затем он подставляется в функцию h 1 / 𝑥 . Мы заменяем 𝑥 на (3𝑥-1) 2 .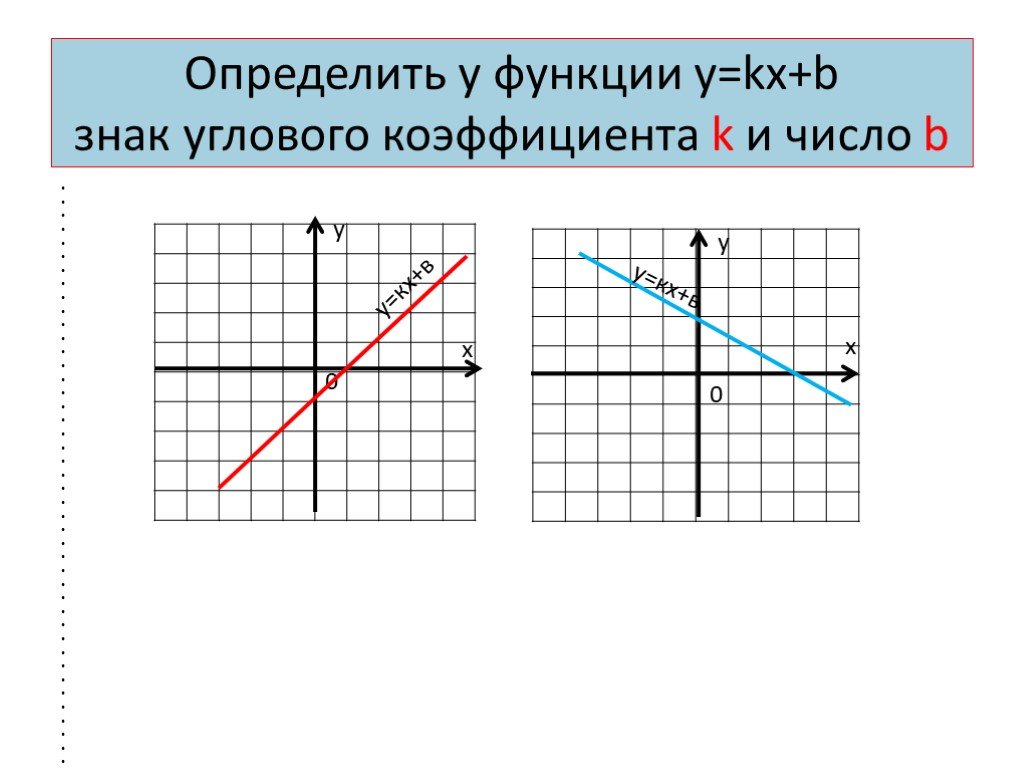
h(g(f(𝑥))) = 1 / (3𝑥-1) 2 .
Примеры композитной функции
Пример композитной функции с квадратными корнями
Если G (𝑥) = 𝑥 2 + 5𝑥 и F (𝑥) = √ 𝑥, Рассчитайте G (F ( 𝑥 ). ). Подставьте √ 𝑥 во все 𝑥 , найденные в функции g( 𝑥 ) . г(f( 𝑥 )) = ( √ 𝑥 ) 2 +5 √ 𝑥 . Здесь √ 𝑥 и квадратная операция отменяется, чтобы оставить g(f( 𝑥 )) = 𝑥 +5 √ 𝑥 .
Пример композитной функции с фракциями
Если G ( 𝑥 ) = 1 / 𝑥 и F ( 𝑥) = 1- 𝑥 и F ( 𝑥) = 1- 𝑥 , FIND G ( 𝑥) = 1- 𝑥 , FIND G ( 𝑥) = 1- 𝑥 .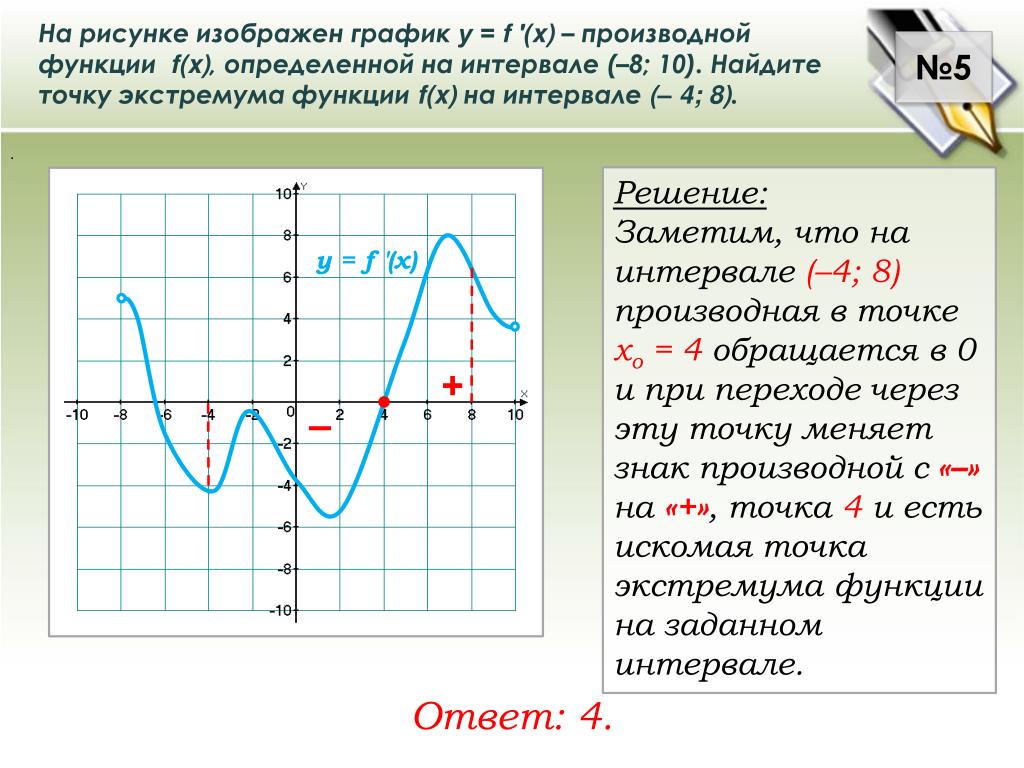 𝑥 )). Замените функцию f на 𝑥 в функции g. г(f( 𝑥))= 1 / (1- 𝑥) . Эта составная функция записывается в виде дроби.
𝑥 )). Замените функцию f на 𝑥 в функции g. г(f( 𝑥))= 1 / (1- 𝑥) . Эта составная функция записывается в виде дроби.
Пример составной функции с Sin(𝑥)
Если g(𝑥) = 2𝑥 + 1 и f(𝑥) = sin( 𝑥), вычислить f(g( 𝑥 )). Подставьте 2 𝑥 +1 в каждое 𝑥 , найденное в функции f( 𝑥 ) . f(g( 𝑥 )) = sin(2 𝑥+1) .
Пример составной функции с e
𝑥 e 𝑥 и ln( 𝑥) являются обратными функциями. При записи в виде составной функции эти две функции компенсируют друг друга. Если g( 𝑥)=e 𝑥 и f( 𝑥)=ln( 𝑥 )- 𝑥, вычислить f(g( ). Каждая 𝑥 в f( 𝑥) заменяется на e 𝑥 и т. д.0007 𝑥 . Это упрощается до 𝑥-e 𝑥 .
д.0007 𝑥 . Это упрощается до 𝑥-e 𝑥 .
Функция, состоящая из самой себя
Функция, f( 𝑥 ) может быть составлена из самой себя, чтобы сформировать f(f( 𝑥)), которая также может быть записана как f504. ( 𝑥). Это означает, что функция помещается как вход самой себе. Например, если f( 𝑥)=5 𝑥-2, то в f(f( 𝑥)), 𝑥 в f( 𝑥)=5 𝑥-2 будет заменено на 5 𝑥-2 . F (F ( 𝑥)) = 5 (5𝑥-2) -2, что Simplifies до 25 (5𝑥-2) -2. 𝑥 -12.
Область определения составных функций
Чтобы вычислить область определения составной функции gf(𝑥):
- Найдите значения, исключенные из области определения внешней функции g(𝑥).

- Установите f(𝑥) равным этим исключенным значениям и решите относительно 𝑥, чтобы найти значения, которые должны быть исключены из домена.
- Найдите любые другие значения, исключенные из области определения внутренней функции f(𝑥).
- Объедините эти результаты, чтобы сформировать общую область составной функции.
Например, если и , найдите домен .
Шаг 1. Найдите значения, которые исключены из области определения g(𝑥)
В функции g(𝑥) не может быть знаменателя, равного 0.
x≠0, так как мы не можем делить на 0
Шаг 2. Установите f(𝑥) равным этим исключенным значениям и найдите 𝑥
.
Мы решаем это для 𝑥, чтобы найти любые дополнительные значения, которые должны быть исключены из домена.
Возводим в квадрат обе части уравнения.
Затем мы видим, что .
Шаг 3. Найдите любые значения, которые исключены из внутренней функции, f( 𝑥 )
.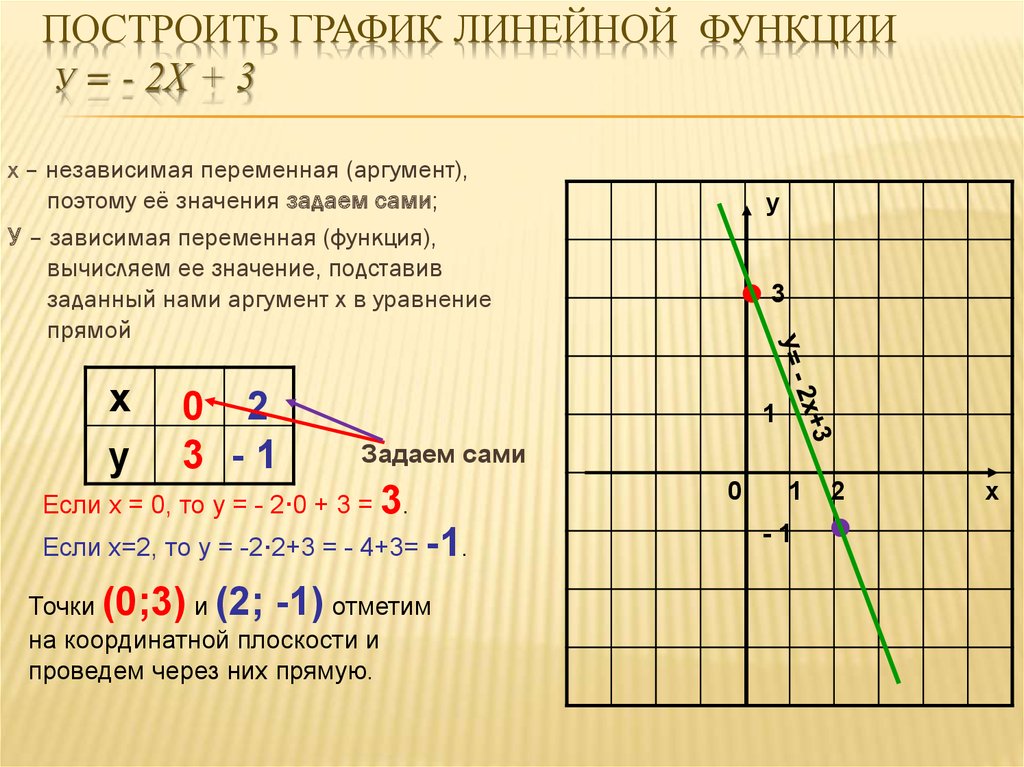 Мы не можем извлекать корень из отрицательного числа.
Мы не можем извлекать корень из отрицательного числа.
Следовательно .
Шаг 4. Объедините эти результаты, чтобы определить область определения составной функции
В , областью является то .
Однако на шаге 2 мы сталкиваемся с проблемами, потому что это приводит к нулевому знаменателю составной функции.
Таким образом, конечный домен составной функции равен .
Составные функции из графиков
Чтобы найти значение составной функции из графика:
- Используйте ввод составной функции для считывания вывода с графика внутренней функции.
- Используйте этот вывод как ввод графика внешней функции.
Например, функции f(𝑥) и g(𝑥) показаны ниже.
Используйте графики для расчета значения составной функции g(f(5)).
Шаг 1. Используйте вход составной функции для считывания вывода с графика внутренней функции
Число на входе составной функции равно 5.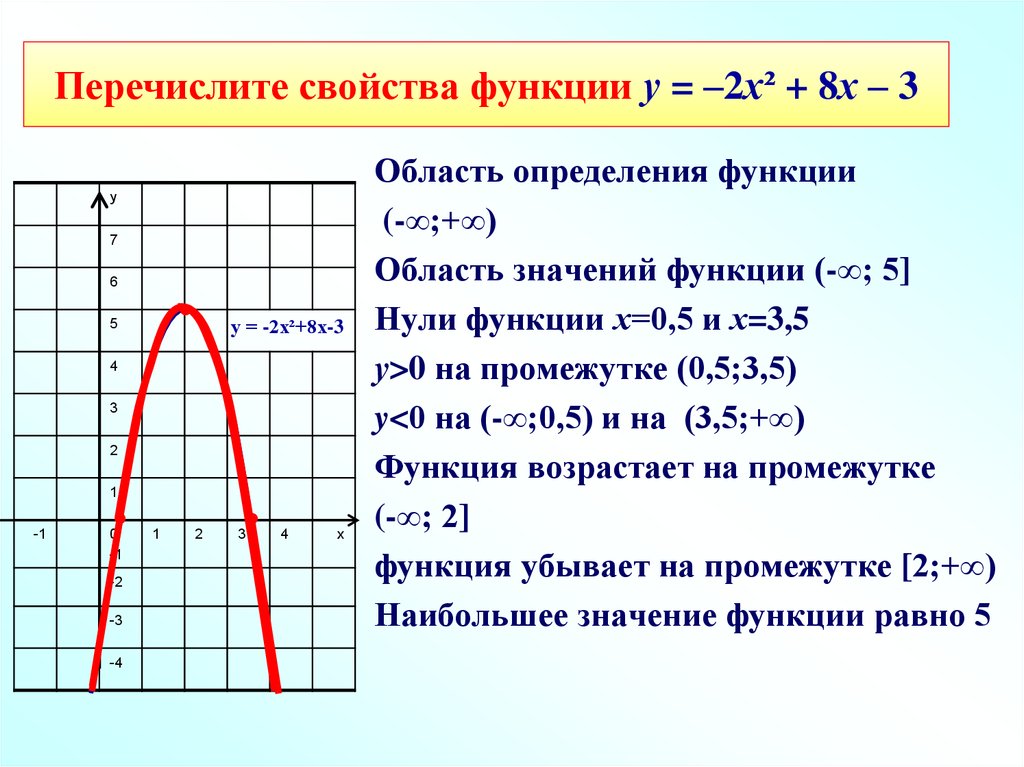
Мы читаем график внутренней функции f( 𝑥) в точке, где 𝑥 = 5.
Когда 𝑥 = 5, функция f(𝑥) имеет выход 4.
Шаг 2. Используйте этот выход как вход графика внешней функции
Мы используем выход 4 из первого графика в качестве входных данных для внешней функции g(𝑥).
Когда 𝑥 = 4, g(𝑥) имеет выход 5.
Следовательно, g(f(𝑥)) = 5.
Вот еще один пример.
Чтобы вычислить g(f(2)), мы сначала подставляем 2 в качестве входных данных в график f(𝑥).
Это дает нам результат 2 по оси Y.
Затем мы используем этот вывод 2 из графика f(𝑥) в качестве входных данных для графика g(𝑥).
Когда 𝑥 = 2, g(𝑥) имеет выход 7.
Следовательно, g(f(2)) = 7.
Составные функции с использованием таблицы
Чтобы вычислить значение составной функции из таблицы:
- Считать вывод внутренней функции из ее таблицы с требуемым значением.
- Используйте этот вывод как ввод в таблицу внешней функции и прочитайте новый вывод.

Например, рассчитайте значение составной функции g(f(3)) с помощью приведенных ниже таблиц.
Шаг 1. Считайте вывод внутренней функции из ее таблицы по требуемому значению
Вход составной функции: 𝑥 = 3.
Из первой таблицы, когда 𝑥 = 3, значение f(𝑥) = 5.
Шаг 2. Используйте этот вывод в качестве входных данных в таблице внешнюю функцию и прочитать новый вывод
Выход таблицы f(𝑥) был 5.
Это используется в качестве входных данных в таблице g(𝑥).
Когда 𝑥 = 5, g(𝑥) = 17.
Следовательно, g(f(3)) = 17.
Исчисление I. Форма графика, часть I (практические задачи)
Онлайн-заметки Пола
Главная
/
Исчисление I
/
Применение производных
/ Форма графика, часть I
Показать мобильное уведомление Показать все примечания Скрыть все примечания
Уведомление для мобильных устройств
Похоже, вы используете устройство с «узкой» шириной экрана ( т. е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
Раздел 4.5. Форма графика, часть I
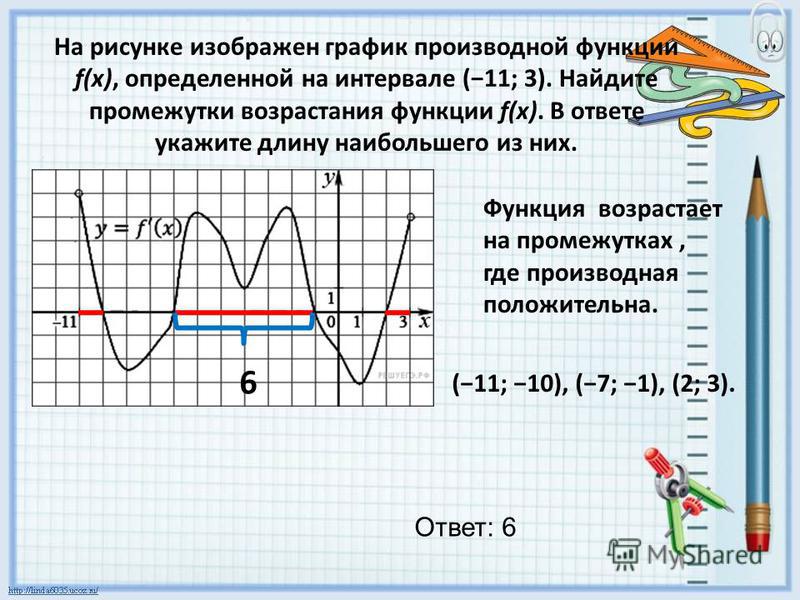
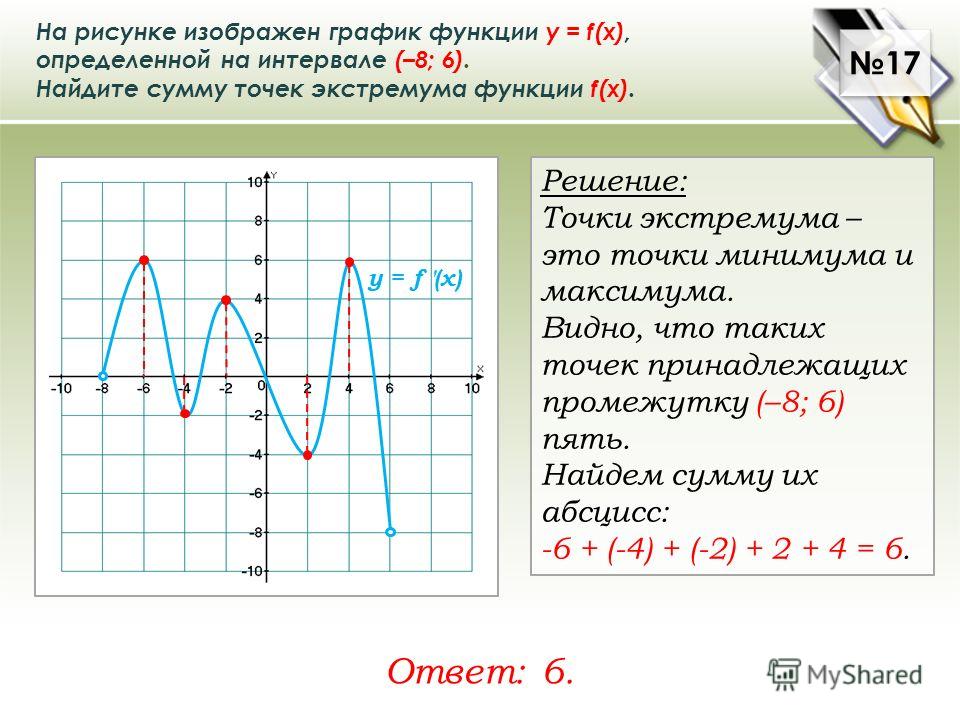
Для задач 1 и 2 дан график функции. Определить промежутки возрастания и убывания функции.
- Решение
- Решение
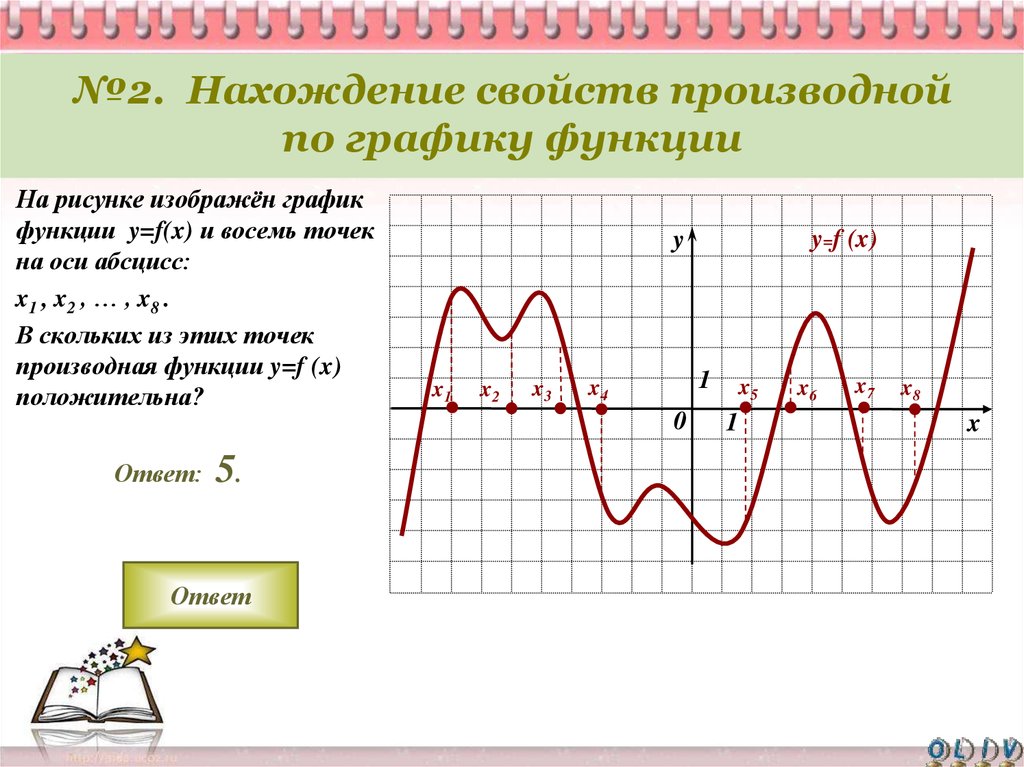
Ниже приведен график производной функции. По этому графику определите интервалы, в которых функция возрастает и убывает.
- Решение
- Эта проблема касается какой-то функции. Все, что мы знаем о функции, это то, что она существует везде, и мы также знаем приведенную ниже информацию о производной функции.
 Ответьте на каждый из следующих вопросов об этой функции.
Ответьте на каждый из следующих вопросов об этой функции.- Определите критические точки функции.
- Определите интервалы возрастания и убывания функции.
- Классифицируйте критические точки как относительные максимумы, относительные минимумы или ни то, ни другое.
Для задач 5 – 12 ответьте на каждый из следующих вопросов.
- Определите критические точки функции. 92}} \справа)\) Решение
- Для некоторой функции \(f\left( x \right)\) известно, что существует относительный максимум в точке \(x = 4\). Ответьте на каждый из следующих вопросов об этой функции.


 Ответьте на каждый из следующих вопросов об этой функции.
Ответьте на каждый из следующих вопросов об этой функции.