Как узнать объем куба формула: Как вычеслить объём куба если длина его ребра 2.5см

Как рассчитать объем куба? – Обзоры Вики

Формула для определения объема умножает длину на ширину и высоту. Хорошая новость для куба заключается в том, что измерение каждого из этих измерений точно такое же. Следовательно, длину любой стороны можно умножить в три раза. Это приводит к формуле: Объем = сторона * сторона * сторона.

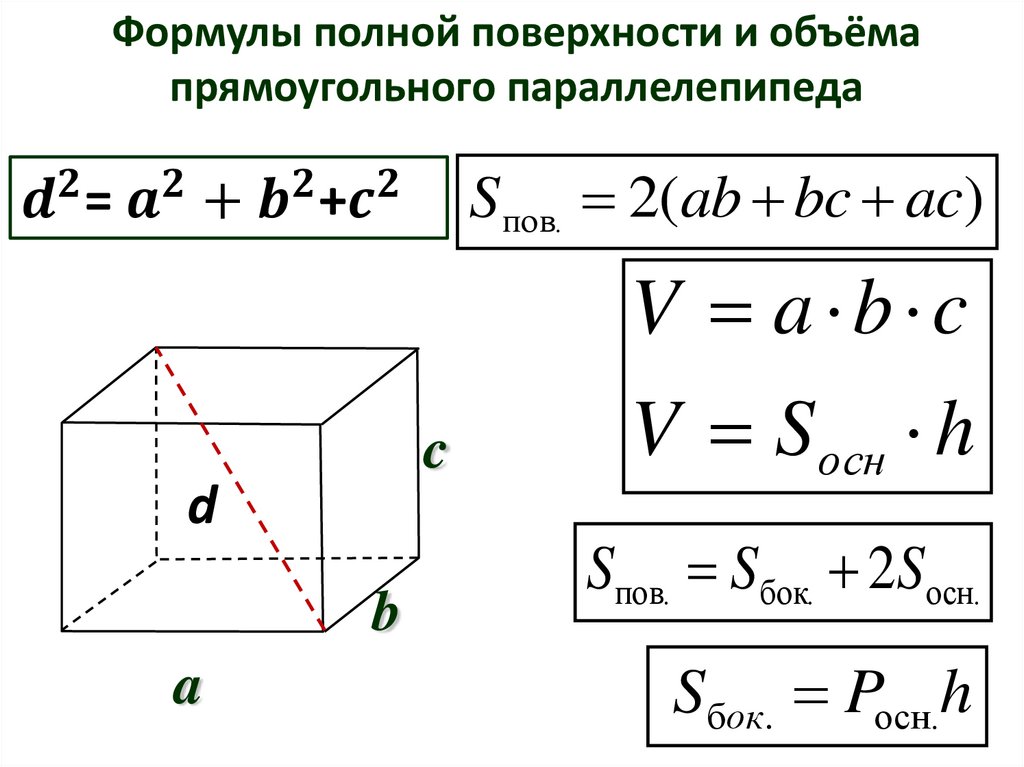
Каков объем формулы прямоугольного параллелепипеда? Какова формула объема прямоугольного параллелепипеда? Формула объема прямоугольного параллелепипеда = Длина × Ширина × Высота.

Во-вторых, какова формула прямоугольного параллелепипеда? Формулы куба и прямоугольного параллелепипеда

Cubo,en	Кубоид
Объем куба = (Сторона) 3	Объем кубоида = ( длина × ширина × высота )
Диагональ куба = √3l	Диагональ кубоида = √ (l 2 + b 2 +h 2 )
Периметр куба = 12 сторон	Периметр кубоида = 4 (длина + ширина + высота)

Что такое кубик 8?

Как кубический корень из 8 целое число, 8 — идеальный куб.
…
Кубический корень из 8 в радикальной форме: ∛8.

1.	Что такое кубический корень из 8?
3.	Является ли кубический корень из 8 иррациональным?
4.	Часто задаваемые вопросы о Cube Root of 8

то Как найти объем куба и прямоугольного параллелепипеда? Теперь для расчета объема куба нужно просто найти куб данного значения стороны. Объем прямоугольного параллелепипеда — это произведение длины, ширины и высоты, в просторечии называемое «lbh». Для любого прямоугольного параллелепипеда длины L, ширины B и высоты H объем V равен LxBxH.

Как найти количество кубов прямоугольного параллелепипеда? Чтобы найти количество кубиков в каждом слое прямоугольного параллелепипеда, умножьте длину на ширину. 4 х 3 = 12 и так, в этом слое 12 кубиков.

Как вы решаете задачи на куб и кости?

Сколько кубиков вы можете определить на данном изображении?

Следовательно, ‘216‘ — правильный ответ.

Что такое диагональ кубоида? Объяснение: Пусть «а» — длина стороны куба. Формула диагонали куба = 3⎷a. Пусть «l» — длина, «b» — ширина, а «h» — высота прямоугольного параллелепипеда. Формула диагонали прямоугольного параллелепипеда = ⎷ (l² + b² + ч²)

Является ли куб прямоугольным параллелепипедом?

Куб — это частный случай квадратного прямоугольного параллелепипеда, у которого все шесть граней — квадраты.
…

Прямоугольный кубоид
Тип	Призма Плезиоэдр
Лики	6 прямоугольника
Ребра	12
вершины	8

Что такое куб 3 7?

Это реальное решение уравнения x ³ = 7. Кубический корень из 7 выражается как ∛7 в радикальной форме и как (7) ^⅓ или (7) ^{0 . 33} в экспоненциальной форме.
…
Кубический корень из 7 в радикальной форме: ∛7.

1.	Что такое кубический корень из 7?
4.	Часто задаваемые вопросы о Cube Root of 7

Что такое куб 10? Кубический корень из 10 выражается как ∛10 в радикальной форме и как (10) ^⅓ or (10) ^{0 . 33} в экспоненциальной форме.
…
Кубический корень из 10 в радикальной форме: ∛10.

1.	Что такое кубический корень из 10?
2.	Как вычислить кубический корень из 10?
3.	Является ли кубический корень из 10 иррациональным?

Что такое куб от 1 до 10? Числа в кубе от 1 до 100

Число	Cubo,en
8	512
9	729
10	1000
11	1331

• 4 июня 2020 г.

Как найти диагональ куба и прямоугольного параллелепипеда?

Ответ: Диагональ куба = 3⎷a , Диагональ прямоугольного параллелепипеда = ⎷(l² + b² + ч²)

Сколько диагоналей в кубоиде? Кубоид имеет не менее 4 диагоналей.

Сколько кубиков в одном кубоиде?

Разница между кубом и кубоидом

Cubo,en	Кубоид
В кубе все шесть лиц квадраты	У прямоугольного параллелепипеда все шесть граней прямоугольники.
Куб, состоящий из 12 диагоналей с одинаковой площадью поверхности	Всего у кубоида 12 диагоналей, из которых 3 диагонали различны по мере.

Сколько маленьких кубиков в кубоиде? Есть 16 маленьких кубиков прикреплены к наружным стенкам куба.

Сколько кубиков может поместиться в параллелепипед?

Объем прямоугольного параллелепипеда = длина × ширина × высота = 15 × 4 × 8 = 60 × 8 = 480 см.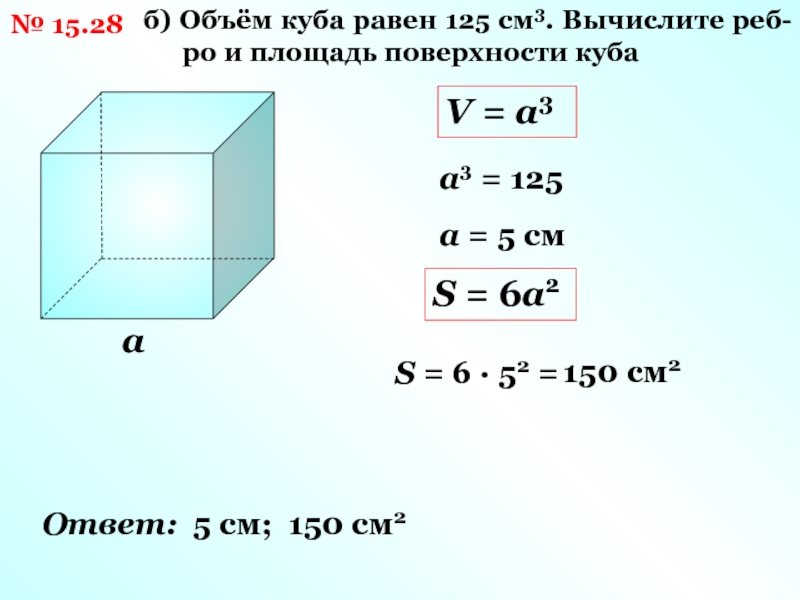 ³. Так 480 кубика подойдет.

Как ты делаешь трюк с кубиками?

Как вы решаете кости умственных способностей? DICE REASONING: концепции и хитрости

1. К одной грани примыкают четыре грани.
2. Есть пары противоположных граней, например, напротив DEFH находится ABCG и так далее.
3. CDEG — это верхняя грань куба.
4. ABHF — нижняя грань куба.

Объем куба — онлайн калькулятор

• Справочник
• Онлайн-калькуляторы
• Тесты с ответами

Объем куба равен произведению длины, ширины и высоты фигуры.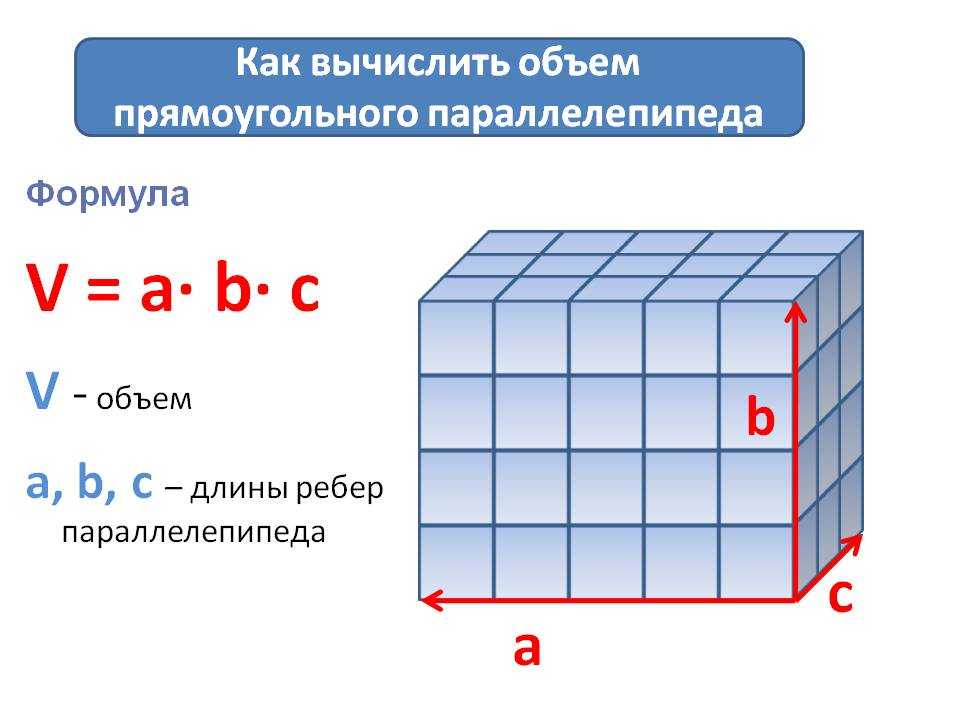 Так как все ребра фигуры одинакового размера, то итогом будет длина, возведенная в третью степень. Такое несложное вычисление можно произвести самостоятельно. Но если предстоит переводить величины из одной в другую, лучше воспользоваться нашим сервисом.

На сайте собраны калькуляторы, которые помогают справиться с решением задач по алгебре и геометрии. Вам необходимо только ввести данные, программа сама выполнит нужные преобразования, выдаст пошаговый расчет и ответ.

1. Введите ребро куба.
   
2. Отметьте единицы измерения для ребра куба и искомого объема. Отправьте задание на расчет кнопкой «Найти».
   
3. Получите решение и ответ.
   ​​​​​​​

Ответ:

Решение

Ответ:

• list» :key=»`error-${eIdx}`» v-html=»e»/>

Похожие калькуляторы:

• Объем пирамиды
• Объем цилиндра (Радиус основания и высота)
• Объем цилиндра (Площадь основания и высота)
• Объем конуса (Радиус основания и высота)
• Объем конуса (Площадь основания и высота)
• Объем шара
• Объем параллелепипеда
• Объем прямоугольного параллелепипеда

Для решения задач применяется формула объема куба:

​​​​​​​

где a – длина ребра фигуры.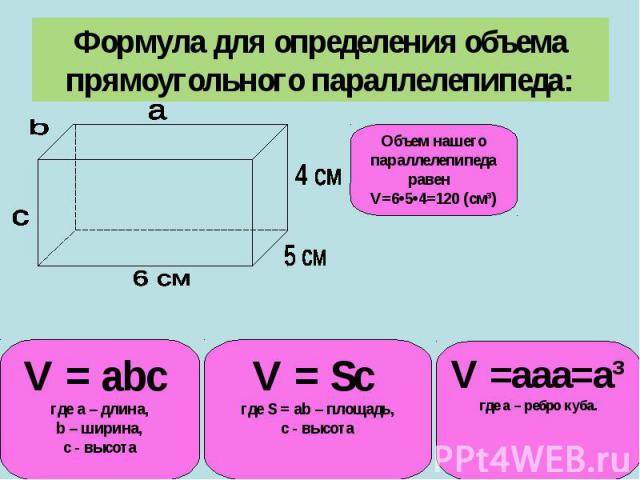

С помощью сайта школьники могут готовиться к урокам, контрольным, поступлению в университет. Студентам легче сдавать зачеты, экзамены. Для родителей, учителей ускоряется процесс проверки выполненных заданий. Также программы используют инженеры и строители при расчете требуемых для работы материалов.

Чем полезен сервис:

• Минимум ожидания. Вычисления и ответ доступны сразу после отправки на расчет.
• Отсутствие регистрации. При срочной необходимости получить ответ нет времени на лишние действия.
• Круглосуточный доступ. Вы сможете получить решение задачи в любое время.
• Безлимитные проверки. Количество подсчетов не ограничивается.

Для учеников калькуляторы – это возможность самостоятельно готовиться к урокам и экзаменам, проверять собственные вычисления. Пошаговые подсчеты, чертежи позволяют запоминать алгоритм и применять его в других заданиях. Сервис работает бесплатно. Любой желающий может воспользоваться набором программ, чтобы повысить свою успеваемость по алгебре и геометрии.

Понравился калькулятор? Поделись с друзьями!

Разделы калькуляторов

• Процент
• Решение матриц
• Точка, прямая, плоскость
• Конвертеры
• Объем фигур
• Калькуляторы площади фигур
• Решение уравнений
• Операции над векторами
• Периметр фигур

Поможем с любой работой

• Дипломные работы
• Курсовые работы
• Рефераты
• Контрольные работы
• Решение задач
• Отчеты по практике

Все наши услуги

Узнай бесплатно стоимость работы

Не получается написать работу самому?

Доверь это кандидату наук!

Как найти объем куба

Все ресурсы по промежуточной геометрии

8 Диагностические тесты 250 практических тестов Вопрос дня Карточки Learn by Concept

← Предыдущая 1 2 3 4 Следующая →

Справка по геометрии среднего уровня » Твердая геометрия » Кубики » Как найти объем куба

Ребра куба в три раза длиннее ребер меньшего куба.

Объем большего куба во сколько раз больше объема меньшего куба?

Возможные ответы:

Правильный ответ:

Объяснение:

Если представить длину ребра меньшего куба, его объем будет равен .

Ребра большего куба в три раза длиннее, поэтому длину можно представить как . Объем , который есть .

Объем большого куба  в 27 раз больше объема маленького куба  .

 

Сообщить об ошибке

Длина стороны куба – дюймы.

Какой объем?

Возможные ответы:

Правильный ответ:

Объяснение:

Объем куба равен

Таким образом, при длине стороны 7 дюймов объем равен

Сообщить об ошибке

Длина стороны куба равна футам.

Каков объем ?

Возможные ответы:

Правильный ответ:

Объяснение:

Объем куба равен

Таким образом, при длине стороны 2 фута объем равен

Сообщить об ошибке

Найдите объем куба с длиной ребра .

Возможные ответы:

Правильный ответ:

Объяснение:

Объем куба можно определить с помощью уравнения , где  обозначает длину одной стороны куба. Уравнение состоит в том, что все ребра куба имеют одинаковую длину. Нужно просто подставить значение данного ребра в уравнение для  , чтобы найти объем куба.

Сообщить об ошибке

Если сторона куба имеет длину, то каков объем куба?

Возможные ответы:

Правильный ответ:

Пояснение:

Чтобы найти объем куба, мы просто трижды умножаем длину одной из сторон куба на саму себя, или, другими словами, возводим ее в куб. Если назвать длину стороны куба, то:

Сторона нашего кубика имеет длину, поэтому мы можем подставить это в уравнение и решить:

Сообщить об ошибке

Кубик Рубика состоит из трех квадратных слоев с девятью одинаковыми кубиками меньшего размера. каждый слой. Если один из меньших кубиков имеет длину стороны 1,5 см, каков приблизительный объем всего кубика Рубика?

Возможные ответы:

Правильный ответ:

Объяснение:

Это большая проблема, потому что есть два подхода к ней. Проще всего понять, что, поскольку каждое ребро кубика Рубика состоит из 3 меньших кубиков, мы можем найти длину ребра всего кубика Рубика:

(ребро всего кубика Рубика)

Теперь, когда мы знаем длина ребра найти объем легко, мы просто умножаем длину, ширину и высоту куба, чтобы найти объем. Это легко, потому что длина, ширина и высота равны 4,5 см.

(том кубик Рубика)

Это ответ. Другой способ решить проблему — найти объем одного из меньших кубов, затем умножить его на 9, чтобы найти объем одного слоя, а затем умножить на три, потому что слоев 3.

(объем одного маленького кубика)

(объем одного слоя кубика Рубика)

(объем кубика Рубика)

Два разных метода и мы получили одинаковый ответ!

Сообщить об ошибке

Из куба вырезается цилиндр, как показано на рисунке ниже.

Найдите объем фигуры.

Возможные ответы:

Правильный ответ:

Пояснение:

Чтобы найти объем фигуры, мы должны сначала найти объемы куба и цилиндра.

Вспомним, как найти объем куба.

Подставьте заданную длину стороны куба, чтобы найти объем.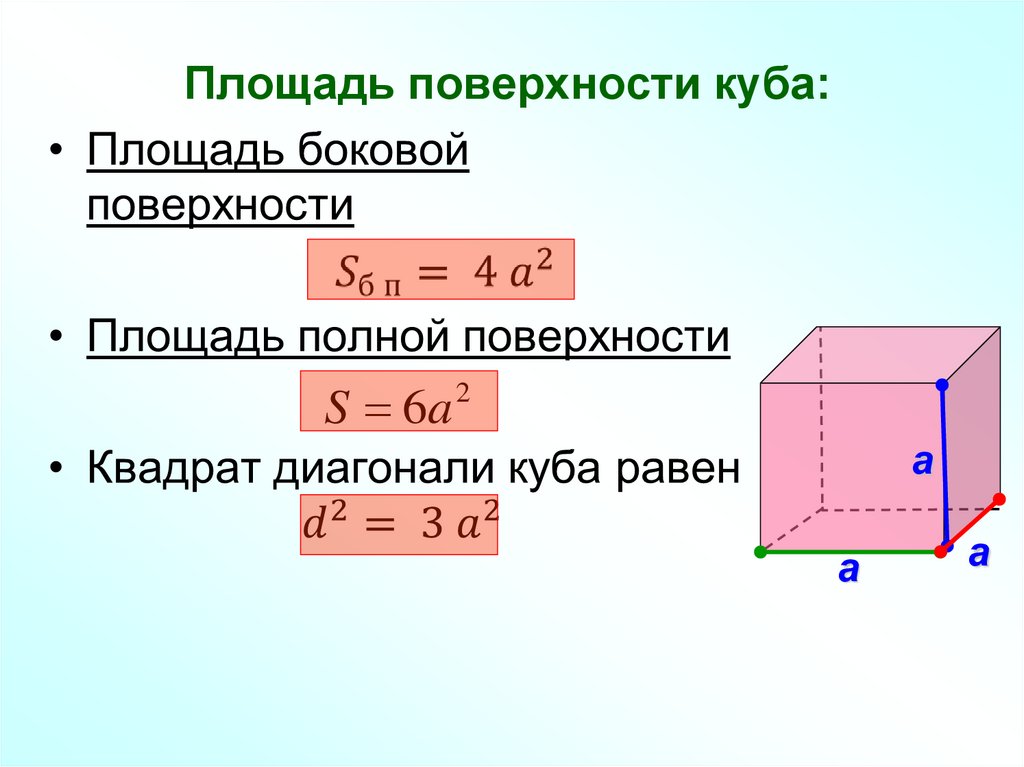

Далее вспомним, как найти объем цилиндра.

Используйте заданный диаметр, чтобы найти длину радиуса.

Найдите объем цилиндра.

Чтобы найти объем фигуры, вычтите объем цилиндра из объема куба.

Обязательно округляйте до десятичных знаков.

Сообщить об ошибке

Цилиндр вырезается из куба, как показано на рисунке ниже.

Найдите объем фигуры.

Возможные ответы:

Правильный ответ:

Пояснение:

Чтобы найти объем фигуры, мы должны сначала найти объемы куба и цилиндра.

Вспомним, как найти объем куба.

Подставьте заданную длину стороны куба, чтобы найти объем.

Далее вспомним, как найти объем цилиндра.

Используйте заданный диаметр, чтобы найти длину радиуса.

Найдите объем цилиндра.

Чтобы найти объем фигуры, вычтите объем цилиндра из объема куба.

Обязательно округляйте до десятичных знаков.

Сообщить об ошибке

Цилиндр вырезается из куба, как показано на рисунке ниже.

Найдите объем фигуры.

Возможные ответы:

Правильный ответ:

Пояснение:

Чтобы найти объем фигуры, мы должны сначала найти объемы куба и цилиндра.

Вспомним, как найти объем куба.

Подставьте заданную длину стороны куба, чтобы найти объем.

Далее вспомним, как найти объем цилиндра.

Используйте заданный диаметр, чтобы найти длину радиуса.

Найдите объем цилиндра.

Чтобы найти объем фигуры, вычтите объем цилиндра из объема куба.

Обязательно округляйте до десятичных знаков.

Сообщить об ошибке

Цилиндр вырезается из куба, как показано на рисунке ниже.

Найдите объем фигуры.

Возможные ответы:

Правильный ответ:

Пояснение:

Чтобы найти объем фигуры, мы должны сначала найти объемы куба и цилиндра.

Вспомним, как найти объем куба.

Подставьте заданную длину стороны куба, чтобы найти объем.

Далее вспомним, как найти объем цилиндра.

Используйте заданный диаметр, чтобы найти длину радиуса.

Найдите объем цилиндра.

Чтобы найти объем фигуры, вычтите объем цилиндра из объема куба.

Обязательно округляйте до десятичных знаков.

Сообщить об ошибке

← Предыдущая 1 2 3 4 Следующая →

Уведомление об авторских правах

Все промежуточные ресурсы по геометрии

8 Диагностические тесты 250 практических тестов Вопрос дня Карточки Learn by Concept.

Формула объема куба

Диагонали куба — грани и пространство

Как найти объем куба?

Наш кубический калькулятор поможет вам найти все параметры куба. Хотите ли вы определить объем коробки или проверить площадь кубика, этот гибкий инструмент — то, что вам нужно. Введите один параметр из пяти — объем куба, площадь поверхности куба, диагональ грани, диагональ куба или сторону куба — и в мгновение ока мы покажем вам остальные. Попробуй! Если вы все еще не знаете, как найти объем формулы куба, продолжайте прокручивать до части описания, где мы все подробно объясним.

Куб и другие

Начнем с самого начала — что такое куб? Это трехмерный твердый объект, ограниченный шестью квадратными гранями, по три грани которых сходятся в каждой вершине. Это обычная квадратная призма в трех ориентациях. Куб — единственный правильный шестигранник, и у него

• 6 граней;
• 12 ребер; и
• 8 вершин.

Вас интересует калькулятор с прямоугольной призмой? У нас есть только инструмент для вас.

Площадь поверхности куба

Формула площади поверхности куба очень проста — это площадь одной грани, умноженная на 6, так как каждый куб имеет шесть одинаковых квадратных граней. Площадь квадрата равна a² , где a — длина одного ребра, поэтому уравнение площади поверхности куба:

площадь_площади = 6 × a²

Формула объема куба объем, возведите длину ребра в третью степень:

объем = a³

Вы можете думать о формуле объема куба как о вычислении объема любой другой призмы — просто умножьте площадь основания раза высота твердого тела. Наше основание представляет собой квадрат, поэтому его площадь равна х , а наша высота также равна х , так как все ребра одинаковы. Вот мы и получили ту же формулу — а³ — как и ожидалось.

Диагонали куба — грань и пространство

Если вам интересно, как найти диагонали куба, подумайте немного о диагонали квадрата. Формула квадратной диагонали — это длина стороны, умноженная на квадратный корень из 2, и она исходит из теоремы Пифагора:

диагональ грани = √(a² + a²) = √2a² = a√2 — это наш куб × диагональ грани*

Для диагонали куба все, что вам нужно сделать, это еще раз применить теорему Пифагора:

диагональ куба = √((a√2)² + a²) = √3a² = a√3

Таким образом, диагональ куба равна длине стороны, умноженной на квадратный корень из 3.

Хотите узнать больше о теореме Пифагора? Посетите наш калькулятор теоремы Пифагора.

Как найти объем куба?

Рассчитаем объем кубика Рубика:

1. Введите известное значение . В нашем случае мы знаем, что размер стандартного кубика Рубика составляет 5,7 сантиметра (2 1⁄4 дюйма) с каждой стороны.
2. Ого, как быстро! Появляются все остальные параметры . Благодаря кубическому калькулятору мы только что узнали, что:

• Объем 11,4 куб.

  No related posts.