|
Random converter |
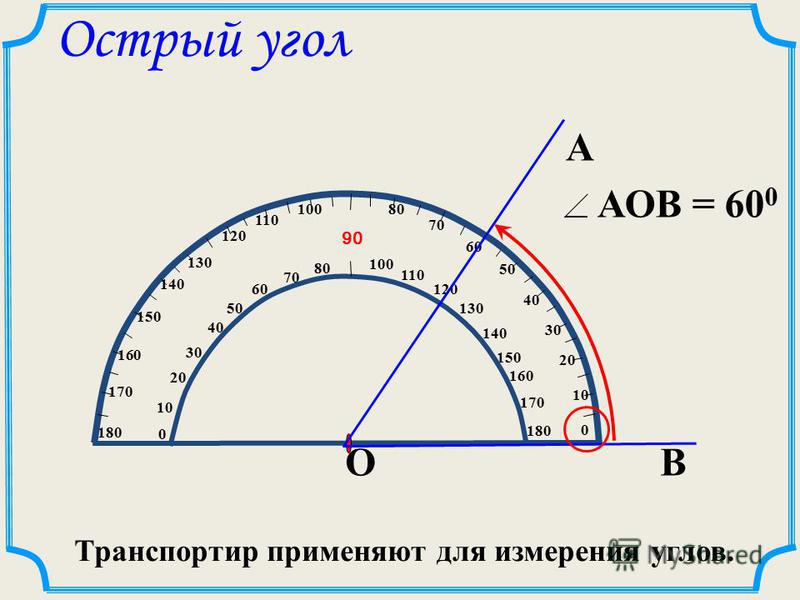
Перевести единицы: градус [°] в окружность [окружность]Конвертер длины и расстоянияКонвертер массыКонвертер мер объема сыпучих продуктов и продуктов питанияКонвертер площадиКонвертер объема и единиц измерения в кулинарных рецептахКонвертер температурыКонвертер давления, механического напряжения, модуля ЮнгаКонвертер энергии и работыКонвертер мощностиКонвертер силыКонвертер времениКонвертер линейной скоростиПлоский уголКонвертер тепловой эффективности и топливной экономичностиКонвертер чисел в различных системах счисления.Конвертер единиц измерения количества информацииКурсы валютРазмеры женской одежды и обувиРазмеры мужской одежды и обувиКонвертер угловой скорости и частоты вращенияКонвертер ускоренияКонвертер углового ускоренияКонвертер плотностиКонвертер удельного объемаКонвертер момента инерцииКонвертер момента силыИмпульс (количество движения)Импульс силыКонвертер вращающего моментаКонвертер удельной теплоты сгорания (по массе)Конвертер плотности энергии и удельной теплоты сгорания топлива (по объему)Конвертер разности температурКонвертер коэффициента теплового расширенияКонвертер термического сопротивленияКонвертер удельной теплопроводностиКонвертер удельной теплоёмкостиКонвертер энергетической экспозиции и мощности теплового излученияКонвертер плотности теплового потокаКонвертер коэффициента теплоотдачиКонвертер объёмного расходаКонвертер массового расходаКонвертер молярного расходаКонвертер плотности потока массыКонвертер молярной концентрацииКонвертер массовой концентрации в раствореКонвертер динамической (абсолютной) вязкостиКонвертер кинематической вязкостиКонвертер поверхностного натяженияКонвертер паропроницаемостиКонвертер плотности потока водяного параКонвертер уровня звукаКонвертер чувствительности микрофоновКонвертер уровня звукового давления (SPL)Конвертер уровня звукового давления с возможностью выбора опорного давленияКонвертер яркостиКонвертер силы светаКонвертер освещённостиКонвертер разрешения в компьютерной графикеКонвертер частоты и длины волныОптическая сила в диоптриях и фокусное расстояниеОптическая сила в диоптриях и увеличение линзы (×)Конвертер электрического зарядаКонвертер линейной плотности зарядаКонвертер поверхностной плотности зарядаКонвертер объемной плотности зарядаКонвертер электрического токаКонвертер линейной плотности токаКонвертер поверхностной плотности токаКонвертер напряжённости электрического поляКонвертер электростатического потенциала и напряженияКонвертер электрического сопротивленияКонвертер удельного электрического сопротивленияКонвертер электрической проводимостиКонвертер удельной электрической проводимостиЭлектрическая емкостьКонвертер индуктивностиКонвертер реактивной мощностиКонвертер Американского калибра проводовУровни в dBm (дБм или дБмВт), dBV (дБВ), ваттах и др. 1 градус [°] = 0,00277777777777778 окружность [окружность] Исходная величина градусрадианградгонминутасекундазодиакальный сектортысячнаяоборотокружностьоборотквадрантпрямой уголсекстант Преобразованная величина градусрадианградгонминутасекундазодиакальный сектортысячнаяоборотокружностьоборотквадрантпрямой уголсекстант Объемная плотность зарядаЗнаете ли вы, что один и тот же электровакуумный прибор можно найти на кухне и в радаре? Всего один щелчок — и вы узнаете какой это прибор! Общие сведения Виды углов Измерение углов Транспортир Использование углов в архитектуре и искусстве Общие сведенияПлоский угол — геометрическая фигура образованная двумя пересекающимися линиями. Виды угловПрямые углы равны 90°, острые — меньше 90°, а тупые — наоборот, больше 90°. Углы, равные 180° называются развернутыми, углы в 360° называются полными, а углы больше развернутых но меньше полных называются невыпуклыми. Когда сумма двух углов равна 90°, то есть один угол дополняет другой до 90°, они называются дополнительными. Если они дополняют друг друга до 180°, они называются смежными, а если же до 360° — то сопряженными. В многоугольниках углы внутри многоугольника называются внутренними, а сопряженные с ними — внешними. Когда сумма двух углов равна 90°, то есть один угол дополняет другой до 90°, они называются дополнительными. Если они дополняют друг друга до 180°, они называются смежными, а если же до 360° — то сопряженными. Два угла, образованные при пересечении двух прямых и не являющихся смежными, называются вертикальными. Они равны. Измерение угловДва транспортира: обычный и цифровой Углы измеряют с помощью транспортира или вычисляют по формуле, измерив стороны угла от вершины и до дуги, и длину дуги, которая эти стороны ограничивает. Углы обычно измеряют в радианах и градусах, хотя существуют и другие единицы. Можно измерять как углы, образованные между двумя прямыми, так и между кривыми линиями. Для измерения между кривыми используют касательные в точке пересечения кривых, то есть в вершине угла. Транспортир Транспортир — инструмент для измерения углов. Большинство транспортиров имеют форму полукруга или окружности и позволяют измерить углы до 180° и до 360° соответственно. В некоторых транспортирах встроена дополнительная вращающаяся линейка для удобства в измерении. Использование углов в архитектуре и искусствеДом с лофтами и квартирами «Pure Spirits» в центре Торонто, Онтарио, Канада Художники, дизайнеры, мастера и архитекторы издавна используют углы для создания иллюзий, акцентов и других эффектов. Чередование острых и тупых углов или геометрические узоры из острых углов часто используются в архитектуре, мозаике и витражах, например в строении готических соборов и в исламской мозаике. Музей Турецкого и исламского искусства. Стамбул, Турция. Фотография помещается с разрешения автора. Одна из известных форм исламского изобразительного искусства — украшение с помощью геометрического орнамента гирих. Этот рисунок применяют в мозаике, резьбе по металлу и дереву, на бумаге и на ткани. Руб аль-хизб и звезда аль-кудс В исламском изобразительном искусстве и архитектуре часто используется руб аль-хизб — символ в форме одного квадрата, наложенного на другой под углом в 45°, как на иллюстрациях. «Флэтайрон-билдинг» или здание «Утюг», Нью-Йорк Острые углы часто используют в архитектуре как декоративные элементы. Они придают зданию строгую элегантность. Тупые углы, наоборот, придают зданиям уютный вид. Так, например, мы восхищаемся готическими соборами и замками, но они выглядят немного печально и даже устрашающе. А вот дом себе мы скорее всего выберем с крышей с тупыми углами между скатами. Углы в архитектуре также используют для укрепления разных частей здания. Обычно здания строят вертикально, но иногда бывают исключения. Некоторые здания специально строят с наклоном, а некоторые наклоняются из-за ошибок. Один из примеров наклонных зданий — Тадж-Махал в Индии. Четыре минарета, которые окружают главное строение, построены с наклоном от центра, чтобы в случае землетрясения они упали не вовнутрь, на мавзолей, а в другую сторону, и не повредили основное здание. Иногда здания строят под углом к земле в декоративных целях. Например, Падающая башня Абу-Даби или Capital Gate наклонена на 18° к западу. А одно из зданий в Мире Головоломок Стюарта Лэндсборо в городе Ванка в Новой Зеландии наклоняется к земле на 53°. Это здание так и называется, «Падающая башня». Иногда наклон здания — результат ошибки в проектировании, как например наклон Пизанской башни. Строители не учли структуру и качество почвы, на которой ее возводили. Башня должна была стоять прямо, но плохой фундамент не смог поддерживать ее вес и здание осело, покосившись на один бок. Башню много раз реставрировали; самая последняя реставрация в 20-м веке остановила ее постепенное оседание и увеличивающийся наклон. Ее удалось выровнять с 5.5°до 4°. Башня церкви СуурХусен в Германии тоже наклонена из-за того, что ее деревянный фундамент прогнил с одной стороны после осушения болотистой почвы, на которой она построена. На данный момент эта башня наклонена больше, чем Пизанская — примерно на 5°. Литература Автор статьи: Kateryna Yuri Перевести единицы: градус в квадрант Перевести единицы: градус в секстант Перевести единицы: градус в тысячная Перевести единицы: секунда в градус Перевести единицы: градус в оборот Перевести единицы: град в окружность Перевести единицы: гон в оборот Перевести единицы: градус в минута Перевести единицы: радиан в окружность Перевести единицы: град в градус Вас могут заинтересовать и другие конвертеры из группы «Популярные конвертеры единиц»:Конвертер длины и расстояния Конвертер массы Конвертер мер объема сыпучих продуктов и продуктов питания Конвертер площади Конвертер объема и единиц измерения в кулинарных рецептах Конвертер температуры Конвертер давления, механического напряжения, модуля Юнга Конвертер энергии и работы Конвертер мощности Конвертер силы Конвертер времени Конвертер линейной скорости Конвертер тепловой эффективности и топливной экономичности Конвертер чисел в различных системах счисления. Конвертер единиц измерения количества информации Конвертер десятичных приставок Передача данных Курсы валют Размеры мужской одежды и обуви Размеры женской одежды и обуви Компактный калькулятор Полный калькулятор Определения единиц Вы затрудняетесь в переводе единицы измерения с одного языка на другой? Коллеги готовы вам помочь. |
Функция Excel TAN: как найти касательный угол
Если вы работаете с любым треугольником, у которого где-то есть прямой угол, очень легко найти касательный угол, если вы знаете длину двух сторон треугольника.
В Microsoft Excel это еще проще , потому что есть встроенные функции, которые вы можете использовать.
Что такое касательный угол?
Угол касания — это угол в треугольнике, где вы знаете длину стороны, противоположной углу, и длину стороны, прилегающей к нему.
Представьте, например, что ваш босс говорит вам отрегулировать лестницу точно на 70 градусов от земли. Если у вас нет специальных инструментов, вам будет очень трудно измерить, составляет ли угол между лестницей и землей ровно 70 градусов.
Однако, если у вас есть измерительная лента, вы можете измерить расстояние от нижней части лестницы до стены. Поскольку лестница у стены образует треугольник, это будет сторона, которая «прилегает» к углу касательной, который вы пытаетесь вычислить.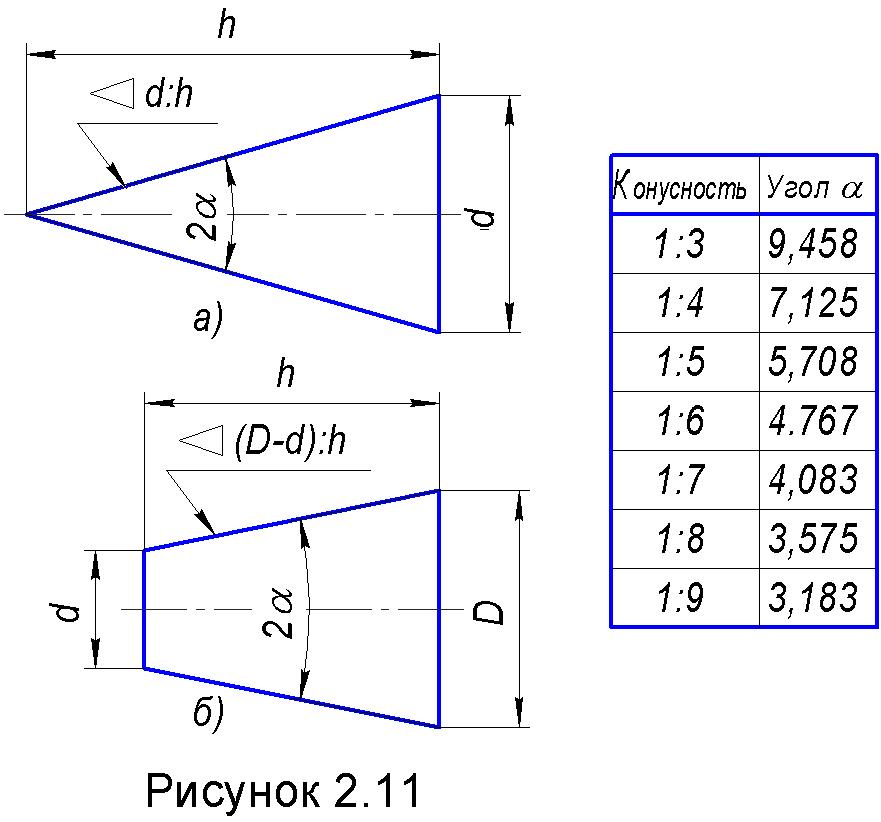
Затем вы должны измерить расстояние от нижней части стены до точки, где верхняя часть лестницы касается ее. Это расстояние стороны, «противоположной» от угла касания.
Имея только противоположные и смежные стороны, вы можете рассчитать угол у основания лестницы, используя функцию арктангенса.
Если стена (противоположная) сторона составляет 10 футов, а наземная (смежная) сторона — 5 футов, формула для угла касания — это противоположная сторона, разделенная на соседнюю сторону. Это 10 делится на 5 или 0,5.
Чтобы найти значение для самого угла, нужно взять арктангенс 0,5.
Нахождение касательного угла с помощью Excel
Вы можете попытаться найти калькулятор, который может вычислить арктангенс значения, но в Excel есть встроенная функция ATAN, которую вы можете использовать.
Формула возвращает угол в радианах, который ваш начальник, вероятно, не поймет.
Вы хотите конвертировать радианы в градусы, умножив их на 180 / пи.
К счастью, в Excel также есть функция PI, которую вы можете использовать для этой цели.
Ответ в этом случае составляет 63,43 градуса. Это означает, что вам нужно отрегулировать одну из длин, пока угол не составит ровно 70 градусов.
В Excel это легко, потому что вы можете просто изменить значение противоположной стороны, пока результат арктангенса не станет равен 70.
Вы выяснили, как разместить лестницу, и ваш босс счастлив!
Использование ASIN и ACOS в Excel
В этом же сценарии предположим, что у вас недостаточно рулетки, чтобы измерить стену. Вы знаете только, что лестница составляет 15 футов, и вы измерили, что она находится в 5 футах от стены.
Как вы рассчитываете угол?
К счастью, в Excel есть две другие функции, которые вы можете использовать в этой ситуации.
Длина лестницы — это «гипотенуза» треугольника, а расстояние от земли — это смежная сторона с углом. До тех пор, пока треугольник имеет один прямой угол (90 градусов), имеющаяся у вас информация определяет формулу, которую вам нужно использовать.
- Косинус : Вы вычисляете угол косинуса, если знаете длину гипотенузы и соседней стороны.

- Синус : Рассчитайте угол синуса, если вы знаете длину гипотенузы и противоположную сторону.
В этом случае угол аркозина соседней стороны делится на гипотенузу.
Поскольку вы знаете, что соседняя сторона (расстояние до земли) составляет 5 футов, а длина лестницы (гипотенуза) составляет 15 футов, косинус угла 5 делится на 15 или 0,333.
Чтобы рассчитать угол, вам нужно использовать формулу арккозина в Excel.
Результат функции arccosine — Excel в радианах, поэтому вам нужно умножить его на 180 / PI, чтобы преобразовать в градусы.
В этом случае у 15-футовой лестницы с основанием в 5 футах от стены угол составляет 70,53 градуса.
Если вы знали, что высота стены (противоположная сторона) составляет 10 футов, а не расстояние от стены (соседняя сторона) от земли, вам нужно будет использовать формулу арксинуса в Excel.
В этом случае синус угла противоположной стороны делится на гипотенузу.
После преобразования в градусы угол в этом случае будет 48,12 градуса.
Зачем использовать ATAN, ACOS или ASIN?
Вы можете быть удивлены тем, как часто возникают ситуации, когда вам может понадобиться использовать одну из этих функций в Excel.
Вот лишь несколько примеров:
- В столярном деле и строительстве углы и длины используются во всех аспектах строительства домов и зданий.
- Фотографы используют углы, чтобы тщательно выровнять освещение и свои творческие снимки.
- В спорте понимание углов может улучшить навыки и улучшить стратегию.
- Корабли и самолеты расположены на радаре с использованием углов и расстояний.
- Если вы хотите быть уверенным, что мебель будет вписываться в вашу комнату, вам нужно знать, как рассчитать длину и углы!
Вы можете выполнить эти вычисления на научном калькуляторе. Но если у вас нет под рукой, Excel может помочь вам сделать эти вычисления лучше, чем что-либо еще.
Как вычислить углы в градусах
••• joxxxxjo/iStock/GettyImages
Обновлено 13 марта 2018 г.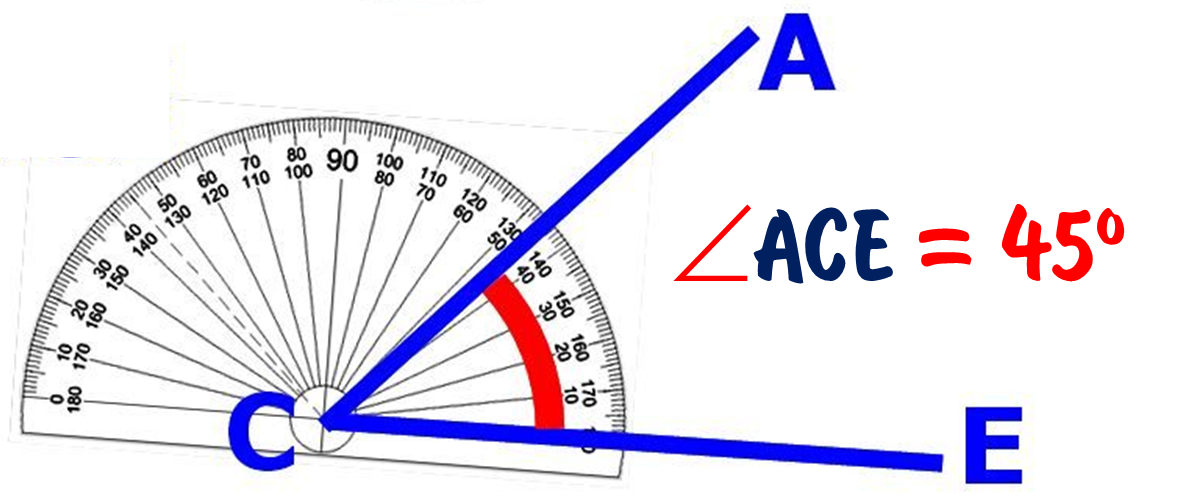
Автор Susan Revermann области, такие как астрономия, архитектура и инженерия. Умение находить градусы угла — необходимый навык, которым вы должны овладеть, прежде чем углубляться в более сложные понятия, такие как радианы, длина дуги и площадь сектора. В зависимости от уровня математики, на котором вы находитесь, и конкретного угла, с которым вы имеете дело, вы можете вычислить градусы угла несколькими различными методами.
Использование транспортира
Транспортир используется для измерения углов так же, как линейка для измерения длины. Это пластиковый или металлический полукруг с градациями через равные промежутки времени от 0 до 90 градусов вправо и влево от нулевого положения. Его легко использовать: совместите градацию «0» на транспортире с одним из лучей угла и расположите средний круг на транспортире на вершине угла. Обратите внимание, где другой луч угла совпадает с транспортиром — это даст вам градусы угла.
Треугольники предсказуемы
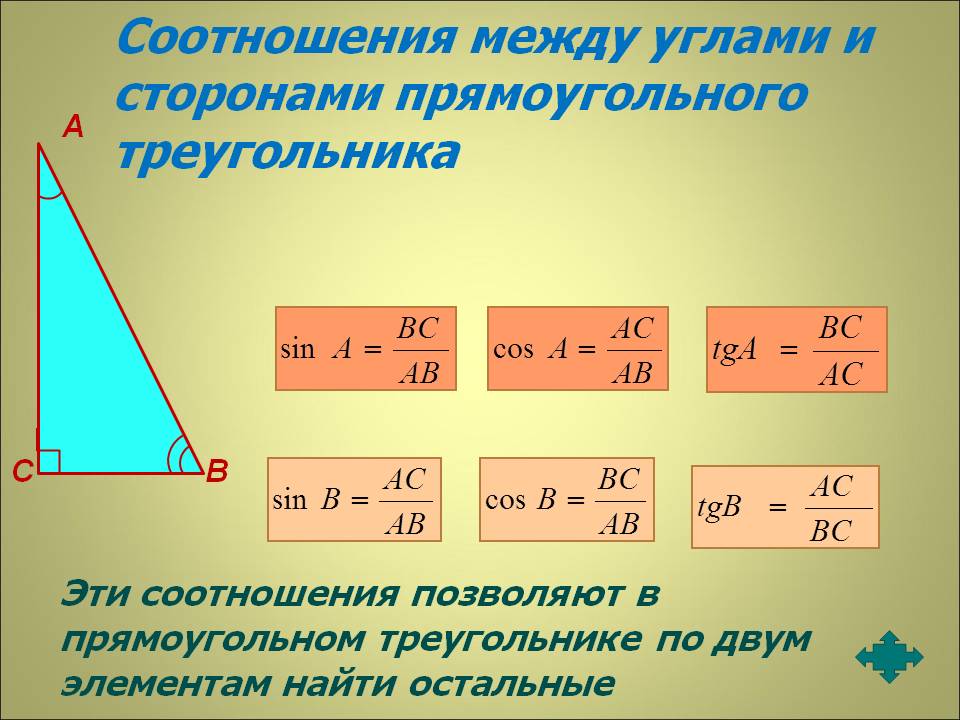
Треугольник всегда имеет три угла, и их сумма всегда равна 180 градусам.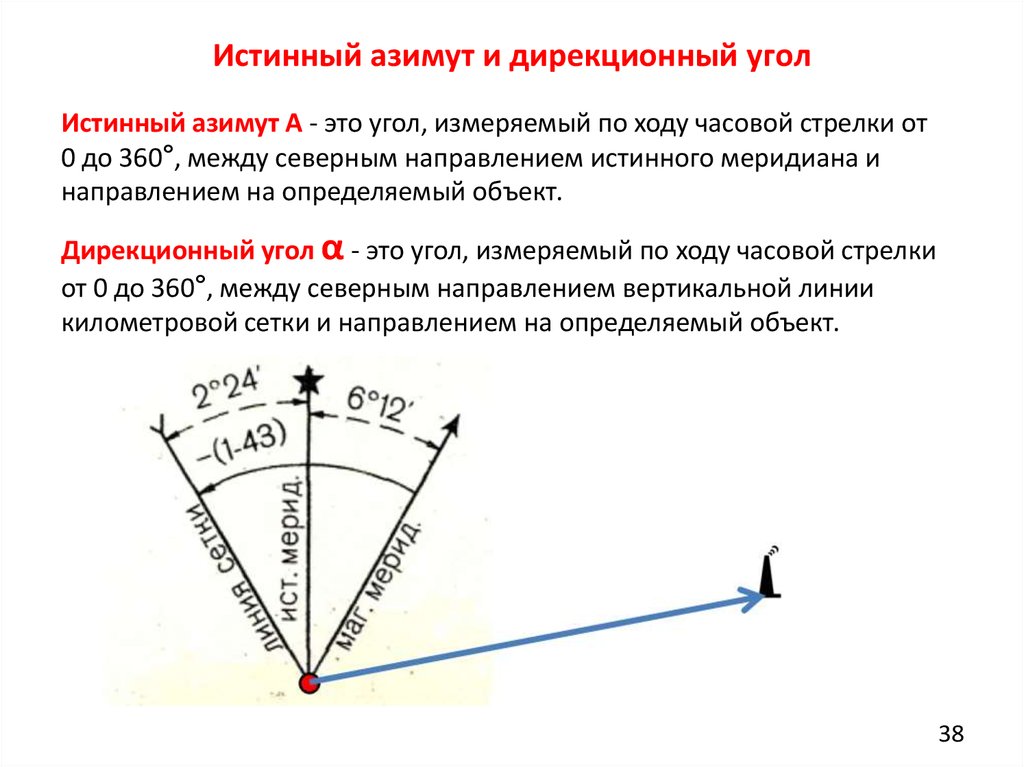 Зная это, всегда можно вычислить значение одного из углов, если известны значения двух других. Просто сложите эти два значения и вычтите из 180. Однако это не поможет, если вы не знаете значений ни одного из углов. В таком случае может помочь тригонометрия прямоугольных треугольников.
Зная это, всегда можно вычислить значение одного из углов, если известны значения двух других. Просто сложите эти два значения и вычтите из 180. Однако это не поможет, если вы не знаете значений ни одного из углов. В таком случае может помочь тригонометрия прямоугольных треугольников.
Тригонометрия в помощь
Прямоугольный треугольник — это треугольник, содержащий 9Угол 0 градусов. Таким образом, два других угла в сумме составляют 90 градусов, поэтому, если вы сможете найти один из них, вы узнаете и другой. В любой неправильный треугольник можно вписать прямоугольный треугольник и определить один из углов по таблицам синусов и косинусов.
Значение любого угла в прямоугольном треугольнике можно определить по длинам образующих его линий, которые можно измерить. Деление длины линии, противоположной углу, на гипотенузу дает дробь, известную как «синус» угла, а деление длины линии, прилегающей к углу, на гипотенузу дает «косинус». Вы можете посмотреть обе эти дроби на диаграммах, чтобы найти угол.
Вы можете посмотреть обе эти дроби на диаграммах, чтобы найти угол.
Пример
У вас есть треугольник с тремя неизвестными углами. Вы проводите линию, перпендикулярную одной из линий в треугольнике, чтобы разделить один из углов пополам, таким образом образуя прямоугольный треугольник. Как только вы измерите длины линий, у вас будет все необходимое для определения значений всех углов.
Легче всего определить угол, который вы не делили пополам. Предположим, что длина нарисованной вами линии, противоположной углу, равна 3 дюймам, а длина гипотенузы прямоугольного треугольника равна 6 дюймам. Таким образом, синус угла равен 3/6 = 0,5, и если вы посмотрите на таблицу, вы обнаружите, что угол равен 30 градусам. Это означает, что другой угол в прямоугольном треугольнике равен 60 градусам, потому что в сумме эти два должны быть равны 9.0. Вы разделили угол исходного треугольника пополам, когда рисовали прямоугольный, поэтому значение этого угла равно 120 градусам.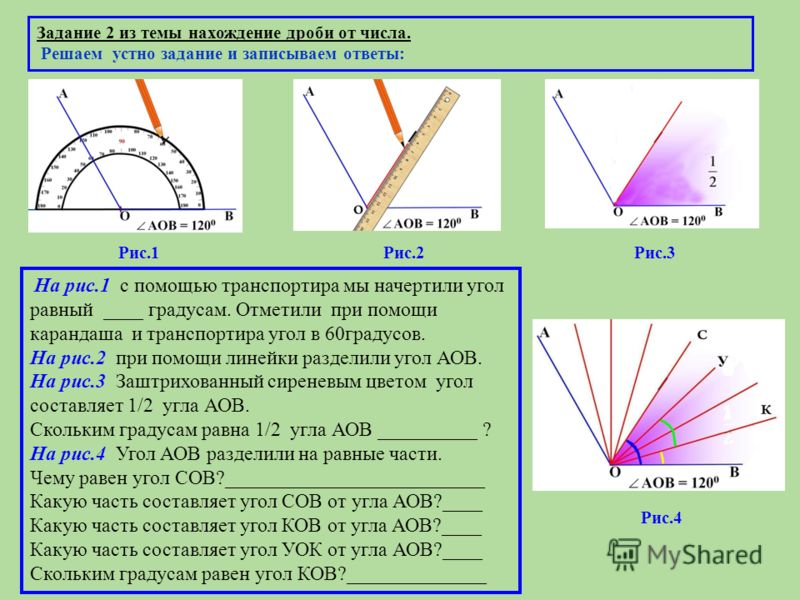 Это означает, что значение третьего угла в исходном треугольнике должно быть 30 градусов, так как сумма значений всех углов должна составлять 180.
Это означает, что значение третьего угла в исходном треугольнике должно быть 30 градусов, так как сумма значений всех углов должна составлять 180.
Углы треугольника — Бесплатная помощь по математике
Можно складывать углы
Точно так же, как и обычные числа, углы можно складывать для получения суммы, возможно, с целью определения меры неизвестного угла. Иногда мы можем определить недостающий угол, потому что знаем, что сумма должна быть определенной величиной. Помните: сумма градусных мер углов любого треугольника равна 180 градусам. Ниже приведено изображение треугольника ABC, где угол A = 60 градусов, угол B = 50 градусов и угол С = 70 градусов.
Если сложить все три угла любого треугольника, получится 180 градусов. Итак, градусная мера угла А + угол В + угол С = 180 градусов. Это верно для любого треугольника в мире геометрии.
Нахождение недостающего угла
В треугольнике ABC ниже угол A = 40 градусов, а угол B = 60 градусов. Чему равен угол С?
Мы знаем, что сумма мер любого треугольника равна 180 градусам. Используя тот факт, что угол A + угол B + угол C = 180 градусов, мы можем найти меру угла C.
угол A = 40
угол B = 60
угол C = мы не знаем.
Чтобы найти угол C, мы просто подставляем в приведенную выше формулу и находим C. Чтобы проверить правильность 80 градусов, добавим все три меры угла. Если мы получим 180 градусов, то наш ответ для угла C правильный.
Вот так:
40 + 60 + 80 = 180
180 = 180… Проверяет!
Вам не всегда нужно подставлять эти значения в уравнение и решать. Как только вы освоитесь с такой задачей, вы сможете сказать: «Хорошо, 40 + 60 = 100, значит, другой угол должен быть равен 80!» и это намного быстрее.
Равносторонние треугольники
Если треугольник равносторонний, какова градусная мера каждого из его углов?
Помните, все стороны равностороннего треугольника имеют равную меру . Они также, как вы узнаете, имеют равные углы! Пусть x = градусная мера каждого угла. У треугольников три угла, поэтому мы прибавим х ТРИ раза.
У нас есть это:
x + x + x = 180
3x = 180
x = 60
Логично, правда? Если все углы равны и в сумме дают 180, то должно быть 60 градусов!
Отношение углов
Градусы углов треугольника относятся как 4 : 5 : 9.
Какова градусная мера НАИМЕНЬШЕГО угла треугольника?
Обратите внимание, что наименьший угол представлен наименьшим числом в заданном соотношении. Наименьшее данное число равно 4, верно? Поскольку это отношение, мы должны умножить все эти значения (4,5,9) на некоторый общий коэффициент, чтобы получить фактические углы. (Например, 60 и 80 находятся в соотношении 3:4 с коэффициентом 20)
Пусть 4x = мера наименьшего угла треугольника.


 Плоский угол состоит из двух лучей с общим началом, и эта точка называется вершиной луча. Лучи называются сторонами угла. У углов много интересных свойств, например, сумма всех углов в параллелограмме — 360°, а в треугольнике — 180°.
Плоский угол состоит из двух лучей с общим началом, и эта точка называется вершиной луча. Лучи называются сторонами угла. У углов много интересных свойств, например, сумма всех углов в параллелограмме — 360°, а в треугольнике — 180°.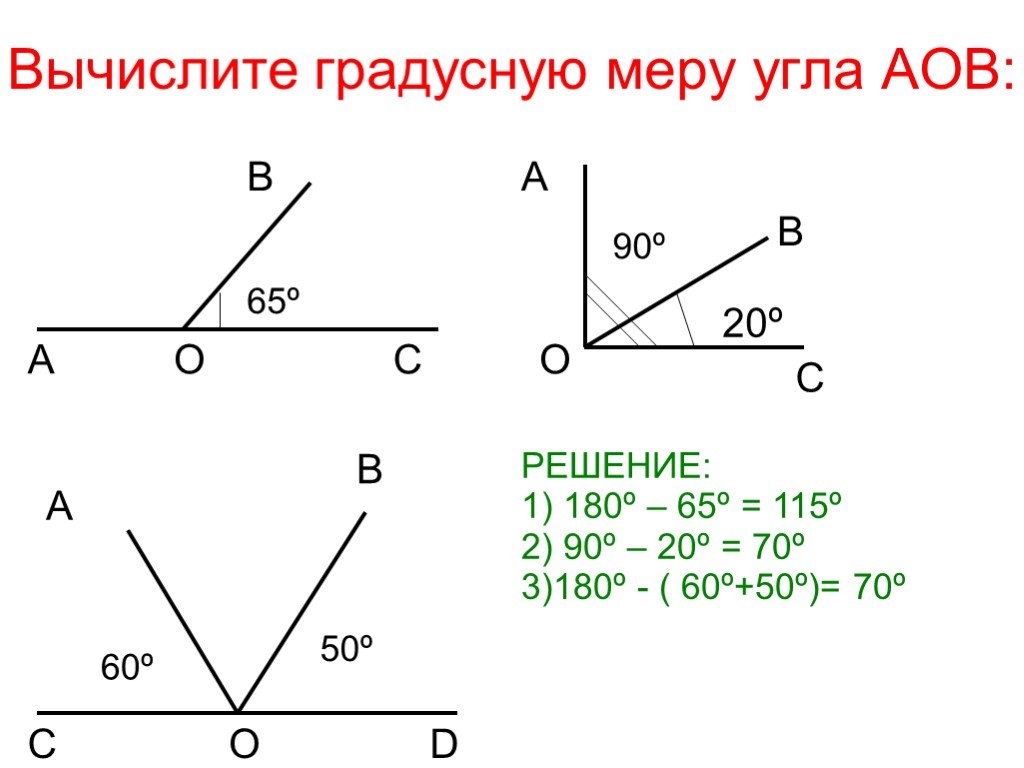 В многоугольниках углы внутри многоугольника называются внутренними, а сопряженные с ними — внешними.
В многоугольниках углы внутри многоугольника называются внутренними, а сопряженные с ними — внешними.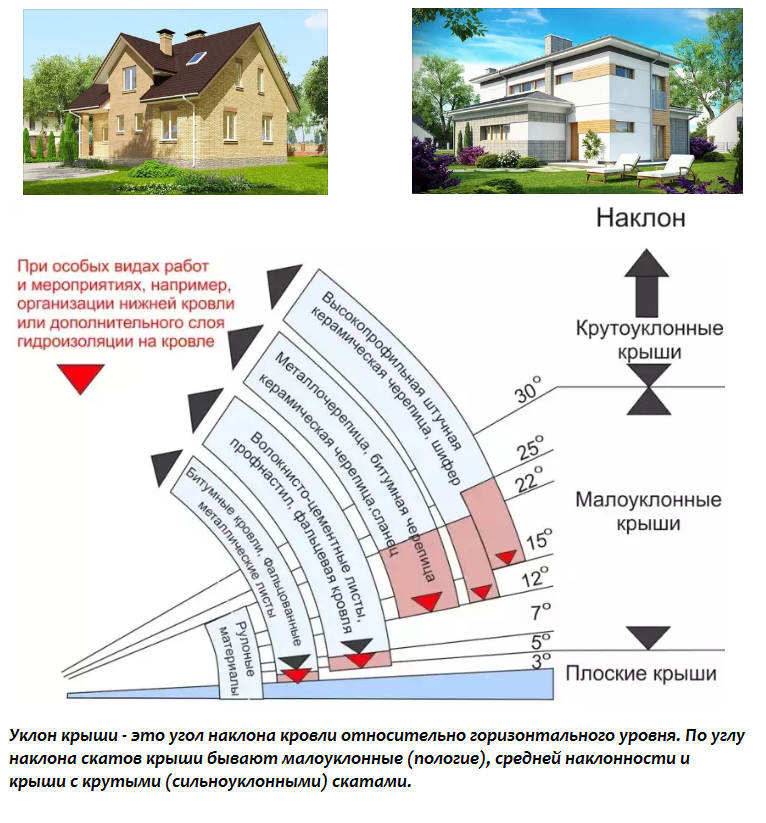 Шкалы на транспортирах наносят чаще в градусах, хотя иногда они бывают и в радианах. Транспортиры чаще всего используют в школе на уроках геометрии, но их также применяют в архитектуре и в технике, в частности в инструментальном производстве.
Шкалы на транспортирах наносят чаще в градусах, хотя иногда они бывают и в радианах. Транспортиры чаще всего используют в школе на уроках геометрии, но их также применяют в архитектуре и в технике, в частности в инструментальном производстве.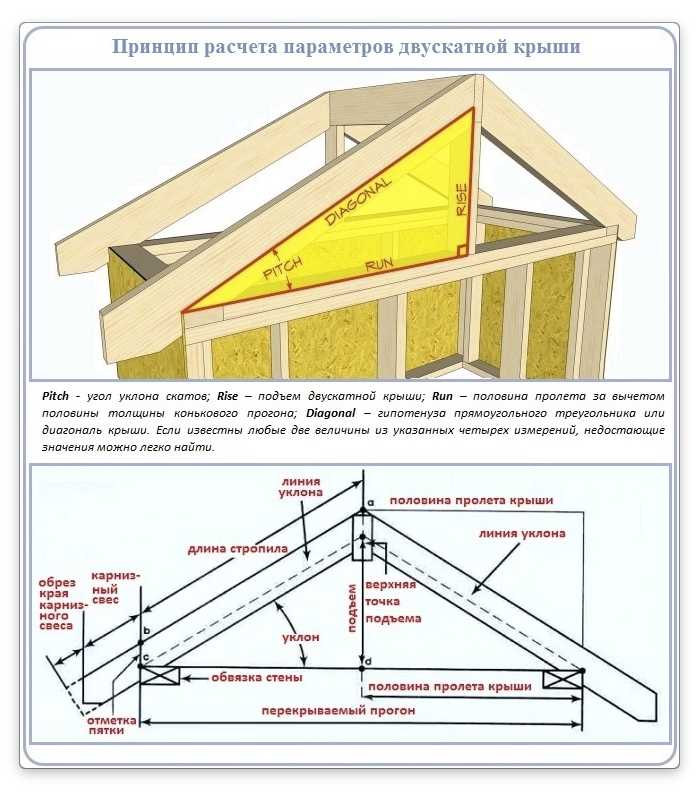 Рисунок создается с помощью чередования геометрических фигур. Традиционно используют пять фигур со строго определенными углами из комбинаций в 72°, 108°, 144° и 216°. Все эти углы делятся на 36°. Каждая фигура разделена линиями на несколько более маленьких симметричных фигур, чтобы создать более тонкий рисунок. Изначально гирихом назывались сами эти фигуры или кусочки для мозаики, отсюда и пошло название всего стиля. В Марокко существует похожий геометрический стиль мозаики, зулляйдж или зилидж. Форма терракотовых изразцов, из которых складывают эту мозаику, не соблюдается так строго, как в гирихе, и изразцы часто более причудливой формы, чем строгие геометрические фигуры в гирихе. Несмотря на это, мастера зулляйджа также используют углы для создания контрастных и причудливых узоров.
Рисунок создается с помощью чередования геометрических фигур. Традиционно используют пять фигур со строго определенными углами из комбинаций в 72°, 108°, 144° и 216°. Все эти углы делятся на 36°. Каждая фигура разделена линиями на несколько более маленьких симметричных фигур, чтобы создать более тонкий рисунок. Изначально гирихом назывались сами эти фигуры или кусочки для мозаики, отсюда и пошло название всего стиля. В Марокко существует похожий геометрический стиль мозаики, зулляйдж или зилидж. Форма терракотовых изразцов, из которых складывают эту мозаику, не соблюдается так строго, как в гирихе, и изразцы часто более причудливой формы, чем строгие геометрические фигуры в гирихе. Несмотря на это, мастера зулляйджа также используют углы для создания контрастных и причудливых узоров. Он может быть изображен как сплошная фигура, или в виде линий — в этом случае этот символ называется звездой Al-Quds (аль кудс). Руб аль-хизб иногда украшают небольшими кругами на пересечении квадратов. Этот символ используют в гербах и на флагах мусульманских стран, например на гербе Узбекистана и на флаге Азербайджана. Основания самых высоких в мире на момент написания (весна 2013) башен близнецов, башен Петро́нас построены в форме руб аль-хизба. Эти башни находятся в Куала-Лумпуре в Малайзии и в их проектировании участвовал премьер-министр страны.
Он может быть изображен как сплошная фигура, или в виде линий — в этом случае этот символ называется звездой Al-Quds (аль кудс). Руб аль-хизб иногда украшают небольшими кругами на пересечении квадратов. Этот символ используют в гербах и на флагах мусульманских стран, например на гербе Узбекистана и на флаге Азербайджана. Основания самых высоких в мире на момент написания (весна 2013) башен близнецов, башен Петро́нас построены в форме руб аль-хизба. Эти башни находятся в Куала-Лумпуре в Малайзии и в их проектировании участвовал премьер-министр страны. Архитекторы проектируют форму, размер и угол наклона в зависимости от нагрузки на стены, нуждающиеся в укреплении. Этот принцип укрепления с помощью наклона использовали еще с древних времен. Например, античные строители научились строить арки без цемента и иных связующих материалов, укладывая камни под определенным углом.
Архитекторы проектируют форму, размер и угол наклона в зависимости от нагрузки на стены, нуждающиеся в укреплении. Этот принцип укрепления с помощью наклона использовали еще с древних времен. Например, античные строители научились строить арки без цемента и иных связующих материалов, укладывая камни под определенным углом.
 Угол является мерой поворота такого луча.
Угол является мерой поворота такого луча.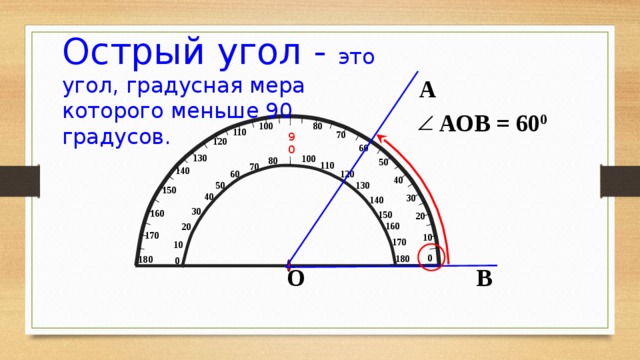 », то есть «…умножить на десять в степени…». Компьютерная экспоненциальная запись широко используется в научных, математических и инженерных расчетах.
», то есть «…умножить на десять в степени…». Компьютерная экспоненциальная запись широко используется в научных, математических и инженерных расчетах. com на YouTube
com на YouTube